1 Introduction

In this paper, we describe a new variant of the Feasibility Pump algorithm to find feasible solutions for mixed integer nonlinear programming (MINLP) problems. We consider an implementation of the Feasibility Pump within a global solver, in our case Couenne.

An MINLP is an optimization problem of the form

$$\begin{aligned} \begin{array}{llll} \min \quad &{} c^\mathsf {T} x \\ \mathrm {s.t.}\quad &{} g_j(x) \le 0 \quad &{}&{} \text {for } j=1,\ldots ,m, \\ &{} L_i \le x_i \le U_i &{}&{} \text {for } i=1,\ldots ,n, \\ &{} x_i \in \mathbb {Z} &{}&{} \text {for } i\in \mathcal {I}, \end{array} \end{aligned}$$
(1)

where \(\mathcal {I}\subseteq \{1,\ldots ,n\}\) is the index set of the integer variables, \(d\in \mathbb {R}^n\), \(g_j:\mathbb {R}^n \rightarrow \mathbb {R}\) for \(j=1,\ldots ,m\), and \(L\in (\mathbb {R}\cup \{-\infty \})^n\), \(U\in (\mathbb {R}\cup \{+\infty \})^n\) are lower and upper bounds on the variables, respectively. Since fixed variables can always be eliminated, we assume w.l.o.g. that \(L_i<U_i\) for \(i=1,\ldots ,n\), i.e., that the interior of [L, U] is nonempty. Note that a nonlinear objective function can always be reformulated by introducing one additional constraint and variable. We chose the convention of assuming a linear objective for the ease of presentation; the presented algorithm and the conducted experiments address general MINLPs.

There are many subclasses of MINLP; the following four will play a role in this article:

  • If all constraint functions \(g_j\) are convex, problem (1) is called a convex MINLP.

  • If all constraint functions \(g_j\) are affine, problem (1) is called a mixed integer linear program (MIP).

  • If \(\mathcal {I} = \varnothing \), problem (1) is called a nonlinear program (NLP).

  • If \(\mathcal {I} = \varnothing \) and all \(g_j\) are affine, problem (1) is called a linear program (LP).

Primal heuristics are algorithms that try to find feasible solutions of good quality for a given optimization problem within a reasonably short amount of time. They are incomplete methods, hence there is usually no guarantee that they will find any solution, let alone an optimal one.

For mixed-integer (linear) programming it is well-known that general-purpose primal heuristics are able to find high-quality solutions for a wide range of problems [8, 27]. For mixed-integer nonlinear programming, research in the last five years has shown an increasing interest in general-purpose primal heuristics [9–12, 15, 16, 19, 20, 33, 36, 37].

Discovering good feasible solutions at an early stage of the MINLP solving process has several advantages:

  • The bounding step of the branch-and-bound [32] algorithm depends on the quality of the incumbent solution; a better primal bound leads to more nodes being pruned and hence to smaller search trees.

  • The same holds for presolving and domain propagation strategies such as reduced cost fixing. Better solutions can lead to tighter domain reductions. Besides cut generation, bound tightening is one of the most important features for an efficient implementation of a branch-and-bound algorithm for nonconvex MINLPs, see, e.g., [6, 29].

  • In practice, it is often sufficient to compute a heuristic solution whose objective value is within a certain quality threshold. For hard MINLPs that cannot be solved to optimality within a reasonable amount of time, it might still be possible to generate good primal solutions quickly.

  • Improvement heuristics such as RINS  [12, 14, 21] or Local Branching [12, 26, 37] need a feasible solution as starting point.

Feasibility Pump (FP) algorithms follow the idea of decomposing the set of constraints of a mathematical programming problem into two parts: integer feasibility and constraint feasibility. At least for MIP and convex MINLP, both are “easy” to achieve: the former by rounding, the latter by solving an LP or a convex NLP, respectively. Each can be done in polynomial time. Two sequences of points \(\{\tilde{x}^k\}_{k=1}^K\) and \(\{\bar{x}^k\}_{k=1}^K\), for \(K \in {\mathbb {Z}}\), are generated such that \(\tilde{x}\) contains integral points that may violate constraints \(g_j(x)\le 0\) for one or more \(j=1,2,\ldots {},m\) and \(\bar{x}\) contains points that are feasible for a continuous relaxation to the original problem but might not be integral. These two sequences are related to each other in that the points of \(\{\tilde{x}^{k}\}\) are obtained through rounding of the integral coordinates of points in \(\{\bar{x}^{k}\}\) and these, in turn, are obtained via projections of points in \(\{\tilde{x}^{k}\}\).

One focus of this chapter is the application of a Feasibility Pump inside a global solver such as Baron [41], Couenne [6], LindoGlobal [34], Bonmin [14] or SCIP [2], whereas previous publications considered the Feasibility Pump as a standalone procedure. This has an impact on the design choices carried out in developing the heuristic, in particular balancing efficiency versus completeness. If primal heuristics are applied as supplementary procedures inside a global solver, the overall performance of the solver is the main objective. To this end, it is often worth sacrificing success on a small number of instances for a significant saving in average running time. The enumeration phase of the Feasibility Pump presented in [7] is a typical example of a component that is crucial for its impressive success rate as a standalone algorithm, but it will not be applied when the Feasibility Pump is used inside a global solver, see [8].

This paper features three novel contributions aimed at a more flexible use of a Feasibility Pump within a nonconvex MINLP solver:

  1. (i)

    a hierarchy of rounding procedures, ranked by efficiency (typically converse to the quality of the provided points) for finding integral points; which routine to use is decided and automatically adapted at runtime;

  2. (ii)

    an improved and parameterized distance function for the rounding step, taking into account second-order information of the continuous NLP relaxation; and

  3. (iii)

    the separation of linearization cuts that approximate the convex envelope of the nonconvex feasible set of the NLP relaxation of (1), as opposed to employing Outer Approximation cuts [24] only for the convex part of the problem. We know of no other FP that generates linearization cuts.

2 Feasibility Pumps for MINLP

The Feasibility Pump (FP) algorithm was originally introduced by Fischetti, Glover, and Lodi in 2005 [25] for mixed binary programs, i.e., for the special case of MIPs in which \(l_j=0\) and \(u_j=1\) for all \(j \in \mathcal {I}\). The principal idea is as follows. The LP relaxation of a MIP is solved. The LP optimum \(\bar{x}\) is then rounded to the closest integral point. This part of the FP algorithm is called the rounding step. If \(\tilde{x}\) is not feasible for the linear constraints, the objective function of the LP is changed to an \(\mathcal {\ell }_{1}\) distance function:

$$\begin{aligned} \Delta (x, \tilde{x}) := \sum _{j \in \mathcal {I}}\left| x_j - \tilde{x}_j \right| = \sum _{j \in \mathcal {I} :\tilde{x}_j = 0} x_j + \sum _{j \in \mathcal {I} :\tilde{x}_j = 1} (1-x_j) \end{aligned}$$
(2)

and a new \(\bar{x}\) is obtained by minimizing \(\Delta (x,\tilde{x})\) over the LP relaxation of the MIP. The process is iterated until \(\tilde{x} = \bar{x}\) which implies feasibility (w.r.t. the MIP). The operation of obtaining a new \(\bar{x}\) from \(\tilde{x}\) is known as the projection step, as it consists of projecting \(\tilde{x}\) to the feasible set of a continuous relaxation of the MIP along the direction \(\Delta (x,\tilde{x})\).

The original work by Fischetti et al. [25] led to many follow-up publications [3, 4, 7, 13, 22, 23, 28, 30] on Feasibility Pumps for MIP that improve the performance mostly by extending one of the two basic steps of rounding and projection. Most important for the present paper is the work by Achterberg and Berthold [3] who suggest to replace function (2) by a convex combination of (2) and the original objective \(c^{\mathsf {T}}x\) in order to produce higher-quality solutions.

Versions of the Feasibility Pump for convex MINLP have been presented by Bonami et al. [15] and Bonami and Gonçalves [16]. The only publication for nonconvex MINLP that we are aware of is D’Ambrosio et al. [20]. Bonami and Gonçalves [16] keep the rounding step as in [25] and replace solving an LP in the projection phase by solving a convex NLP, using again the distance function (2) as an objective. Recently, Sharma et al. [38, 39] presented an integration of the Objective Feasibility Pump idea by Achterberg and Berthold and the algorithm of Bonami and Gonçalves: a scaled sum of the distance function and the original objective is used as an objective for the convex NLP. In [15], the authors suggest using an \(\mathcal {\ell }_2\) norm for the projection step. Further, their implementation of the rounding step differs significantly from all previous FP variants. Instead of performing an instant rounding to the nearest integer, they solve an MIP relaxation which is based on an outer approximation [24] of the underlying MINLP. The particular difficulty addressed in [20] is that of handling the nonconvex NLP relaxation if adapting the algorithm of [15] to the nonconvex case. The authors suggest using a stochastic multistart approach, feeding the NLP solver with different randomly generated starting points, and solving the NLP to local optimality as if it was a convex problem. In the following three sections, we present our suggestions to extend the Feasibility Pump for nonconvex MINLP. The first one mainly aims at saving computation time, while the second and the third incorporate the nonlinear problem structure directly into the FP algorithm.

3 A hierarchy of rounding procedures

In the preceding publications on Feasibility Pump heuristics, several ideas have been proposed to generate good integer points during the rounding step. The original work [25] and one of the nonlinear FPs [16] suggest plain rounding in order to get a point which is closest w.r.t. the \(\mathcal {\ell }_2\) norm. The Feasibility Pump 2.0 [28] uses an iterated “round-and-propagate” procedure in order to get a point which is close w.r.t. the \(\mathcal {\ell }_2\) norm but “more feasible” for the relaxation. The nonlinear Feasibility Pumps suggested by [15, 20] solve an MIP to get the closest integer point w.r.t. the \(\mathcal {\ell }_1\) norm that fulfills all constraints of the linear relaxation.

The observed shift from “stay close to the previous point” to “stay close, but also fulfill the relaxation” leads us to the idea of trying several rounding procedures which address these goals in various ways. Similar to other FPs for MINLP, the rounding step is performed by solving a MIP that is a relaxation of the original MINLP. In convex MINLP, such a MIP can be obtained by applying Outer Approximation [24] and maintaining integrality constraints, while in the nonconvex case the MIP is obtained as a LP relaxation of the MINLP with the integrality constraints.

In order to obtain a point \(\tilde{x}\) that satisfies the integrality constraints, we select a procedure from the following list:

  1. (i)

    Solve the MIP relaxation with a node limit and an emphasis on good solutions.

  2. (ii)

    Solve the MIP relaxation with a node limit (smaller than in (i)), disabling time-consuming cutting plane separation, branching and presolving strategies.

  3. (iii)

    Solve the root node of the MIP relaxation of method (i), then apply the RENS heuristic, see [10].

  4. (iv)

    Solve the root node of the MIP relaxation, then apply the Objective Feasibility Pump 2.0 [28] for MIPs.

  5. (v)

    Apply the round-and-propagate algorithm of [28]: selectively round a fractional variable to the nearest integer and then apply a domain propagation to restrict the feasible set, until either a feasible solution is found or the remaining MIP is proven infeasible. In the latter case, round all remaining unfixed variables to the nearest integer.

  6. (vi)

    Choose an integral point from a solution pool (e.g. from suboptimal solutions of applying procedure (i)), see below.

  7. (vii)

    Apply a random perturbation to \(\bar{x}^{k-1}\) and round to the nearest integer \(\tilde{x}^k\).

Note that the integral points generated by procedures (v–vii) might be infeasible for the MIP problem of the current iteration. While procedures (i–iv) might terminate without an integral point, procedure (v) will always produce an integral point. The last two procedures are implemented solely to avoid cycling, i.e. for the case that a point constructed by procedure (v) is identical to one visited in a previous iteration. Further, procedures (v–vii) are ordered by their expected running time and the expected likelihood to produce a good integral point. The higher in the list a procedure is, the more expensive it is and the more likely it is to produce high-quality (w.r.t. the distance function) solutions.

Having this variety of options to produce integral points, the question remains which to apply when. At the first iteration of the FP, we employ procedure (ii). If the current procedure successfully provides us with a “new” (not yet visited) integer point for three iterations in a row, we proceed with the next (cheaper and less aggressive) method of the above list. If, at any iteration, the current procedure does not terminate within the given limits or produces a point that was already visited, we proceed with the previous (more expensive and more powerful) method of the above list. Note that the list of procedures from (ii) to (vii) has decreasing complexity and, in general, declines in solution quality. At subsequent iterations of the FP we use the procedure that was successful previously, but switch down to a cheaper routine when there were three successful iterations in a row.

In principle, the list could be prepended at the head to include methods that capture constraint feasibility even better (and are most likely more time consuming), for instance a convex (nonlinear) relaxation of the nonconvex MINLP. However, computational results presented in [20] indicate that this results in a significant computational overhead with little impact.

If procedures (i), (ii), or (iii) are used for the rounding step, these may produce more than one MIP-feasible solution. The suboptimal points might be used for later iterations, and are therefore stored in a solution pool. This approach is motivated by two observations: first, in (i) we solve similar MIPs over and over again, mainly using a different objective (plus some new cuts). Each known feasible point from a previous call may be used as a starting solution in subsequent calls. Procedures (iii) and (iv) will also benefit from a given upper bound as they consider a restricted search space. Second, considering a point which was initially a candidate, but was then discarded carries more information about the problem than one generated through random perturbation. Thus, the previously collected points are used in (vi). We rank the points in the pool by the value of the distance function at the current iteration.

4 Follow the Hessian: an improved distance function

Feasibility Pumps for MIP use the \(\mathcal {\ell }_1\) norm for the projection and the rounding step; the nonlinear FPs by Bonami et al. [15] and D’Ambrosio et al. [20] use \(\mathcal {\ell }_2\) for the projection and \(\mathcal {\ell }_1\) for rounding. De Santis et al. [22] present variants of the distance function that help draw a connection with the Frank-Wolfe algorithm and that show some computational advantage w.r.t. the more traditional distance functions. Either way, exclusively using these norms as objective functions for auxiliary optimization problems ignores the fact that a “close” solution is not necessarily a good one: the original objective function is completely neglected and no information is used on how much the constraints are violated.

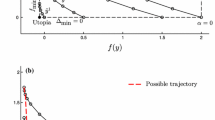
To overcome this issue, we use the norm of a vector obtained from a linear transformation applied to \(x-\bar{x}^k\). As a motivating example, consider first an unconstrained integer nonlinear optimization problem \(\min \{f(x) :x\in \mathbb {Z}^n\}\), where \(f\in \mathcal {C}^2(\mathbb {R}^{n},\mathbb {R})\). Note that this example diverges from our assumed MINLP formulation in that it uses a nonlinear objective function. We find this digression necessary to explain the idea expressed in this section, which ultimately refers to the MINLP standard we specified in (1). Assume that \(\bar{x}\) is a local optimum of the continuous relaxation \(\min \{f(x) :x\in \mathbb {R}^n\}\). Level curves of the \(\mathcal {\ell }_1\) and the \(\mathcal {\ell }_2\) distance functions w.r.t. \(\bar{x}\) are given in Fig. 1. In either norm, \(\tilde{x}\) is the closest integer point (the result is norm-invariant on \(\mathbb Z^n\)).

Fig. 1
figure 1

Level curves (gray) of different norm functions \(\Delta \)(\(x\),\(\bar{x}\)). The closest integer point to \(\bar{x}\) is \(\tilde{x}\). In a and b, the norm \(||\cdot ||_p\) is used for \(p=1\) and \(p=2\) respectively

Full size image

Now consider the second-degree Taylor series approximation of \(f\) at \(\bar{x}\):

$$\begin{aligned} f(x) \approx f(\bar{x}) + \nabla f\Big |_{\bar{x}}^\mathsf {T} (x-\bar{x}) + \frac{1}{2}(x-\bar{x})^\mathsf {T} H(x-\bar{x}) \end{aligned}$$
(3)

which is convex and quadratic. We want to use (3) for constructing an improved distance function which uses information about \(f\). Since the problem is unconstrained, the gradient of \(f\) is null, i.e., \(\nabla f|_{\bar{x}}= 0\), and its Hessian is positive semidefinite, i.e., \(H = \nabla ^2 f|_{\bar{x}}\succeq 0\). Thus, minimizing (3) is equivalent to minimizing \( (x-\bar{x})^\mathsf {T} H(x-\bar{x}) \) given that the first two terms can be ignored.

Fig. 2
figure 2

Level curves (grey) of different norm functions using second order information associated with the objective function of the original problem. The distance function in b and its piecewise linear approximation in a both lead to \(\tilde{x}^{\prime }\) as best integral point in the vicinity of \(\bar{x}\)

Full size image

As shown in Fig. 2b, the level curves of this new function are ellipsoids whose axes and axis lengths are defined by the eigenvectors and eigenvalues of \(H\). Note that this relation is inverse proportional, i.e., the larger the eigenvalue, the steeper the ascent, the shorter the corresponding axis. A convex, piecewise linear approximation of this objective function is \(||{H}^{\frac{1}{2}}(x-\bar{x})||_1\). Its level curves are represented in Fig. 2a. This is a distance function that incorporates information about the original objective function. Both functions that are displayed in Fig. 2 find \(\tilde{x}^{\prime }\) as best (w.r.t. the Hessian) integral point near \(\bar{x}\). Note that, in general, neither \(||H^{\frac{1}{2}}(x-\bar{x})||_1\) nor \(||H^{\frac{1}{2}}(x-\bar{x})||_2\) yield a minimum in the hypercube \(\left[ \lfloor \bar{x} \rfloor ,\lceil \bar{x} \rceil \right] \) containing \(\bar{x}\). Also, the closest point changes with the norm as one could construct an example where \(\text {argmin}_{x\in \mathbb Z^n}||H^{\frac{1}{2}}(x-\bar{x})||_p\) depends on p.

The advantage of using the Hessian \(H\), which incorporates second-order information about the current optimal solution of the nonlinear problem, is that a minimizer of \(||{H}^{\frac{1}{2}}(x-\bar{x})||_1\), while possibly far from \(\bar{x}\) in terms of the \(\mathcal {\ell }_1\) norm, corresponds to an integer point whose objective function is close to that of \(\bar{x}\), hence providing a “good” solution from the objective function standpoint.

Let us now generalize this to the constrained version. If we consider an MINLP with a nonlinear objective function, the Hessian of the objective function is, in general, indefinite at the optimum \(\bar{x}\) of the relaxation as there might be active constraints. In case of a linear objective (as in our definition (1)), the Hessian is constant zero. As an alternative, we use the Hessian of the Lagrangian function of the NLP relaxation of the original MINLP:

$$\begin{aligned} \tilde{H} = \left( \frac{\partial ^{2} \mathcal L}{\partial x_{i} \partial x_{j}}\right) _{i,j=1,2,\ldots {}, n}. \end{aligned}$$

While this is a straightforward generalization of the unconstrained case, it must be pointed out that there might be one or more active constraints a local optimum. Sufficient conditions for optimality in the constrained case dictate that \(\tilde{H}\) is only positive semidefinite on the null space of the gradient [5], i.e., in \(\{x \in \mathbb R^{n}: c^{\mathsf {T}}x = 0\}\). We hence correct \(\tilde{H}\) as follows: if an eigenvalue decomposition of \(\tilde{H}\) has q negative eigenvalues \(\lambda _1, \lambda _2, \ldots {}, \lambda _q\) whose eigenvectors have non-zero component in the null space of the gradient, we replace each of those eigenvalues with a value that is higher than the maximum eigenvalue of \(\tilde{H}\). This allows us to focus the search on solutions that are closer to the active constraints rather than along the direction expressed by c.

Definition 1

(Hesse-distance) Let \(\tilde{H} \in \mathbb {R}^{n\times n}\) be the Hessian of the Lagrangian (possibly modified as described above) and a reference point \(\bar{x} \in [l,u]\) be given. We call

$$\begin{aligned} \tilde{\Delta {}}_{\text {int}}(x,\bar{x}) = ||\tilde{H} ^{\frac{1}{2}}(x-\bar{x})||_1 \end{aligned}$$

the \(\ell _1\) Hesse-distance of \(x\) to \(\bar{x}\).

We suggest to incorporate the Hesse-distance into the objective functions of the auxiliary MIPs that are solved in the rounding step of the nonlinear Feasibility Pump. While there have been several publications for improving the distance function for the projection step [3, 15, 20, 22], this is, up to our knowledge, the first attempt of drawing information from the constraint functions into the distance function definition of a Feasibility Pump algorithm. In the spirit of the Objective Feasibility Pump, we came up with the following combination:

$$\begin{aligned} \begin{array}{llll} \Delta _{\text {int}} (x,\bar{x}) &{}=&{} \alpha _{\text {dist}}||x - \bar{x}^k||_1 + \alpha _{\text {H}} \tilde{\Delta }_{\text {int}}(x,\bar{x}) + \alpha _{\text {orig}} c^\mathsf {T} x. \\ \end{array} \end{aligned}$$

Typically, one would increase \(\alpha _{\text {dist}}\) in every iteration, making it converge to one and fade out the other two, thereby shifting the focus from solution quality towards pure feasibility. Note that for any value of these parameters the objective function is piecewise linear and convex. Note also that one can easily extend the definition of the Hesse-distance to the Euclidean case and incorporate it into the objective function for the projection phase. Preliminary experiments revealed, however, that this is not beneficial.

5 Separation of linearization cuts and postprocessing

Techniques to generate a linear relaxation of a MINLP can be used in an incremental fashion as a separation procedure: given a solution \(\tilde{x}\) to a MIP relaxation that is not feasible for the MINLP itself, find a linear cut \(a^{\mathsf {T}}x \le d\) that is fulfilled by all solutions of the MINLP, but \( a^{\mathsf {T}}\tilde{x} > d\) (or show that no such inequality exists). LP-based branch-and-bound solvers for MINLP, such as Couenne or SCIP, typically solve such separation problems to improve local dual bounds at each node. For details on branch-and-cut for MINLP, see, e.g., [40, 42]. In marked difference to previous nonlinear Feasibility Pumps, our implementation also separates linear over- and underestimators for nonconvex functions and not exclusively Outer Approximation cuts for convex parts of the problem.

A typical problem occurring in iterative heuristics such as the FP is cycling. Some versions prevent cycling by adding no-good cuts. Our FP variant attempts to avoid cycling in two ways. First, linear inequalities for nonconvex MINLPs are added to eliminate infeasible integer points. For convex constraints, Outer Approximation cuts are added. For nonconvex constraints, the situation is more involved. As for most global optimization solvers Couenne uses the standard approach of reformulating nonconvex constraints via an expression tree whose nodes are variables and elementary nonlinear functions. For these nonlinear functions, underestimators are used to produce valid linear relaxations. For instance, nonconvex bilinear terms can be addressed via McCormick underestimators [35]. This might still allow for permanently separating the MIP solution from the feasible region.

However, when the MIP terminates with an optimal solution that is infeasible for the (nonconvex) MINLP, but inside the convex hull of its feasible set, no linear cut can be added to separate the solution from its feasible set. This leads to the second way of avoiding cycling: we forbid particular assignments to the integer variables by the use of a tabu list.

A final component of our Feasibility Pump implementation is the postprocessing of feasible solutions. If a MINLP feasible solution \(\tilde{x}\) is found, the values for the continuous variables are only optimal for the distance objective used at the last iteration. To check whether there are better solutions, we run a simple local search improvement heuristic: we obtain a restriction of the original MINLP by fixing all integer variables to the values of the Feasibility Pump solution \(\tilde{x}\) and solve it to local optimality with a convex NLP solver such as Ipopt.

6 Computational experiments

We implemented the Feasibility Pump within Couenne 0.4.7 [6], which is a MINLP solver that uses CBC 2.8.9 [18] as a branch-and-bound manager. Within our implementation, the auxiliary MIP problems are solved by SCIP 3.0.2 [2], linked against Soplex 1.7.2 [44]. The auxiliary NLPs are solved by Ipopt 3.11.7 [31, 43]. The results were obtained on a cluster of 64bit Intel Xeon X5672 CPUs at 3.20 GHz with 12 MB cache and 48 GB main memory, running openSUSE 12.3 with a gcc 4.7.2 compiler. Turboboost was disabled. In all experiments, we ran only one job per node to reduce fluctuations in the measured running times that might be caused by interference between jobs that share resources, in particular the memory bus.

As a test set, we used the MinlpLib [17]. We excluded all instances that were solved by Couenne before the Feasibility Pump was called or that got linearized by presolving, and four instances for which Couenne triggered an error. This resulted in a test set of 218 instances. We compared the following six different settings of the nonlinear Feasibility Pump:

  • Default uses a Manhattan distance function, without contributions of the Hessian of the Lagrangian or the original objective, i.e., \(\alpha _{\text {H}} = \alpha _{\text {orig}} = 0\); this setting does not add convexification cuts for non-convex parts of the problem; the auxiliary MIP is always solved by running SCIP with a stall node limit of 1000 and aggressive heuristic settings; this resembles the Feasibility Pump of [20].

  • Cuts uses cuts for nonconvex parts of the problem (in addition to standard MIP cuts and Outer Approximation cuts); otherwise the same as default;

  • Hierarchy uses different algorithms to solve the MIP in different iterations of the Feasibility Pump, see Sect. 3; otherwise the same as default;

  • Hessian constructs the objective of the auxiliary MIP as a combination of the Manhattan distance and the Hessian of the Lagrangian, see Sect. 4; we chose \(\alpha _{\text {dist}} = 1-0.95^{k}\) and \(\alpha _{\text {H}} = 0.95^{k}\) at the k-th iteration; otherwise the same as default;

  • Objective constructs the objective of the auxiliary MIP as a combination of the Manhattan distance, the Hessian of the Lagrangian and a linear approximation of the original objective; we chose \(\alpha _{\text {dist}} = 1-0.95^{k}\), \(\alpha _{\text {H}} = 0.95^{k}\), and \(\alpha _{\text {orig}} = 0.9^{k}\) at the k-th iteration, otherwise the same as default;

  • Simple applies rounding to the nearest integer instead of solving an auxiliary MIP in the rounding phase, compare [16].

Table 1 shows aggregated results of our experiments. For each of the six settings, we give three performance indicators: feas, the number of instances (out of 218) for which this setting found a feasible solution; bet : wor, the number of instances for which this setting found a better/worse solution (in terms of the objective function value) as compared to the default setting; and time, the running time in shifted geometric mean (see, e.g., [1, 9]), including Couenne’s presolving and reformulation algorithms being applied, i.e., the time needed for processing the root node with one single call to the Feasibility Pump algorithm. We used a shift of 10 s for the running time.

Table 1 Performance of different Feasibility Pump versions for a single call at the root node (aggregated results)
Full size table

First of all, we observe that each of the five non-default settings outperforms the default in at least one of the three measures of performance. The hierarchy setting is the only one to outperform the default in all three measures, albeit only slightly in the quality of the solution found.

We further see that the cuts and the hessian setting both lead to slightly more solutions being found. This could be expected since both attempt to better incorporate the structure of the nonlinear feasibility region into the auxiliary MIP formulation. While using the Hessian leads to better solutions being found, applying cutting plane separation for nonconvex constraints deteriorates the quality of the solution found more often than it improves it. Computing the Hessian of the Lagrangian itself might take considerable time, both settings that make use of this feature show an increase in running time by more than 50 %.

Similar to results for linear Feasibility Pumps, using the original objective often leads to better solutions being produced by the Feasibility Pump, but at the same time reduces the number of solutions being found. Note that the bet : wor statistic includes those cases for which only one of the settings found a solution. Finally, the “simple” setting, which does not use an auxiliary MIP at all, is only slightly faster than the default setting, but much worse in terms of found solutions and solution quality. It can be seen as an implementation of [16] for nonconvex MINLP.

In our implementation, we observe another behavior typical of Feasibility Pumps: although they are very successful in finding feasible solutions (about 75 % of the instances for the hierarchy setting), these solutions are often of a mediocre quality. In geometric mean, the primal gap (as defined in, e.g., [9]) of the solutions found was  34 %. This is almost in line with the Objective Feasibility Pump for MIP that was shown in [3] to reduce the average gap from 55 % for the original Feasibility Pump to 29.5 %.

From our results we conclude that within a global solver, one should use the hierarchy setting and, at least in the initial runs of the FP (i.e., in the first BB nodes), a dynamic setting of \(\alpha _{\text {H}}\) that makes use of the Hesse-distance. For a standalone FP or when there is an emphasis on feasibility, a concurrent run between the hierarchy (most solutions) and the objective setting (highest solution quality) seems most promising.

7 Conclusion

We presented and evaluated three novel ideas for solving nonconvex MINLPs with a Feasibility Pump: the generation of valid cutting planes for nonconvex nonlinearities, using a hierarchy of MIP solving procedures, and applying an objective function for the auxiliary MIPs that incorporates second-order information. For the latter, we introduced the so-called Hesse-distance.

In our computational experiments, the dynamic use of various MIP solving strategies showed the favorable behavior to produce more solutions and better solutions in a shorter average running time. A convex combination of the Hesse-distance function and the Manhattan distance likewise improved the number of solutions found and their quality.