Introduction

Polymer electrolytes are mixtures of polymer and inorganic material. They combine electric conductivity and flexible mechanical properties making them attractive for solid-state devices as batteries or electrochromic displays [1–3]. Especially, systems comprising poly(ethylene oxide) (PEO) attracted much attention in the last decades. This interest was fed by the hope to form materials with sufficiently high electric conductivity applicable in solid-state devices. From an academic point of view, activities were driven by exploring mechanism of conductivity in those or other systems [4–18]. Indeed, progress in the field depends strongly on revealing and understanding of the charge transport process. Prominent contributions to dynamics of charge transport in the frequency range of universal dielectric response (UDR) were provided in Refs. [19, 20]. In the following, we focus on the range of DC conductivity below UDR where conductance is independent of frequency. The remarkable point, PEO, displays not only after addition of an inorganic salt conductivity but also without salt when the molecular mass of chains is sufficiently low. An eminent point, chains are below the entanglement molecular mass in the low-molecular PEO (M w ≈ 1000 g mol−1, M entangle ≈ 3500 g mol−1 [21]). This experimental finding suggests that diffusion-controlled association/dissociation equilibrium plays a prominent role in systems under discussion. Dipole-dipole interactions in the low-molecular PEO induce an electric field leading to mobility-related diffusive relaxation.

There have been discussed several elementary processes ruling proton conductivity in those systems. The most prominent model takes a hydrogen bonding network as base for indirect motion of protons by folding down of bonds. Concomitantly, conductivity is supplemented by self-dissociation of species which contributes also to conductivity [22]. It is obvious that strong correlations exist between mobility of solvated proton complexes and tracer-like diffusion of protons, rendering the situation quite complex. As a result, separation of the elementary processes proves to be difficult [23].

Polymer electrolytes are characterized by dipole-dipole interactions between constituents. But, these hydrogen bond-like interactions are connected with loss of orientation entropy of interacting species. Therefore, interaction becomes only possible if donor and acceptor groups keep the correct orientation to each other. Under dynamic conditions, only the mobile part of charge carriers determines conductivity. Effective concentration itself depends on characteristic length scales ruling decay of concentration gradients. As a result, potent number of particles is intimately allied to mobility. In the following, we conceive this effective concentration in phenomenological way. Thus, DC conductivity is seen as the result of dielectric relaxation. Short-range disorder coupled with correlations between salt and chain segments preserves Gaussian transport process. Velocity correlations are neglected in the diffusion-controlled process; the transport process is seen in mean-field approximation. This approximation yields mean-square displacement growing strictly linearly with time, which corresponds to frequency-independent diffusion coefficient and concomitantly to frequency-independent conductivity.

From thermodynamic point of view, the polymer electrolyte might be characterized simply by ideal electrochemical potential of charged entities or by homogeneous distribution of charge carriers among chains. However, association of the constituents and long-range electric interactions destroy random mixing. Dielectric relaxation towards equilibrium is driven by an entropy loss related to structure formation under influence of the dynamic electric field. In other words, conductivity is governed by kinetic diffusion coefficient and by thermodynamic capacitance density.

The paper is organized as follows. From impedance spectrum Z(ω), one gets information on characteristic relaxation properties of the system. These properties, bordering the low-frequency range where conductivity stays constant, are discussed in thermodynamic terms as well as related to an adequate electric circuit. Eventually, dynamic equilibrium of association/dissociation is established that allows for discussing transport properties as function of effective concentration of relaxing species.

Preliminaries

Preparation of the salt-polymer mixtures and most experimental data are published elsewhere [13, 14, 18, 24]. Therefore, we do not mention experimental details.

Polymer electrolytes are mixtures of polymer and inorganic salt. They are formed by patches of dielectric and conducting domains. Impedance spectroscopy was intensively employed for studies of their properties. In impedance spectroscopy, a film of a polymer electrolyte is embedded between two blocking electrodes. Electric bulk properties of the film might be represented by a capacitor C b in parallel with the bulk resistance R b. Since the ions moving in the film cannot enter the electrode, there is some accumulation of charges at the sample/electrode interface; that is, a double-layer capacitance C dl in series with the resistor-capacitor (RC) circuit exists. In electric terms, the polymer electrolyte might be simulated by the equivalent RC circuit as given in Fig. 4. The following discussion is based on that circuit. Details are given in Refs. [13, 14].

Results and discussion

Impedance

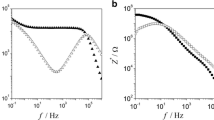
Impedance Z(ω), as provided by spectroscopy, may display different characteristics as a function of frequency. These are maximum and minimum of imaginary part of impedance Z″(ω) at frequencies ω max and ω min and crossing of real and imaginary parts of impedance. When crossing occurs at frequency ω max, we observe Debye relaxation. It corresponds to exponential decay of polarization. Dispersion of relaxation times leads to shift of crossing frequency to ω > ω max. Impedances for two different PEOs are shown in Fig. 1. One recognizes that the low-molecular PEO shows perfectly Debye relaxation and the high-molecular mass PEO with 9 wt% of Li-salt displays it to a good approximation.

Fig. 1
figure 1

Real (solid marker) and imaginary (open marker) parts of reduced impedance; R b Ohm’s resistance of sample. a PEO with M w = 300 kg mol−1 and filled with 9 wt% of LiClO4 at room temperature; data after [13]. b PEO with M w = 1 kg mol−1 without salt at 40 °C; data after [24]

Full size image

Figure 2 summarizes characteristic frequencies of the two PEO samples as functions of salt content and temperature, respectively. We notice that frequency ω max increases with ascending salt content at T = const as well as with temperature at salt content zero. It means that relaxation decays faster with both increasing salt content and temperature. More precisely, we have to distinguish two regions, low and high temperatures, for frequency ω max of the low-molecular mass PEO. The transition of slope (dω/dT) occurs at melting point of the PEO-1 k, T m = 37 °C. The lowest-frequency ω max was monitored at 22 °C, that is, ω max< 0.628 s−1 for T < 22 °C. Frequency ratio ω min/ω max stays roughly constant under conditions studied here. Below, it will turn out that this corresponds to approximately constant capacitance ratio, interface capacity electrode/electrolyte, and sample capacity. We note that frequency ω min can only be monitored after melting of the PEO-1 k sample.

Fig. 2
figure 2

Characteristic frequencies of PEO samples; black square—ω max and white triangle—(ω max/ω min). a PEO-300 k versus mass fraction of LiClO4 at room temperature; data after [13]. b PEO-1 k without salt versus temperature; data after [24]

Full size image

Spectral plots of Z″(ω) as in Fig. 1 allow for determination of Ohm’s resistance R b via |Z″|max = R b/2. An equivalent way for determination of R b starts from the well-known relationship σ DC = L/[A(Z′2 + Z″2)1/2] with L as the thickness of the sample and A as the area of the electrode (for details, cf. Refs. [13, 14]). It is obvious that a plot of impedance Z″ = Z″ (Z′) in Z′–Z″ plane results in a semicircle with radius R b. Resistances R b obtained after both procedures were found to be in perfect agreement. In summary, from impedance spectra as in Fig. 1, we get Ohm’s resistance R b of the film sample. This allows for determination of DC conductivity, σ DC ∝ 1/R b. Results are presented in Fig. 3.

Fig. 3
figure 3

Conductivity σ DC of PEO samples. a PEO-300 k versus mass fraction of LiClO4 at room temperature; data after [13]. b PEO-1 k without salt versus temperature; data after [24]; for comparison, white triangle is σ DC of PEO-300 k plus salt as indicated

Full size image

One observes increasing conductivity with both added salt at T = const as well as with temperature. For PEO-1 k, variation of conductivity with temperature resembles well with the very variation of frequency ω max. We observe low- and high-temperature regions. The discussion below about transport properties will show that low-temperature region is coined just by ω max, whereas high-temperature region is additionally governed by ratio ω min/ω max. There is one exception just below the melting temperature. At T = 36 °C, σ DC is also ruled by the frequency ratio but is precisely integrated in the low-temperature branch. Conductivity displays Arrhenius-like behavior with respect to temperature. The corresponding activation energies amount in the low- and high-temperature ranges to 416 kJ mol−1 (24 to 36 °C) and 14 kJ mol−1 (40 to 50 °C), respectively. We note that PEO-1 k exhibits the same conductivity at 40 °C as high-molecular mass PEO comprising around 10 wt% of LiClO4 at 25 °C.

Conductivity in the low-frequency region (cf. below) is given by mobility u of charge carriers and their molar concentration c S

$$ {\sigma}_{DC}={c}_{\mathrm{S}}Fu $$
(1)

Quantity F symbolizes Faraday’s constant.

Transport properties

In impedance experiment, moving molecules experience some drift velocity due to electric force f, which is superimposed to the random walk originating from collisions with other molecules. The ratio of drift velocity and electric field, v drift/E, is the phenomenological coefficient u occurring in Eq. (1). Drift velocity equals acceleration multiplied by average time τ between two collisions. Accordingly, we may formulate flux generated by electric field or drift velocity

$$ {J}_{\mathrm{drift}}={c}_{\mathrm{S}}uE $$
(2)

The low-frequency region that is the region where conductivity σ is independent of frequency is coined by balance between mass flow and drift flow caused by electric force. In other words, there is no entropy production since J x  + J drift = 0 and we have an equilibrium or steady state situation. The corresponding diffusion coefficient reads after Nernst and Einstein

$$ {D}_{NE}=\frac{u}{F}RT $$
(3)

Diffusing particles are arranged under equilibrium conditions according to Maxwell-Boltzmann distribution as it becomes obvious with vanishing flux, J = 0. We get for Eq. (1) with relationship (3)

$$ {\sigma}_{DC}=\frac{F^2}{RT}{c}_{\mathrm{S}}{D}_{NE} $$
(4)

Diffusion coefficient D NE might be seen as tracer diffusion coefficient. It is not identical with diffusion coefficient D Fick occurring in Fick’s law. This coefficient describes diffusion under action of a concentration gradient including gradient of chemical potential. It causes mass transport after Fick’s diffusion equation. Thus, coefficient D Fick refers in contrast to tracer diffusion to a non-equilibrium process generating entropy production and driving the system towards equilibrium. We approximate mobility u by characteristic time constant τ given by Debye relaxation frequency, ω max = τ −1. As Fig. 1 clearly shows, we are a little bit outside of the frequency independent range of σ(ω) if we select ω max (or ω min) as the characteristic frequency governing mobility u. We are outside the equilibrium situation, and flow is connected with entropy production. The region where conductivity σ is independent of frequency is bordered by the two characteristic frequencies

$$ {\omega}_{\min}\le \omega \le {\omega}_{\max }. $$

Thus, we are replacing D NE in Eq. (4) by D Fick and note that D Fick = D NE in mean field approximation. This might be justified as long as efficient concentration c S is low.

Diffusion coefficient D Fick is related to characteristic frequencies ω min and ω max occurring in imaginary part of impedance, Zʺ(ω); they reflect electrode polarization and Debye relaxation, respectively. Diffusion coefficient is given by mean-free path l times drift velocity, \( D=\frac{1}{3}l{v}_{\mathrm{drift}} \). These quantities are specified in terms of the circuit given in Fig. 4. When C dl = 0, one observes Z′(ω) → R b and Z″(ω) → 0 in the limit ω → 0 and time constant of Debye relaxation amounts to τ = R b C b.

Fig. 4
figure 4

Equivalent circuit for polymer electrolyte film between two blocking electrodes, R b and C b, bulk resistance and capacitance, and C dl, double-layer capacitance electrolyte/electrode

Full size image

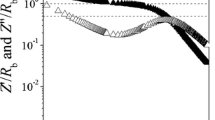
Figure 1 shows that this is not obeyed for the PEO samples under discussion. Results indicate that charge carriers are located in a surface layer close to electrodes. The system becomes a condenser in the DC limit; capacitances C dl ≠ 0 are related to the surface layers. We introduce the capacitance ratio C b/C dl = l/L Footnote 1 with L being sample thickness. Electrode polarization and Debye relaxation coin the length ratio. Analysis of the circuit yields to a good approximation [13, 14]

$$ \frac{l}{L}\approx 0.5{\left(\frac{\omega_{\min }}{\omega_{\max }}\right)}^2\kern0.5em for\ l/L<<1 $$
(5)

Accordingly, diffusion coefficient readsFootnote 2

$$ {D}_{\mathrm{Fick}}=\frac{1}{12}{\left(\frac{\omega_{\min }}{\omega_{\max }}\right)}^4{\omega}_{\max }{L}^2 $$
(6)

This is the diffusion coefficient governing the relaxation process in close proximity to DC region. Ratio l/L describes the capacitance effect in the system. It equals volume ratio v surface/v sample and accounts for the probability that charge carriers are accumulated in the surface layer. Thus, one may approximate the entropy of structure formation in the system as follows

$$ \frac{\Delta S}{R}= \ln \left(\frac{l}{L}\right) $$
(7)

Relationship (7) gives the entropy loss compared to random distribution of charges in the system. Equation (6) allows for separation of product Dc S ∝ σ DC in Eq. (4). Let us reformulate Eq. (4) as follows

$$ \alpha D=\frac{\sigma_{DC}}{\varepsilon_{\mathrm{o}}}\cdot \frac{RT{\varepsilon}_{\mathrm{o}}}{F^2{c}^{*}} $$
(8)

Coefficient α denotes the ratio c S/c * with c * being the concentration of added salt. The first factor of relationship (8) equals characteristic frequency ω max, and the second factor gives some squared length λ close to Debye length; diffusion coefficient reads D = ω max λ 2/α. Comparison with Eq. (6) yields

$$ {c}_{\mathrm{S}}=3\frac{{\left(\lambda /L\right)}^2}{{\left(l/L\right)}^2}{c}^{*} $$
(9)

Separation bases on diffusion coefficient D Fick given by Eq. (6); that is, separation refers to timescale τ max and length ratio (5) derived from equivalent circuit (Fig. 4) or on Debye relaxation and electrode polarization. It becomes obvious that electrically active concentration, participating in conduction, depends on length ratio λ/l. The more diffuse the double layer develops as compared to Debye length, the smaller concentration c S is. Engaging Eq. (7), one may also state that concentration c S is governed by the difference in dissipated energies, |TΔS λ| − |TΔS l|. In the salt-free system, we see c S as the molar concentration of dipole-dipole interactions moving under action of electric field.

Inspection of Fig. 2 gives qualitative notice about concentration and temperature dependence of diffusion coefficient for the systems under discussion. We note only in the high-temperature range that, from 36 to 50 °C, PEO-1 k displays characteristic frequencies ω min and ω max (see Fig. 2). For lower temperatures, frequency shifts to f min < 0.1 s−1. Therefore, we used for calculation of diffusion coefficient ω min/ω max(36 °C) = const in the low-temperature range. This is marked by small solid squares in Fig. 5b. For both systems, one observes only minor variation of frequency ratio ω min/ω max with respect to concentration and temperature, respectively, whereas ω max increases under these conditions but very weakly only for the low-molecular PEO. Weak variation of frequency ratio carries over to characteristic length and also to entropy (7). Thus, we expect increase of diffusion coefficient with salt content but very weak variation with temperature in the salt-free system. Inspection of Figs. 2 and 3 prompts σ DC/D ≈ const. It follows also c S ≈ const for salt-comprising PEO-300 k and in the high-temperature branch of PEO-1 k. Constancy of c S reveals thermal stability of structures formed under action of electric field. Moreover, fraction of electrically active charge carriers, α = c S/c *, diminishes with increasing added salt concentration c * and stays approximately constant for the PEO-1 k. These qualitative conclusions are confirmed in Fig. 5.

Fig. 5
figure 5

Diffusion coefficient D (black square) and effective concentration c S (white markers) after Eqs. (4) and (6), respectively (cf. text). a Versus salt content for PEO-300 k at 25 °C; data after [13]. b Versus temperature for PEO-1 k; data after [24]

Full size image

We may see \( {c}_{\mathrm{S}}^{-1} \)as molar volume and calculate via v S/v sampleentropy (refer to Eq. (7)). Constancy of c S yields also constancy of entropy. Moreover, we get information about Stokes’ friction force f = ϕv drift by applying data of the mentioned figures. Mobility under dynamic electric conditions is given by

$$ u=\frac{e}{m}\tau $$
(10)

with e and m being charge and mass of the diffusing entity. We select again as timescale τ max, inverse Debye relaxation frequency. It follows for Stokes’ friction force f acting under conditions where σ DC has been measured

$$ f=\frac{e}{u}{v}_{\mathrm{drift}} $$
(11)

Ratio e/u ≡ ϕ is the friction coefficient. Mobility is related via Eq. (3) to the appropriate diffusion coefficient (6). It follows for friction force

$$ f\propto \frac{T}{\left(\frac{l}{L}\right)} $$
(12)

Friction force is inversely proportional to electric screening length; the smaller characteristic length l is, the higher friction force is. Entropy production or the rate of dissipated energy is given by

$$ T\dot{S}=f{v}_{\mathrm{drift}} $$
(13)

where drift velocity is the relative velocity between chains and charged entities. It rules together with friction between them relaxation of concentration fluctuations. The corresponding diffusion coefficient ascends with added salt concentration (cf. Fig. 5). This is so because entropy production increases with relaxation frequency ω max. It follows with Eq. (11)

$$ \frac{\dot{S}}{R}\propto {\omega}_{\max } $$
(14)

Systems under discussion display l/L ≈ const with respect to concentration as well as temperature. Hence, one observes f ≈ const for the high-molecular mass PEO with salt and weak variation with temperature for the PEO-1 k. However, we note that magnitude of friction force in the low-molecular system exceeds that one in the salt-comprising system since the frequency ratio or l is smaller for the low-molecular PEO as Fig. 2 shows. Also after Fig. 2, entropy production increases with salt content at T = const and varies weakly with temperature for the PEO-1 k in the high-temperature region. Entropy production tends towards approximately the same distance to equilibrium in both systems at sufficiently high salt content and sufficiently high temperature, respectively.

Selected results are listed in Table 1 for the two PEO systems under condition of approximately equal DC conductivity. We find that relaxation time constants are equal to good approximation. In other words, we compare the systems under equal timescale. We see a huge disparity between characteristic lengths due to variation in the frequency ratios. This coins also variation in drift velocity and, consequently, in diffusion coefficient being very large in the salt-comprising system as compared to the salt-free PEO. Inverse molar concentration c S represents molar volume of the surface layer and is therefore proportional to characteristic length l; consequently, c S is small for the salt-comprising system and quite large for PEO-1 k. The difference in characteristic lengths points to rather diffuse double layer in the salt-comprising system and to sharp layer in the low-molecular PEO. Consequently, friction force is low in the former case and much stronger in the latter. The same effect is true for entropy (7). All properties listed in Table 1 are consistently comprehensive in the framework of dielectric relaxation shown in Fig. 1.

Table 1 Dynamic properties of the PEO systems under conditions of equal DC conductivity
Full size table

Association

As Debye relaxation shows, there exist dipole-dipole interactions in mixtures of high-molecular mass PEO and Li salt as well as in pure PEO consisting of oligomers (M = 1 kg mol−1). Thus, conductivity is related to association/dissociation and it is diffusion controlled. In both cases, hydrogen bonds lead to associations or complex formation in dynamic equilibrium with dissociation. Salt molecules mediate association in first case. In low-molecular PEO, association of chains may occur owing to hydrogen bonding with each other via ether oxygen or via −OH end groups. We note that effective concentration c S of relaxing entities depends critically on orientation of donor and acceptor groups. They have to occupy correct orientation in vicinity to each other. Variation of effective concentration c S, as shown in Fig. 5a, b, suggests that keeping correct arrangement is more important for the polymer-salt mixture as for the PEO oligomer. We note also that dipole-dipole interactions could not be observed in salt-free high-molecular PEO at room temperature.

In the polymer electrolyte, we have distribution of salt molecules among chains but not just random mixing as Eq. (7) shows. One may see the mixture as segment-related association between Li salt (S) and segments (M) in the high-molecular PEO mixed with salt. More precisely, we see it as association/dissociation equilibrium which is diffusion controlled.

$$ SM\leftrightarrow S+M $$

We symbolize here the electrically active concentration c S after Eq. (4) by αc * with c * being the added concentration of salt. Factor α might be grasped for the moment as degree of dissociation. We get for the relevant concentrations c S = c M = αc * and c SM = (1 − α) c *. The corresponding dissociation constant reads.

$$ {K}_{\mathrm{c}}=\frac{\alpha^2{c}^{*}}{1-\alpha}\approx \frac{{\left(\alpha {c}^{*}\right)}^2}{c^{*}} $$
(15)

In the last expression, it is assumed α ≪ 1. Quantity K c depends on concentration. We get the thermodynamic equilibrium constant K a by replacing concentration c S by activity a, that is, introducing mean activity coefficient γ ±. It follows

$$ {K}_a={K}_c/{\left({\gamma}_{\pm}\right)}^2=\frac{k_{\mathrm{ass}}}{k_{\mathrm{diss}}} $$
(16)

Activity coefficient γ ± 2 refers to standard state pure salt in the state of infinitely high dilution, γ ± 2 c * = 1. In Eq. (16), equilibrium constant is expressed by ratio of kinetic rate constants (for dissociation and association), underlining that involved species are in dynamic equilibrium. Hence, we have for rate constant k diss = \( {\tau}_{\max}^{-1} \) with \( {\tau}_{\max}^{-1} \) = ω max. Timescale τ max is related to bond lifetime or to the strength of the transient dipole-dipole interaction. A nice confirmation is presented by comparison of results shown in Figs. 3b and 2. PEO-300 k plus W S = 0.09 LiClO4 displays at room temperature approximately the same DC conductivity as salt-free PEO-1 k at 40 °C. The corresponding frequencies ω max amount to 4.7 × 105 and 4.4 × 105 s−1, respectively.

It results with Eqs. (13) and (14) and using for lg γ ± 2 Debye-Hückel approach

$$ \lg {K}_{\mathrm{c}}= \lg {K}_{\mathrm{a}}+ \lg {\gamma_{\pm}}^2= \lg {K}_{\mathrm{a}}+A\kern0.5em {\left(\alpha {c}^{*}\right)}^{1/2} $$
(17)

where A is a constant. Figure 6 gives the ratio K c versus (c S)1/2; the intercept marks the dissociation constant K a. It results

$$ {K}_{\mathrm{a}}=2.0\times {10}^{-22},\alpha =1.4\times {10}^{-11},\varDelta {G^{\mathrm{o}}}_{298}=123.9\ \mathrm{kJ}\ {\mathrm{mol}}^{-1} $$
(18)
Fig. 6
figure 6

Dissociation ratio K c versus (c S)1/2 after Eq. (17) and K c versus temperature after Eq. (19). a Thermodynamic dissociation constant K a (white square) for PEO-300 k at 298 °C. b Dissociation ratio for PEO-1 k versus temperature; high-temperature range (white square)

Full size image

with α = (c S/c *)equil. Results (18) reveal shifting of equilibrium strongly towards association.

For the PEO of low-molecular mass, we assume molecule-related association/dissociation

$$ {P}_{\mathrm{k}}\ \overset{K_{\mathrm{c}}}{\leftrightarrow }{P}_{\mathrm{k}-1}+{P}_1\kern0.75em \mathrm{with}\ k-1=1,2,3,... $$

P k denotes an aggregate composed of k unimers P 1. Since equilibrium constant of molecule-related association/dissociation is independent of degree of association k, one gets simply for dissociation constant K c analogous to Eq. (13) with use of ρ S/M o = c S, M o segment molar mass

$$ {K}_{\mathrm{c}}={\alpha}^2{c}^{*} $$
(19)

Comparison of Figs. 6a, b shows that dissociation constant K c in the high-temperature range is much higher in PEO-1 k as in the salt-containing PEO. Note that constant K c is inversely proportional to molar volume, V * = M o/ρ. Hence, we get

$$ {K}_a={K}_c/{c}_S=\alpha $$
(20)

Figures 5b and 6b reveal that both K c and c S vary weakly with temperature in the high-temperature branch. Therefore, we apply mean values of these quantities in Eqs. (19) and (20) and refer to T = 318 K. It follows

$$ \begin{array}{cc}\hfill \alpha =1.4\times {10}^{-4}\ \hfill & \hfill \varDelta {G^{\mathrm{o}}}_{318}=23.5\ \mathrm{kJ}\ {\mathrm{mol}}^{-1}\hfill \end{array} $$

After Eq. (7), one gets TΔS = −30.4 kJ mol−1; that is, moderate interactions are acting in the system, ΔH o 318 ≈ −7 kJ mol−1. Constant K a reflects only dissociation/association equilibrium in the range above 40 °C that is in the molten state. Equilibrium at lower temperatures shifts stronger to association.

There is a pronounced difference between the two PEO systems. The salt-comprising polymer electrolyte follows (after Fig. 6a) Debye-Hückel approximation. In agreement with Table 1, DC conductivity is chiefly determined by diffusion coefficient. The opposite is true for temperature dependence of conductivity in the low-molecular PEO. Diffusion coefficient is low, due to high friction force, and approximately constant, whereas apparent inverse partial molar volume, equal to apparent concentration c S, is quite high at high temperature due to the sharp double layer.

Molar conductivity is presented in Fig. 7. Again, one may state that effective concentration c S acts as suitable variable for representing behavior of polymer electrolytes. The salt-comprising PEO obeys precisely Kohlrausch’s law up to c S ≈ 1 × 10−11 mol cm−3.

$$ \varLambda ={\varLambda}_{\mathrm{o}}\hbox{--} B{\left({c}_{\mathrm{S}}\right)}^{1/2} $$
(21)
Fig. 7
figure 7

Molar conductivity versus effective concentration (c S)1/2 and temperature. a PEO-300 k at 25 °C; white square—Λ o. b PEO-1 k; black square—high-temperature range and white square—low-temperature range

Full size image

We note that Λ o exceeds the corresponding value in aqueous solution of Li salt by four orders of magnitude, Λ o ≈ 1 × 106 cm2 (Ω mol)−1. The polymer electrolyte with PEO represents an extremely weak electrolyte.

Molar conductivity of the salt-free PEO-1 k stays approximately constant in the high-temperature range. In agreement with Fig. 5 and preceding discussion, molar conductivity of PEO-1 k remains markedly below that of the salt-comprising PEO. The course in the low-temperature region is only of qualitative meaning since we adopted ω min/ω max (36 °C) = const in the low-temperature branch. It increases with increasing temperature due to rapidly increasing diffusion coefficient (cf. Fig. 5b). The activation energy amounts to E A ≈ 125 kJ mol−1.

When molar conductivity follows Kohlrausch’s law, then we expect also

$$ D={D}_{\mathrm{o}}\left[1\hbox{--} B{\left({c}_{\mathrm{S}}\right)}^{1/2}\right] $$
(22)

with

$$ {D}_{\mathrm{o}}=\frac{RT}{F^2}{\varLambda}_{\mathrm{o}} $$

This is precisely obeyed for PEO-300 k. We get with data of Fig. 7

$$ \begin{array}{ccc}\hfill {\varLambda}_{\mathrm{o}}=1.3\times {10}^6{\mathrm{cm}}^2{\left(\varOmega\ \mathrm{mol}\right)}^{-1}\hfill & \hfill {D}_{\mathrm{o}}=0.35\ {\mathrm{cm}}^2{\mathrm{s}}^{-1}\hfill & \hfill {\sigma}_{\mathrm{o}}=1.8\times {10}^{-5}{\left(\varOmega\ \mathrm{cm}\right)}^{-1}\hfill \end{array} $$

from σ o = (F 2/RT)D o α.

Conclusion

Dielectric relaxation in the low-frequency range is coined by charge accumulation in interfacial layer electrode/electrolyte. Development of the double layer turns the system in a capacitance. Under dynamic conditions, efficient charge carrier density and mobility are bound to characteristic length ratio and to a timescale of reference. Accordingly, timescale was obtained from Debye relaxation frequency displayed by imaginary part of complex impedance. Both transport quantities are prominently ruled by length ratio, double-layer l over sample thickness L. This ratio in turn is given by ratio of characteristic frequencies of Zʺ(ω), (ω min/ω max)2. Double-layer formation causes deviation of charge distribution from homogeneity, or formation of double-layer corresponds to an entropy loss given by ln (l/L). It becomes obvious that the smaller length ratio l/L is, the higher magnitude of entropy loss is, the higher charge carrier density is, and concomitantly, the smaller mobility due to increasing friction force is. Moving charged entities through melt of chains experience some friction. The dissipated energy is given by the product of friction force and drift velocity. These quantities govern relaxation of concentration fluctuations in the system. The disentangled melt of PEO-1 k appears as damped liquid, at least in the neighborhood of melting point, due to high magnitude of entropy loss and high friction force. It turns out that the high-molecular PEO with added salt and the neat low-molecular PEO at higher temperatures behave as weak electrolytes. The former system obeys precisely Kohlrausch’s law. In that sense, it can be also seen as strong electrolyte owing to very low efficient concentration c S.