1 Introduction

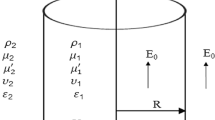
A Hele-Shaw cell is a technical device introduced in [18], formed by two parallel plates separated by a narrow gap of thickness b. The equations verified by the mean velocities of a Stokes fluid in a Hele-Shaw cell are similar with the Darcy’s law for the flow in a porous medium—see [2, 20]. The interface between two immiscible Stokes fluids in a Hele-Shaw cell is unstable when the displacing fluid is less viscous—see Saffman and Taylor [33]. The important parameter of the displacing process is the small number \(\epsilon = b/l\), where l is the length of the Hele-Shaw cell.

The Hele-Shaw model can be used to study the secondary oil recovery. Since 1960, good results were obtained by using a polymer solution as “forerunner” in the oil recovery process—see [14] and the references therein. The oil can often be considered a non-Newtonian fluid, so it is useful to study the stability of the non-Newtonian displacements in Hele-Shaw cells.

The non-Newtonian fluids and their stability analysis are studied in a large number of papers—see [4, 9, 10, 13, 15, 25, 31, 34, 35]. These fluids exhibit at least two characteristics not present in Newtonian case: shear-thinning and elasticity. Two important constitutive models exist in order to describe these effects. The Ostwald–de Waele power-law fluid shows shear-thinning properties but is inelastic. The Oldroyd-B model exhibits elasticity but not shear-thinning.

Important results about the stability of non-Newtonian displacements in Hele-Shaw cells were obtained in [1, 3, 11, 22, 23, 32, 37].

A formula of the growth rate of perturbations was obtained in [37], when a power-law fluid (with exponent q) is displaced by air in a rectilinear cell. It is multiplied by \(q^{-1/2}\) as compared with the Newtonian case, but there is no qualitative change.

In [1] is studied the flow near an arbitrary corner for any power-law fluid. The variational calculus is used in [3], to investigate the time-dependent injection rate that minimizes the Saffman–Taylor instability, when shear-thinning fluids or polymer-solutes (with slowly or fast gelling properties) are displacing. In [11] are studied some methods to minimize the fingering phenomenon when an inviscid fluid displaces a power-law fluid. The problem of bubble contraction in a Hele-Shaw cell is studied in [22], when the surrounding fluid is of power-law type, related with a small perturbation of the radially symmetric problem. The stability of the displacement of two power-law fluids in a radial Hele-Shaw cell has been considered in [23]. The displacement of a high-viscosity power-law fluid by a low-viscosity Newtonian fluid in a radial Hele-Shaw cell is studied in [32] and a detailed analysis of the flow is given, concerning the fractal fingering patterns.

Numerical results concerning the displacement of Oldroyd-B and Maxwell upper—convected fluids by air in rectilinear Hele-Shaw cells are given in [26, 27, 37]. Very high values of the growth constant were reported in [37], when the relaxation (in time) constant is increasing up to a critical value. This phenomenon may be related with the fractures observed in the flows of complex fluids in Hele-Shaw cells—see [28, 29, 38] and the references therein.

In this paper we study the linear instability of the displacement of two Oldroyd-B fluids in a rectilinear Hele-Shaw cell. We use the same depth-averaged interface conditions as in [33, 37]. The thickness of the narrow gap is much smaller compared with the cell length, then we can neglect some terms in the perturbations equations. The new element is the explicit formula (57) of the growth rate of perturbations, which depends on \((C_i-D_i)\), where \(C_i, D_i\) are the Weissenberg numbers of the two fluids. Most numerical methods fail when the Weissenberg numbers are near 1. A blow-up of our growth rates (57) appears for some critical values \((C_i-D_i)=O(1)\). Therefore our results give a sharp indication that the instability is due to the model .

The paper is organized as follows. In Sect. 2 we describe the Hele-Shaw cell and the constitutive equations of the Oldroyd-B fluids. The basic solution is given in Sect. 3. In Sect. 4 we get the linear perturbation system. The stability analysis is performed in Sect. 5. A special Fourier decomposition used in Sect. 5.1 allows us to avoid the unbounded growth of the partial derivatives of the perturbed velocities near the interface between the two fluids. The perturbations are considered as series of powers of the small parameter \(\epsilon \)—see the first paragraph of this section. In Sect. 5.2 we get the leading order terms of the extra-stress tensor and the amplitude of the velocity perturbations. In Sect. 6 we obtain the growth rate formula. In Sect. 7 we give new results on the effects of superficial tension in the instability of the displacement process. Some dispersion curves are plotted. They are in good agreement with previous numerical results. We conclude in Sect. 8. The calculations and complex formulas required for exposure are detailed in “Appendices 1–3”.

2 The Oldroyd-B fluids

We consider two incompressible and immiscible Oldroyd-B fluids in a Hele-Shaw cell parallel with the xOy plane. The distance between cell plates is b, which is much lower compared to the cell length l. We use the small parameter

$$\begin{aligned} \epsilon = b/l<<1. \end{aligned}$$
(1)

The fluid 1 is displacing the fluid 2 in the positive direction of the Ox axis. On the sharp interface between the fluids, the jump of the averaged normal stress should equal the surface tension multiplied by the curvature of averaged interface and the normal velocity should be continuous (the “depth-averaged” Laplace’s law). The no-slip conditions are imposed on the cell plates.

The velocities, the pressures, the viscosities and the extra—stress tensors for both fluids \(i=1,2\) are denoted by

$$\begin{aligned} { { \underline{\mathbf{u}}^i}} = ({ \underline{u}}^i,{ \underline{v}}^i,{ \underline{w}}^i), \,\, { \underline{p}}^i, \,\, \mu _i, \,\, { \underline{\tau }}^i . \end{aligned}$$

The stress \({\underline{\Sigma }} ^i\) and the strain-rate \({\underline{\mathbf{S}}^i}\) are given by

$$\begin{aligned}&{{ \underline{\Sigma }} ^i }= {\underline{p}}^i \mathbf{I} - { \underline{\tau }}^i,\\&{\underline{\mathbf{S}}}^{\mathbf{i}} = ({\underline{\mathbf{V}}}^{\mathbf{i}} + {{\underline{\mathbf{V}}}^{\mathbf{iT}} })/2,\\&{{\underline{\mathbf{V}}}^{\mathbf{i}} = \nabla { \underline{\mathbf{u}}^i}}, \end{aligned}$$

where \(\mathbf{I}\) is the unit tensor and \(\nabla \) is the gradient operator.

We have the following flow equations, divergence-free condition and constitutive relations, with \(c_i> d_i \ge 0, \,\,\, i=1,2\):

$$\begin{aligned}&- {\nabla } { \underline{p}^i} + {\nabla } \cdot { \underline{\tau }}^i =0,\nonumber \\&{\underline{u}}^i_{x} + { \underline{v}}^i_y + { \underline{w}}^i_z =0, \end{aligned}$$
(2)
$$\begin{aligned}&{{ \underline{\tau }}}^1 + c_1 {{ \underline{\tau }}}^{1 \nabla } = 2 \mu _1 ( {{\underline{\mathbf{S}}}}^1 + d_1 {{\underline{\mathbf{S}}}}^{1 \nabla } ) ; \end{aligned}$$
(3)
$$\begin{aligned}&{{ \underline{\tau }}}^2 + c_2 {{ \underline{\tau }}}^{2 \nabla } = 2 \mu _2 ( {\underline{\mathbf{S}}}^2 + d_2 { \underline{\mathbf{S}}}^{2 \nabla } ) . \end{aligned}$$
(4)

Here \((c_1, d_1), \,\, (c_2, d_2) \) are the relaxation and the retardation (time) constants of the fluids. The lower indices \(_x\), \(_y\), \(_z\) are denoting the partial derivatives; \({{ \underline{\tau }}}^{ i \nabla }, \quad {{\underline{S}}}^{ i \nabla } \) are the upper convected derivatives. We consider a steady flow, then

$$\begin{aligned}&{{ \underline{\tau }}}^{ i \nabla }= {{ \underline{\mathbf{u}}}} ^i\cdot { \nabla } { \underline{\tau }}^i - ({ \underline{\mathbf{V}}}^i { \underline{\tau }}^i + { \underline{\tau }}^i { \underline{\mathbf{V}}}^{iT}),\quad \nonumber \\&{\underline{\mathbf{S}}}^{ i \nabla }= {\underline{\mathbf{u}}}^i \cdot {\nabla } { \underline{\mathbf{S}}}^i - ({ \underline{\mathbf{V}}}^i \mathbf{{ \underline{S}}}^i + { \underline{\mathbf{S}}}^i{ \underline{\mathbf{V}}}^{iT}). \end{aligned}$$
(5)

3 The basic flow

We study the linear instability of the following basic flow, denoted by the upper index \(^{0i}\), \(i=1,2\):

$$\begin{aligned}&{\nabla } p^{0i} = ( p^{0i}_{x}(x), 0 , 0); \quad \mathbf{u}^{0i} = ( u^{0i}(z), 0, 0 );\nonumber \\&\mathbf{V}^{0i}_{13}=u^{0i}_z; \quad \mathbf{V}^{0i}_{mn}=0, \,\, (mn)\ne (13);\nonumber \\&\mathbf{S}^{0i} = (\mathbf{V}^{0i} + \mathbf{V}^{0iT} )/2 . \end{aligned}$$
(6)

The basic extra-stress tensor \(\tau ^{0i}\) is depending only on z and is given by the Eqs. (75)–(77) in “Appendix 1”. It follows (see also [37]):

$$\begin{aligned}&\tau ^{0i}_{11} = 2 \mu _i (c_i-d_i) (u^{0i}_z)^2; \end{aligned}$$
(7)
$$\begin{aligned}&\tau ^{0i}_{13} = \mu _i u^{0i}_z; \quad \tau ^{0i}_{mn}=0, \,\, (mn)\ne (11), (13). \end{aligned}$$
(8)

Therefore we obtain the following equations of the basic pressures

$$\begin{aligned}&p^{0i}_{x} = \tau ^{0i}_{11,{x}} + \tau ^{0i}_{12,y} + \tau ^{0i}_{13,z} = \tau ^{0i}_{13,z},\nonumber \\&p^{0i}_y = p^{0i}_z = 0. \end{aligned}$$
(9)

From the relation (9)\(_1\) we get

$$\begin{aligned} p^{0i}_{x} = \tau ^{0i}_{13, z} = G_i = \mu _i u^{0i}_{zz} \end{aligned}$$
(10)

where \(G_i\) are two negative constants. We suppose \(u^{0i}= 0\) for \(z=0, z=b\), then

$$\begin{aligned} u^{0i} = (G_i / 2 \mu _i )z(z-b), \quad i=1,2 . \end{aligned}$$
(11)

The normal velocity must be continuous across the interface. Our basic velocity has only the normal component, then \(u^{01}=u^{02}\) and we have the important relation

$$\begin{aligned} \frac{G_1}{\mu _1} = \frac{G_2}{\mu _2} . \end{aligned}$$
(12)

The basic velocity\(u^0\) is given by

$$\begin{aligned} u^{0}:= u^{0i} = (G_i / 2 \mu _i )z(z-b), \quad i=1,2. \end{aligned}$$
(13)

We define the average operator

$$\begin{aligned} \quad <h > = (1/b) \int _0^b h(z)dz \end{aligned}$$
(14)

and we introduce the characteristic velocity U:

$$\begin{aligned} U= <u^{0}> = -\frac{b^2}{12 \mu _i} G_i , \quad G_i = -\frac{12 U \mu _i}{b^2}. \end{aligned}$$
(15)

The relation (15) is similar with the Darcy’s law for a porous medium with permeability \((-b^2/12)\).

We consider the following basic interface between the displacing fluids

$$\begin{aligned} x=Ut, \end{aligned}$$
(16)

where t is time and we introduce the moving coordinate system

$$\begin{aligned} {\overline{x}}=x-Ut. \end{aligned}$$
(17)

The basic (material) interface becomes

$$\begin{aligned} {\overline{x}} = {\overline{x}}_0:= 0. \end{aligned}$$
(18)

In the following we still use the notation x instead of \({\overline{x}}\).

It is noteworthy that in [37] is considered the planar interface \(x=Ut\), by using the relation (15). In [27], after the formula (10), it is specified that “since b is much smaller than any lateral lengthscale in a Hele-Shaw device, then any z dependence of the basic interface is not relevant”.

The flow is due to the pressure gradients. The pressures contain two unknown constants, used latter in order to obtain the Laplace’s law for perturbations.

4 The perturbations system

The linear perturbations of the basic solution (6) are denoted by

$$\begin{aligned} u^i,v^i, w^i, p^i, \mathbf{V}^i, \mathbf{S}^i, \tau ^i, \quad i=1,2. \end{aligned}$$

We assume \( u^i=v^i=w^i=0\) for \(z=0, z=b\). The perturbation of the basic interface (18) is denoted by \(\psi (y,z, t)\) and we have

$$\begin{aligned} \psi _t = u^1|_{x_0}= u^2|_{x_0} . \end{aligned}$$
(19)

The basic velocities are divergence-free. In the frame of linear perturbations we obtain \(u^i_x+v^i_y+w^i_z=0\). We use the average operator (14) and the boundary conditions for w, then

$$\begin{aligned} <u^i_x+v^i_y >=0. \end{aligned}$$

This condition is verified if \(u^i_x+v^i_y=0\), from which we get \(w^i_z=0\). In this paper we consider

$$\begin{aligned} u^i_x+v^i_y=0, \quad w^i=0. \end{aligned}$$
(20)

The following relations (21)–(26) are concerning both fluids 1 and 2, then we omit the upper index \(^i\). The small perturbations are inserted in (3)–(5) and we obtain

$$\begin{aligned}&{\tau }^0 + {\tau } + \theta ({\tau }^0 + {\tau })^{{\nabla }} \nonumber \\&\quad =2 \mu [\mathbf{S}^0 + \mathbf{S} + \eta (\mathbf{S}^0 +\mathbf{S})^{\nabla }], \end{aligned}$$
(21)
$$\begin{aligned}&({\tau }^0 + {\tau })^{{\nabla }} = u^0 {\tau }_x-[\mathbf{V}^0{\tau }^0+{\tau }^0 \mathbf{V}^{0T}]\nonumber \\&\qquad -[\mathbf{V}^0 {\tau } + \mathbf{V} {\tau }^0 + {\tau }^0 \mathbf{V}^T + {\tau } \mathbf{V}^{0T}], \end{aligned}$$
(22)
$$\begin{aligned}&(\mathbf{S}^0 + \mathbf{S})^{{\nabla }} = u^0 \mathbf{S}_x - [\mathbf{V}^0 \mathbf{S}^0 + \mathbf{S}^0 \mathbf{V}^{0T}] \nonumber \\&\qquad -[\mathbf{V}^0 \mathbf{S} + \mathbf{V} \mathbf{S} ^0 + \mathbf{S}^0 \mathbf{V}^T + \mathbf{S} \mathbf{V}^{0T}] \end{aligned}$$
(23)

where \(\mu , \theta , \eta \) verify the relations

$$\begin{aligned}&\mu = \mu _1 \text{ for } x < x_0; \quad \mu = \mu _2 \text{ for } x > x_0; \end{aligned}$$
(24)
$$\begin{aligned}&\theta = \left\{ \begin{array} {c} c_1, x<x_0 \\ c_2, x>x_0 \end{array} \right. ; \quad \eta = \left\{ \begin{array} {c} d_1, x<x_0 \\ d_2, x>x_0 \\ \end{array} \right. . \end{aligned}$$
(25)

In the frame of the linear stability (by neglecting the second order terms in perturbations) it follows

$$\begin{aligned} {\tau } + \theta ( u^0 {\tau }_x- \mathbf{E})= \mu \{ 2\mathbf{S} + \eta ( u^0 {2\mathbf S}_x - \mathbf{F})\}, \end{aligned}$$
(26)

where the tensors \(\mathbf{E}, \mathbf{F}, \mathbf{S}\) are given in “Appendix 2”–see the relations (78)–(80).

The perturbed normal stresses in both fluids are (see [5, 31])

$$\begin{aligned} T^i_{11} = p^{0i} + p^i - (\tau ^{0i}_{11}+ \tau ^i_{11} ). \end{aligned}$$
(27)

We search for the limit values \( T^-_{11}= lim_{ \,\, x<x_0, \,\, x\rightarrow x_0 \,\,}T^1_{11} \quad \) and \( \quad T^+_{11}= lim_{ \,\, x>x_0, \,\, x\rightarrow x_0 \,\,}T^2_{11}\).

The basic pressure is not depending on z, then we have the Taylor’s first-order development near the basic interface \(x_0\):

$$\begin{aligned}&p^{0i}(x_0+ \psi ) = p^{0i}(x_0+<\psi>) \nonumber \\&\quad =p^{0i}(x_0) + p^{0i}_x(x_0)<\psi> = p^{0i}(x_0) + G_i <\psi >. \end{aligned}$$
(28)

From (19), (27), (28), near the interface \(x=x_0\) we get

$$\begin{aligned}&T^-_{11} = p^{01}(x_0)+ G_1<\psi> + p^1 - (\tau ^{01}_{11}+ \tau ^1_{11} ),\nonumber \\&T^+_{11} = p^{02}(x_0)+ G_2 <\psi > + p^2 - (\tau ^{02}_{11}+ \tau ^2_{11} ). \end{aligned}$$
(29)

The depth-averaged dynamic Laplace’s law (near the basic interface \(x=x_0\)) is

$$\begin{aligned}< T^+_{11}- T^-_{11}>= \gamma \times <interface \,\, curvature > \end{aligned}$$

where \(\gamma \) is the surface tension. From  (28), (29) it follows

$$\begin{aligned}&p^{02}(x_0) + G_2<\psi> + {< p^2 } - \tau ^{02}_{11}+ \tau ^2_{11}> \nonumber \\&\qquad -\{ p^{01}(x_0) + G_1<\psi> + {< p^1 } - \tau ^{01}_{11}+ \tau ^1_{11}> \}\nonumber \\&\quad =\gamma (x_0) < x_{0yy} + x_{0zz} + \psi _{yy} + \psi _{zz} >, \end{aligned}$$
(30)

where the curvature of \(\psi \) is approximated by \((\psi _{yy}+\psi _{zz})\). The basic normal stress verify the Laplace’s law on the basic interface \(x=x_0\), so we should have the relationship

$$\begin{aligned}&(p^{02} -<\tau ^{02}_{11}>)|_{x_0} - (p^{01} -<\tau ^{01}_{11}>)|_{x_0}\nonumber \\&\quad =\gamma (x_0) < x_{0yy} + x_{0zz} >=0. \end{aligned}$$
(31)

Only the basic pressures gradients are given, then the basic pressures contain two additive constants. As in [37] (where the displacing fluid is air), for appropriate values of these constants we get the above relation—see also the last two lines of Sect. 4. Therefore the relations (30)–(31) are giving us the Laplace’s law for perturbations:

$$\begin{aligned}&(G_2-G_1)<\psi> + {<p^2 - \tau ^2_{11}> -<p^1 - \tau ^1_{11}> } \nonumber \\&\quad = \gamma (x_0) < \psi _{yy} + \psi _{zz} >. \end{aligned}$$
(32)

5 Linear stability analysis

5.1 Fourier decomposition

The system (26) is linear in the disturbance quantities. We consider the perturbations of the velocities in the following form, with \(k \ge 0, \quad \alpha >0 \) :

$$\begin{aligned}&u^1 = f(z) {E_1} \cos (ky), \nonumber \\&v^1 = - f(z){E_1} \sin (ky), \quad x < x_0; \end{aligned}$$
(33)
$$\begin{aligned}&u^2 = f(z) { E_2} \cos (ky), \nonumber \\&v^2 = f(z){ E_2}\sin (ky), \quad x >x _0; \end{aligned}$$
(34)
$$\begin{aligned}&f(z) = \beta u^0(z), \quad \beta = O(\epsilon ^2); \end{aligned}$$
(35)
$$\begin{aligned}&{E_1}= \exp ( - k \alpha + kx + \sigma t ), \,\, x \le x_0;\nonumber \\&{E_2}= \exp ( - k \alpha - kx + \sigma t ), \,\, x \ge x_0. \end{aligned}$$
(36)

The dimension of \(\alpha \) is length. On \(x_0\) we have

$$\begin{aligned}&u^1=u^2, \quad v^{1-}\ne v^{2+}, \nonumber \\&v^1_y = -kf { E_1}|_{x_0} \cos (ky), \nonumber \\&v^2_y = kf { E_2} |_{x_0}\cos (ky), \end{aligned}$$
(37)

where \(^-, ^+\) are the lateral limits values. The perturbations decay to zero away from \(x_0\) and \(u^i_x+v^i_y=0\), \(i=1,2\). We have \(k \cdot \exp (-k \alpha ) \le 1/(\alpha e)\). Then \(u_x, u_y, v_x, v_y\) near \(x_0\) are bounded with respect to k. We justify the form of the amplitude f in Sect. 5.2.

The relations (19), (33)–(36) give us \(\psi =u/\sigma \) and from (32) it follows

$$\begin{aligned} \sigma = \frac{ \gamma<u_{yy} + u_{zz}> +(G_1-G_2)<u> }{<p^2 - \tau ^2_{11}> - <p^1 - \tau ^1_{11}> } \end{aligned}$$
(38)

where \(u=u^1(x_0)=u^2(x_0)\). We look for \(<p^i - \tau ^i_{11}> \) as functions of \(u^{0}\) and \(u^i\).

In this paper we use the following dimensionless quantities, denoted by \('\) :

$$\begin{aligned}&x'=x/l, \quad y' = y/l, \quad z'=z/b,\nonumber \\&u^{'i}=u^i/ U, \quad v^{'i} =v^i/ U,\nonumber \\&p^{'i}=p (l/\mu _i U), \quad \gamma '= \gamma /(\mu _1 U), \quad \mu _0= \mu _2/\mu _1 ,\nonumber \\&\alpha ' = \alpha / l, \quad k'=kl, \quad \sigma ' = \sigma / (U/l), \quad t' = t(U/l).\nonumber \\&\{ (\tau ^i _{11})' , (\tau ^i_{ 12})', (\tau ^i_{ 22})' \} = \{ \tau ^{i}_{11} ,\tau ^{i}_{ 12}, \tau ^{i}_{ 22} \} (l/\mu _i U),\nonumber \\&\{ (\tau ^i_{13})' ,(\tau ^i_{ 23})', (\tau ^i_{ 33})' \} = \{ \tau ^{i}_{13} ,\tau ^{i}_{ 23}, \tau ^{i}_{ 33} \} (b/\mu _i U),\nonumber \\&C_i = c_i U/b, \quad D_i= d_i U/b. \end{aligned}$$
(39)

Here \(C_i, D_i\) are the Weissenberg numbers. We consider that \(C_i,D_i, \exp (\sigma ' t')\) are of order O(1).

5.2 First order terms for \(\tau , p\)

In this subsection we use only the dimensionless quantities, but we omit the \('\). We obtain approximate formulas of \(\tau _{ij}, p_z, p_x, p_y\) in terms of \(u^0, u, v\).

The first order terms for all components of \(\tau \) are given in “Appendix 3”. For both fluids (\(i=1,2\)) we have

$$\begin{aligned}&\tau ^i_{33}=0, \, \tau _{31}^i=u^i_z , \, \tau ^i_{32}=v^i_z, \end{aligned}$$
(40)
$$\begin{aligned}&\tau ^i_{12,y} = (u^i_y+v^i_x)_y + 2 (C_i -D_i) u^0_{z} v^i_{zy}/ \epsilon , \end{aligned}$$
(41)
$$\begin{aligned}&\tau ^i_{ {11,x}} = 2u^i_{xx} + 4 (C_i-D_i) u^0_zu^i_{zx}/ \epsilon . \end{aligned}$$
(42)

We get \(p^i_z, p^i_x\) by using the flow equations and the divergence-free condition:

$$\begin{aligned} p^i_z= & {} \tau ^i_{31,x}+\tau ^i_{32,y} = u^i_{zx}+ v^i_{zy} = 0; \end{aligned}$$
(43)
$$\begin{aligned} p^i_{x}= & {} \tau ^i_{11,x}+\tau ^1_{12,y}+\tau ^i_{13,z} / \epsilon ^2 \nonumber \\= & {} \quad 2 u^i_{xx} + 4 (C_i-D_i)u^{0}_{z}u^i_{zx} / \epsilon \nonumber \\&+\,(u^i_{y}+v^i_{x})_{y} + 2 (C_i-D_i)u^{0}_{z} v^i_{zy} / \epsilon + u^i_{zz} / \epsilon ^2 . \end{aligned}$$
(44)

We also have \( u^i_{zx} + v^i_{zy} =0, \quad u^i_{xx}+ v^i_{xy}=0, \quad { u^i_{xx} + u^i_{yy} =0} \) and from (44) it follows

$$\begin{aligned} p^i_{x} = 2(C_i-D_i)u^{0}_{z} u^i_{zx} / \epsilon + u^i_{zz} / \epsilon ^2. \end{aligned}$$
(45)

On the same way we get

$$\begin{aligned} p^i_{y} = 2(C_i-D_i)u^{0}_{z} v^i_{zx} / \epsilon + v^i_{zz} / \epsilon ^2. \end{aligned}$$
(46)

As \(u^i_{zxx}+ v^i_{zxy}=0, \,\, u^i_{zzx}+v^i_{zzy}=0\), from (45)–(46) we obtain

$$\begin{aligned} p^i_{xx} + p^i_{yy} =0. \end{aligned}$$
(47)

The form of the amplitude f is justified as follows. From (43), (45) we should have

$$\begin{aligned} p^1_{xz}= 2 ( C_1-D_1) (u^0_z u^1_{zx})_z/ \epsilon + u^1_{zzz}/ \epsilon ^2 =0. \end{aligned}$$
(48)

We prove that \(p^1_{xz} =O(\epsilon )\). For this, we recall \( \beta = O( \epsilon ^2)\) and we use the inequality

$$\begin{aligned}&max_k \{u^1_x\} \le max_k \{ k \exp (-k \alpha + kx) \} \le \\&max_k \{ k \exp (-k \alpha ) \} = { 1/(\alpha e),} \end{aligned}$$

which is verified for \(x<0\) and \(k>0\). Then

$$\begin{aligned} { (u^0_z u^1_{zx})_z/ \epsilon } =\beta O(1)/\epsilon = O(\epsilon ) , \quad ( C_1-D_1) (u^0_z u^1_{zx})_z / \epsilon =O(\epsilon ). \end{aligned}$$

The decomposition (33)–(36) is giving us \(u^1_{zzz}=0\). Then \(f(z)=\beta u^0(z)\) verifies (48) with the precision order \( O(\epsilon ) \), if \(\alpha \) is large enough.

6 The growth rate formula

In this section we use both dimensional and dimensionless quantities (the last are denoted by \(^{\prime }\)) and obtain the growth-rate formula. The flow equations and the decomposition (33)–(36) give us

$$\begin{aligned}&p^1 - \tau ^1_{11} = \frac{1}{k}(\tau ^1_{12,y} + \tau ^1_{13,z} ), \, x<x_0;\nonumber \\&p^2 - \tau ^2_{11} = \frac{-1}{k} ( \tau ^2_{12,y} + \tau ^2_{13,z} ), \, x>x_0. \end{aligned}$$
(49)

The dimensional forms of the Eqs. (89), (100) in “Appendix 3” are

$$\begin{aligned}&\tau ^i_{12,y} = \mu _i[(u^i_y + v^i_x)_y + 2(c_i-d_i) u^{0}_z v^i_{zy}],\nonumber \\&\tau ^i_{13}= \mu _i u^i_z, \,\, \tau ^i_{23}= \mu _i v^i_z, \,\,\tau ^i_{33}= 0. \end{aligned}$$
(50)

From the relations (33), (34), (37) and (49)–(50) we obtain

$$\begin{aligned} (u^1_y+v^1_x)_y= & {} -2 k^2 f(z) { E_1} \cos (ky); \nonumber \\ (u^2_y+v^2_x)_y= & {} -2 k^2 f(z) { E_2} \cos (ky);\nonumber \\ p^1 - \tau ^1_{11}= & {} \frac{1}{k} \mu _1 [(u^1_y+v^1_x)_y + 2 (c_1-d_1) u^{0}_zv^1_{zy} + u^1_{zz} ] \nonumber \\= & {} \frac{1}{k}\mu _1[ -2k^2 f { -} 2k(c_1-d_1)u^{0} f_z + f_{zz} ] { E_1} \cos (ky); \end{aligned}$$
(51)
$$\begin{aligned} p^2 - \tau ^2_{11}= & {} \frac{- 1}{k} \mu _2 [(u^2_y+v^2_x)_y + 2 (c_2-d_2) u^{0}_zv^2_{zy} + u^2_{zz} ]\nonumber \\= & {} \frac{-1}{k}\mu _2[-2k^2 f + 2 k(c_2-d_2) u^{0} f_z + f_{zz} ] { E_2} \cos (ky). \end{aligned}$$
(52)

We use (32), (51), (52) and get

$$\begin{aligned}&(G_2-G_1) \frac{<u^0>}{\sigma } - \frac{\gamma }{\sigma }<-k^2 u^0 + u^0_{zz}> +\nonumber \\&-\frac{1}{k} <-2k^2 u^0 M + 2k N(u^0_z)^2 + u^0_{zz} M > =0,\nonumber \\&M= (\mu _2+\mu _1), \,\, M'= (\mu _0+1),\nonumber \\&N = \mu _2(c_2-d_2) -\mu _1(c_1 - d_1),\nonumber \\&N' = \mu _0(C_2-D_2) -(C_1 - D_1). \end{aligned}$$
(53)

From (11)–(15) we obtain the following averages

$$\begin{aligned}&<u^0>=U,\\&<(u^0_z)^2>= 12 U^2/b^2 ,\\&<u^0_{zz}>= - 12 U/b^2, \end{aligned}$$

then (53)\(_1\) leads us to:

$$\begin{aligned} \sigma = \frac{ U k (\mu _2-\mu _1) - \gamma (k^3 b^2 /12 + k)}{ M k^2 b^2 /6 - 2k N U + M }. \end{aligned}$$
(54)

Let \(Ca= (\mu _2-\mu _1) U/ \gamma \) be the capillary number, then the relation (54) becomes

$$\begin{aligned} \sigma = \frac{ U k (\mu _2-\mu _1)(1- Ca^{-1}) - \gamma (k^3 b^2 /12)}{ M k^2 b^2 /6 - 2k N U + M }. \end{aligned}$$
(55)

The dimensional Saffman–Taylor formula is

$$\begin{aligned} \sigma _{ST} = \frac{Uk(\mu _2- \mu _1) - \gamma ( k^3 b^2/12)}{ M }. \end{aligned}$$
(56)

When \(Ca>> 1\) we have the same numerators in (55) and (56); only the denominator of (55) contains the two new terms \((M k^2b^2/6 - 2k N U)\) instead of M.

From (39), (53), (54) and (56) we get the dimensionless expressions

$$\begin{aligned}&\sigma ' = \frac{ k' (\mu _0-1) - \gamma ' (k'^3 \epsilon ^2 /12 + k')}{ k'^2 M' \epsilon ^2 /6 - 2k' N'\epsilon + M'}, \end{aligned}$$
(57)
$$\begin{aligned}&\sigma '_{ST} = \frac{ k{'}(\mu _0- 1) - \gamma ' ( k'^3 \epsilon ^2/12)}{M'}. \end{aligned}$$
(58)

Remark 1

We have

$$\begin{aligned}<\psi>= & {} {<u>/ \sigma }\nonumber \\= & {} \frac{1}{\sigma } < f(z) > \exp (-k \alpha ^+_- kx + \sigma t) \cos (ky). \end{aligned}$$
(59)

Then, near the basic interface, \(p^{0i}\) given by (28) is depending on y. But our basic pressures must depend only on x—see (9). We can partially overcome this inconsistency by using the parameter \(\alpha \). For this, we estimate the partial derivative of the perturbed interface with respect to y. As we mentioned at the end of Sect. 5.1, we consider \(\exp (\sigma ' t' ) = O(1)\). Then we have

$$\begin{aligned}&<\psi >_y \le \frac{1}{\sigma } | f(z)| F(k),\\&F(k):= k \exp ( - k \alpha )\quad { \le } \quad \frac{1}{\alpha e}. \end{aligned}$$

A large enough value of \(\alpha \) is giving us an arbitrarily small value of \(p^{0i}_y\). If \(\alpha =0\) in the decomposition (33)–(36), then for \(x \rightarrow 0\) and \(k \rightarrow \infty \) we get \( <\psi >_y, |u_x|, \, |u_y|, \, |v_x|, \, |v_y| \rightarrow \infty \). \(\square \)

Remark 2

Our model can describe the case when the air is displacing an Oldroyd-B fluid. For this, we consider (12) in the form \(G_1= \mu _1 G_2/ \mu _2\). As the displacing fluid is air, then \(\mu _1 \approx 0\) and from (12), (49), (50) we get

$$\begin{aligned} G_1 =0, \quad p^1 - \tau ^1_{11}=0. \end{aligned}$$

In this case the Laplace’s law (32) becomes

$$\begin{aligned} G_2<\psi> +<p^2 - \tau ^2_{11}> = \gamma (x_0) <\psi _{yy} + \psi _{zz}>. \end{aligned}$$
(60)

This form of the Laplace’s law (by neglecting the meniscus curvature \(\psi _{zz}\)) was used in [37], based on the additional hypothesis

$$\begin{aligned} p^{02} = G_2(x-Ut), \quad x >x_0, \end{aligned}$$

which in fact it’s not necessary. If \(\mu _1=0, c_1=d_1=0\) then the formula (54) becomes

$$\begin{aligned} \sigma = \frac{ U k \mu _2 - \gamma (k^3 b^2 /12 + k)}{ \mu _2 [ k^2 b^2 /6 +1] - 2k \mu _2(c_2-d_2) U}. \end{aligned}$$
(61)

In (39)\(_3\) we put \( \gamma '=\gamma /(\mu _2 U) \text{ instead } \text{ of } \gamma '=\gamma /(\mu _1 U)\). Moreover, \(\mu _0=1\). Then we get the dimensionless growth rate

$$\begin{aligned} \sigma '_{AIR} = \frac{ k' - \gamma ' (k'^3 \epsilon ^2 /12 + k')}{ k'^2 \epsilon ^2 /6 - 2k' (C_2-D_2) \epsilon + 1}. \end{aligned}$$
(62)

The dimensionless Saffman–Taylor formula is

$$\begin{aligned} \sigma '_{ST-AIR} = k' - \gamma ' k'^3 \epsilon ^2 /12. \end{aligned}$$
(63)

\(\square \)

7 Discussion and results

A. We consider \(C_i=D_i=0\) or \(C_i=D_i, \,\, i=1,2\), or \((C_1-D_1)= \mu _0 (C_2-D_2) \). Then the growth constant (57) becomes

$$\begin{aligned} \sigma ' = \frac{ k' (\mu _0-1) - \gamma ' (k'^3 \epsilon ^2 /12 + k')}{ (\mu _0+ 1) [ k'^2 \epsilon ^2 /6 +1] }, \end{aligned}$$
(64)

therefore \(\sigma ' < \sigma '_{ST}\). Two new terms appear in (64), compared with the formula (58):

(i) \( (\mu _0+ 1)k'^2 \epsilon ^2/6 \) in the denominator;      (ii) \( - k' \gamma ' \) in the numerator.

The dispersion curves are given in Fig. 1. The new terms in the formula (64) appear from two reasons:

(a) we did not neglect \(u_x,v_x, u_y, v_y\) with respect to \(u_z, v_z\);

(b) we used the total curvature of the perturbed interface in the Laplace law (32).

As a consequence, we obtain the following results:

(A1) Even if the surface tension\(\gamma '\)on the interface is zero, the growth constant is bounded with respect to the wave number\(k'\). Equation (64) with \(\gamma '=0\) gives us

$$\begin{aligned}&\sigma ' = R \frac{ k'}{(1 + k'^2 \epsilon ^2/6)} < R \frac{(1+ \delta ) \sqrt{3}}{ \epsilon \sqrt{2}}, \quad \forall \delta >0,\nonumber \\&\quad R = \frac{(\mu _0-1)}{(\mu _0+ 1)}. \end{aligned}$$
(65)

Indeed, we have

$$\begin{aligned}&\frac{ k'}{ 1+ k^{'2} \epsilon ^2/ 6 }< B, \,\, \forall \,\, k' \ge 0\Leftrightarrow 1- \frac{2 \epsilon ^2}{3} B^2 <0 \Leftrightarrow B > \frac{ \sqrt{3}}{ \epsilon \sqrt{2}}. \end{aligned}$$

\(\bullet \)

Fig. 1
figure 1

Dispersion curves (58) (upper) and (64) for \(\gamma ' =0.1, \epsilon =0.006, \mu _0=2\)

Full size image

(A2) If the surface tension \(\gamma '\) on the interface is zero, then the growth constant tends to zero for very large wave numbers \(k'\).

We mention here some results obtained for displacements of immiscible Newtonian fluids with very small (or zero) surface tensions on the interface, in 2D Hele-Shaw cells. In [36] (Introduction) it is stated that “One asks whether a non-zero-surface-tension model approximates the zero-surface-tension one. The answer is negative in the case of a receding fluid (see numerical evidence in [8, 30]). In the case of injection the answer is supposed to be affirmative but is still unknown”. In [21] is given a perturbation theorem for strong polynomial solutions to the zero surface tension Hele-Shaw equation driven by injection or suction, the so called Polubarinova–Galin equation. In the case of suction, by using some additional hypothesis, it is proved that the most part of the fluid will be sucked before the strong solution blows up.

The above results (A1) and (A2) are in contradiction with the Saffman–Taylor formula (58), where \(\gamma '=0\) is giving an unbounded growth constant (with respect to \(k'\)). \(\bullet \)

(A3) From (64) we get

$$\begin{aligned} \sigma ' < \frac{k' \{(\mu _0-1) - \gamma ' \}}{(\mu _0+1)(1 + k'^2 \epsilon ^2/6)} \end{aligned}$$
(66)

and it follows

$$\begin{aligned} \gamma '> \mu _0-1 >0 \Rightarrow \sigma ' \le 0. \end{aligned}$$
(67)

The growth constant is negative or zero when the surface tension \(\gamma '\) is large enough, even if the displacing fluid is less viscous (that means \(\mu _2>\mu _1\)). This is in contradiction with the Saffman–Taylor criterion derived from (56). This is an important result of our paper: the displacement instability in a 3D Hele-Shaw cell is determined not only by the ratio of the viscosities of the two fluids, but also by the surface tension on the interface. When the displacing fluid is less viscous, the sufficient condition for the almost stability (that means \( \sigma ' \le 0\)) is

$$\begin{aligned} \gamma ' > \mu _0-1. \end{aligned}$$
(68)

A quite similar result is given by the formula (19) of [24]: the growth-rate can not be positive for large enough surface tension. But in our formula (68) we have also the viscosities ratio. \(\bullet \)

A different contradiction of the Saffman and Taylor stability criterion was observed in [6, 7, 12, 16, 17, 19]. All these papers are related with the displacement of air (then \(\mu _2\) is almost zero) by a fluid with surfactant properties in a Hele-Shaw cell with preexisting surfactant layers on the plates; it is pointed out that a more viscous displacing fluid can give us an unstable air-fluid interface. The experiments and the numerical results are in good agreement—but in a 3D frame. We can consider that our result is a complementary one, compared with the above experiments with surfactants fluids and Hele-Shaw cells. We proved that for a large enough surface tension, even if the displacing fluid is less viscous, the air-fluid interface is almost stable. \(\bullet \)

B. We consider now the case when at least one of the Weissenberg numbers is not equal to zero and \((C_1-D_1) \ne \mu _0 (C_2-D_2) \).

(B1) Let \((C_i-D_i) \ne 0, \, i=1,2\). We use the notations (53) and introduce the new quantity \(\Delta \):

$$\begin{aligned} \Delta = (N')^2 -(M')^2 /6. \end{aligned}$$
(69)

In the formula (57) we must avoid the critical value

$$\begin{aligned} (N'_{cr})^2 = (M')^2 / 6. \end{aligned}$$
(70)

The denominator of the growth rate (57) is strictly positive in the range \(\Delta <0\). As a consequence, from (57) we get the following instability criterion:

$$\begin{aligned}&0< \gamma '<(\mu _0-1) \text{ and } (N') ^2< (\mu _0+1)^2 /6 \Rightarrow \nonumber \\&\sigma ' > 0 \quad \text{ for } \quad (k')^2 < 12 (\mu _0-1- \gamma ')/( \epsilon ^2 \gamma ' ). \end{aligned}$$
(71)

Moreover, when

$$\begin{aligned} (N') ^2 \le (\mu _0+1)^2/6, \end{aligned}$$

the denominator of (57) is close to zero and we get an “explosion” of the growth rate. Then a strong destabilizing effect appears, compared with the case of Newtonian displacing fluids.

We have also

$$\begin{aligned}&(\mu _0-1)<0 \text{ and } (N') ^2 < (\mu _0+1)^2 / 6 \Rightarrow \nonumber \\&\sigma ' \le 0 . \end{aligned}$$
(72)

(B2) If \(C_2-D_2 \ne 0\) and \( (C_1 - D_1) =0 \) or \(C_1=D_1=0\) we have a Stokes displacing fluid. In this case, with \( N'= [\mu _0 (C_2-D_2)] \) we obtain the above results (71)–(72).\(\bullet \)

7.1 Numerical results

We consider an Oldroyd-B fluid (\(C_2-D_2\ne 0\)) displaced by a Stokes fluid (\(C_1=D_1=0\)). In Figs. 2, 3 we compare our dispersion curves (57) and Saffman–Taylor formula (58), in the case \( \gamma '=0.1, \,\, \epsilon =0.006\), for \(\mu _0=2\) and \(\mu _0=4\). The maximum value of \(\sigma '\) given by (57) is increasing as function of \((C_2-D_2)\) until the “explosion” of the growth rates appears, when a critical value \((C_2-D_2)_{cr}\) is reached. The formula (70) gives us

$$\begin{aligned} (C_2-D_2)_{cr} = \frac{\mu _0+1}{\mu _0 \sqrt{6} }> \frac{1}{\sqrt{6} }, \quad \mu _0 = \frac{\mu _2}{\mu _1}. \end{aligned}$$
(73)

If the ratio \(\mu _0\) is increasing, then the critical numbers for which the blow-up of the growth rate appears is decreasing. For \(\mu _0 \rightarrow \infty \) we get \((C_2-D_2)_{cr} \rightarrow 1/\sqrt{6}\). This is natural: if the viscosity of the displacing fluid is decreasing to zero then the blow-up of \(\sigma '\) appears “earlier”, for smaller values of \((C_2-D_2)_{cr} \).

Fig. 2
figure 2

Dispersion curves (57) and (58) for \(\mu _0=2, \gamma ' =0.1, \epsilon =0.006, C_1=D_1=0 \)\( C_2-D_2= 0.1 \, ({\text {lower}}), 0.3, 0.4, 0.5, 0.55, 0.58, 0.58, 0.595 \, ({\text {upper}}) \)

Full size image
Fig. 3
figure 3

Dispersion curves (57) and (58) for \(\mu _0=4, \gamma ' =0.1, \epsilon =0.006, C_1=D_1=0 \)\( C_2-D_2= 0.1 \, ({\text {lower}}), 0.2, 0.3, 0.35, 0.37, 0.375 \, ({\text {upper}}) \)

Full size image
Fig. 4
figure 4

Dispersion curves (62) and (63) for \(\gamma ' =0.1, \epsilon =0.006, C_1=D_1= 0 \)\( C_2-D_2= 0.1 \, ({\text {lower}}), 0.2, 0.3, 0.35, 0.37, 0.375 \, ({\text {upper}}) \)

Full size image
Fig. 5
figure 5

Dispersion curves (62) for \(\gamma ' =0.1, \epsilon =0.006, C_2=0.375, r=D_2/C_2 \)\( r= 1 \, ({\text {lower}}), 0.7, 0.5, 0.3, 0.1, 0 \, ({\text {upper}}) \)

Full size image

In Figs. 4, 5 are plotted the growth rates (62) when air (then \(C_1=D_1=\mu _1=0\)) is displacing an Oldroyd-B fluid. In Fig. 4 we compare (62) and (63) for \(\gamma '=0.1, \quad \epsilon =0.006\). The maximum value of \(\sigma '\) is increasing in terms of \((C_2-D_2)\) until we get the blow-up of the growth rate for the critical value

$$\begin{aligned} (C_2-D_2)_{cr} = \frac{1}{\sqrt{6}} . \end{aligned}$$
(74)

In Fig. 5 are plotted the growth rates (62) when \(C_2= 0.375\) and \(r= D_2/C_2\), for r= 1, 0.7, 0.5, 0.3, 0.1, 0. The dispersion curves given in Figs. 4, 5 are quite similar with the numerical results given in Figures 1, 3 of [37].

8 Conclusions

In the last decades, some important results were established concerning the linear instability of the displacement of immiscible non-Newtonian fluids in 3D Hele-Shaw cells.

The displacement of a power-law fluid by the air in a rectilinear cell was studied by Wilson [37] and a formula of the growth rate of perturbations was given, but there is no qualitative change compared with the Saffman–Taylor result. The case of radial displacements is different and was studied in subsequent papers; the effect of the interfacial tension was highlighted.

Numerical results were obtained concerning the displacement of an Oldroyd-B fluid by the air in rectilinear cells. A blow-up of the numerical growth rate was reported, in accord with some experimental results concerning the flow of complex fluids in Hele-Shaw cells. On the other hand, most numerical methods show the existence of a critical value of the Weissenberg numbers beyond which no discrete solutions can be obtained.

In this paper we study the linear instability of the steady displacement of two Oldroyd-B fluids in a rectilinear Hele-Shaw cell. We use the Fourier decomposition (35) for the velocities (u, v) and obtain the formula (57) of the growth rate of disturbances, which presents a blow-up for some critical values of the Weissenberg numbers.

In the case of two Newtonian displacing fluids in a 3D cell, our growth rate is less than the Saffman–Taylor value, but no qualitative change appears—see Fig. 1. We prove that the flow instability is decided not only by the ratio of the viscosities, but also by the surface tension on the interface—see the relations (66)–(68). The Saffman–Taylor viscous fingering problem in rectangular geometry is studied in [24], highlighting the link between interface asymmetry and viscosity contrast. The equation (19) of [24] shows that the growth rates will not become positive if the surface tension is large enough. This is in agreement with our result (A3) in Sect. 7.

In the case of two Oldroyd-B displacing fluids we get the instability criterion (71). A strong destabilization effect appears, compared with the Newtonian displacements. The dispersion curves for Stokes (or air) displacing fluids are plotted in Figs. 2, 3, 4 and 5. Our analytical results are quite similar with numerical results already obtained in [37]. So there is strong enough evidence that the instability is due to the flow model, at least for the flow geometry considered here.