Vectorization and parallelization of 2-D wavelet lifting

Abstract

With the start of the widespread use of discrete wavelet transform in image processing, the need for its efficient implementation is becoming increasingly more important. This work presents several novel SIMD-vectorized algorithms of 2-D discrete wavelet transform, using a lifting scheme. At the beginning, a stand-alone core of an already known single-loop approach is extracted. This core is further simplified by an appropriate reorganization of operations. Furthermore, the influence of the CPU cache on a 2-D processing order is examined. Finally, SIMD-vectorizations and parallelizations of the proposed approaches are evaluated. The best of the proposed algorithms scale almost linearly with the number of threads. For all of the platforms used in the tests, these algorithms are significantly faster than other known methods, as shown in the experimental sections of the paper.

1 Introduction

The discrete wavelet transform (DWT) [13] is a mathematical tool which is suitable for the decomposition of a discrete signal into low-pass and high-pass frequency components. Such a decomposition is often performed at several scales. It is frequently used as the basis of sophisticated compression algorithms. An inverse transform has a symmetric nature compared to the forward version of the transform. For this reason, this article discusses only the forward transform.

Considering the number of arithmetic operations, a lifting scheme [9] can be an efficient way for computing the discrete wavelet transform. The transform using this scheme can be computed in several successive lifting steps. A simple approach of the lifting scheme evaluation directly follows the lifting steps. This approach suffers from the necessity of using several reads and writes of intermediate results, which slows down the computation. Anyhow, there are ways [1, 7] of lifting evaluation more efficiently.

This paper focuses on the Cohen–Daubechies–Feauveau (CDF) 9/7 wavelet [8], which is often used for image compression (e.g., JPEG 2000 or Dirac standards). Responses of this wavelet can be computed by a convolution with two FIR filters, one with 7 and the other with 9 real-valued coefficients. The transform employing such a wavelet can be computed in four successive lifting steps, as shown in [9].

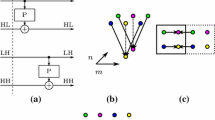
In the case of two-dimensional transform, the DWT can be realized using the separable decomposition scheme [12]. In this scheme, the coefficients are evaluated by successive horizontal and vertical 1-D filtering, resulting in four disjoint groups (LL, HL, LH and HH subbands). A naive algorithm of 2-D DWT computation directly follows the horizontal and vertical filtering loops. Unfortunately, this approach is encumbered with several accesses to intermediate results. State-of-the-art algorithms fuse the horizontal and vertical loops into a single one, which results in the single-loop approach [11].

This paper presents a SIMD-vectorized algorithm for calculation of the 2-D discrete wavelet transform through the lifting scheme. The algorithm is based on the single-loop approach introduced earlier in [11]. At the beginning, a stand-alone core of such an approach is extracted. The core is further simplified by appropriately reorganizing and merging some of the operations inside. Moreover, the complicated treatment of image borders is also omitted in this step. At this stage, the influence of the CPU cache on the 2-D processing order is studied and discussed. Furthermore, several SIMD-vectorizations of the cores are proposed here. Finally, a complete image processing using these vectorized cores is broken into independent parts and parallelized using threads. The best of the proposed algorithms scale almost linearly with the number of threads .

In present-day personal computers (PCs), general-purpose microprocessors with SIMD instruction set are almost always found. For example, in the x86 architecture, the appropriate instruction set is streaming SIMD extensions (SSE). This fourfold SIMD set fits exactly the CDF 9/7 lifting data flow graph when using the single-precision floating-point format. This paper is focused on the present computers with x86 architecture. All the methods presented in this paper are evaluated using mainstream PCs with Intel x86 CPUs. Intel Core2 Quad Q9000 running at 2.0 GHz was used. This CPU has 32 kiB of level 1 data cache and 3 MiB of level 2 shared cache (two cores share one cache unit). The results were verified on a system with AMD Opteron 2380 running at 2.5 GHz. This CPU has 64 kiB of level 1 data, 512 kiB of level 2 cache per core and 6 MiB of level 3 shared cache (all four cores share one unit). Another set of verification measurements was made on Intel Core2 Duo E7600 at 3.06 GHz (32 kiB level 1 data, 3 MiB level 2) and on AMD Athlon 64 X2 4000+ at 2.1 GHz (65 kiB level 1 data, 512 kiB level 2). Due to limited space, the details are not shown for these platforms with the exception of a summarizing table. All the algorithms below were implemented in the C language, using the SSE compiler intrinsics.¹ In all cases, a 64-bit code compiled using GCC 4.8.1 with -O3 flag was used.

The rest of the paper is organized as follows. The Sect. 2 discusses the state of the art—especially the lifting scheme, vertical and diagonal vectorizations and the 2-D single-loop approach. The Sect. 3 roposes a method eliminating the problems of complicated implementation of the original approach. The Sect. 4 studies the influence of CPU caches on the 2-D transform using the proposed method. The Sect. 5 vectorizes the proposed cores to make good use of the SIMD instruction set. In addition, the Sect. 6 illustrates how the core approach can be employed with the widely used symmetric border extension. The Sect. 7 demonstrates that the proposed approaches perform better when parallelized compared to the known ones. Finally, the Sect. 8 summarizes the paper and outlines the future work.

2 Related work

On many architectures, the lifting scheme [9, 16] is the most efficient scheme for computing the discrete wavelet transform. Any discrete wavelet transform with finite filters can be factorized into a finite sequence of $N$ pairs of predict and update convolution operators $P_n$ and $U_n$. Such a lifting factorization is not generally unique. For symmetric filters, the non-uniqueness can be exploited to maintain the symmetry of lifting steps. In detail, each predict operator $P_n$ corresponds to a filter $p_{i}^{(n)}$ and each update operator $U_n$ to a filter $u_{i}^{(n)}$.

In Daubechies and Sweldens [9] demonstrated an example of CDF 9/7 transform factorization which resulted in four lifting steps ($N=2$ pairs) plus final scaling of the coefficients. In their example, the individual lifting steps use 2-tap symmetric filters for the prediction as well as the update. During this calculation, intermediate results can be appropriately shared between neighboring pairs of coefficients. The calculation operates as an in-place algorithm, which means the DWT can be calculated without allocating auxiliary memory buffers. The resulting coefficients are interleaved in place of the input signal. The calculation of the complete CDF 9/7 DWT is depicted in Fig. 1 (coefficient scaling is omitted).

Fig. 1

Complete data flow graph of CDF 9/7 wavelet transform. The input signal is at the top, output at the bottom. The vertical (dashed) as well as the diagonal (dotted) vectorization is outlined

Originally, the problem of minimum memory implementations of the lifting scheme was adressed in [7] by Chrysafis and Ortega. However, their approach is very general and it is not focused on parallel processing. A variation of this implementation was presented by Kutil in [11], which is specifically focused on a vectorized CDF 9/7 wavelet transform. The author splits the lifting data flow graph into vertical areas (see the dashed area in Fig. 1). Due to the dependencies of individual operations, computations inside these areas cannot be parallelized. However, this approach is advantageous thanks to the locality of data required to compute output coefficients. This algorithm can be vectorized by handling the coefficients in blocks. In this paper, Kutil’s method is called vertical vectorization.

In contrast to the previous method, we have presented a diagonal vectorization (the dotted area in Fig. 1) of the algorithm described in [1]. This vectorization allows the use of SIMD processing without grouping coefficients into blocks. Unlike the vertical vectorization, which handles coefficients in blocks, our method processes pairs of coefficients one by one immediately when available. This strategy can be especially useful on systems equipped with a small CPU cache.

Many papers are focused on 2-D transforms. For instance, in Chatterjee and Brooks [3] proposed two optimizations of the 2-D transform. The first optimization interleaves the operations of the 1-D transform on multiple columns. The second optimization modifies the layout of the image data so that each sub-band is laid out contiguously in memory. Furthermore, in [4], the authors address the implementation of a 2-D transform focusing on memory hierarchy and SIMD-parallelization. Here, the pipelined computation is applied in vertical direction on subsequent rows. The abovementioned work was later extended to [6], where vectorization using SSE instructions is proposed to be used on several rows in parallel. In [5], the same authors introduced a new memory organization for 2-D transforms, which is a trade-off between the in-place and the Mallat organizations. In [5, 6], the authors vectorized a transform using an approach similar to the one described in [11]. In [14, 15], several techniques for reducing cache misses for 2-D transforms were proposed. Moreover, two techniques for avoiding address aliasing were proposed in [15].

Fig. 2

A core of the single-loop approaches. Already read/written area is shown in light/dark gray

Further in [11], the author focuses on the 2-D transform in that he merges vertical and horizontal passes into a single loop. Two nested loops (an outer vertical and an inner horizontal loop) are considered as a single loop over all pixels of the image. The author called it the single-loop approach. Specifically, two vertically vectorized loops are merged into a single one. Since the output of horizontal filtering is the input of vertical filtering, the output of the first filtering is used immediately when it is available. Kutil’s single-loop approach is based on the vertical vectorization. One step of the vertical vectorization requires two values (a pair) to perform an iteration (see the dataflow graph in Fig. 1). Thus, the algorithm needs to perform two horizontal filterings (on two consecutive rows) at once. For each row, a low-pass and a high-pass coefficient are produced, which makes $2\times 2$ values in total. The image processing by this core is outlined in Fig. 2. The vertical vectorization algorithm passes four values from one iteration to the other in horizontal direction for each row (eight in total). In vertical direction, the algorithm needs to pass four rows between iterations. The length of the coresponding prolog as well as epilog phases is $F = 4$ coefficients. The situation is illustrated in Fig. 3.

Fig. 3

Simplified view of the single-loop approach showing the prolog and epilog phases. The length $F$ of these phases is 4 (vertical vectorization) or 10 (diagonal one) coefficients

In [2], we have proposed a combination of the above-described approach with our algorithm of diagonal vectorization presented in [1]. In this case, the single-loop pass over all pixels of the image remains. In contrast to Kutil’s work, we employed the diagonal vectorization in the heart of our algorithm. The diagonal vectorization uses two values to perform one iteration. Thus, also this algorithm needs to perform two horizontal filterings at once. The kernel also has the size of $2\times 2$ values in total. In the horizontal direction, the diagonal vectorization passes four values from one iteration to the other for each row. However, the algorithm needs to pass 12 rows between iterations in the vertical direction. The lengths of the coresponding prolog and epilog phases are $F = 10$ coefficients now. Unlike the vertical vectorization, the diagonal can be simply SIMD-vectorized in the 1-D and thus also in the 2-D case. Finally, a large part of the $2\times 2$ diagonally vectorized kernel is written using SSE instructions which perform 4 operations in parallel. A drawback of this method is the three times greater memory required for row buffers.

The implementation of 2-D DWT was also studied on modern programmable graphics cards (GPUs). In this scenario, the input image has to be initially transferred from the main memory into the memory on the graphics card. Analogously, the resulting coefficients have to be transferred back. For instance, when implemented in GPU’s fragment shaders, the filter-bank scheme often outperforms lifting scheme filtering for shorter wavelets, as reported in [17]. In contrast, the authors of [18] compared the preceding approach with lifting and convolution implementation of various integer-to-integer wavelet transforms using CUDA and found the lifting scheme more advantageous.

As can be seen, the problem of efficient 2-D discrete wavelet transform implementation was widely studied. Despite this fact, we propose several improvements that lead to additional speedups.

Since this work is based on our previous work in [1] and [2], it should be explained what the difference between this work and [1, 2] is. In [1], we have presented the diagonal vectorization of the 1-D lifting scheme. This vectorization cuts a data flow diagram of the lifting scheme for the purpose of exploiting SIMD instructions easily. Moreover, in [2], we have proposed a combination of the 2-D single-loop approach [11] with our algorithm of 1-D diagonal vectorization. This combination allows a SIMD-vectorization of a newly formed 2-D image processing algorithm while preserving its minimum memory requirements. In this paper, we further develop the 2-D single-loop approach into the so-called core approach. This newly proposed approach is further tuned, vectorized and parallelized.

3 Core approach

In this section, several single-loop algorithm optimization techniques are proposed. They are applicable on vertical as well as diagonal vectorization. In all cases, these optimizations led to a speedup in comparison with the original single-loop approach.

To solve the complicated border treatment problem described above (see Fig. 3), we decided to remove these difficult parts of the border area processing code. We kept only the $2\times 2$ core of 2-D lifting, which produces a four-tuple of coefficients (LL, HL, LH and HH). This was done in both vectorizations—the vertical as well as the diagonal one. Such a modification requires two additional changes in image processing.

First, the row and column buffers must be prefilled before the core calculation. The simplest way is to fill them with zeros, which corresponds to extending the image borders with zeros.

The second change is to place a filtered input image into the enveloping frame as seen in Fig. 4. This is necessary for two reasons. First, the core can process only images with sizes which are multiples of two in both directions. Second, the core produces resulting coefficients with a lag of $F$ samples in both directions. Thus, to place the coefficients into corresponding positions as in the input image, the $2\times 2$ core needs to store the results to $(x-F,y-F)$ coordinates with respect to input coordinates $(x,y)$. Note that $F$ is equal to $4$ for the vertical and $10$ for the diagonal vectorization for the CDF 9/7 wavelet. The disadvantage of this change is a slightly higher memory consumption.

The approach just proposed above corresponds to the zero-padding signal extension. One can simply employ the proposed approach with a widely used symmetric-padding as illustrated in the Symmetric Extension section.

Fig. 4

Simplified view of implementation of the core approach showing the zero padding (light gray). The zero padding in the dotted area needs not be read because its zero effect is known in advance. An initial position of the core from Fig. 2 is shown in the top left corner

This proposed simplification allows the programmer to write a much simpler code. Another consequence is that the code has a reduced footprint in level 1 instruction cache [10] possibly allowing faster execution. Moreover, with this approach, we tried another $2\times 2$ core optimization. This 2-D core is actually composed of four 1-D cores (two in the horizontal and two in the vertical direction). With the scaling constant $\zeta$, the scaling of one pair of coefficients can be written as element-wise multiplication by a vector $[\zeta ^{-1}\;\zeta ]$. For horizontal filtering, this results in element-wise multiplication by a matrix $Z$ as in (1).

$$Z = \left[ {\begin{array}{*{20}l} {\zeta ^{{ - 1}} } & \quad{\zeta } \\ {\zeta ^{{ - 1}} } & \quad {\zeta } \\ \end{array} } \right]$$

(1)

For the vertical direction, the scaling is done with the transposed matrix $Z^{T}$. Since the output of the first two $2\times 2$ cores is the input of the second two cores and since the lifting is just a linear transform, we have merged the two coefficient scalings from the first $2\times 1$ cores into the second $1\times 2$ cores. This can be conjointly written as element-wise multiplication by (2).

$$Z \cdot Z^{T} = \left[ {\begin{array}{*{20}l} {\zeta ^{{ - 2}} } &\quad {1} \\ 1 &\quad {\zeta ^{2} } \\ \end{array} } \right]$$

(2)

The optimized cores produce exactly the same results as the original ones. A comparison of execution times is shown in Figs. 5 and  6. Both axes are shown in a logarithmic scale. Above 1 megapixel, the core approach becomes faster than the single-loop approach. It is true especially thanks to the omission of complicated prolog and epilog phases, which makes the code short and simple.

Fig. 5

Comparison of the single-loop and the core approaches on Intel CPU

Fig. 6

Comparison of the single-loop and the core approaches on AMD CPU

Table 1 Reference platforms

Table 2 Alternative platforms

All of the above approaches (naive, single-loop and core) in combination with vectorizations (vertical, diagonal) are compared in Tables 1 and  2. The naive algorithm is used as the reference one. All the measurements were performed on a 58 megapixel image. See the Sect. 1 for a detailed explanation of the platforms. The naive algorithm of 2-D DWT computation directly follows the horizontal and the vertical filtering loops. Therefore, these loops are not fused together and remain separated.

Our implementations can deal with identical (in-place processing) as well as distinct (out-of-place) source and destination memory areas. However, this paper evaluates solely the in-place variant. Since our cores are parametrized by four pointers (LL, HL, LH and HH coefficients), changing the memory layout is a trivial modification. The paper uses the interleaved layout.

4 CPU cache influence

This section studies the influence of CPU caches on a 2-D transform using the core approach. Some type of the CPU cache is present in all modern platforms. However, all the experiments presented in this paper are closely focused on the x86 architecture. For details, see [10].

In the cache hierarchy, the individual coefficients of the transform are stored inside larger and integral blocks (called cachelines). A hardware prefetcher attempts to speculatively load these blocks in advance, before they are actually required. Due to the limited size of the cache, the least recently used blocks are evicted (discarded or stored into the memory). Moreover, due to a limited cache associativity, it is also impossible to hold in the cache the blocks corresponding to arbitrary memory location at the same time.

Kutil studied [11] a performance degradation in the vertical filtering (especially when the row stride is a power of two). This degradation is a consequence of a limited set associativity of the CPU cache. Since every image pixel is visited only once in the single-loop approach as well as in the core one, such a degradation is completely avoided in these two cases. To avoid doubts about possible caching issues, we use the prime stride between subsequent rows of the image as suggested in [11].

Even though every four-tuple of pixels is visited only once, certain caching issues can be expected due to the mutual shift of read and write heads of the cores (either the vertical core or the diagonal one). This mutual shift of heads guarantees that the resulting coefficients are placed into the same $(x,y)$-coordinates as the corresponding input pixels. However, this is not the only possible memory layout. The read and write heads of the cores can point to the same or, on the contrary, to completely different memory locations. For the reason described above, several processing orders have been evaluated to find the most friendly one with respect to CPU caches [10]. In all the cases studied below, the adjacent pixels (coefficients) in image rows were stored without gaps. Note that the coefficients are represented as 32-bit floating-point numbers.

Two different fundamental orders are possible—the horizontal order (also known as a raster order) and the vertical order. Considering the limited sizes and possibly limited set associativities of CPU caches, the processing can be performed on the appropriate strips or blocks. This results in six combinations in total. Note that other (more complicated) processing orders also exist. The strip processing order (referred to as strip mining or aggregation) was used earlier, e.g., in [3, 4] or [5]. All the evaluated processing orders are depicted in Fig. 7.

Fig. 7

Processing orders evaluated with both cores (vertical and diagonal)

A subset of the results of this experiment is shown in Fig. 8 (vertical core on Intel), Fig. 9 (diagonal core on Intel), Fig. 10 (vertical core on AMD) and Fig. 11 (diagonal core on AMD). On the Intel as well as AMD platforms employed, all the horizontal orders perform in most cases almost equally well. On the other hand, all the vertical orders are clearly slower. This is the expected behavior since the hardware prefetcher can prefetch the coefficients only to an extent of one 4 KiB page.² The horizontal processing order is the fastest one for both cores—the diagonal and the vertical one. Note that these results are not generic and they are dependent on the CPU cache parameters. The measurements performed suggest that the horizontal order should be the best choice for platforms with unknown cache parameters. A summarization of the measurement for 58 megapixel images is shown in Tables 3 and  4. Note also that the implementations used are slightly different from those used in the previous section.

Fig. 8

Evaluation of processing orders. Vertical core on Intel platform

Fig. 9

Evaluation of processing orders. Diagonal core on Intel platform

Fig. 10

Evaluation of processing orders. Vertical core on AMD platform

Fig. 11

Evaluation of processing orders. Diagonal core on AMD platform

Table 3 Intel platform

Table 4 AMD platform

5 Vectorizing cores

This section describes how several vertical as well as diagonal $2\times 2$ cores are fused together to better exploit SIMD instructions.

Quite a similar fusion was developed by Kutil in [11] employing his version of vertical core (with two separated coefficient scalings). He used a different memory layout (accessing memory through packed words) and especially a different variant of the single-loop approach (buffering up to 16 whole rows). In contrast to Kutil’s work, we do not access memory through packed words at all. Instead, we access the input samples and the output coefficients through distinct pointers. Thus, our algorithm is more general and can be used for multichannel images or for data in more than two dimensions.

Fig. 12

Best-performing vectorized cores. The image is processed in blocks of the indicated size. For each block, the auxiliary buffers are updated during the computation, as indicated by arrows

A more detailed description of the individual cores follows. The best-performing vectorized cores are shown in Figure  12. Moreover, the complete image processing using the $4\times 4$ vertical core is illustrated in Fig. 14.

5.1 2 × 2 vertical core

This core is not actually vectorized. Two adjacent vertical and two subsequent adjacent horizontal iterations of the 1-D vertical vectorization were combined into one compact 2-D core. In addition, a simple optimization was performed. The coefficient scaling from the first vertical iterations bubbled through the subsequent horizontal iterations and was merged with their scalings. The result of a core optimized in this way is exactly the same as the result of a non-optimized version employing two independent scalings. Although no SIMD instructions are used in the core, some speedup can be expected thanks to the single-loop approach as well as the hardware prefetching into CPU caches. The core formed requires one four-tuple of intermediate results per one pair of coefficients in one direction. The total number of intermediate results is $2\times 4$ horizontally and $2\times 4$ vertically.

5.2 4 × 4 vertical core

This core consists of two parts. In the first part, two adjacent vertical core iterations are performed on four independent subsequent rows. This can be called $2\times 4$ vertical core iterations. The $4\times 4$ matrix of intermediate results is now transposed.³ In the second part, two adjacent core iterations are performed on four subsequent columns. Finally, the matrix of coefficients is scaled at once, as explained in the previous core description. Note that the result need not be transposed again. A similar $4\times 4$ core was also used in [11], where the packed words are accessed directly in the main memory. In his work, he have to read two $4\times 4$ blocks at once and store them separately. Figure 13 explains how the vectorization of the $4\times 4$ vertical core is actually implemented. The SSE registers are outlined by a dotted line. For simplicity, the buffers are omitted.

Fig. 13

$4\times 4$ vertical core. In $2\times 4$ blocks, all operations of the vertical vectorization are performed over SSE vector registers instead of ordinary scalar ones

5.3 8 × 2 and 2 × 8 vertical cores

The cores are composed of two $8\times 1$ SIMD-vectorized horizontal filterings followed by two $2\times 4$ adjacent vertical core iterations. In the case of the $8\times 1$ horizontal filtering, two (even and odd coefficients) whole packed words are now transformed using SIMD instructions. This actually evaluates four subsequent pairs of lifting coefficients at once. This $8\times 1$ core was also used in [11], working directly over the memory. The $2\times 4$ vertical core iterations were explained in the $4\times 4$ vertical core description. These are applied on even and odd coefficients from $8\times 1$ filterings separately. No transposition is performed in this case.

5.4 2 × 2 diagonal core

This core merges two horizontal and two vertical SIMD-vectorized 1-D diagonal cores. Thus, all operations of this core are pure SIMD instructions (with the exception of loads and stores of the coefficients). The optimization of joint scaling operations as mentioned in the description of the $2\times 2$ vertical core is also used here. This newly formed core requires three four-tuples of intermediate results per one pair of coefficients in one direction. The total number of intermediate results is therefore $2\times 12$ horizontally plus $2\times 12$ vertically.

5.5 6 × 2 and 2 × 6 diagonal cores

A series of three consecutive $2\times 2$ diagonal cores can be combined together. At the end of each vertical core iteration, three appropriate auxiliary buffers are exchanged. After three such iterations, the meanings of these buffers are again returned to the original states. It is therefore possible to omit this buffer exchange at all if the following diagonal cores are appropriately modified. Note that the three buffers represent the left, center and right input coefficients of the elementary lifting operations.

Fig. 14

Complete image processing using the $4\times 4$ core. The auxiliary buffers are shown on the left and top image edges. The light gray cores have to be evaluated before evaluating the dark gray one

The performance of the above-described cores was evaluated. In all cases, a raster scan pattern was used. The results are summarized in Figs. 15 and  16 as well as in Tables 5 and  6.

Fig. 15

Vectorized cores. Performance comparison on Intel platform

Fig. 16

Vectorized cores. Performance comparison on AMD platform

Table 5 Intel platform

Table 6 AMD platform

6 Symmetric extension

This section illustrates how the core approach can be employed with the widely used symmetric border extension.

The symmetric border extension method assumes that the input image can be recovered outside its original area by symmetric replication of boundary values. There are a few differences compared to the zero-padding extension presented in the Sect. 3. Depending on the platform, the symmetric extension can run slightly faster or slower, as shown below. This extension, too, does not require placing the input image into the enveloping frame. However, several conditional branches are placed inside of the computing core. This may or may not cause a performance degradation. Still, special prolog or epilog parts are not needed.

The best-performing $4\times 4$ core using the vertical vectorization was chosen for this purpose. Initially, this core was split into three consecutive parts. The first part loads data from the memory and places them into auxiliary variables.⁴ The subsequent second part performs the actual calculation. Finally, the last part stores the results back in the memory. The programmer should be able to fully reuse the already written code. No special prolog or epilog parts are required here.

The only change here is a simple memory addressing treatment in the first and the last parts. In the first one, the coefficient addresses pointing outside of an image region are mirrored back inside it. In a similar way, the memory accesses outside of the image in the last part are completely discarded. As shown below, these changes do not significantly affect the performance.

Fig. 17

Image processing with the symmetric border extension. In the central (blue) area, no core modification is required. The buffers are shown on the sides of the virtual image

The whole image processing using a core modified in this manner is shown in Fig. 17. The source and destination areas may (in-place processing) or may not be identical. The image must be virtually extended according to the filter length (four coefficients in the case of the CDF 9/7 wavelet). A slightly faster core with a hardcoded memory access pattern can be used in the central part of the virtually extended image. This central part is indicated by blue color in Fig. 17. In the case of the in-place processing, a code processing an area to the right and bottom of this central part have to be written carefully. Otherwise, the core might overwrite the area that will still be read.

Fig. 18

Performance of the $4\times 4$ cores using different border extensions (zero padding and symmetrization). Intel platform

Fig. 19

Performance of the $4\times 4$ cores using different border extensions (zero padding and symmetrization). AMD platform

The performance comparison with an implementation using the zero border extension is plotted in Figs. 18 and  19. The vertical vectorization is used in all of the implementations. The naive implementation is shown only for comparison. No significant difference in the performance is observed.

Table 7 Intel platform

Table 8 AMD platform

The time in nanoseconds per one pixel and speedup factors for a 58 megapixel image are given in Tables 7 and  8. Note that the implementations slightly differ from the previous ones.

7 Parallelization

This section shows the effect of parallelization of the above-discussed approaches. With the optimizations proposed in the previous sections, both of the vectorizations scale almost linearly with the number of threads.

Table 9 Performance evaluation using threads on Intel platform

Table 10 Performance evaluation using threads on AMD platform

Fig. 20

Comparison of the parallelized naive and the parallelized core approaches on Intel CPU

Fig. 21

Comparison of the parallelized naive and the parallelized core approaches on AMD CPU

The naive approach that uses horizontal and vertical 1-D transform was parallelized using multiple threads. The same was done with vectorized core single-loop approaches ($4\times 4$ vertical and $6\times 2$ diagonal, both with merged scaling). In the latter case, the image was split into several rectangular regions assigned to different threads. In the first case, this was done twice—for the horizontal and for the vertical filtering. Both multi-threaded implementation were written using the diagonal as well as the vertical vectorizations, resulting in four implementations in total. The performance comparison is shown in Figs. 20 and  21. Both axes are shown in logarithmic scale. It can be seen that the naive approach, even when parallelized, is, in fact, always slower in comparison to just the single-threaded core approach utilizing the vertical vectorization.

The original single-loop approach was not parallelized, due to its irregular nature.

Table 11 Numbers of lines required by threads for initialization (prolog) and buffering due to overlap

The parallelization of the single-loop core approach is not as straightforward as the parallelization of the naive approach. To produce correct results, each thread must process a segment (several rows) of input image before its assigned area. In this segment, no coefficients are written to output. Therefore, this phase can be understood as a prolog. Without the prolog, the threads would produce independent transforms, each with zero border extension. The lengths of prologs for vertical and diagonal vectorization are shown in Table 11. The above fact leads to overlapping computation and thus mutual thread synchronization (using barriers). Moreover, no subsequent thread can start producing output coefficients immediately at the segment beginning. Otherwise, it would lead to overwriting a part of the segment which is assigned to the corresponding previous thread (a race condition). To resolve this issue, the initial part (several first rows) of each thread output is buffered and written out after the completion of the calculation of the whole thread assigned area. This leads to a second barrier synchronization. The sizes of buffers are shown in Table 11. The latter of the described solutions (buffering of output) is not necessary if the output is placed into a distinct memory area. On the other hand, using distinct memory areas can lead to flooding the CPU cache with two memory regions. The synchronization happens at certain points (not each row), which are identified by arrows in Fig. 22.

Fig. 22

The synchronization barriers identified by arrows. They are necessary only in conjunction with the in-place transform

Finally, a summarizing comparison of parallelizations is shown in Tables 9 and  10. The measurements were performed on a 58-megapixel image. The single-threaded algorithm is used as a reference one. Using the core approach, both the vectorizations scale almost linearly with the number of threads.

In summary, our method is very suitable for parallelization and vectorization. In contrast to [11], the size of auxiliary memory buffers does not grow with increasing core size (for vertical vectorization, 4 rows for $2\times 2$ as well as $4\times 4$ core). Moreover, the core approach can SIMD-vectorize even $2\times 2$ core (diagonal vectorization). Further, as opposed to [11], our method can handle arbitrary memory layouts and process the data in-place as well as out-of-place; also, in case of the symmetric extension, we have radically simplified the border treatment and the overhead is now completely hidden in memory latencies. Finally, our approach can be easily vectorized as well as parallelized as opposed to [11], where parallelization using threads is not considered at all.

8 Conclusion

We have presented a novel approach to the 2-D wavelet lifting scheme, reaching speedups of at least $10\times$ on AMD and at least $5\times$ on Intel platform for large data. Initially, this approach was based on the fusion of the single-loop and vertical as well as diagonal vectorization approaches. We have proposed a simplification which drops the complicated prolog and epilog phases. This allowed us to easily merge scalings of two subsequent filterings into a single one. The proposed core approach is simple to implement in comparison with the classical single-loop approach. With increasing image size (above 1 megapixel), this approach becomes faster compared to the original one. We have also discussed a CPU-cache-friendly processing order. For the memory layout that we used, the horizontal processing order shows the best performance in most cases. Furthermore, we have vectorized newly formed cores to exploit the advantages of the SIMD instruction set. In addition, we have illustrated how the proposed core approach can be employed with the widely used symmetric border extension. Finally, we parallelized these vectorized approaches using threads and achieved a speedup of nearly $40\times$ on AMD and $15\times$ on Intel, using $4$ threads. The proposed approach scales almost linearly with the number of threads.

All the methods compared in this paper were evaluated using ordinary personal computers with x86 CPUs (Intel Core2 Quad, AMD Opteron, Intel Core2 Duo, AMD Athlon 64 X2).

Further work will focus on exploring the behavior of proposed approaches on other architectures (vector processors, many-core systems) or with other wavelets (different lifting factorizations).