Binary polyp-size classification based on deep-learned spatial information

Abstract

Purpose

The size information of detected polyps is an essential factor for diagnosis in colon cancer screening. For example, adenomas and sessile serrated polyps that are $\ge 10$ mm are considered advanced, and shorter surveillance intervals are recommended for smaller polyps. However, sometimes the subjective estimations of endoscopists are incorrect and overestimate the sizes. To circumvent these difficulties, we developed a method for automatic binary polyp-size classification between two polyp sizes: from 1 to 9 mm and $\ge 10$ mm.

Method

We introduce a binary polyp-size classification method that estimates a polyp’s three-dimensional spatial information. This estimation is comprised of polyp localisation and depth estimation. The combination of location and depth information expresses a polyp’s three-dimensional shape. In experiments, we quantitatively and qualitatively evaluate the proposed method using 787 polyps of both protruded and flat types.

Results

The proposed method’s best classification accuracy outperformed the fine-tuned state-of-the-art image classification methods. Post-processing of sequential voting increased the classification accuracy and achieved classification accuracy of 0.81 and 0.88 for polyps ranging from 1 to 9 mm and others that are $\ge 10$ mm. Qualitative analysis revealed the importance of polyp localisation even in polyp-size classification.

Conclusions

We developed a binary polyp-size classification method by utilising the estimated three-dimensional shape of a polyp. Experiments demonstrated accurate classification for both protruded- and flat-type polyps, even though the flat type have ambiguous boundary between a polyp and colon wall.

Introduction

The size information of detected polyps is an essential factor for diagnosis in colon cancer screening [1]. The American [2] and European [3] guidelines for colonoscopy surveillance define what treatments should be chosen after a physician finds polyps with respect to their size estimations.

Fig. 1

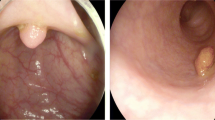
Difficulty of polyp-size estimation from a colonoscopic image: a Loss of three-dimensional information by projection to an image plane: Appearance size highly depends on distance from image plane $\pi$ to an object. In (a), ${\varvec{c}}$ denotes optical centre. b Examples of appearance sizes of polyps: Polyps of different sizes (2, 6, and 10 mm) can appear to be almost identical. c Gross morphology of polyps

In both definitions, the size determination of whether a polyp size is equalling or exceeding 10 mm, or not is critical. Adenomas and sessile serrated polyps of 10 mm are considered advanced, and shorter surveillance intervals are recommended for smaller polyps [1, 2]. The determination of polyp size is based on subjective estimation by endoscopists rather than objective measurements by pathologists. However, subjective estimation tends to be overestimation, where small polyps are mistakenly considered 10 mm or larger [4].

Subjective estimations are essentially an ill-posed problem, as depicted in Figs. 1a and b, since the two-dimensional endoscopic view fails to completely capture all of the three-dimensional information. Furthermore, several kinds of gross morphology shown in Fig. 1c complicate estimations. To circumvent this difficulty, subjective observations with a device have been proposed [5,6,7]. Rex et al. measured polyp size by comparing the size of open forceps [5]. Hyun et al. [6] and Kaz et al. [7] developed graduated measuring devices, which have scale marks of 5-mm intervals to measure a polyp in vivo. Hyun et al. achieved classification accuracy of 0.93, 0.16 and 0.58 with their graduated device for polyps ranging 0–5 mm, 6–9 mm and $\ge$10 mm, respectively [7]. Even if endoscopists use a device, there is a terminal digit preference bias for aesthetically pleasing numbers, where endoscopists are apt to determine in such increments as 5, 10, 15, 20, $\dots$ mm [8]. As a device-free method, Itoh et al. proposed image-based binary polyp-size classification using convolutional neural networks (CNNs), and achieved classification accuracy of 0.79 for 50 protruded polyps [9].

In this paper, instead of polyp-size estimation, we tackle binary polyp-size classification between polyps of 1-9 mm and those of $\ge 10$ mm. This approach bases on the following two reasons. The first reason is that the determination of whether a polyp size is equalling and exceeding 10 mm, or not is critical for diagnosis in colon cancer screening. The second one is that precise polyp-size estimation under the ill-posed condition is still too challenging at this point. Therefore, we propose a new polyp-size classification method as a natural extension of our previous method [9]. In this extended method, we introduce new techniques: model-based precise depth estimation and polyp localisation. We used the unsupervised estimation of relative depth in previous work, which has no physical length. Instead of relative depth, we adopted a depth with a physical length obtained from a model-based RGBD-GAN that achieved accurate depth estimation with an average error less than 1 mm [10]. We combine the depth and polyp location information to express the three-dimensional shape of a polyp with physical length for the classification.

Methods

Single-shot classification

This paper assumes that a three-channel colonoscopic image ${\mathcal {X}} \in {\mathbb {R}}^{H \times W \times 3}$ with height H and width W expresses only one polyp, and refer to ${\mathcal {X}}$ as a polyp image.

The straightforward estimation of polyp size s from an image appearance of $\mathcal {X}$ is expressed with a parameter vector ${\varvec{\theta }}$ as a function $f({\mathcal {X}}; {\varvec{\theta }})=s$. As the regression problem for pairs of polyp image ${\mathcal {X}}_i$ and ground-truth size $s^{*}_i$ of each polyp in ${\mathcal {X}}_i$ for index $i=1,2,\dots , N$, we obtain the optimised parameter vector $\hat{{\varvec{\theta }}}$ by

$$\begin{aligned} \mathrm {arg} \ \underset{{\varvec{\theta }}}{\mathrm {min}} \ \underset{i}{{\mathbb {E}}} \Bigl [ \Vert f({\mathcal {X}}_i; {\varvec{\theta }}) - s^{*}_i \Vert _2^2 \Bigr ], \end{aligned}$$

(1)

where $\Vert \cdot \Vert _2$ is the Euclidean norm. However, an obtained function $f({\mathcal {X}}; \hat{{\varvec{\theta }}})$ does not work for an unseen image ${\mathcal {X}} \notin \{ {\mathcal {X}}_i \}_{i=1}^N$ due to the ill-posed condition as shown in Figs. 1a and b.

To circumvent the ill-posed condition, depth information is essential. Previous work [9] estimated a depth image ${\varvec{D}} \in {\mathbb {R}}^{H \times W}$ from ${\mathcal {X}}$ by an unsupervised method. By expressing all the parameters for depth estimation as ${\varvec{\theta }}_{{D}}$, we have a depth-estimation function

$$\begin{aligned} g({\mathcal {X}}; {\varvec{\theta }}_{{D}}) = {\varvec{D}}. \end{aligned}$$

(2)

Furthermore, we relaxed polyp-size estimation to the binary polyp-size classification. In this classification, we use category labels 0 and 1 to express the 1–9 mm and $\ge 10$ mm polyps, respectively. By using binary cross-entropy ${\mathscr {H}}$, optimised depth estimation $g({\mathcal {X}}_i ; \hat{{\varvec{\theta }}}_D)={\varvec{D}}_i$, and ground truth $t_i^{*}$, we define a parameter optimisation as

$$\begin{aligned}&\arg \ \underset{{\varvec{\theta }}}{\min } \ {\mathscr {H}}\bigl ( t_{i}^{*}, f({\mathcal {X}}_i, {\varvec{D}}_i; {\varvec{\theta }}) \bigr ), \end{aligned}$$

(3)

$$\begin{aligned}&\quad = \arg \, \underset{{\varvec{\theta }}}{\min } \, \underset{i}{{\mathbb {E}}} \left[ t_i^{*} \log \biggl ( \frac{1}{f({\mathcal {X}}_i, {\varvec{D}}_i; {\varvec{\theta }}) } \biggr )\right. \nonumber \\&\left. \quad \quad + (1 - t_i^{*}) \log \biggl ( \frac{1}{ 1 - f({\mathcal {X}}_i, {\varvec{D}}_i; {\varvec{\theta }}) } \biggr ) \right] . \end{aligned}$$

(4)

By thresholding a probability $f({\mathcal {X}}, {\varvec{D}};\hat{{\varvec{\theta }}})$ with $\xi$, we obtain a category label for input . To solve Eq. (4), we used RGB-D CNN [9]. However, this CNN must learn how to detect polyp locations from training images without annotations of polyp locations.

In our method, we estimate a polyp-location map ${\varvec{W}} \in \{ 0, 1 \}^{H \times W}$, whose elements of 0 and 1 express polyp’s in-existence and existence, respectively. By expressing all the parameters for a polyp detection as ${\varvec{\theta }}_{{L}}$, we have a polyp detector $h({\mathcal {X}}; {\varvec{\theta }}_{{L}})$ that outputs ${\varvec{W}}$ and a likelihood $p \in [0, 1]$ for a polyp existence. Using a detector with an optmised parameter vector $\hat{{\varvec{\theta }}}_L$, we define polyp localisation by

$$\begin{aligned} {\mathscr {G}} (h({\mathcal {X}}; \hat{{\varvec{\theta }}}_{{L}})) = {\varvec{W}}, \ \mathrm {if} \ p > \tau , \end{aligned}$$

(5)

where $\tau$ is a criterion. We then integrate ${\varvec{W}}$ to ${\varvec{D}}$, since the combination of the depth and location information expresses a polyp’s three-dimensional shape. By expressing a localised-depth image ${\varvec{D}}_i \odot {\varvec{W}}_i$ with the Hadamard product $\odot$ for ${\mathcal {X}}_i$, we search the solution $\hat{{\varvec{\theta }}}$ of

$$\begin{aligned}{} & {} \arg \ \underset{{\varvec{\theta }}}{\min } \ {\mathscr {H}} \bigl ( t_{i}^{*}, f({\varvec{D}}_i \odot {\varvec{W}}_i; {\varvec{\theta }}) \bigr ) \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \ \ \ \ \ \ \ \ \ \ \ \ \ = \arg \, \underset{{\varvec{\theta }}}{\min } \, \underset{i}{{\mathbb {E}}} \Biggl [ t_i^{*} \log \biggl ( \frac{1}{f({\varvec{D}}_i \odot {\varvec{W}}_i ; {\varvec{\theta }}) } \biggr ) \Biggr . \nonumber \\ \Biggl .{} & {} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \quad \quad + (1 - t_i^{*}) \log \biggl ( \frac{1}{ 1 - f({\varvec{D}}_i \odot {\varvec{W}}_i; {\varvec{\theta }}) } \biggr ) \Biggr ] .\qquad \end{aligned}$$

(7)

We then defined binary classification with a criterion $\xi$ as

$$\begin{aligned} {\mathscr {F}}\bigl ( f({\varvec{D}} \odot {\varvec{W}}; \hat{{\varvec{\theta }}}) \bigr ) = {\left\{ \begin{array}{ll} 1, &{} \text {if} \ f({\varvec{D}} \odot {\varvec{W}}; \hat{{\varvec{\theta }}}) > \xi , \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(8)

Figure 2a illustrates the proposed method. For the practical construction of $g({\mathcal {X}}; \hat{{\varvec{\theta }}}_D), h({\mathcal {X}}; \hat{{\varvec{\theta }}}_L), f({\varvec{D}} \odot {\varvec{W}}; \hat{{\varvec{\theta }}})$ , we optimise RGBD-GAN [10], YOLOv3 [11], and a three-layer CNN, respectively. We explain how to optimise them in Sect. 4: Optimisations.

Fig. 2

Proposed binary polyp-size classification methods: a Single-shot classification; b Sequential-voting classification; In (a), the top and bottom numbers in images and square boxes express the spatial resolutions and channel sizes, respectively

Sequential-voting classification

We propose a voting-based classification shown in Fig. 2b for a short colonoscopic video. Single-shot classification often suffers from illumination changes, motions, colour blurs, and so on. To achieve a robust polyp-size classification, we use sequential polyp images ${\mathcal {X}}_i, i=1,2, \dots , M$ extracted from a short colonoscopic video. Using $\hat{{\varvec{\theta }}}$ obtained from Eq. (7), we obtain a set $\{ p_i \}_{i=1}^M$ of probabilities $p_i = f( {\varvec{D}}_i \odot {\varvec{W}}_i; \hat{{\varvec{\theta }}})$, $i=1,2, \dots , M$ for each ${\mathcal {X}}_i$. Let ${\varvec{v}} \in \{0, 1\}^{M}$ be a binary vector defined by

$$\begin{aligned} {\varvec{v}}= (v_i), \ \ v_i = {\left\{ \begin{array}{ll} 1, &{} \text {if} \ p_i > \xi , \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(9)

With ${\varvec{v}}$ and $L_0$ norm $\Vert \cdot \Vert _0$, we classify an input video as

$$\begin{aligned} f_v({\varvec{v}}) = {\left\{ \begin{array}{ll} 1, &{} \Vert {\varvec{v}} \Vert _0 \ge \frac{M}{2},\\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(10)

Dataset construction

Dataset for depth estimation

To optimise RGBD-GAN, we select the real-and-virtual colonoscopy dataset [10]. This dataset offers 9189 colonoscopic images and 8085 RGB-D virtual colonoscopic images. These colonoscopic images are extracted from colonoscopic videos of 30 patients at five frames per second. In the video collection, we used a high-definition colonoscope (CF-HQ290ZI; Olympus). The virtual colonoscopic images are generated from CT colonography data of seven patients with CT colonography software [12]. For the generation of the virtual depth image, pixel values are set to a range of [0, 255] for distances in the range of [0, 10] cm.

Table 1 Summary of number of colonoscopic images in training, validation, and test data: Number in parentheses expresses the number of polyps

Fig. 3

Examples of training dataset for binary polyp-size classification: As pre-processing, we generated localised-depth images using our trained YOLOv3 and RGBD-GAN

Fig. 4

Size and gross-morphology distributions in our dataset: a Gross-morphology distribution of all data; b Size distribution of all data; c Size distribution of training data; d Size distribution of validation data; e Size distribution of test data

Dataset for polyp localisation

To optimise YOLOv3, we selected 67,824 polyp images and 1028 non-polyp images collected at five hospitals [13]. Each polyp image includes one polyp of protruded or flat type, which has a bounding box annotation of its location. Each non-polyp image includes one of eight typical hard negative elements, such as bubbles, halation, droplets, ..., with a bounding box annotation.

To evaluate localisation accuracy, we used publicly available SUN database [14]. This database offers 49,136 images of 100 different polyps, which are protruded- and flat-type polyps, and 109,554 images of no-polyp scenes with their location annotation.

Dataset for polyp-size classification

We constructed a polyp-size dataset. First, we collected colonoscopic videos during typical colonoscopies at two hospitals using a colonoscope (CF-HQ290ZI; Olympus) and a video recorder (IMH-10; Olympus) with Institutional Review Board approval. Expert endoscopists with experience of over 5000 colonoscopy cases measured polyps by comparing the tip of an inserted sheath and the polyp diameters. We used sheaths of polypectomy snares (snare master; Olympus, captivator; Boston Scientific), whose tips have diameters of 2.6 and 2.4 mm. To reduce personal bias in their measurements, two or three expert endoscopists checked a polyp’s size and reached a consensus. Endoscopists annotated the polyp-existing frames with labels of gross morphology (Ip, Isp, Is, and IIa) and size (1, 2, 3, $\dots$, 14, 15 mm) with an annotation tool [15].

Next, we divided these videos into training, validation, and test data without duplication of polyp cases. We extracted still images from these data at 30 frames per second (fps). We removed such inappropriate images as motion blurred, colour blurred, bubbles, out-of-focus, and successive images with a similar appearance from only the training data. The test dataset has 84 polyps, each of which has an average of 185 successive images.

Finally, we generated depth and localised-depth images for the all images by using RGBD-GAN and YOLOv3. Table 1 summarises the number of images in the constructed dataset. Figure 3 shows examples of the training data. Figure 4 shows the image-number-based distributions of size and gross morphology in our dataset.

Fig. 5

Architecture for depth estimation and polyp localisation: a RGBD-GAN [10] for depth estimation; b YOLOv3 [11] for polyp detection; In (a) and (b), numbers above and below square boxes express the spatial resolutions and channel sizes, respectively. As the exception, a number below a residual unit in (b) expresses the number of residual units

Optimisations

${\varvec{\theta }}_{{\mathcal {D}}}$ for depth estimation

For the domains ${\mathcal {R}}_{\mathrm {RGB}}$ and ${\mathcal {V}}_{\mathrm {RGBD}}$ of RGB colonoscopic and RGB-D virtual colonoscopic images, respectively, we define $F: {\mathcal {R}}_{\mathrm {RGB}} \rightarrow {\mathcal {V}}_{\mathrm {RGBD}}$ and $G: {\mathcal {V}}_{\mathrm {RGBD}} \rightarrow {\mathcal {R}}_{\mathrm {RGB}}$. For the generation of RGB channel of these virtual images, we assume the Lambertian-reflection model. For given images ${\mathcal {X}}_i \in {\mathcal {R}}_{\mathrm {RGB}}$ and ${\mathcal {Y}}_j \in {\mathcal {V}}_{\mathrm {RGBD}}$ for $i=1, 2, \dots , n_{{\mathcal {R}}}$ and $j=1, 2, \dots , n_{{\mathcal {V}}}$, we introduce discriminators $D_{{\mathcal {V}}}$ and $D_{{\mathcal {R}}}$, which distinguish ${\mathcal {Y}}_j$ from $\{ F({\mathcal {X}}_i) \}_{i=1}^{n_{{\mathcal {R}}}}$, and ${\mathcal {X}}_i$ from $\{ G({\mathcal {Y}}_j) \}_{i=1}^{n_{{\mathcal {V}}}}$, respectively. We then obtain an object function

$$\begin{aligned} {\mathscr {L}}(G, F, D_{{\mathcal {V}}}, D_{{\mathcal {R}}})= & {} {\mathscr {L}}_{\mathrm {GAN}}(F, D_{{\mathcal {V}}},{\mathcal {V}}_{\mathrm {RGBD}}, {\mathcal {R}}_{\mathrm {RGB}}) \nonumber \\&+ \, {\mathscr {L}}_{\mathrm {GAN}}(G, D_{{\mathcal {R}}},{\mathcal {R}}_{\mathrm {RGB}}, {\mathcal {V}}_{\mathrm {RGBD}})\nonumber \\&+\, \lambda {\mathscr {L}}_{\mathrm {cyc}}(F,G), \end{aligned}$$

(11)

where $\lambda$ controls the importance of adversarial losses ${\mathscr {L}}_{\mathrm {GAN}}$ and a cycle-consistency loss ${\mathscr {L}}_{\mathrm {cyc}}$ [10]. By expressing the all parameters of F and G as ${\varvec{\theta }}_D$ and ${\varvec{\theta }}_R$, respectively, we search $\hat{{\varvec{\theta }}}_D$ by solving the min–max problem

$$\begin{aligned} \mathrm {arg} \ \underset{{\varvec{\theta }}_D, {\varvec{\theta }}_R}{\mathrm {min}} \ \underset{D_{{\mathcal {V}}},D_{{\mathcal {R}}}}{\mathrm {max}} {\mathscr {L}}(F, G, D_{{\mathcal {V}}}, D_{{\mathcal {R}}}). \end{aligned}$$

(12)

With the obtained $\hat{{\varvec{\theta }}}_D$, we estimate depth image ${\varvec{D}}$ as the fourth channel of $\hat{{\mathcal {Y}}} = F({\mathcal {X}})$ [10].

Figure 5a shows the architecture of F for depth estimation. By using training data described in Sect. 3.1: Dataset of depth estimation, we optimised RGBD-GAN with Adam of base learning $lr=0.002$, minibatch size of 64, leaky ReLU coefficient $\alpha =0.2$, $\lambda =10$, and data argumentation of random flips for 300 epochs.

${\varvec{\theta }}_{{L}}$ for polyp localisation

We briefly summarise the optimisation of YOLOv3 [11], since YOLO has a few versions and partial updates presented by different papers.

As shown in Fig. 5b, YOLOv3 comprises two parts: backbone and head. The backbone part is Darknet-53 which extracts image features from input. The head part outputs predictions for three scales. In the i-th scale, YOLOv3 divides an input image ${\mathcal {X}}$ into $S_i \times S_i$ regions as cells and predicts B candidates of an object’s location for each cell.

YOLOv3 uses bounding box priors. The k-th bounding box prior of the i-th scale has predefined width $A_{w_{ik}}$ and height $A_{w_{ik}}$. Furthermore, YOLOv3 adopts gird-cell coordinate $(c_{x_{ij}}, c_{y_{ij}})$ in the divided ${\mathcal {X}}$. The origin in grid-cell coordinate is the left-top corner of ${\mathcal {X}}$, and $(c_{x_{ij}}, c_{y_{ij}})$ represents grid-corner indices for the j-th cell in the i-th scale. YOLOv3 predicts $t_{x_{ijk}}, t_{y_{ijk}}, t_{w_{ijk}}, t_{h_{ijk}}$, and outputs a centre $(b_{x_{ijk}}, b_{y_{ijk}})$, width $b_{w_{ijk}}$ and height $b_{h_{ijk}}$ of a location for an object by

$$\begin{aligned} b_{x_{ijk}}= & {} \sigma (t_{x_{ijk}}) +c_{x_{ij}}, \end{aligned}$$

(13)

$$\begin{aligned} b_{y_{ijk}}= & {} \sigma (t_{y_{ijk}}) + c_{y_{ij}}, \end{aligned}$$

(14)

$$\begin{aligned} b_{w_{ijk}}= & {} A_{w_{ik}} \mathrm {e}^{t_{w_{ijk}}},\end{aligned}$$

(15)

$$\begin{aligned} b_{h_{ijk}}= & {} A_{h_{ik}} \mathrm {e}^{t_{h_{ijk}}}, \end{aligned}$$

(16)

where $\sigma (\cdot )$ is a sigmoid function. Furthermore, YOLOv3 predicts an objectness score $\sigma (t_{o_{ijk}})$ and category scores $\sigma (t_{c_{ijk1}})$, $\sigma (t_{c_{ijk2}})$, $\dots \sigma (t_{c_{ijkC}})$ for the k-th bounding box of the j-th cell in the i-th scale. Therefore, for the i-th scale, YOLOv3 outputs a tensor ${\mathcal {T}}_{i} \in {\mathbb {R}}^{S_i \times S_i \times (B(4+1+C)))}$. As the outputs of $h({\mathcal {X}}; {\varvec{\theta }}_L)$, we obtain ${\varvec{W}}$ by Eqs. (16)-(19) and $p=\sigma (t_{c_{ijk1}})$.

YOLOv3 ignores low-confident predictions by thresholding object scores with $\eta$. For each object, YOLOv3 finds the best localisation by computing IoU (Intersection over Union) $S \cap S^{*} / S \cup S^{*}$ between a predicted region S and ground truth $S^{*}$. We set weights $\mathbbm {1}^{\mathrm {obj}}_{ijk}=1$ and $\mathbbm {1}^{\mathrm {obj}}_{ijk} =0$ for the best localisation and the others, respectively, for each object. Furthermore, we set $\mathbbm {1}^{\mathrm {non}}_{ijk}=1 - \mathbbm {1}^{\mathrm {obj}}_{ijk}$. By using ground truth $t_{x_{ijk}}^{*}$, $t_{y_{ijk}}^{*}$, $t_{w_{ijk}}^{*}$, $t_{h_{ijk}}^{*}$, $t_{c_{ijk1}}^{*}$, $t_{c_{ijk2}}^{*}$, $\dots t_{c_{ijkC}}^{*}$, for ${\mathcal {X}}$, we have a loss functional by

$$\begin{aligned}&{\mathscr {L}}( h({\mathcal {X}}; {{\varvec{\theta }}_{L}} )) = \lambda _{\mathrm {box}} \sum _{i=1}^3 \sum _{j=1}^{S_i^2} \sum _{k=1}^{B} \mathbbm {1}^{\mathrm {obj}}_{ijk} \Bigl ( | t_{x_{ijk}} - t_{x_{ijk}}^{*}|^2 + |t_{y_{ijk}} - t_{y_{ijk}}^{*}|^2 \Bigr . \Biggr . \nonumber \\ \Bigl .&{} \ \ \ + |t_w - t_w^{*}|^2 +|t_h - t_h^{*}|^2 \Bigr ) - \sum _{i=1}^3 \sum _{j=1}^{S_i^2} \sum _{k=1}^{B} \Bigl ( \mathbbm {1}^{\mathrm {obj}}_{ijk} \log \bigl ( \sigma (t_{o_{ijk}}) \bigr ) \Bigr . \nonumber \\ \Biggl . \Bigl .&{} \ \ \ + \mathbbm {1}^{\mathrm {non}}_{ijk} \log \bigl (1 - \sigma (t_{o_{ijk}}) \bigr ) \Bigr )\nonumber \\&\ \ \ - \sum _{i=1}^3 \sum _{j=1}^{S_i^2} \sum _{k=1}^{B} \sum _{l=1}^{C} \mathbbm {1}^{\mathrm {obj}}_{ijk} \Bigl ( t_{c_{ijkl}}^{*} \log \bigl (\sigma (t_{c_{ijkl}}) \bigr ) \Bigr . \Biggr . \nonumber \\ \Biggl . \Bigl .&{} \ \ \ + (1 - t_{c_{ijkl}}^{*}) \log \bigl (1 - \sigma (t_{c_{ijkl}}) \bigr ) \Bigr ). \end{aligned}$$

(17)

By using a training set $\{ {\mathcal {X}}_m \}_{m=1}^N$, we search $\hat{{\varvec{\theta }}}_{L}$ by solving

$$\begin{aligned} \mathrm {arg} \ \underset{{\varvec{\theta }}_{L}}{\mathrm {min}} \ \underset{m}{{\mathbb {E}}} \Bigl [ {\mathscr {L}}(h({\mathcal {X}}_m ; {{\varvec{\theta }}_{{L}}}) ) \Bigr ]. \end{aligned}$$

(18)

To optimise ${\varvec{\theta }}_{{L}}$, we used 68,852 images described in Sect. 3.2: Dataset for polyp localisation. We set $C=9$ and $\eta =0.6$. As shown in Fig. 6b, we used $S_1=6, S_2=12, S_3=24$ and $B=3$. We used the same bounding-box priors as the original [11]. Setting $\alpha =0.1$ for all leaky ReLU and $\lambda _{\mathrm {box}}=1.0$ for Eq. (17), we applied fine-tuning to the weights of the pre-trained backbone [11] with the stochastic gradient descent and the same data augmentations of Ref. [13]. With a minibatch size of 64, we used a burn-in of 1000 iterations and obtained a learning rate of $lr = 1.0 \times 10^{-4}$. We then started a model training of 70,000 iterations where lr was multiplied with 0.10 at 56,000 and 63,000 iterations.

Fig. 6

Evaluation of polyp localisation with SUN colonoscopy video database: a ROC curves with IoU thresholding $\rho$ for all images in the database; b Mean IoU for score thresholding $\tau$ for all images in the database

${\varvec{\theta }}$ for polyp-size classification

To solve Eq. (7), we optimised the three-convolution CNN shown in Fig. 2a with the training data described in Sect. 3.3: Dataset for polyp-size classification. Setting leaky ReLU coefficient $\alpha =0.3$ and dropout ratio 0.2, we used He’s weight initialisation, Adam of a learning rate $lr=1.0 \times 10^{-5}$, and weighted binary cross-entropy loss for 150 epochs. As the data argumentation, we used random shift, rotation, horizontal and vertical flips, and a small perturbation of the pixel values. In this optimisation, we multiplied 0.1 to lr at 15 epochs. Based on the evaluations with the validation data, we selected the early stopping model at 25 epochs.

Experimental evaluations

Evaluation of localisation

First, we evaluated the accuracy of polyp detection and localisation, by using the SUN database described in Sect. 3.2: Dataset for polyp localisation. We detected polyps in these images using YOLOv3. Although it outputs several predictions for input, we selected only one output of the highest likelihood for input and applied thresholding in Eq. (5). Furthermore, we added IoU thresholding in this evaluation. If IoU is less than criterion $\rho \in [0, 1]$, we reject the detection results. We defined sensitivity and specificity as the ratios of the correctly detected polyp images and the correctly undetected non-polyp images, respectively. Figure 6a shows the ROC curves for the criteria of likelihood $\tau = 0.025, 0.050, \dots , 0.975$ and IoU $\rho =0.0, 0.1, 0.2, \dots , 0.5$, where area under curve is 0.98 for $\rho =0.0$. Figure 6b shows the mean IoU.

Fig. 7

Quantitative evaluation of proposed method: a Comparative evaluation among proposed method, Xception, InceptionResNet-v2, NASNet-A, and BseNet for single-shot classification; b Comparison between single-shot and sequential voting classifications

Fig. 8

Classification accuracy with respect to sizes: a InceptionResNet-v2 for RGB images; b Proposed method as single-shot classification; c Proposed method as sequential-voting classification

Fig. 9

Examples of correctly classified images: Each is given by pair of input RGB and localised-depth images

Evaluation of single-shot classification

Next, we evaluated the accuracy of the single-shot classification method by comparing the proposed and CNN architectures. As comparison methods, we adopted NASNet-A [16], InceptionResNet-v2 [17], and Xception [18], which achieved the best-, second-, and third-ranked top-1 image classification accuracies in the ImageNet dataset. As the depth-based method, we added to this comparison our previous work: BseNet [9]. In this evaluation, we used images described in Sect. 3.3: Dataset for polyp-size classification.

For NASNet-A, InceptionResNet-v2, and Xception, we applied fine-tuning to their pre-trained models of ImageNet using the colonoscopic images of our training data. Just for InceptionResNet-v2, we applied fine-tuning using the depth images in our training data. In such fine-tuning, we used only the feature extraction part of each architecture and added a classification part, which consists of global average pooling and a fully connected layer. For the optimisation of BseNet, we used the colonoscopic and depth images in our training data.

Fig. 10

Typical comparison between correctly and incorrectly classified cases in sequential-voting classification: Blue rectangles depict predicted location of a polyp. Yellow rectangles depict correct location of a polyp in case of incorrect localisation. Two cases show different flat polyps of 11 mm

Fig. 11

Distributions of probabilities in correctly and incorrectly classified cases in sequential-voting classification: a and b are distributions for correct and incorrect classified cases in Fig. 10

We classified the test data by the six trained models. We defined sensitivity and specificity of the ratios of the correctly classified images of polyps over 10 mm and those in the 1 to 9 mm range, respectively. Figure 7a summarises the ROC curves with the criteria of likelihood $\xi = 0.05, 0.10, \dots , 0.95$. Figures 8a and b show the classification accuracy in each size for the InceptionResNet-v2 and the proposed method. In Figs. 8a and b, we set $\xi$ to 0.4 and 0.7, respectively. Figure 9 illustrates examples of the correctly classified inputs by the proposed method.

Evaluation of sequential-voting classification

Finally, we evaluated our sequential-voting classification with the test dataset described in Sect. 3.3: Dataset for polyp-size classification. Figure 7b summarises the classification results of the sequential-voting and single-shot classifications. We defined accuracy as the ratio of correctly classified scenes. Figure 8c shows the accuracy in each size of the sequential-voting classification. Figure 10 shows a typical comparison between correctly and incorrectly classified scenes. Figure 11a and b show the distributions of the likelihoods for the correctly and incorrectly classified scenes in Figs. 10a and b.

Discussion

In Fig. 7a, the proposed method achieved the best result among the six methods, demonstrating the importance of combining a polyp’s location and depth information. BseNet with RGB-D images achieved almost the same performance as Xception, even though this method used RGBD-GAN for depth estimation. These results emphasise the importance of location information.

InceptionResNet-v2 with colonoscopic images achieved the second-best classification accuracy, even though it achieved meaningless random classification with depth images in Fig. 7a. These results imply that deep learning might not identify polyps just using depth images, since there is no texture information of a polyp.

Figure 8a shows that InceptionResNet-v2 with colonoscopic images only correctly classified polyps from 2 to 9 mm. On the other hand, our proposed method correctly classified the polyps of every size except 9 and 11 mm in Fig. 8b. These two sizes are difficult queries, since they exist around the border of the binary categories. Figure 9 shows the correct classification for both small- and large-appearance polyps. These results suggest that the proposed method captured the three-dimensional information of polyps.

In Figs. 7b and 8c, we improved the classification accuracy by sequential voting. The classifications of the polyps from 1 to 9 mm and those of $\ge$ 10 mm achieved accuracies of 0.81 and 0.88. Figures 11a and b show the probability distributions for the correctly and incorrectly classified polyps in Fig. 10. In the former case, the proposed method captured the correct location of a polyp, whereas miss-localisations exist in many frames in the latter case. These miss-localisations can happen in the images when a flat polyp exists far from a colonoscope.

From Fig. 4b, we confirmed a less-biased size distribution over our dataset than subject estimation results [4, 8]. In subjective estimation, including size determination with measurement devices, estimated sizes tend to concentrate on only specific sizes such as 5, 10, 15, 20 mm [8]. In Ref. [4], among 99 polyps determined as 10 mm in subjective estimation, 71 polyps were actually <10 mm. On the other hand, the polyp-size distribution of our dataset is a smooth continuum in Fig. 4b. Therefore, the distribution of our dataset implies that our polyp-size measurement achieved the reduction in the terminal digit bias. Furthermore, the distribution of our dataset has a similar size distribution as the one of pathological measurement [4]. These observations imply that our measurements reduced the overestimation, too. The expert endoscopists in our group reached a consensus that a possible measurement error might be less than 1 mm.

Even though our localisation is imperfect for the SUN database as shown in Fig. 6, we can handle possible localisation errors. Since our purpose is polyp-size classification, we can get close enough to a polyp to correctly capture its location. The possible errors both in the ground truth data and depth estimation results [10] might cause lower classification accuracy for polyp sizes from 8 to 12 mm than the other sizes in Figs. 8b and c. However, our method achieved 88% classification accuracy for large polyps, whereas only 58% of 34 endoscopists correctly recognised large polyps in subjective-estimation tests with artificial polyps and the graduated device [7]. Compared with the subjective estimation [7], our method has an advantage in the correct recognition of large polyps.

Furthermore, our binary polyp-size classification has an advantage compared with the polyp-size regression. As shown in Fig. 4, the distribution of polyp sizes is imbalanced. If we adopt the regression, a trained model might overfit the dominant sizes of the distribution such as 2, 3, $\dots$, 7 mm polyps. However, by splitting sizes into 1–9 mm and $\ge 10$ mm as binary polyp-size categories, we can prevent the overfitting to the dominant sizes.

Conclusions

We developed a new method for binary polyp-size classification by integrating the deep-learning-based estimation of a polyp’s spatial information, since spatial information is essential for classifying object sizes in a three-dimensional space. In this method, precise polyp localisation and depth estimation with physical length contributed to estimating the three-dimensional shape of a polyp. Furthermore, the binary classification is not suffered from the imbalanced distribution of polyp sizes. Experimental results demonstrated accurate classification for both protruded- and flat-type polyps. Our method achieved 88% classification accuracy for large polyps, whereas only 58% of 34 endoscopists correctly recognised large polyps in the subjective estimation [7]. Moreover, the implementation of our method is feasible, since the pipeline in our method bases on deep-learning frameworks. Therefore, in the future, we can improve our method by integrating more precise depth-estimation and localisation methods into the pipeline.