A Mathematical Model Supports a Key Role for Ae4 (Slc4a9) in Salivary Gland Secretion

Abstract

We develop a mathematical model of a salivary gland acinar cell with the objective of investigating the role of two $\mathrm{Cl}^-/\mathrm{HCO}_3^-$ exchangers from the solute carrier family 4 (Slc4), Ae2 (Slc4a2) and Ae4 (Slc4a9), in fluid secretion. Water transport in this type of cell is predominantly driven by $\mathrm{Cl}^-$ movement. Here, a basolateral $\mathrm{Na}^+/ \mathrm{K}^+$ adenosine triphosphatase pump (NaK-ATPase) and a $\mathrm{Na}^+$–$\mathrm{K}^+$–$2 \mathrm{Cl}^-$ cotransporter (Nkcc1) are primarily responsible for concentrating the intracellular space with $\mathrm{Cl}^-$ well above its equilibrium potential. Gustatory and olfactory stimuli induce the release of $\mathrm{Ca}^{2+}$ ions from the internal stores of acinar cells, which triggers saliva secretion. $\mathrm{Ca}^{2+}$-dependent $\mathrm{Cl}^-$ and $\mathrm{K}^+$ channels promote ion secretion into the luminal space, thus creating an osmotic gradient that promotes water movement in the secretory direction. The current model for saliva secretion proposes that $\mathrm{Cl}^-/ \mathrm{HCO}_3^-$ anion exchangers (Ae), coupled with a basolateral $\mathrm{Na}^+/\hbox {proton}$ ($\hbox {H}^+$) (Nhe1) antiporter, regulate intracellular pH and act as a secondary $\mathrm{Cl}^-$ uptake mechanism (Nauntofte in Am J Physiol Gastrointest Liver Physiol 263(6):G823–G837, 1992; Melvin et al. in Annu Rev Physiol 67:445–469, 2005. https://doi.org/10.1146/annurev.physiol.67.041703.084745). Recent studies demonstrated that Ae4 deficient mice exhibit an approximate $30\%$ decrease in gland salivation (Peña-Münzenmayer et al. in J Biol Chem 290(17):10677–10688, 2015). Surprisingly, the same study revealed that absence of Ae2 does not impair salivation, as previously suggested. These results seem to indicate that the Ae4 may be responsible for the majority of the secondary $\mathrm{Cl}^-$ uptake and thus a key mechanism for saliva secretion. Here, by using ‘in-silico’ Ae2 and Ae4 knockout simulations, we produced mathematical support for such controversial findings. Our results suggest that the exchanger’s cotransport of monovalent cations is likely to be important in establishing the osmotic gradient necessary for optimal transepithelial fluid movement.

1 Introduction

Saliva is an exocrine secretion composed of water, a combination of electrolytes, and proteins (Gordon 1982). Among its many roles, saliva initiates digestion by facilitating mastication, swallowing and appreciation of foods. A low salivary flow (hyposalivation) causes a subjective feeling of dry mouth, otherwise known as xerostomia (Locker 1995). Oral pain, caries, mouth infections, problems with digestion and speech are associated with hyposalivation. Common pathologies that precede the latter include cystic fibrosis, pancreatitis and Sjögren’s syndrome (Mignogna et al. 2005). Neck and head irradiation therapies to treat cancer have also been linked to hyposalivation (Niedermeier et al. 1998).

In humans, the majority of saliva is secreted by three major pairs of glands situated at the side of the face, the submaxillary triangle, and underneath the tongue, i.e. the parotid, submandibular and sublingual glands, respectively. Saliva is also secreted in lesser quantities by a multitude of minor glands scattered around the oral cavity. Salivary glands are multi-lobular glands composed of different types of cells. For instance, secretory cells are arranged in clusters to form acini, which consist of a single layer of epithelial cells connected to a ductal system that ends in the oral cavity. The type of secretion produced by the different salivary glands varies: some glands produce a watery serous-like saliva, others a more dense viscous secretion, and some generate a mixture of both (Melvin et al. 2005).

Saliva formation starts in the acinar epithelium where water is taken from the blood stream and transported to the luminal space. Water transport is driven by an osmotic gradient created by the transport of ions (Yusuke et al. 1973) (Fig. 1). To explain this, Thaysen et al. (1954) proposed a ‘two-stage secretion’ model. Studies in the rat submandibular gland demonstrated that acinar cells secrete a salt (NaCl)-rich ‘primary’ fluid (stage1). The fluid is then modified after its passage through a series of ducts; most of the NaCl is reabsorbed and potassium ($\mathrm{K}^+$) is secreted (stage 2) (Young and Schögel 1966).

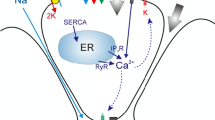
The molecular basis for epithelial fluid transport was first described by Silva et al. (1977). According to this model, secondary active $\mathrm{Cl}^-$ transport is the driving force of fluid secretion. Transepithelial $\mathrm{Cl}^-$ movement across acinar cells requires a $3\mathrm{Na}^+/2 \mathrm{K}^+$ adenosine triphosphatase pump (NaK-ATPase) at the basolateral membrane for generating an inwardly directed $\mathrm{Na}^+$ electrochemical gradient that is used by a basolateral $\mathrm{Na}^+$–$\mathrm{K}^+$–$2 \mathrm{Cl}^-$ cotransporter (Nkcc1) to accumulate intracellular $\mathrm{Cl}^-$ above its equilibrium potential. Acetylcholine (ACh) released by parasympathetic nerve terminals binds to muscarinic receptors located at the plasma membrane of acinar cells. This triggers a complex intracellular cascade of events that culminates in the release of intracellular calcium ($\mathrm{Ca}^{2+}$) from internal stores. This increase in $[\mathrm{Ca}^{2+}]_i$ is responsible for the activation of $\mathrm{Cl}^-$ and $\mathrm{K}^+$ membrane channels that extrude $\mathrm{K}^+$ ions into the interstitium and $\mathrm{Cl}^-$ ions into the acinar lumen (Catalán et al. 2009).

Novak and Young (1986) showed that the $\mathrm{Na}^+$–$\mathrm{K}^+$–$2 \mathrm{Cl}^-$ (Nkcc1) cotransporter is the primary pathway involved in $\hbox {Cl}^-$ uptake by acinar cells. Martinez and Cassity (1983) demonstrated that loop diuretics furosemide and bumetanide severely impair Nkcc1-mediated ion transport and as a result salivary gland fluid secretion is decreased by approximately $65\%$. Later experiments by Evans et al. (2000) showed that Nkcc1-deficient mice exhibit reduced salivation (approximately $70\%$).

It was then proposed that an additional $\mathrm{HCO}_3^-$-dependent transport system may be involved in the uptake of $\mathrm{Cl}^-$ ions (Novak and Young 1986). Acinar cells express a paired $\mathrm{Na}^+/\hbox {H}^+$ (Nhe1) and $\mathrm{Cl}^-/ \mathrm{HCO}_3^-$ exchanger system that regulates intracellular pH and at the same time supports intracellular accumulation of $\mathrm{Cl}^-$. This paired exchanger ion transport mechanism relies on intracellular carbonic anhydrase activity (Ogawa et al. 1998). Carbon dioxide ($\hbox {CO}_2$) enters the cytoplasm through the membrane and is rapidly hydrated forming carbonic acid ($\hbox {H}_2\hbox {CO}_3$). This acid is dissociated into $\hbox {H}^+$ and $\mathrm{HCO}_3^-$ by intracellular carbonic anhydrases. Cholinergic receptor activation leads to Nhe1 transporter activation thus causing intracellular alkalinisation and consequently promoting intracellular $\hbox {HCO}_3^-$ accumulation. $\mathrm{Cl}^-/ \mathrm{HCO}_3^-$ exchangers use this outward $\mathrm{HCO}_3^-$ gradient to support $\mathrm{Cl}^-$ uptake (Peña-Münzenmayer et al. 2015, 2016).

It has long been suspected that the $\mathrm{Cl}^-/ \mathrm{HCO}_3^-$ anion exchanger (Ae2-Slc4a2), ubiquitous to almost all cell types, is responsible for the majority of the $\mathrm{HCO}_3^-$-dependent $\mathrm{Cl}^-$ uptake in secretory epithelia (Roussa 2011; Nguyen et al. 2004; Evans et al. 2000; Frizzell and Hanrahan 2012). However, recent experiments have demonstrated expression in salivary gland acinar cells of another exchanger from the Slc4 family, a monovalent cation-dependent $\mathrm{Cl}^-/ \mathrm{HCO}_3^-$ transporter (Ae4-Slc4a9) (Peña-Münzenmayer et al. 2016). Surprisingly this transporter, previously thought to be expressed primarily in ductal cells, appears to be an essential $\mathrm{Cl}^-$ uptake pathway for the salivary gland acinar cell. Through a series of experiments, Peña-Münzenmayer et al. (2015) demonstrated that Ae4-deficient mice suffered an approximate $30\%$ salivary reduced flow. In contrast, Ae2-deficient mice exhibited no reduction in salivary fluid. The exact reason behind the cellular preference for Ae4 over the Ae2 remains controversial.

In the present study, we describe a mathematical model that extends the work of Gin et al. (2007), Maclaren et al. (2012) and Palk et al. (2010) to include the two $\mathrm{HCO}_3^-$-dependent $\mathrm{Cl}^-$ uptake mechanisms (Ae2 and Ae4) in question. Through computational simulations, we investigate the effect of the absence of Ae2 and Ae4 on fluid secretion. Based on the model results, we propose a theoretical explanation as to why the gland acinar cell may favour Ae4 over Ae2 as a main $\mathrm{HCO}_3^-$-dependent $\mathrm{Cl}^-$ uptake mechanism in the secretory process.

2 Model

2.1 Assumptions and Notation

The model is based on fluxes responsible for changes in ion concentrations of three main compartments: the interstitium, cytoplasm and the acinar lumen. We denote these by subscripts $e, \ i \ \text {and}\ l$, respectively (Fig. 1). Each flux, denoted by J, is represented by a mathematical sub-model based on experimental observations and previous mathematical models (refer to ‘Appendix’ for full details on each flux model).

Fig. 1

Schematic diagram of the salivary acinar cell model. We distinguish the basal and lateral sides (basolateral) to the apical side of the plasma membrane. Perfusion studies demonstrated different potentials on each portion of the acinar membrane (Young 1968). In the diagram, these are separated by a yellow line. The basolateral membrane portion contains Nkcc1 (green), NaK-ATPase (yellow), Ae4 (red), Ae2 (blue), Nhe1 (white) and $\mathrm{Ca}^{2+}$-activated $\mathrm{K}^+$ channels. The cell membrane is permeable to $\hbox {CO}_2$; carbonic anhydrases in the cytoplasm catalyse the reaction of $\hbox {CO}_2$ and water to form carbonic acid, which dissociates into $\mathrm{HCO}_3^-$ and $\hbox {H}^+$. The apical membrane contains a $\mathrm{Ca}^{2+}$-activated $\mathrm{Cl}^-$ channel. Both apical and basolateral membranes are permeable to water. Finally, we have included paracellular $\mathrm{K}^+$ and $\mathrm{Na}^+$ currents along with a paracellular water flow. Although the apical membrane also contains $\mathrm{Ca}^{2+}$-activated $\mathrm{K}^+$ channels, these are omitted from the model for simplicity (Color figure online)

The model assumes that the concentration of each ionic species is spatially homogeneous. In addition, the interstitial ionic concentrations are assumed to be constant. This is equivalent to placing a single homogeneous cell in an infinite bath of ions. Although we know this assumption to be incorrect (for example, interstitial [$\hbox {K}^+$] rises as much as twofold during stimulation), our model here provides a necessary first step towards the construction of a more complex model that includes dynamic variation of extracellular concentrations.

2.2 Ion Channels and Fluxes

The osmotic gradient needed for passive water movement in the secretory direction is maintained primarily by transcellular $\hbox {Cl}^-$ transport. In our model, the primary $\hbox {Cl}^-$ uptake mechanism is the Nkcc1. We use the model of Palk et al. (2010) to describe Nkcc1-related ion fluxes. It consists of a two-state model simplification based on an earlier model constructed by Benjamin and Johnson (1997) (‘Appendix 1’).

Along with the Nkcc1, the Ae2 exchanger supports $\hbox {Cl}^-$ influx but at the expense of intracellular $\hbox {HCO}_3^-$ efflux. We use the model of Falkenberg and Jakobsson (2010) (‘Appendix 5’). The Nhe1 antiporter model is also based on Falkenberg and Jakobsson (2010) (‘Appendix 6’).

In addition to the Nkcc1 and Ae2, the model includes another mechanism that supports $\hbox {Cl}^-$ influx. The Ae4 is a $\hbox {Cl}^-/\hbox {HCO}_3^-$ exchanger that is non-selective for monovalent cations (Peña-Münzenmayer et al. 2016). In our model, $\hbox {K}^+$ and $\hbox {Na}^+$ are extruded by the mechanism to accommodate for this feature. Its stoichiometry is 1:1:2, that is, one $\hbox {Cl}^-$ ion in exchange for 2 $\hbox {HCO}_3^-$ and one monovalent cation per cycle (‘Appendix 7’).

To maintain a $\hbox {Na}^+$ electrochemical gradient and energise secondarily active transports, the NaK-ATPase pump extrudes 3 $\hbox {Na}^+$ ions in exchange for 2 $\hbox {K}^+$ ions. We use the model of Palk et al. (2010), which is a simplification of the model of Smith and Crampin (2004) (‘Appendix 2’).

The efflux of intracellular $\mathrm{K}^+$ ions to the interstitial compartment occurs via basolateral membrane $\hbox {Ca}^{2+}$-activated $\mathrm{K}^+$ channels (Fig. 1). In our model, these generate a current that is dependent on the channel’s open probability. Such probability is assumed to be directly proportional to the $[\mathrm{Ca}^{2+}]_i$ (Takahata et al. 2003) (‘Appendix 3’).

The efflux of $\mathrm{Cl}^-$ from the cellular compartment to the acinar lumen occurs via apical membrane $\hbox {Ca}^{2+}$-activated $\mathrm{Cl}^-$ channels (Fig. 1). Their current is dependent on the channel’s open probability, which in turn is assumed to be directly proportional to the $[\mathrm{Ca}^{2+}]_i$ (Takahata et al. 2003) (‘Appendix 4’).

2.3 Intracellular Ionic Concentrations

In our model, $\hbox {Cl}^-$ enters the cell via the Nkcc1 cotransporter and the Ae2 and Ae4 exchangers and is extruded through an apical $\hbox {Ca}^{2+}$-activated-$\hbox {Cl}^-$ current (CaCC):

$$\begin{aligned} \frac{\mathrm{d}([\text {Cl}^-]_i \omega _i)}{\mathrm{d}t}=2J_{\mathrm{Nkcc1}}+J_{\mathrm{Ae4}} +J_{\mathrm{Ae2}}-\frac{I_{\mathrm{CaCC}}}{Fz_{\mathrm{Cl}}}. \end{aligned}$$

(1)

The factor of 2 in the ($J_{\mathrm{Nkcc1}}$) term reflects the stoichiometry of the cotransporter. The variable $\omega _i$ denotes the cell volume, while $z_{\mathrm{Cl}}=-1$ denotes the valence of $\hbox {Cl}^-$. Note that the units of the left-hand side of this equation are moles per unit time. Thus, all fluxes must be expressed in moles per unit time, i.e. each flux describes the total number of moles of an ion entering or leaving the cell per unit time.

$\hbox {Na}^+$ enters the cell via Nkcc1 cotransporter activity and the Nhe1 antiporter and is extruded through the Ae4 exchanger and the NaK-ATPase pump:

$$\begin{aligned} \frac{\mathrm{d}([\text {Na}^+]_i\omega _i)}{\mathrm{d}t}=J_{\mathrm{Nkcc1}} +J_{\mathrm{Nhe1}}-\left( \frac{[\text {Na}^+]_i}{[\text {Na}^+ ]_i+ [\text {K}^+]_i} \right) J_{\mathrm{Ae4}}-3J_{\mathrm{NaK}}. \end{aligned}$$

(2)

The factor of 3 in the ATPase pump flux expression indicates the hydrolysis of 1 ATP molecule to extrude three $\hbox {Na}^+$ in exchange for 2 $\hbox {K}^+$ per cycle. The expression $\left( \frac{[\text {Na}^+]_i}{[\text {Na}^+]_i+ [\text {K}^+]_i} \right)$ determines the amount of Ae4 flux due to Na$^+$ transport.

The rate at which [$\hbox {K}^+$] varies depends on the Nkcc1 cotransporter, $\hbox {Ca}^{2+}$-activated-$\hbox {K}^+$ current (CaKC), NaK-ATPase pump and Ae4 cotransporter.

$$\begin{aligned} \frac{\mathrm{d}([\text {K}^+]_i\omega _i)}{\mathrm{d}t}=J_{\mathrm{Nkcc1}}+2J_{\mathrm{NaK}} -\frac{I_{\mathrm{CaKC}}}{F z_{\mathrm{K}}}-\left( \frac{[\text {K}^+]_i}{[\text {Na}^+]_i + [\text {K}^+]_i} \right) J_{\mathrm{Ae4}}. \end{aligned}$$

(3)

The factor of 2 in the NaK-ATPase pump flux expression accounts for the stoichiometry of the mechanism. The parameter $z_{\mathrm{K}}=+1$ represents the valence of $\hbox {K}^+$ ions. The expression $\left( \frac{[\text {K}^+]_i}{[\text {Na}^+]_i + [\text {K}^+]_i} \right)$ determines the amount of Ae4 flux due to $\hbox {K}^+$ transport.

In our model, $\hbox {HCO}_3^-$ and $\hbox {H}^+$ are a product of the dissociation of carbonic acid ($\hbox {H}_2\hbox {CO}_3$). We include an intracellular buffer term, whose activity is directly proportional to the influx of $\hbox {CO}_2$ across the plasma membrane (‘Appendix 8’). Efflux of $\hbox {HCO}_3^-$ is a direct consequence of Ae2 and Ae4 transporter activity. Exit of $\hbox {H}^+$ ions is a result of Nhe1 $\hbox {Na}^+$ exchange. No other $\hbox {H}^+$ or $\hbox {HCO}_3^-$ transport mechanisms are included.

$$\begin{aligned}&\frac{\mathrm{d}([\text {HCO}_3^-]_i \omega _i)}{\mathrm{d}t}=J_{\mathrm{Buffer}}-2J_{\mathrm{Ae4}}-J_{\mathrm{Ae2}}, \end{aligned}$$

(4)

$$\begin{aligned}&\frac{\mathrm{d}([\text {H}^+]_i\omega _i)}{\mathrm{d}t}=J_{\mathrm{Buffer}}-J_{\mathrm{Nhe1}}, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\mathrm{d}([\text {CO}_2]_i \omega _i)}{\mathrm{d}t}=J_{\mathrm{CO}_2}-J_{\mathrm{Buffer}}. \end{aligned}$$

(6)

2.4 Two-Membrane Model and the Tight Junction

Observations by Young (1968) revealed the presence of two different membrane potentials on portions of the same cellular membrane: the apical and the basolateral (Fig. 1). To obtain the potential at each membrane portion, we use Kirchhoff’s current law for a simple resistor–capacitor circuit:

$$\begin{aligned}&C_m \frac{\mathrm{d}V_b}{\mathrm{d}t}=-I_{\mathrm{CaKC}}-I_{\mathrm{NaK}}+\left( I_\mathrm{K}^t +I_{\mathrm{Na}}^t\right) , \end{aligned}$$

(7)

$$\begin{aligned}&C_m \frac{\mathrm{d}V_a}{\mathrm{d}t}=-I_{\mathrm{CaCC}}-\left( I_\mathrm{K}^t+I_{\mathrm{Na}}^t\right) , \end{aligned}$$

(8)

The right-hand side of Eqs. (7) and (8) represents the sum of the currents for each ion species through the respective membrane segment. In Eq. (8), the term $I_{\mathrm{CaCC}}$ represents the apical $\hbox {Ca}^{2+}$-activated $\hbox {Cl}^-$ channel current. The terms $I_{\mathrm{CaKC}}$ and $I_{\mathrm{NaK}}$ in Eq. (7) represent the current due to $\hbox {Ca}^{2+}$-activated $\mathrm{K}^+$ channels and NaK-ATPase pumps located in the basolateral plasma membrane of the cell, respectively. The terms $I_\mathrm{K}^t$ and $I_{\mathrm{Na}}^t$ in Eqs. (7) and (8) represent the $\mathrm{Na}^+$ and $\mathrm{K}^+$ currents through the tight junctions (‘Appendix 10’). The latter are driven by the negative transepithelial potential generated upon $\hbox {Cl}^-$ secretion into the luminal space and contribute to changes in both membrane potentials ($V_a$ and $V_b$). Finally, $C_m$ is the capacitance of the cell membrane.

We used the convention that the apical membrane potential is negative as it is measured from the lumen to the cytoplasm. The basolateral membrane potential, on the other hand, is measured from the interstitium to the cytoplasm.

2.5 Fluid Transport

In salivary gland acinar cells, water moves across the plasma membrane through water-specific channels called aquaporins. Parotid gland acinar cells express the aquaporin 5 gene (AQP5) which has been shown to be involved in selective membrane water transport (Delporte and Steinfeld 2006). We model the water fluxes due to aquaporins as a direct consequence of the osmotic gradient between the three neighbouring compartments (intersititum, cellular and the acinar lumen) and assume that the plasma membrane cannot withstand hydrostatic pressure gradients. The difference between the apical and basolateral fluid flow drives a change in cellular volume ($\omega _i$):

$$\begin{aligned} \frac{\mathrm{d}\omega _i}{\mathrm{d}t}=q_a-q_b. \end{aligned}$$

(9)

The terms $q_a$ and $q_b$ represent the water fluxes across the basolateral membrane and the apical membrane: subscripts a and b, respectively. These are defined by:

$$\begin{aligned}&q_a=P_a \Bigg [ \sum [c]_{l} + \varPsi _l - \sum [c]_{i} -\frac{x_i}{\omega _i}\Bigg ], \end{aligned}$$

(10)

$$\begin{aligned}&q_b=P_b \Bigg [ \sum [c]_{i}+ \frac{x_i}{\omega _i} - \sum [c]_{e} \Bigg ], \end{aligned}$$

(11)

where $P_i$ ($i=a$ or b) represents the permeability of the respective plasma membrane portion (‘Appendix 11’), and

$$\begin{aligned}&\sum [c]_{l}=[\text {K}^+]_l+[\text {Na}^+]_l +[\text {H}^+]_l+[\text {Cl}^-]_l+[\text {HCO}_3^-]_l, \\&\sum [c]_i=[\text {K}^+]_i+[\text {Na}^+]_i+[\text {H}^+]_i +[\text {Cl}^-]_i+[\text {HCO}_3^-]_i+[\text {CO}_2]_i,\\&\sum [c]_e=[\text {K}^+]_e+[\text {Na}^+]_e +[\text {H}^+]_e +[\text {Cl}^-]_e+[\text {HCO}_3^-]_e+[\text {CO}_2]_e. \end{aligned}$$

The value $x_i$ in Eqs. (10) and (11) represents the moles of negatively charged particles with valence $(z_x) \le -1$ in the cellular media that are impermeable to the plasma membrane. To obtain its value, we used the electroneutrality condition described in ‘Appendix 9’. The term $\varPsi _l$ in Eq. (10) accounts for the uncharged impermeable ionic species and proteins (e.g. amylase) present in the acinar lumen that we do not keep track of in the model but contribute to the osmolarity of the compartment. This term is a parameter of the model, and its value was found by solving Eq. (9) at steady state. In doing so, we are ensuring the correct volume and fluid flow.

According to these equations, the osmolarity of the interstitium is 292.6 mM, the osmolarity in the cell is 296.6 mM, and the osmolarity in the acinar lumen is 297.4 mM (see Table 1). Thus, at rest there is a small flux from the interstitium into the cell and from the cell into the lumen.

Similarly, the transport of fluid through the tight junctions (i.e. from the interstitial to the acinar lumen paracellularly) occurs as a consequence of the osmotic gradient between the two compartments,

$$\begin{aligned} q_t=P_t \Bigg [ \sum [c]_{l} + \varPsi _l - \sum [c]_{e} \Bigg ]. \end{aligned}$$

(12)

$P_t$ represents the tight junction’s permeability to water (‘Appendix 11’). Finally, the total flux of water into the lumen (apical and paracellular) is given by:

$$\begin{aligned} q_{\mathrm{tot}}=q_a+q_t. \end{aligned}$$

(13)

Note that an important consequence of assuming a constant luminal volume ($\omega _l$) is that Eq. (13) also represents the flux of water out of the lumen (into the salivary ducts).

2.6 Lumen Ion Concentrations

The ionic concentrations in the acinar lumen depend on the apical membrane and tight junction fluxes. For instance, $\hbox {Na}^+$ and $\hbox {K}^+$ enter the lumen through the tight junction, while $\hbox {Cl}^-$ enters the lumen via a CaCC channel located on the apical membrane:

$$\begin{aligned}&\omega _l \frac{\mathrm{d}[\text {Na}^+]_l}{\mathrm{d}t}=\frac{I_{\mathrm{Na}}^t}{F z_{\mathrm{Na}}}-q_{\mathrm{tot}}[\text {Na}^+]_l, \end{aligned}$$

(14)

$$\begin{aligned}&\omega _l \frac{\mathrm{d}[\text {K}^+]_l}{\mathrm{d}t}=\frac{I_\mathrm{K}^t}{Fz_{\mathrm{K}}} -q_{\mathrm{tot}}[\text {K}^+]_l, \end{aligned}$$

(15)

$$\begin{aligned}&\omega _l \frac{\mathrm{d}[\text {Cl}^-]_l}{\mathrm{d}t}=\frac{I_{\mathrm{CaCC}}}{F z_{\mathrm{Cl}}} -q_{\mathrm{tot}}[\text {Cl}^-]. \end{aligned}$$

(16)

In Eqs. (14)–(16), the term $q_{\mathrm{tot}}$ removes the associated ion out of the acinar lumen and into the ductal passage. We use this expression because Eq. (13), unlike Eqs. (10)–(12), does not model water flow through a water selective channel (aquaporin). Here the expression $q_{\mathrm{tot}}$ is a simple convective flux; thus, in addition to water, it removes the respective ions from the luminal compartment.

2.7 Summary of the Model

$$\begin{aligned} \frac{\mathrm{d}([\text {Cl}^-]_i \omega _i)}{\mathrm{d}t}= & {} 2J_{\mathrm{Nkcc1}}+J_{\mathrm{Ae4}} +J_{\mathrm{Ae2}}-\frac{I_{\mathrm{CaCC}}}{F z_{\mathrm{Cl}}}, \\ \frac{\mathrm{d}([\text {Na}^+]_i \omega _i)}{\mathrm{d}t}= & {} J_{\mathrm{Nkcc1}}+J_{\mathrm{Nhe1}} -3J_{\mathrm{NaK}}-\left( \frac{[\text {Na}^+]_i}{[\text {Na}^+ ]_i + [\text {K}^+]_i} \right) J_{\mathrm{Ae4}}, \\ \frac{\mathrm{d}([\text {K}^+]_i\omega _i)}{\mathrm{d}t}= & {} J_{\mathrm{Nkcc1}}+2J_{\mathrm{NaK}} -\frac{I_{\mathrm{CaKC}}}{F z_{\mathrm{K}}}-\left( \frac{[\text {K}^+]_i}{[\text {Na}^+]_i + [\text {K}^+]_i} \right) J_{\mathrm{Ae4}},\\ \frac{\mathrm{d}([\text {H}^+]_i \omega _i)}{\mathrm{d}t}= & {} J_{\mathrm{Buffer}}-J_{\mathrm{Nhe1}}, \\ \frac{\mathrm{d}([\text {CO}_2]_i \omega _i)}{\mathrm{d}t}= & {} J_{\mathrm{CO}_2}-J_{\mathrm{Buffer}}, \\ \frac{\mathrm{d}([\text {HCO}_3^-]_i \omega _i)}{\mathrm{d}t}= & {} J_{\mathrm{Buffer}} -2J_{\mathrm{Ae4}}-J_{\mathrm{Ae2}},\\ \omega _l \frac{\mathrm{d}[\text {Na}^+]_l}{\mathrm{d}t}= & {} \frac{I_{\mathrm{Na}}^t}{F z_{\mathrm{Na}}} -q_{\mathrm{tot}}[\text {Na}^+]_l,\\ \omega _l \frac{\mathrm{d}[\text {K}^+]_l}{\mathrm{d}t}= & {} \frac{I_\mathrm{K}^t}{Fz_{\mathrm{K}}} -q_{\mathrm{tot}}[\text {K}^+]_l, \\ \omega _l \frac{\mathrm{d}[\text {Cl}^-]_l}{\mathrm{d}t}= & {} \frac{I_{\mathrm{CaCC}}}{F z_{\mathrm{Cl}}} -q_{\mathrm{tot}}[\text {Cl}^-]_l,\\ C_m \frac{\mathrm{d}V_b}{\mathrm{d}t}= & {} -I_{\mathrm{CaKC}}-I_{\mathrm{NaK}}+\left( I_\mathrm{K}^t +I_{\mathrm{Na}}^t\right) ,\\ C_m \frac{\mathrm{d}V_a}{\mathrm{d}t}= & {} -I_{\mathrm{CaCC}}-\left( I_\mathrm{K}^t+I_{\mathrm{Na}}^t\right) ,\\ \frac{\mathrm{d}\omega _i}{\mathrm{d}t}= & {} q_b-q_a,\\ q_{\mathrm{tot}}= & {} q_a+q_t. \end{aligned}$$

2.8 $\hbox {Ca}^{2+}$ Signalling

Salivary gland secretion can be achieved by stimulating the salivary glands with a variety of agonists that raise intracellular $\hbox {Ca}^{2+}$ levels in an oscillatory manner. Previous models by Palk et al. (2010) and Gin et al. (2007) investigate the effects of $\hbox {Ca}^{2+}$ oscillations on saliva secretion. Here, however, we do not consider the effects of $\mathrm{Ca}^{2+}$ oscillations. Instead, we assume that $[\mathrm{Ca}^{2+}]_i$ is a given function of time (Fig. 2), where this function is based on the overall qualitative behaviour of the oscillations observed by Foskett and Melvin (1989) and Soltoff et al. (1989) and experimental data from Bruce et al. (2002). This approach allows us to bypass the complicated dynamics of $\hbox {Ca}^{2+}$ signalling and solely focus on membrane activity.

Fig. 2

Theoretical curve that qualitatively reproduces the acinar cell $[\hbox {Ca}^{2+}]_i$ response to agonist stimulation at room temperature (based on observations by Bruce et al. 2002). Stimulation occurs between minutes 6 and 12. Before and after this period, the $[\hbox {Ca}^{2+}]_i$ lies at its resting concentration of 58 nM (Foskett and Melvin 1989). This curve is a fixed input to the model, which thus, for simplicity, ignores the complexity of $\mathrm{Ca}^{2+}$ signalling

2.9 Numerical Simulations

The small membrane capacitance $C_m$ renders the system stiff. Thus, we ignore the fast dynamics of the membrane potentials and use a quasi-steady-state (QSS) approximation to the membrane potentials:

$$\begin{aligned}&-I_{\mathrm{CaKC}}-I_{\mathrm{NaK}}+\left( I_\mathrm{K}^t+I_{\mathrm{Na}}^t \right) =0,\\&-I_{\mathrm{CaCC}}-\left( I_\mathrm{K}^t+I_{\mathrm{Na}}^t \right) =0. \end{aligned}$$

The QSS approximation reduces the model to a system of 10 differential equations and 2 algebraic constraints. This type of problem is known as a differential–algebraic equation system or DAE. The MATLAB routine ‘ode15s’ is well equipped to handle DAE systems like this. A good review of the theory of DAEs is given by Kunkel and Mehrmann (2006).

3 Results

3.1 Ionic Resting States and Agonist Stimulation

For the wild-type case (and in the absence of agonist), we determined values for the ion conductances and transporter densities by requiring a physiological reasonable steady state (Table 1).

Table 1 Comparison of steady-state results

Fig. 3

Response of intracellular ion concentrations to agonist stimulation. $\mathrm{Cl}^-$, $\mathrm{K}^+$ and $\mathrm{HCO}_3^-$ concentrations all decrease significantly, while $\mathrm{Na}^+$ concentration increases. Neither $[\hbox {CO}_2]_i$ nor pH change significantly

Fig. 4

a, b, c Response of the luminal ion concentrations to agonist stimulation. d In response to agonist stimulation, the cell volume shrinks by approximately $28\%$. e, f Response of the membrane potentials to agonist stimulation

Fig. 5

Figure depicts a sharp increase in total fluid flow rate from its resting state of $0.24\hbox {e}{-}08\, \upmu \hbox {L}/\hbox {min}$ to a maximal flow rate (under agonist stimulation) of $3.2\hbox {e}{-}08\ \upmu \hbox {L}/\hbox {min}$, an approximate 13-fold increase. Upon removal of agonist (minute 15), the flow rate returns to its resting value. Note that at rest the flow rate is not zero. This is because the model is constructed in such a way that there is always an ionic concentration gradient between the 3 compartments, which drives fluid flow at rest

Addition of agonist was simulated by specifying $[\mathrm{Ca}^{2+}]_i$ as a given function of time (Sect. 2.8 and Fig. 2). The responses of the intracellular ion concentrations are shown in Fig. 3, while the response of the membrane potentials and the lumenal concentrations is shown in Fig. 4.

In response to agonist stimulation, there is a significant decline in $[\mathrm{Cl}^-]_i$ and $[\mathrm{K}^+]_i$ (Fig. 3c, b), as $\mathrm{Ca}^{2+}$ opens $\mathrm{Cl}^-$ and $\mathrm{K}^+$ channels to allow for efflux of those ions. This decline in $[\mathrm{Cl}^-]_i$ leads to an increased $\mathrm{Cl}^-$ uptake through the Nkcc1, Ae4 and Ae2, which results in a rise in $[\mathrm{Na}^+]_i$ and a fall in $[\mathrm{HCO}_3^-]_i$ (Fig. 3a, d).

Nauntofte (1992) describes the Nhe1 exchanger as the main $\hbox {Na}^+$ pathway of salivary gland acinar cells (approximately $70\%$). In our model, this task is divided between the Nkcc1 and the Nhe1, where the principal pathway is the Nkcc1. Agonist stimulation promotes $\mathrm{Cl}^-$ influx and $\mathrm{HCO}_3^-$ efflux through Ae2 and Ae4. The resultant decrease in $[\mathrm{HCO}_3^-]_i$ increases the activity of carbonic anhydrase, thus increasing $\hbox {CO}_2$ influx and intracellular [$\hbox {H}^+$]. This in turn increases the activity of the Nhe1, leading to an increase in $[\mathrm{Na}^+]_i$ (Fig. 3a), as experimentally observed. This sequence highlights the model’s capability to regulate cellular pH (Fig. 3e, f).

The increased basal $\mathrm{K}^+$ conductance hyperpolarizes the basolateral membrane (Fig. 4f), while the increased apical $\mathrm{Cl}^-$ conductance depolarises the apical membrane (Fig.  4e). The apical and basolateral membrane potentials agree with experimentally observed results. Pedersen and Petersen (1973) found that at rest the basolateral portion of the acinar cell has a potential of approximately −62.5 mV, our model reaches −62.5 mV. After agonist stimulation, they observed a hyperpolarisation of about (10–15 mV), while our model predicts that the basolateral membrane hyperpolarizes by 14.7 mV. Following stimulation, the apical membrane is depolarised from −50.24 to −41 mV followed by a hyperpolarisation to −55 mV (Fig. 4e, f).

$\mathrm{Cl}^-$ current from the cell into the lumen increases the lumenal $\mathrm{Cl}^-$ concentration (Fig. 4c), which in turn increases the flow of cations through the tight junctions, leading to increases in lumenal $\mathrm{Na}^+$ and $\mathrm{K}^+$ concentrations also (Fig. 4a, b).

Finally, the ionic concentration dynamics of the cell lead to a $27.3\%$ loss of cellular volume at maximal stimulation (Fig. 4d) and an increase in the total flow rate. At maximal stimulation (by agonist), the model cell experiences a sharp increase in its total fluid flux from $0.24\hbox {e}{-}08\ \upmu \hbox {L}/\hbox {min}$ at rest, to $3.2\hbox {e}{-}08\ \upmu \hbox {L}/\hbox {min}$. This is an approximate 13-fold increase (Fig. 5).

These results validate the model’s qualitative behaviour allowing us to proceed with ‘in-silico’ experimentation (Nauntofte 1992; Melvin et al. 2005).

3.2 Simulations of Ae2 and Ae4 Knockouts

Ae2 expression is ubiquitous in nearly all secretory epithelia (Frizzell and Hanrahan 2012), and its activity has been linked to cellular pH regulation. Thus, in acinar cells, it has been suspected to support the secretion process (Roussa 2011; Evans et al. 2000; Nguyen et al. 2004). Recent studies by Peña-Münzenmayer et al. (2015) provided evidence for an alternative $\hbox {Cl}^-$ uptake mechanism dependent on the expression of the anion exchanger Ae4. Ae4, like Ae2, is $\hbox {HCO}_3^-$ dependent. Saliva secretion experiments performed on Ae2 and Ae4 knockout mice showed that Ae4 is important for saliva secretion. Surprisingly, saliva secretion rates were not affected in salivary glands lacking Ae2 exchangers. We use our mathematical model to try to understand the mechanism by which Ae4, but not Ae2, is important for saliva secretion.

To simulate the absence of either the Ae2 or Ae4, we set their respective transporter densities, $G_{\mathrm{Ae2}}$ and $G_{\mathrm{Ae4}}$, to zero (‘Appendix 11’). Under such conditions, the model reaches new steady states that reveal the dynamics associated with the loss of a particular transporter. These new steady states were compared to the complete model, i.e. when there was no deletion of any flux (we call this ‘control’, see Figs. 3, 4, 5).

When the Ae2 flux term is removed, the model behaves qualitatively the same as the control cell. In Fig. 6, we compare intracellular ion concentrations in the model with either Ae2 or Ae4 removed (blue and red lines, respectively). The control case is shown as a black line. Since, in each panel, the blue and black lines are very similar, we see that removal of Ae2 has no significant effect on intracellular ion concentrations, or on $[\hbox {CO}_2]_i$ or pH.

Conversely, when the Ae4 flux term is removed, we see a drop in resting $[\mathrm{Cl}^-]_i$ (Fig. 6c) and increases in $[\mathrm{K}^+]_i$, $[\mathrm{Na}^+]_i$ and $[\mathrm{HCO}_3^-]_i$ (Fig. 6a, b, d, respectively). As with Ae2 removal, there is no significant effect on $[\hbox {CO}_2]_2$ or pH (Fig. 6e, f).

After application of agonist, $[\mathrm{Cl}^-]_i$ reaches a significantly lower steady state than that of the control. This corresponds to the data shown in Fig. 1C, D of Peña-Münzenmayer et al. (2015). These data show that recovery of $[\mathrm{Cl}^-]_i$ is slower in Ae4 knockout mice than in control mice or Ae2 knockout mice. Our model results (Fig. 6c) show the same qualitative behaviour, with $[\mathrm{Cl}^-]_i$ recovery being the same speed in control and Ae2 knockout simulations, and being significantly slower in the Ae4 knockout case (minutes 10–20).

A similar pattern is seen in the membrane potentials and the lumenal concentrations (Fig. 7). Removal of Ae2 makes no significant difference, while removal of Ae4 causes a hyperpolarisation of the apical membrane (Fig. 7d), a small depolarisation of the basolateral membrane (Fig. 7e) and significant decreases in all lumenal concentrations (Fig. 7a–c).

Fig. 6

Intracellular ion concentrations in the model with either Ae2 or Ae4 removed (blue and red, respectively) compared to the control cell (black). Knockout of Ae2 has no significant effect on the model responses. (The blue and black lines are very similar in each panel.) Knockout of Ae4 causes a significant decrease in $[\mathrm{Cl}^-]_i$ (c), and significant increases in $[\mathrm{K}^+]_i$, $[\mathrm{Na}^+]_i$ and $[\mathrm{HCO}_3^-]_i$ (a, b, d). For both knockouts, pH and $[\hbox {CO}_2]_i$ remain almost unchanged (panels E and F) (Color figure online)

Fig. 7

Voltages and lumenal ion concentrations in the model with either Ae2 or Ae4 removed (blue and red, respectively) compared to the control cell (black). a, b, c Removal of Ae4 causes less $\mathrm{Cl}^-$ transport, and thus lower lumenal ion concentrations. d, e Ae2 deletion does not result in changes in the membrane potentials. Ae4 deletion, which causes a decrease in $\hbox {Cl}^-$ concentration (lumenal and intracellular), leads to hyperpolarisation of the apical membrane. At the basolateral membrane, a decreased NaK-ATPase and CaKC flux results in a small membrane depolarisation (Color figure online)

These differences in ion concentrations are reflected in the rates of secretion in the Ae2 or Ae4 knockout simulations (Fig. 8). Since Ae2 knockout has little effect on ion concentrations or membrane potentials, it has little effect on fluid transport also. However, the decreased lumenal $\mathrm{Cl}^-$ concentration as a result of Ae4 knockout results in significantly decreased fluid transport. However, it is important to note that our model does not capture the correct kinetics of changes in fluid flow. According to Fig. 1A, B of Peña-Münzenmayer et al. (2015), upon agonist stimulation, fluid transport in Ae4 knockout mice first reaches a peak (of approximately the same magnitude as in control mice), but then gradually decreases, over a period of approximately 10 min, to a lower level. Our model displays the same qualitative behaviour, but the fluid flow rate in the model Ae4 knockout simulation reaches a new, lower, steady state after only about 2 min, considerably faster than what was observed experimentally. The reason for this discrepancy is unclear.

Fig. 8

Ae2 knockout cell (blue) displays no significant change in flow rate compared to the control (black), but the Ae4 knockout cell (red) displays around $24\%$ reduction in salivary flow rate compared to the control cell (Color figure online)

These results suggest that the cell is able to adapt well to loss of the Ae2, but not to loss of the Ae4. We tested the hypothesis that this difference is due to the fact that Ae4 transports cations as well as $\mathrm{Cl}^-$ and $\mathrm{HCO}_3^-$.

In Fig. 9, we show the fluxes in the model in control conditions, and under Ae4 or Ae2 knockout. Knockout of Ae2 causes upregulation of Ae4 (Fig. 9a) and vice versa (Fig. 9b). However, and counterintuitively, the model indicates that neither Ae2 nor Ae4 knockout leads to significant activation of the Nkcc1 to compensate for the missing $\hbox {Cl}^-$ (Fig. 9c). This result is in agreement with experimental observations by Peña-Münzenmayer et al. (2015) who observed no difference in Nkcc1 activity between control cells and Ae knockouts.

Instead, the rise in $[\mathrm{Na}^+]_i$ caused by Ae4 knockout causes a significant decrease in the Nhe1 flux (Fig. 9d). Conversely, Ae2 knockout causes an increase in Ae4 activity, which decreases $[\mathrm{Na}^+]_i$ slightly (Fig. 6a), which causes a slight increase in the Nhe1 flux.

Thus, in summary,

• When Ae2 is knocked out, a rise in Ae4 activity increases the outward flow of $\mathrm{Na}^+$ and $\mathrm{K}^+$, which is offset by a very small rise in Nkcc1 activity, which not only brings in $\mathrm{Na}^+$ and $\mathrm{K}^+$, but also serves to increase $\mathrm{Cl}^-$ uptake slightly. A slight rise in Nhe1 activity offsets the fall in $[\mathrm{Na}^+]_i$ and $[\mathrm{K}^+]_i$, leading to a new steady state where the ion concentrations remain almost unchanged (as shown in Fig. 6).

• On the other hand, when Ae4 is knocked out, $[\mathrm{Na}^+]_i$ and $[\mathrm{K}^+]_i$ rise, while $[\mathrm{Cl}^-]_i$ falls. The cell cannot compensate for the rise in $[\mathrm{Na}^+]_i$ and $[\mathrm{K}^+]_i$ by decreasing the Nkcc1, as this would decrease $[\mathrm{Cl}^-]_i$ even further. In fact Nkcc1 flux is raised slightly, exacerbating the problem of increased $[\mathrm{Na}^+]_i$ and $[\mathrm{K}^+]_i$. This leads to a significant decline in Nhe1 flux and changes to the acid-base balance. The cell finally reaches a steady state with high $[\mathrm{Na}^+]_i$, $[\mathrm{K}^+]_i$ and $[\mathrm{HCO}_3^-]_i$, and low $[\mathrm{Cl}^-]_i$, leading to a significant decline in fluid transport.

Fig. 9

Model fluxes under control conditions and Ae4 or Ae2 knockout. a On Ae2 knockout, the Ae4 increases its activity. b On Ae4 knockout, the Ae2 increases its activity. c In Ae2 and Ae4 knockout cells, upregulation of the Nkcc1 is minimal. d Loss of Ae2 causes an increase in Ae4 activity, which leads to a slight decrease in $[\mathrm{Na}^+]_i$. As a response, the Nhe1 increases its activity slightly. In contrast, in the Ae4 knockout cell, a high $[\hbox {Na}^+]_i$ causes a significant decrease in Nhe1 activity (red) (Color figure online)

4 Discussion

We constructed a mathematical model with the aim of understanding the experimental results of Peña-Münzenmayer et al. (2015). In salivary gland acinar cells, transcellular movement of $\hbox {Cl}^-$ has been observed to be the rate-limiting step for gland fluid secretion. Ever since the observations of Silva et al. (1977) it has been accepted that the Nkcc1 is responsible for the majority of the $\hbox {Cl}^-$ influx. Experiments by Evans et al. (2000) demonstrated that an additional mechanism is partly responsible for introducing $\hbox {Cl}^-$ into the cell. The Ae2, a $\hbox {Cl}^-/\hbox {HCO}_3^-$ exchanger which has been identified as mainly involved in cellular pH regulation, was hypothesised to be responsible for supporting this influx as the mechanism can be found in nearly all secretory epithelia (Melvin et al. 2005; Nauntofte 1992). However, the results of Peña-Münzenmayer et al. (2015) demonstrate that the Ae2 might not be involved in the secretory process of acinar cells. Instead, a cation-dependent $\hbox {Cl}^-/\hbox {HCO}_3^-$ exchanger, the Ae4, may be the primary mechanism supporting $\hbox {Cl}^-$ influx through the Nkcc1, and hence a key mechanism in salivary gland acinar fluid secretion. Our model aimed to explore two basic questions:

• Can a mathematical model explain these experimental results?

• If so, can we explain the cell’s preference for Ae4 (as opposed to Ae2) involvement in the secretion process?

To answer these questions, we constructed a mathematical model based on previous work by Gin et al. (2007), Maclaren et al. (2012) and Palk et al. (2010). The Ae2 knockout model’s behaviour was similar to that of the control cell, while the Ae4 knockout model had a significantly decreased fluid flow. One of the most non-intuitive features of this simulation was the response of the Nkcc1. Given that the Nkcc1 is responsible for at least $70\%$ of the cellular $\hbox {Cl}^-$ intake (Evans et al. 2000), we expected to see an increased response to account for the loss of a $\hbox {Cl}^-$ influx pathway, but no such increase was observed in the model, in either the Ae2 or Ae4 knockouts. This result is in agreement with observations by Peña-Münzenmayer et al. (2015) which saw no difference in Nkcc1 activity between knockouts and control.

The Ae4 knockout cell is significantly different from the control cell. Again, we see no large difference in Nkcc1 activity. However, unlike the Ae4 in the absence of Ae2, the Ae2 is unable to increase its activity sufficiently to account for the loss of Ae4. In addition, we see that higher concentrations of $\hbox {K}^+$ and $\hbox {Na}^+$ also prevent the Nkcc1 from increasing its activity. On the one hand, the Ae2 tries to extrude the required $\hbox {HCO}_3^-$ to prevent alkalinisation of the cell, while the $\hbox {HCO}_3^-$ buffer rate slows down to support this. This leads to a decrease in Nhe1 activity which serves to prevent higher $[\hbox {Na}^+]_i$. Interestingly, this is consistent with the observations of Nauntofte (1992). On the other hand, there is a decreased NaK-ATPase activity which prevents higher $[\hbox {K}^+]_i$, and which comes at the expense of depolarising the basolateral membrane and preventing the efflux of $\hbox {K}^+$. This result supports the observations of Peña-Münzenmayer et al. (2015).

Thus, our model results support the findings of Peña-Münzenmayer et al. (2015) and provide a possible explanation for the difference in behaviour seen in Ae4 knockout and Ae2 knockout mice. In particular, the model predicts that the cation dependence of Ae4 $\hbox {Cl}^-/\hbox {HCO}_3^-$ exchange is critical for its role in $\mathrm{Cl}^-$ uptake.

Appendices

Appendix

$\hbox {Na}^+$–$\hbox {K}^+$–$2\hbox {Cl}^-$ Cotransporter (Nkcc1)

The Nkcc1 cotransporter expression is ubiquitous in nearly all cells and secretory epithelia (Wang et al. 2003). The Nkcc1-mediated-$\hbox {Cl}^-$ uptake mechanism is a secondary active transport, i.e. the energy required for its activity comes indirectly from ATP hydrolysis. The Nkcc1 model we use was first constructed by Benjamin and Johnson (1997). The model assumes equilibrium ion binding, binding symmetry and identity of $\hbox {Cl}^-$ binding sites. This results in a 10 state model. Palk et al. (2010) and Gin et al. (2007) simplified it to a two-state model that assumes simultaneous binding and unbinding of $\hbox {Cl}^-$, $\hbox {K}^+$ and $\hbox {Na}^+$. The reaction occurs as follows:

$$\begin{aligned} O + \text {K}^+_e \text {Na}^+_e (\text {Cl}_e)^2 \underset{k_1^-}{{\mathop {\rightleftharpoons }\limits ^{k_1^+}}} I \underset{k_2^-}{{\mathop {\rightleftharpoons }\limits ^{k_2^+}}} O + \text {K}^+_i \text {Na}^+_i (\text {Cl}_i^-)^2. \end{aligned}$$

The steady-state flux is given by

$$\begin{aligned} J_{\mathrm{Nkcc1}}=\alpha _{\mathrm{Nkcc1}} \left( \frac{a_1-a_2 [\text {Na}^+]_i [\text {K}^+]_i [\text {Cl}^-]_i^2}{a_3+a_4 [\text {Na}^+]_i [\text {K}^+]_i [\text {Cl}^-]_i^2}\right) , \end{aligned}$$

(17)

where $\alpha _{\mathrm{Nkcc1}}$ is the density of the cotransporter.

Nkcc1	Description	Value	Units
$\alpha _{\mathrm{Nkcc1}}^{\tiny {\dagger }}$	Membrane density	2.15	$\hbox {amol}/\upmu \hbox {m}^3$
$a_1$	Rate	157.5	$\hbox {s}^{-1}$
$a_2$	Rate	$2.0096\times 10^7$	$\hbox {mM}^{-4}$ $\hbox {s}^{-1}$
$a_3$	Rate	1.0306	$\hbox {s}^{-1}$
$a_4$	Rate	$1.3852\times 10^6$	$\hbox {mM}^{-4}\ \hbox {s}^{-1}$

1. $^{\dagger }$Parameter value determined from the model
2. Parameter values taken from Palk et al. (2010)

$\hbox {Na}^+/\hbox {K}^+$ ATPase Pump (NaK)

The $\hbox {Na}^+/\hbox {K}^+$ ATPase pump extrudes 3 $\hbox {Na}^+$ ions while introducing 2 $\hbox {K}^+$ ions against their electrochemical gradients at the expense of hydrolysing an ATP molecule per cycle. The net reaction for the pump cycle is

$$\begin{aligned} \text {ATP} + 3 \text {Na}_i^+ + 2 \text {K}_e^+ \leftrightarrow \text {ADP} + \text {P}_i + 3\text {Na}_e^+ +\text {K}_i^+, \end{aligned}$$

where $\text {P}_i$ represents the intracellular concentration of phosphate (a result of ATP conversion to ADP). Smith and Crampin (2004) constructed a mathematical model of the NaK-ATPase pump intended to be used as a component in whole-cell myocyte modelling with the objective to predict pump function and whole myocyte behaviour when cellular metabolism is compromised. Palk et al. (2010) reduced the model to two states:

$$\begin{aligned} \text {O} + 2\text {K}_e \underset{k_1^-}{{\mathop {\rightleftharpoons }\limits ^{k_1^+}}} \text {I}+ 3\text {Na}_e,\\ \text {I} + 3\text {Na}_i \underset{k_2^-}{{\mathop {\rightleftharpoons }\limits ^{k_2^+}}} \text {O} + 2\text {K}_i. \end{aligned}$$

where I refers to an ‘Inside’ state and O to an ‘Outside’ state. The simplification assumes that external $\hbox {Na}^+$ and internal $\hbox {K}^+$ ions simultaneously bind and unbind and are supplied at a constant rate. In addition, the forward reaction rates are higher than the reverse and that the steady-state flux through the pump is given by

$$\begin{aligned} J_{\mathrm{NaK}}=\alpha _{\mathrm{NaK}}\left( r \frac{[\text {K}^+]_e^2 [\text {Na}^+]_i^3}{[\text {K}^+]_e^2+\alpha [\text {Na}^+]_i^3}\right) , \end{aligned}$$

(18)

where $\alpha _{\mathrm{NaK}}$ is the density of the pump.

NaK-ATPase	Description	Value	Units
$\alpha _{\mathrm{NaK}}^{\dagger }$	Membrane density	4.84	$\hbox {amol}/\upmu \hbox {m}^3$
r	Rate	$1.305\times 10^6$	$\hbox {mM}^{-3}\ \hbox {s}^{-1}$
$\alpha _1$	Half saturation	0.641	$\hbox {mM}^{-1}$

1. $^{\dagger }$Parameter value determined from the model
2. Parameter values taken from Palk et al. (2010)

$\hbox {Ca}^{2+}$-Activated-$\hbox {K}^+$ Channel (CaKC)

Takahata et al. (2003) characterised the biophysical and pharmacological properties of native TEA-insensitive $\hbox {Ca}^{2+}$ activated currents in bovine parotid acinar cells. In their study, they developed a mathematical model that describes the basolateral CaKC current. The open probability of the channel is given by

$$\begin{aligned} P_{\mathrm{CaKC}}=\left( \frac{[\text {Ca}^{2+}]_i}{[\text {Ca}^{2+}]_i+K_{\mathrm{CaKC}}}\right) ^{\eta _2}, \end{aligned}$$

(19)

where $\eta _2=2.54$ is the Hill coefficient and $K_{\mathrm{CaKC}}$ the dissociation constant (a function of the potential difference across the membrane). We used the value found by Palk et al. (2010) of $0.182\ \upmu \hbox {M}$, as we require a small open probability at steady-state $\hbox {Ca}^{2+}$ concentrations. The flux is defined as

$$\begin{aligned} J_{\mathrm{CaKC}}=\frac{G_{\mathrm{CaKC}}P_{\mathrm{CaKC}}}{F}\left( V_b-V_{\mathrm{CaKC}} \right) , \end{aligned}$$

(20)

with Nernst potential

$$\begin{aligned} V_{\mathrm{CaKC}}=\frac{RT}{F z^\text {K}}\ln \left( \frac{[\text {K}^+]_e}{[\text {K}^+]_i} \right) , \end{aligned}$$

(21)

where $z^\text {K}=+1$, the ion’s valence.

$\hbox {Ca}^{2+}$-Activated-$\hbox {Cl}^-$ Channel (CaCC)

Frizzell and Hanrahan (2012) demonstrated that the apical CaCC channels are activated at low $\hbox {Ca}^{2+}$ concentrations by membrane depolarisation and when $\hbox {Ca}^{2+}$ reaches micromolar concentrations. As a simplification, we used a model similar to that of Takahata et al. (2003). Previous mathematical models for the acinar cell have used the model of Arreola et al. (2002). We found that there is no qualitative difference between the models. The CaCC model predicts a large maximum single channel conductance. With a Hill coefficient of $\eta _1=1.46$ and a dissociation constant of $K_{\mathrm{CaCC}}=0.26 \,\upmu \hbox {M}$. The open probability is given by

$$\begin{aligned} P_{\mathrm{CaCC}}=\left( \frac{[\text {Ca}^{2+}]_i}{[\text {Ca}^{2+}]_i+K_{\mathrm{CaCC}}}\right) ^{\eta _1}. \end{aligned}$$

(22)

In this way, the flux is defined as

$$\begin{aligned} J_{\mathrm{CaCC}}=\frac{G_{\mathrm{CaCC}}P_{\mathrm{CaCC}}}{F} \left( V_a-V_{\mathrm{CaCC}} \right) , \end{aligned}$$

(23)

with Nernst potential

$$\begin{aligned} V_{\mathrm{CaCC}}=\frac{RT}{z^{\text {Cl}}F}\ln \left( \frac{[\text {Cl}^-]_l}{[\text {Cl}^-]_i}\right) , \end{aligned}$$

(24)

where $z^{Cl}=-1$, the ion’s valence.

SLC4A2 Anion Exchanger (Ae2)

We use a model created by Falkenberg and Jakobsson (2010). It relies on a concentration gradient, i.e. it uses the $\hbox {HCO}_3^-$ gradient to pump $\hbox {Cl}^-$ into the cell. The energy required for this exchange is derived from the NaK-ATPase activity (Roussa et al. 2001). Its flux depends on the ionic concentrations in the cytoplasm and interstitium, the number of binding sites and the half saturation constants. The model evaluates the product of two terms and the exchanger’s conductance which is proportional to the density of active membrane proteins. The contribution from the concentrations and binding site properties represented by the Michaelis–Menten terms. Additionally as a simplification, we include the difference of the transporter in reverse which renders the exchanger bidirectional.

$$\begin{aligned} J_{\mathrm{Ae2}}&=G_{\mathrm{Ae2}}\Bigg [ \left( \frac{[\text {Cl}^-]_e}{[\text {Cl}^-]_e+K_{\mathrm{Cl}}}\right) \left( \frac{[\text {HCO}_3^-]_i}{[\text {HCO}_3^-]_i+K_\mathrm{B}}\right) \nonumber \\&\quad -\left( \frac{[\text {Cl}^-]_i}{[\text {Cl}^-]_i+K_{\mathrm{Cl}}}\right) \left( \frac{[\text {HCO}_3^-]_e}{[\text {HCO}_3^-]_e+K_\mathrm{B}} \right) \Bigg ]. \end{aligned}$$

(25)

Ae2	Description	Value	Units
$G_{\mathrm{Ae2}}^{\tiny {\dagger }}$	Ae2 activity	0.01807	$\text {fmol}/\text {s}$
$K_{\mathrm{Cl}}$	Half saturation	5.6	mM
$K_\mathrm{B}$	Half saturation	$10^{4}$	mM

1. $^{\dagger }$Parameter derived from the model
2. Parameters from Falkenberg and Jakobsson (2010)

$\hbox {Na}^+/\hbox {H}^+$ Exchanger (Nhe1)

Similarly to the Ae2 exchanger, our model for the Nhe1 exchanger is based on Falkenberg and Jakobsson (2010). Its flux is given by

$$\begin{aligned} J_{\mathrm{Nhe1}}&=G_{\mathrm{Nhe1}} \Bigg [ \left( \frac{[\text {H}^+]_i}{[\text {H}^+]_i+K_\mathrm{H}}\right) ^2 \left( \frac{[\text {Na}^+]_e}{[\text {Na}^+]_e+K_{\mathrm{Na}}} \right) \nonumber \\&\quad -\left( \frac{[\text {Na}^+]_i}{[\text {Na}^+]_i+K_{\mathrm{Na}}}\right) \left( \frac{[\text {H}^+]_e}{[\text {H}^+]_e+K_\mathrm{H}} \right) ^2 \Bigg ]. \end{aligned}$$

(26)

Nhe1	Description	Value	Units
$G_{\mathrm{Nhe1}}^{\tiny {\dagger }}$	Nhe1 activity	0.0305	$\text {fmol}/\text {s}$
$K_\mathrm{H}$	Half saturation	$4.5\times 10^{-4}$	mM
$K_{\mathrm{Na}}$	Half saturation	15	mM

1. $^{\dagger }$Parameter derived from the model
2. Parameters from Falkenberg and Jakobsson (2010)

SLC4A9 Anion Exchanger (Ae4)

The anion exchanger 4 transports interstitial $\hbox {Cl}^-$ into the cell while extruding 2 $\hbox {HCO}_3^-$ ions and $\hbox {Na}^+$-like monovalent cations (per cycle). In our model, the only monovalent cation, other than $\hbox {Na}^+$, is $\hbox {K}^+$. However, it has been suggested that $\hbox {Cs}^+$, $\hbox {Li}^+$ and $\hbox {Rb}^+$ are also extruded through the Ae4 (Peña-Münzenmayer et al. 2016).

Fig. 10

Schematic diagram of the Markov state model of a bidirectional Ae4 exchanger

We modelled the Ae4 exchanger as a Markov state model for a single exchanger (Dupont et al. 2016). We assume 2 conformational states: (1) the exchanger working forwards and the backward reaction with the $\hbox {HCO}_3^-$ binding site exposed in the interior ($A_i$ and $B_i$) and (2) with the $\hbox {HCO}_3^-$ binding site exposed on the exterior ($A_e$ and $B_e$), respectively (Fig. 10). The lower-case notation $\hbox {cl}$, $\hbox {hco}_3^-$, $\hbox {na}^+$ and $\hbox {k}^+$ denotes the concentration of each ion, respectively. As a simplification, we have assumed simultaneous binding and unbinding of ions to the exchanger. The equations that describe the exchanger under this model are

$$\begin{aligned}&\frac{\mathrm{d}A_i}{\mathrm{d}t}=k_{-1} \hbox {cl}_i B_i+ k_{4} A_e - A_i( k_1 \beta _i + k_{-4}), \end{aligned}$$

(27)

$$\begin{aligned}&\frac{\mathrm{d}B_i}{\mathrm{d}t}=k_1 \beta _i A_i + k_{-2} B_e - B_i(k_{-1} \hbox {cl}_i + k_2), \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\mathrm{d}A_e}{\mathrm{d}t}=k_3 \hbox {cl}_i B_i + k_{-4}A_i - A_e (k_{-3} \beta _e + k_{4}), \end{aligned}$$

(29)

$$\begin{aligned}&A_i+A_e+B_i+B_e=1. \end{aligned}$$

(30)

where $\beta _j=(\hbox {hco}_3^-)^2 (\hbox {na}^+ + \hbox {k}^+)$; for $j=i,e$. Eq. (30), is a conservation equation. The steady-state flux is

$$\begin{aligned} J_{Ae4}=k_{4}A_e-k_{-4}A_i=\frac{\beta _i \hbox {cl}_e - K_1K_2K_3K_4 \hbox {cl}_i \beta _e}{\beta _i \gamma _1+\left( \gamma _2+\gamma _3 \beta _i\right) \beta _e+ \left( \gamma _4 + \gamma _5 \beta _e\right) \hbox {cl}_i + \left( \gamma _6 + \gamma _7 \hbox {cl}_i\right) \hbox {cl}_e}, \end{aligned}$$

where $K_i=k_{-i}/k_i$, and $i=1,\ldots ,4$. The values $\gamma _j$, where $j=1,\ldots ,7$, are a condensed form to write the combination of the different parameters that make the equation. After some careful algebraic manipulation, it can be shown that the expression above simplifies to:

$$\begin{aligned} J_{Ae4}=G_{Ae4}\left[ \hbox {k}_+ \hbox {cl}_e (\hbox {hco}_3^-)_i^2 (\hbox {na}^+_i+\hbox {k}^+_i) - \hbox {k}_- \hbox {cl}_i (\hbox {hco}_3^-)_e^2 (\hbox {na}^+_e+\hbox {k}^+_e)\right] , \end{aligned}$$

(31)

where $G_{Ae4}$ (with units of $\text {fmol}$) denotes the density of exchangers. Thus, $J_{Ae4}$ has units of concentration/time. The parameters, $\hbox {k}_+$ and $\hbox {k}_-$, are the association and dissociation rates, respectively. These were found by solving the bicarbonate steady-state equation (Eq. 4).

Ae4	Description	Value	Units
$G_{\mathrm{Ae4}}$	Density of Ae4	0.66	$\hbox {amol}/\upmu \hbox {m}^{3}$
$\hbox {k}_+$	Rate	$1.92\times 10^{-2}$	$\hbox {mM}^{-4}\ \hbox {s}^{-1}$
$\hbox {k}_-$	Rate	$1.3 \times 10^{-5}$	$\hbox {mM}^{-4}\ \hbox {s}^{-1}$

1. Parameter values determined from the model

$\hbox {CO}_2$ Transport and $\hbox {HCO}_3^-$ Buffering

The acinar cell’s membrane is permeable to $\hbox {CO}_2$ which diffuses down its concentration gradient into the cytoplasm where it combines with water to form carbonic acid ($\hbox {H}_2\hbox {CO}_3$). Carbonic anhydrases catalyse the reaction and dissociate the acid quickly into $\hbox {H}^+$ ions and $\hbox {HCO}_3^-$ ions. For simplicity, we assume the reaction occurs as follows:

$$\begin{aligned} \text {CO}_2+\text {H}_2\text {O} \underset{k_{-1}}{{\mathop {\rightleftharpoons }\limits ^{k_{1}}}}\text {H}^+ + \text {HCO}_3^-. \end{aligned}$$

Using the law of mass action, and assuming chemical equilibrium, we have

$$\begin{aligned}&[\text {CO}_2]_l=\frac{k_{-1}}{k_{1}}[\text {HCO}_3^-]_l[\text {H}^+]_l, \\&[\text {CO}_2]_i=\frac{k_{-1}}{k_{1}}[\text {HCO}_3^-]_i[\text {H}^+]_i. \end{aligned}$$

Diffusion across both membranes is modelled as

$$\begin{aligned}&J_{\mathrm{CO}_{2_{a}}}=P_{\mathrm{CO}_2}\left( [\text {CO}_2]_l-[\text {CO}_2]_i \right) ,\\&J_{\mathrm{CO}_{2_{b}}}=P_{\mathrm{CO}_2}\left( [\text {CO}_2]_e-[\text {CO}_2]_i \right) , \\&J_{\mathrm{CO}_2}=P_{\mathrm{CO}_2} \left( 2[\text {CO}_2]_i-[\text {CO}_2]_l-[\text {CO}_2]_e \right) . \end{aligned}$$

$P_{\mathrm{CO}_2}$ is the membrane permeability to $\hbox {CO}_2$ (same for both membranes). From the reaction above, we can derive (using the law of mass action) a term for the production of $\hbox {HCO}_3^-$ and $\hbox {H}^+$ that is proportionally dependent on the influx of $\hbox {CO}_2$,

$$\begin{aligned} J_{\mathrm{Buffer}}=k_1[\text {CO}_2]_i-k_{-1}[\text {H}^+]_i[\text {HCO}_3^-]_i. \end{aligned}$$

$\hbox {HCO}_3^-$ Buffer	Description	Value	Units
$k_{1}$	Rate	11	$\hbox {s}^{-1}$
$k_{-1}$	Rate	$2.6\times 10^4$	$\hbox {s}^{-1}$
$P_{\mathrm{CO}_2}$	Membrane $\hbox {CO}_2$ transport rate	$1.97\times 10^{-13}$	$\hbox {s}^{-1}$

1. Parameter values taken from Sharp et al. (2015)

Electroneutrality

It is a constraint of the model that the interstitium, the cellular media and the acinar lumen must maintain electroneutrality. For instance, in the cellular compartment we keep track of 6 ionic species. However, in reality there are many more. The number of moles of large negatively charged molecules (with valence $z_x \le -1$) that are impermeable to the cellular membrane and thus trapped inside the cell is denoted $x_i$. To find its value, we note

$$\begin{aligned}{}[\text {K}^+]_i+[\text {Na}^+]_i+[\text {H}^+]_i-[\text {Cl}^-]_i -[\text {HCO}_3^-]_i-\frac{x_i}{\omega _i}=0, \end{aligned}$$

(32)

where $\omega _i$ is the volume of the cell. We solve for $x_i$,

$$\begin{aligned} x_i=\omega _i\left( [\text {K}^+]_i+[\text {Na}^+]_i+[\text {H}^+]_i -[\text {Cl}^-]_i-[\text {HCO}_3^-]_i \right) . \end{aligned}$$

(33)

Similarly, in the acinar lumen and the interstitium we must have:

$$\begin{aligned}&[\text {K}^+]_l+[\text {Na}^+]_l +[\text {H}^+]_l-[\text {Cl}^-]_l-[\text {HCO}_3^-]_l=0, \end{aligned}$$

(34)

$$\begin{aligned}&[\text {K}^+]_e+[\text {Na}^+]_e +[\text {H}^+]_e-[\text {Cl}^-]_e-[\text {HCO}_3^-]_e=0. \end{aligned}$$

(35)

Tight Junction

The tight junction currents are given by a linear current–voltage (I–V) relationship:

$$\begin{aligned}&J_\mathrm{K}^t=\frac{g_\mathrm{K}^t}{z^\text {K}F}\left( V_t-V_\mathrm{K}^t \right) , \end{aligned}$$

(36)

$$\begin{aligned}&J_{\mathrm{Na}}^t=\frac{g_{\mathrm{Na}}^t}{z^{\text {Na}}F}\left( V_t-V_{\mathrm{Na}}^t \right) . \end{aligned}$$

(37)

Here $z^{\text {Na}}=+1$ and $z^\text {K}=+1$, correspond to the valence of each ion species, respectively. $V_{Na}^t$ and $V_K^t$ are their respective Nernst potentials:

$$\begin{aligned}&V_{\mathrm{Na}}^t=\frac{RT}{F} \ln \left( \frac{[\text {Na}^+]_l}{[\text {Na}^+]_e}\right) , \\&V_{\mathrm{K}}^t=\frac{RT}{F} \ln \left( \frac{[\text {K}^+]_l}{[\text {K}^+]_e} \right) . \\ \end{aligned}$$

The potential at the tight junction, $V_t$, is given as:

$$\begin{aligned} V_t=V_a-V_b. \end{aligned}$$

Other Parameters of the Model

See Table 2.

Table 2 Parameters of the model