1 Introduction

Many infectious diseases such as measles, whooping cough, chickenpox, polio, mumps and rubella take special interest in children. The major reason for this is that they have not yet developed immunity to them. Although vaccination has reduced the infection from these diseases and eradicated some of them like small pox, they continue to kill thousands of children around the world every year. Thus, understanding childhood disease transmission and control remains essential. Because there are enough infection data, mathematical models are increasingly useful for these purposes. Most of these models are compartmental models which classify the population with respect to various stages of disease infection.

The classical compartmental model for childhood infectious diseases is the McKendrick–Kermack SIR model with vital dynamics. This model has three compartments:

  • Susceptible S(t) individuals who are currently susceptible to the disease;

  • Infectious I(t) individuals who are currently infected with the disease;

  • Removed R(t) individuals who have recovered from the disease and therefore possess immunity.

It is assumed that the birth rate and the natural death rates are both \(\mu \). This assumption keeps the population size constant at a normalized value one. Infected children recover at a constant rate \(\nu \) and then become immune to the disease. Finally, it is assumed that the incidence is proportional to the product of the number of susceptible and infected individuals. These lead to the following system of equations:

$$\begin{aligned} \frac{\mathrm{d}S(t)}{\mathrm{d}t}&=\mu -\beta (t) S(t)I(t)-\mu S(t),\\ \frac{\mathrm{d}I(t)}{\mathrm{d}t}&=\beta (t)S(t)I(t)-\nu I(t)-\mu I(t),\\ \frac{\mathrm{d}R(t)}{\mathrm{d}t}&=\nu I(t)-\mu R(t), \end{aligned}$$

where \(S(t)+I(t)+R(t)=1\). Many authors have extended this model to include individuals who are exposed (E) to infection, but are not yet infectious. They assumed that children leave the exposed compartment and enter the infectious (I) compartment at some constant rate a, the reciprocal of which equals the mean latent period. This model, called the SEIR model, is described by the following system of equations:

$$\begin{aligned} \frac{\mathrm{d}S(t)}{\mathrm{d}t}&=\mu -\beta (t) S(t)I(t)-\mu S(t),\\ \frac{\mathrm{d}E(t)}{\mathrm{d}t}&=\beta (t)S(t)I(t)-aE(t)-\mu E(t),\\ \frac{\mathrm{d}I(t)}{\mathrm{d}t}&=aE(t)-\nu I(t)-\mu I(t),\\ \frac{\mathrm{d}R(t)}{\mathrm{d}t}&=\nu I(t)-\mu R(t). \end{aligned}$$

The rate at which susceptibles become infected is called the transmission rate \(\beta \). This transmission rate depends on factors such as the frequency and closeness of contacts, the infectivity of the infectious individuals, and the susceptibility of susceptible individuals. Thus, the transmission rate will be higher when children are packed together and lower when they are not. Since children turn to be crowded together in school seasons and separated during holidays, the transmission rate will therefore be extremely high when children are in school and extremely low when they are on holidays. This means that the transmission rate for a childhood disease varies dramatically in time.

According to Section 3.4.9 of Anderson and May (1991), ‘...the direct measurement of the transmission rate is essentially impossible for most infections. But if we wish to predict the changes wrought by public health programmes, we need to know the transmission rate ....’ Thus, unlike other parameters of infectious disease models, such as recovery rate, birth rate and death rate, that can be easily measured directly via public health databases, it is essentially impossible to measure the transmission rate directly for certain infectious diseases. Moreover, other parameters are relatively stable, while the transmission rate varies dramatically. Given that the important events of disease transmission are incorporated in the transmission rate, there is urgent need to have an estimate for this parameter. Some researchers model the transmission rate using a step function based on school calendars (Earn et al. 2000). Other authors use the sinusoidal function \(\beta (t)=\beta _0(1+\alpha \cos (2\pi t))\), where \(\beta _0\) is the mean transmission rate and \(\alpha \) is the amplitude of the seasonal variation (Glendinning and Perry 1997).

These models do not take into account all the seasonal factors that drive the transmission rate of childhood infectious diseases. Even though the neglected factors are of little importance, including them in the model will paint a complete picture of the nature of the transmission rate of these diseases. One additional drawback of these models is the lack of transmission data to validate them with. There is therefore a need to extract the time-dependent transmission rate through a solution of an inverse problem so as to have a complete picture of the transmission rate of these diseases and equally validate the assumed transmission rate functions in the literature.

Some researchers (Becker 1989; Fine and Clarkson 1985) used the discrete time SI or SIR model to extract the time-dependent transmission rate. Fine and Clarkson (1985) used the model:

$$\begin{aligned} I(t+1)&=I(t)S(t)\beta (t)\\ S(t+1)&=S(t)-I(t+1)+B(t)-V(t) \end{aligned}$$

where I(t) and \(I(t+1)\) denote the infected population at time periods t and \(t+1\), \(S(t+1)\) and S(t) the susceptible population at time periods t and \(t+1\), \(\beta (t)\) the time-dependent transmission parameter, B(t) the number of susceptible introduced or born into the population, V(t) the vaccinated population. From this model, the authors obtained the recursive formula:

$$\begin{aligned} \beta (t)=\frac{I(t+1)}{\beta (t)S(t)}. \end{aligned}$$

This formula requires S(t), which is often difficult to estimate especially for outbreaks in which a reasonable percentage of the population is immune to infection. Also the formula is not explicit. For other drawbacks of this formula, see Pollicott et al. (2010, 2012), Hadeler (2011). Pollicott et al. (2010, 2012) originally introduced the inverse method for estimating a continuous time transmission rate from prevalence data. Hadeler (2011) extended the inverse method for incidence data and other possibilities. This inverse method does not require the knowledge of S(t) and leads to an explicit formula for \(\beta (t)\). The inverse method for deriving these algorithms is applicable to a majority of infectious diseases, but the algorithms have only been constructed and applied to pre-vaccination data so far.

One can reduce the number of susceptible children with vaccines. Vaccination is the administration of antigenic material to stimulate an individual’s immune system to develop adaptive immunity to a pathogen. Vaccines can ameliorate both mortality and morbidity. The effectiveness of vaccination has been widely studied and verified since the first work of Edward Jenner on smallpox (Lombard et al. 2007). In this paper, we first derive the algorithms with vaccination which is dominantly important in the control of infectious diseases nowadays.

Assuming that all children grow to adults at some point in the future, in this paper, we extend the SEIR model for childhood diseases to an SEIRA model by adding the adult compartment (A). The SEIRA model is extended to include a compartment for children that have been vaccinated, and the effect of vaccination on the dynamics of I(t) is studied. We carry out stability and sensitivity analyses of these two models and extend both the prevalence and incidence algorithms, respectively. Our sensitivity analysis emphasizes the importance of the transmission rate in controlling outbreaks and thus the need to estimate this key parameter. The applicability of our derived incidence algorithm is illustrated with pre- and post-vaccination measles data from Liverpool and London. The transmission rate estimated using our algorithm has two dominant spectral peaks of frequencies 1 and 3 times per year. These dominant frequencies are the same for pre- and post-vaccination situations for both cities. The dominant frequency of 1 per year is consistent with common belief that measles is driven by seasonal factors and the 3 times per year frequency indicates the superiority of school contacts in driving measles transmission over other seasonal factors. The peak values of 1 per year and the 3 per year frequencies are comparable for both pre- and post-vaccination data from Liverpool, while the 1 per year peak value is larger than the 3 per year peak value for both pre- and post-vaccination data from London. This is because London is a landlocked city and thus has relatively high-temperature variations which strongly affect the seasonality of the measles virus with subsequent influence on its transmission. Liverpool, on the other hand, is a coastal city with relatively stable temperature, and thus, the main modulator of the transmission of measles virus for this city was school dates. We find that the dominant frequencies of the Fourier transform of the transmission rate in London have less noise than that of the Fourier transform of the transmission rate in Liverpool. This could be attributed to the city size as London is a much larger city than Liverpool.

2 The SEIRA Model

Recall that in the derivation of the SEIR model, the total population is divided into four compartments: susceptible, exposed, infective and recovered. This model can be applied to all infectious diseases satisfying its assumptions. However, it is not suitable for childhood infectious diseases since, in the SEIR model, adults who have never been infected nor vaccinated are also considered as susceptibles.

When studying childhood infectious diseases, we first classify the population into the adult ( A ) and the juvenile groups. Then, divide the juvenile group into susceptibles ( S ), exposed ( E ), infective ( I ) and recovered ( R ).

With SEIR model, we consider natural death rate for every group. But children usually do not die naturally. They die only because of some specific reasons such as accidents or diseases and their death rate is much lower than the natural death rate. Therefore, here, we ignore natural death rate for the juvenile group. Instead, we consider growth rate as children will grow up and no longer be susceptible. We assume that children grow to become adults at a rate g , i.e., people under 1 / g years old will be considered as juvenile. Transition terms between S,  E,  I and R are the same as in SEIR model.

Our model, called the SEIRA model, is described by the following system of equations:

$$\begin{aligned} \frac{\mathrm{d}S(t)}{\mathrm{d}t}&= \delta A(t)-\beta (t) S(t) I(t) - g S(t),\nonumber \\ \frac{\mathrm{d}E(t)}{\mathrm{d}t}&= \beta (t) S(t) I(t)-aE(t)-gE(t), \nonumber \\ \frac{\mathrm{d}I(t)}{\mathrm{d}t}&= aE(t)-\nu I(t)-gI(t),\nonumber \\ \frac{\mathrm{d}R(t)}{\mathrm{d}t}&=\nu I(t)-g R(t),\nonumber \\ \frac{\mathrm{d}A(t)}{\mathrm{d}t}&=g(S(t)+E(t)+I(t)+R(t))-\delta A(t). \end{aligned}$$
(1)

The parameters are described in Table 1, which also contains the default values of these parameters for measles.

Values of the parameters a and \( \nu \) for measles are taken from Anderson and May (1991) and “The weekly OPCS reports”: \( a=52/\hbox {year} \) and \( \nu =52/\hbox {year} .\) Thus, the infectious period is the same as the exposed period which is \( 1~\hbox {year}/52=1~\hbox {week} \). We assume that the average life span is 80 years and only kids under 16 are susceptible to measles. Therefore, \( g=1/16/\hbox {year}\) and natural death rate \( \delta =1/64/\hbox {year} .\) Values of p and q are mainly determined by a vaccination policy, which can be as low as 0 % if there is no vaccination or as high as 100 % if every individual is vaccinated. p will be used in Sect. 7.

In Sects. 3 and 4, we assume that \(\beta \) is a constant and in Sects. 5, and 6, it is considered to be a function of time.

Table 1 Parameter descriptions and values for measles
Full size table

3 Qualitative Analysis

In this section, we list qualitative results such as positivity, boundedness, equilibria and their stability of the SEIRA model. The proofs of the theorems in this section are presented in “Appendix”.

Theorem 1

The compact set \(\Omega =\) {( S, E, I, R, A ): \(S\ge 0,E\ge 0,I\ge 0,R\ge 0,A\ge 0, S+E+I+R+A=1\)} is positively invariant for the semiflow generated by system (1).

Theorem 2

System (1) has two equilibria: the disease-free equilibrium point \((S_1^*,~E_1^*,~I_1^*,~R_1^*,~A_1^*)= \left( \frac{\delta }{g+\delta },~0,~0,~0,~\frac{g}{g+\delta }\right) \) and the endemic equilibrium point

$$\begin{aligned} \left( S_2^*,~E_2^*,~I_2^*,~R_2^*,~A_2^*\right)= & {} \left( \frac{(a+g)(\nu +g)}{a\beta },~\frac{g\delta }{(a+g)(g+\delta )}\right. \\&\left. -\frac{g(\nu +g)}{a\beta },~\frac{ag\delta }{(a+g)(g+\delta )(\nu +g)}\right. \\&\left. -\frac{g}{\beta }, \frac{a\nu \delta }{(a+g)(g+\delta )(\nu +g)} -\frac{\nu }{\beta },~\frac{g}{g+\delta }\right) . \end{aligned}$$

If \( a\delta \beta <(a+g)(g+\delta )(\nu +g) \), the disease-free equilibrium will be locally asymptotically stable and the endemic equilibrium will not be feasible. On the other hand, if \( a\delta \beta >(a+g)(g+\delta )(\nu +g) \), the endemic equilibrium will be locally asymptotically stable and the disease-free equilibrium will be unstable.

Conjuncture 1

When \( R_0<1,~\lim _{t \rightarrow +\infty } (S(t),~ E(t),~I(t),~R(t),~A(t))\ \longrightarrow \) Disease-free equilibrium (DFE) and when \( R_0>1,~\lim _{t \rightarrow +\infty } (S(t),~ E(t),~I(t),~R(t), A(t))\ \longrightarrow \) Endemic equilibrium (EE), where \(R_0= \frac{a\delta \beta }{(a+g)(g+\delta )(\nu +g)} \) is the basic reproduction number.

Recall that when \( R_0>1 \), the disease can spread and when \( R_0<1 \), the disease will finally disappear. We can rewrite \( R_0 \) as

$$\begin{aligned} R_0=\frac{\beta }{\nu +g}\cdot \frac{a}{a+g}\cdot \frac{\delta }{\delta +g}. \end{aligned}$$

We know that \( \beta S I \) is the number of new cases over a unit time. Hence, the average number of new cases caused by one infective individual is \( \frac{\beta S I}{I}=\beta S \). Therefore, the number of susceptibles an infective individual can infect is the average number over a unit time multiply by the average length of duration an infective individual stay infectious which is \( \beta S \cdot \frac{1}{\nu +g} \). The fraction of the infected individuals who can finally become infective is the probability that an exposed individual will become infective in a unit time multiply by the time duration of an exposed individual stay exposed which is \( a \cdot \frac{1}{a+g} \). The expected fraction of susceptibles is \(\frac{\delta }{\delta +g} \) which is the value of susceptibles at the disease-free steady state. Therefore, \( \beta S \cdot \frac{1}{\nu +g}\cdot \frac{a}{a+g}= \beta \cdot \frac{\delta }{\delta +g}\cdot \frac{1}{\nu +g}\cdot \frac{a}{a+g}\) is the average number of susceptibles that one infective individual can infect.

Using the parameter values in Table 1, one gets \(R_0=49.88.\) This value is higher than the average value for \(R_0\), usually between 12 and 18. This is due to the maximum susceptible age and live span assumptions made above. Imposing an upper susceptible age of 6 years and an appropriate life span will yield a lower \(R_0\) value.

4 Sensitivity Analysis

In this section, we calculate, analyze and compare the normalized forward sensitivity indices of the outbreak peak value, time of outbreak peak and steady state value of I(t) , to the parameters of the system by computing

$$\begin{aligned} \hbox {S.I.}=\frac{p}{X^*}\frac{\partial X^*}{\partial p} , \end{aligned}$$
(2)

where \( X^* \) is the quantity being considered and p is the parameter which \( X^* \)depends upon. Sensitivity indices can be positive or negative which indicate the nature of the relationship. The magnitude of S.I. indicates the strength of the relationship.

When studying quantities like the peak value or the peak time which do not have explicit formulas, we compute an approximate value of their S.I. as follows

$$\begin{aligned} \hbox {S.I.}=\frac{p}{X^*(p)}\frac{ X^*(p+\Delta p)-X^*(p-\Delta p)}{2\Delta p}. \end{aligned}$$
(3)

We calculate S.I. with respect to one specific parameter by perturbing this parameter only and keeping the others unchanged. Here, we take \( \Delta p=1\, \% p \).

4.1 Sensitivity Analysis of the Outbreak Peak Value

The sensitivity indices of the amplitude of the outbreak peak show how the first epidemic depends on the parameters as seen in Table 2.

Table 2 The sensitivity indices of the value of the outbreak peak with respect to the parameters values \( \delta =1/64/12/\hbox {month},~ \beta =55/\hbox {month}, ~g=1/16/12/\hbox {month},~ \nu =52/12/\hbox {month}, a=52/12/\hbox {month} \) and initial values \( S(0)=0.2,~ E(0)=0.002, ~I(0)=0.002, ~R(0)=0.006,~ A(0)=0.79 \)
Full size table

The removal rate \(\nu \) has the strongest relationship to the magnitude of the outbreak peak. The negative value tells us that a lower removal rate would lead to a more severe epidemic. In contrast to the birth/death rate \(\delta \) which has among the lowest of sensitivity indices, \(\nu \) would thus be an important parameter to control in order to reduce the harm of an outbreak.

Both the average transmission rate \( \beta \) and a have strong positivity relationship to the peak outbreak as a higher \( \beta \) value would lead to a higher number of people in the exposed compartment and a higher a would move more exposed to the infectives compartment.

The sensitivity index with respect to the human birth/death rate \(\mu \) is very low in comparison with all the others. This makes sense, because the initial peak of an epidemic occurs relatively quickly after the introduction of sick people, and the birth and death of new susceptibles would take much longer time.

The sensitivity of the growth rate g to the outbreak peak is negative because a larger growth rate will move people from the invectives compartment to the adult compartment faster, thus reducing the outbreak peak. Similar to birth/death rate \( \delta \), growth rate g has a small influence on the peak value.

In fact, parameters related to demography, such as birth/death rate and growth rate, would have small influence on the outbreak level as the initial peak appears relatively quickly. Parameters which are directly related to infection would have important influence on the initial peak. For instance, the following parameters: a which determines how fast exposed individuals will become infectious, \( \nu \) which determines how quickly infectives will move to the recovered compartment and \( \beta \) which determines how many susceptibles will be infected all have a strong relationship with the outbreak as expected because they are directly related to infection.

4.2 Sensitivity Analysis of the Outbreak Peak Time

Sensitivity indices of the outbreak peak time measure how the first epidemics outbreak time depends on different parameters as seen in the Table 3.

Table 3 The sensitivity of the outbreak peak time with respect to the parameters with values \(\delta =1/64/12/\hbox {month}, \beta =55/\hbox {month}, g=1/16/12/\hbox {month}, \nu =52/12/\hbox {month}, a=52/12/\hbox {month}\) and initial values \( S(0)=0.2,~ E(0)=0.002, ~I(0)=0.002, ~R(0)=0.006,~ A(0)=0.79 \)
Full size table

As outlined previously, we have the same reason that birth/death rate \( \delta \) and growth rate g have less influence on the outbreak time than the other three parameters.

We can see from Table 3 that the average transmission rate \(\beta \) has the strongest influence on the dynamics of the system. This suggests that \( \beta \) is a more important parameter to control to prevent outbreaks. The negative relationship tells us that a larger average transmission rate would lead to a quicker outbreak.

The relationship between rate a and the time of the maximum outbreak is negative, because a higher contact rate (shorter latent period) will cause more new infections and the timing of the maximum would be attained earlier.

The removal rate still has an important effect on the outbreak time. The positive relationship between \( \nu \) and the outbreak time is because patients will recover faster with a larger \( \nu \) value, thereby postponing the outbreak time.

4.3 Sensitivity Analysis of the Endemic Steady State

Endemic steady state determines the levels of the different groups of an endemic infectious disease. It represents the expectation of the final size of all the groups. In Table 4, we list sensitivity indices of \( I_2^* \) with respect to all the parameters.

Table 4 Sensitivity of the endemic steady state with respect to the parameters with values \( \delta =1/64/12/\hbox {month}, \beta =55/\hbox {month}, g=1/16/12/\hbox {month}, \nu =52/12/\hbox {month}, a=52/12/\hbox {month}\)
Full size table

The endemic level of infective individuals is most sensitive to the recovery rate \(\nu \) and birth/death rate \(\delta \). It has a strong negative relationship with \(\nu \) because recovering is the main way that infectives leave the infected compartment. The relationship with \(\delta \) is positive as a larger \( \delta \) means more susceptible newborns will possibly become infectives. Rate a has a weak but positive relationship with \(I_2^*\) as expected because a larger a causes more people in the exposed compartment to become infectives. The average transmission rate \( \beta \) is also of great importance in controlling the endemic level of the infectives. The positive relationship is obvious since larger \( \beta \) means more susceptibles will get infected.

5 Extracting the Time-Dependent Transmission Rate \(\beta (t)\) from Prevalence Pre-vaccination Data

In this section, we assume that \(\beta (t)\) is a function of time, compute the formula for \( \beta (t) \) based on prevalence pre-vaccination data and then use it to construct an algorithm.

Theorem 3

Suppose the epidemic is observed over the time interval [0, T], where \(t=0\) and \(t=T\) are, respectively, the start and end of observations, then the time-dependent transmission function \(\beta (t)\) for System (1) satisfy \( M{\beta ''\beta ^2}+N{(\beta ')^2\beta }+ P{\beta '\beta ^2}-L{\beta ^4}-Q{\beta ^3}=0\) where f(t) is a smooth positive function which matches the infection data in the interval [0, T],

$$\begin{aligned} H(t)&\triangleq f''(t)+(\nu +2g+a)f'(t)+(a+g)(\nu +g)f(t)\\ M&=D=-Hf^3,\\ N&=C=2Hf^3,\\ P&=B-(2g+\delta )Hf^3=2Hf'f^2-2H'f^3-(2g+\delta )Hf^3,\\ Q&=-(A+(2g+\delta )H'f^3-(2g+\delta )Hf'f^2+g(g+\delta )Hf^3)\\&=-(H''f^3-Hf''f^2-2H'f'f^2+2H(f')^2f+(2g+\delta ) H'f^3\\&\quad -(2g+\delta )Hf'f^2+g(g+\delta )Hf^3),\\ L&=-(H'f^4+(g+\delta )Hf^4-ag\delta f^4). \end{aligned}$$

Proof

See “Appendix”. \(\square \)

Based on the formula for \(\beta (t)\) derived above, we now construct a prevalence algorithm for extracting the transmission rate from the SEIRA model.

Step 1 Smoothly interpolate the infection data with a spline or trigonometric function to generate a smooth function, f(t).

Step 2 Calculate the function \(H(t)= f''(t)+(\nu +2g+a)f'(t)+(a+g)(\nu +g)f(t)\). Compute M, N, P, Q and L by plugging H(t) into (12).

Step 3 Choose \( \beta (0) , \beta '(0)\) and interval T, use an ODE solver to solve equation \(M{\beta ''\beta ^2}+N{(\beta ')^2\beta }+P{\beta '\beta ^2}-L{\beta ^4}-Q{\beta ^3}=0\) for \( \beta (t) \) on interval the [0, T].

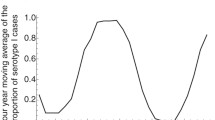
In the absence of real prevalence data, we use simulated data to test this algorithm. To this end, consider the following function \(f(t)=10^{-3}[1.4+\cos (2\pi t/12)] \) that approximates fractions of infectives from a typical infectious disease with periodic outbreaks. Figure 1 contains the dynamics of \( \beta (t)\) for this data set, using the algorithm above.

Fig. 1
figure 1

\( \beta (t) \) extracted from fake prevalence data \(f(t)=10^{-3}[1.4+\cos (2\pi t/12)] \) with initial value \(\beta (0)=56,\beta '(0)= -1 \), and parameters \( \nu =52/12,a=52/12,g=1/16/12,\delta =1/64/12 \)

Full size image

6 Extracting the Time-Dependent Transmission Rate from Pre-vaccination Incidence Data

In this section, we compute the formula for \( \beta (t) \) that depends on incidence data and use it to construct the incidence algorithm. As in the previous section, we assume that the transmission rate depends on time.

6.1 Solution of the Inverse Problem for the SEIRA Model

To construct the algorithm, we first rewrite \(\beta (t)\) in terms of \( \omega (t). \) With \( \omega (t)=\beta SI \) and \( S+E+I+R+A=1 \), the SEIRA model can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}S(t)}{\mathrm{d}t}&= (\delta A(t)-\omega (t))-gS(t) \end{aligned}$$
(4)
$$\begin{aligned} \frac{\mathrm{d}E(t)}{\mathrm{d}t}&= \omega (t)-(a+g)E(t), \end{aligned}$$
(5)
$$\begin{aligned} \frac{\mathrm{d}I(t)}{\mathrm{d}t}&= aE(t)-(\nu +g)I(t),\end{aligned}$$
(6)
$$\begin{aligned} \frac{\mathrm{d}R(t)}{\mathrm{d}t}&=\nu I(t)-g R(t),\end{aligned}$$
(7)
$$\begin{aligned} \frac{\mathrm{d}A(t)}{\mathrm{d}t}&=g-(g+\delta )A(t). \end{aligned}$$
(8)

We have the following theorem:

Theorem 4

For the SEIRA, given a continuous function w(t) generated from the incidence data, \(\beta (t)\) can be estimated by \(\frac{\omega (t)}{S(t)I(t)}\) with S(t) and I(t) given by (9) and (10), respectively.

$$\begin{aligned} S(t)&= S(0)e^{-gt}+\int _0^t\left( \delta \left( A(0) e^{-(g+\delta )s}\right. \right. \nonumber \\&\left. \left. \quad +\int _0^s g e^{(g+\delta )(\sigma -s)}\mathrm{d}\sigma \right) -\omega (s)\right) e^{g(s-t)}\mathrm{d}s\end{aligned}$$
(9)
$$\begin{aligned} I(t)&= I(0) e^{-(\nu +g)t}+\int _0^ta (E(0) e^{-(a+g)s}\nonumber \\&\quad +\int _0^s \omega (\sigma ) e^{(a+g)(\sigma -s)}\mathrm{d}\sigma )e^{(\nu +g)(s-t)}\mathrm{d}s \end{aligned}$$
(10)

Proof

See “Appendix”. \(\square \)

We now turn the above theorem into an algorithm to extract time-dependent transmission rate \(\beta (t)\) numerically, using incidence data:

Step 1  Smoothly interpolate incidence data with a spline or trigonometric function to generate a smooth \( \omega (t)\) ( in fact, we only need \(\omega (t)\) to be continuous, not necessarily smooth).

Step 2  Let T be the whole period of data. Compute \(\beta (t)=\frac{\omega (t)}{S(t)I(t)},\) for \(t \in [0,T]\).

Because we have real incidence data, we test the latter algorithm using both fake and real data. Firstly, we test the performance of the incidence algorithm using fake data. As before, we use the function \( f(t)=10^{-3}[1.4+\cos (2\pi t/12)]\) to generate the data. Figure 2 shows \( \beta (t) \) plotted against time using simulated data. Our algorithm estimates the transmission rate perfectly well, using this data.

Fig. 2
figure 2

\( \beta (t) \) extracted from fake incidence data \(f(t)=10^{-4}[2.7+1.5sin(2\pi t/12)] \) with initial value \(S(0)=0.25,E(0)=0.0009,I(0)=0.0001,A(0)=0.7 \), and parameters \(\nu =52/12,a=52/12,g=1/16/12,\delta =1/64/12 \). \( \beta (t) \) from time 0 to 40

Full size image

Secondly, we use real incidence data from Liverpool and London given in Fig. 3 to test the efficiency of our prevalence algorithm.

Fig. 3
figure 3

Measles weekly notification data in Liverpool and London from 1944 to 1986

Full size image

Figure 4a shows \( \beta (t) \) extracted from pre-vaccination measles weekly notification data of Liverpool from 1944 to 1966 using the prevalence algorithm. There are more noises with the weekly data. This is because Liverpool is a relatively smaller city compare to London. The population of Liverpool is less then 1/10 that of London. Figure 4b plots modulus of Fourier transform of \( \beta (t) \) in Liverpool. We observe two dominant peaks with frequencies 1/year and 3/year.

Figure 5a illustrates \( \beta (t) \) extracted from post-vaccination measles weekly notification data of London from 1944 to 1966 by the prevalence algorithm. Figure 5b plots modulus of Fourier transform of \(\beta (t) \) in this city. As with that in Liverpool, two dominant peaks with frequencies 1/year and 3/year are observed.

Fig. 4
figure 4

Time-dependent transmission rate \( \beta (t) \) of Liverpool from year 1944 to 1966 and the modulus of its Fourier transform. The parameters are \( \delta =1/64/52/\hbox {week}, a=52/52/\hbox {week}, \nu =52/52/\hbox {week}, g=1/16/52/\hbox {week} \) and initial values \( S(0)=0.2, E(0)=0.001, I(0)=0.001, A(0)=0.78.\) a \(\beta (t)\) of Liverpool from 1944 to 1966. b Modulus of the Fourier transform of \(\beta (t)\) in Liverpool from 1944 to 1966

Full size image
Fig. 5
figure 5

Time-dependent transmission rate \( \beta (t) \) of London from year 1944 to 1966 and the modulus of its Fourier transform. The parameters used are \( \delta =1/64/52/\hbox {week}, a=52/52/\hbox {week}, \nu =52/52/\hbox {week}, g=1/16/52/\hbox {week} \) and initial values \( S(0)=0.2, E(0)=0.001, I(0)=0.001, A(0)=0.78.\) a \(\beta (t)\) of London from 1944 to 1966. b Modulus of the Fourier transform of \(\beta (t)\) in London from 1944 to 1966

Full size image

The 1/year peak is consistent with common belief that measles is driven by seasonal factors such as environmental changes and immune system changes and the 3/year peak indicates the superiority of school contacts in driving measles transmission over other seasonal factors and thus support authors in Grassly and Fraser (2006), Keeling and Rohani (2008) that ignore other seasonal factors in determining the transmission rate of measles. The 1/year frequency peak value is about twice the value of the 3/year frequency for the Fourier transform of the transmission rate in London, whereas there is no great difference in the peak values of the dominant frequencies for that in Liverpool. This might be linked to the geographical location of the two cities. Also, the dominant frequencies are robust with respect to initial values. Moreover, the dominant frequencies in London have less noise than those in Liverpool because the population of London is greater than that of Liverpool and it is less sensitive to unexpected factors.

7 The SEIRA Model with Vaccination

In this section, we investigate the effect of vaccination on the SEIRA epidemic model. Vaccination is the process by which a vaccine stimulates the immune system of an individual to build immunity against a pathogen. Vaccination can ameliorate both mortality and morbidity. The effectiveness of vaccination has been widely studied and verified since the first work of Edward Jenner on smallpox (Lombard et al. 2007).

Different vaccination strategies are used to deal with different situations. Pediatric vaccination is an efficient way in preventing dangerous human infectious diseases. Much work has focused on the vaccination of newborn babies or infants to reduce the prevalence of diseases such as measles, mumps and rubella. Mathematical treatment of vaccination is straight forward and only needs a single addition to the SEIRA model. Using p to denote the fraction of the newborns that are successfully vaccinated, we obtain the following model:

$$\begin{aligned} \frac{\mathrm{d}S(t)}{\mathrm{d}t}&= \delta (1-p) A(t)-\beta (t) S(t) I(t) - g S(t),\nonumber \\ \frac{\mathrm{d}E(t)}{\mathrm{d}t}&= \beta (t) S(t) I(t)-aE(t)-gE(t),\nonumber \\ \frac{\mathrm{d}I(t)}{\mathrm{d}t}&= aE(t)-\nu I(t)-gI(t), \nonumber \\ \frac{\mathrm{d}R(t)}{\mathrm{d}t}&=\nu I(t)-g R(t)+\delta p A(t), \nonumber \\ \frac{\mathrm{d}A(t)}{\mathrm{d}t}&=g(S(t)+E(t)+I(t)+R(t))-\delta A(t). \end{aligned}$$
(11)

However, it is not cost-effective to control rare infectious diseases by pediatric vaccination. To this end, another vaccination policy, random vaccination is conducted for rare infectious diseases or any potential outbreak. With this policy, all unvaccinated susceptibles and not just newborns are vaccinated.

It is difficult for a disease to spread as long as the fraction of susceptibles is kept low. Therefore, it is more reasonable that we should vaccinate less if the fraction of susceptibles is lower and vice versa.

In Sects. 8 and 9, we assume that \(\beta \) is a constant, and in Sects. 10 and 11, it is considered to be a function of time.

8 Qualitative Analysis

In this section, we list qualitative results such as positivity, boundedness, equilibria and their stability of system (11). The proofs of the theorems in this section are presented in “Appendix”.

Theorem 5

The compact set \(\Gamma = \{( S, E, I, R, A \)): \(S\ge 0,E\ge 0,I\ge 0,R\ge 0,A\ge 0, S+E+I+R+A=1\)} is positively invariant for the semiflow generated by system (11).

Theorem 6

System (11) has two equilibria: the disease-free equilibrium \(~(S_1^*,~E_1^*,~I_1^*, R_1^*,~A_1^*)=\left( \frac{\delta (1-p)}{g+\delta },~0,~0,~\frac{\delta p}{g+\delta },~\frac{g}{g+\delta }\right) \) and the endemic equilibrium \((S_2^*,~E_2^*,~I_2^*,~R_2^*, A_2^*)= \left( \frac{(a+g)(\nu +g)}{a\beta },~\frac{g\delta (1-p)}{(a+g)(g+\delta )}-\frac{g(\nu +g)}{a\beta },~\frac{ag\delta (1-p)}{(a+g)(g+\delta )(\nu +g)}-\frac{g}{\beta }, \frac{a\nu \delta (1-p)}{(a+g)(g+\delta )(\nu +g)}-\frac{\nu }{\beta }+\frac{\delta p}{g+\delta },~\frac{g}{g+\delta }\right) \)

When \( {a\delta (1-p)\beta }<{(a+g)(g+\delta )(\nu +g)} \), the disease-free equilibrium is locally asymptotically stable and the endemic equilibrium is not feasible ,and when \( a\delta (1-p) \beta >(a+g)(g+\delta )(\nu +g) \), the endemic equilibrium is locally asymptotically stable and the disease-free equilibrium is unstable.

The basic reproduction number is

$$\begin{aligned} R_0=\frac{a\beta \delta (1-p) }{(a+g)(g+\delta )(\nu +g)}. \end{aligned}$$

It can be rewritten as

$$\begin{aligned} R_0=\frac{\beta }{\nu +g}\cdot \frac{a}{a+g}\cdot \frac{\delta }{\delta +g}\cdot (1-p). \end{aligned}$$

The first three terms have the same meanings as before. When considering vaccination, the level of susceptibles will be ‘discounted’ by \( p \times 100\,\% \) because vaccinated newborns are not susceptible.

9 Sensitivity Analysis

In this section, we focus only on the sensitivity of the outbreak peak value, time of outbreak peak and steady state value of I(t) , to the Vaccinated fraction p,  since we have discussed the sensitive indices of these quantities to the other parameters of the model in one of the previous sections.

9.1 Sensitivity Analysis of the Outbreak Peak Value

Table 5 shows the sensitivity of the outbreak peak value to all the parameters of our model. Comparing sensitivity analysis of this model with that of the previous model, we can see that the absolute value of sensitivity indices with respect to all parameters are smaller, but vaccination does not change ranks of their importance. This is because it is applied only to newborn babies, and newborns constitute only a very small proportion of the total child population. The Vaccinated fraction p has a negative relationship with the outbreak peak since more pediatric vaccination will result in less infectives.

9.2 Sensitivity Analysis of the Outbreak Peak Time

From Table 6, we can see that the Vaccinated fraction p is the least important to control in preventing outbreaks. This is because the vaccination here is pediatric vaccination and there are fewer newborns compare to all children.

Table 5 Sensitivity of the value of the outbreak peak to the parameters with the parameter values \(p=0.5, \delta =1/64/12/\hbox {month},~ \beta =150/\hbox {month}, ~g=1/16/12/\hbox {month},~ \nu =52/12/\hbox {month},~ a=52/12/\hbox {month} \) and initial values \( S(0)=0.0998,~ E(0)=0.0001, ~I(0)=0.0001, ~R(0)=0.11,~ A(0)=0.79 \)
Full size table
Table 6 Sensitivity of the outbreak peak time to the parameters with parameter values \(p=0.5, \delta =1/64/12/\hbox {month},~ \beta =150/\hbox {month}, ~g=1/16/12/\hbox {month},~ \nu =52/12/\hbox {month},~ a=52/12/\hbox {month} \) and initial values \( S(0)=0.0998,~ E(0)=0.0001, ~I(0)=0.0001, ~R(0)=0.11,~ A(0)=0.79 \)
Full size table

9.3 Sensitivity Analysis of the Endemic Steady State

Table 7 shows that the Vaccinated fraction p has the greatest importance in determining the endemic level of infectives. Long-term vaccination to newborn babies will give immunity to most kids after many years, and thus, the Vaccinated fraction p is critical in endemics. The negative relationship is because more vaccination will reduce the fraction of susceptibles. Infectives will be less with less susceptibles.

Table 7 Sensitivity of the endemic steady state to the parameters with parameter values \(p=0.5, ~\delta =1/64/12/\hbox {month},~ \beta =150/\hbox {month}, ~g=1/16/12/\hbox {month},~ \nu =52/12/\hbox {month},~ a=52/12/\hbox {month} \)
Full size table

10 Extracting the Time-Dependent Transmission Rate \(\beta (t)\) from Prevalence Post-vaccination Data

In this section, we derive the formula for \( \beta (t)\) from the SEIRA model with vaccination based on prevalence data that can be used to construct an algorithm for extracting transmission rate from post-vaccination prevalence data as with \(\beta (t)\) that we constructed for pre-vaccination data. We will omit the algorithm here as the steps of the algorithm are the same as when extracting \(\beta (t)\) from prevalence pre-vaccination data.

Theorem 7

Suppose the epidemic is observed over the time interval [0, T], where \(t=0\) and \(t=T\) are, respectively, the start and end of observations, then the time-dependent transmission function \(\beta (t)\) for System (11) satisfying (12),

$$\begin{aligned} My^{\prime \prime }+Py'^{\prime }Qy+L=0 \end{aligned}$$
(12)

where f(t) is a smooth positive function which matches the infection data in the interval [0, T],

$$\begin{aligned} y&=\beta ^{-1} \\ H&=f''(t)+(a+2g+\nu )f'(t)+(a+g)(\nu +g)f(t),\\ M&=-(1-p)Hf^3,\\ N&=2(1-p)Hf^3,\\ P&=(1-p)(2Hf'f^2-2H'f^3-(2g+\delta )Hf^3)-p'Hf^3,\\ Q&=-(1-p)(H''f^3-Hf''f^2-2H'f'f^2+2H(f')^2f\\&\quad +(2g+\delta )H'f^3-(2g+\delta )Hf'f^2\\&\quad +g(g+\delta )Hf^3)-p'H'f^3+p'Hf'f^2-gp'Hf^3,\\ L&=-(1-p)(H'f^4+(g+\delta )Hf^4-ag\delta (1-p) f^4)-p'Hf^4. \end{aligned}$$

The formula for the coefficients seems quiet different from the previous ones. In fact, the formula presented above combines the situation when \( 0\le p <1 \) and when \( p=1 \). From the first equation of (11), we can see that when \( p=1 , \frac{\mathrm{d}S}{\mathrm{d}t}\) is independent of A(t) . Thus, we have the same behavior as with an SEIR model. We present formulae for both cases: \( p=1 \) and \( 0\le p<1 \).

  • when \(p(t)=1\), we have

    $$\begin{aligned} P{\beta '}-L{\beta ^2}-Q{\beta }=0 \end{aligned}$$

    This is a Bernoulli equation. By letting \(y(t)=\frac{1}{\beta (t)} \), the Bernoulli equation can be rewritten as a first-order linear differential equation \( Py'(t)+Qy(t)+L=0 \) with

    $$\begin{aligned} P&=-Hf,\\ Q&=-(H'f-Hf'+gHf),\\ L&=-Hf^2. \end{aligned}$$

  • when \(0\le p(t)<1 \), we have \( M{\beta ''\beta ^2}+N{(\beta ')^2\beta }+P{\beta '\beta ^2}-L{\beta ^4}-Q{\beta ^3}=0\) with

    $$\begin{aligned} M&=-Hf^3,\\ N&=2Hf^3,\\ P&=2Hf'f^2-2H'f^3- \left( \frac{p'}{1-p}+2g+\delta \right) Hf^3,\\ Q&=-(H''f^3-Hf''f^2-2H'f'f^2+2H(f')^2f+\left( \frac{p'}{1-p}+2g+\delta \right) H'f^3\\&\quad - \left( \frac{p'}{1-p}+2g+\delta \right) Hf'f^2+g\left( \frac{p'}{1-p}+g+\delta )Hf^3\right) ,\\ L&=-\left( H'f^4+\left( \frac{p'}{1-p}+g+\delta \right) Hf^4-ag\delta (1-p) f^4\right) . \end{aligned}$$

We omit the proof of this theorem since it is similar to that of Theorem 3. Same as before, the lack of post-vaccination prevalence data prevented us from testing the algorithm with real data. But as can be seen from the experiment with fake data demonstrated before, the prevalence algorithm works well.

11 Extracting the Time-Dependent Transmission Rate \(\beta (t)\) from Incidence Post-vaccination Data

Here, we derive the formula for \( \beta (t)\) from the SEIRA model with vaccination based on incidence data that can be used to construct an algorithm for extracting transmission rate from post-vaccination incidence data as with \(\beta (t)\) that we constructed for pre-vaccination data. As above, we will omit the algorithm for extracting \(\beta (t)\) from post-vaccination incidence data as the steps of the algorithm are the same as when extracting \(\beta (t)\) from incidence pre-vaccination data.

Theorem 8

For the vaccinated SEIRA model with time-dependent vaccinated fraction p, the time-dependent transmission rate is \(\beta (t)=\frac{\omega (t)}{S(t)I(t)}\) where S(t) and I(t) are

$$\begin{aligned} S(t)&= S(0) e^{-gt}+\int _0^t(\delta (\mathbf{1-p(s) }) (A(0) e^{-(g+\delta )s}\\&\quad +\int _0^s g e^{(g+\delta )(\sigma -s)}\mathrm{d}\sigma )-\omega (s))e^{g(s-t)}\mathrm{d}s'\\ I(t)&= I(0)e^{-(\nu +g)t}+\int _0^ta (E(0) e^{-(a+g)s}\\&\quad +\int _0^s \omega (\sigma ) e^{(a+g)(\sigma -s)}\mathrm{d}\sigma )e^{(\nu +g)(s-t)}\mathrm{d}s. \end{aligned}$$

The only difference between this Theorem and Theorem 4 is the present of \(1-p(t)\) in the equation for I(t) above. We omit the proof of this theorem, as it is almost identical to the proof of Theorem 4.

Since we have post-vaccination measles weekly notification data of Liverpool and London from 1974 to 1986 (see Fig. 3), we use it to illustrate the efficiency of this algorithm.

Figure 6a presents \( \beta (t) \) extracted from post-vaccination measles weekly notification data of Liverpool from year 1974 to 1986. Figure 6b plots the modulus of Fourier transform of \( \beta (t) \) in Liverpool. Same as with pre-vaccination incidence algorithm, we observe dominant peaks of 1/year and 3/year periods. Figure 7a illustrates \( \beta (t) \) extracted from post-vaccination measles weekly notification data of London from year 1974 to 1986 by the incidence algorithm. Figure 7b shows the modulus of Fourier transform of \( \beta (t) \) in London. The modulus of the Fourier transform of \(\beta (t)\) in this city has the same number of dominant spectral peaks all having the same periods like that in the city of Liverpool before and after vaccination and in it prior to vaccination.

Fig. 6
figure 6

Time-dependent transmission rate \( \beta (t) \) of Liverpool from year 1974 to 1986 and the modulus of its Fourier transform. The parameters are \( \delta =1/64/52/\hbox {week}, a=52/52/\hbox {week}, \nu =52/52/\hbox {week}, g=1/16/52/\hbox {week} \) and initial values are \( S(0)=0.25, E(0)=0.001, I(0)=0.001, A(0)=0.7.\) a \(\beta (t)\) of Liverpool from 1974 to 1986. b Modulus of the Fourier transform of \(\beta (t)\) in Liverpool from 1974 to 1986

Full size image
Fig. 7
figure 7

Time-dependent transmission rate \( \beta (t) \) of London from year 1974 to 1985 and the modulus of its Fourier transform. The parameters are \( \delta =1/64/52/\hbox {week}, a=52/52/\hbox {week}, \nu =52/52/\hbox {week}, g=1/16/52/\hbox {week} \) and initial values are \( S(0)=0.15, ~E(0)=1\hbox {e}{-05}, ~\hbox {I}(0)=1\hbox {e}{-04}, ~ \hbox {A}(0) =0.7\) a \(\beta (t)\) of London from 1974 to 1985. b Modulus of the Fourier transform of \(\beta (t)\) in London from 1974 to 1985

Full size image

Although the dominant frequencies for pre-vaccination and post- vaccination data from both cities are the same, the peak values are greater in the pre-vaccination case.

For the same reason as with the pre-vaccination data, the dominant frequencies in London have less noise than those in Liverpool. Also, as with pre-vaccination data, there is no significant difference in the values of the dominant frequencies in Liverpool as opposed to London where there is a noticeable difference in the values. The fact that vaccination does not change the dominant frequencies in both cities strengthens our belief that transmission of measles is driven by school seasons as well as other seasonal factors. We find the transmission cycles to be synchronized in different cities.

12 Discussion

We present an efficient model with and without vaccination for childhood infectious diseases. Our mathematical and numerical investigations have revealed a number of biologically and mathematically significant results that provides theoretical framework for public health interventions.

We conjecture that when \( R_0\ge 1 \), the solutions of the SEIRA system go to the endemic equilibrium and when \(R_0<1\), they go to the disease-free equilibrium. \(R_0=\frac{a\beta \delta (1-p) }{(a+g)(g+\delta )(\nu +g)}\) is the basic reproduction number.

Sensitivity analysis proves the importance of quarantining patients to prevent an epidemic outbreak. It reveals that birth and removal rate are the most important factors in controlling the endemic level of patients which indicts the importance of medication treatment. We equally find out from our sensitivity analysis that the transmission rate is one of the most important parameter in controlling the endemic level of infectives, when an outbreak occurs and the number of people that are infected in an outbreak.

We equally present algorithms to compute the time-dependent transmission rate from pre- and post-vaccination prevalence and incidence data. We illustrate the efficiency of these algorithms using London and Liverpool measles data. The extracted transmission rate functions have two dominant spectral peaks with frequencies 1/year and 3/year. These dominant frequencies are neither affected by vaccination nor the city in question. The 1/year dominant frequency is consistent with common belief that measles is driven by seasonal factors such as environmental changes and immune system changes and the 3/year frequency indicates the superiority of school seasons in driving measles transmission over other seasonal factors. The 1 per year and the 3 per year peaks are comparable for both pre- and post-vaccination data from Liverpool, whereas the 1 per year peak is larger than the 3 per year peak for both pre- and post-vaccination data from London. This is because London is a landlocked city and thus has large temperature variations which strongly affect Paramyxovirus (measles virus) seasonality with subsequent influence on its transmission. Weather variation thus is as important as school seasons in modulating the transmission of paramyxovirus when it comes to landlocked cities. Liverpool on the other hand is a coastal city with stable temperature, and thus, the main modulator of the transmission of paramyxovirus for this city was school seasons. The dominant frequencies in London have less noise than those in Liverpool because the population of London is greater than that of Liverpool and it is less sensitive to unexpected factors. The MATLAB inbuilt function fft was used to compute the fast Fourier transforms (FFTs) of the data. The frequencies resolve by fft are \(\frac{1}{T}, \frac{2}{T}, \frac{3}{T}, \ldots , \frac{N}{2T}, T=N\Delta t\) where \(N=\) sampled points, \(\Delta t\) sampling time interval. The first frequency is called the dominant frequency, and the last one is the Nyquist critical frequency. By taking the absolute value of the FFT, we obtained the amplitude spectrum shown in Figs. 4b, 5b, 6b and 7b.

Fine and Clarkson (1985) estimated the transmission parameter using the notification data from England and Wales from 1950 to 1979. To compare our results to those of these authors, we equally apply our algorithm to these data shown in Fig. 8. The figure shows that the outbreaks within this period were biennial in nature, with the magnitude of those in even numbered years higher than those in the odd numbered years.

Fig. 8
figure 8

1950–1966 weekly notification data for England and Wales

Full size image

Figure 9 shows the results obtained by applying our algorithm to these data. As in Fine and Clarkson (1985), the form of the transmission rate for odd and even numbered years’ outbreaks differs only in magnitude. This difference in magnitude can be credited to the difference in the number of susceptibles available. Since the trend is similar, to analyze our extracted transmission parameter, we consider just the data for few outbreaks. The figure shows that the trend of the transmission rate is similar to that of the notified measles cases in Fig. 8. English schools have three terms: autumn, spring and summer. These terms, respectively, run from September to mid-December (followed by 2 weeks Christmas holidays), January to late March (followed by 2 weeks Easter holidays) and March to mid-July (followed by 6 weeks of Summer holidays). Each term is divided into half by a half term break. The transmission parameter drops down whenever students were on either major holidays or midterm breaks and begin rising immediately as soon as school resumes, reaching a peak value sometime within the term. There are three main lengthy decline and steep rise. The lengthy decline could be attributed to major school holidays and the steep rise to school openings after major school holidays. The lowest incidence was reported during period when students were on summer holidays. These support the assertion in Grassly and Fraser (2006), Keeling and Rohani (2008) that measles transmission is mostly driven by school contacts.

Fig. 9
figure 9

England and Wales time-dependent transmission rate \( \beta (t) \) from 1950 to 1952. The parameters are \( \delta =1/64/52/\)week, \(a=52/52/\)week, \(\nu =52/52/\)week, \(g=1/16/52/\)week and initial values are \( S(0) =0.2, E(0)=0.003, I(0)=0.003, A(0)=0.79\)

Full size image

We believe that our algorithms could be used to estimate the transmission rate of another infectious childhood disease. The choice of the algorithm to use depends on the available data and on weather or not vaccination has been applied to a percentage of children in the region. For almost any type of infectious diseases, the derivations of our prevalence and incidence formulas can be applied with necessary modifications in disease transmission models.