Wavelength Selection in Gyrotactic Bioconvection

Abstract

We investigate pattern formation by swimming micro-organisms (bioconvection), when their orientation is determined by balance between gravitational and viscous torques (gyrotaxis), due to being bottom heavy. The governing equations, which consist of the Navier–Stokes equations for an incompressible fluid coupled with a micro-organism conservation equation, are solved numerically in a large cross section chamber with periodic boundary conditions in the horizontal directions. The influence of key parameters on wavelength selection in bioconvection patterns is investigated numerically. For realistic ranges of parameter values, the computed wavelengths are in good agreement with the experimental observations provided that the diffusion due to randomness in cell swimming behaviour is small, refuting a recently published claim that the mathematical model becomes inaccurate at long times. We also provide the first computational evidence of “bottom-standing” plumes in a three-dimensional simulation.

1 Introduction

Bioconvection is the name given to the phenomenon of spontaneous pattern formation in suspensions of swimming micro-organisms (Pedley and Kessler 1992; Hill and Pedley 2005). It occurs due to the collective behaviour of many micro-organisms swimming in a fluid and is realized as patterns, similar to those of thermal convection which occurs when a layer of fluid is heated from below. Bioconvection patterns can be observed in the laboratory in suspensions of micro-organisms, but these have also been found in situ in micropatches of zooplankton (Kils 1993). The micro-organisms are 3–5 % denser than the water they swim in and on average they swim upwards, so that they aggregate at the top layer of the suspension. This leads to an overturning instability and formation of convection patterns, which have some similarities with those due to thermal convection, but are driven solely by the swimming micro-organisms, as the following observations make clear. Direct thermal convection can occur in a suspension if the suspension chamber is heated from below or from the sides. However, bioconvection has been observed in a suspension layer that is strongly cooled from below, and hence it is not a thermal effect (Platt 1961). Further, the sedimentation velocity of a typical micro-organism is negligible compared with its swimming speed, and the patterns disappear when the micro-organisms stop swimming.

Micro-organisms respond to stimuli by swimming, on average, in particular directions. These responses are called taxes, examples of which include gravitaxis, chemotaxis, gyrotaxis and phototaxis. Gravitaxis is a response to gravity or acceleration, and swimming upwards is known as negative gravitaxis. Chemotaxis corresponds to swimming up or down chemical gradients, and phototaxis denotes swimming towards or away from light. The centre of mass of many micro-organisms is displaced from the centre of buoyancy towards the rear of the body, and as such they are bottom heavy. These bottom-heavy micro-organisms swim, on average, upwards in absence of bulk fluid motions resulting in negative gravitaxis. In a bulk fluid motion with horizontal vorticity component, a micro-organism experiences a viscous torque that tends to tip it away from the vertical. On the other hand, the gravitational torque, which is countered by the viscous torque, tends to make it swim up. The swimming response when the direction is obtained by balancing the gravitational and viscous torques is called gyrotaxis. A gyrotactic micro-organism swims at an angle to the vertical when the bulk fluid motion has a horizontal component of vorticity. Gravitaxis and gyrotaxis are passive orientation mechanisms, unlike active responses such as phototaxis and chemotaxis.

Kessler (1985) demonstrated that many swimming micro-organisms are gyrotactic and made observations of regular patterns in shallow suspensions a few millimetres deep and of gyrotactic plume formation in a tall cylinder filled with the suspension. Usually, two types of structures are observed in deep suspensions. One consists of plumes plunging from the concentrated top surface, and the other structure shows irregular tall thin bottom-standing plumes, some of which do not extend to the top of the suspension (Pedley and Kessler 1992). A quantitative study of bioconvection patterns in a gyrotactic algal suspension was performed by Bees and Hill (1997). They measured the wavelengths of the planforms of bioconvection patterns as a function of the depth and concentration of the suspension.

Most of the bioconvection experiments were carried out in chambers having large horizontal cross-sectional areas. Numerical simulation in such a domain offers significant computational challenges. Hence, most previous bioconvection simulations were carried out in two dimensions. The structure and stability of a single plume in a two-dimensional chamber were examined by Ghorai and Hill (1999). The parametric dependence of the wavelengths was investigated in a two-dimensional wide chamber by Ghorai and Hill (2000). The structure and stability of a single plume in axisymmetric and three-dimensional chambers have also been investigated numerically (Ghorai and Hill 2002, 2007). Recently, Karimi and Paul (2013) have examined three-dimensional gyrotactic bioconvection in a spatially extended domain. They have studied the variation in pattern wavelength with respect to the Rayleigh number. All these computations described are based on the continuum models. In contrast, Hopkins and Fauci (2002) simulated two-dimensional bioconvection using discrete models based on point particles.

Bioconvection patterns show polygonal cells such as squares and hexagons each with a thin descending central core surrounded by a broad column of rising fluid. Hence, bioconvection is intrinsically a three-dimensional phenomenon, and we must solve the full three-dimensional problem to gain insight into this phenomenon. A chamber with a large horizontal cross-sectional area generates bioconvection patterns consisting of several plumes that are periodic in the $x$ and $y$ directions. We thus consider a chamber that is periodic in the horizontal directions and examine the influence of the governing parameters on the wavelengths of patterns. This paper differs in several aspects from that of Karimi and Paul (2013). Their chamber had rigid as well as periodic walls, and the long-time wavelengths reported by them are large compared with those of the experiments (Bees and Hill 1997), leading them to suggest that “model modifications may be required for quantitative agreement in the long-time nonlinear regime”. We are able to resolve this problem by demonstrating that wavelengths from the numerical simulations become comparable with those of the experiments for suitable values of the diffusion coefficient. We also discuss the effects of depth and concentration on the pattern wavelengths and show the evidence of bottom-standing plumes that are observed in experiments.

This paper is organized as follows. The mathematical formulation of the problem is described in Sect. 2. A brief description of the computational method is given in Sect. 3, and the results of the numerical computations are described in Sect. 4. Finally, we discuss the numerical results and draw conclusions.

2 Mathematical Formulation

Consider the motion of a suspension of gyrotactic micro-organisms confined in a three-dimensional chamber of side dimensions $L_1,L_2$ and depth $H$ referred to Cartesian coordinates with the $z$-axis pointing upwards. The horizontal lower boundary is rigid, and the vertical boundaries are periodic. The horizontal boundary at the top is open to the air, and it is assumed to be stress free.

2.1 Governing Equations

As in Pedley et al. (1988), we assume a monodisperse cell population that can be modelled by a continuous distribution. The suspension is dilute so that the volume fraction of the cells is small and cell–cell interactions are negligible. Each cell has a volume $\vartheta$ and density $\rho +\delta \rho$, where $\rho$ is the density of water in which the cells swim and $0 < \delta \rho /\rho \ll 1$. Let ${\varvec{u}}$ and $n$, respectively, denote the velocity and concentration in the suspension. Supposing that the suspension is incompressible, conservation of mass leads to

$$\begin{aligned} \varvec{\nabla }\varvec{\cdot }{\varvec{u}} = 0. \end{aligned}$$

(1)

The momentum equation is given by

$$\begin{aligned} \frac{\partial {\varvec{u}}}{\partial t} + (\varvec{u}\varvec{\cdot }\varvec{\nabla }){\varvec{u}} = -\frac{1}{\rho }\varvec{\nabla }p_e + \nu {\nabla ^2}{\varvec{u}} - \frac{g \vartheta \delta \rho \,n}{\rho }\hat{\varvec{z}}, \end{aligned}$$

(2)

where $p_e$ is the excess pressure above the hydrostatic pressure, $g$ is the magnitude of the acceleration due to gravity, $\nu$ is the kinematic viscosity of the suspension which is assumed to be that of the water, and $\hat{\varvec{z}}$ is a vertical unit vector. Equation (2) is derived under the Boussinesq approximation, neglecting all effects of the micro-organisms on the flow except their negative buoyancy.

The equation for cell conservation implies that concentration of cells, $n$, satisfies

$$\begin{aligned} \frac{\partial n}{\partial t} = -{\varvec{\nabla }}\varvec{\cdot }{\varvec{J}}, \end{aligned}$$

(3)

where the flux of the cells is

$$\begin{aligned} {\varvec{J}} = n {\varvec{u}}+{n}V_c <{\varvec{p}}> - \, \varvec{\mathsf D}\varvec{\cdot }{\varvec{\nabla }}{n}. \end{aligned}$$

(4)

The first term, $n {\varvec{u}}$, on the right-hand side of equation (4) is the flux due to the advection of the cells by the bulk flow, and the second term, ${n}V_c <{\varvec{p}}>$, is the flux due to the swimming of the cells. The unit vector ${\varvec{p}}$ denotes a cell’s swimming direction, and $<{\varvec{p}}>$ is the mean swimming direction that is estimated from the deterministic torque balance equation (see Sect. 2.2 below). The swimming speed $V_c$ is assumed to be constant. The third term on the right-hand side of Eq. (4) represents the random component of the cell locomotion. We choose the diffusivity tensor $\varvec{\mathsf D}$ to be isotropic and constant, $\varvec{\mathsf D}=D \varvec{\mathsf I}$, and thus the flux of cells becomes

$$\begin{aligned} {\varvec{J}} = n {\varvec{u}}+{n}V_c <{\varvec{p}}> - \, D {\varvec{\nabla }}{n}, \end{aligned}$$

where $D$ is the diffusion coefficient. The assumptions of constant isotropic diffusivity and deterministic $<{\varvec{p}}>$ in equation (4) are ad hoc, and modifications have been considered using a probability density function that satisfies a Fokker–Planck equation (Hill and Bees 2002; Manela and Frankel 2003). However, closed-form solutions are available only for some special flows. The simplified ad hoc model is a good first model that contains the essential features of the flow.

Fig. 1

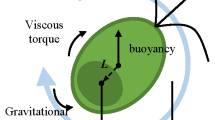
An idealized spherical algal cell. The swimming direction ${\varvec{p}}$ is specified by spherical polar angles $\theta$ and $\phi$ relative to a right-handed system of Cartesian coordinates with origin at the centre. Here $h$ denotes the distance of the centre of gravity from the centre of the cell

2.2 Calculation of the Mean Swimming Direction

For simplicity, we approximate an algal cell as a sphere of radius $a$ with its centre of gravity displaced by $-h{\varvec{p}}$ from the geometric centre of the cell (see Fig. 1). The gravitational torque acting on the cell is

$$\begin{aligned} {\varvec{T}}_g = m g h {\varvec{p}} \times \hat{\varvec{z}}. \end{aligned}$$

(5)

The viscous torque on the algal cell of radius $a$ is given by

$$\begin{aligned} {\varvec{T}}_{\mu }=4\pi \mu a^3 \left( \varvec{\nabla }\times {\varvec{u}}-2{\varvec{\Omega }} \right) , \end{aligned}$$

(6)

where ${\varvec{\Omega }}$ is the angular velocity of the spherical cell. Neglecting inertial effects at the low Reynolds number flow associated with the motion of the algal cells, their swimming orientation is specified by the torque balance equation, ${\varvec{T}}_g + {\varvec{T}}_\mu ={\varvec{0}}$, which on simplification gives (Leal and Hinch 1972)

$$\begin{aligned} \dot{{\varvec{p}}}=\frac{1}{2B}\Big (\hat{\varvec{z}}-(\hat{\varvec{z}} \cdot {\varvec{p}}){\varvec{p}}\Big )+\frac{{\varvec{\omega }}\times {\varvec{p}}}{2}, \end{aligned}$$

(7)

where ${\varvec{\omega }}=(\omega _1,\omega _2,\omega _3)$ is the local vorticity field and $B=4\pi \mu a^3/mgh$ is called the gyrotactic reorientation parameter. The equations describing the equilibrium orientation are (Pedley and Kessler 1987)

$$\begin{aligned} \displaystyle -\omega _1\sin \phi +\omega _2\cos \phi= & {} \sin \theta /B, \end{aligned}$$

(8)

$$\begin{aligned} \displaystyle \omega _1\cos \phi +\omega _2\sin \phi= & {} \omega _3\tan \theta . \end{aligned}$$

(9)

Let $\omega =|{\varvec{\omega }}|$ be the magnitude of the vorticity vector. The equilibrium orientation, ${\varvec{p}}_e$, obtained by solving equations (8) and (9) is always stable for $\omega _3\ne 0$. For flows with $\omega _3=0$, there exists a stable equilibrium solution ${\varvec{p}}_e$ of Eqs. (8) and (9) with $\sin \theta =B\omega$ if $B\omega < 1$, but no stable equilibrium if $B\omega >1$. When $B\omega >1$ and $\omega _3=0$, the cells tumble and we can find an average swimming direction $\bar{\varvec{p}}$ by integrating ${\varvec{p}}$ over a tumbling period (Ghorai and Hill 1999). The mean swimming orientation, $<{\varvec{p}}>$, is taken to be equal to ${\varvec{p}}_e$ when the equilibrium orientation is stable and equal to $\bar{\varvec{p}}$ when the algal cells tumble.

2.3 Scaling of the Equations

Let $\bar{n}$ be the mean cell concentration. We use the scales $H$, $D/H$, $\mu D/H^2$, $H^2/D$ and $\bar{n}$ for length, velocity, pressure, time and cell concentration, respectively. For convenience, we keep the same notations for the dimensional and dimensionless variables. In terms of the dimensionless variables, the bioconvection equations become

$$\begin{aligned}&\varvec{\nabla }\varvec{\cdot }{\varvec{u}} = 0, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{1}{S_c}\left( \frac{\partial {\varvec{u}}}{\partial t} + (\varvec{u}\varvec{\cdot }\varvec{\nabla }){\varvec{u}}\right) = -\varvec{\nabla }p_e + {\nabla ^2}{\varvec{u}} - R\,n\,\hat{\varvec{z}}, \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial n}{\partial t} = -{\varvec{\nabla }}\varvec{\cdot }\Big ({ \left( {\varvec{u}}+ V_s<{\varvec{p}}>\right) n - {\varvec{\nabla }}{n}}\Big ), \end{aligned}$$

(12)

where $S_c=\nu /D$ is the Schmidt number, $V_s=V_c H/D$ is the scaled swimming speed, and $R=\bar{n} \vartheta g \delta \rho H^3/\rho \nu D$ is the Rayleigh number. Since the gyrotactic reorientation parameter $B$ has a dimension of inverse time, the dimensionless gyrotaxis parameter $G$ is defined by $G=BD/H^2$.

2.4 Initial and Boundary Conditions

Due to scaling, the horizontal boundaries are now at $z=0,1$. The bottom boundary is rigid no slip, and the top boundary is stress free. Further, there is no flux of cells through the top and bottom boundaries. If ${\varvec{u}}=(u,v,w)$, then these boundary conditions are given by

$$\begin{aligned}&u=v=w={\varvec{J}}\varvec{\cdot }\hat{\varvec{z}}=0 \text { at }z=0, \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\partial u}{\partial z} = \frac{\partial v}{\partial z} = w = {\varvec{J}}\varvec{\cdot }\hat{\varvec{z}} = 0 \text { at } z=1. \end{aligned}$$

(14)

The vertical boundaries are at $x=0,\lambda _1$ and $y=0,\lambda _2$, where $\lambda _1=L_1/H$ and $\lambda _2=L_2/H$ are the horizontal aspect ratios of the chamber. These vertical boundaries are assumed to be periodic.

The initial conditions are that of a zero flow together with a small random perturbation to the uniform concentration of cells:

$$\begin{aligned} {\varvec{u}}= \varvec{0},\quad n=1+\epsilon \mathcal {A}(x,y,z), \end{aligned}$$

(15)

where $\epsilon =10^{-5}$ and $\mathcal {A}(x,y,z)$ is a random number between $-1/2$ and $1/2$ at $(x,y,z)$.

3 Numerical Procedure

The governing equations are discretized on a staggered mesh using the gauge method developed by Weinan and Liu (2003). The use of the staggered mesh has many advantages, one of them being that the no-cell flux boundary condition can be satisfied automatically when discretized. There are boundary layers at the top due to the high cell concentration and at the bottom due to the presence of the rigid no-slip wall. In order to resolve these boundary layers, a non-uniform mesh is used in the vertical direction. However, the mesh in the horizontal directions is taken to be uniform.

In the gauge formulation, we introduce a gauge variable $\phi$ and an auxiliary vector field ${\varvec{A}}={\varvec{u}}-\varvec{\nabla }\phi$. The method leads to transport equations for ${\varvec{A}}$ and a Poisson equation for $\phi$. The discretized transport equations are solved using an approximate factorization method. The solution of the Poisson equation for $\phi$ is obtained in two steps. First, the application of the fast Fourier transform (FFT) in the horizontal directions leads to a system of uncoupled tridiagonal matrix equations in the vertical direction, and these equations are inverted in the usual manner. Second, the solution for $\phi$ is then reconstructed via inverse FFT. Further, the discretized cell conservation equation preserves the positivity of the cell concentration. The numerical results agree well with those obtained using a second-order projection method (Ghorai and Hill 2007). The code can also be applied with minor changes to the two-dimensional problem, and the two-dimensional results agree well with those that were obtained using vorticity-stream function formulation (Ghorai and Hill 1999).

4 Results

We examine the effects of the values of the diffusion coefficient, concentration and depth on the bioconvection patterns. To this end, we take a three-dimensional chamber of large horizontal, 4 cm x 4 cm, cross-sectional area. The ranges of the parameter values used in the simulations are given in Table 1 (Pedley et al. 1988). Because of the computational time taken by the simulations, most of the results in this paper use the selected parameter values listed in the last column of Table 1, which correspond to those for the gyrotactic alga, C. nivalis. The gyrotactic parameter $B$ is approximately 3.4 s. The dimensional depth and mean concentration are taken from the experimental data in Bees and Hill (1997). Their experimental data were recorded for the first 10–15 min after mixing of the suspension. Most of the results presented below are given in terms of dimensional time up to 20 min, and the results are plotted in dimensional coordinates. We choose a $256\times 256$ mesh in the horizontal directions. In the absence of flow, the steady-state concentration at the top of the chamber is

$$\begin{aligned} c_{\text {max}}=\frac{\bar{n}HV_c}{D\left( 1-\exp (-HV_c/D)\right) }. \end{aligned}$$

Thus, for a fixed value of $V_c$, $c_{\text {max}}$ increases with $H$ but decreases as $D$ increases. To resolve such a high concentration, more grid points are used in the vertical direction for higher values of $H$ and lower values of $D$. For example, 56 and 66 points are taken for $D=2.5\times 10^{-4}$ cm$^{2}$ s$^{-1}$ and $D=10^{-4}$ cm$^{2}$ s$^{-1}$ with $H=0.469$ cm. Similarly, 86 points are taken for $D=10^{-4}$ cm$^{2}$ s$^{-1}$ with $H=0.723$ cm.

Table 1 Estimates of typical parameters for the model taken from Pedley et al. (1988)

Table 2 Dimensional and dimensionless parameters used in the simulations described in this paper

The average horizontal wavelength, $\Lambda$, is defined by (Tomita and Abe 2000)

$$\begin{aligned} \Lambda = \sum _{k_x=-N/2}^{N/2} \sum _{k_y=-N/2}^{N/2}\frac{2\pi }{\sqrt{k_x^2+k_y^2}}{\hat{n}}^2(k_x,k_y) {\Big /}\sum _{k_x=-N/2}^{N/2} \sum _{k_y=-N/2}^{N/2}{\hat{n}}^2(k_x,k_y), \end{aligned}$$

(16)

where $k_x$ and $k_y$ represent the wavenumbers in the $x$ and $y$ directions, respectively; $\hat{n}(k_x,k_y)$ is the horizontal concentration spectrum, and $N$ is the horizontal grid number. The average horizontal wavelength is obtained using FFT from the concentration values near the upper surface of the chamber.

Given a basic state, linear stability theory predicts the critical Rayleigh number, above which the suspension becomes unstable. The critical Rayleigh number for the onset of bioconvection in a suspension of gyrotactic micro-organisms was calculated in the absence of flow ($\varvec{u} = \varvec{0}$) for two different initial concentration profiles, viz. a uniform profile that is appropriate for a deep layer (Pedley et al. 1988) and an exponential equilibrium profile for a layer of finite depth (Hill et al. 1989). The critical Rayleigh number based on the uniform profile is an approximation to an initially well-mixed suspension, such as that at the beginning of the experiments reported by Bees and Hill (1997), since the profile does not satisfy the no-flux conditions at the top and bottom boundaries of the finite depth chamber. Let $R_c^{(e)}$ and $R_c^{(u)}$ denote the critical Rayleigh numbers based on the exponential and uniform profiles, respectively. Pedley et al. (1988) give $R_c^{(u)}=16\pi ^2/V_s G$. Table 2 shows the dimensional and dimensionless parameter values used in the simulations described in this paper. For some parameter values, the value of $R_c^{(e)} < R < R_c^{(u)}$, where $R$ is the Rayleigh number used in the simulation as defined in Eq. (11). In such cases, the suspension is not initially unstable, and the uniform profile evolves towards an exponential profile as the cells swim upwards. The evolving profile eventually becomes linearly unstable and bioconvection begins.

4.1 Effect of Cell Diffusivity

We consider experiments 17, 18 and 19 of Bees and Hill (1997) which were conducted in a layer of depth $H=0.469$ cm and mean concentration $\bar{n}=1.89\times 10^6$ cells cm$^{-3}$. We take three cell diffusivity values of $5\times 10^{-4}$, $2.5\times 10^{-4}$ and $10^{-4}$ cm$^2$ s$^{-1}$. For comparison, the dimensionless parameter values with $D=5\times 10^{-4}$ cm$^2$ s$^{-1}$ match with those of Karimi and Paul (2013). The Rayleigh number $R$ based on these parameter values is approximately 956, and we have computed the corresponding variation in the mean horizontal wavelength $\Lambda$ with time for these parameter values, as described in detail below. They also examined the time dependence of $\Lambda$ for other values of Rayleigh number while keeping rest of the parameters fixed, including the cell diffusivity, swimming speed and depth. In contrast, we varied the last three parameters, which leads to changes in Rayleigh number as well as other dimensionless parameters.

Fig. 2

Evolution of the cell concentration in a 0.469-cm-deep chamber with mean concentration $\bar{n}=1.89\times 10^6$ cells cm$^{-3}$: a $D=5\times 10^{-4}$, b $D= 2.5\times 10^{-4}$ and c $D=10^{-4}$ cm$^2$ s$^{-1}$. The concentration is plotted as contours on the cross-sectional surface near the top ($z=0.465$ cm), and the contours take the values 0.3, 0.5, 0.7, 0.9 of $n^{\text {s}}_{\text {ref}}$ (see text for details). The values of $n^{\text {s}}_{\text {ref}}$ at the initial and final time are a $9.5,14.3$, b $18.6,21.5$, c $34.3,37.3$

Fig. 3

Variation in the average horizontal wavelength with time: a $D=5\times 10^{-4}$, b $D= 2.5\times 10^{-4}$ and c $D=10^{-4}$ cm$^2$ s$^{-1}$. The cell swimming speed is 100 $\upmu$m s$^{-1}$, and the depth and the mean concentration are i 0.469 cm and $\bar{n}=1.89\times 10^6$ cells cm$^{-3}$ and ii 0.282 cm and $4.30\times 10^6$ cells cm$^{-3}$

The concentration at the top of the chamber increases with time due to cells swimming up, and the cells accumulate at the top, where the no-cell flux condition holds. Plumes start developing near the top surface at around $t=60, 50$ and 40 s for $D=5\times 10^{-4}, 2.5\times 10^{-4}$ and $10^{-4}$ cm$^2$ s$^{-1}$, respectively. The concentration gradient at the top is steeper when the cell diffusivity is smaller. This leads to the initiation of bioconvection at an earlier time for the smaller cell diffusivity. The evolution of the concentration at an early time (3 min) and at a later time (20 min) is shown in Fig. 2, where the concentration is plotted as contours on a horizontal cross-sectional surface near the top. The concentration is scaled with $n^{\text {s}}_{\text {ref}}$, a reference value of concentration $n$ on the cross-sectional surface. It is seen that the number of plumes decreases significantly with time for the highest cell diffusivity $D=5\times 10^{-4}$ cm$^2$ s$^{-1}$, as was also observed in the simulations by Karimi and Paul (2013). For the intermediate value of $D=2.5\times 10^{-4}$ cm$^2$ s$^{-1}$, the number of plumes at 20 min has decreased somewhat less than that of the highest value of $D$, while the number of plumes almost remains constant for the lowest value of $D=10^{-4}$ cm$^2$ s$^{-1}$. The same can be seen from the variation in the average horizontal wavelength $\Lambda$ against time shown in Fig. 3i. The average horizontal wavelength in experiments 17, 18 and 19 of Bees and Hill (1997) is around 0.330 cm. The wavelength for $D=10^{-4}$ cm$^2$ s$^{-1}$, in the time interval from 15 to 20 min, varies in the range from 0.27 to 0.32 cm. Thus, the wavelength with lower cell diffusivity agrees well with the experimental findings. Further, the wavelength usually decreases with time in the experiments. In the numerical simulations, the wavelength increases with time for higher cell diffusivity but does not change significantly for lower cell diffusivity. Next we consider experiments 26, 27, 28 and 29 of Bees and Hill (1997) that were conducted in a layer of depth $H=0.282$ cm and mean concentration $\bar{n}=4.30\times 10^6$ cells cm$^{-3}$. The variation in the numerical wavelength with time is shown in Fig. 3ii. Here also, the variation in the wavelength with time changes little for the lower cell diffusivity. The wavelength for $D=10^{-4}$ cm$^2$ s$^{-1}$, in the time interval from 15 to 20 min, varies in the range from 0.20 to 0.22 cm which agrees well with experimental wavelength 0.226 cm. Next, we again consider experiments 17, 18 and 19 of Bees and Hill (1997), but we reduce the cell swimming speed from 100 to $50\,\upmu$m s$^{-1}$. The variation in the average horizontal wavelength $\Lambda$ against time is shown in Fig. 4. The wavelength increases with time for $D=10^{-4}$ cm$^2$ s$^{-1}$ for the lower swimming speed of $50\,\upmu$m s$^{-1}$, but it changes little with time at the higher cell swimming speed $100\,\upmu$m s$^{-1}$ [see Fig. 3i]. To realize little variation with time, the cell diffusivity needs to be lower. From Fig. 4, we see that the horizontal wavelength changes little with time for lower cell diffusivity, such as with $D=5\times 10^{-5}$ cm$^2$ s$^{-1}$. Thus the ratio of the cell swimming speed to the cell diffusivity plays an important role in the selection of pattern wavelengths. For $R$ above its critical value, the wavelength of the maximum growth rate gives an estimate of the pattern wavelength at the initiation of bioconvection. The wavelength of the maximum growth rate is finite, and it decreases as $R$ increases. The initial pattern wavelength approaches the wavelength of the maximum growth rate, and this leads to decrease in the wavelength at an initial stage in Fig. 4. However, the nonlinear effects become dominant after the initial stage.

4.2 Effect of Varying the Depth

Here we study the effects of the depth on the wavelengths keeping other parameters fixed. We choose the sets of data from Bees and Hill (1997) in which the mean concentrations are kept fixed and the depths are different. The cell swimming speed and the cell diffusivity are kept fixed at 100 $\upmu$m s$^{-1}$ and $D=10^{-4}$ cm$^2$ s$^{-1}$, respectively.

Fig. 4

Variation in the average horizontal wavelength with time: a $D=10^{-4}$, b $D= 7.5\times 10^{-5}$ and c $D=5\times 10^{-5}$ cm$^2$ s$^{-1}$. The cell swimming speed is 50 $\upmu$m s$^{-1}$, and the depth and the mean concentration are 0.469 cm and $\bar{n}=1.89\times 10^6$ cells cm$^{-3}$. The sudden changes in the initial stage mark the transition from the static state to the convective state

First, we choose three sets of data in experiments 14, 17 and 20 from Bees and Hill (1997). The mean concentration is kept fixed at $\bar{n}=1.89\times 10^6$ cells cm$^{-3}$, and the depths are 0.384, 0.469 and 0.723 cm, respectively. The solutions for the 0.469-cm-deep chamber at two different times have already been shown in Fig. 2c, and the corresponding solutions for the 0.384-cm-deep chamber are similar in appearance. We observe bottom-standing plumes for the $0.723$-cm-deep chamber in which the plumes are quite irregular. Figure 5 shows a snapshot of the cell concentration in the mid-vertical plane of the chamber located at $x=2$ cm. Most of the plumes are found at the bottom of the chamber and do not extend to the top. There is also an accumulation of cells at the upper surface leaving almost clear fluid in the interior outside the plumes themselves. This confirms the existence of bottom-standing plumes that were also observed in experiments. On the other hand, the plumes become more regular in a shallow-depth chamber. To verify this, we change the depth to $0.2$ cm keeping the rest of the parameters fixed. Figure 6 shows the concentration in the mid-vertical plane located at $x=2$ cm. The plumes are symmetric, are more organized and mostly extend from the top to the bottom of the chamber.

Fig. 5

Snapshot of two-dimensional contour map of concentration sliced on the mid-vertical plane located at $x=2$ cm at around $t=20$ min. The contours take values of 0.025, 0.05, 0.1, 0.2, 0.4 of $n^{\text {s}}_{\text {ref}}$, where $n^{\text {s}}_{\text {ref}} =40.0$

Fig. 6

Snapshot of two-dimensional contour map of concentration sliced on the mid-vertical plane located at $x=2$ cm at around $t=20$ min. The contours take values of $0.025,0.05,0.1,0.2,0.4$ of $n^{\text {s}}_{\text {ref}}=20.0$

Table 3 Comparisons between the experimental wavelengths and numerical results

To check the dependence of the solutions on the initial conditions, we performed two sets of numerical computations with different random perturbations to the initial uniform concentration that satisfy equation (15). The maximum and minimum wavelengths in the time interval from 15 to 20 min were calculated. The mean of the maximum and minimum values is taken to be the wavelength for each numerical experiment. The numerical values based on these two simulations together with the experimental values of Bees and Hill (1997) are shown in Table 3. The table shows that the numerical values of the wavelengths agree well with the experimental values.

Table 4 Comparisons between the experimental wavelengths and numerical results

Fig. 7

Evolution of the cell concentration in a 0.186-cm-deep chamber of mean concentration $\bar{n}=4.19\times 10^6$ cells cm$^{-3}$ but of different cell volumes: a $\vartheta =5\times 10^{-10}$ cm$^3$, b $\vartheta =3\times 10^{-10}$ cm$^3$. The concentration is plotted as contours on the cross-sectional surface near the top ($z=0.184$ cm), and the contours take values of 0.2, 0.4, 0.6, 0.8 of $n^{\text {s}}_{\text {ref}}$. The values of $n^{\text {s}}_{\text {ref}}$ at the initial and final time are a 24.3, 29.3, b 43.0, 40.2

Next we choose three sets of data given in experiments 23, 24 and 25 from Bees and Hill (1997) with a mean concentration $\bar{n} = 4.19 \times 10^6$ cells cm$^{-3}$, and the depths are 0.468, 0.291 and 0.186 cm, respectively. The range of wavelengths based on two simulations with different random perturbations together with the experimental values of Bees and Hill (1997) is shown in Table 4. The wavelength decreases slightly with the depth of the chamber in the experiments. The numerical wavelengths agree well with the experimental wavelengths for the 0.291- and 0.468-cm-deep chambers, but the numerical wavelength for the shallow 0.186-cm-deep chamber is larger than the experimental value. Also, the variation in the wavelength with time changes little for the 0.291- and 0.468-cm-deep chambers, but it gradually increases for the 0.186-cm-deep chamber. To investigate this, we plotted the solutions for the 0.186-cm-deep chambers at two different times in Fig. 7a. The wavelength at the initial stages is very small which is evident from the many plumes at $t=3$ min. The wavelength increases due to merging of plumes which occurs at higher Rayleigh number. The solution at $t=20$ min shows clusters of star-shaped patterns due to the merging of nearby plumes. Similar clusters of patterns were also observed earlier in both the closed box and periodic boundary condition simulations [see Fig. 1(d), and Fig. 3(a) and (b) in Karimi and Paul (2013)]. The cell volume $\vartheta$ occurs only in the Rayleigh number. The cell volume $\vartheta =5\times 10^{-10}$ cm$^3$ corresponds to Fig. 7a. Next we decrease the cell volume to $\vartheta =3\times 10^{-10}$ cm$^3$ and thereby decrease the Rayleigh number. The corresponding solution is shown in Fig. 7b. Here, the number of plumes also decreases due to merging of nearby plumes, but the clustering is less prominent here. Thus, if the plumes in the initial stages are very close to each other, then the nonlinear effects at higher Rayleigh number cause merger of nearby plumes, leading to an increase in wavelength with time.

4.3 Effects of Varying the Mean Concentration

Here we examine the effects of varying the mean cell concentration on the patterns. For a fixed depth, we take three sets of concentration values, $\bar{n} = 2\times 10^6$, $\bar{n} = 4\times 10^6$ and $\bar{n} = 6\times 10^6$ cells cm$^{-3}$, which represent typical mean concentration values used in the experiments of Bees and Hill (1997).

Fig. 8

Variation in the average horizontal wavelength with time in i 0.3-cm- and ii 0.5-cm-deep chambers with different mean concentration: a $\bar{n}=2\times 10^{6}$, b $\bar{n}=4\times 10^{6}$ and c $\bar{n}=6\times 10^{6}$ cells cm$^{-3}$. The sudden changes in the initial stage mark the transition from the static state to the convective state

First, we choose a relatively shallow 0.3-cm-deep chamber. The variation in the average horizontal wavelength is shown in Fig. 8i. The average wavelengths of the patterns are approximately 0.242, 0.218 and 0.200 cm for $\bar{n}=2\times 10^{6}$, $\bar{n}=4\times 10^{6}$ and $\bar{n}=6\times 10^{6}$ cells cm$^{-3}$, respectively. Thus, the wavelength decreases slightly with an increase in the mean concentration. Also, the wavelength varies little with time for all the three concentration values.

Next we consider the solutions in a 0.5-cm-deep chamber with the same mean concentrations as in the previous numerical solutions. The variation in the average horizontal wavelength is shown in Fig. 8ii. The average wavelengths of the patterns are approximately 0.300, 0.264 and 0.250 cm for $\bar{n}=2\times 10^{6}$, $\bar{n}=4\times 10^{6}$ and $\bar{n}=6\times 10^{6}$ cells cm$^{-3}$, respectively. As in the previous case, the wavelength decreases slightly with an increase in the mean concentration and it varies little with time for all the three concentration values.

5 Conclusions

Using a fully three-dimensional computational model, we have examined the dependence of the bioconvection pattern wavelengths on the diffusivity of the cells, the depth of the chamber and the mean cell concentration. The conclusions are based on the numerical experiments reported in this paper. Among all the parameter values, the ratio of the cell swimming speed to the cell diffusivity has the most significant effects on the wavelength of the patterns. In particular, we have demonstrated that Karimi and Paul’s (2013) numerical experiments disagree with Bees and Hill’s (1997) experimental measurements of long-time pattern wavelengths, because Karimi and Paul chose too large a value of the swimming diffusion parameter, leading to a qualitative change in the evolution of the plumes.

For a fixed swimming speed, the wavelength increases with time at higher cell diffusivity but changes little at lower cell diffusivity. In the experiments, the wavelengths usually decreased with time, but this change is not always monotonic (Bees and Hill 1997). In the numerical experiments, the variation in the wavelength with time is not monotonic either for smaller cell diffusivity. The wavelengths in the experiments decreased slightly with an increase in the depth of the chamber, but again the trend is not clearly marked. Similar characteristics have also been observed in the numerical experiments. In the case of small depth and high Rayleigh number, plumes sometimes merge with nearby plumes leading to higher wavelengths. Finally, well-developed wavelength decreases slightly with an increase in the mean concentration. We have also observed bottom-standing plumes in deep chambers. In the case of bottom-standing plumes, most of the cells are transported to the bottom of the chamber and many plumes at the bottom do not extend to the top of the chamber.

The model assumed in this paper has some simplifying assumptions. The most important is that the dispersion of swimming cells due to randomness in their swimming direction has been modelled by a constant isotropic diffusion term in the cell conservation equation. We have shown that good qualitative and quantitative agreement with experiments is obtained by an appropriate choice of this diffusion term. However, in experiments, there are a number of different complementary dispersion mechanisms including:

• (i) generalized Taylor dispersion due to the interaction of swimming across streamlines and advection by the flow;

• (ii) variation in swimming direction for a population of cells;

• (ii) variation in swimming speed for a population of cells;

• (iv) hydrodynamic cell–cell interactions that change swimming directions and are significant in regions, such as plumes, where the volume fraction of cells is high;

• (v) variations in size and age, and hence swimming behaviour, of cells in a suspension.

Variability in swimming direction in the absence of flow was successfully modelled as a rotational Brownian diffusivity by Hill and Häder (1997), was extended to calculate spatial diffusion in unbounded linear flows using generalized Taylor dispersion theory by Hill and Bees (2002) and by Manela and Frankel (2003) and has subsequently been studied in pipe flows (Bearon et al. 2012) and channels (Croze et al. 2013). The effects of shear on the cell diffusivity can be gauged from the magnitude of $\zeta =B|{\varvec{\omega }}|$, where $B$ is the gyrotaxis number and ${\varvec{\omega }}$ is the vorticity vector. In many situations, cells tumble for $\zeta >1$ and some components of diffusion tensor decrease with increase in $\zeta$. In our simulations, we found that $\zeta$ varies from $\zeta =0$ to $\zeta =7$ and hence could potentially decrease some components of diffusion tensor. However, the spatial diffusion based on the generalized Taylor dispersion is a long-time asymptotic analysis, whereas, here, cells move relatively quickly between different flow regions, and there is no theory for the dispersion of swimming cells in regions of the flow that are hyperbolic, such as local stagnation points. There have been computational studies of pairwise hydrodynamic interaction between idealized swimming cells (e.g. Ishikawa et al. 2006) and its effects on rotational diffusivity (Ishikawa and Pedley 2007), but the theory is incomplete and there are no results for higher concentrations. The mean and standard deviation of swimming speed were measured in the absence of flow by Hill and Häder (1997). The effect of variation in swimming speed was identified by Bees and Hill (1999) in a fixed-correlation-time approximation to the spatial diffusion given by Pedley and Kessler (1990), but the theory has not been extended further. Given the current state of the theory, the number of different dispersion mechanisms and the agreement between our numerical results and experiments, we conclude that the use of a constant isotropic diffusion may be regarded as a good first approximation to the dispersion of swimming cells in bioconvection in simple constrained geometries, and it is not at all obvious that any improvement could be obtained by introducing more complicated expressions for dispersion without much more refined experimental data.

Some other simplifying assumptions in the model are the following. We have considered spherical cells only, whereas a typical algal cell closely resembles a spheroid. However, it has been shown that, averaged over a swimming cycle, the C. nivalis cell reorients as though it was spherical (O’Malley and Bees 2012). The physical parameters used in the numerical experiments are the best estimates currently available, but many may not be accurate. The experiments of Bees and Hill (1997) were carried out in a closed circular Petri dish, whereas our simulations were carried out in a rectangular periodic chamber. Thus, the effects of rigid boundary and cylindrical geometry on the patterns are absent in our simulations. Despite these discrepancies, the numerical results agree well, both qualitatively and quantitatively, with the experimental observations.