A Stochastic Model of Cancer Growth Subject to an Intermittent Treatment with Combined Effects: Reduction in Tumor Size and Rise in Growth Rate

Abstract

A model of cancer growth based on the Gompertz stochastic process with jumps is proposed to analyze the effect of a therapeutic program that provides intermittent suppression of cancer cells. In this context, a jump represents an application of the therapy that shifts the cancer mass to a return state and it produces an increase in the growth rate of the cancer cells. For the resulting process, consisting in a combination of different Gompertz processes characterized by different growth parameters, the first passage time problem is considered. A strategy to select the inter-jump intervals is given so that the first passage time of the process through a constant boundary is as large as possible and the cancer size remains under this control threshold during the treatment. A computational analysis is performed for different choices of involved parameters. Finally, an estimation of parameters based on the maximum likelihood method is provided and some simulations are performed to illustrate the validity of the proposed procedure.

1 Introduction

Tumor is one of the main causes of death in the modern society, so in the last decades a lot of attempts have been made to describe the tumor dynamic. From the mathematical point of view, the studies in this direction have also affected the construction and the analysis of some models aimed at predicting the evolution of the disease under particular conditions or under the influence of specific therapies. Most of these models are based on the assumption that the growth curve is exponential type (see, for instance, Gerlee (2013), for historical development of tumor growth laws). These models describe the increase in the tumor size over time via differential equations. Since the exponential curve seems unable to explain tumor growth in the longer term, different models have been formulated for describing the tumor dynamic. More accurate models are characterized by the presence of an inflection point. This point determines a sigmoidal shape whose limit value, called “carrying capacity”, is imposed by some environmental limitation such as nutrients. In particular, the law of Gompertz plays an important role in the dynamic of solid tumor because in several contexts it seems to fit experimental data in a reasonable precise way (cf., for example, Migita et al. 2008; Wang et al. 2007). Specifically, the Gompertz equation has proven to be a useful tool to describe human cancer evolution. For example, in Cameron (1997), Norton (1988), Speer et al. (1984), Spratt et al. (1992), and Hausten and Schumacher (2012), Gomperztian model of breast cancer growth has been formulated and analyzed. In Maronski (2008), the problem of optimal chemotherapy is considered based on the Gompertz cancer model. In Marusic et al. (1994), fourteen deterministic mathematical models have been studied to describe the tumor growth in vivo. In this context, the authors showed that the Gompertz model best fit data from colon carcinoma. The Gompertz law has been also used to describe the interaction between the cancer and the immunological system. In this direction, in Albano et al. (2007), de Vladar et al. (2003) and de Vladar and Gonzalez (2004), models that include the principal characteristics of the T-cell-mediated reaction against cancer were proposed. Moreover, in Kozusko and Bajzer (2003), it has been considered also the dynamics between proliferating and quiescent cells that form the tumor mass.

However, often some discrepancies exist between clinical data and theoretical predictions, due to more or less intense environmental fluctuations depending on various factors that are not measurable or are not known. So, to take into consideration such environmental fluctuations, generally associated with the dynamics of real systems, the notion of growth in random environment has been formulated. Various contributions that following the stochastic approach are present in the literature. In Lo (2007, 2010), the proposed models take account of both cell fission and mortality. In Abundo and Rossi (1989), the growth of tumor size under the effect of therapies that modify the growth rates of the phenomenon was studied. In Albano and Giorno (2006), a stochastic Gompertz model was used to describe the evolution of a solid tumor treated with a time-dependent therapy able to modify the birth rate of the cancer cells. Since then, various other models have been formulated to include the interesting parameters of the phenomenon. Specifically, in Albano and Giorno (2008), the interactions between proliferating and quiescent cells have been analyzed under the effect of two kinds of therapies: non-specific cycle drugs (that can damage tumor cells in any phase of the cellular cycle) and specific cycle drugs (that act on tumor cells only in a fixed phase of their cycle). In Albano et al. (2013), the authors have studied the growth of tumor size under the effect of anti-proliferative and/or pro-apoptotic therapies that modify both growth rates of the phenomenon.

Moreover, various studies have been made to describe methods to estimate the involved parameters (cf., for example, Abundo et al. 1993) and the time-dependent functions representing the effect of a therapy treatment (cf. Albano et al. 2011, 2012; Román-Román and Torres-Ruiz 2012). In Weedon-Fekjaer et al. (2008), the authors have used a new procedure to estimate the tumor growth through mammography screening data. To take into account the real cases in which different therapies are jointly applied, in Albano et al. (2014), the authors have proposed a methodology to estimate the functions representing the effect of a therapy that can affect growth and/or death rate when one of the functions is known or can be estimated previously. The proposed procedure allows to establish the nature, or at least the prevalent effect, of a single therapy.

Recently, some models have been proposed to describe the tumor dynamic under the effect of therapies that instantly reduce an intrinsic factor of the tumor worsening at predefined levels. In particular, in Hirata et al. (2010) and Tanaka et al. (2010), models of prostate tumor growth under intermittent hormone therapy have been studied. The models are categorized into a hybrid dynamical system because switching between on-treatment and off-treatment intervals is considered in addition to continuous dynamics of tumor growth.

In the following, we consider the tumor size as the intrinsic factor to control. In this direction, in order to describe the effect of a therapeutic program that produces an intermittent suppression of the intrinsic factor, in Giorno and Spina (2013) a stochastic process with jumps, based on a Gompertz diffusion process, has been proposed. Each jump, representing the effect of an application of a therapy, shifts the process to a certain return value that in general we can assume random. The constructed stochastic process is composed by recurring cycles representing the time interval between a jump and the other. The duration of the cycles is the time interval between two successive applications of therapy. In Giorno and Spina (2013), the attention is paid on the effect produced by the randomness of the return point of the process. In particular, the simulations show that the mean of the process is not influenced by the distribution of the return point, so this one can be assumed constant.

In the present paper, we reformulate the model proposed in Giorno and Spina (2013) to take into account the effect that the therapy can have on the individual. Indeed, since when a therapy is applied there is a selection event in which only the most aggressive clones survive, we assume that after an application of the therapy, the tumor size returns to a fixed value from which the evolution starts with an increased growth rate. For example, this perspective could be applied to targeted drugs that have a much lower toxicity for the patient. Specifically, we consider a stochastic return process built on a Gompertz diffusion process such that each return occurs at variable intervals of time and shifts the process in a predetermined state. From here, the process restarts according to the Gompertz law, whose parameters are modified to take into account the effect of a selection event. The obtained process is composed of independent cycles that can be of variable durations if the inter-jump intervals are not constant. Moreover, we assume that, after each jump, the process starts with a gradually increased growth rate, depending on the number of applications made. Hence, each therapeutic application involves a reduction in the tumor mass, but it also implies an increase in the speed of growth. This raises the problem of finding a compromise between these two aspects. In this paper, we analyze the stochastic process with jumps, and from the study of the first passage time (FPT) through a constant boundary, we provide information on how to choose the application times so that the cancer size remains bounded during the treatment. The remainder of the paper is organized as follows.

In Sect. 2, the deterministic model is introduced and the assumption of random environment is considered to obtain the stochastic process. Since the analysis of the return stochastic process requires the study of the single processes active in each cycle, some information concerning the single processes are provided. In Sect. 3, we introduce the FPT problem for the process with jumps through a constant control threshold. We note that the FPT problem for one-dimensional diffusion processes with jumps is studied also in Abundo (2010). In the present paper, a numerical procedure to compute the FPT probability density function (pdf) and its mean is proposed. In Sect. 4, the analysis of the FPT is used to provide a criterion to select the times in which to apply the therapy and some numerical evaluations are performed to point out the efficiency of the proposed strategy. The choice of these times depends on parameters involved in the model that can be known only via statistical procedures. So, in Sect. 5, an estimation of parameters based on the maximum likelihood method is provided and some simulations are carried out.

2 The Model

We want to analyze the effect of a therapeutic program that provides intermittent suppression of cancer cells. Each application of the therapeutic program shifts the cancer mass to a return state $\rho$; moreover, to take into account the selection event in which only the most aggressive clones survive, we assume that the growth rate of the cancer cells increases after each application.

We suppose that the return state $\rho$ is equal to the initial tumor mass, i.e., the tumor size recorded at the time of diagnosis. The therapeutic program consists of $N$ applications of the therapy. We denote by $\zeta _k$, ($k=1,2,\ldots ,N$) the inter-jump intervals.

Let $x(t)$ be the deterministic process describing the tumor size at the time $t$. Then, $x(t)$ consists of independent cycles, each of one we suppose is described by Gompertz law with different growth rates. In particular, starting at $\rho >0$, the process evolves according to the Gompertz law with parameters $\alpha _0=\alpha$ and $\beta$, where $\alpha >0$ and $\beta >0$ are the natural growth parameters of the tumor cells in the absence of therapies. After a time $\zeta _1$, a therapy is applied, the effect of which is to reduce the tumor size to $\rho$ on the one hand and to increase the growth rate with an amount $\gamma _1$ on the other hand. Thus proceeding, after the $k$-th application, the process will evolve from the state $\rho$ following the Gompertz law with the birth parameter $\alpha _k=\alpha +\gamma _k$, while the death parameter remains constant. For each $k=1,2,\ldots ,N$, the constant $\gamma _k>0$ describes the toxicity of the drug for the patient. Generally, assuming that the therapy is applied $N$ times, the cancer size at time $t$ can be described by using the indicator function $1_A$ as following:

$$\begin{aligned} x(t)=\sum _{k=0}^{N} x_k(t) 1_{\left[ \tau _k,\tau _{k+1}\right) }(t), \end{aligned}$$

(1)

with $x(\tau _k^-)=x_{k-1}(\tau _k)$, $x(\tau _k)=\rho$, $\tau _0=0$, $\tau _k=\zeta _1+\ldots +\zeta _k$, $k=1,2,\ldots , N$, $\tau _{N+1}=\infty$ and where

$$\begin{aligned} x_k(t)=\exp {\left\{ \frac{\alpha _k}{\beta }+\left( \log \rho -\frac{\alpha _k}{\beta }\right) e^{-\beta (t-\tau _k)}\right\} },\quad x_k(\tau _k)=\rho , \end{aligned}$$

(2)

with $\alpha _0=\alpha$ and $\alpha _k=\alpha +\gamma _k$, for $k\ge 1$. Equation (2) describes the evolution of tumor size after the $k$-th application of the therapy.

Note that $x_k(t)$ is bounded by

$$\begin{aligned} C_k=\lim _{t\rightarrow \infty }x_k(t)=\exp \left\{ {\alpha _k\over \beta }\right\} . \end{aligned}$$

Specifically, if $\rho <C_k$, then $x_k(t)$ increases until $C_k$, being this value an upper bound, else $x_k(t)$ decreases until $C_k$. Here, we consider the case $\rho <C_k$.

To include in the model (1) environmental fluctuations, in the line of Ricciardi (1979), we propose the stochastic process $X(t)$ defined by

$$\begin{aligned} {X(t)}=\sum _{k=0}^{N} {X_k(t)} 1_{\left[ \tau _k,\tau _{k+1}\right) }(t), \end{aligned}$$

(3)

where $X_k(t)$, for $k=0,\ldots ,N$, is the stochastic process solution of the stochastic differential equation

$$\begin{aligned} \mathrm{d}X_k(t)=[\alpha _k-\beta \ln X_k(t)]\,X_k(t)\mathrm{d}t+\sigma X_k(t) \mathrm{d}W(t),\quad X_k(\tau _k)=\rho \quad (t\ge \tau _k), \end{aligned}$$

with $\sigma >0$ measures the width of environment fluctuations and $W(t)$ is a standard Brownian motion.

Concretely, $X_k(t)$ is the Gompertz diffusion process, introduced in Capocelli and Ricciardi (1974), and characterized by drift and infinitesimal variance

$$\begin{aligned} A_1^{(k)}(x)=(\alpha _k-\beta \ln x)x,\quad A_2^{(k)}(x)=\sigma ^2x^2, \end{aligned}$$

respectively.

The transition probability density function of $X_k(t)$ (see Albano et al. 2011 for details) is

$$\begin{aligned} f_k(x,t|\rho ,\tau _k)={1\over x\sqrt{2\pi V^2(t|\tau _k)}}\exp \left\{ -{[\ln x-M_k(t|\ln \rho ,\tau _k)]^2\over 2V^2(t|\tau _k)}\right\} , \end{aligned}$$

(4)

where

$$\begin{aligned} M_k(t|y,\tau _k)&= y\,e^{-\beta (t-\tau _k)}-{\sigma ^2/2-\alpha _k\over \beta }(1-e^{-\beta (t-\tau _k)}),\\ V^2(t|\tau _k)&= {\sigma ^2\over 2\beta }\left( 1-e^{-2\beta (t-\tau _k)}\right) , \end{aligned}$$

whereas their moments are given by

$$\begin{aligned} E[X_k^n(t)|X_k(\tau _k)=\rho ]=\exp \left\{ nM_k(t|\ln \rho ,\tau _k)+{n^2\over 2}V^2(t|\tau _k)\right\} \quad (n=1,2,\ldots ). \nonumber \\ \end{aligned}$$

(5)

The moments of $X(t)$ can be calculated by virtue of (3) making use of (5).

In order to show graphically the behavior of the process $X(t)$, Fig. 1 contains several simulated sample paths. In the simulation analysis, we assume that the rates are measured in years$^{-1}$ and the tumor size is given by the tumor cell density. Specifically, following Parfitt and Fyhrie (1997), we consider $\alpha =6.46\, \hbox {year}^{-1},\, \beta =0.314\, \hbox {year}^{-1},\, X_k(0)=\rho =10^8$. Note that the value $1.074\,\times \,10^8$ is representative of a 0.1 g tumor mass (namely the smallest diagnosable mass). In Fig. 1, a sample path of $X(t)$ is plotted for $N=5$ with $\alpha _k=\alpha +0.1 k\, (k=0,1,\ldots ,5),\, \sigma =0.1$ and different choices of the inter-jump intervals. On the left of Fig. 1, the instants of therapy applications are (1, 3, 5.5, 7), in the center are (2, 6, 10, 13) and on the right we have chosen (2, 4, 6, 8, 10). The blue and red curves represent $X(t)$ and $X_0(t)$, respectively. Note that for this choice of the parameters, during the treatment, the process $X(t)$ is below $X_0(t)$, corresponding to the natural evolution of the illness.

Fig. 1

The sample paths $X(t)$ are plotted for $\rho =10^8,\,\alpha _k=6.46+0.1 k,\,\beta =0.314,\,\sigma =0.1$ and therapeutic application times (1, 3, 5.5, 7), (2, 6, 10, 13) and (2, 4, 6, 8, 10) (from left to right). The red line represents $X_0(t)$ (Color figure online)

3 The First Passage Time problem

In this section, we focus on the FPT problem for the process $X(t)$ through a constant threshold $S$. Since $X(t)$ is defined in terms of the single processes $X_k(t)$, we firstly remark some aspects about the FPT of $X_k(t)$ through $S$.

3.1 FPT for the Process $X_k(t)$

Let

$$\begin{aligned} T_k(S|\rho )=\inf _{t>\tau _k}\{t:X_k(t)>S|X_k(\tau _k)=\rho \},\quad S>\rho \end{aligned}$$

be the random variable FPT of $X_k(t)$ through the threshold $S$ and let $g_k(S,t|\rho ,\tau _k)$ be its pdf. For $S>\rho$, the density $g_k$ is the solution of the following second-kind Volterra integral equation (cf., for example, Buonocore et al. 1987; Giorno et al. 1989)

$$\begin{aligned} g_k(S,t|\rho ,\tau _k)=-2\varPsi _k(S,t|\rho ,\tau _k)+2\int _{\tau }^tg_k(S,u|\rho , \tau _k)\varPsi _k(S,t|S,u)\,\mathrm{d}u, \end{aligned}$$

where

$$\begin{aligned} \varPsi _k(S,t|z,u)\!=\!-\!{S\over 2}\left[ \!\left( \!\alpha _k\!-\!\beta \ln S-{3\sigma ^2\over 2}\right) \!f_k(S,t|z,u)-\sigma ^2S{\partial \over \partial x}f_k(x,t|z,u)\bigg |_{x=S}\right] . \end{aligned}$$

Note that $T_k(S|\rho )=\tau _k+T_k^0(S|\rho )$, where $T_k^0(S|\rho )$ is the FPT of the process $X_k(t)$ translated to the initial time 0. Therefore, one has

$$\begin{aligned} E[T_k(S|\rho )]=\tau _k+E\left[ T_k^0(S|\rho )\right] . \end{aligned}$$

Moreover, following Ricciardi et al. (1999), we can prove that $T_k^0(S|\rho )$ is an honest random variable and its mean can be evaluated by means of

$$\begin{aligned} E[T_k^0(S|\rho )]= \int _\rho ^S \mathrm{d}z h_k(z) \int _0^z s_k(u)\mathrm{d}u, \end{aligned}$$

(6)

where

$$\begin{aligned} h_k(x)&= \exp \left\{ -2 \int ^x {A_1^{(k)}(\xi )\over A_2^{(k)}(\xi )}\mathrm{d}\xi \right\} = x^{-2\alpha _k/\sigma ^2}\exp \Bigl \{{\beta \over \sigma ^2}\ln ^2x\Bigr \},\\ s_k(x)&= {2\over {A_2^{(k)}(x)h_k(x)}} , \end{aligned}$$

are the scale function and speed density of $X_k(t)$, respectively.

3.2 FPT for the Process $X(t)$

Let

$$\begin{aligned} T(S|\rho )=\inf _{t>0}\{t:X(t)>S|X(0)=\rho \},\quad S>\rho \end{aligned}$$

be the FPT of $X(t)$ through $S$ and let $g(S,t|\rho ,0)$ be its pdf. We obtain an expression for $g$ as it follows. Let $I_k=[\tau _k,\tau _{k+1})$ for $k=0,1,\ldots , N$. If $t\in I_0$ then no treatment has yet been applied, so $X(t)$ evolves as $X_0(t)$ and $g(S,t|\rho ,0)=g_0(S,t|\rho ,0)$. If $t\in I_k$ with $k\ge 1$, i.e., $k$ applications of the therapy have been done, $X(t)$ reaches $S$ for the first time at $t$ if and only if $X_k(t)$, starting from $\rho$ at time $\tau _k$, crosses $S$ for the first time at $t$ and no previous processes have crossed $S$ before $\tau _k$. Moreover, since $X(t)$ consists of independent cycles, we have:

$$\begin{aligned} g(S,t|\rho ,0) = \left\{ {\begin{array}{*{20}{l}} {{{g}_0}(S,t|\rho ,0)}&{}\quad {t \in {I_0}}\\ {\prod \limits _{j = 0}^{k - 1} {\left[ {1 - \int \limits _{{\tau _j}}^{{\tau _{j + 1}}} {{g_j}} (S,\tau |\rho ,{\tau _j})\mathrm{d}\tau } \right] } {g_k}(S,t|\rho ,{\tau _k}),}&{}\quad {t \in {I_k}}. \end{array}} \right. \end{aligned}$$

We compute the FPT pdf $g$ recalling that $g_k(S,t|\rho ,\tau _k)$ can be approximated with the function $\tilde{g}_k(S,t|\rho ,\tau _k)$, for $t\in I_k$ $(k=0,1,\ldots , N)$, obtained via the following numerical algorithm (cf. Buonocore et al. 1987; Giorno et al. 1989):

$$\begin{aligned} \tilde{g}_k(S,\tau _k+H|\rho ,\tau _k)&= -2\varPsi _k(S,\tau _k+H|\rho ,\tau _k)\\ \tilde{g}_k(S,\tau _k+iH|\rho ,\tau _k)&= -2\varPsi _k(S,\tau _k+iH|\rho ,\tau _k)\\&{+\,}{2}H\sum _{r=1}^{i-1}\tilde{g}_r(S,\tau _k+rH|\rho ,\tau _k) {\varPsi }_k(S,\tau _k+iH|S,\tau _k+rH)\\&\qquad (i=2,3,\ldots ) \end{aligned}$$

where $H$ represents the integration step. In Fig. 2, the FPT pdf of $X(t)$ is plotted for $\alpha _k = 6.46 + 0.1k, \,\beta = 0.314,\,\sigma = 0.1,\,S = 8\,\times \,10^8,\,\rho = 10^8$ and various choices of the application times.

Fig. 2

The FPT pdf of $X(t)$ for $\alpha _k=6.46+0.1\, k,\,\beta =0.314,\,\sigma =0.1,\,S=8\,\times \,10^8,\,\rho =10^8$ and therapeutic application times (1, 3, 5.5, 7), (2, 6, 10, 13) and (2,4,6,8,10) (from left to right)

The mean of $T$

$$\begin{aligned} E[T(S|\rho )]=\int _0^\infty t \,g(S,t|\rho ,0)\,\mathrm{d}t, \end{aligned}$$

can be computed by using the numerical evaluation of $g(S,t|\rho ,0)$.

4 A Proposed Scheduling

The effectiveness of an intermittent treatment depends on the range of the inter-jump intervals. The choice of $\zeta _k$ has to balance the positive effect (the reduction in the cancer mass) and the negative effect (the survival of the most aggressive clones) of the treatment.

Denoting by $S$ a control threshold, we require that $X(t)<S$ during the treatment. Hence, we propose to apply therapy before $X(t)$ reaches $S$. So, $\zeta _k$ can be determined from the FPT of the process $X_{k-1}(t)$ through $S$. Rather than considering the random variable FPT $T_k(S|\rho )$, we refer to its mean. Therefore, for $k=1,2,\ldots ,N$, we choose $\zeta _k<E[T_{k-1}^0(S|\rho )]$. One could consider $\zeta _k=E[T_{k-1}^0(S|\rho )]- A,$ where $A>0$ is an arbitrary constant such that $\zeta _k>0$, but this is not an objective choice because $A$ is not related to the involved values. It is more plausible that $A=h\, E[T_{k-1}^0(S|\rho )]$ is proportional to the FPT mean. Thus, we consider $\tau _k=\tau _{k-1}+\zeta _k$, with

$$\begin{aligned} \zeta _k=(1-h)\,E\left[ T_{k-1}^0(S|\rho )\right] \end{aligned}$$

(7)

where $0<h<1$ is the proportion of reduction with respect to $E[T_{k-1}^0(S|\rho )]$. Hence, increasing values of $h$ (that correspond to decreasing inter-jump intervals) are safer in terms of not passing the control threshold. Generally, the maximum number of applications $N$ is chosen such that for $k>0$ one has $\tau _{k+1}-\tau _k>\theta$, where $\theta$ can be considered as the minimum waiting time between consecutive applications.

In the following, we consider fixed values of $\alpha ,\,\beta ,\,\gamma ,\,\sigma$ and $S$ and we calculate the mean FPT of $X_k(t)$ through $S$ via (6) to determine $(\tau _1,\tau _2,\dots ,\tau _N)$. Then, we compute the mean FPT of $X(t)$ via the numerical evaluation of $g(S,t|\rho ,0)$, and we make sure that the therapy is effective by verifying that $E[T(S|\rho )]>E[T_{0}(S|\rho )]$, where $E[T_{0}(S|\rho )]$ is the mean of FPT in the absence of therapy. Moreover, we monitor the mean state of $X(t)$ to verify that it is below $S$ until the end of the treatment.

To illustrate the proposed procedure, we assume that the parameters are $\alpha _k=6.46+k\gamma ,\,\beta =0.314$, $\sigma =0.1$ and $\rho =10^8$ and we choose various values of $\gamma$ and $S$. We consider three values for the inter-jump intervals and for the application times of the therapy:

• Case (a): $h=0.10,\quad \zeta _{k+1}^a=90\%\,E[T_{k}^0(S|\rho )],\quad \tau _1^a=\zeta _1^a,\quad \tau _{k+1}^a= \tau _k^a+\zeta _{k+1}^a,$

• Case (b): $h=0.05,\quad \zeta _{k+1}^b=95\%\,E[T_{k}^0(S|\rho )], \quad \tau _1^b=\zeta _1^b,\quad \tau _{k+1}^b= \tau _k^b+\zeta _{k+1}^b,$

• Case (c): $h=0.01,\quad \zeta _{k+1}^c=99\%\,E[T_{k}^0(S|\rho )],\quad \tau _1^c=\zeta _1^c,\quad \tau _{k+1}^c= \tau _k^c+\zeta _{k+1}^c.$

The maximum number of applications $N$ is chosen such that $\zeta _{k+1}^a\ge 0.5$, so it is also $\zeta _{k+1}^b\ge 0.5$ and $\zeta _{k+1}^c\ge 0.5$

For the considered three cases, in Table 1, the means of $T_k^0(S|\rho )$ through $S=6\times 10^8$ for $\gamma =0.1$ are listed in the second column; in the other columns, we report the amplitude of inter-jump intervals $(\zeta _{k+1})$, the application times $(\tau _{k+1})$ and the corresponding mean of $T(S|\rho )$ if the therapeutic program consists of $k+1$ applications. We note that $E[T(S|\rho )]$ is always greater than $E[T_0(S|\rho )$ and it increases as the number of the applications increases. In Fig. 3, to summarize the results of Table 1, we plot the mean FPT of $X(t)$ when the therapy is applied $N$ times. As shown in Fig. 4, the strategy (7) is effective for the considered values of $h$; indeed, the mean of $X(t)$ (blue curve) is always below $S$ (black line) and $E[X_0(t)|X_0(0)=\rho ]$ (red curve) during the treatment. However, since the mean FPT of $X(t)$ for the Case (c) is greater with respect to the other considered cases (cf. Table 1; Fig. 3), it is best waiting as long as before applying the therapy.

Fig. 3

The mean FPT of $X(t)$ for the same choice of the parameters of Table 1

Fig. 4

$E[X(t)|X_0(0)=\rho ]$ (blue curve), $E[X_0(t)|X_0(0)=\rho ]$ (red curve) and $S= 6\times 10^8$ (black line) for the same parameters of Table 1 and for $\zeta _k$ given in (7) with $h$=10, 5, 1 % (from left to right) (Color figure online)

In Table 2 and in Figs. 5 and 6, the analysis is realized for the same choices of Table 1 but assuming $\gamma =0.5$. In this case, since $\gamma$ is greater, the number of therapeutic applications and the mean FPT of $X(t)$ are considerably lower than the previous case. However, as the previous case, the best results are for the Case (c).

Fig. 5

The mean FPT of $X(t)$ for the same choice of the parameters of Table 2

Fig. 6

$E[X(t)|X_0(0)=\rho ]$ (blue curve), $E[X_0(t)|X_0(0)=\rho ]$ (red curve) and $S= 6\cdot 10^8$ (black line) for the same parameters of Table 2 and for $\zeta _k$ given in (7) with $h$=10, 5, 1% (from left to right) (Color figure online)

Table 1 For $\alpha =6.46,\, \beta =0.314,\, \gamma =0.1,\,\sigma =0.1$ and $\rho =10^8$, the FPT means of $X_k(t)$ and of $X(t)$ through $S= 6\times 10^8$ are listed

In Table 3 and in Figs. 7 and 8, in order to show as the control threshold influences the mean of FPT of $X(t)$, we propose the same analysis for $S=3\times 10^8$ and $\gamma =0.1$; since the threshold is lower, the mean FPT of $X(t)$ and the number of therapeutic applications decrease with respect to the results of Table 1 obtained for the same value of $\gamma$. Also, for decreasing values of the threshold $S$, the Case (c) gives larger mean FPT (cf. Table 3; Figs. 7, 8).

Fig. 7

The mean FPT of $X(t)$ for the same choice of the parameters of Table 3

Fig. 8

$E[X(t)|X_0(0)=\rho ]$ (blue curve), $E[X_0(t)|X_0(0)=\rho ]$ (red curve) and $S= 3\times 10^8$ (black line) for the same parameters of Table 3 and for $\zeta _k$ given in (7) with $h$=10, 5, 1% (from left to right) (Color figure online)

In conclusion, the Case (c) gives always the best results; in particular, the mean FPT is larger for smaller values of $\gamma$ and for higher control threshold.

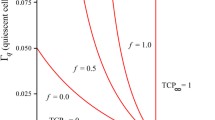
We summarize the obtained results for the mean FPT of $X(t)$ and for $N$ associated with the Case (c) for different values of $\gamma$ (Fig. 9) and of $S$ (Fig. 10). Specifically, from Fig. 9, we note that the product $\gamma E[T(S|\rho )]\in (4,8)$ increases as $\gamma$ increases, whereas $\gamma N\in (2,2.8)$ decreases as $\gamma$ increases. Moreover, from Fig. 10, we conclude that the ratios $E[T(S|\rho )]/S\in (1.3\times 10^{-8},1.83\times 10^{-8})$ and $N/S\in (1.3\times 10^{-8},1.83\times 10^{-8})$ increase as $S$. To underline the effect of the stochasticity, in Fig. 11 for the Case (c) and $N=6$, we plot the mean FPT of $X(t)$ for various values of $\sigma$ and some choices of $S$ (on the left) and of $\gamma$ (on the right). The results for $\sigma =0$, corresponding to the deterministic case, have been determined as the intersection points of the curve $x(t)$ defined in (1) and the threshold $S$. We note that the mean FPT increases as $\sigma$ increases even if the rise is slow for $\sigma \le 0.5$. Indeed, the deterministic curve goes up to the carrying capacity while the sample paths of the stochastic process grow with upward and downward fluctuations and the last ones delay the crossing of $S$.

Fig. 9

Case (c): means of $T$ (on the left) and values of $N$ (on the right) for $S=6\times 10^8$ and various choices of $\gamma$

Fig. 10

Case (c): means of $T$ (on the left) and values of $N$ (on the right) for $\gamma =0.1$ and various choices of $S$

Fig. 11

Case (c): means of $T$ for various values of $\sigma$ and $N=6$ with $\gamma =0.1$ and $S=3\times 10^8, 6\times 10^8$ (on the left) and with and $S=6\times 10^8$ and $\gamma =0.1,0.5$ (on the right)

The proposed model allows to make predictions for any choice of the parameters and of the inter-jumps intervals. On the other hand, the choice of application times depends on parameters involved in the model that can be known via statistical procedures as it is shown in the next section.

5 Estimation of the Parameters

The aim of the present section is to estimate the parameters of the processes $X(t)$. In order to use the maximum likelihood method, we consider the transformation:

$$\begin{aligned} v_\beta =\frac{\sqrt{\beta }\left[ \log x -e^{-\beta (t-\tau )}\log y \right] }{\sqrt{1-e^{-2\beta (t-\tau )}}}, \end{aligned}$$

(8)

so the transition pdf of $X_k(t)$ (4) can be rewritten as it follows:

$$\begin{aligned} f_k^{\beta }(v_\beta ,t|y_\beta ,\tau )=\frac{1}{\sqrt{\pi \sigma ^2}}\exp \left( -\frac{[v_\beta -a_kT_\beta ]^2}{\sigma ^2}\right) , \quad (\tau _k\le \tau <t<\tau _{k+1}) \end{aligned}$$

where $\alpha _k=\alpha +\gamma _k$ and

$$\begin{aligned} a_k=\displaystyle \alpha _k-\frac{\sigma ^2}{2}, \quad T_\beta =\frac{1-e^{-\beta (t-\tau )}}{\sqrt{\beta \left( 1-e^{-2\beta \,(t-\tau )}\right) }}. \end{aligned}$$

(9)

For $k=0,1,\ldots , N$, we consider a discrete sampling of the process $X_k(t)$ based on $d$ sample paths. Let $\{x_{ij}^k\}$ be the sample paths for the inferential study observed at times $t_{ij}^k$ with $\tau _{k}\le t_{ij}^k<\tau _{k+1}(i=1,2,\ldots ,d; j=1,2,\ldots , n_{i_{k}})$. Making use of (8) and (9), we have

$$\begin{aligned} T_{\beta ,k}^{ij}=\frac{1-e^{-\beta (t_{ij}^k-t_{i,j-1}^k)}}{\sqrt{\beta \left( 1-e^{-2\beta \,(t_{ij}^k-t_{i,j-1}^k)}\right) }},\quad v_{\beta ,k}^{ij}=\frac{\sqrt{\beta }\left[ \log x_{ij}^k -e^{-\beta (t_{ij}^k-t_{i,j-1}^k)}\log x_{i,j-1}^k \right] }{\sqrt{1-e^{-2\beta (t_{ij}^k-t_{i,j-1}^k)}}}. \end{aligned}$$

Denoting by $\mathbf {v}$ the vector of the values $v_{\beta ,k}^{i,j}$ and making use of the independence of the processes $X_k(t)$, the log-likelihood function for the transformed sample is

$$\begin{aligned} \log \mathbb {L}_{\mathbf {v}}(a,\varGamma ,\sigma )&= -\frac{M-d}{2}\log \sigma ^2-\frac{M-d}{2}\log \pi \\&{-\,}\frac{1}{\sigma ^2}\sum _{k=0}^{N}\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}} \left[ v_{\beta ,k}^{ij}-(a+\gamma _k)T_{\beta ,k}^{ij}\right] ^2, \end{aligned}$$

where $a=\alpha -\sigma ^2/2,\,\varGamma =(\gamma _1,\ldots ,\gamma _N)$ and $M= \sum _{k=0}^{N}\sum _{i=1}^{d}n_{i_k}$.

Table 2 For $\alpha =6.46,\, \beta =0.314,\, \gamma =0.5,\,\sigma =0.1$ and $\rho =10^8$, the FPT means of $X_k(t)$ and of $X(t)$ through $S= 6\times 10^8$ are listed

Table 3 For $\alpha =6.46,\, \beta =0.314,\, \gamma =0.1,\,\sigma =0.1$ and $\rho =10^8$, the FPT means of $X_k(t)$ and of $X(t)$ through $S= 3\times 10^8$ are listed

Deriving the log-likelihood function with respect to $\gamma _l,\,a,\,\beta$ and $\sigma ^2$ and making the derivatives equal to zero, we obtain the following system of equations:

$$\begin{aligned} \frac{\partial \log \mathbb {L}_{\mathbf {v}}(a,\varGamma ,\sigma )}{\partial \gamma _l}&= 0 \Longleftrightarrow \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}v_{\beta ,l}^{ij}T_{\beta ,l}^{ij}\!=\!(a\!+\!\gamma _l) \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}(T_{\beta ,l}^{ij})^2,\quad l\!=\!1,\ldots ,N\nonumber \\\end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial \log \mathbb {L}_{\mathbf {v}}(a,\varGamma ,\sigma )}{\partial a}&= 0 \Longleftrightarrow \sum _{k=0}^{N}\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}v_{\beta ,k}^{ij}T_{\beta ,k}^{ij}= \sum _{k=0}^{N}(a+\gamma _k)\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}(T_{\beta ,k}^{ij})^2\nonumber \\&\Longleftrightarrow \sum _{i=1}^{d}\sum _{j=2}^{n_{i_0}}v_{\beta ,0}^{ij}T_{\beta ,0}^{ij}= a\sum _{i=1}^{d}\sum _{j=2}^{n_{i_0}}(T_{\beta ,0}^{ij})^2\end{aligned}$$

(11)

$$\begin{aligned} \frac{\partial \log \mathbb {L}_{\mathbf {v}}(a,\varGamma ,\sigma )}{\partial \beta }&= 0 \Longleftrightarrow \sum _{k=0}^{N}\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}v_{\beta ,k}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}v_{\beta ,k}^{ij}\nonumber \\&-\sum _{k=0}^{N}(a+\gamma _k)\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}T_{\beta ,k}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}v_{\beta ,k}^{ij}\nonumber \\&-\sum _{k=0}^{N}(a+\gamma _k)\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}v_{\beta ,k}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}T_{\beta ,k}^{ij}\nonumber \\&+\sum _{k=0}^{N}(a+\gamma _k)^2\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}T_{\beta ,k}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}T_{\beta ,k}^{ij}=0\end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial \log \mathbb {L}_{\mathbf {v}}(a,\varGamma ,\sigma )}{\partial \sigma ^2}&= 0 \Longleftrightarrow \sigma ^2(M-d)=2\sum _{k=0}^{N}\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}} \left[ v_{\beta ,k}^{ij}-(a+\gamma _k)T_{\beta ,k}^{ij}\right] ^2.\nonumber \\ \end{aligned}$$

(13)

For $l=0,\ldots ,N$, we denote by

$$\begin{aligned}&Y_{1,l}^{\beta }=\displaystyle \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}v_{\beta ,l}^{ij}T_{\beta ,l}^{ij}\quad Y_{2,l}^{\beta }=\displaystyle \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}(T_{\beta ,l}^{ij})^2 \quad Y_{3,l}^{\beta }=\displaystyle \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}T_{\beta ,l}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}v_{\beta ,k}^{ij}\\&Y_{4,l}^{\beta }=\displaystyle \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}v_{\beta ,l}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}T_{\beta ,k}^{ij}\quad Y_{5,l}^{\beta }=\displaystyle \sum _{i=1}^{d}\sum _{j=2}^{n_{i_l}}T_{\beta ,l}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}T_{\beta ,k}^{ij} \end{aligned}$$

and

$$\begin{aligned} Z^{\beta }=\sum _{k=0}^{N}\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}v_{\beta ,k}^{ij}\frac{\mathrm{d}}{{\mathrm{d}\beta }}v_{\beta ,k}^{ij}. \end{aligned}$$

So, from (10), (11) and (13), one has:

$$\begin{aligned} a_{\beta }=\frac{Y_{1,0}^{\beta }}{Y_{2,0}^{\beta }}, \quad (a+\gamma _k)_{\beta }=\frac{Y_{1,k}^{\beta }}{Y_{2,k}^{\beta }}, \quad k=1,\ldots ,N \end{aligned}$$

and

$$\begin{aligned} \sigma ^2_{\beta }=\frac{2}{M-d}\left\{ \sum _{k=0}^{N}\sum _{i=1}^{d}\sum _{j=2}^{n_{i_k}}(v_{\beta ,k}^{ij})^2 -\sum _{k=0}^{N}\frac{(Y_{1,k}^{\beta })^2}{Y_{2,k}^{\beta }}\right\} . \end{aligned}$$

Moreover, from (12), it follows

$$\begin{aligned} Z^{\beta }-\sum _{k=0}^{N}\frac{Y_{1,k}^{\beta }}{Y_{2,k}^{\beta }} \left[ Y_{3,k}^{\beta }+Y_{4,k}^{\beta }-\frac{Y_{1,k}^{\beta }}{Y_{2,k}^{\beta }}Y_{5,k}^{\beta }\right] =0. \end{aligned}$$

This last equation does not have an explicit solution, so the estimation of $\beta$ can be found via numerical methods. After the estimation $\widehat{\beta }$ of $\beta$ has been obtained we can find the estimation of $\widehat{a_{\beta }}=a_{\widehat{\beta }}$, $\widehat{(a+\gamma _k)_\beta }=(a+\gamma _k)_{\widehat{\beta }}$, $k=1,\ldots ,N$, so $\widehat{\gamma }_k=\widehat{(a+\gamma _k)_\beta }-\widehat{a_{\beta }}$. Moreover, $\widehat{\sigma ^2_{\beta }}=\sigma ^2_{\widehat{\beta }}$, and hence, $\widehat{\alpha }=\widehat{a_{\beta }}+\widehat{\sigma ^2_{\beta }}/2$.

In the following, we present a simulation study in order to validate the estimation procedure previously developed. We have chosen to apply the therapy five times at the instants $(\tau _0,\tau _1,\tau _2,\tau _3,\tau _4,\tau _5)=(0,10,20,30,40,50)$. Hence, in this case $N=5$ and the involved processes are $X_0(t),\ldots ,X_5(t)$. The process $X(t)$ is observed in the interval $[0,\,100]$. We have fixed for each process $\alpha =6.46,\,\beta =0.314,\,\alpha _k=\alpha +k\,\gamma$, and we have considered $\gamma =0.1,\,0.25,\,0.50$ and $\sigma =0.01,\,0.025,\,0.05,\,0.075,\,0.1$. We have simulated 25 sample paths of $X(t)$. Each sample path of $X(t)$ is obtained by means of (3) from the simulated sample paths associated with the processes $X_k(t)$ into $[\tau _k,\tau _{k+1})$, with $X_k(\tau _k)=\rho =10^8$, by using the step $H=0.1$. Hence, we have considered 100 data for each $X_i(t)$ ($i=0,1,\ldots ,4$) and 501 for $X_5(t)$. After the simulation, we have chosen a sample for each process starting from the first value and using the step $H_1=1$. Hence, a sample of 101 data is obtained [10 data for each $X_i(t)$ for $i=0,1\ldots ,4$ and 51 for $X_5(t)$]. The algorithm has been implemented with MATHEMATICA 9.0. In Table 4, the obtained estimations are listed. We note that the estimation procedure is valid for each choice of the parameters even if, due to the increasing variability of the sample paths, it gives worse results for values of $\sigma$ greater than 0.5.

Table 4 Estimated values for $\alpha ,\,\beta ,\,\sigma$ and $\gamma _k=k\,\gamma$ for some combinations of $\gamma$ and $\sigma$, taking $\alpha = 6.46, \beta = 0.314$

6 Conclusions

We propose a stochastic cancer growth model to study the effect of an intermittent therapy. We assume that each therapeutic application reduces the cancer size at a fixed level and produces an increase in the growth rate of the cancer cells of a term $\gamma _k$ that depends on the number of followed applications. The obtained stochastic process $X(t)$ is a combination of different Gompertz processes, $X_k(t)$, that describe the phenomenon in each inter-jump interval. Various simulations have been performed by choosing some control thresholds and different $\gamma _k$. Moreover, we propose a strategy based on the mean FPT of $X_k(t)$ through a control threshold to select the inter-jump intervals and different amplitudes of such intervals are considered. Specifically, $X(t)$ is reset before the reaching of control threshold $S$. The goodness of the obtained results is measured via the increase in the mean FPT of $X(t)$ through $S$. Furthermore, we verify that the mean size of the cancer is under $S$ during the treatment. The performed analysis shows that better results are obtained when the therapy is applied as later as possible, for higher control thresholds and smaller $\gamma _k$. However, the proposed model allows to make predictions for any choice of the parameters and of the inter-jumps intervals. On the other hand, the choice of application times depends on parameters involved that are estimated via the maximum likelihood method. Moreover, to validate the estimation procedure, various simulations are performed by using an algorithm implemented with MATHEMATICA 9.0.

Various future directions are possible, for example, the inclusion of delay times after each application of the therapeutic program. Indeed, it is reasonable to think that the effect of an application is not instantaneous, but it needs a time interval to observe the effect of the treatment. Such interval can have random duration imagining that the reaction times are different for different individuals. Moreover, we would extend the proposed model by considering that each application reduces the tumor size of a different quantities so that the return points are different. Finally, the proposed strategy can be compared with other ones. This analysis would be useful to establish when it is preferable to choose inter-jump intervals based on the FPT, as proposed in the present paper, with respect to other choices which consist, for example, in considering constant inter-jump intervals.