Characteristics of Quantum Plasmonic Waves Guided by a Symmetric Metal–Gap–Dielectric Nano-system

Abstract

The guiding properties of a symmetric conductor–gap–dielectric system consists of a metal film symmetrically surrounded by media of two dielectrics, and is theoretically analyzed by using the quantum hydrodynamic model and Maxwell’s equations. We found that the quantum effects, including the Fermi pressure and the Bohm potential, facilitate the propagation of the hybrid surface waves at higher values of the wavenumber. The results show that the permittivity of the surrounding dielectric mediums and the geometric effects (namely, the thickness of the metal film and gap layers) significantly modify the basic behaviors of the hybrid surface waves. Our results provide a good understanding of the basic features of the wave propagation phenomenon in hybrid waveguide systems.

Introduction

Surface plasmon polaritons (SPPs) are waves that propagate at the interface between a conductor and a dielectric medium. SPP wave has been intensively investigated, due to its potential to confine the light beam on the subwavelength scale [1, 2]. This confinement increases the field amplitude in the metal and reduces the propagation length of the SPP waves. Thus, the typical plasmonic structures are unsuitable for many practical implementations.

The compromise between confinement and propagation loss is one of the major challenges in SPP technology. In recent decades, various types of SPP structures have been proposed for the solution to the ohmic loss of SPP modes. One of the most appealing candidates is the dielectric–metal–dielectric (DMD) structure which consists of a thin metal film sandwiched by a dielectric medium. In this structure, many kinds of geometries have been studied theoretically and experimentally [3,4,5,6]. Results show that if the metal film thickness is thin enough, the SPP waves on the two metal-dielectric interfaces can be coupled efficiently and create two plasmon wave modes: the long-range SPP (LR-SPP) mode with the symmetric field profile and the short-range SPP (SR-SPP) mode with the antisymmetric field profile.

Although the LR-SPP wave has a high propagation length compared with the SPP mode, it suffers from very weak confinement owing to the trade-off between the propagation and confinement. In recent years, many researchers have examined a conductor–gap–dielectric (CGD) structures to achieve the hybrid plasmon polariton (HPP) waves with strong optical field confinement and low propagation loss [7,8,9,10,11,12,13,14,15,16,17]. The CGD structures consist of a high-index dielectric medium separated from a metal surface by a low index dielectric layer (gap).

Wei et al. investigated the dispersion equation of HPP modes in a symmetric conductor–gap–dielectric (SCGD) system, consisting of a finite-thickness metal film symmetrically sandwiched by two-layer dielectrics with low-index nanoscale gaps inside. They showed that if the thickness of the gap is thin enough, the SCGD structure can support ultra-long-range surface mode [18].

When the thickness of the metal film in the plasmonic structures, approaches the nanoscale, the quantum effects are no longer negligible. Such fine effects play a vital role in the dynamic properties of the surface waves [19, 20]. Jung and Hong in 2013 studied SR-SPP and LR-SPP modes on a thin quantum plasma layer by using the plasma dielectric function with the kinetic dispersion model [21]. Moradi analyzed the propagation of bulk and surface waves in a thin quantum plasma film [22]. In our recent work, we studied quantum effects, including the Fermi pressure, the Bohm potential, and the exchange–correlation interaction [23, 24] in the planar CGD system by using a quantum hydrodynamic (QHD) model. It is shown that the presence of the gap nanolayer modifies the behavior of the HPP waves in quantum plasma systems [25].

To the best of our knowledge, the influence of quantum effects has not yet studied on the guided mode in hybrid waveguides. This motivated us to study the influence of quantum effects on the guided modes in a planar symmetric conductor–gap–dielectric system (SCGD).

The present paper is organized as follows: in “Assumptions and Equations,” the dispersion relation of SR-HPP mode and LR-HPP mode in a quantum SCGD system has been derived by using the QHD model. In “Numerical Analysis Results and Discussions,” the propagation characteristics of the hybrid modes in quantum plasma are analyzed and numerically solved for certain special cases. Finally, a brief discussion has been provided in “Conclusions.”

Assumptions and Equations

The proposed planar SCGD system consists of a thin metallic film with the thickness t, sandwiched symmetrically with a low-index dielectric (gap layer), and semi-infinite high-index dielectric (surrounding medium). If the height of each low-index dielectric between the metal film and the cladding medium is sufficiently small, the guided modes in the SCGD system have a high propagation length with strong fields localized on a subwavelength scale. The geometry of the symmetric metal-gap-dielectric structure is presented schematically in Fig. 1.

Fig. 1

Schematic diagram of the planar symmetric conductor–gap–dielectric (SCGD) system

Here, we consider the linear theory of surface waves and study the TM polarization hybrid waves (E_x, E_y, B_z) in the y-direction (y is the propagation direction). We assume that the permittivity of metal, gap, and high-index dielectric are ${\varepsilon }_{1}, {\varepsilon }_{2}$ and ${\varepsilon }_{3}$, respectively. The ions are immobile and all materials are lossless. We also considered the sharp boundaries of the layers are at x = 0, x = t, x = t + d, and x = −d.

Given that the dispersion properties of the surface waves are a useful tool for investigation of the physical characteristic of a plasmonic system, in this section we obtained the dispersion relation of the HPP by using the Maxwell equations coupled with the quantum hydrodynamic model (QHD) includes quantum force due to the electron tunneling through the Bohm potential and quantum statistical pressure effects. The continuity equation and the momentum equation for a quantum plasma are as follows:

$$\frac{\partial {n}_{e}}{\partial t}+\nabla .({n}_{e}V)=0,$$

(1)

$$\frac{\partial V}{\partial t}=-\frac{e}{m}E-\frac{{{v}_{Fe}}^{2}}{{n}_{0}}\nabla {n}_{e}+ \frac{{{\hbar }}^{2}}{4{n}_{0}{m}^{2}} \nabla {\nabla }^{2}{n}_{e}.$$

(2)

The second and third terms on the right-hand side of Eq. (2) refer to the contribution of the Fermi electron temperature and Bohm potential effects, respectively. The Maxwell equations for the electrons are given by

$$\nabla \times E=-\frac{1}{c}\frac{\partial B}{\partial t} ,$$

(3)

$$\nabla \times B=\frac{1}{c}\frac{\partial E}{\partial t}-\frac{4\pi e{n}_{e}}{c}V,$$

(4)

$$\nabla .B=0 ,$$

(5)

$$\nabla .E=-4\pi e{n}_{e}$$

(6)

In the above equations $c$, e, ${n}_{e}, m$, and $\hbar$ are the speed of light in vacuum, the electric charge, the electron number density, the mass of electrons, and the Planck constant divided by 2π, respectively. $E$, $B,$ V, and ${v}_{\mathrm{Fe}}$ are the electric fields, magnetic field, velocity of electrons, and electron Fermi velocity, respectively. We assume that the electron density perturbation and electromagnetic field perturbation depend on the time and spatial coordinate in the following form: $f\left(x, y, t\right)=f\left(x\right)exp\left[i({k}_{y}y-\omega t)\right]$, where $\omega$ is the wave frequency and ${k}_{y}$ is the wave vector along the y-direction.

Using Eqs. (1), (2), and (6), the wave equation for the perturbed electron density inside the metal film can be obtained as

$$n=A\mathrm{exp}\left(\gamma x\right)+{A}^{{^{\prime}}}\mathrm{exp}\left(-\gamma x\right) \qquad 0<x<t,$$

(7)

where A and ${A}^{^{\prime}}$ refer to the amplitude of the perturbed density, ${\gamma }^{2}={k}_{y}^{2}+({\omega }_{p}^{2}-{\omega }^{2})/{(v}_{Fe}^{2}+{\hbar }^{2}{k}_{y}^{2}/4{m}^{2})$ where ${\omega }_{p}=\sqrt{4\pi {n}_{0}{e}^{2}/{m}_{e}}$ is the electron plasma frequency. By employing the over-critical density plasma limit $({(v}_{Fe}^{2}{k}_{y}^{2}\ll \left|{\omega }_{p}^{2}-{\omega }^{2}\right|)$, $\gamma$ reduces to $\gamma =\sqrt{{(\omega }_{p}^{2}-{\omega }^{2})/{(v}_{Fe}^{2}+{\hbar }^{2}{k}_{y}^{2}/4{m}^{2})}.$

The perturbed electromagnetic field components in the metal film ($0<x<t$), gap layers ($t<x<d, -d<x<0$), and cladding dielectric regions ($t+d<x , x<-d$), by neglecting the very slow non-local varieties${(k}_{y}^{2}{\partial }^{4}/\partial {x}^{4}\ll {\partial }^{2}/\partial {x}^{2}\ll {k}_{y}^{2})$ are obtained in the following forms:

$$\begin{cases}{B}_{z}={c}_{1}\mathrm{exp}\left({\alpha }_{1}x\right)+{c}_{1}^{{^{\prime}}}\mathrm{exp}\left(-{\alpha }_{1}x\right) &\\& 0< x<t, \\ {E}_{y}=\frac{i}{{\omega }_{p}^{2}-{\omega }^{2}} [c\omega {\alpha }_{1}\left({c}_{1}\mathrm{exp}\left({\alpha }_{1}x\right)-{c}_{1}^{{^{\prime}}}\mathrm{exp}\left(-{\alpha }_{1}x\right)\right)&\\-4\pi e{k}_{y}{v}_{Fe}^{2}(1+\frac{{{\hbar }}^{2}}{4{m}^{2}{v}_{Fe}^{2}}({k}_{y}^{2}-{\gamma }^{2}))(Aexp\left(\gamma x\right)+{A}^{{^{\prime}}}exp\left(-\gamma x\right))]&\end{cases}$$

(8)

$$\begin{cases}{B}_{z}={c}_{2}exp({\alpha }_{2}x)+{c}_{2}^{{^{\prime}}}exp(-{\alpha }_{2}x) &\\& t<x<d, \\ {E}_{y}=\frac{c{\alpha }_{2}}{i\omega {\varepsilon }_{2}}\left({c}_{2}\mathrm{exp}({\alpha }_{2}x){-c}_{2}^{{^{\prime}}}\mathrm{exp}(-{\alpha }_{2}x)\right)&\end{cases}$$

(9)

$$\begin{cases}{B}_{z}={c}_{3}exp({-\alpha }_{3}x) &\\& t+d<x,\\ {E}_{y}=\frac{-c{\alpha }_{3}}{i\omega {\varepsilon }_{3}}{c}_{3}exp({-\alpha }_{3}x) &\end{cases}$$

(10)

$$\begin{cases}{B}_{z}={c}_{4}exp({\alpha }_{2}x)+{c}_{4}^{{^{\prime}}}exp(-{\alpha }_{2}x) &\\& -d<x<0,\\ {E}_{y}=\frac{c{\alpha }_{2}}{i\omega {\varepsilon }_{2}}\left({c}_{4}\mathrm{exp}({\alpha }_{2}x){-c}_{4}^{{^{\prime}}}\mathrm{exp}(-{\alpha }_{2}x)\right)&\end{cases}$$

(11)

$$\begin{cases}{B}_{z}={c}_{5}exp({\alpha }_{3}x) &\\& x<-d,\\ {E}_{y}=\frac{c{\alpha }_{3}}{i\omega {\varepsilon }_{3}}{c}_{5}exp({\alpha }_{3}x)&\end{cases}$$

(12)

where ${\alpha }_{1}^{2}={k}_{y}^{2}+({\omega }_{p}^{2}-{\omega }^{2})/{c}^{2}$ and ${\alpha }_{\mathrm{2,3}}^{2}={k}_{y}^{2}-{\omega }^{2}{\varepsilon }_{\mathrm{2,3}}/{c}^{2}$. And ${c}_{1}$,${c}_{1}^{{^{\prime}}},{c}_{2}$, ${c}_{2}^{{^{\prime}}},{c}_{3}$, ${c}_{4}$ $, {c}_{4}^{{^{\prime}}}$, and ${c}_{5}$ are unknown constants to be obtained later by the appropriate electromagnetic boundary conditions through the interface plane in all regions, x = 0, x = t, x = t + d, and x = −d, together with the specular reflection condition ${V}_{x}=0$ in x = 0 and x = t interfaces. After some long, but straightforward algebraic manipulations, the dispersion relation of the HPP modes in the planar SCGD system can be obtained in the following forms:

$$2-Y+Y\frac{{\omega }^{2}{\alpha }_{1}{\varepsilon }_{2}}{{\alpha }_{2}\left({\omega }_{p}^{2}-{\omega }^{2}\right)}\mathrm{tan}h \ \left(\frac{{\alpha }_{1}t}{2}\right)=Y\frac{{k}_{y}^{2}{\omega }_{p}^{2}{\varepsilon }_{2}}{{\gamma \alpha }_{2}\left({\omega }_{p}^{2}-{\omega }^{2}\right)}\mathrm{tan}h \ \left(\frac{\gamma t}{2}\right)$$

(13)

$$2-Y+Y\frac{{\omega }^{2}{\alpha }_{1}{\varepsilon }_{2}}{{\alpha }_{2}\left({\omega }_{p}^{2}-{\omega }^{2}\right)}\mathrm{cot}h \ \left(\frac{{\alpha }_{1}t}{2}\right)=Y\frac{{k}_{y}^{2}{\omega }_{p}^{2}{\varepsilon }_{2}}{{\gamma \alpha }_{2}\left({\omega }_{p}^{2}-{\omega }^{2}\right)}\mathrm{cot}h \ \left(\frac{\gamma t}{2}\right)$$

(14)

where $Y=1+\mathrm{exp}(2{\alpha }_{2}d)({\alpha }_{2}{\varepsilon }_{3}+{\alpha }_{3}{\varepsilon }_{2})/({\alpha }_{2}{\varepsilon }_{3}-{\alpha }_{3}{\varepsilon }_{2})$. Equations (13) and (14) represent the long-range HPP mode and the short-range HPP mode in the quantum symmetric metal–gap-dielectric system, respectively.

In the limit of $t\to \infty$, the SCGD system reduces to a CGD system that guides the typical HPP modes within the nanometer-scale gap region. In this case, the dispersion relation of hybrid surface waves takes the following form:

$$\gamma ={k}_{y}^{2}{\omega }_{p}^{2}{\varepsilon }_{2}\frac{\left({\varepsilon }_{3}{\alpha }_{2}-{\varepsilon }_{2}{\alpha }_{3}\right)\mathrm{exp}\left(-2{\alpha }_{2}d\right)+{\varepsilon }_{3}{\alpha }_{2}+{\varepsilon }_{2}{\alpha }_{3}}{\left({\varepsilon }_{3}{\alpha }_{2}-{\varepsilon }_{2}{\alpha }_{3}\right)\left[{\alpha }_{2}\left({\omega }_{p}^{2}-{\omega }^{2}\right)+{\alpha }_{1}{\omega }^{2}{\varepsilon }_{2}\right]\mathrm{exp}\left(-2{\alpha }_{2}d\right)-\left({\varepsilon }_{3}{\alpha }_{2}+{\varepsilon }_{2}{\alpha }_{3}\right)\left[{\alpha }_{2}\left({\omega }_{p}^{2}-{\omega }^{2}\right)-{\alpha }_{1}{\omega }^{2}{\varepsilon }_{2}\right]}$$

(15)

The dispersion relation (15) is in good agreement with that we obtained in the previous work in the absence of the exchange–correlation (EC) term [25]. In the classical limit, it is found that Eqs. (13) and (14) reduce to the following forms:

$$\mathrm{tan}h \ \left(\frac{{\alpha }_{1}t}{2}\right)=\frac{{\alpha }_{2}{\varepsilon }_{1}}{{\alpha }_{1}{\varepsilon }_{2}} \frac{2-Y}{Y}$$

(16)

$$\mathrm{tan}h \ \left(\frac{{\alpha }_{1}t}{2}\right)=\frac{{\alpha }_{1}{\varepsilon }_{2}}{{\alpha }_{2}{\varepsilon }_{1}} \frac{Y}{2-Y}$$

(17)

These results are the same as the dispersion relations of HPP modes in the classical SCGD structure derived by Wei et al [18]. On the other hand, in absence of the gap layers (i.e., h = 0), we obtain the well-known dispersion relation of the LR-SPP mode and SR-SPP mode in the DMD system [2] as follows:

$$\mathrm{tan}h \ \left(\frac{{\alpha }_{1}t}{2}\right)=-\frac{{\alpha }_{3}{\varepsilon }_{1}}{{\alpha }_{1}{\varepsilon }_{3}}$$

(18)

$$\mathrm{tan}h \ \left(\frac{{\alpha }_{1}t}{2}\right)=-\frac{{\alpha }_{1}{\varepsilon }_{3}}{{\alpha }_{3}{\varepsilon }_{1}}$$

(19)

At room temperature, the electromagnetic component of the plasmonic surface waves is unaffected by the quantum effects [19], so we are going to investigate the dispersion relation of LR-HPP mode in the electrostatic limit ($c\to \infty$).

$${\omega }_{\mathrm{LR}-\mathrm{HPP}}=\frac{{\omega }_{p}}{\sqrt{z}}\left[1+\frac{{k}_{y}{\varepsilon }_{2}\sqrt{{v}_{\mathrm{Fe}}^{2}+\frac{{{\hbar }}^{2}{k}_{y}^{2}}{4{m}^{2}}}}{2{\omega }_{p}\sqrt{1-1/z}}\frac{{\varepsilon }_{3}+{\varepsilon }_{2}+\left({\varepsilon }_{3}-{\varepsilon }_{2}\right)\mathrm{exp}\left(-2{k}_{y}d\right)}{{\varepsilon }_{3}+{\varepsilon }_{2}-\left({\varepsilon }_{3}-{\varepsilon }_{2}\right)\mathrm{exp}(-2{k}_{y}d)}\mathrm{tan}h(\frac{t{\omega }_{p}\sqrt{1-1/z}}{2\sqrt{{v}_{Fe}^{2}+\frac{{{\hbar }}^{2}{k}_{y}^{2}}{4{m}^{2}}}})\right]$$

(20)

where

$$z=\frac{\left({\varepsilon }_{3}-{\varepsilon }_{2}\right)\left({\varepsilon }_{2}\mathrm{tan}h\left(\frac{{k}_{y}t}{2}\right)-1\right)\mathrm{exp}\left(-2{k}_{y}d\right)+({\varepsilon }_{3}+{\varepsilon }_{2})\left({\varepsilon }_{2}\mathrm{tan}h\left(\frac{{k}_{y}t}{2}\right)+1\right)}{{\varepsilon }_{3}+{\varepsilon }_{2}-({\varepsilon }_{3}-{\varepsilon }_{2})\mathrm{exp}(-2{k}_{y}h)}$$

(21)

The above equations can be used to investigate the propagation characteristic of LR-HPP mode in the quantum SCGD system.

To numerically analyze the dispersion relations of the LR-HPP mode, we introduce the dimensionless parameters $W={\omega }_{\mathrm{LR}-\mathrm{HPP}}/{\omega }_{p} , K={k}_{y}{v}_{\mathrm{Fe}}/{\omega }_{p} , D=d{\omega }_{p}/{v}_{\mathrm{Fe}} ,T=t{\omega }_{p}/{v}_{\mathrm{Fe}} ,$ and $H=\hbar {\omega }_{p}/2m{v}_{\mathrm{Fe}}^{2}$, to derive the normalized forms of Eqs. (20) and (21) as follows:

$$W_{LR-HPP}=\frac{1}{\sqrt{Z}}\left[1+\frac{K{\varepsilon }_{2}\sqrt{1+\frac{{K}^{2}{H}^{2}}{4}}}{2\sqrt{1-1/Z}}\frac{{\varepsilon }_{3}+{\varepsilon }_{2}+\mathrm{exp}(-2KD)({\varepsilon }_{3}-{\varepsilon }_{2})}{{\varepsilon }_{3}+{\varepsilon }_{2}-\mathrm{exp}(-2KD)({\varepsilon }_{3}-{\varepsilon }_{2})}\mathrm{tan}h \ (\frac{T\sqrt{1-1/Z}}{2\sqrt{1+\frac{{K}^{2}{H}^{2}}{4}}})\right]$$

(22)

where

$$Z=\frac{\mathrm{exp}\left(-2KD\right)({\varepsilon }_{3}-{\varepsilon }_{2})\left({\varepsilon }_{2}\mathrm{tan}h \ \left(\frac{KT}{2}\right)-1\right)+\left({\varepsilon }_{3}+{\varepsilon }_{2}\right)\left({\varepsilon }_{2}\mathrm{tan}h \ \left(\frac{KT}{2}\right)+1\right)}{{\varepsilon }_{3}+{\varepsilon }_{2}-\mathrm{exp}\left(-2KD\right)({\varepsilon }_{3}-{\varepsilon }_{2})}$$

(23)

Numerical Analysis Results and Discussions

As shown in Eq. (20), parameters such as the Fermi pressure and the Bohm potential effects, the thickness of the metal and gap layers, and the refractive index of the gap and the cladding dielectric mediums play an important role in the dispersion properties of the long-range HPP mode. In this section, we numerically solved the dispersion relation of the electrostatic LR-HPP modes and examine the effect of these parameters on the dispersion properties of LR-HPP modes in the SCGD system.

The typical characteristic parameters in the present multilayer system are as follows: gold for the metal layer with the typical physical parameter values ${V}_{\mathrm{Fe}}=1.4\times {10}^{6}\left(m/s\right)$ and ${\omega }_{p}=1.37\times {10}^{16}\left(1/s\right)$ at room temperature [26]; Ge for the high index dielectric with permittivity ${\varepsilon }_{3}=18.27$, and SiO₂, CdS, Si, or Ge for the low-index dielectric with permittivity ${\varepsilon }_{2}=2.07$, $5.29, 11.93$, and $18.27$, respectively [18].

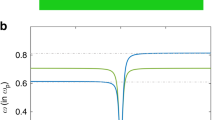
We first examined the effect of the quantum parameter on the dispersion relation of LR-HPP mode. In Fig. 2, we plotted the normalized frequency (W) versus the normalized wavenumber (K) for three values of H (H = 0, H = 0.2, and H = 0.4.

Fig. 2

Dispersion relations of electrostatic LR-HPP modes in the SCGD system for the different quantum parameters H = 0, H = 0.2, and H = 0.4. With d = 2.5 nm, t = 10 nm, ${\varepsilon }_{3}=18.27$, and ${\varepsilon }_{2}=2.07$

Figure 2 shows that the frequency of LR-HPP waves experiences an enhancement due to the Fermi pressure and the Bohm potential parameters at higher values of the normalized wavenumber. One can also see from this figure that by increasing the quantum parameter H, the group velocity and the normalized frequency of the LR-HPP waves increase for the end region of the wavenumber.

To illustrate how the geometrical dimensions affect the LR-HPP modes, we plotted the normalized frequency as a function of the normalized wavenumber for (a) different values of the metal thickness (t = 0.5 nm, t = 1 nm, t = 5 nm, and t = 10 nm) at gap layers with the fixed thickness d = 2.5 nm and (b) different values of the gap thickness (d = 0, d = 1 nm, d = 2 nm, and d = 3 nm) at a fixed metal thickness (t = 10 nm) in Fig. 3.

Fig. 3

Dispersion relations of electrostatic LR-HPP modes in the SCGD system for (a) the gap thickness d = 2.5 nm and various metal thicknesses t = 0.5 nm, 1 nm, 5 nm, 10 nm and (b) the metal thickness t = 10 nm and various gap thicknesses d = 0, 1 nm, 2 nm, 3 nm. With H = 0.4, ${\varepsilon }_{3}=18.27$ and ${\varepsilon }_{2}=2.07$

The results show that the normalized frequency at the beginning of excitation of LR-HPP modes decreases when the metal film thickness is bigger and the propagation velocity of LR-HPP mode is changed when the thickness of the metal layer increases. It turns out that the metal film thickness has more important effect on the hybrid plasmonic modes.

In Fig. 3b, we have compared the dispersion relation of the LR-HPP mode in the SCGD system with the LR-SPP mode in the case of zero-gap layer thickness (d = 0) for the DMD structure. It can be seen that an increase of the gap layer thickness increases the normalized frequency in the region of $K<0.25$ and decreases the normalized frequency in the region of $K>0.25$.

In Fig. 4, we have considered different dielectric materials in the gap layers, to show how the dispersion properties of LR-HPP modes are controlled by the index contrast ratio between the gap and the cladding dielectric medium. We have considered the SCGD system with four different materials SiO₂, CdS, Si, or Ge in the gap layers. In this figure, H = 0.4, the high index dielectric is Ge; the thickness of the gap layers and the metal film are d = 2.5 nm and t = 10 nm, respectively. We found that for the higher values of the relative dielectric constant of gap and cladding regions, the group velocity of LR-HPP mode (solid line) experiences a decrease, and in the case of the DMD structure for ${\varepsilon }_{2}={\varepsilon }_{3}$, the HPP mode appears with higher group velocity (dashed line). It is seen that the cutoff frequency decreases with the increase of permittivity ${\varepsilon }_{2}$; however, it leads to increase the phase velocity of LR-HPP mode.

Fig. 4

Dispersion relations of electrostatic LR-HPP modes in the SCGD system for four different materials as the gap layers. For the chosen parameter values H = 0.4, t = 10 nm, d = 2.5 nm, and ${\varepsilon }_{3}=18.27$

Conclusions

In this paper, we derived a new dispersion relation for hybrid plasmonic waves supported by the planar quantum symmetric conductor–gap–dielectric (SCGD) system which allows us to study the effect of physical and geometrical properties (namely, the quantum parameters, the thickness of different layers, dielectric constant), on the dispersion properties of LR-HPP modes.

It is shown that the group velocity and the normalized frequency of LR-HPP waves increase in the presence of the quantum effects. It was found that the thickness of the metal and gap layers has a great effect on the LR-HPP modes. Also, we found that the normalized frequency of the LR-HPP mode experiences an increase (a decrease) in the certain range of the normalized wavenumber for $K<0.25$ ($K>0.25$).

We also investigated the influence of the relative dielectric constant of cladding dielectric and the gap mediums. It is shown that in the case of SiO₂/Ge with a large relative dielectric constant, the LR-HPP mode has a smaller group velocity than that of the long-range mode in the DMD structure for the case of ${\varepsilon }_{2}={\varepsilon }_{3}$.

We believe that our work provides a good understanding to investigate the propagation properties of the hybrid plasmonic waves in the quantum SCGD systems. These structures are suitable for applications in the ultra-long-range SCGD waveguides, plasmonic nanolasers, plasmonic sensors, etc.