Introduction

ACUTE shortage of spectrum in the lower frequency range and benefit of using higher frequencies led the researchers to think of using beyond gigahertz frequency and towards terahertz (THz). The THz (= 1012 Hz) radiation refers to electromagnetic radiation in 0.1–10 THz range. In recent years, THz technology has gained more research attention which can be marked from the application of this in fields like defense, medical, earth and space science, material characterization, communication, sensing and imaging, etc., [1,2,3,4,5,6,7].

Presently, the focus is more towards the lower THz range because of the availability of the sources in this range [8,9,10]. A thorough literature survey reveals the use of metals, carbon nanotube (CNT), and graphene as the materials for antenna design in low-THz frequency. Copper is the most widely used metal in radio frequency and microwave frequency range. But, the design of THz copper antenna faces many challenges starting from the technological limitation of micro fabrication up to the requirement for consideration of the electromagnetic interaction at nanoscale. At THz frequency, conductivity and skin depth of conventional copper metal decreases. Low conductivity of copper leads to degradation of radiation efficiency of copper antenna and small skin depth of copper leads to high propagation losses at THz frequencies. To overcome these difficulties in nanoscale antenna at THz band, materials other than conventional copper were explored by the microwave engineers. The outcome was the use of materials made of carbon atoms, such as, CNT and graphene that opens up the possibility to design nanostructure antennas at THz frequency.

Although many THz antennas design using copper, graphene, and carbon nanotubes (CNTs) materials have been reported in the literature [11,12,13,14,15,16,17,18,19,20]. But on keen observation, it can be observed that the reason of using of such materials and the best material out of these, for THz antenna applications, is missing from antenna literature. Because this information is important from THz antenna designer’s point of view, here, in this communication, we have made an effort to answer the query with technical justification. The phenomenon of surface plasmon polariton (SPP) is used in order give reasoning for the use of suitable materials for THz antenna applications. Performance of THz antennas is carried out by analyzing their surface conductivity and surface impedance. A specific length dipole was taken as the candidate antenna for the analysis. Simulation results show that the antenna made up of graphene has better performance in terms of radiation efficiency, directivity, and compactness. For this reason, a thorough analysis has been done for the graphene plasmonic antenna.

This paper is organized as follows. SPP concept is first introduced in “Surface Plasmons and Plasmonic Resonance,” and an analytical formulation of plasmonic resonance of the graphene dipole antenna at THz band is discussed. Then, “Surface Conductivity and Surface Impedance” presents the analytical treatment of the surface conductivity and surface impedance of graphene, CNT, and copper at THz band. To verify the inferences drawn from this section, simulation results for graphene, CNT, and copper dipole antenna at low-THz frequencies are presented in “Results and discussion.” Finally, conclusions are drawn in “Conclusion.”

Surface Plasmons and Plasmonic Resonance

Under appropriate conditions, light can interact with the free electrons present on the surface of a metal to yield surface plasmon polariton mode. Incidence of light on metal nanostructures creates electron oscillations in the metal. The quantum state of oscillation of electron is known as plasmons. The term plasmon is chosen because it is a quantum of electron plasma just as photon is a quantum of light. Plasmon may comprise volume plasmon or surface plasmon. Plasmon of the surface of metal is known as surface plasmons. Volume plasmons are longitudinal oscillations and thus cannot be excited by transverse electromagnetic wave. However, surface plasmons strongly interact with photon. When photon interacts with surface plasmons at metal-dielectric interface, it results SPP [21]. SPPs confine strongly to metal surface and propagate along metal-dielectric interface. Major properties of SPPs are field enhancement, long range propagation, and short wavelength [22]. SPP mode is transverse magnetic (magnetic field is in y-direction and electric field is oriented in z-direction). This character leads the electric field component being enhanced near the surface and decay exponentially with distance away from it. In metal medium, the decay length of the field δm is determined by skin depth, whereas decay length of field in dielectric medium δd is of the order of half of wavelength of light involved.

It is noteworthy to mention that all metals cannot support surface plasmon. Following two conditions must satisfy for good plasmonic materials. First, surface plasmons exists if the real part of dielectric constant is negative, i.e., ε’ < 0 if ε = ε’ + iε“. Second, the imaginary part should be much less than the negative real part of dielectric constant, i.e., ε”<<−ε’ [23]. So far, most of the SPP related research work has been studied on noble metals, such as silver and gold. Metal plasmonic materials support propagation of SPP waves at infrared and visible frequency regime. These materials support the propagation of SPP waves with high propagation lengths of the order of a few SPP wavelengths λspp [24]. However, the propagation of SPP waves on best metal plasmonic materials exhibits large Ohmic losses and cannot be easily tuned. In contrast, carbon-based materials, such as, graphene and CNT, support the propagation of SPP waves at THz frequencies with more unique properties including tuning capability.

Novoselov et al. discovered graphene in 2004 by extracting from graphite using micro-mechanical cleavage technique [25]. It is a two-dimensional single layer of sp2-bonded carbon atoms packed in a honeycomb lattice, as shown in Fig. 1(a), with a carbon atom spacing of 0.142 nm. The extraordinary electronic, optical, mechanical, and thermal properties of graphene stimulated a great research interest in numerous fields. Its unique attractive properties such as zero-overlap semimetal or zero-gap semiconductor with very high electrical conductivity have made it the unique material of the twenty-first century. This nanomaterial graphene has very high electronic mobility of 2 × 105 cm2 V−1 S−1 [26], high current density of the order of 109 A/cm [27], and Fermi velocity (velocity of electron) of the order of 106 m/s, which is 300 times smaller than velocity of light [28].

Fig. 1
figure 1

a Lattice vector and position vector in graphene sheet. b Carbon nanotube

Full size image

The major advantage of graphene is that, it supports the propagation of SPP waves at THz frequency regime [29], which is much lower than plasmonic frequency of metals. In graphene, the complex wave vector Kspp of SPP waves determines the propagation properties of the waves. SPP wavelength is determined by the real part of the wave vector, Re{Kspp} = 2π/λspp. SPP decay and SPP propagation length are determined by the imaginary part of the wave vector Im{Kspp} and 1/Im{Kspp}, respectively. Due to the two-dimensional nature of graphene, SPP wave strongly confines at sub-wavelength scales. Surface plasmons in graphene layer exhibit unique properties of low losses, strong confinement, and high tunability. Major advantages of graphene SPP waves in comparison to noble metal SPP waves are (i) SPP waves are strongly confined to the graphene layer, with wavelength (λSPP) much smaller than free space wavelength λ0 (λSPP < <λ0) [30]. (ii) The capability of dynamically tuning the graphene conductivity via chemical potential by means of chemical doping or electrostatic bias voltage. In the THz frequency range, interband transitions in graphene are forbidden by the Pauli exclusion principle; hence, losses are small and the SPP waves can propagate [31]. SPP waves in graphene propagate for frequencies ħω < 2μc, where ħ is the reduced Planck’s constant and μc is the graphene chemical potential. Graphene supports transverse magnetic SPP mode at THz frequency range. The dispersion relation of TM SPP mode of graphene is given by [31]

$$ {K}_{SPP}=\frac{i\left({\varepsilon}_1+{\varepsilon}_2\right){\varepsilon}_0c}{\sigma \left(\omega \right)}{K}_0 $$
(1)

where KSPP is wave vector of SPPs in graphene, K0 is the free space wave vector, є1 and є2 are the relative dielectric permittivities of the substrate beneath graphene and the medium above graphene, respectively, є0 is the vacuum permittivity, c is the velocity of light in vacuum, and σ(ω) is the frequency-dependent conductivity of graphene, and graphene layer supports TM SPP waves with an effective mode index, which can be expressed as [32].

$$ {\eta}_{eff}=\sqrt{1-4\frac{\mu_0}{\varepsilon_0}\frac{1}{\sigma {\left(\omega \right)}^2}} $$
(2)

where σ(ω) is the frequency-dependent conductivity of graphene, μ0 and ε0 are permeability and permittivity of free space, respectively.

The propagation of SPP wave in graphene antenna and graphene arrays structure was found in the literature [11,12,13,14, 33,34,35]. Plasmonic resonances associated to SPP waves propagating along graphene open the era of THz antennas. The plasmonic resonance condition can be written as [36].

$$ \frac{m}{2}\frac{\lambda }{\eta_{eff}}=L $$
(3)

where L is the graphene plasmonic antenna length, λ is the wavelength of the incident electromagnetic radiations, and m is an integer which determines the order of the resonance. Since the effective mode index ηeff = λ/λSPP, length of graphene plasmonic antenna can be expressed as

$$ L=\frac{m}{2}{\lambda}_{SPP}=m\frac{\pi }{K_{SPP}} $$
(4)

where λSPP is the SPP wavelength and KSPP is the SPP wave vector. In considered frequency range, graphene SPP wave vector can be expressed as [30].

$$ {K}_{SPP}\approx \frac{\hslash {\omega}^2}{2{\alpha \mu}_cc} $$
(5)

where ω is the angular frequency, ħ is reduced plank’s constant, μc is the chemical potential of graphene, c is the velocity of light, and \( \alpha =\frac{e^2}{\hslash c}\frac{1}{4\pi {\varepsilon}_0}=\frac{1}{137} \) is the fine structure constant [37].

Therefore, length of the graphene plasmonic antenna can be written as

$$ L=m\frac{2{\pi \alpha \mu}_cc}{\hslash {\omega}^2} $$
(6)

and resonant frequency of the graphene plasmonic antenna for first order of resonance (m = 1) can be expressed as

$$ {f}_r=\sqrt{\frac{{\alpha \mu}_cc}{2\pi L\hslash }} $$
(7)

A carbon nanotube can be formed by rolling a graphene sheet. CNT was first discovered by Sumio Iijima in 1991 [38]. Zigzag and armchair CNTs can be formed by wrapping a graphene sheet along x-axis and y-axis, respectively. If the sheet is rolled around another axis, that is neither x- nor y-, then the forming tube is called chiral CNT. Lattice basis vectors a1 and a2 and relative position vector R = ma1 + na2, (m and n are integers) of graphene are shown in Fig. 1(a) and CNT is shown in Fig. 1(b). CNTs are characterized by the dual indices (m, n), for example (m, 0) designates zigzag CNTs, (m, m) armchair CNTs and (m, n), 0 < n ≠ m, chiral CNTs. CNTs can also be categorized as single-walled or multiwalled. CNTs have high mobility (≈ 8 × 104 cm2 V−1 S−1) and large current density (≈ 109 A/cm) [39]. Since, the bandgap of CNTs can be controlled by the size of applied magnetic field, they are tunable. Plasmonic waves in CNT can propagate at THz frequencies regime.

All above-mentioned plasmonic materials such as graphene, CNT, and noble metals including Au, Ag, etc. support the propagation of SPP waves at subwavelength scales. But, important differences among these plasmonic materials are (i) noble metals support SPP waves at the infrared and visible frequency regime, whereas, both carbon materials, that is, graphene and CNT, allow the propagation of SPP waves at THz frequencies regime. (ii) The propagation of SPP waves on metal plasmonic materials exhibits more plasmonic losses than graphene and CNT. (iii) Tunability is not possible for a fixed metal plasmonic structure or devices; whereas, capability of tuning is easily achieved in both graphene and CNT. Due to the curvature effect, more plasmonic losses occur in CNT with less tunability as compared to 2D graphene plasmonic material at THz frequency regime. Hence, it can be traced that the unique properties of graphene surface plasmons provide more advantages at THz frequency regime, which make it as a best material at THz frequency.

Surface Conductivity and Surface Impedance

Surface Conductivity and Surface Impedance of Graphene

Due to complicated many body interactions of electron in graphene, surface conductivity σs consists of both intraband conductivity σintra and interband conductivity σinter, which can be modeled using Kubo formalism [40].

$$ {\sigma}_s={\sigma}_{\mathrm{intra}}+{\sigma}_{\mathrm{inter}} $$
(8)

Both intraband and interband conductivity depend on the angular frequency ω, chemical potential μc, relaxation time τ, and temperature T as

$$ {\displaystyle \begin{array}{l}{\sigma}_s\left(\omega, {\mu}_c,\tau, T\right)=\frac{j{e}^2\left(\omega -j{\tau}^{-1}\right)}{\pi {\hslash}^2}\times \\ {}\left[\frac{1}{{\left(\omega -j{\tau}^{-1}\right)}^2}\underset{0}{\overset{\infty }{\int }}\varepsilon \left(\frac{\partial {f}_d\left(\varepsilon \right)}{\partial \varepsilon }-\frac{\partial {f}_d\left(-\varepsilon \right)}{\partial \varepsilon}\right) d\varepsilon -\underset{0}{\overset{\infty }{\int }}\frac{f_d\left(-\varepsilon \right)-{f}_d\left(\varepsilon \right)}{{\left(\omega -j{\tau}^{-1}\right)}^2-4{\left(\varepsilon /\hslash \right)}^2} d\varepsilon \right]\end{array}} $$
(9)

First and second terms represent intraband and interband contribution for graphene’s surface conductivity respectively. In the low-THz band and room temperature, the intraband conductivity dominates over interband conductivity, given by

$$ {\displaystyle \begin{array}{l}{\sigma}_{\mathrm{intra}}\left(\omega, {\mu}_c,\tau, T\right)\\ {}=-j\frac{e^2{\kappa}_BT}{\pi {\hslash}^2\left(\omega -j{\tau}^{-1}\right)}\left[\frac{\mu_c}{\kappa_BT}+2\kern0.3em \ln \left({e}^{-{\mu}_c/{\kappa}_BT}+1\right)\right]\end{array}} $$
(10)

In the near-infrared and visible spectrum, the interband conductivity dominates over intraband conductivity, given by

$$ {\sigma}_{\mathrm{inter}}\left(\omega, {\mu}_c,\tau, T\right)=-\frac{j{e}^2}{4\pi \hslash}\ln \left[\frac{2\mid {\mu}_c\mid -\hslash \left(\omega -j{\tau}^{-1}\right)}{2\mid {\mu}_c\mid +\hslash \left(\omega -j{\tau}^{-1}\right)}\right] $$
(11)

where \( {f}_d\left(\varepsilon \right)={\left[{e}^{\left(\varepsilon -{\mu}_c\right)/{\kappa}_BT}+1\right]}^{-1} \) is the Fermi-Dirac distribution, ε is energy, j is the imaginary unit, μc is the chemical potential, T is temperature, kB is the Boltzmann’s constant, e is the electron charge, ћ is the reduced Planck’s constant, and τ is the relaxation time.

The relaxation time can be expressed as, \( \tau =\hslash {\mu}_g\sqrt{\pi n}/{ev}_f \) where n is carrier density, μg is the electron mobility in graphene (≈ 2 × 105 cm2 V−1 S−1) and vf is Fermi velocity (≈ 106 m/s in graphene). Carrier density is related to chemical potential of graphene as

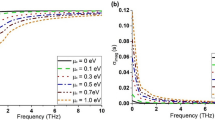
$$ n=\frac{2}{\pi {\hslash}^2{v_f}^2}\underset{0}{\overset{\infty }{\int }}\varepsilon \left[{f}_d\left(\varepsilon -{\mu}_c\right)-{f}_d\left(\varepsilon +{\mu}_c\right)\right] d\varepsilon $$
(12)

Chemical potential μc depends on carrier density n, which can be tuned by applying external voltage and/or chemical doping. Surface conductivity of graphene increases with increase of chemical potential. The surface conductivity of graphene calculated with the help of eq. (10) is shown in Fig. 2, for chemical potential μc = 0.2 eV, transport relaxation time τ = 1 ps at room temperature T = 300 K. Real part of the intraband conductivity corresponds to absorption and the imaginary part is allowing plasmonic modes. The graphene layer behaves as a constant resistance in series with inductive reactance that increases with increasing frequency. At 1.5-THz frequency, the surface impedance of graphene ZS = 42 + j401 Ω, which shows the highly inductive nature of graphene surface conductivity at low-terahertz frequencies. At a constant frequency, graphene conductivity can be tuned with chemical potential μc, which can be controlled by applying electrostatic bias voltage at the graphene layer. Therefore, radiation properties of graphene nanoantenna can be tuned via chemical potential. Figure 3 shows the complex conductivity of graphene in 0–2 THz range for different chemical potentials when relaxation time τ = 1 ps at room temperature T = 300 K. Furthermore, graphene shows the tunable behavior of surface conductivity at low-terahertz frequencies with the variation of relaxation time as shown in Fig. 4.

Fig. 2
figure 2

Complex conductivity of graphene for μc = 0.2 eV, τ = 1 ps and T = 300 K

Full size image
Fig. 3
figure 3

Complex conductivity of graphene for different chemical potentials at τ = 1 ps and T = 300 K

Full size image
Fig. 4
figure 4

Complex conductivity of graphene for different relaxation times at μc = 0.2 eV and T = 300 K

Full size image

The surface conductivity of graphene plays a major role for determining the resonance of graphene plasmonic antenna since wavelength of SPP waves within graphene plasmonic antenna is expressed as λSPP = λ / neff where neff is effective mode index and depends upon conductivity. Surface impedance of a graphene sheet can be expressed as ZS = 1/σs. Surface impedance ZS of graphene can be written as

$$ {Z}_S\left({V}_b\right)={R}_S\left({V}_b\right)+{jX}_S\left({V}_b\right) $$
(13)

where Vb is the bias voltage.

\( {R}_S=\frac{\pi {\hslash}^2{\tau}^{-1}}{e^2{\kappa}_BT\left[\frac{\mu_c}{\kappa_BT}+2\kern0.3em \ln \left({e}^{-{\mu}_c/{\kappa}_BT}+1\right)\right]} \) is the surface resistance, and \( {X}_S=\frac{\pi {\hslash}^2\omega }{e^2{\kappa}_BT\left[\frac{\mu_c}{\kappa_BT}+2\kern0.3em \ln \left({e}^{-{\mu}_c/{\kappa}_BT}+1\right)\right]} \) is the surface reactance.

Both surface resistance RS and surface reactance XS can be tuned by application bias voltage within ranges of 50 Ω–2 kΩ and 0.2–3 Ω, respectively. If Vd is bias voltage for highly doped graphene, then conductivity of graphene can be maximum when bias voltage Vb = Vd and minimum when bias voltage Vb = 0. Hence, graphene has two modes such as low resistance mode when Vb = Vd and high resistance mode when Vb = 0.

Conductivity and Surface Impedance of CNT

The electronic properties of CNT depend on the diameter and chirality of CNT. The (m, n) indices determine the semiconducting or metallic behavior of nanotubes. Armchair CNTs are always metallic. They exhibit no energy band gap. Zigzag and chiral CNT show both metallic and semiconducting behavior. Zigzag CNTs are metallic when m = 3q, where q is an integer, otherwise semiconducting. Chiral CNTs are metallic when (2 m + n)/3 is an integer, otherwise semiconducting. The conductivity of CNTs mainly depends on its chirality. CNT’s conductivity consists two parts: intraband conductivity and interband conductivity. In low-THz frequency range, intraband conductivity is more significant. In the present case, we have assumed armchair SWCNT. The intraband conductivity of armchair CNTs of small radius can be expressed as [17].

$$ {\sigma}_{CNT}=-j\frac{2{e}^2{v}_f}{\pi^2\hslash r\left(\omega -j{\tau}^{-1}\right)} $$
(14)

where e is electron charge, r is the radius of CNT, vf is Fermi velocity (vf ≈ 9.71 × 105 m/s for CNT), τ is the electron relaxation time, ω is angular frequency, and ћ is reduced plank’s constant. The surface impedance of CNT can be calculated as.

$$ {\displaystyle \begin{array}{l}{Z}_{CNT}=\frac{1}{2\pi r{\sigma}_{CNT}}=\frac{j\pi \hslash \left(\omega -j{\tau}^{-1}\right)}{4{e}^2{v}_f}\\ {}=\frac{\pi \hslash {\tau}^{-1}}{4{e}^2{v}_f}+ j\omega \frac{\pi \hslash }{4{e}^2{v}_f}={R}_{CNT}+ j\omega {L}_{CNT}\\ {}{R}_{CNT}=\frac{\pi \hslash {\tau}^{-1}}{4{e}^2{v}_f}\\ {}{L}_{CNT}=\tau {R}_{CNT}=\frac{\pi \hslash }{4{e}^2{v}_f}=3.3\mathrm{nH}/\upmu \mathrm{m}.\end{array}} $$
(15)

RCNT and LCNT are overall scattering resistance and kinetic inductance of CNT. Real part and imaginary part of CNT surface impedance are of the same order in the THz range. These expression and values of scattering resistance and kinetic inductance agree with that obtained in [41]. Scattering resistance depends on relaxation time which accounts for electron interaction with acoustic phonons. Relaxation time can be expressed as [42] τ = 2r/(αT), where α is a constant and ranging from 9.2 to 12. Therefore, scattering resistance and surface impedance of CNT can be expressed as

$$ {R}_{CNT}=\frac{\pi \hslash }{4{e}^2{v}_f}\frac{\alpha T}{2r} $$
$$ {Z}_{CNT}=\frac{\pi \hslash }{4{e}^2{v}_f}\frac{\alpha T}{2r}+ j\omega \frac{\pi \hslash }{4{e}^2{v}_f} $$

Surface impedance (10, 10) armchair CNT at 1 and 2 THz are ZCNT1 = (4.2+ j20) kΩ/μm and ZCNT2 = (4.2+ j40) kΩ/μm. Radius of (10, 10) armchair CNT calculated as

\( r=\frac{\sqrt{3}}{\pi }b\sqrt{m^2+ mn+{n}^2} \), where b = 0.142 nm is the inter atomic distance in graphene and m = n = 10. It can be seen that kinetic inductance increases with increase of frequency in THz range. Scattering resistance is independent of frequency. Therefore, scattering resistance of CNT remains constant with frequency in low-THz range.

Conductivity and Surface Impedance of Copper at THz

The surface impedance and conductivity of copper in the THz frequency region can be expressed, using Drude theory as [43]

$$ {Z}_{cu}=\sqrt{\frac{j{\omega \mu}_0}{\sigma_D^{cu}+j{\omega \varepsilon}_0}} $$
(16)
$$ {\sigma}_D^{cu}=\frac{ne^2\tau }{m\left(1+ j\omega \tau \right)}=\frac{\sigma_0^{cu}}{1+ j\omega \tau} $$
(17)

σ0cu = (ne2τ/m) is the dc-conductivity, ω is the angular frequency, τ is the electron relaxation time, e is the electron charge, m is the mass of electron, and n is the density of conduction electron in material. Surface impedance of copper wire for small radius r can be expressed as,

$$ {\displaystyle \begin{array}{l}{Z}_{cu}={R}_{cu}+ j\omega \left({L}_{cu}^i+{L}_{cu}^k\right)\\ {}{R}_{cu}=\frac{\sigma_{re}}{\pi {r}^2\left({\sigma}_{re}^2+{\sigma}_{im}^2\right)}\kern0.5em \mathrm{is}\kern0.5em \mathrm{ohmic}\kern0.5em \mathrm{resistance},\\ {}{L}_{cu}^i=\frac{\mu_0}{8\pi}\kern0.5em \mathrm{is}\kern0.5em \mathrm{internal}\kern0.5em \mathrm{inductance},\kern0.5em \mathrm{and}\\ {}{L}_{cu}^k=\frac{\sigma_{re}}{\pi {r}^2\left({\sigma}_{re}^2+{\sigma}_{im}^2\right)}\kern0.5em \mathrm{is}\kern0.5em \mathrm{the}\kern0.5em \mathrm{kinetic}\kern0.5em \mathrm{inductance}.\end{array}} $$

σre and σim represent real and imaginary part of conductivity, respectively. Kinetic inductance is much more than internal inductance and less than the ohmic resistance at low-THz frequencies (where ωτ < < 1). At 6.45 THz, ωτ = 1 for copper. Therefore, ohmic resistance Rcu is the dominant contribution to surface impedance of copper wire below 6.45 THz frequency.

A comparison of electronic properties of graphene, CNT, and copper is shown in Table 1. Since CNT is formed from graphene material; some properties of graphene and CNT are similar. Due to structural differences, they exhibit few different properties. The current density of both graphene and CNT is same, while current density of copper is less than CNT and graphene. The electron mobility of graphene is more than CNT and the electron mobility of copper is much smaller than CNT and graphene. Therefore, we can note that graphene is a best conductor and CNT is better conductor than copper in THz frequency regime.

Table 1 Comparison of electronic properties of graphene, CNT, and copper
Full size table

Results and Discussion

A center-fed THz dipole of length 71 μm was taken as the candidate antenna for comparison of the radiation performance for these three materials. Silicon dioxide (εr = 3.9) substrate of dimension (80 × 15 × 1) μm3 is chosen for graphene, CNT, and copper dipole antennas. Antennas were simulated using Ansys HFSS, a finite element method (FEM)-based electromagnetic solver. In the simulation, graphene dipole antenna was modeled as planar structure of graphene sheet, whereas CNT and copper dipole antenna was modeled as cylindrical structure of graphene and copper material, respectively. The modeled structure of graphene, CNT, and copper dipole antenna is shown in Fig. 5. Graphene dipole antenna resonates at 0.81 THz, whereas CNT and the copper dipole antenna resonate at 1.42 and 1.90 THz, respectively, which is illustrated in Fig. 6.

Fig. 5
figure 5

(i) Cross-sectional view of modeled THz dipole antenna, and (ii) top view of modeled THz dipole antenna. a Graphene dipole antenna. b CNT dipole antenna. c Copper dipole antenna

Full size image
Fig. 6
figure 6

Reflection coefficient and the far-field pattern of (a) graphene, (b) CNT, and (c) copper dipole antenna

Full size image

Numerically, resonant frequency of graphene dipole antenna over silicon dioxide substrate can be obtained from eq. 7 as fr = (αμcc/2πLћεeff)1/2 = 0.81 THz, where L = 71 μm, μc = 0.3 eV, α = 1/137, ћ = 1.05 × 10−34 Js, and εeff (effective dielectric constant) = 3.34. This numerical result is exactly equal to simulation result. Also, it can be noted that, graphene antenna resonates at lowest frequency compared to CNT and copper dipole antenna. Radiation patterns of graphene, CNT, and copper dipole antenna at their resonant frequencies are shown in Fig. 6. From these results, it can be seen that, radiation pattern of graphene, CNT, and copper dipole nanoantenna is identical, but with varied directivities. The resonant frequency of these three antennas and the corresponding directivities at these frequencies are given in Table 2. It can be noticed that graphene dipole antenna has higher directivity than CNT dipole antenna and directivity of CNT dipole antenna is higher than copper dipole antenna at low-THz frequency range.

Table 2 Radiation characteristics of graphene, CNT, and copper dipole antenna
Full size table

CNTs are characterized by slow wave propagation and large kinetic inductance. At THz frequency, kinetic inductance of CNT increases as frequency increases, as discussed in “Conductivity and Surface Impedance of CNT.” Due to kinetic inductive effect, the electromagnetic wave propagates at a much slower speed along the nanotube, which allows the CNT antenna to resonate at THz band. In case of copper, ohmic resistance is more than kinetic inductance and is a dominant contribution to surface impedance at low-THz frequency range, as discussed in “Conductivity and Surface Impedance of Copper at THz.” It is noteworthy to mention that CNT is a better conductor than copper wires at the THz band. Owing to slow wave propagation along CNT and high conductivity compared to metallic copper wire at THz frequency range, CNT dipole antenna radiates at lower frequency with higher directivity than copper dipole antenna.

At THz frequency, graphene is characterized by SPP and highly inductive nature of surface conductivity, as discussed in “Surface Plasmons and Plasmonic Resonance” and “Surface Conductivity and Surface Impedance of Graphene,” respectively. Due to propagation of TM SPP waves and excellent electronic properties at THz frequency range, graphene dipole antennas are able to radiate at the lowest frequency with the highest directivity compared to CNT and copper dipole antenna of same size. Furthermore, radiation characteristics of graphene dipole antenna can be controlled via chemical potential by electrostatic field tuning.

Conclusion

Due to the properties of conductivity function and plasmonic effect at THz frequencies, performance of graphene, carbon nanotube, and copper dipole antenna of same length is quite different. In comparison to carbon nanotube and copper dipole antenna, graphene plasmonic dipole antenna resonates at the lowest frequency with the highest directivity due to support of transverse magnetic surface plasmon polariton wave at terahertz band. This paper has provided the theoretical background for the choice of materials for low-THz antennas. Experimental results could be carried out to further validate the proposed theoretical analyses.