1 Introduction

The small-strain shear modulus (i.e., Gmax) is a key parameter in many geotechnical applications, such as seismic ground response analyses [56], site characterization [42] and liquefaction potential evaluation [2, 68], which could be considered as an indicator to represent the current state of the soils, including the void ratio and stress state [21, 23, 62]. Previous studies indicated that the small-strain shear modulus of soil is generally anisotropic [32, 36].

Natural and engineered soil deposits undergo different depositional processes, including dry and hydraulic depositions, and are subjected to complex stress conditions, resulting in significant effect on the fabric of soil [47, 51, 65]. The fabric refers to the packing or spatial arrangement [12], characteristics of contact normal [14] and void distribution [50] of discrete particles, which affects mechanical properties of soil [37]. Many laboratory and field tests were conducted to indicate that the small-strain shear modulus is anisotropic at general stress state. Zeng and Ni [66] found that the significance of stress-induced anisotropy is controlled by the value of K0 by using multi-directional bender element device. He et al. [22] showed that the anisotropic stress path has significantly influenced on stiffness anisotropy. However, it is generally accepted the anisotropy of small-strain shear modulus is result from inherent and stress-induced fabric anisotropy, and the two are not well distinguished [12, 17].

The anisotropy of small-strain shear modulus under an isotropic stress state is typically referred to as inherent anisotropy [25, 57, 58], verified through various methods of sample preparation in laboratory tests and numerical simulations. For example, specimens prepared by the air pluviation and vibration under isotropic consolidation have lower small-strain shear modulus in the vertical direction than in the horizontal direction [4, 11, 13], while tend to be isotropic prepared by the tamping and de-compaction method [11, 25], and the contact orientation of the specimens prepared by rain deposition is more likely to deviate [10]. The anisotropy of stiffness in an anisotropic stress state is commonly referred to as stress-induced anisotropy, which is widely prevalent in situ field conditions [6]. However, for the inherent and stress-induced anisotropy, it is still a challenge to explore the mechanism that how the soil fabric affects the small-strain shear modulus, respectively, due to the difficulty to quantifying the fabric anisotropy.

Based on the advanced technologies and instrument facilities, the fabric features were attempted to be observed and measured by experimental micromechanical observations, including photo-elastic techniques [15, 31], particle image velocimetry [30] and X-ray tomography [49], which are extremely costly and complicated when used in practice. Fortunately, the proposed DEM method provides an effective way to investigate the mechanical behavior of granular materials at the microscopic level using contact-based fabric indicators [28, 35, 48, 50, 55, 60, 61]. By performing wave velocity measurement using DEM simulations, Xu et al. [52] and Gu et al. [18] showed that the small-strain shear modulus could be influenced by contact connectivity networks, and Dutta et al. [8] found a close relationship between shear wave velocity and coordination number exists during shearing. Li et al. [27] investigated the evolution of both the shear modulus and elastic modulus during triaxial compression, and the results showed that the elastic modulus correlates with the fabric anisotropy. Gu et al. [17] performed a series of simple shear tests with exceedingly strain increments, extracting the microstructural information at each stress state. And they revealed distinct relationships between the small-strain shear modulus and contact normal under anisotropic triaxial compression and extension conditions. Yang and Huang [59] used three-dimensional DEM-clump simulations to model the morphology of Toyoura sand, and accurately characterized the role of inherent and strain-induced soil fabrics. However, previous studies have only qualitatively illustrated the relationship between small-strain shear modulus and fabric anisotropy, and the quantitative researches and microscopic mechanism have been neglected. Furthermore, research on the consideration of both inherent and stress-induced anisotropy lacks a systematic approach.

In the present study, specimens are generated using three-dimensional DEM method to simulate wave velocity measurement tests with different combinations of stress state, void ratio and initial soil fabrics. The objective is to investigate these influences on the small-strain shear modulus of granular materials. Meanwhile, the microscale evolutions are subjected to further examination, including the mechanical coordination number and the contact normals distribution of particle assembly, to explain the underlying mechanism of how fabric anisotropy affects small-strain modulus. And the relationship between the small-strain shear modulus anisotropy and fabric anisotropy is also investigated, which indicates that the degree of anisotropy in practice could be determined by wave measurement.

2 DEM modeling

2.1 Material and sample preparation

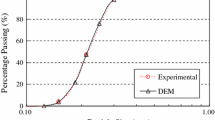
The established commercial software PFC3D was used to perform the DEM simulation. In this study, around 38,000 spherical particles with diameters ranging from 0.15 to 0.20 mm were randomly generated in a cylindrical region (diameter 8 mm × height 8 mm) with rigid frictionless walls. The walls were subjected to stress control to achieve a desired stress state. The particle size distribution of an assembly is shown in Fig. 1. The Hertz–Mindlin contact model was employed in this study which could reflect the stress dependent characteristic of the specimen stiffness [46]. The contact normal secant stiffness (i.e., Kn) and contact shear tangent stiffness (i.e., ks) are given by Eq. (1–3) [24]. The modeling parameters used in the simulations are provided in Table 1.

$$ K_{{\text{n}}} = \frac{{2G\sqrt {2R} }}{{3\left( {1 - \nu } \right)}}u_{{\text{n}}}^{1/2} , $$
(1)
$$ k_{{\text{s}}} = \frac{{2\left( {3G^{2} \left( {1 - \nu } \right)R} \right)^{1/3} }}{2 - \nu }F_{{\text{n}}}^{1/3} , $$
(2)
$$ F_{{\text{n}}} = \frac{{2G\sqrt {2R} }}{{3\left( {1 - \nu } \right)}}u_{{\text{n}}}^{3/2} , $$
(3)

where G is the average shear modulus of the contacting particles, ν is the average Poisson ratio of the contacting particles, R is the average radius of the contacting particles, Fn is the normal contact force between the particles, and un is the overlap of the contacting particles.

Fig. 1
figure 1

Particle size distribution selection for DEM simulations

Full size image
Table 1 Parameters used in DEM simulation
Full size table

The specimen was prepared using the radius expansion method. Then each specimen was brought to a desired isotropic stress state by using a numerical servo-control mechanism. During the assembly generation stage, the inter-particle friction coefficients (i.e., μ) were adjusted by trial and error to ensure the sample achieved the desired void ratio. The maximum void ratio (i.e., emax) and minimum void ratio (i.e., emin) of the granular soils under 100 kPa are 0.766 and 0.632 for temporary inter-particle friction coefficients of 0.5 and 0.01, respectively. After reaching initial equilibrium, the specimens were subjected to creation of soil fabric and bender element tests with the adjusted inter-particle friction coefficient of 0.5.

Energy was dissipated in DEM simulations via the local damping ratio. The local damping was set to the default value (i.e., 0.7), 0.9 and 0.01 during the probe test, quiet after consolidation and wave measurement, respectively [24, 39], which would be introduced in the following chapter. No friction work or kinetic energy was generated in this study, indicating that there was no relative sliding between the particles, and the specimens remained elastic.

2.2 Micromechanical quantities

Coordination number (i.e., CN) is commonly used to characterize the inter-particle contacts, referring to the average number of contacts per particle, based on the criterion that the normal contact force between contacts is greater than zero. However, there is always a small fraction of particles with only one or zero contact, which do not contribute to the stable state of stress. Therefore, the mechanical coordination number (i.e., MCN) proposed by Thornton [45] is adopted in this study, which could be expressed as Eq. (4).

$$ {\text{MCN}} = \frac{{2N_{{\text{c}}} - N_{{{\text{b}}1}} }}{{N_{{\text{b}}} - N_{{{\text{b}}0}} - N_{{{\text{b}}1}} }}, $$
(4)

where Nb and Nc are total number of particles and contacts, respectively; Nb1 and Nb0 are total number of particles with only one and zero contacts, respectively. In the three-dimensional space, the minimum MCN needed to support a stable load-bearing structure is 4 [9].

A fabric tensor is employed as an index to describe the orientation of inter-particle contacts, which generally characters the contact normals distribution. The fabric tensor is the nth moment of contact normals distribution function and could usually be expressed in the form of a second-order tensor (i.e., Fij) as defined in Eq. (5) [38].

$$ {\varvec{F}}_{ij} = \int\limits_{\Omega } {n_{i} } n_{j} E\left( n \right){\text{d}}\Omega , $$
(5)

where ni is the contact normals in the i-direction, E(n) is the contact normals probability distribution density, and Ω is the unit sphere. And E(n) for cross-anisotropy, without terms higher than the second-order Fourier expansion, could be expressed in the following Eq. (6) [5].

$$ \left\{ {\begin{array}{*{20}l} {E\left( n \right) \approx \frac{1}{4\pi }\left( {1 + a_{ij}^{{\text{c}}} n_{i} n_{j} } \right)} \hfill \\ {a_{ij}^{{\text{c}}} = a_{ji}^{{\text{c}}} ,a_{ii}^{{\text{c}}} = 0,} \hfill \\ \end{array} } \right. $$
(6)

where \(a_{ij}^{{\text{c}}}\) is the tensor of anisotropy. If the contact normals distribution is uniform in the unit sphere, the assembly could be considered as isotropic (i.e., \(a_{ij}^{{\text{c}}}\) = 0). Conversely, the assembly is anisotropic (i.e., \(a_{ij}^{{\text{c}}}\) ≠ 0). Substituting Eq. (6) in Eq. (5) and integration, one has:

$$ a_{ij}^{{\text{c}}} = \frac{15}{2}F_{ij}^{\prime } , $$
(7)

where \(F_{ij}^{\prime }\) is the deviatoric part of Fij. To quantify the degree of anisotropy, the following deviatoric invariant scalar (i.e., contact normal anisotropy) is usually used as Eq. (8) [16, 55, 57, 58, 67].

$$ a_{{\text{c}}} = {\text{sign}}\left[ {\cos \left( {2\theta } \right)} \right]\sqrt {\frac{3}{2}a_{ij}^{{\text{c}}} a_{ij}^{{\text{c}}} } , $$
(8)

where θ defines the angle between the principal direction of \(a_{ij}^{{\text{c}}}\) and the Z-axis. The sign[cos(2θ)] indicates the orientation of the principal direction of \(a_{ij}^{{\text{c}}}\). A positive sign of ac indicates the principal direction of \(a_{ij}^{{\text{c}}}\) along the vertical direction with θ = 0° and a negative sign for ac otherwise with θ = 90°.

2.3 Creation and microscale evolution of the initial soil fabric

In this study, two series of anisotropic specimens were generated. In series I, all specimens were generated with isotropic stress states and nearly the same void ratio to investigate the influence of inherent fabric anisotropy. In series II, the stress states of the specimens were designed using a stress ratio (i.e., SR) defined as the ratio of the axial stress to the radial stress. These specimens were subjected to anisotropic stress states with a certain degree of inherent anisotropy, representing the more complex conditions, serving as supplementary conditions to Series I.

2.3.1 Specimens with inherent fabric anisotropy

In order to create different initial soil fabrics at isotropic stress states, specimens experienced initial consolidation were subjected to undrained pre-shearing which produces large maximum strains. Then the specimens should be reconsolidated back to the initial isotropic stress state by servo-control [63]. The undrained pre-shearing could be performed either in compression or extension. Figure 2 shows the stress path and volumetric strain evolution during the sample preparation. The mean effective stress p′ and the deviatoric stress q′ are defined as Eq. (9):

$$ \begin{aligned} p^{\prime} & = \frac{{\sigma^{\prime}_{1} + 2\sigma^{\prime}_{3} }}{3} \\ q^{\prime} & = \sigma^{\prime}_{1} - \sigma^{\prime}_{3} , \\ \end{aligned} $$
(9)
Fig. 2
figure 2

Stress path and volumetric strain evolution during the sample preparation: a stress path of 0.702_100_− 0.294; b volumetric strain of 0.702_100_− 0.294; c stress path of 0.702_100_0.275; d volumetric strain of 0.702_100_0.275

Full size image

It could be observed that specimens 0.702_100_− 0.294 and 0.702_100_0.275 produce maximum axial strains of − 4.7% and 4%, respectively, during undrained pre-shearing. The negative axial strain represents extension of the specimen, while the positive represents compression. Although experiencing pre-shearing performed in different directions, both specimens produced a volumetric strain of − 0.83% during reconsolidation and eventually achieved the desired void ratio (i.e., e = 0.702). It should be noted that the negative volumetric strain represents specimen contraction and vice versa for specimen expansion. Generally, the specimen with strong anisotropy should experience the large pre-shearing strain and volumetric strain. The specimens subjected to pre-shearing in compression exhibited a preferential alignment of contact normals along the vertical direction (i.e., ac > 0), whereas pre-shearing in extension resulted in a concentration of contact normals predominantly along the horizontal direction (i.e., ac < 0). However, the void ratio of the specimens after reconsolidation changes significantly due to alterations in particle arrangement induced by pre-shearing, which is especially pronounced in loose specimens. To examine the influence of ac, the specimens with the same void ratio were generated by selecting samples with higher initial void ratio to different degrees of pre-shearing. The response of the specimens with anisotropic soil fabrics was compared with that of specimens having isotropic fabric (i.e., ac ≈ 0), where no pre-shearing was conducted. The specimens with isotropic stress states and fabrics were generated as listed in Table 2 column 1. And the conditions of the specimens with inherent fabric anisotropy (i.e., series I) are given in Table 2 column 2. The specimen IDs listed in Table 2 column 1 and 2 are sequentially consisted of the void ratio after quiet, the initial confining pressure and the ac value. It should be noted that the specimens in Table 2 column 1 are considered isotropic; therefore, the final columns of IDs are all marked as 0.

Table 2 Test program for DEM simulation
Full size table

To investigate the influence of the method for creating the initial soil fabrics in series I, the evolutions of some microscale parameters in the typical specimens were analyzed. Three specimens were consolidated at 100 kPa with different ac. As shown in Fig. 3, the stress state of the specimens with different fabric anisotropy is nearly identical, the generated specimens have almost no shear stress, and the normal stress components are consistent with the stresses monitored by the macro walls. The same stress tensor information provides comparability for subsequent analysis. The orientation distributions of contact normal probability density and normal contact force (i.e., NCF) are shown in Fig. 4. For the specimen that has not been subjected to the creation of the initial soil fabric (i.e., ac = 0.021), distributions of contact normal probability density and NCF are nearly isotropic. However, the contact normals distribution is adjusted significantly due to the direction of pre-shearing, with vertical orientation for compression (i.e., ac = 0.275) and horizontal orientation for extension (i.e., ac = − 0.294). In pre-shearing specimens, an interesting phenomenon is observed where the distribution of NCF is consistently perpendicular to the contact normals distribution, unlike the anisotropically consolidated samples. This could be attributed to the isotropic stress distribution, which results in a sparse distribution of NCF where the contact normals distribution is concentrated.

Fig. 3
figure 3

The stress tensor information of typical specimens of series I

Full size image
Fig. 4
figure 4

Evolution of the a contact normal probability density and b NCF distributions

Full size image

Furthermore, the distributions of contact normals, NCF and contact normal tangent stiffness projected in the XY and XZ planes are shown in Fig. 5. It could be observed that the projected distributions of all microscale parameters in the XY plane are generally consistent, indicating that the specimen exhibits a state of transverse isotropy. The contact normals distribution in Fig. 5a is consistent with that in Fig. 4, and the distribution of NCF perpendicular to contact normals is particularly pronounced as shown in Fig. 5b. Figure 5c shows the distribution of contact normal tangent stiffness, and it exhibits the same distribution as that of the contact normals, indicating that the arrangement of inter-particle governs the macroscopic stress–strain behaviors.

Fig. 5
figure 5

Evolution of the a contact normals, b NCF and c contact normal tangent stiffness distribution in XY and XZ planes

Full size image

2.3.2 Specimens with stress-induced anisotropy

The monotonic tests were conducted under drained condition to obtain the desired anisotropic stress states following the initial consolidation of the specimens to the isotropic stress state of 100 kPa. The lateral stresses (i.e., σ′3) were kept constant, while the axial stresses (i.e., σ′1) were increased or decreased monotonically by moving the top and bottom plates of DEM model. The stress path is shown in Fig. 6.

Fig. 6
figure 6

Stress path of monotonic loading tests

Full size image

To ensure the generality of the results, two specimens with different initial void ratios were selected to represent the loose and dense samples. The response of drained compression tests of the two specimens shows different typical types, as shown in Fig. 7. 0.709_1.0_0.024 shows the typical contract behavior where volumetric contraction and q hardening observed until reaching the critical state, representing the specimen is loose. The specimen IDs are composed in sequence of the void ratio after quiet, the SR value, and the ac value. And 0.619_1.0_0.013 represents the dilatant behavior of the dense specimen: q exhibits an initial sharp increase with a slight volumetric contraction and then softens toward the critical state with significant volumetric dilation [34]. The maximum and minimum SR values of the very dense specimen are 2.4 and 0.4, respectively, and 1.8 and 0.5 for medium-dense specimen. The difference value for SR value is 0.2 in each state during axial compression, while 0.1 for extension. The details of the specimens of series II are presented in Table 2 column 3.

Fig. 7
figure 7

Two typical behaviors of two specimens under drained condition

Full size image

As shown in Fig. 8, the values of ac and MCN remain constant within a certain range of SR values, and then adjust significantly when SR values exceed the range. For the dense specimens of e0 = 0.619, the range tends to be wider, suggesting that the specimens exhibit a greater capacity to resist the external load. And the increase of ac coincides with the decrease of MCN, indicating that the inhomogeneous arrangement of particles leads to a decrease in the local particle contacts and, consequently, a decrease in the total number of effective particle contacts.

Fig. 8
figure 8

The evolution of ac and MCN under different SR values

Full size image

2.4 Shear wave velocity measurement

Before performing the shear wave velocity measurement, it is essential to ensure that the specimen has reached a further equilibrium state. Therefore, the local damping was set to a high value (i.e., 0.9) to dissipate kinetic energy more efficiently. After additional numerical cycles, the velocities of the particles would eventually become low enough compared to the excitation magnitude (i.e., quiet). After the specimens were prepared, shear wave velocities tests were simulated using a pair of circular disks as a wave transmitter and receiver, as shown in Fig. 9. The diameter of each disk was half the size of the specimen, and the thickness corresponded to the median particle diameter (i.e., d50). In this study, shear wave velocities were measured in both the vertical plane (i.e., XZ plane) for isotropic and anisotropic specimens and the horizontal plane (i.e., XY plane) specifically for anisotropic specimens. To eliminate the generation of frictional work, the amplitude of the sinusoidal input was set at 10−5 m/s [19]. And a low value of damping ratio (i.e., 0.01) was used as recommended by O’Donovan [39] to keep balance between the high-quality arrival signal and properly damp out coda waves.

Fig. 9
figure 9

A cross-section of a typical DEM specimen with two pairs of wave transmitters and receivers

Full size image

To select an appropriate input frequency (i.e., fin), a set of bi-directional wave velocities tests were carried out on an isotropic specimen (Specimen ID: 0.702_100_0). Figure 10 shows the input and output shear wave signals in the XY plane with different input frequencies ranging from 5 to 500 kHz. The time of wave arrival was determined using the first arrival method, and the corresponding timings were indicated by arrows in Fig. 10. It shows that the velocities are consistent when the input frequencies are high enough, that is, the ratio of propagation distance to wavelength is large enough.

Fig. 10
figure 10

Wave signals in the horizontal plane (X–Y plane) with different input frequencies in an isotropic specimen

Full size image

The actual shear wave velocity value (i.e., Vs0) was derived from the probe test, which served as a benchmark for the measurements conducted in the bender element tests. During the probe test, a small-strain increment was applied at a slow rate (i.e., 10−5 m/s) in the vertical direction until the shear strain reached 10−6, while maintaining constant stress components in the horizontal direction. A dimensionless inertia parameter I could be defined as follows:

$$ I = \dot{\varepsilon }\sqrt {\left( {m_{{\text{g}}} /d_{50} \sigma_{0} } \right)} , $$
(10)

where \(\dot{\varepsilon }\) is the strain rate, mg is the particle mass, and σ0 is the confining pressure. The parameter I for a loading rate of 10−5 and the confining pressure of 100 kPa was calculated to be 3.37 × 10−8 in this study, indicating that the loading is sufficiently slow to satisfy quasi-static loading conditions [1, 41]. Subsequently, the small-strain modulus of isotropic specimens (i.e., Gmax0) was determined from the stress–strain curve, as shown in Fig. 11. Then the Vs0 could be calculated by using Eq. (11):

$$ V_{{{\text{s}}0}} = \left( {\frac{{\Delta \sigma_{1} - \Delta \sigma_{3} }}{{2\rho \left( {\Delta \varepsilon_{1} - \Delta \varepsilon_{3} } \right)}}} \right)^{\frac{1}{2}} , $$
(11)

where Δσ1 and Δσ3 are the axial and radial stress increments, Δε1 and Δε3 are the axial and radial strain increments correspondingly, and ρ is the density of the specimen [34].

Fig. 11
figure 11

Stress–strain curve obtained from the probe test

Full size image

The variation of the normalized shear wave velocities Vs/Vs0 against the input frequencies is shown in Fig. 12, where the black square dots represent the results in the vertical plane and the blue dots represent results in the horizontal plane. The shear wave velocities appear to be frequency dependent in DEM simulation. The figure shows that Vs/Vs0 is less than 1.0 at low input frequencies and the results for the two planes show discretization. As shown in Fig. 10, the receiver detects the output signal before a complete sine wave is fully excited with a low input frequency. As a result, the received wave signals at low input frequencies are unreliable, because the main components of the signal are refracted and reflected by the walls. Figure 13 shows the combination of the transmitter plane and the section of the specimen where it is located. It could be observed that the distance from the transmitter to the boundary of the specimen in the X–Y plane is shorter, so the waves propagating in this plane are more prone to refraction and reflection [39], resulting in significant near-field effect [3, 44]. However, if the input frequency is high enough (i.e., exceeds 100 kHz), the near-field effect diminishes and the first arrival of the received signal is directly identified, which leads to repeatable measurement. Therefore, the input frequency of 200 kHz was chosen in this study to security the wavelength is long enough and satisfy the relationship L > 2λ (i.e., 4λ in this study) [19, 40, 54], where L and λ are the propagation distance and wavelength, respectively. Subsequently, the validated wave measurements were employed to simulate anisotropic specimens with the selected input frequency [19, 53].

Fig. 12
figure 12

Shear wave velocities determined by first arrival method at different input frequencies

Full size image
Fig. 13
figure 13

The transmitter plane and the section of the specimen where it is located: a in the XZ plane; b in the XY plane

Full size image

3 Results and discussion

3.1 Results of isotropic specimens

According to the elastic constitutive equations proposed by Hardin [21], the relationship could be expressed as Eq. (12):

$$ G_{\max \_ij} = S_{ij} F\left( e \right)\left( {\frac{{\sigma_{i}^{\prime } }}{{P_{{\text{a}}} }}} \right)^{\frac{n}{2}} \left( {\frac{{\sigma_{j}^{\prime } }}{{P_{{\text{a}}} }}} \right)^{\frac{n}{2}} , $$
(12)

where Gmax_ij is the value of Gmax in the ij stress plane which could be expressed as Gmax0 in isotropic granular materials, Sij is an elastic stiffness coefficient which will be further explained sequentially below, F(e) is a measure of particle concentration, σ′iσ′j accounts for current state of stress, n is the stress exponential constant, and Pa is the atmospheric pressure (i.e., 101 kPa).

Figure 14 shows the relationship between Gmax0 and the void ratio for isotropic specimens consolidated at 100 and 200 kPa. As seen in Fig. 14, Gmax0 exhibits a strong linear relationship with the void ratio, indicating that F(e) should be a linear function which would be illustrated below. However, the values of Gmax0 for each void ratio at 200 kPa are significantly higher than those at 100 kPa as expected due to the stress exponential constant. The results show that n = 0.377 in this study, which is slightly higher than 1/3 for the Hertz–Mindlin contact law. The reason is that the particle assembly in this study exists a certain particle gradation, which results in the increase of the number of particle contacts [20].

Fig. 14
figure 14

The relationship between Gmax0 and the void ratio at different stress

Full size image

To eliminate the influence of the stress on Gmax0, the stress normalized small-strain shear modulus (i.e., Gmax1) is defined as follows:

$$ G_{\max 1} = G_{\max 0} \left( {\frac{{P_{{\text{a}}} }}{{\sigma_{i}^{\prime } }}} \right)^{\frac{n}{2}} \left( {\frac{{P_{{\text{a}}} }}{{\sigma_{j}^{\prime } }}} \right)^{\frac{n}{2}} = S_{ij} F\left( e \right) = S_{ij} (B - e), $$
(13)

where F(e) = B − e is the function of the void ratio and B is defined as the phase-change void ratio, representing the transition of particle materials from the solid phase to the liquid phase, resulting in the loss of their capability to transmit shear waves, and should be taken as 0.81 in this study; Sij is a constant parameter reflecting the soil fabrics, with a value of 102.02 MPa in this study.

The Gmax1 is plotted against the void ratio in Fig. 15. It could be observed that the Gmax1 under different confining stress exhibits a consistent relationship with the void ratio. The result shows that Gmax1 could be effectively expressed using the void ratio by selecting an appropriate function of the void ratio. The evolution of Gmax1 with MCN of the particle assembly is shown in Fig. 16. It convincingly indicates that MCN has a similar effect on Gmax1 as the void ratio and could be expressed as Eq. (14):

$$ G_{\max 1} = C^{\prime } \left( {{\text{MCN}} - {\text{MCN}}_{0} } \right), $$
(14)

where MCN0 refers to the MCN when the stiffness of the particle assembly is zero, corresponding to the phase-change void ratio at a macroscopic scale, should be taken as 3.812 in this study. And C′ is a constant parameter. As seen in Fig. 16, Gmax1 of isotropic specimens is primarily governed by MCN, which is directly related to the contact density of the total granular assembly.

Fig. 15
figure 15

The relationship between Gmax1 and e0 of isotropic specimens

Full size image
Fig. 16
figure 16

The evolution of Gmax1 with MCN of isotropic specimens

Full size image

If Gmax1 is divided by the selected F(e), the variation of the parameter Sij in Eq. (13) with the void ratio could be obtained as shown in Fig. 17. It could be observed that the parameter Sij remains a constant value regardless of the confining pressure and the void ratio, fluctuating within the range of 102.02 MPa ± 2 MPa. Therefore, Sij is defined as the reference fabric (i.e., Gmax1/F(e)) in this study, representing the Gmax0 normalized by the state of stress and density, and it effectively reflects the current fabric state of the particle assembly.

Fig. 17
figure 17

The results of Gmax1/F(e) with void ratio at different stress state

Full size image

3.2 Results of anisotropic specimens

In order to investigate the influence of ac on the Gmax, the normalized reference fabric (i.e., Norm. Gmax1/F(e)) is proposed, which is defined as the ratio between the reference fabric of anisotropic specimens and that of isotropic specimens (i.e., Norm. Gmax1/F(e) = Gmax1(a ≠ 0)/Gmax1(a ≈ 0)). It should be noted that, due to the difference in Gmax within the two stress planes of anisotropic specimens, the normalized reference fabric in the XZ stress plane (i.e., Norm. Gmax1_XZ/F(e)) should be discussed separately from that in the XY plane (i.e., Norm. Gmax1_XY/F(e)). Figure 18 shows the evolution of Norm. Gmax1/F(e) with ac in different stress planes of series I and II. As shown in Fig. 18a, Norm. Gmax1_XZ/F(e) increases first with increasing ac and then decreases with further increase of ac, but the degree of decrease is less significant than increase. Figure 18b shows a different trend that Gmax1_XY/F(e) always decreases approximately linearly as ac increases. The normalized reference fabric in the XZ and XY plane could be expressed as follows:

$$ {\text{Norm}}.\;G_{\max 1\_XZ} /F\left( e \right) = 1 + 0.14a_{{\text{c}}} - 0.23a_{{\text{c}}}^{2} , $$
(15)
$$ {\text{Norm}}.\;\;G_{\max 1\_XY} /F\left( e \right) = 1 - 0.27a_{{\text{c}}} - 0.04a_{{\text{c}}}^{2} . $$
(16)
Fig. 18
figure 18

The evolution of normalized Gmax1/F(e) with ac in different stress planes: a in the XZ stress plane; b in the XY stress plane

Full size image

According to the linear contact model presented by Yimsiri and Soga [64] using micromechanics theory, Gmax is related to the radius of particle, the volume of the particle, CN, kn, ks, and ac. If Gmax of anisotropic specimens is normalized by the value of that of isotropic specimens, the influence of particle radius, particle volume and CN could be eliminated. As shown in Fig. 19, the hollow dots represent the simulation results of this study, and the dotted lines represent the derived results from Yimsiri's study. The results show that the fabric anisotropy has a primary effect on Gmax, while the ratio of ks/kn has a secondary effect on Gmax. And the relationship of different ratios of ks/kn is similar to that observed in this study using the Hertz–Mindlin contact model.

Fig. 19
figure 19

The comparison of the relationship between Norm. Gmax1 and ac of this study with that of Yimsiri's research

Full size image

Figure 20a and b illustrate the distribution of contact normals in the XZ and XY stress planes of 0.702_100_− 0.294, respectively, and Fig. 20c provides a sectional view of the 3D distribution. The approximation for the distribution of contact normals could be obtained by Eq. (17) [43]:

$$ Y = b + a \cdot \cos \left[ {2\left( {x \cdot \frac{\pi }{180} + x_{0} } \right)} \right], $$
(17)

where Y is the number of contacts obtained from the statistics in each region, x is angular distribution of regions, b is a constant that represents the average number of contacts in the assembly, a refers to the magnitude of the directional variation of average number of contacts, and x0 defines the direction of average number of contacts which should be approximated to 0 or π/4 in this study.

Fig. 20
figure 20

The distribution of contact normal of 0.702_100_− 0.294: in the XZ stress plane; b in the XY stress plane; c section view of 3D distribution

Full size image

The number of contacts in the direction of wave propagation (i.e., corresponding to 0° and 180°) and that in the direction of particle perturbation (i.e., corresponding to 90° and 270°) was calculated by b + a and b − a, respectively. It could be observed that the four marked points are connected to form a diamond shape. The value of half area of the diamond represents the product of the number of contacts in the direction of wave propagation and that in the direction of particle perturbation, which could be defined as PXZ and in PXY in the XZ and XY plane, respectively, as shown in Fig. 20a and b. The areas of the diamond obtained by the projection of all anisotropic specimens were calculated as above.

The ratio of PXZ or PXY to MCN, normalized by that of the isotropic specimens (i.e., Norm. P/MCN), along with Norm. Gmax1/F(e) of two series, is plotted in Fig. 21. It could be observed that Norm. P/MCN exhibits a good linear relationship with Norm. Gmax1/F(e), indicating that Norm. Gmax1/F(e) is primarily determined by the number of contacts in the direction of wave propagation and particle perturbation. The compact arrangement of particles in the direction of particle perturbation improves vibration efficiency, while in the direction of wave propagation, it directly accelerates wave transmission. As a result, the specimens that subjected to pre-shearing in compression tend to exhibit a sparse arrangement of particles in the XY stress plane where the contact density remains homogeneous, leading to lower shear wave velocities or Norm. Gmax1_XY/F(e). Conversely, specimens subjected to pre-shearing in extension tend to exhibit a more compact arrangement of particles in this plane, leading to higher Norm. Gmax1_XY/F(e) in Fig. 18a. However, the evolution of Norm. Gmax1_XZ/F(e) is more complex, due to the opposite development pattern of contact density in two directions on the anisotropic plane. When the granular material is horizontally anisotropic, particles are loosely and densely arranged in the Z and X directions of the plane, respectively; when vertically anisotropic, particles are loosely arranged in the X direction and densely in the Z direction. Therefore, regardless of the anisotropic state, there is a “competing effect” on particle contact density in the XZ stress plane, where an increase in particle contact density in the Z direction coexists with a decrease in the X direction. Figure 22a shows an extreme case of horizontal anisotropy, where particles are significantly overlapped in the horizontal direction. The shear waves generated by particle vibrations in the X direction cannot propagate in the Z direction. Conversely, particles are overlapped in the vertical direction with extreme vertical anisotropy, preventing effective wave vibrations in the X direction, as shown in Fig. 22b. In these two extreme cases, shear waves cannot effectively propagate in both stress planes. However, shear waves effectively propagate in intermediate cases, leading to a qualitative observation that PXZ and Norm. Gmax1_XZ/F(e) increases first and then decreases with the development of ac in Fig. 18b.

Fig. 21
figure 21

The evolution of Norm. P/MCN with Norm. Gmax1/F(e) in different stress plane

Full size image
Fig. 22
figure 22

Extreme cases of anisotropy: a horizontal anisotropy; b vertical anisotropy

Full size image

The ratio of Gmax1 in the XZ stress plane to that in the XY stress plane (i.e., Gmax1_XZ/Gmax1_XY) against ac of two series is shown in Fig. 23. In this study, the difference of Gmax1 between the XZ and XY stress plane could reach up to approximately 45% when − 0.6 ≤ ac ≤ 0.4, significantly influencing other mechanical behaviors of granular materials [68]. It is noted that Gmax1_XZ/Gmax1_XY increases in an approximately linear relationship with ac, could be expressed as follows:

$$ \frac{{G_{\max 1\_XZ} }}{{G_{\max 1\_XY} }} = 1 + 0.42a_{{\text{c}}} . $$
(18)
Fig. 23
figure 23

The relationship between Gmax1_XZ/Gmax1_XY and ac

Full size image

When the specimen is in an isotropic state (i.e., ac = 0), the Gmax1 in both stress planes should be equal. It is recommended that the ratio Gmax1_XZ/Gmax1_XY could be an indicator of fabric anisotropy of granular soils, which obtained by wave measurement. In engineering practice, various spatial distributions of shear wave velocities could be obtained by different borehole configurations in the cross-hole and in-hole seismic tests [26, 33], or directly obtained by multi-directional bender element tests. Combining the stress conditions and measured shear wave velocities, the degree of anisotropy of the in situ field could be determined as follows:

$$ a_{{\text{c}}} = f\left( {\frac{{G_{\max 1\_XZ} }}{{G_{\max 1\_XY} }}} \right) = f\left[ {\left( {\frac{{V_{{{\text{S}}\_XZ}} }}{{V_{{{\text{S}}\_XZ}} }}} \right)^{2} \left( {\frac{{\sigma^{\prime}_{Y} }}{{\sigma^{\prime}_{Z} }}} \right)^{\frac{n}{2}} } \right], $$
(19)

where VS_XZ and VS_XY are the shear wave velocity in XZ and XY stress plane and σ′Z and σ′Y are the effective stress in the vertical and horizontal direction. The degree of anisotropy of granular soils is large when the calculated results are shifted by 1.0.

Figure 24 shows the ratio of the number of contacts between the XZ and XY planes (i.e., PXZ/PXY) with Gmax1_XZ/Gmax1_XY of two series. At the microscale, it could be observed that the difference in the number of contacts between the direction of wave propagation and the direction of particle perturbation emerges as a dominant factor influencing the degree of stiffness and fabric anisotropy.

Fig. 24
figure 24

The evolution of PXZ/PXY with Gmax1_XZ/Gmax1_XY

Full size image

3.3 Discussion on the expression of G max

In addition to Eq. (12), the Gmax of the soil also could be expressed by Eq. (20), which is related to the effects of stress history [7, 29].

$$ G_{\max \_ij} = \frac{{{\text{OCR}}^{k} S_{ij} }}{{F\left( e \right)2\left( {1 + \nu } \right)}}\left( {\frac{{\sigma_{i}^{\prime } }}{{P_{{\text{a}}} }}} \right)^{\frac{n}{2}} \left( {\frac{{\sigma_{j}^{\prime } }}{{P_{{\text{a}}} }}} \right)^{\frac{n}{2}} , $$
(20)

where OCR is over-consolidation ratio, k is the soil constant depending on the plasticity index (i.e., PI) of the soil, ν is the elastic Poisson’s ratio, and the remaining variables are consistent with those in Eq. (12). Under the condition of the same stress state, F(e), ν and Sij, OCRk plays a significant role, which is similar to the effect of Norm. Gmax1/F(e) in Eqs. (15) and (16). In fact, Sij could be considered as a variable, and the influence of over-consolidation could be explained as the evolution of the reference fabric, thus providing a specific physical interpretation of the expression of Gmax.

4 Conclusions

A micromechanical study was presented to investigate the small-strain modulus of granular materials at different degree of fabric anisotropy by DEM simulations. After creating different initial soil fabrics of two series, the wave measurement tests were performed and the microscale evolution was examined. The relationship between the Gmax and ac was analyzed and attempts were made to link the microscale fabric anisotropy with the macroscale wave velocity. The main findings of the study are summarized as follows:

  1. 1.

    In series I, the distribution of NCF is perpendicular to the distribution of contact normals due to the isotropic stress distribution. In series II, the microscopic MCN and contact normals distribution essentially remain constant until a threshold SR is reached and then adjust significantly, especially for the dense specimens.

  2. 2.

    The reference fabric Gmax1/F(e) is a constant value of the isotropic specimens, fluctuating within the range of 102.02 MPa ± 2 MPa in this study. Both series of anisotropic specimens exhibit consistent evolution patterns: Gmax1/F(e) increases as ac increases first and then decreases with further increase of ac in the XZ stress plane, while always decreases approximately linearly as ac increases in the XY stress plane. Norm. Gmax1_XY/F(e) exhibits a monotonic and wider range of variation during its evolution, where the influence of the evolution of ac is uniformly distributed in the entire isotropic plane.

  3. 3.

    The evolution of microscopic contact density is closely related to macroscopic wave velocity and stiffness. Norm. P/MCN increases from 0.75 to 1.25 as Norm. Gmax1/F(e) increases from 0.8 to 1.2 in two series of specimens. The result shows that Norm. P/MCN is linearly proportional to Norm. Gmax1/F(e), indicating that the reference fabric is predominantly dominated by the density of contacts in the direction of wave propagation and particle perturbation.

  4. 4.

    Gmax1_XZ/Gmax1_XY has a linear relationship with ac and passes through (0,1), with a range of variation of 45%, resulting from the difference in the number of contacts in the direction of wave propagation and the direction of particle perturbation. The fabric anisotropy ac could be calculated based on the shear wave velocities in both XZ and XY stress plane by Eq. (19), which could be potentially determined in engineering practice and laboratory testing as long as the orthogonal stress conditions are known.