Study of the dynamics of water-enriched debris flow and its impact on slit-type barriers by a modified SPH–DEM coupling approach

Abstract

Slit-type barriers serve as active countermeasures against debris flow. However, the dynamic interaction between debris flows and slit-type barriers is extremely complicated. To model the fluid-solid behavior of debris flows, a coupled approach of smoothed particle hydrodynamics (SPH) and discrete element method (DEM) is developed. We use the model to investigate the dynamics of how debris flows impact slit-type barriers. The proposed approach is able to simulate the embedding of arbitrarily shaped particles in viscous debris flows. A GPU acceleration technique is employed to overcome large computational costs. The approach is first validated by comparing numerical results to experimental observations for some standard conditions. Subsequently, experiments of the impact of water-enriched debris on slit-type barriers are modeled and validated. Moreover, the effects of barrier arrangement, solid volume fraction and boulder shape on debris-barrier interactions are further explored. This study analyzes the interaction between debris flows and slit-type barriers by coupled SPH–DEM and provides insight into the optimal design of barriers.

1 Introduction

Debris flows are gravity-driven multiphase mixtures with complicated composition and rheological behavior, which may present viscous laminar or dilute turbulent flow [35]. As one of the most destructive natural disasters, debris flows pose significant hazards to human lives, infrastructures and lifeline facilities worldwide, threatening populated areas located far away from the slope source region due to their sudden outbreak, ferocity, short duration and severity [24, 33, 47, 85]. Debris flow barriers have thus been widely constructed to reduce the debris velocity and mitigate the subsequent destructive effects. Generally, there are two types of debris flow barriers: closed-type barriers, which are designed to capture all components of debris flows, the other is the open-type barrier that intends to intercept boulders and allow fluid and fine particles in debris flows to pass through. Slit-type barriers, as open-type barriers, have been widely used in recent years due to their convenient construction and low environmental influence.

Dynamic interactions between debris flows and barriers are complicated because they depend not only on kinematics (such as velocity and fluid viscosity), but also on stiffness and geometric characteristics of the barriers [8, 11, 32, 81]. Researchers have utilized various methods to explore the impact dynamics of debris flows on barriers [1, 10, 42, 83]. Some field experiments have been conducted at Jiangjia Ravine in China [29, 30, 36] and Ohya in Japan [34, 86, 87]. Due to the unpredictable and destructive nature of debris flow disasters, it is a significant challenge to track the impact force acting on the barriers during disasters in real time. Alternatively, some semi-empirical methods have been applied to the construction of debris flow barriers in engineering practice, such as the hydrostatic approach [4, 43], the shock wave approach [19, 72] and the hydrodynamic approach [76, 80]. However, it remains demanding to reconcile theoretical concepts with field and experimental results by these means, which can result in significant discrepancies [43]. Recently, the debris-barrier interaction has been addressed by a number of laboratory flume experiments [7]. Moriguchi et al. [63] investigated the effect of slope angle on debris-barrier interactions through small-scale laboratory physical modeling and concluded that the impact force increases with increasing slope angle. Jiang and Towhata [38] studied debris-barrier interactions through a series of experiments on dry debris flows impacting rigid barriers. They verified that the impact force acting on the barriers is comprised of drag force, gravity, friction force and passive earth force. Jiang et al. [] explored the effect of particle characteristics on the process of debris flows impacting rigid barriers. Their results showed that particle characteristics can directly affect the flow velocity of the debris flows and the flow deposition regime of debris flows behind barriers. Song et al. [81] examined the effect of the solid fraction on the impact of debris flows against rigid barriers through a series of centrifuge experiments. They observed that the transition from the pile-up mechanism to the run-up mechanism is governed by the solid fraction. Wang et al. [90] developed three different barrier shapes and investigated the effect of barrier shape on debris-barrier interactions. They found that trapezoidal-shaped barriers reduced the velocity of debris flow impacting the barrier to a greater extent. Huang et al. [32] investigated the effect of barrier stiffness on debris flows impact barriers using flume experiments. They derived that the reduction in barrier stiffness had a buffering effect on debris flow impact and diminished the peak impact force.

Due to the development of the numerical simulations, various numerical methods have been extensively implemented to analyze the impact dynamics of debris flows on barriers. To the best of our knowledge, the commonly available numerical models include continuum models [96, 98], discrete medium models [84, 95, 99], and coupled computational models [53]. For example, Rickenmann et al. [75] applied the finite element model (FEM) and the finite volume method (FVM) model to simulate a debris flow event in the Wartschenbach torrent in Austria. Jeong et al. [37] used the Eulerian-Lagrangian FEM to examine the impact force of debris flows on a closed-type barrier. Leonardi et al. [50] explore possible applications of the Lattice-Boltzmann method (LBM) for the simulation of geophysical flows. Choi et al. [9] presented a methodology for modeling debris flows described as a single-phase medium using the arbitrary Lagrangian Eulerian (ALE) method. Zhang et al. [105] developed a novel three-dimensional computational fluid dynamics (CFD) code to acquire the affected areas, runout distances, deposition depths, and velocities of potential debris flows at Xiaojia Gully, located in Sichuan Province, China. However, the aforementioned methods are grid-based methods that suffer from unavoidable drawbacks such as difficulty in capturing free fluid surface, mesh distortion and mesh redivision when dealing with free fluid surface, large deformation and multiphase flow. Meshless techniques, which include the smoothed particle hydrodynamics (SPH) method [59, 100], the particle finite element method (PFEM) [65], and the material point method (MPM) [82, 94], have been developed to avoid these problems. SPH has proven to be robust and reliable in simulating fluid dynamics with large deformations due to the absence of computational grids [23, 57, 67, 68, 107]. Dai et al. [17] applied SPH to model debris flows as a viscous fluid, predicted the propagation behavior of debris flows, and obtained the evolution of debris flow impact on the barriers. Favero Neto et al. [22] present an updated Lagrangian continuum particle method to gain insight into the accuracy and robustness of the SPH framework for modeling debris flows. Choi et al. [13] investigated the effect of barrier location, especially the distance from the source to the barriers, on the velocity and volume of debris flows using SPH. They found that the installation of barriers close to the source seemed to be more effective in the case of long flow paths. More recently, the discrete element method (DEM) has been widely used for numerical modeling of rockfalls and debris flows [21, 39, 45, 73, 77] and has been found to be an effective way to simulate solid boulders in debris flows. Wu et al. [93] simulated the process of a dry debris flow impacting a rigid wall using DEM. Shen et al. [79] further quantified the effect of dry debris flows on rigid barriers using DEM simulations. They identified three stages of the interaction of the dry debris flow with rigid barriers, namely frontal impact, run-up and pile-up. The aforementioned methods simplified debris flow as an equivalent fluid. Nevertheless, it is apparent that both the solid and fluid phases significantly affect the dynamics of debris flow [35] and the gross simplifications of using an equivalent fluid approach limit the comprehensive understanding of two-phase interaction. Therefore, several coupling approaches have been proposed, such as the coupled CFD-DEM model [53, 58, 97, 101], the coupled SPH–DEM model [74, 102], the coupled ALE-SPH model [69], and the FEM-DEM-LBM model [48]. Li [52] used the coupled CFD-DEM model to simulate debris flows and to analyze the impact of debris flows on rigid or flexible barriers. Their simulations resulted in a new, physically based model of the impact pressure of debris flows on rigid barriers. Leonardi and Pirulli [49] validated the developed DEM-FEM model by the concordance of field measurements and numerical simulations. Liu et al. [54] investigated complicated fluid-particle-structure interactions using the coupled SPH–DEM-FEM approach, and the impact of debris flows on barriers was accurately predicted. The DEM models used in the above studies are all spherical particles because of their computational convenience and low cost. However, simplifying arbitrarily shaped solids to spherical particles will inevitably lead to computational discrepancies.

This study proposes a coupled SPH–DEM approach in which arbitrarily shaped solids can be considered. The numerical code of the proposed approach is fully accelerated by GPU devices to model large numbers of particles. The goal is to reveal the detailed mechanisms of debris-barrier interactions and to explore the effects of different factors on debris-barrier interactions. The remainder of this paper is organized as follows: Section 2 illustrates the methodology of the SPH–DEM. Section 3 compares the numerical simulations with the results of two classical experiments to validate the proposed approach. Section 4 establishes and validates the numerical model of water-enriched debris flow impacting slit-type barriers. Section 5 analyzes the effects of barrier arrangement, solid volume fraction and boulder shape on debris-barrier interactions. Section 6 provides the main conclusions of this study.

2 Methodology

2.1 Fluid phase governed by SPH

SPH is a meshless Lagrangian approach that was originally proposed by [25] for astrophysical applications and has been extensively applied in fluid hydrodynamics. SPH has been proven to be a significant strength in dealing with free surface flows [], highly deformable geometries [78] and multiphase flows [55].

In SPH, the computational domain of the fluid is discretized into a set of particles with material properties and kinematics. The continuous fluid field can be obtained by a weighted average of neighboring particles through kernel functions. Thus, the properties of the fluid particle at position ${\textbf {r}}$ are approximated by using an integral representation of the smooth kernel function ($W({\textbf {r}}-{\textbf {r}}^{\prime },h)$) as follows:

$$\begin{aligned} \left\langle F({\textbf {r}})\right\rangle =\int _{\Omega }{F({{\textbf {r}}^{\prime }})}{W({\textbf {r}}-{{\textbf {r}}^{\prime }},h)d{{\textbf {r}}^{\prime }}} \end{aligned}$$

(1)

where $\left\langle \cdot \right\rangle$ represents the kernel approximation; $\Omega$ is the support domain of a particle with position vector r; ${\textbf {r}}^{\prime }$ is a neighboring particle position vector in $\Omega$; h is the smoothing length, which defines the influence domain of the kernel. The smoothing kernel function $W({\textbf {r}}-{\textbf {r}}^{\prime },h)$ is an important factor in determining the performance of SPH simulations, which not only dictates the interpolation accuracy of SPH approximation, but also is relevant to numerical stability.

Various kernel functions have been developed and used in SPH, among which the most commonly used are the cubic spline kernel function [62] and the Wendland kernel function [92]. In this study, the Wendland kernel function is chosen as the smoothing kernel function in three dimensions because it can achieve a favorable balance between numerical accuracy [56] and computational cost [20]:

$$\begin{aligned} W(q,h)=\alpha _D{\left\{ \begin{array}{ll} \left( 1-\frac{q}{2}\right) ^4(1+2q), &{} 0\le q \le 2 \\ 0, &{} q \ge 2 \\ \end{array}\right. } \end{aligned}$$

(2)

where $q=|{\textbf {r}}-{\textbf {r}}^{\prime }|/h$, which is the normalized distance between particle ${\textbf {r}}$ and ${\textbf {r}}^{\prime }$; $\alpha _D$ is a normalized factor which is $7/({4\pi h^2}$) in 2-D cases and $21/(16\pi h^3)$ in 3-D cases [26].

Fig. 1

Particle approximations for particle i within the support domain kh of the kernel function W

As mentioned above, the support domain in SPH is represented by a set of particles associated with material properties. By estimating the field variables on these arbitrarily distributed particles within the support domain, the particle approximation discretizes the continuous form of the SPH kernel approximation as a summation of neighboring particles, as shown in Fig. 1. As a result, the final form of Eq. (1) is approximated as:

$$\begin{aligned} \left\langle F({\textbf {r}}_i)\right\rangle =\frac{m_j}{\rho _j}\sum _{j=1}^{N}F({\textbf {r}}_j)W({\textbf {r}}_i-{\textbf {r}}_j,h) \end{aligned}$$

(3)

where i and j in the subscript denote the concerning particle and the neighboring particle, respectively; N is the number of particles within the support domain of the kernel function; m is the mass of the particle; and $\rho$ is the density of the particle.

The continuity and momentum equations for the fluid phase in the Lagrangian frame are written as follows:

$$\begin{aligned} \frac{\text {d}{} {\textbf {v}}}{\text {d}t}&=-\frac{\nabla p}{\rho }+\frac{\mu }{\rho }\nabla ^2{\textbf {v}}+{\textbf {g}} \end{aligned}$$

(4)

$$\begin{aligned} \frac{\text {d}\rho }{\text {d}t}&=-\rho \nabla \cdot {\textbf {v}} \end{aligned}$$

(5)

where ${\textbf {v}}$ represents the velocity field; p represents pressure; $\rho$ is fluid density; and $\mu$ and ${\textbf {g}}$ represent kinematic viscosity and gravitational acceleration, respectively.

The fluid is usually assumed to be weakly compressible in SPH, so the equation of state is applied to estimate the pressure in the density field [14]:

$$\begin{aligned} p_i=\frac{\rho _0c_0^2}{\gamma }\left[ \left( \frac{\rho _i}{\rho _0}\right) ^\gamma -1\right] \end{aligned}$$

(6)

where $\rho _0=1000 kg/m^3$ is the reference density; $c_0$ is the speed of sound and $\gamma$ is a constant (usually taken as 7.0 for ideal fluid according to []). It is worth noting that the speed of sound $c_0$ is not an actual physical property in SPH, but a parameter intended to control the compressibility. When the speed of sound is high enough, the fluid is incompressible. Typically, $c_0$ is selected to be 10 times larger than the expected maximum velocity in the flow. The purpose of this, according to [60], is to ensure that the relative density fluctuates by less than 1$\%$.

The discretized form of the continuity equation in SPH can be written as:

$$\begin{aligned} \frac{\text {d}\rho _i}{\text {d}t}=\sum _{j}m_j({\textbf {v}}_i-{\textbf {v}}_j)\cdot \nabla W({\textbf {r}}_{ij},h)+\Phi _i \end{aligned}$$

(7)

where the subscripts i and j denote fluid particles; ${\textbf {r}}_{ij}={\textbf {r}}_{i}-{\textbf {r}}_{j}$; $m_j$ is the mass of fluid particle j; $\rho _i$ is the density of fluid particle i; ${\textbf {v}}_i$ and ${\textbf {v}}_j$ are the velocities of fluid particles i and j, respectively; $\nabla$ represents the kernel gradient taken with respect to the coordinates of particle i; and $\Phi _i$ is an additional density diffusion term called $\delta$-SPH [3], which is employed to eliminate spurious numerical noise in the pressure field and is written as:

$$\begin{aligned} \Phi _i=2\delta h c_0\sum _j(\rho _j-\rho _i)\frac{{\textbf {r}}_{ij}\cdot \nabla W({\textbf {r}}_{ij},h)}{|{\textbf {r}}_{ij}|^2}\frac{m_j}{\rho _j} \end{aligned}$$

(8)

where the constant $\delta$ is used to control the intensity of density diffusion. Based on many numerical calculations and theoretical analysis [51, 70, 104], it is identified that $\delta$ = 0.1 is an appropriate value for both Newtonian and non-Newtonian flows in SPH simulations.

The discretized momentum conservation equation can be expressed as:

$$\begin{aligned} \begin{aligned} \frac{\text {d}{} {\textbf {v}}_i}{\text {d}t}=&-\sum _jm_j\left( \frac{p_i}{\rho _i^2}+\frac{p_j}{\rho _j^2}\right) \nabla W({\textbf {r}}_{ij},h)+\sum _jm_j\left( \frac{4\mu {\textbf {r}}_{ij}\nabla W({\textbf {r}}_{ij},h)}{(\rho _i+\rho _j)|{\textbf {r}}_{ij}|^2}\right) {\textbf {v}}_{ij}\\&+\sum _jm_j\left( \frac{{\varvec{\tau }}_i}{\rho _i^2}+\frac{{\varvec{\tau }}_j}{\rho _j^2}\right) \nabla W({\textbf {r}}_{ij},h)+{\textbf {F}}_{i}^{D}+{\textbf {g}} \end{aligned} \end{aligned}$$

(9)

where the first term on the right-hand side represents the symmetric, balanced form of the pressure term, respecting the action-reaction principle [60]; the second and third terms denote the viscous stresses [64] and sub-particle scale (SPS) stresses [27], respectively, where $\mu$ is the kinematic viscosity of the fluid; ${\textbf {F}}_{i}^{D}$ denotes the external forces from DEM grains. The SPS term is introduced to represent the effect of turbulent motion at scales smaller than the kernel scale (the effective filtration scale of the system). The SPS stress tensor ${\varvec{\tau }}$ can be written as:

$$\begin{aligned} \frac{{\varvec{\tau }}}{\rho }=2v_t\left( {\textbf {S}}-\frac{1}{3}\delta _ktr({\textbf {S}})\right) -\frac{2}{3}C_I|{\textbf {r}}_{ij}|^2\delta _k|{\textbf {S}}|^2 \end{aligned}$$

(10)

where $v_t=(C_S|{\textbf {r}}_{ij}|)^2|{\textbf {S}}|$ is the turbulent eddy viscosity; $C_S=0.12$ is the Smagorinsky constant; $C_I=0.0066$; the Kronecker delta $\delta _k=1$; and ${\textbf {S}}$ is the local strain rate tensor, with $|{\textbf {S}}|=\sqrt{2{\textbf {SS}}}$.

Current studies in three-dimensional numerical simulation of debris-flow based on SPH mainly select the Bingham model to describe the complex rheological behavior of debris-flow [16, 31]. For this study, the Herschel-Bulkley-Papanastasiou (HBP) model proposed by Papanastasiou was used to describe the rheological behavior of debris flows [66]. In HBP model, the shear stress tensor can be calculated by the effective viscosity:

$$\begin{aligned} \tau ^{\alpha \beta }=2\mu _{eff}\epsilon ^{\alpha \beta }=2\left[ K(\dot{\gamma })^{n-1}+\frac{\tau _y}{2\dot{\gamma }}\left( 1-e^{-2m\dot{\gamma }}\right) \right] \epsilon ^{\alpha \beta } \end{aligned}$$

(11)

where $\tau _y$ is the yield stress, which is commonly calculated by the Mohr–Coulomb yield criterion as:

$$\begin{aligned} \tau _y=c+p\textrm{tan}\varphi \end{aligned}$$

(12)

where c and $\varphi$ denote the cohesion and the frictional angle of debris-flow mass, respectively; p is the pressure.

$\epsilon ^{\alpha \beta }$ is local strain rate tensor defined as:

$$\begin{aligned} \epsilon ^{\alpha \beta }=\frac{1}{2}\left[ \frac{\partial v^\alpha }{\partial x^\beta }+\frac{\partial v^\beta }{\partial x^\alpha }\right] \end{aligned}$$

(13)

$\dot{\gamma }$ is the shear rate, which can be calculated by:

$$\begin{aligned} \dot{\gamma }=\sqrt{\frac{1}{2}\epsilon ^{\alpha \beta }\epsilon ^{\alpha \beta }}=\sqrt{\frac{1}{2}\left[ \left( \frac{\partial v^\alpha }{\partial x^\alpha }\right) ^2+\left( \frac{\partial v^\beta }{\partial x^\beta }\right) ^2+\frac{1}{2}\left( \frac{\partial v^\alpha }{\partial x^\beta }+\frac{\partial v^\beta }{\partial x^\alpha }\right) ^2\right] } \end{aligned}$$

(14)

K, m and n present constant coefficients. At the same, the second term of the right-hand side of Eq. (11) satisfies:

$$\begin{aligned} lim_{\dot{\gamma }\rightarrow 0}\frac{1}{2\dot{\gamma }}\left( 1-e^{-2m\dot{\gamma }}\right) =m \end{aligned}$$

(15)

Compared with the widely accepted Bingham model, two additional coefficients, m and n, are involved in the HBP model. The coefficient m mainly controls the initial rapid growth of shearing stress, and the coefficient n majorly controls the linear or nonlinear behavior in the high shearing rate range.

2.2 Solid phase governed by DEM

DEM, first proposed by [15], has been extensively applied to the simulation of rock avalanches and debris flows [2, 103]. The basic principle of DEM is to simulate solids with a series of discrete particles, each of which serves as a unit with a specific size and shape. These particles can squeeze and overlap each other within a small area, generating interaction forces. The motion parameters of the particles are then calculated by Newton’s law of motion. By such iterative calculations, the movements of the studied elements are tracked. Furthermore, the shape and type of elements in DEM are not constrained to spherical granular elements and can include arbitrary shaped block elements, or composite elements consisting of several single elements.

Considering the contact between grains of arbitrary shape or between grains and boundaries, the DEM proposed here allows to calculate the distance at which any two grains overlap and the corresponding contact forces and moments between the grains. Nevertheless, it works on the same principle as the classical DEM: for each grain in the system, here denoted as particle a, its dynamics is simulated by numerically integrating the Newton’s equations of motion for translational and rotational degrees of freedom once all the forces acting on it are known:

$$\begin{aligned}&m_a\frac{\textrm{d}{} {\textbf {v}}_a}{\textrm{d}t}=\Sigma _{k\in a}{} {\textbf {F}}^{c,k}+m_a{\textbf {g}}+\left( {\textbf {F}}_a^b+{\textbf {F}}_a^d+{\textbf {F}}^{v}m_a\right) \end{aligned}$$

(16)

$$\begin{aligned}&\frac{\textrm{d}\left( {\textbf {I}}_a\cdot {\varvec{\omega }}_a\right) }{\textrm{d}t}=\Sigma _{k\in a}({\textbf {x}}^{c,k}-{\textbf {x}}_a)\times {\textbf {F}}_{c,k,n} \end{aligned}$$

(17)

where $m_a$ and ${\textbf {v}}_a$ are the mass and translational velocity of grain a; subscript k denotes any one particle, belonging to set of particles a; ${\textbf {F}}_c$ denotes the contact force; ${\textbf {F}}_b$ is the buoyant force; ${\textbf {F}}_d$ represents the drag force; ${\textbf {F}}^{v}m$ is the virtual mass force; ${\textbf {I}}_a$ is the 3$\times$3 inertia matrix; ${\varvec{w}}_a$ denotes the angular velocity; ${\textbf {x}}^c$ is the contact point position vector of the particles; and ${\textbf {x}}_a$ is the centroid position vector of the grain.

DEM considers each simulated particle as rigid, yet allows a small interpenetration d between the particles in order to calculate the contact force ${\textbf {F}}_a^c$ and moment ${\textbf {T}}_a^c$ according to the selected contact model. In fact, various contact models with different levels of sophistication have been developed, such as Herztian or Hookean contact with particle-scale dampfig [70, 104], incorporating rolling resistance [27, 64], considering hysteresis [61]. In this study, a master–slave approach is proposed [40] to detect the contact between two particles, where a slave level set function is applied to evaluate the values of all nodes of the master. If the value of the level set function for any node is negative, then contact exists and the force and moment for each penetrating node are calculated and then summed to give the total contact force and moment between the two particles, as shown in Fig. 2b. In the proposed DEM implementation, the total force ${\textbf {F}}^c$ exerted by particle b on a is calculated according to the following equations:

$$\begin{aligned} {\textbf {F}}^c&={\textbf {F}}_n^c+{\textbf {F}}_t^c \end{aligned}$$

(18)

$$\begin{aligned} {\textbf {F}}_n^c&=\Sigma _{k=1}^{M}{} {\textbf {F}}_{n,k}=\Sigma _{k=1}^{M}k_nd_k\hat{{\textbf {n}}}_k \end{aligned}$$

(19)

$$\begin{aligned} {\textbf {F}}_t^c&=\Sigma _{k=1}^M{\textbf {F}}_{t,k}=-\Sigma _{k=1}^{M}\frac{{\varvec{\Delta }}{} {\textbf {s}}}{|{\varvec{\Delta }}{} {\textbf {s}}_k|}min(k_t|{\varvec{\Delta }}{} {\textbf {s}}|,\mu _s|{\textbf {F}}_{n,k}|) \end{aligned}$$

(20)

where M is the total number of nodes where grain a penetrates grain b; ${\textbf {F}}_{n,k}$ and ${\textbf {F}}_{t,k}$ are the normal and tangential forces computed at node k, respectively; $d_k$, $\hat{{\textbf {n}}}_k$ and ${\varvec{\Delta }}{} {\textbf {s}}_k$ have the same meaning as in the above statement, but are now computed at each node k. By utilizing this level set function approach, contact detection between two arbitrarily shaped grains becomes extremely trivial and requires very little computational effort.

Fig. 2

a An example of constructing one grain with arbitrary shape using level set function; b Schematic representation of contact between two grain

In addition, each individual grain is represented by two quantities: a set of spatially distributed discrete points $\left\{ {\textbf {x}}_1,{\textbf {x}}_2,......,{\textbf {x}}_n\right\}$ on the grain surface and a discretized level set function $\phi ({\textbf {p}})$, where ${\textbf {p}}$ are the grid points in the DEM herein, as shown in Fig. 2a. $\left\{ {\textbf {x}}_1,{\textbf {x}}_2,......,{\textbf {x}}_n\right\}$ provides the geometric information of the particle, while the discretized level set function $\phi ({\textbf {p}})$ is scalar-valued and implicit, giving the distance from a point ${\textbf {p}}$ to the particle surface, which is formed by connecting $\left\{ {\textbf {x}}_1,{\textbf {x}}_2,......,{\textbf {x}}_n\right\}$: $\phi ({\textbf {p}})>0$ when ${\textbf {p}}$ is outside the surface; $\phi ({\textbf {p}})=0$ when ${\textbf {p}}$ is on the surface; and $\phi ({\textbf {p}})<0$ when ${\textbf {p}}$ is inside the surface.

2.3 SPH–DEM coupling algorithm

In the resolved coupling between SPH and DEM, the surface of the DEM particles is considered as a rigid moving boundary of the SPH fluid phase. The interaction forces are calculated by integrating the stresses on the surface of DEM particles. In this work, the focus is placed on particles with arbitrary shapes; therefore, an approach should be developed that can calculate the interactions along arbitrarily complex moving interfaces.

Fig. 3

Schematic diagram of the coupling approach of SPH particles with arbitrarily shaped DEM particles

In this approach, the density of solid particles is obtained from ghost positions within the fluid domain by linear extrapolation. Thanks to an additional boundary interface, located half a particle spacing from the layer of the closest boundary particles to the fluid, a ghost node is mirrored, with respect to this interface, into the fluid domain. In this ghost node, the fluid properties are found through a first-order consistent SPH spatial interpolation over the surrounding fluid particles only. Once the density and its gradient are computed at the ghost nodes, the density of the boundary particle is obtained by means of a linear extrapolation with the found values. In this way, the boundary density is presented as part of the fluid continuum and pressure from the equation of state gives smoother and more physical pressure fields, avoiding the non-physical gap between the boundary and the fluid.

Thus, the density of the solid boundary particle $\rho _B$ is expressed as:

$$\begin{aligned} \rho _B=\rho _G+({\textbf {r}}_B-{\textbf {r}}_G)\cdot \langle \nabla \rho _G\rangle \end{aligned}$$

(21)

where ${\textbf {r}}_B$ and ${\textbf {r}}_G$ are the position of the boundary particle and associated ghost node, respectively, with $B\bigcap G$, and $\langle \nabla \rho _G\rangle$ is the corrected SPH gradient at the ghost node. The velocity at the ghost node is found using a Shepard filter sum:

$$\begin{aligned} {\textbf {v}}=\frac{\sum _{b\in F} V_b{\textbf {v}}_bW}{\sum _{b\in F} V_bW} \end{aligned}$$

(22)

where F is the floating solid and b is the particle on it.

The boundary particle then receives this velocity with the direction reversed to create a no-slip condition at the boundary interface. With this method, it is also possible to create a free-slip boundary by assigning the exact tangential velocity found at the ghost node to the boundary particles.

In addition, proper determination of the time step size plays an essential role in numerical integration since it affects the stability and accuracy of the calculated results. In the coupled SPH–DEM algorithm, the Courant-Friendrich-Lewy (CFL) criterion condition can be written as:

$$\begin{aligned} \Delta t&=C_{CFL}{\min }[\Delta t_f;\Delta t_{cv};\Delta t_{DEM}] \end{aligned}$$

(23)

$$\begin{aligned} \Delta t_f&=_i^{\min }\left( \sqrt{\frac{h}{|{\textbf {f}}_i|}}\right) \end{aligned}$$

(24)

$$\begin{aligned} \Delta t_{cv}&=_i^{\min }\left( \frac{h}{c_0+\max _j|\frac{{\textbf {v}}_{ij}{} {\textbf {r}}_{ij}}{{\textbf {r}}_{ij}^2}|}\right) \end{aligned}$$

(25)

$$\begin{aligned} \Delta t_{DEM}&=^{\min }_a\left( \frac{\pi }{50}\sqrt{\frac{k_{n,ab}}{m_{ab}}}\right) \end{aligned}$$

(26)

where $C_{CFL}$ is the Courant number of the order of $10^{-1}$; $\Delta t_f$ is considered from the perspective of force []; $\Delta t_{cv}$ is an item that considers the CFL conditions and the restrictions on viscous items []; $\Delta t_{DEM}$ is the term obtained under DEM stability constraints []. Therefore, the time step is variable in this study.

A flowchart of the coupled SPH–DEM is shown in Fig. 4. First, the particle data are initialized. All particle information is uploaded to the GPU memory, and subsequently computations are performed in a massive parallel manner based on the GPU. At the beginning of each loop, a neighbor particle search is first performed to create two cell chains for SPH particles and DEM particles, and the time step is estimated. Then the SPH–DEM interactions are calculated using Eq. (9). For fluid particles, the SPH-SPH interaction is calculated, and the combined force of the SPH particles is obtained by combining the effect of the solid boundary on the SPH particles and updating the particle velocity and position information. For solid particles, the DEM is used to calculate the contact forces between the solid particles, and all the forces applied to the DEM particles are added up and then summed. The forces and moments of the rigid body are calculated, and the velocity, position, and rotation information are updated. Thus, a full calculation cycle is completed. The Verlet algorithm is used for time integration. All intensive operations are performed by the GPU, which greatly improves the computational efficiency.

Fig. 4

Calculation flowchart of coupling SPH–DEM algorithm

2.4 GPU implementation

The coupled SPH–DEM approach is realized using C++ and CUDA developed by NVIDIA. GPU acceleration is implemented through the use of the SPMD technique [18], in which a single program is simultaneously executed by multiple threads. Due to the discrete nature of particle-based methods, the GPU acceleration technique seamlessly supports the coupled SPH–DEM algorithm. GPU threads are assigned to perform different GPU kernel functions for each particle, such as neighbor search, force calculation, and time integration. However, an important difference between the GPU implementations of DEM and SPH is that the former requires recording contact information between the particles in contact, while the latter does not. This contact information is typically utilized to determine the friction state, either static or dynamic, and typically requires a large amount of memory for recording the contact history. For efficient computation, parameters that remain constant during the computation, such as material properties, are stored in GPU cache memory (a GPU memory with extremely fast data fetch speeds), while other data, such as particle position, velocity, and force, are stored in GPU global memory.

In addition, double precision floating point accuracy is required to minimize numerical errors. Therefore, it is important to optimize the algorithm to balance memory consumption and computational efficiency to efficiently solve large-scale problems. For this purpose, only a list of neighbors is constructed for the DEM particles since each SPH particle can have a large number of neighbors due to the size of its support domain. Particle mapping steps for SPH particles are performed occasionally, while all levels of search steps are performed at each time step. When the cumulative displacement of any particle exceeds the specified threshold, the reconstruction of DEM neighbor list and the particle mapping step of SPH particles are triggered. We also note that all simulation cases in this study were run on GeForce RTX 3060Ti GPUs.

3 Validation examples

3.1 Verification of SPH: dam break experiment

The dam break experiment conducted by [44] is utilized to validate the capability of the proposed numerical approach in solving the fluid problem. The constructed numerical model is depicted in Fig. 5. A water column of 0.146 m $\times$ 0.2 m $\times$ 0.292 m is generated on the left side of a tank of 0.584 m $\times$ 0.2 m $\times$ 0.35 m, where the water column is simulated of SPH particles with an initial particle spacing of 2.0 mm. The SPH particles are initialized with hydrostatic pressure in accordance with their positions and reference densities. The simulation parameters are listed in Table 1. The entire simulation domain is discretized into 1.05 million fluid particles. The numerical simulation completed in 7755 s (approximately 2.15 h).

Table 1 Parameters in the simulation of the dam break experiment

Fig. 5

Numerical model setup of the dam break experiment

The results of the simulation and experiment on the flow pattern of the water column in the tank at selected time instances are shown in Fig. 6. We observed that at 0.2 s the collapsing water rushes along the bottom of the tank at an increasing velocity to the right boundary, and then the water in front is blocked by the right vertical wall at 0.4 s, thus moving upward. After, a significant amount of water is deflected vertically and then falls back under the effect of gravity, producing a swooping surface wave that flows back toward the left side of the tank. The flow patterns that are obtained from the simulations are in good agreement with those observed in laboratory tests, which indicates that the SPH approach in this study can qualitatively capture the flow behavior of the fluid.

Fig. 6

Comparisons of experimental and simulated flow pattern evolution at different times

Fig. 7

Water surface elevations for numerical simulations and experiments at different times

Additionally, we note that the numerical results of the water surface elevation are approximately in agreement with the experimental results at different moments, as shown in Fig. 7. Clearly, the trends of water surface elevations are essentially the same, with minimal differences at different horizontal distances. These slight differences may be attributed to the initial particle spacing and the smoothing length, although its effect is negligible [28, 106]. This result further demonstrates the robustness and reliability of the proposed approach in this study in simulating the fluid phase.

3.2 Verification of the HBP model: column collapse experiment

The performance of the HBP model was tested through the 2D column collapse experiment of [5]. In the experimental setup, aluminum bars with diameters of 0.001 m and 0.0015 m and lengths of 0.05 m were used to simulate 2-D conditions. The dimensions of the column were 0.2 m $\times$ 0.1 m $\times$ 0.05 m, and the collapse was triggered by the rapid removal of the support wall on the right side of the column.

This experiment was simulated by the HBP-based SPH model. In the simulation, the soil column was modeled by 5,430 fluid particles with an initial particle spacing of 2 mm. Based on the results of four shear box tests on aluminum bars, the following material parameters were used in the HBP model: density $\rho$ = 2650 $\mathrm {kg/cm^3}$, yield shear stress $\tau _y$ = 0.36 kPa, and key coefficients of the HBP model m = 0.15 and n = 1.01. The numerical simulation cost 300 s (approximately 0.08 h).

Fig. 8

Column collapse comparison between: a the experimental results of [5], b results of HBP model and c final surface height profile and yield lines in experiment and simulation

Figure 8 shows a comparison between the experimental and numerical results of the HBP model including the surface profile and yielded area comparison with the experimental results. The numerical results obtained by the HBP model match well with the experimental results in terms of the height profile of the deposit and in terms of the yield lines inside the column. Overall, the HBP model utilized in this study demonstrated a good ability to simulate frictional flow.

3.3 Verification of DEM: rock collapse experiment

This section demonstrates the reliability of the proposed DEM approach in simulating solid particles of arbitrary shapes. For this purpose, gravity-driven rock collapse experiments were chosen because they are simple to perform and are widely used as validation experiments for modeling solid particles [71, 91].

Fig. 9

Setups and materials used in rock collapse experiments and simulations

The laboratory rock collapse experiments were conducted in a container made of acrylic panels with dimensions of 5 cm in width, 35 cm in length, and 25 cm in height. A pumpable baffle was located 5 cm from the left side of the container, as shown in Fig. 9a. The rocks used in the experiments were trigonal cone-shaped crushed rocks of approximately the same size, shape and composition (see Fig. 9b). Initially, an assembly of approximately 960 rocks was placed on the left side of the container, confined by the baffle. The rock assembly was 5 cm in width, 5 cm in length, and 13 cm in height. Once the experiments began, the baffle was lifted at a low speed to ensure optimal spreading of the material. During the lifting of the baffle, the crushed rocks were observed to collapse, roll and form a slope under gravity. Finally, after the collapsed crushed rocks were stabilized, the repose angle was measured using a protractor. These experiments were repeated five times, and the results revealed that the average repose angle of the collapsed rocks is 31$^{\circ }$, as shown in Fig. 10. A Dimax HS4 high-speed camera was operated to record the entire experiment at 500 frames per second.

Table 2 Parameters in the simulation of the rock collapse experiments

Fig. 10

Comparisons of experimental and simulated rock collapse patterns at different times

Fig. 11

Evolution of experimental and simulated rock collapse at different times

Rock collapse experiments are also simulated using the proposed approach. The configuration of the numerical model of rock collapse corresponds to the experiment, as shown in Fig. 9c. The solid particles in the simulation were obtained by scanning real crushed rocks using a 3D laser scanner, and the resulting rock assembly consisting of 960 crushed rocks was populated to the left part of the constructed numerical model. Furthermore, the dimensions of the initial sample are consistent with the experimental configuration. Since the numerical model of discrete particles differs from the experimental crushed rocks, to accurately reflect the actual kinetics of the crushed rock flow, the key parameters of the discrete model of rock collapse, including the kinetic friction coefficient and the restitution coefficient, first must be calibrated through trial and error. The parameters used in the simulation are listed in Table 2. When the assembly reached a steady state, the baffle was set to lift upward at a constant velocity of 4 m/s, which was consistent with the average speed recorded by the high-speed camera during the experiment. Driven by gravity, the rock assembly collapsed and rolled to the right side of the container. The entire simulation domain is discretized into 1.9 million solid particles. The numerical simulation completed in 23,036 s (approximately 6.39 h).

Figure 10 compares the experimental and numerical studies of rock collapse at different times. The simulated and experimental rock collapse patterns at the same moments are essentially in agreement. At first, the rock assembly was in a stable state, and as the baffle moved upward, the lower part of the rock assembly started to slide down to the right. Due to the effect of contact friction, the rocks in contact with the baffle were resistant to sliding and even had a tendency to move upward with the baffle. At t = 6.5 s, the rocks and the baffle were exactly not in contact at all. Subsequently, the rock assembly slid under the effect of gravity and eventually formed a slope. The comparison reveals that the repose angles measured by the experiment and the simulation are identical, which qualitatively validates the robustness of the approach.

Quantitative comparisons of rock collapse heights at different times are depicted in Fig. 11. The simulated results at different times agreed with the experimental results in terms of the collapse trend, movement pattern and surface profile of the rocks. Moreover, the propagation distances of both the experimental and simulated rock assemblages were approximately 15 cm. Therefore, it is reasonable and accurate to simulate arbitrarily shaped solids with the proposed DEM model.

4 Debris flow impacting slit-type barriers

DEM has been proven to be effective in simulating arbitrarily shaped solids, while SPH can accurately simulate the fluid phase, as shown in previous benchmarks. In this section, a model of a water-enriched debris flow impacting a slit-type barrier is developed to understand the role of fluid-solid interaction in the mobility of the flow by comparison with [12]’s experiments. Using this model, the effects of debris flow characteristics and barrier geometric features on debris-barrier interactions, including barrier arrangement, boulder shape and solid volume fraction, are further investigated.

4.1 Numerical model setup

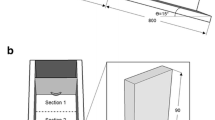
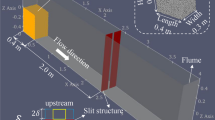
The numerical model configuration for the flume experiments is shown in Fig. 12. (The unit of value marked in the figure is mm by default.) The length, width and height of the flume are 1.4 m, 0.4 m and 0.3 m, respectively, with an inclination of 15$^{\circ }$. A debris flow generating box with dimensions of 0.2 m $\times$ 0.4 m $\times$ 0.3 m is placed at the top of the flume. A set of slit-type barriers is installed 0.8 m from the end of the channel. This set of slit barriers is made of seven identical rectangular walls, each with dimensions of 50 mm in width, 90 mm in height and 13 mm in thickness.

Fig. 12

Schematic diagram of the setup for the flume experiment by [12]

Prior to the initiation of the simulations, all debris flow components are generated in the debris flow generating box. The debris flow consists of a water-sand mixture and boulders. The water-sand mixture with a total mass of 4.5 kg is assumed to be a viscous fluid with a density of 1300 $\mathrm {kg/m^3}$ and is simulated by SPH. The boulders with a total mass of 0.149 kg in the experiments, represented by glass beads with a diameter of 16 mm, are simulated by DEM. In addition, both the rigid barriers and the flume in the experiments are modeled by solid DEM particles. By comparison, we found that a better simulation effect, including time and computational savings, can be obtained when the spacing between SPH particles (dp) is 1.5 mm, namely, the ratio of SPH particle spacing to DEM particle diameters is 0.09375. Both SPH and DEM simulations are performed with an average time step of 0.105 s. Gravity is considered during the simulations, and the gravitational acceleration is 9.81 $\mathrm {m/s^2}$. The duration of the whole simulation is 6.0 s. Furthermore, according to Kuwabara and Kono [46], the Froude number ($F_r$), which is the ratio of inertial force to gravity, can reflect the dynamic similarity of the physical model of open channel flows including debris flows. $F_r$ is obtained from the following equation:

$$\begin{aligned} F_r=\frac{\nu }{\sqrt{gh\textrm{cos}\theta }} \end{aligned}$$

(27)

where $\nu$ is the frontal velocity; h represents the flow depth; and $\theta$ denotes the channel inclination. To ensure that the results observed in the simulation and the flume experiment are as consistent as possible, some parameters are set by trial and error so that $F_r$ is 11, which is the same as the experimental Froude value. The parameters used in the simulations are listed in Table 3. The entire simulation domain is discretized into 2.2 million solid particles and 1.4 million fluid particles. The numerical simulations completed in 77,135 s (approximately 21.43 h).

Table 3 Parameters used in the simulation of flume experiments

4.2 Numerical model validation and analysis

The numerical model of the water-enriched debris flow impacting slit-type barriers using the modified SPH–DEM approach was validated by comparison with the experiments conducted by [12]. Several groups of experiments were simulated, as shown in Fig. 13, including four cases “A”, “B”, “C” and “D”. Case A represents the barrier arrangement P00 (rectangular walls are uniformly arranged with 0$^{\circ }$ to the horizontal direction of the channel) and the boulders are not contained in the debris flow; Case B represents the barrier arrangement P30 with a debris flow that contains boulders; Case C represents the barrier arrangement V30 (rectangular walls are arranged in a V-shape and at an angle of 30$^{\circ }$ to the horizontal direction of the channel) and the debris flow does not contain boulders; Case D represents the barrier arrangement V30 with a debris flow that contains boulders.

Fig. 13

Comparisons of numerical simulations and experiments for several different cases

Fig. 14

Evolution of fluid velocity for Case A and Case C in experimental and numerical experiments

The numerically simulated and experimental debris flow interactions with slit-type barriers for the four cases are illustrated in Fig. 13. For Case B, the directional deflection of the debris flow due to the barrier is reproduced; for Case D, the boulders in the debris flow are blocked behind the barrier and the accumulation is reproduced. Thus, the numerical model can effectively morphologically simulate the movement of the two-phase debris flow in the flume and its interaction with the barrier. This qualitatively verifies the reliability and robustness of the modified SPH–DEM coupling approach in simulating debris flow dynamics. The evolution of the average velocity of the fluid in the debris flow along the channel direction is shown in Fig. 14 for Case A and Case C. We observe that in both cases, the simulation results mostly match the experimental data numerically. The results of the numerical simulation at the first velocity measurement point are lower in both cases, which likely occurs because the debris flow reaches a steady state in the generating box before it is released in the simulations, while there will be a certain initial velocity in the experiments. Nevertheless, overall, the results justify that the numerical approach can quantitatively simulate the movement of the debris flow in the flume, which leads to the following analysis.

5 Numerical results analysis

Understanding and predicting the factors that influence debris flow-barrier interactions is a critical task for assessing and managing risk in many worldwide mountainous regions that are heavily influenced by debris flows. Many researchers have explored and found that barrier configuration [89], landslide volume [], and landslide material [88] all affect the impact dynamics of debris flows on barriers. In view of the above, the flume experiment model constructed is further analyzed to investigate the effects of different factors on the interaction between the water-enriched debris flow and the slit-type barrier, in terms of both the features of the barrier and the initial characteristics of the debris flow. The total impact force of the debris flow on the barrier and the run-up height of the debris flow along the barrier are adopted as two evaluation indicators.

5.1 Dynamics of debris flow impacting slit-type barriers

The dynamics of the water-enriched debris flow impacting the slit-type barrier are presented in this section. Figure 15 shows the evolution of the motion of the debris flow for Case D. At the initial instance, the debris flow is generated in the debris flow generating box located at the top of the flume, with the gate closed to ensure that the debris flow is sufficiently well mixed and in a steady state. At t = 2.5 s, the gate is removed, and the debris flow then travels downward along the flume. Clearly, the velocity of the boulder at t = 3.0 s is less than that of the fluid. Subsequently, the fluid front reaches the barrier. The velocity of the fluid decreases owing to the barrier and is partially bounced back and partially flows down the slit. Simultaneously, we note that some of the fluid continues to move forward across the barrier due to a continuous stream of subsequent fluid convergence. On the other hand, the boulders keep moving forward due to the interaction with the fluid and are then blocked at the back of the barrier. From t = 5.0 s onward, the fluid behind the barrier can only flow down the slit in streams due to its low kinetic energy.

Fig. 15

Evolution of debris flow motion during debris flow impact on slit-type barriers for Case D

Fig. 16

Evolution of the velocity field of the fluid during the interaction of the debris flow with the barrier

To better understand the mechanism of the interaction between the debris flow and the barrier, Fig. 16 reveals the variation in the velocity field of the fluid in the debris flow with time. When the fluid front touches the barrier, part of the fluid velocity direction goes vertically upward and reflects backward after reaching a certain height, and the velocity magnitude sharply decreases, while part of the fluid flows through the slit, and the velocity magnitude gradually increases. At t = 3.2 s, with a massive surge of fluid toward the barrier, carrying the boulder forward, the movement of the fluid is divided into three parts: part of it bounces back after running up along the barrier, part of it flows forward across the barrier, and part of it flows through along the slit. The rebounded fluid hits the subsequent fluid, which decreases the velocity of the subsequent fluid at t = 3.4 s. After t = 3.6 s, the velocity of the fluid behind the barrier gradually decreases to 0. Most of the boulders are deposited at the bottom of the barrier except for a small amount that is wrapped by the fluid across the barrier.

5.2 Influence of barrier arrangement

In fact, the arrangement of the barrier effectively affects the interaction of the debris flow with the slit-type barriers by reducing the velocity of the debris flow and the trap ratio of the barrier to the debris flow, according to [12] and [41]. Therefore, it is worthwhile to further investigate the effect of barrier arrangement on the impact force to which the barrier is subjected and on the movement of the debris flow. This section simulates the interaction process between the debris flow and the barrier for the barrier arrangements of P00, P30, P45, V30 and V45. These barrier arrangements are shown in Fig. 17. Furthermore, in exploring the barrier performance, this study considered the effective opening ratio, which is defined as the ratio of the effective opening width of the flow to the total width of the channel. The effective opening ratios for these barrier arrangements of P00, P30, P45, V30 and V45 are 0.125, 0.485, 0.613, 0.128 and 0.220, respectively.

Fig. 17

Several different arrangements of slit-type barriers

Fig. 18

Snapshots of debris flow-barrier interaction under different barrier arrangements

Figure 18 shows the water-enriched debris flow as it impacts the slit-type barrier at t = 3.2 s and t = 4.5 s for five different barrier arrangements. The differences in the movement morphology of the debris flow impacting the barrier under different arrangements are clearly observed: at t = 3.2 s, the debris flow mainly climbs vertically upward along the barrier and partly crosses the barrier to flow forward when the barrier arrangement is P00, while for the barrier arrangements P30 and P45, most of the debris flow flows through the slit. Clearly, the flow velocity is faster for P45. Moreover, both phenomena of debris flow climbing upward along the barrier and flowing through the slit occur when the arrangements are V30 and V45, and the flow velocity is greater for V45. Therefore, we conclude that the larger the effective opening ratio of the barrier is, the easier it is for the debris flow to pass through the slit, and at the same time, the greater the fluid front flow velocity. In addition, the smaller the effective opening ratio is, the more significant the backwater effect is, which is consistent with what was observed in the experiments of Choi et al. The backwater effect refers to the fact that part of the debris flow is bounced back from the barrier and collides with the following body and tail, leading to a reduction in kinetic energy and velocity and ultimately to the deposition of debris and trapping by the barrier. Additionally, we note that the larger the effective opening ratio of the barrier is, the smaller the volume of fluid located at the back of the barrier at t = 4.5 s. This result suggests that reducing the effective opening ratio of the barrier can, to some extent, impede the movement of the fluid.

Impact force, as one of the critical factors in assessing barrier performance, is a key parameter to consider during barrier design. The dynamic impact force on the barrier for different barrier arrangements is shown in Fig. 19a. We note that for the slit-type barriers in this study, the impact force data for the rectangular walls marked in red in Fig. 17 are extracted because, when the barriers are arranged in a row, the middle barrier tends to be subjected to the greatest impact force in the collision between the debris flow and the barrier. Figure 19b shows that the trend of the impact force on the barrier is essentially the same for different barrier arrangements: the front end of the debris flow contacts the barrier at t = 2.9 s, resulting in a sharp increase in impact force, and the peak impact force is reached at t = 3.2 s; then, the impact force gradually decreases until it stabilizes. Furthermore, the peak impact force of the V-shaped barrier is larger than that of the P-shaped barrier. For the P-shaped barrier, the larger the effective opening ratio of the barrier is, the smaller the peak impact force. This occurs because the increase in the effective opening ratio allows more debris flow to pass through the slit, thereby weakening the impact on the barrier and implying that the barrier has a weaker effect in trapping the debris flow. In contrast, this phenomenon is not significant for the V-shaped barrier. Additionally, we note that there are significant fluctuations in the impact force until it reaches stability for both V30 and P00. This fluctuation is caused by the backwater effect after the debris flow impacts the barrier and the repeated impacts of the debris flow on the barrier. It further indicates that the larger the barrier opening ratio is, the weaker the backwater effect is, while the static impact force is smaller.

Fig. 19

Comparisons of a Impact force on barriers; b Water surface elevation along the channel with different barrier arrangements

In addition, the water surface elevation of the debris flow on the cross section where the central axis of the flume is located for different barrier arrangements at t = 3.2 s is extracted, as shown in Fig. 19b. We observe that the maximum water surface elevation decreases as the effective opening ratio increases, which is true for both P-type barriers and V-type barriers. For P-type barriers, the greater the effective opening ratio is, the further the distance from the top of the flume at the maximum water surface elevation, while for V-type barriers, the opposite is true. Additionally, for a given angle, the maximum water surface elevation for the P-type barrier is smaller. In fact, to some extent, the water surface elevation correlates with the performance of the barrier. For different barrier arrangements, the front of the debris flow almost touches the barrier at the same time, while a low run-up height indicates weak barrier interception performance against debris flows. Therefore, it is clear that the overall performance of P00 in the P-type barrier is better. For specific angles, V-type barriers show better performance than P-type barriers.

5.3 Influence of solid volume fraction

The contribution of boulders in debris flows cannot be neglected, despite the nature of water-enriched debris flows. To further investigate the effect of boulders in water-rich debris flows, this section considers the effect of the degree of fluid-solid interaction on the mobility of the debris flow and its impact against slit-type barriers. The degree of fluid-solid interaction is represented by the solid volume fraction $\nu$, which is the ratio of the solid volume to the total volume of the packing. Five values of solid volume fractions are adopted in this section: 0, 0.167$\%$, 0.334$\%$, 0.822$\%$, and 1.176$\%$.

The general flow trend of the debris flow remains the same, and all flows exhibit significant upward jets after the impact, suggesting that a run-up mechanism exists despite the inconsistent solid volume fractions. Upon reaching the maximum run-up height, part of the debris flow begins to roll back and pile up at the back of the barrier, while some other fluids flow through the slit. Figure 20 compares the morphologies of debris flows for different solid volume fractions as they interact with the barrier at t = 4.5 s and t = 5.5 s. The data clearly show that the increase in boulders in the debris flow leads to a weakening of the fluid-barrier interaction so that more fluid is retained at the back of the barrier at the same moment. This occurs because the fluid-solid interaction strengthens with the increase in the solid volume fraction, which further reduces the energy dissipation when the fluid impacts the barrier.

Fig. 20

Snapshots of the debris flow impact slit-type barriers for different solid volume fractions

Fig. 21

Comparisons of a Impact force on barriers; b Water surface elevation along the channel with different solid volume fractions

Figure 21a shows the development of the dynamic impact of the fluid on the barrier for several solid volume fractions. The impact force of each debris flow first exhibits a rapid increase until it reaches a peak and then decreases dramatically to a final static force. Nevertheless, it is also evident that the larger the solid volume fraction is, the larger the peak impact force of the fluid on the barrier in the debris flow. This phenomenon may be attributed to dynamic pressure coefficient increases as the solid volume fraction increases, which leads to an increase in the dynamic pressure of the fluid on the barrier. Moreover, we note that there is a significant fluctuation in the impact force curve until the final static impact force is reached. This fluctuation becomes more pronounced as the solid volume fraction decreases, with the exception of $\nu$ = 0. Each reduction in impact force during the fluctuation is due to the separation of the fluid from the debris flow and its convergence toward the subsequent fluid. Similar findings were reported in the studies of [6] and [].

In addition, the water surface elevation at t = 3.2 s when the fluid impacts the barrier at different solid volume fractions is extracted in Fig. 21b. The process of fluid-barrier interaction at the same moment is essentially consistent, but the larger the solid volume fraction is, the lower the maximum water surface elevation at which the fluid runs up along the barrier. This is because the increase in the number of boulders leads to more fluid–solid contact, and thus, the fluid exerts more buoyancy and drag force on the solid, resulting in more energy dissipation. Thus, the energy dissipated on the barrier is weaker, and the run-up height is lower.

5.4 Influence of boulder shape

Currently, the majority of numerical simulations employ spheres instead of arbitrarily shaped boulders to simplify calculations in debris flow modeling. However, this simplification affects the accuracy of the simulation. Therefore, the effect of spherical and irregular boulders in debris flows on the impact of water-enriched debris flows against slit-type barriers is compared. To ensure that other factors do not affect the simulation, arbitrary irregular boulders of similar volume to spherical boulders are selected. Snapshots of the debris flow movement in the two cases are shown in Fig. 22. We notably observe that the fluid flow is faster in the debris flow containing irregular boulders. An interesting phenomenon occurs in the evolution of the dynamic impact of the fluid on the barrier, as shown in Fig. 23a, where the peak impact force of the debris flow containing irregular boulders on the barrier is greater, yet its static impact at final stabilization is smaller. We speculate that this occurs due to the smaller contact between the irregular boulders and the fluid, resulting in less energy dissipation in the fluid-boulder interaction and thus a greater dynamic impact on the barrier. The smaller final static impact may be attributed to more fluid crossing the barrier in a debris flow that contains irregular boulders. The water surface elevation of the fluid was further compared for both cases at t = 3.2 s (see Fig. 23b). We also found that debris flows containing irregularly shaped boulders had greater run-up heights. This result is consistent with our expectations.

Fig. 22

Snapshots of numerical simulation of flume experiments with the types of boulders of spherical boulders and irregular boulders at different times

Fig. 23

Comparisons of a Impact force on barriers; b Water surface elevations as the distance along the channel with the types of boulders of spherical boulders and irregular boulders

6 Conclusions and recommendations

In this study, a modified SPH–DEM coupling approach is proposed to study the impact dynamics of debris flows on barriers. The fluid phase is modeled by SPH, while DEM simulates arbitrarily shaped solids. The robustness and reliability of the proposed approach are validated by comparing the results with those of two classical tests, namely, the dam-break experiment and the rock-collapse experiment. Subsequently, a model of a water-enriched debris flow impacting a slit-type barrier is constructed and calibrated, and the model is used to further investigate the effects of the solid volume fraction of the debris flow, boulder shape, and barrier arrangement on the debris flow-barrier interaction. Based on the limited number of simulation cases and the parameters used, the conclusions of this study are as follows:

$\bullet$ The main mechanism of water-enriched debris flow movement along slit-type barriers is a run-up mechanism. The main mechanism of water-enriched debris flow movement along slit-type barriers is also a run-up mechanism. Three types of motion patterns are observed after the front fluid impacts the barrier: climbing along the barrier and crossing it; passing through the slit between the rectangular walls; climbing along the barrier and then falling and rebounding; and rolling back and impeding the advance of the subsequent debris flow.

$\bullet$ Barriers with different arrangements are all subjected to the maximum impact force of the debris flow at the same moment. The static impact force and maximum water surface elevation decrease with increasing effective opening ratio for both P-type and V-type barriers. For a specific angle, the V-type barrier is subjected to a larger peak impact force than the P-type barrier, and the debris flow climbing along the V-type barrier has a larger maximum water surface elevation.

$\bullet$ Changes in the solid volume fraction affect the movement of the fluid in the debris flow. The dynamic impact force of fluid on the barrier decreases with increasing solid volume fraction, whereas the run-up height along the barrier demonstrates the opposite trend. A useful phenomenon is obtained by changing the shape of the boulder: debris flows containing irregular boulders have higher peak impact forces, while those containing spherical boulders have greater static impact forces.

All the simulations modeled in this study were carried out at a small scale, which might not correspond to physical instances of debris flow. The water-sand mixture is simplified as a non-Newtonian fluid rather than being considered as a mixture, which is at odds with the actual situation. Extending this design method and installation technique to a current debris flow barrier and actual field cases should be considered. Additionally, it is necessary to confirm that our same conclusions would be drawn from other numerical models or equations. In addition, when designing multiple barriers in actual field cases, there are many possible shapes, scales, and geometries that exist; it is difficult to select suitable barrier locations and designs for all possible cases. The developed simulation approach and obtained results provide an effective tool and insight that can contribute to the optimum design of debris flow barriers.