Stability analysis of reservoir slopes under fluctuating water levels using the combined finite-discrete element method

Abstract

Fluctuating water levels are responsible for many reservoir slope failures. This work develops a novel slope analysis model (Y-slopeW) to evaluate the reservoir slope stability under water–rock coupling effect, based on the combined finite-discrete element method (FDEM). The transient fluid fields under water level fluctuations are first calculated, and then slope stability under water–rock interaction is evaluated in terms of the safety factor using the strength reduction method. Several benchmark tests are proposed to validate the present model. Stability analysis of an ideal slope under reservoir water level fluctuation is analyzed, where the effect of reservoir fluctuation rate and rock permeability coefficient on slope stability are discussed in detail. A practical slope case (Majiagou slope) in the Three Gorges Reservoir area is studied. Results show that the fluctuating reservoir water level plays an important role in slope stability, and a rapid drawdown is the most unfavorable condition to the slope stability. The work detailed herein proposes an efficient tool to better understand the failure mechanism and stability evolution for slopes under water level fluctuation.

1 Introduction

Slope failure is particularly detrimental to the safety of human life and engineering infrastructure, causing thousands of fatalities and billions in economic losses every year [1, 2]. Groundwater conditions are considered to be one of the most influential factors that control the stability of natural slopes [3, 4]. Particularly for reservoir slopes, the fluctuating water level can have significant adverse effects on the hydrological conditions, stress condition and geomaterials properties in the reservoir area, inducing reservoir slope failures [5, 6]. Attention to reservoir slope stability has been growing since the catastrophic event of the Vaiont reservoir slope failure, which left behind a catastrophic 2600 fatalities [7]. With the rapid development of renewable water resources, numerous hydraulic engineering projects have been constructed in recent years (e.g., the Three Gorges project, Jinping II project), with profound effects on slope stability [4, 8]. For example, following the construction of the Three Gorges Dam on the Yangtze River, more than 4200 landslides were observed along the banks of this huge reservoir (Fig. 1) [4, 9, 10]. Therefore, a better understanding of the failure mechanism of reservoir slopes under the effects of water level fluctuation is fundamentally important for the safety of both human lives and engineering projects.

Fig. 1

The landslides distribution and two representative landslides in Three Gorges Reservoir area (after [4, 10, 11])

The intricate impacts of groundwater fluctuation on reservoir slope stability requires an understanding of the complex multiphysics interaction between the water and geomaterials, e.g., physical, mechanical, and chemical effects [12, 13]. The water–rock interactions significantly alter the seepage field, stress field and geomaterials properties, ultimately leading to the deformation (even failure) of the bank slope. Extensive research has been performed to study the slope failure problems under groundwater effect with a variety of techniques. Field investigation and monitoring data analysis [14,15,16] are widely used to reveal the relationship between slope displacement and reservoir water level, and help to propose an early warning to active landslides. In addition, laboratory tests [17,18,19], that can intuitively reflect the failure process and failure mechanism, are also used to investigate the slope problems under different water conditions. Although the use of field and laboratory methods have the advantage of investigating influential factors, mechanisms, and establishing empirical equations, they are costly and require a prolonged period to perform and monitor. In lieu of which limit equilibrium methods (LEM), which quantitatively assesses the slope stability conditions in terms of safety factors, have also been developed to assess and analyse slope stability under groundwater effects [20,21,22]. Commercial software based on the LEM, e.g., GeoStudio [23] and Slide [24], represent an important tool to help and guide engineers in solving slope problems. However, LEM suffers from some limitations, for instance, the sliding body is assumed as a rigid block and the material constitutive relationship is ignored. Alternatively, the development of numerical methods provides a new approach to slope problems, where nonlinear material behavior, complex boundary, and loading conditions can be accounted for. Griffiths and Lan [25] first explored the use of finite element method (FEM) to assess slope stability under drawdown conditions. Then more numerical methods, e.g., finite difference method (FDM) [26], discrete element method (DEM) [27], discontinuous deformation analysis (DDA) [11], and numerical manifold method (NMM) [28] became prevalent to the slope stability analysis under water effect. Even though the above numerical methods achieved decent results for the slope problems, the underlying failure mechanism caused by the water–rock coupling effect is still poorly understood. In fact, some of the above models suffer from oversimplifications, for example, the water effect is simplified to hydrostatic pressure or using submerged density to represent soil under water, and physical/mechanical parameters are kept constant during the analysis. In order to develop a comprehensive understanding of the water–rock coupling effect on the slope stability, the hydrodynamic pressure (i.e., seepage force) and wetting-induced material weakening are necessary in the slope stability evaluation [27, 29]. Additionally, instead of steady-state conditions that assume a linear water table, the transient seepage process with fluctuating water level should be examined to understand the impacts associated with the fluctuation of the water table. Thus, a robust model that considers the impacts of water–rock coupling effects is essential to the slope stability analysis.

The combined finite discrete element method (FDEM) [30], which combines advantages of continuum and discontinuum techniques, has attracted wide attention and has also been applied to slope problems [31,32,33,34,35]. Recently, Sun et al. [35, 36] proposed an FDEM framework (named Y-slope) for simulating the entire slope failure process (involving the initiation, transport to deposition), proposing a promising tool for slope problems. However, water–rock coupling effects on slope stability have not been considered in the aforementioned FDEM work. In this paper, a novel reservoir slope analysis model (Y-slopeW) is proposed to investigate the slope stability under water effects, by incorporating a seepage algorithm into the Y-slope model. The transient fluid field within the slope subject to water level variations is first calculated by the seepage algorithm, and then the corresponding water–rock coupling effect, including physical and mechanical interactions, are rigorously considered in the Y-slope model. Based on the obtained seepage field and water–rock interactions, the slope stability in terms of the safety factor is solved with the strength reduction method (SRM). Several benchmark tests are proposed to validate the proposed model. An ideal slope model is proposed to investigate the slope stability variation with the reservoir level fluctuations, where the sensitivity of the rate of water level fluctuation and rock permeability coefficient are discussed in detail. Finally, a case study of Majiagou slope in the Three Gorges region is presented.

2 Fundamentals of FDEM

The FDEM, which combines the advantages of both finite and discrete element methods, has been employed in a variety of continuum-discontinuum simulations [37,38,39,40,41], as well as hydro-mechanical coupling problems [42,43,44,45,46,47] in recent years. In this section, basic principles of FDEM are briefly introduced. The reader is referred to Munjiza et al. [48] and Munjiza [30] for more in-depth information pertaining to the FDEM.

In FDEM, the rock mass (Fig. 2a) is discretized into 3-node triangular elements, and 4-node zero-thickness joint elements (Fig. 2b). These joint elements represent the bond between the edges of the triangular nodes. Pre-existing or newly generated cracks are represented by crack elements (i.e., broken joint elements). The stress and deformation of each discrete block is calculated using FEM formulations, while the interaction of multiple blocks is simulated by the DEM formulations. The transition from continuum to discontinuum is simulated by the breakage of the joint element.

Fig. 2

The rock mass is discretized into triangular elements, joint elements, and crack elements

An explicit time integration scheme is applied to solve the motion of the discretized system and to update the nodal coordinates, where the governing equations can be expressed as [30]:

$${\mathbf{M}}\frac{{\partial^{2} {\mathbf{x}}}}{{\partial t^{2} }} + {\mathbf{F}}_{{{\text{int}}}} ({\mathbf{x}}) - {\mathbf{F}}_{{{\text{ext}}}} ({\mathbf{x}}) - {\mathbf{F}}_{{\text{c}}} ({\mathbf{x}}) - {\mathbf{F}}_{{\text{j}}} ({\mathbf{x}}) - {\mathbf{F}}_{{\text{w}}} ({\mathbf{x}}) = \mathbf{0}$$

(1)

where M is the lumped mass matrix of the system, x is the vector of the nodal coordinates. F_int, F_ext, F_c, F_j, F_w represent the internal forces, external loads, contact forces, joint forces and water pressure (including both static and dynamic pressure), respectively.

The stress–strain relationship of the constant-strain triangular finite element, representing the material being modelled, is based on the traditional FEM formulations [30, 49]:

$${\mathbf{T}}{ = }\frac{\lambda }{2}\left( {J - \frac{1}{J}} \right){\mathbf{I}} + \frac{\mu }{J}({\mathbf{B}} - {\mathbf{I}}) + c{\mathbf{D}}$$

(2)

where T is the Cauchy stress tensor, J is determinant of the deformation gradient, λ and μ are the Lame constants, I is the identity matrix, c is the damping coefficient, B is the left Cauchy-Green strain tensor, D is the rate of deformation tensor. Then, the internal nodal force (F_int) can be given by:

$${\mathbf{F}}_{{\text{int}}} { = }\frac{1}{2}{\mathbf{Tn}}l$$

(3)

where n is the normal vector of the triangular edge, l is the length of the corresponding edge, 1/2 means the edge force is evenly distributed on the two end nodes.

When two discrete bodies come in contact, the contact forces are calculated by a potential function method [50]. The distributed contact force (dF_c) between the contactor and target elements can be expressed as:

$$d{\mathbf{F}}_{c} = \left[ {{\text{grad}}\phi_{c} (P_{c} ) - {\text{grad}}\phi_{t} (P_{t} )} \right]dA$$

(4)

where P_c and P_t are the overlapping points of the contactor and target, respectively, and ϕ_c and ϕ_t is the corresponding potential function, A is the overlap area. The total normal contact force (F_cn) and tangential friction force (F_ct) between the two discrete bodies are given by:

$$\begin{array}{*{20}c} {{\mathbf{F}}_{{{\text{cn}}}} = - {\mathbf{n}}\int_{0}^{A} {{\mathbf{F}}_{c} dA} } & , & {{\mathbf{F}}_{{{\text{ct}}}} = \mu \left\| {{\mathbf{F}}_{{c{\mathbf{n}}}} } \right\|\frac{{{\mathbf{v}}_{{\mathbf{r}}} }}{{\left\| {{\mathbf{v}}_{{\mathbf{r}}} } \right\|}}} \\ \end{array}$$

(5)

where n is the normal vector of the fracture edge, v_r is the relative velocity, and μ is the friction coefficient.

The mechanical behavior of the joint elements is simulated using an intrinsic cohesive-zone approach [51]. Upon exceeding the peak strength of the material, a fracture process zone (FPZ), characterized by nonlinear behavior, forms ahead of the cracks (Fig. 3a) which albeit damaged can still transfer load. The normal and tangential tractions (σ_j and τ_j) of joint elements are functions of the normal and tangential displacement (δ_o and δ_s), respectively, as illustrated in Fig. 3b. The strain-softening response developing in the FPZ ultimately leads to the formation of new cracks via Mode I (i.e., tensile failure), Mode II (i.e., shear failure) or mixed Mode I-II [30].

Fig. 3

a Schematic of FPZ in the FDEM and b the constitutive model of joint elements. δ_op and δ_sp are the critical opening and sliding displacement, corresponding to the material tensile and shear strength (f_t and f_s), respectively. δ_or and δ_sr are the maximum opening and sliding displacement, relating to the Mode I and II fracture energies (G_IC and G_IIC), respectively. f_r is the residual shear strength

3 Water–rock coupling model for slope stability analysis: Y-slopeW

The water–rock coupling effect is essential to accurately simulate the response of the reservoir slope stability under varying groundwater conditions. In this section, the basic theory and implementation procedure of slope stability analysis under water–rock interactions are introduced. A transient seepage algorithm is proposed for the fluid field analysis inside the slope and the water–rock interactions are superimposed into the numerical simulation. The obtained transient hydro-mechanical conditions are used for the slope stability analysis with the strength reduction method.

3.1 Seepage field in slope

A seepage model is proposed to calculate the transient fluid field inside the slope under fluctuating water levels. As shown in Fig. 4, based on the unique FDEM topological connection (i.e., finite triangular elements are bonded by jointed elements), a hydro mesh (blue triangular elements with hydro nodes) is inserted into the FDEM mesh for seepage field calculation. The hydraulic field in this domain can be characterized by the hydraulic pressure at these discrete hydro nodes. Each FDEM node shared the same hydro nodes has the same pressure. To facilitate the seepage simulation, a simplification is made: the slope is divided into dry and wet zone based on the water table, and partial saturation and capillarity in the dry zone is neglected.

Fig. 4

Schematic of hydro mesh inserted into the FDEM mesh

Since the water pressure of hydro nodes are different, fluid flow may occur between these nodes. According to Darcy’s law [52], the fluid flux rate (q) along the i (i = x, y) direction due to pressure head, can be expressed as:

$$q_{i} = - k_{ij} \frac{\partial h}{{\partial x_{j} }}$$

(6)

where kij is the permeability coefficient tensor, h is the total pressure head, which can be calculated as:

$$h = p/\rho_{w} g + y$$

(7)

where p is the hydraulic pressure, ρ_w is the fluid density, g =  − 9.8 m/s² is the acceleration of gravity, and y is the elevation head.

Assuming that the pressure head field in a triangular hydro element obeys a linear distribution, the pressure head gradient in the triangular element is constant and can be expressed by [53]:

$$\frac{\partial h}{{\partial x_{i} }} = \frac{1}{S}\int\limits_{A} {\frac{\partial h}{{\partial x_{i} }}} dS = - \frac{1}{2S}\sum\limits_{m = 1}^{3} {h_{m} } n_{i}^{m} l^{m}$$

(8)

where S is area of the triangular element, h_m is the pressure head of the node m, and l^m is the length of the triangular edge opposite to node m. n_i^m = n_m·n_i is the dot product of the vector n_m and n_i, where n_m is the outer normal unit vector of the triangular face opposite to node m, and n_i is the unit vector along i direction.

Thus, combining Eqs. (6) and (8), the fluid flow rate from a triangular hydro element into the hydro node m can be calculated by:

$$Q_{m} = \begin{array}{*{20}c} { - \frac{{q_{i} n_{i}^{m} l^{m} }}{2}} & {(i = x,y)} \\ \end{array}$$

(9)

The total (net) fluid flow of node m can then be calculated as the summation of fluid flow in all surrounding hydro elements associated with node m (Fig. 4). Then the fluid pressure (p) of hydraulic node can be updated as [47, 54,55,56]:

$$p = p_{0} + MQ\frac{\Delta t}{V} - bM\frac{\Delta V}{{V_{m} }}$$

(10)

where p₀ is the pressure at the previous time step; b is the Biot coefficient (b is assumed to be 1 in this paper); M is the Biot modulus; Q is the total flow rate; and ∆t is the time increasement. V is the volume of hydraulic node domain, which is the n/3 of total volume of all connected hydro element (n is the porosity), as the volume of a hydro element is evenly distributed on three nodes (Fig. 4). V_m is the average volume and ∆V is the volume difference of the hydro node at current time step and previous time step.

3.2 Water–rock interaction on slope stability

The water–rock interaction inside the slope mainly impacts the slope stability in two main ways: (1) physicochemical effect on the physical/mechanical properties of slope materials, and (2) mechanical effect on stress conditions inside slopes [12, 13].

The physicochemical effect is the physical and chemical interactions between the water and slope material (e.g., lubrication, softening, dissolution, etc.), and is directly related to the material composition, water saturation, amongst many other factors. In this paper, two common physicochemical effects are considered. The first physicochemical interaction is the change in bulk density caused by water infiltration. The infiltration into the sliding body will increase the self-weight of the material, thus bringing about an increase in slipping force. The other significant physicochemical effect on slope stability is the wetting-induced weakening effect [27], i.e., the material strength decreases after being wetted. These physicochemical effect are considered in the numerical implementation with the following simplification [27, 57]: materials above the water table are assumed dry, and natural density (ρ_d) and natural strength properties (c_d, φ_d, f_td) are used, while those under the water table are assumed wet (or saturated) and the saturated density (ρ_s) and saturated strength properties (c_s, φ_s, f_ts) are used instead. The change in parameters occurs once the elevation of the material changes from above the water table (dry zone) to below the water table (wet zone) or vice-versa (Fig. 5a), while material weaking under repeated wet-dry cycles is ignored.

Fig. 5

Schematics of a the rock-water interaction in the slope and b its effects on shear strength

The water–rock interaction also has mechanical effects on the stress states within the slope, including static pore pressure and dynamic seepage force. Under static pressure, the reservoir water pressure applied on the submerged slope surfaces induces a stabilizing load (i.e., thrust force, f_st) on the slope. Meanwhile, the pore pressure inside the slope acting as a volume force, directly reduces the effective stress, adversely impacting the stability (Fig. 5). Mohr–Coulomb strength criterion based on the effective stress can be expressed as:

$$\tau^{^{\prime}} = \sigma^{^{\prime}} tan\varphi_{s} + c_{s}$$

(11)

where τ′ is the effective shear strength and σ′ = (σ − p) is the effective stress calculated as the difference between the stress (σ) and the pore water pressure (p).

In addition, the viscous drag of water flowing in slopes imposes a dynamic seepage force (f_d) in the direction of flow, which can be expressed as:

$$f_{d} = \rho_{w} gJ$$

(12)

where J is hydraulic gradient in the slope.

3.3 Slope stability analysis

3.3.1 Strength reduction method and safety factor

The strength reduction method (SRM) [25, 58] is widely used in numerical simulations for slope stability analysis. The gradually decreased material strength naturally reflects the rock degradation under water effect. In the traditional SRM, slopes are assumed to fail in shear mode while considering only friction parameters (i.e., cohesion and friction coefficient). However, tension failure also occurs and has significant influence on slope instability [59, 60]. Therefore, in the Y-slopeW, a developed SRM [35] based on the Mohr–Coulomb model with tensile cutoff is implemented, where both the friction parameters and tensile strength are gradually reduced until the slope becomes unstable (i.e., a failure surface develops through the slope and a sudden increase in displacement occurs), and the critical reduction factor (K_c) is considered as the safety factor (SF) of the slope (Fig. 6). It is noteworthy that the Mode I and Mode II fracture energies (i.e., G_IC and G_IIC), which control the fracturing process, should be also reduced by a reduction factor of energy releases of K² to maintain the relationship of the constitutive model.

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}l} {c_{f} = c/K} \hfill \\ {\varphi_{f} = \arctan (tan\varphi /K)} \hfill \\ {f_{tf} = f_{t} /K} \hfill \\ \end{array} } \right.} & , & {\left\{ {\begin{array}{*{20}c} {G_{{{\text{I}}f}} = G_{{\text{I}}} /K^{2} } \\ {G_{{{\text{II}}f}} = G_{{{\text{II}}}} /K^{2} } \\ \end{array} } \right.} \\ \end{array}$$

(13)

where K is the strength reduction factor. c, φ, f_t, G_I and G_II are the materials’ cohesion, internal friction angle, tensile strength, Mode I and Mode II fracture energies, respectively. c_f, φ_f, f_tf, G_If and G_IIf are the reduced cohesion, internal friction angle, tensile strength, Mode I and Mode II fracture energies, respectively.

Fig. 6

a Field observed tensile crack (after [60]). b Schematic of the SRM in Y-slopeW

3.3.2 Modeling procedure for slope stability

The modeling procedure of the slope stability analysis under groundwater effect in the Y-slopeW comprises of two modules (Fig. 7), the first deals with the seepage field (seepage module) followed by the SF calculation (mechanical module). First, the slope model generated incorporates the slope geometry with an initial groundwater condition. Then the seepage module is carried out to simulate the transient fluid field, including the change in water table level, pore pressure as well as the seepage force inside the rock slopes, subjected to the varying hydraulic boundary. The resulting water conditions are then imported into the mechanical module to evaluate the slope stability conditions, considering the water–rock interactions. During the SF calculation, the slope system first reaches an equilibrium state under the effect of gravity and water pressure (including pore pressure and seepage force) when the total kinetic energy (E_k) is less than a critical value (ε). Then the strength reduction process begins, where strength parameters are gradually decreased and re-inputted in the model for equilibrium analysis. The SF is sought when the slope model meets the critical failure criterion, i.e., becoming unstable. The explicit formulation of the model is well suited to deal with large displacements and rock-water coupling.

Fig. 7

Flowchart of the slope stability analysis under water–rock coupling effect using Y-slopeW

4 Validation tests

A series of numerical tests are conducted to verify the accuracy and robustness of the developed Y-slopeW on evaluating the fluid seepage, hydraulic pressure, and the stability analysis of rock slopes. Unless otherwise stated, the fluid parameters adopted in the validation test have a density ρ = 1000 kg/m³, and bulk modulus K_w = 2.0 GPa. In addition, wherever applicable, the internal and residual friction angle are assumed to be the same.

4.1 Water table calculation

The determination of the water table level is important to determine the water–rock interactions zone, especially when reservoir water level fluctuates. A homogeneous rectangular aquifer model (10 m × 5 m) is proposed to verify the proposed model on water table calculation, as shown in Fig. 8. Constant water heads h₁ = 5 m and h₂ = 2 m are applied on the left and right boundary, respectively, and the bottom boundary is impermeable. The permeability coefficient of the rock is k = 1 × 10^–4 m/s, and gravitational acceleration g =  − 9.8 m/s². The analytical solution of the total discharge and water table location is [61, 62]:

$$\begin{aligned} Q & = k\frac{{h_{1}^{2} - h_{2}^{2} }}{2l} \\ h(x) & = \sqrt {h_{1}^{2} - \frac{{h_{1}^{2} - h_{2}^{2} }}{l}x} \\ \end{aligned}$$

(14)

Fig. 8

a Model geometry and b simulation results of pressure distribution (Pa) and water table location

The simulated hydraulic pressure field and water table at steady-state are shown in Fig. 8b, where the simulated water table using Y-slopeW agrees well with the analytical solution. In addition, the calculated discharge Q = 1.07 × 10^–4 m³/s, which also agrees with the analytical solution (1.05 × 10^–4 m³/s).

4.2 Mechanical effect on water–rock interaction

The mechanical effects of water–rock interaction (including pore pressure and seepage force) are validated by a benchmark test [42, 63] where a rectangular strip (10 m × 4 m) is considered, with roller boundaries placed at the base and sides as mechanical boundary conditions. A sequence of three hydraulic boundary scenarios are simulated, which are: (1) initially, the water table is at the bottom of the layer (i.e., no fluid action), and the layer is subjected to gravity only; (2) then, the water table is raised to the top of the model and the pore pressure is fixed at zero at the top of the model; and (3) then a pore pressure of 0.2 MPa is applied at the base (i.e., upwards flow in the model). The parameters used in the simulation were: Young’s modulus E = 80 MPa, Poisson’s ratio ν = 0.25, porosity n = 0.1, dry density and saturated density are ρ_d = 2000 kg/m³ and ρ_s = 2200 kg/m³, respectively, permeability coefficient k = 10^–6 m/s, and gravitational acceleration g = 9.8 m/s². The analytical solution for the vertical incremental displacement at the top of the model is given by [42, 63]:

$$\begin{aligned} \Delta u_{1} & = - \frac{{\rho_{d} gH^{2} (1 + \nu )(1 - 2\nu )}}{2E(1 - \nu )} \\ \Delta u_{2 - 1} & = \frac{{(\rho_{d} + \rho_{w} - \rho_{s} )gH^{2} (1 + \nu )(1 - 2\nu )}}{2E(1 - \nu )} \\ \Delta u_{3 - 2} & = \frac{{(p_{b3} - p_{b2} )H(1 + \nu )(1 - 2\nu )}}{2E(1 - \nu )} \\ \end{aligned}$$

(15)

where p_b3 = 0.2 MPa and p_b2 = 0.098 MPa are fluid pressures at the bottom of model at stages 3 and 2, respectively.

The simulated incremental displacement fields and vectors at steady state are shown in Fig. 9. The model first settles under gravitational force, and then heaves when the water level is raised, and the heave continues upwards due to the vertical head gradient. The calculated vertical incremental displacement of the model at the top are ∆u = -1.020 × 10^–2 m, 4.09 × 10^–3 m, and 5.23 × 10^–3 m, respectively, which matches the analytical values of –1.021 × 10^–2 m, 4.08 × 10^–3 m, and 5.21 × 10^–3 m, respectively at each stage.

Fig. 9

Incremental displacement (m) of the model under the three scenarios: a water table located at the bottom; b water table raised to the top; and c pore pressure of 0.2 MPa applied at the base

4.3 Stability of a simple slope with water table

A benchmark model, that is widely adopted as a verification test in many previous publications [64, 65] and commercial software (e.g., Phase² [66], Slide [24]), is used to validate slope stability analysis in Y-slopeW. The geometry of the slope model with a linear water table is depicted in Fig. 10, where the left and right boundaries are fixed in the x-direction, while the bottom boundary is fixed in both x- and y-direction. This model is meshed into approximately 15,000 unstructured triangular elements with the average element size h = 0.25 m, and computational time step size Δt = 10^–6 s. Two cases, i.e., in the absence (case 1) and presence (case 2) of hydraulic conditions, are studied, and the fluid pressures inside the slope are calculated assuming hydrostatic conditions. The slope material parameters are: Young’s modulus E = 80 MPa, Poisson’s ratio v = 0.25, porosity n = 0.1, density ρ = 1920 kg/m³, cohesion c = 28.7 kPa, friction angle φ = 20°, tensile strength f_t = 10.2 kPa, fracture energies G_IC = 30 N/m and G_IIC = 300 N/m. The strength parameters of the slope geomaterials in natural (dry) states and wet states are assumed identical, for comparison to the previous methods [24, 66].

Fig. 10

Geometry of the benchmark model

The stress distribution (effective stress for case 2) after the slope system reaches an equilibrium are shown in Figs. 11a, b. The stresses generally follow a layered distribution, gradually increasing from top to bottom under gravity. Under the buoyance (pore pressure) effect, the effective stresses below the water table in case 2 are lower than those in case 1. The pore pressure distribution in case 2 is shown in Fig. 11c, and shows great agreement when compared to the analytical solution (Fig. 11d):

$$p = \rho_{w} gh$$

(16)

where h is the vertical distance to the water table. There is zero pore pressure above the water table.

Fig. 11

The vertical stress distribution (Pa) in a case 1 and b case 2. c The pore pressure distribution for case 2 d compared with analytical results along section-line A, B and C

After the system reaches equilibrium, the strength reduction stage is conducted. As shown in Fig. 12, the slope fails when cracks penetrate through the slope forming a through-going failure surface. In both cases, the failure surfaces are composed of shear failures at the lower part of the slope and tensile/mixed failures at the crest of the slope caused by the traction of the sliding bodies. The failure surfaces agree with those in Phase² [66], as shown in Fig. 12c. However, due to the tensile cut-off being implemented in Y-slopeW, the simulation results show a vertical tensile failure at the slope crest, which is in agreement with the experimental and in-situ observations where slopes display surface tensile cracks at the top of the slope [59, 67]. The SF of the two models can be calculated as 1.93 and 1.71, respectively, agreeing with the results (1.98 and 1.77) given by Phase². The difference is mainly attributed to the incorporation of the failure criterion.

Fig. 12

The slope failure pattern of a case 1 and b case 2 (Shear failures are colored blue, tensile failures are colored red and mixed failure are colored orange.). c the comparison of the failure surface with Phase²

5 Slope stability analysis during reservoir water fluctuation

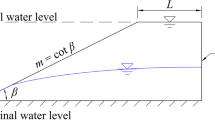
An ideal homogeneous and isotropic bank slope is designed to study the slope stability under reservoir water fluctuation using the proposed Y-slopeW. The slope geometry is shown in Fig. 13, where the slope height and angle are 25 m and 68.2°, respectively. A reservoir filling-drawdown operation is carried out, with the water level changing between an initial level of h₀ = 8 m and top level of h₁ = 20 m. The water table inside the slope is horizontal at the initial state, i.e., the same as the initial reservoir level. The mechanical left and right boundaries are fixed in the x-direction, while the mechanical bottom boundary is fixed in both x- and y-direction. The hydraulic boundary conditions are set as follows: a specific water head boundary equal to the changing reservoir water level is applied on the right bank, while the left boundary and bottom boundary are impermeable (zero-flux) boundaries. The material parameters of the slope are shown in Table 1. The impact of two important factors, i.e., water level change rate and slope permeability coefficient, on slope stability are investigated.

Fig. 13

An ideal slope model with fluctuating water level

Table 1 Mechanical parameters (subscript d and s represent dry and saturated conditions, respectively)

5.1 Effects of water level change rates

To analyze the effects of water level change rates on slope stability, three different change rates (i.e., ∆h = 0.5, 1.0 and 1.5 m/d) are utilized (Fig. 14), while the permeability coefficient is kept constant (i.e., k = 1 × 10^–6 m/s).

Fig. 14

The fluctuation of reservoir water level with time

The transient seepage fields associated with the change of reservoir level was first calculated, and the water pressure distribution and water table in the slope at different times are shown in Fig. 15. During the rising stage (Fig. 15a–c), the water level of the reservoir is higher than that in the slope, thus water seeps into the bank slope from the reservoir. The water pressure in the slope gradually increases, and the pressure increase becomes faster as the slope surface is approached. The water table also gradually rises, however, there is a delayed response with respect to the change in the reservoir level as it exhibits a concave shape (i.e., the water level is higher at the slope and lower as the water table goes inland). In fact, the faster the reservoir water level changes, the more a curved water table and more prominent delayed response can be observed. When the reservoir water level reaches and remains at the top level (Fig. 15c,d), due to the hysteresis of infiltration, pore pressure and water table in the middle and rear part of the slope keep rising until they reach a stable state. At the drawdown stage (Fig. 15e,f), water discharges to the reservoir from the slope, and the water pressure decreases gradually. The water table inclines towards the slope with a convex shape, indicating a lag in the recovery of the reservoir level. In addition, there is a sharp pressure drop near the slope surface as the water table is higher than the reservoir level, indicating that surface runoff occurs. When the reservoir water level remains at the lowest water level (Fig. 15f,g), the water pressure and water table in the slope continue to drop until it reaches stability at the reservoir water level. The change rate of the water table impacts the fluid conditions within the slope. Faster change rates result in an increased water pressure and increase in lag time in the change in the water table, which is consistent with the observation from Sun et al. [21].

Fig. 15

Variation of the fluid pressure (Pa) and water table with the different level change rate

Based on the obtained seepage field, the SF of the slopes are calculated considering the water–rock interaction (including pore pressure, seepage force, and material weakening). As shown in Fig. 16, the variation of SFs under different change rates shares similar trends. Firstly, SF increases during the infilling stage, where seepage forces point into the slope as fluid flows into the slope from the reservoir (as shown in Fig. 17), which is in favor of stability. Besides, the increasing water level provides a thrust force against the slope which aids in stability as its contribution to the SF increasement. The faster the reservoir water level changes, the greater the hydrodynamic pressure and thrust force, leading to higher SFs. The SF then gradually drops to a stable value when the reservoir level remains at the top level. The decrease of SFs is mainly attributed to the dissipated seepage forces as the water pressure equilibrates. The SF at stable state is slightly higher than the initial value caused by the combined effect of pore pressure, thrust force, and material strength weakening. During the drawdown stage of the reservoir water level, the outward seepage forces (Fig. 17b) and the elimination of thrust forces cause the SF to decrease rapidly. Faster rates of reservoir water level change cause a sharp decline in the SF and is lowest at the highest rate. Finally, when the water level drops and maintains the lowest water level, the SF gradually rises to the initial value. The overall variation of the SF shows similar trends to those presented in previous literature [18, 29, 68, 69].

Fig. 16

Variation of the safety factor with time at different change rates

Fig. 17

Seepage force vectors at h = 14 m a point into the slope under rising stage while b point out during drawdown stage. The faster the reservoir water level changes, the greater the seepage force

5.2 Effects of slope permeability coefficient on slope stability

In this section, the slope stability with different slope permeability coefficients (k = 1 × 10^–5, 1 × 10^–6, 1 × 10^–7 m/s) but constant water level change rate (1.0 m/d) is studied.

Figure 18 shows the variation of water table and water pressure with time. Similar to the observations in Sect. 5.1, the pore pressure and water table show a delayed response with respect to the change of reservoir level. During the rising and drawdown process, the water tables form concave and convex shapes, respectively. When the reservoir level is maintained at the maximum/minimum levels, the water table tends to reach a stable level over time. A larger slope permeability coefficient is associated with better permeability and thus less hysteresis to the reservoir change, which can be represented by the pore pressure and water table variation. With an increasing k, the variation of pore pressure is faster, and the water table is smoother.

Fig. 18

Variation of the fluid pressure (Pa) and water table with the different permeabilities

The variation in SF at different permeability coefficients is shown in Fig. 19. Overall, SF increases with the rise of water level at first, slowly decreasing after reaching maximum level. It continuously decreases during the drawdown stage, tending to be smoother after reaching the bottom. Regarding the hydraulic conductivities, the lower the permeability coefficient, the larger the impact on the SF variation, which are consistent with the research presented in [19] and [29]. In other words, the change rate (both increase and decrease rate) of the SF is larger with a smaller permeability coefficient, and the maximum and minimum values also occur with the smallest permeability coefficients. The reason can be explained that the seepage field inside the slope is delayed more with a lower permeability coefficient, inducing a larger seepage force, which is favorable to the slope stability during the infilling stage while unfavorable during the drawdown stage (Fig. 20).

Fig. 19

Variation of the safety factor with time at different change rates

Fig. 20

Seepage force vectors at h = 14 m a point into the slope under rising stage while b point out during drawdown stage. The lower the reservoir permeability, the greater the seepage force

6 Case study: Majiagou slope failure

With the construction of the Three Gorges Dam on the Yangtze River, the periodical water level fluctuation (145–175 m) during the reservoir operation significantly affected the geological environment and hydrological conditions in the reservoir area, inducing large deformation and instability of reservoir slopes [4, 21]. Majiagou slope is a typical unstable bank slope influenced by the construction of the Three Gorges reservoir. A 150 m long, 5–10 cm wide crack (Fig. 6a) at the slope crest developed within 3 months after the reservoir water level rose to 135 m in June 2003, and the slope deformation kept developing since then according to long-term monitoring [60]. In this section, the Y-slopeW is applied to the Majiagou slope stability to investigate the slope stability evolution under the effect of reservoir water level fluctuation.

6.1 Site description

Majiagou landslide (31°01′08′′-31°01′17′′ North latitude, 110°41′48′′-110°42′10′′ East longitude) is located on the left bank of the Zhaxi River, a tributary of the Yangtze River in the Three Gorges reservoir (Fig. 21). The long-narrow tongue-shaped landslide moves along the direction of 290° NWW, which is almost perpendicular to the river. The elevations of the slope toe and crown are 130 and 280 m, respectively, with an average slope of 15°. Surficial deposits and sedimentary bedrock are the main geologic units of the Majiagou landslide based on field investigations [19, 60]. The surficial deposit is colluvial soil consisting of gravel mixed with silty clay and the bedrock is weathered interbedded grey sandstone and purple-red mudstone of the Jurassic Suining Formation. Among them is the sliding zone composed of silty purple-red mudstone with low strength.

Fig. 21

The a location, b view, and c geological section of Majiagou landslide (after [19, 60, 70])

6.2 Numerical simulation with Y-slopeW

6.2.1 Numerical model and hydro-mechanical parameters

A numerical model of the Majiagou slope is established, having dimensions of 625 m in length and 216 m in height (Fig. 22a). The slope is simplified into sliding mass, bedrock, and sliding zone having hydro-mechanical parameters as listed in Table 2. It is worth noting that the sliding zone (0.5–0.8 m in thickness) is relatively small in comparison to the scale of the model, thus it is modelled as a group of joint elements that possess weaker strength properties.

Fig. 22

a Numerical model of Majiagou landslide and b annual water level fluctuation of the Three Gorges reservoir (after [71])

Table 2 Parameter of the Majiagou landslide (after [19, 60]) (subscript d and s represent dry and saturated conditions, respectively)

The left and right mechanical boundaries are fixed in the x-direction, while the bottom mechanical boundary is fixed in both x- and y-direction. The hydraulic boundary conditions are set as: a specific water head boundary equal to the changing reservoir level (145–175 m) is applied on the left bank, and a prescribed water head h = 242 m is applied on the right bank, while the bottom boundary is impermeable (zero-flux) boundaries. The periodical fluctuation of the Three Gorges reservoir (Fig. 22b) is expressed as a piecewise function [Eq. (17)] which is utilized to generalize the water fluctuation in the numerical simulation into 5 stages: (1) impound stage (0.5 m/d), (2) high-level stage (normal level), (3) slow drawdown stage (− 0.1 m/d); (4) rapid drawdown stage (− 0.4 m/d); (5) low-level stage (flood control limit level).

$$h(t) = \left\{ {\begin{array}{*{20}l} {145 + 0.5t} \hfill & {0 \le t < 60} \hfill \\ {175} \hfill & {60 \le t < 120} \hfill \\ {175 - 0.1 \cdot (t - 120)} \hfill & {120 \le t < 220} \hfill \\ {165 - 0.4 \cdot (t - 220)} \hfill & {220 \le t < 270} \hfill \\ {145} \hfill & {270 \le t < 365} \hfill \\ \end{array} } \right.$$

(17)

6.2.2 Simulation results and discussion

The transient seepage field and water table response to the water level fluctuation are shown in Fig. 23. It is noted that the initial condition is obtained by a steady-state analysis in which the reservoir level is maintained at 145 m and water head at the slope right bank is 242 m. During the rising stage (0–60 d), water seeps into the slope, and pore pressures inside the slope gradually increases. However, the pore pressure variation shows a delayed response, where pressure increases faster at the slope front edge than that in the middle or rear part of the slope. Meanwhile, the water table gradually rises, and a lag is observed in the change of reservoir level, showing a concave shape. Then when the water level maintains at 175 m (60–120 d), as the seepage delay inside the slope, the water pressure and water table in the middle and rear part of the slope increases at first until it reaches a steady state. During 120–220 d period, water flows from the slope to the reservoir when the reservoir level decreases, causing a gradual decrease in pore pressure in the slope. The water table also descends gradually and shows a convex form due to the hysteresis effect. Then with the drawdown speed increase (220–270 d), a quicker decrease of water pressure and water table can be observed. Meanwhile, due to the significant delay between the slow seepage flow and the rapid reservoir level change rate, surface runoff can be observed where the water table at slope front is higher than the reservoir water level. Finally, when the reservoir water level reaches and remains at the lowest water level (270–365 d), the water pressure and the water table in the slope first decrease and finally reach stability.

Fig. 23

The variation of pore pressure (Pa) and water table in Majiagour slope with time

To better illustrate the delayed response of the seepage process, the variation of water level at three monitoring sections along the slope are shown in Fig. 24. The water level at the monitoring sections has a similar but delayed variation in response to the reservoir level change. The water level at section A, located at the front edge of the slope, changes almost synchronously with the reservoir water level, while the water level at section B and section C show an obvious delayed response to the changed water level (about 1 and 2 months, respectively), confirming that the farther away from the reservoir, the more the delay in response. Meanwhile, the water fluctuation has a more significant impact on the front edge, while less impact to the middle and rear part, for example, the water fluctuations at section A is 17.5 m, while only 7 m at C. The simulated groundwater level variation inside the slope shows similar trends with the site observation from Zhang et al. [60].

Fig. 24

The variation of the water level at monitoring sections versus reservoir water level

The impact of the change in seepage forces brought about by the change in seepage field is shown in Fig. 25. At the initial stage (t = 0 d), seepage forces point toward the reservoir. When the reservoir water level rises (0–60 d), reservoir water starts flowing into the toe of slope, and seepage forces herein direct into slope and have an increased magnitude. However, the seepage forces in the middle and crest part remains outwards. Then seepage forces at the slope toe gradually dissipates when the water level remains at the high level (60–120 d). This is followed by a drawdown stage (120–220 d), where water flows into reservoir and seepage forces significantly change towards the slope. The magnitude of the seepage forces at the toe continue to increase during the continued drawdown (220–270 d) bringing about the largest seepage force (Fig. 25j). Following which, the seepage forces gradually decrease and return to their initial state as the water level remains at 145 m (270–360 d). It is worth noting that the variation of seepage forces affected by the reservoir water level fluctuation mainly occur at the front part of the slope, while this variation is less to almost negligible inlands of the slope (i.e., the middle and rear parts). These findings are consistent with the variation of the pressure field.

Fig. 25

Variation of the seepage force vector in the Majiagou slope

The fluctuations of the reservoir water level profoundly affect the slope stability. On the one hand, it changes the seepage field of the slope (e.g., pore pressure, seepage force and thrust force), leading to the stress field redistribution. On the other hand, the material strength is weakened under the effect of groundwater. Figure 26 shows the SF variation of the Majiagou slope as the reservoir water level changes. In general, SF increases with the rise of water level at first, slowly decreasing after reaching a maximum level. Then the SF further decreases with drawdown, but gradually increases to a constant value after reaching the bottom. It is noted that a rapid decrease of SF and the lowest SF value (i.e., most dangerous situation) occurs during the rapid drawdown stage, which is also confirmed by the large displacement rate (black box in Fig. 26) recorded by the field displacement monitoring [60]. This highlights the fact that rapid drawdown is extremely detrimental to slope stability. These findings are consistent with the observation of literature [18, 29, 68, 69].

Fig. 26

Variation of the SF with time. The black box indicates the area showing the largest displacement rate

7 Discussions

Extensive evidence indicate that fluctuating water levels have significant adverse effects on the hydrological conditions, stress condition and geomaterials properties in the reservoir area, inducing reservoir slope failures [4, 6, 8]. Our proposed model (Y-slopeW) provides a gateway to investigate the slope failure mechanism and slope stability evolution when the reservoir water level fluctuates. The significance of this model is that transient seepage field and water–rock coupling effect are properly incorporated into FDEM framework to investigate the slope stability analysis. In addition to benchmark tests, the simulation results of the actual slope in the Three Gorges area also demonstrate the robustness and accuracy of the proposed model.

Results show that the water level fluctuations have a profound effect on the hydrological conditions inside a slope and therefore affect slope stability. The varying static/dynamic fluid pressures and material physical/mechanical properties change under water–rock coupling are the main factors that affect the slope stability. According to the ideal slope model and practical Majiagou slope, a similar SF evolution trend can be observed: SF increases in the infilling stage and decreases during the drawdown stage, and stabilizes when the water table is at the top/bottom level, which is consistent with the results found in existing literature [18, 29, 68, 69]. Additionally, a rapid drawdown is critically unfavorable to the slope stability, which agrees with the field observation of large landslide deformation [60, 68, 72].

The change in water level and slope permeability coefficient also play an important role in determining the stability of a slope. Sensitivity analysis, on these two important factors, indicated that the seepage field variation inside the slope shows a delayed response with respect to the reservoir water change, and a higher water change rate and a lower permeability coefficient relate to a more delayed response of the seepage field. These findings are consistent with existing observations [21, 60]. The pressure gradients in the delayed seepage field generate significant seepage force (hydrodynamic pressure) inside the slope: the inward seepage force during the infilling stage is conducive to the slope stability while the outward seepage force during drawdown stage is unfavorable to slope stability. The minimum SF (i.e., the most dangerous hydraulic condition) occurs during the descending period of the water level with a fast change rate or low permeability coefficient, which is accordant with the results of some scholars [29, 60, 68, 72]. Therefore, not only hydrostatic pressure but also seepage forces should be properly considered in slope stability analysis.

The findings in this paper are potentially useful in practical application for reservoir slopes in the Three Gorges project, as well as projects of similar scale. The remarkable, 30-m annual fluctuation in the reservoir water level poses a significant threat to slope stability in this area, and the slope stability obviously decreases under a higher drawdown rate. However, in the case of power generation or flood control, the Three Gorges Reservoir always releases water in a very short timespan. In the 1954 flood for instance, the maximum drawdown of the water level in front of the dam was 17 m with a velocity of 1.2 m/d. This kind of large range and rapid decrease of water level is critical and may pose potential cause of slope instability. Therefore, a reasonable drawdown rate should be determined according to the acceptable risk level, and comprehensive risk mitigation methods should be proposed/employed considering water level control and drainage measures. In addition, the surface runoff and large displacement may occur during the rapid drawdown stage, which potentially propose an early warning to the slope instability.

However, it is noteworthy that slope stability with fluctuating water levels is quite complicated, and depends on the slope geometry, material properties, hydraulic parameters, water level change pattern amongst many other parameters. The conclusions above only pertain to the special cases with specific assumptions in this paper. For example, the increase of SF during the rising is consistent with the many previous work [4, 18, 60], while some researcher observed an opposite trend [7, 73]; In addition, the continuous decline of SF during the drawdown is consistent with the results in literature [18, 29, 68, 69], but somewhat different from the result of some scholars [7, 25, 74], where the lowest SF occurs at a critical reservoir level (not at the highest or the lowest height). The explanation is that the SF is determined based on the combined effect of pore-pressure, seepage force, thrust force and material weakening effect [4, 7, 25, 74]. The rising of the water level will increase the pore pressure of the slope and reduce the strength of the submerged rock mass, which weakens the stability of the slope. At the same time, external loading due to the water pressure on the slope surface, as well as the inward seepage forces will strengthen the stability of the slope. A trade-off between these two factors influences the SF. In addition, some simplifications made in this paper should be improved in further work, e.g., the material parameters should vary with time in long-term cyclical fluctuation conditions, and the saturated–unsaturated flow model should be applied.

Specifically, due to the inheritance of the FDEM, one key advantage of the proposed method is the simulation of entire slope failure processes, from initiation, transport to deposition [35]. The post-failure behavior is out of the scope of this paper, however, the rock fall, deposition, as well as the induced surge is very interesting topic and deserve more attention in our future work.

8 Conclusions

Instability of the reservoir slope under fluctuating water level proposed a major threat to the safety of human life and engineering infrastructure. This paper develops a novel Y-slopeW model to better understand the failure mechanism and stability evolution of the reservoir slopes while honoring and considering the exigent water–rock coupling effect. A major significance in this work is the transient fluid seepage algorithm, which considers fluid flow in both rock matrix and cracks, enabling the calculation of the seepage field with varying water level boundary conditions. Meanwhile, water–rock coupling effect (including physicochemical effect and mechanical effect) are properly incorporated into FDEM to evaluate the slope stability under varying seepage conditions. The proposed Y-slopeW is calibrated by numerical tests and implemented to a practical project (Majiagou slope) in the Three Gorges reservoir.

The outcome of this work shows the profound effect of water level fluctuations, more specifically, the varied seepage field has on the hydrological conditions inside a slope and in turn the slope stability analysis. This variation affects the static/dynamic fluid pressure and material physical/mechanical properties change under water–rock interactions, thus affecting the slope stability. Particularly, the delayed response of seepage field variation inside the slope with respect to the reservoir water change induces significant seepage force (i.e., hydrodynamic pressure), which should be properly considered in the slope stability analysis. The inward seepage force during the infilling stage is conducive to the slope stability while the outward seepage force during drawdown stage is unfavorable to slope stability. Generally, SF increases in the filling stage and decreases in the drawdown stage, while it tends to a stable value at the top/bottom level. In particular, rapid drawdown is critically the most unfavorable condition to the slope stability.

The study of the practical Majiagou slope in the Three Gorges project proposes a suggestion to practical application for the reservoir slopes, where comprehensive risk mitigation method should be proposed by considering water level control, and drainage measures. Periodic geological inspections (e.g., surface runoff and displacement monitoring) could also be helpful to pose early warnings, and accordingly, timely appropriate countermeasures can be taken to avoid hazards.