1 Introduction

Due to stringent limitations of the ground in practice, buildings are often constructed on or near native or engineered slopes [1, 7]. Investigations focused on the presence of slopes can ineluctably have an adverse effect on the ultimate bearing capacity of strip footings. Analytical solutions have been reported by Kusakabe et al. [19], Leshchinsky and Ambauen [20], Meyerhof [28] and Yang et al. [44] to estimate the ultimate bearing capacity of foundations placed atop slopes. Associated with bearing capacity, the corresponding failure mechanism was also observed by Georgiadis [7] based on finite element (FE) analyses. Leshchinsky [21] investigated the bearing capacity and the associated failure mechanism of a strip footing resting on a slope considering the influence of the slope angle, footing width and soil strength properties. Zhou et al. [55, 56] quantitatively defined the threshold between the bearing capacity and slope stability issues and presented detailed design charts under static and seismic conditions. In reality, natural soils are often deposited in layers [10]. Recently, more attention has been drawn to the bearing capacity of foundations placed on the top of two-layered soil slopes. Investigations have been conducted to estimate the ultimate bearing capacity of a layered soil by experiments and numerical modeling [2–4, 6, 13–15, 23, 29, 30, 34, 40, 53, 57]. Merifield et al. [30] investigated the bearing capacity of a rigid footing on horizontal ground composed of two-layered clay. Wu et al. [39] and Xiao et al. [41] conducted a series of parametric studies to investigate the interaction effects of geometrical parameters and soil properties on the ultimate bearing capacity and failure mechanism for footings adjacent to two-layered soil slopes.

Prior works have offered significant guidance to evaluate the ultimate bearing capacity of strip footings resting on two-layered slopes under different situations through deterministic analysis. However, it has been confirmed, in a large proportion of engineering cases, that soil properties such as the shear strength parameters are uncertain with spatial variations [31, 37, 58]. The bearing capacity of rigid footings resting on the top of single-layered slopes considering the spatial variability of soils has received attention. Luo and Bathurst [27] investigated the influence of single-layered soil parameters and geometric conditions on the mean bearing capacity and its variability considering the spatial variability of purely cohesive soils. Halder and Chakraborty [11, 12] quantified the variation trends of bearing capacity in spatially variable soils with various slope angles. They quantified the bearing capacity reduction for footings constructed on the top of a single-layered slope. However, prior assessments of bearing capacity do not involve two-layered soil slopes. Meanwhile, few studies have revealed how the spatial variability of random soil quantitatively affects the interaction of influential factors.

The objective of this paper is to investigate the coupled effect of the spatial variability of undrained shear strength on the ultimate bearing capacity of a rigid footing on a two-layered soil slope with idealized geometry. The analyses are carried out by using a random adaptive finite element limit analysis (RAFELA) [18]. Influential factors, including geometric conditions (e.g., normalized slope height, slope angle), soil parameters (e.g., undrained shear strength) and the soil spatial correlation parameters (i.e., the coefficients of variation (COVs) and the ratio of vertical and horizontal correlation lengths (θy/θx) for two-layered soils), are analyzed to reveal the relationship between the ultimate bearing capacity and the coupled influence of soil parameters. Finally, the sensitivity of the affecting parameters as well as their interaction effects are discussed by adopting a multivariate adaptive regression splines (MARS) procedure.

2 Problem definition and validation

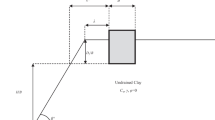
A general layout of the model is illustrated in Fig. 1. A rigid rough footing of width B is positioned adjacent to a two-layered soil slope with height H and angle β. The top layer of clay with undrained shear strength cu1 is underlain by a clay layer with cu2. The value of slope height is equal to that of the thickness of the top layer. The ultimate bearing capacity qu for a rigid footing can be described as [30]:

$$q_{{\text{u}}} = c_{{{\text{u}}1}} \times N_{{\text{c}}} = f\left( {\frac{H}{B},\beta ,\frac{{c_{{{\text{u1}}}} }}{{c_{{{\text{u2}}}} }}} \right)$$
(1)

where qu = average limit pressure under the footing; cu1 = undrained shear strength of the upper layer; cu2 = undrained shear strength of the lower layer; B = footing width; H = slope height; and β = slope angle. The interface between the rigid footing and the soil is assumed to be rough in this study [14]. The bottom and side boundaries are fixed in both the horizontal and vertical directions, whereas vertical displacement is allowed for the side boundaries. To ensure negligible boundary effects, the boundaries are placed far enough away from the footing.

Fig. 1
figure 1

Schematic of the model

Full size image

Owing to acting as a rigorous analytical solution, Finite Element Limit Analysis (FELA) combines the finite element method (FEM) with the limit analysis theory to calculate the collapse load of a structure. To investigate the bearing capacity of footings on horizontal ground [36, 51] and footings on slopes [7, 21, 56], an upper-bound (UB) LA has commonly been employed in prior investigations. The assumption with perfectly plastic soils is proposed, in which an associated flow rule is obeyed for the upper-bound theorem of plasticity. With reference to the rule, the power dissipated for a kinematically admissible velocity field equals that dissipated by external loading, which enables determination of an upper bound for the ultimate bearing capacity and failure geometry [36]. In this study, numerical analyses are carried out with UBLA, and the method is rigorously based on plasticity theorems and has been successfully used in prior investigations [1, 16, 17, 22, 39, 42, 45, 51].

To verify the accuracy of the established model, the bearing capacity of a footing on two-layered cohesive soil slopes (Nc) predicted in this study is compared with the results presented in prior investigations. A series of comparisons between the proposed method and the undrained solutions of Xiao et al. [41], Kalourazi et al. [15] and Izadi et al. [14] are shown in Fig. 2, and the corresponding parameters are shown in Table 1. An agreement in terms of Nc or Nγs/NγLG is found between the calculated results and prior investigations for footings adjacent to two-layered slopes, as shown in Fig. 2.

Fig. 2
figure 2

Comparison of bearing capacity with the results from prior investigations: a Xiao et al. [41]; b Kalourazi et al.[15]; c Izadi et al. [14]

Full size image
Table 1 Parameters of ultimate bearing capacity analysis of a rigid footing on a two-layered soil slope for calibration [14, 15, 41]
Full size table

3 RAFELA modeling

The undrained shear strength of two-layer soils is considered with anisotropic spatial variability for probabilistic investigations of the bearing capacity of footing on slopes. Following previous studies [8, 9, 23,24,25,26, 31], it is assumed that the undrained shear strength in this study obeys a lognormal distribution and can be expressed as follows:

$$f\left( x \right) = \frac{1}{{x\sigma_{\ln x} \sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}\left( {\frac{{\ln x - \mu_{\ln x} }}{{\sigma_{\ln x}^{2} }}} \right)^{2} } \right]$$
(2)

where the mean \(\mu_{\ln x}\) and standard deviation \(\sigma_{\ln x}\) meet:

$$\mu_{\ln x} = \exp \left( {\mu_{\ln x} + \frac{{\sigma_{\ln x}^{2} }}{2}} \right)$$
(3)
$$\sigma_{\ln x} = \sqrt {\exp \left( {2\mu_{\ln x} + \sigma_{\ln x}^{2} } \right)\left[ {\exp \left( {\sigma_{\ln x}^{2} } \right) - 1} \right]}$$
(4)

The mean and standard deviation of undrained shear strength can be described in terms of COV, a dimensionless coefficient that depicts the inherent variability of undrained shear strength in a random field. It can facilitate designers to develop an appreciation for the probable range of variability inherent in the overall evaluation of common design soil properties and therefore identify atypical geotechnical variabilities [8, 31]:

$${\text{COV = }}\frac{{\sigma_{\ln x} }}{{\mu_{\ln x} }}$$
(5)

In a random field, soil properties spatially vary, and the correlation in space is considered. To incorporate the spatial variability of soil, the Karhunen–Loeve (KL) expansion is adopted by identifying a set of orthogonal basis functions that can capture the variability of the field using a small number of terms. The spatial correlation structure is represented by a parameter called “correlation length (θ)” [8, 31], which is a measure of the distance within which the properties are noticeably correlated. A larger θ implies that the fluctuation of the soil property is spatially slower and the soil is more homogeneous, whereas a smaller θ implies that the soil property fluctuates more rapidly in the space and the soil is more homogeneous. To describe the fluctuation of anisotropic random fields, two important terms, the horizontal and vertical correlation lengths (θx and θy, respectively), are introduced. In the context of K-L expansion, a 2D normally distributed random field H(x, y) can be discretized based on the spectral decomposition of its cocorrelation function p[(x1, y1), (x2, y2)]. This field is generally expressed as a truncated series as

$$H\left( {x,y} \right) = \hat{H}\left( {x,y,\theta^{\prime}} \right) = \mu^{\prime} + \sum\limits_{j = 1}^{M} {\sigma^{\prime}\sqrt {\lambda_{j} } } f_{j} \left( {x,y} \right)x_{j} \left( {\theta^{\prime}} \right)$$
(6)

where \(\hat{H}\left( {x,y,\theta^{\prime}} \right)\) represents the simulated random field of H(x, y), θ′ denotes the coordinate in the decomposited outcome space; u′ and σ′ represent the mean and standard deviation of the random field, respectively; fj(x, y) and λj denote the eigenfunctions and eigenvalues of the correlation function p[(x1, y1), (x2, y2)] obtained by solving the homogeneous Fredholm integral equation of the second kind [32, 33]; \(x_{j} \left( \theta \right)\) is a set of uncorrelated random variables with zero mean and unit variance, and M represents the number of K–L expansion terms.

Phoon and Kulhawy [31] comprehensively investigated the effect of the correlation length and summarized a potential range of correlation lengths. To verify an accurate calculation, a sensitivity analysis is performed with adequate Monte Carlo simulations adopted in the discretization, as shown in Fig. 3. Therefore, a total of 1000 Monte Carlo simulations were adopted in each analysis.

Fig. 3
figure 3

Effect of the number of realizations on the bearing capacity factor statistics (baseline case): mean bearing capacity factor and variation in the COV of the bearing capacity factor

Full size image

4 Parametric analysis

4.1 Analysis of deterministic variables

To investigate the bearing capacity of a rigid footing on the top of cohesive soil slopes, a parametric study with a uniform soil domain is presented, covering four geometric parameters, namely, the normalized undrained shear strength Nsu, normalized slope height H/B, slope angle β and normalized footing distance from the crest of the slope λ (footing offset distance/footing width). The UB bearing capacity design chart curves for deterministic analyses are presented in Fig. 4. Three failure mechanisms are observed, including face failure, toe failure and overall slope failure [55]. For the face failure mode and toe failure, failure slips extend to the slope face and toe, respectively, and uniform soils are observed where an asymmetrical rigid wedge occurs directly beneath the footing. However, the slope failure mode, without showing distinct active and passive wedges, is attributed to the slope stability mechanism rather than the bearing capacity issue. The corresponding failure modes are depicted with design chart curves, in which cases serve as the baseline case (i.e., red dots) for the numerical results that appear later in the paper.

Fig. 4
figure 4

Deterministic failure modes of different cases changing with a H/B and b cu1/cu2 (the red dots represent the cases used in this study)

Full size image

4.2 Stochastic analysis

To investigate the influence of affecting parameters on the bearing capacity, a certain parameter is changed from the baseline case (as shown in Table 2), while all other parameters are held constant. Equation 7 is used to calculate the bearing capacity factor Nc for each random field (i.e., each Monte Carlo simulation) as follows [27, 43]

$$N_{{{\text{c}},i}} = q_{{{\text{u}},i}} /\mu_{{\text{c}}}$$
(7)

where qu,i is the ultimate bearing capacity of the rigid footing and i is the counter for the random field realization. The qu value is taken as 0 when slope failure occurs.

Table 2 Soil parameters used in the present study
Full size table

The ratio of the vertical and horizontal correlation distances θy/θx is maintained to represent the anisotropic property of the random field with various coefficients of variation of the soil cohesion COVNc. The COVs of the cohesion in the two layers vary from 0.1 to 0.5, and θy/θx ranges from 0.1 to 0.25 [27, 31]. In this study, the ratio of shear strength from the upper layer and lower layer clay cu1/cu2 varies from 0.5 to 2, which covers most cases in practice [30]. Note that the ratio cu1/cu2 is less than 1, corresponding to the case of a soft clay layer resting over a stiff clay layer, whereas cu1/cu2 is greater than 1 corresponding to the reverse. The value of H/B varies from 3 to 5, corresponding to four different values of cu2/γB, namely, 1, 2, 3, and 4. Following a previous study [7], three slope angles of β = 1:2, 1:1 and 2:1 are taken into consideration. The ranges of the parameters used in nondimensionalizing are γ = 20 kN·m3 and B = 1 m, θx = 10 m and cu1/γB = 2.

4.2.1 Effect of c u1/c u2

Figure 5 presents the effects of various undrained shear strength ratios cu1/cu2 and coefficients of variation of cohesion of the upper layer soil COVcu1 on the mean ultimate bearing capacity factor μNc and coefficients of variation of cohesion COVNc. The deterministic values of the bearing capacity factor for the three cases are shown as dashed lines in Fig. 5a (i.e., Nc,det = 3.44). In general, the presence of spatial variability reduces the stability number compared to its deterministic value. In probabilistic analysis, any consideration of cu1/cu2 yields a linearly decreased μNc with an increasing COVcu1, as shown in Fig. 5a. In contrast, an increasing COVNc for four curves (i.e., cu1/cu2 = 0.5, 1, 1.5 and 2) is captured as COVcu1 increases. Specifically, the results of μNc are similar when a small value (e.g., cu1/cu2 = 0.5, 1 and 1.5), while a noticeable difference for the case with cu1/cu2 = 2 is captured in comparison to these three cases. Similar to μNc, the values of COVcu1 with cu1/cu2 = 0.5, 1 and 1.5 exhibit an insignificant difference, while a larger COVcu1 is observed when cu1/cu2 = 2, as presented in Fig. 5b.

Fig. 5
figure 5

Variation of mean and COV of bearing capacity factor (μNc and COVNc, respectively) with COV of undrained shear strength of upper layer soil COVcu1 for different cu1/cu2 (cu1/cu2 = 2 is the baseline case): a mean of Nc; b COV of Nc

Full size image

The COV of the lower layer soil (i.e., COVcu2) and cu1/cu2 also influence the variability in Nc values. Figure 6a presents the relationships of μNc with varied COVcu2 for different cu1/cu2, and the corresponding change in COVNc is shown in Fig. 6b. In comparison with the effect of COVcu1, the values of μNc and COVNc are insensitive to COVcu2 when cu1/cu2 = 0.5, 1 and 1.5. For the case with cu1/cu2 = 2, a monotonically reduced μNc and an increased COVNc are attained as COVcu2 increases.

Fig. 6
figure 6

Variation of μNc and COVNc with COV of undrained shear strength of lower layer soil COVcu2 for different cu1/cu2 (cu1/cu2 = 2 is the baseline case): a mean of Nc; b COV of Nc

Full size image

In conventional deterministic design, the failure can be defined as the bearing capacities of a footing being less than the corresponding deterministic values based on the uniform soil strength Nc,det [8], and the value divided by a factor of safety (FS) is used to compute the allowable bearing pressure. Therefore, the value of P (Nc,i < Nc,det/FS) is of practical interest to describe the failure probability Pf. The change in the magnitude of Pf with the change in FS with various cu1/cu2 for COVcu1 and COVcu2 is shown in Fig. 7. For FS = 1, the failure probability increases from 60 to 80% when cu1/cu2 increases from 0.5 to 2, indicating a similar risk of failure. When FS = 2 and 3, a significant reduced factor is captured for cu1/cu2 of 0.5, 1 and 1.5, and a larger FS is needed for cu1/cu2 of 2. A relatively larger probability of failure for a larger cu1/cu2 results from the relatively larger COV of the bearing capacity factor.

Fig. 7
figure 7

Relationship between Pf = P (Nc,i < Nc,det/FS) and cu1/cu2 with various FS considering a COVcu1 and b COVcu2

Full size image

Prior investigations have shown that the soil strength has a paramount influence on the bearing capacity that can be attained on two-layered soil slopes, as it governs the failure mechanism that occurs [39, 41, 59]. In stochastic analysis, the spatial soil variability may result in variation of ultimate bearing capacities and potential failure mechanisms. To reveal the variation in the bearing capacity factor Nc when considering spatial soil variability, the failure mechanism of the footing on two-layered slopes is analyzed for various cu1/cu2. In probabilistic analysis, slip surfaces in random soil may develop several paths in weak soil instead of a single shear path [8, 9, 37]. The slip surfaces of various realizations are markedly different from one another because of the difference in the spatial patterns of random soil. In uniform soil, a failure slip extending to the slope face is observed (i.e., face failure mode) with Nc of 3.44 (see Fig. 4b), and an asymmetrical rigid wedge occurs directly beneath the footing. In random soil, Fig. 8a and Fig. 8b selectively show the failure planes for footings with bearing capacity factors of 1.80 and 3.04 when cu1/cu2 = 0.5, which both involve face failure. Failure mechanisms comparable to those in the deterministic case are captured. With reference to a comparable failure mechanism and slip surface length, the corresponding bearing capacity is reduced due to the soil strength along the slip surface. For cu1/cu2 of 2, Fig. 8c also shows that face failure occurs with a bearing capacity factor of 1.81. Figure 8d illustrates that a shear surface extends far from the back corner of the footing (i.e., slope failure mode), which leads to a small resistance of the soil and thus a significantly reduced bearing capacity factor of 0.64. This is because the self-weight of the soil, acting as an external force, causes the failure of the slope rather than the contribution of the bearing capacity. Therefore, both the failure mechanism and the soil strength along the slip surface depend on the spatial pattern of the random field and determine the bearing capacity.

Fig. 8
figure 8

Slip surfaces for different realizations of foundations with bearing capacity factors: a cu1/cu2 = 0.5; b cu1/cu2 = 2

Full size image

4.2.2 Effect of H/B

The effects of COVcu1 and the normalized slope height H/B on the mean bearing capacity μNc and COVNc are presented in Fig. 9a, b, respectively. The deterministic results are also presented as a reference (i.e., Nc, det = 3.44 for H/B = 3, 4 and 5).The three curves have a dip of μNc with increasing COVcu1, especially for the case with H/B = 5, as shown in Fig. 9a. For COVNc, a linear increase in COVNc with increasing COVcu1 is captured for any normalized slope height, as presented in Fig. 9b.

Fig. 9
figure 9

Variation in μNc and COVNc with COVcu1 for different normalized slope heights (H/B = 4 is the baseline case): a mean of Nc and b COV of Nc

Full size image

A parametric study for lower layer soil is also performed to evaluate COVcu2 = 0.1, 0.2, 0.3, 0.4 and 0.5 for H/B of 4, 5 and 6. The effect of COVcu2 and H/B on μNc and COVNc is shown in Fig. 10. When H/B is large (i.e., H/B = 6), the largest influence of lower layer soil variability is observed. Larger H/B values correspond to the largest relative decreases in μNc, and then the increases in COVNc are also most pronounced. In contrast, a smaller H/B causes μNc and COVNc to be less sensitive to changes in COVcu2. The relationship of Pf of various H/B with FS = 1, 2 and 3 is shown in Fig. 11. It is interesting to see that for H/B = 4, 5 and 6 with different COVcu1 and COVcu2 give similar probability of design failure when FS = 1. For FS = 2 and 3, the results demonstrate that a footing with a large H/B has a larger probability of failure.

Fig. 10
figure 10

Variation in μNc and COVNc with COVcu2 for different normalized slope heights (H/B = 4 is the baseline case): a mean of Nc the b COV of Nc

Full size image
Fig. 11
figure 11

Relationship between Pf = P (Nc,i < Nc,det /FS) and H/B with various FS considering a COVcu1 and b COVcu2

Full size image

4.2.3 Effect of β

Figure 12a shows the change in μNc and COVNc with COVcu1 for various slope angles β. The deterministic results are also presented as a reference (i.e., Nc, det = 2.72, 3.44 and 4.17 for β = 2:1, 1:1 and 1:2). As expected, consideration of larger values of COVcu1 resulted in increased μNc. The largest proportional decrease in μNc occurs for steeper slopes. As shown in Fig. 12b, a trend of linear increase in COVNc is represented for all slope angles in this study. However, a larger slope angle is less sensitive to changes in COVcu1.

Fig. 12
figure 12

Variation of μNc and COVNc with COV of COVcu2 for different slope gradients, β (β = 1:1 is the baseline case): a mean of Nc b COV of Nc

Full size image

To investigate the influence of COVcu2 and slope angle β, the change in μNc and COVNc for β = 1:2, 1:1 and 2:1 with various COVcu2 is shown in Fig. 13. Similar to the effect of the upper layer soil variability, a monotonous decrease in μNc and an increase in COVNc are also caused by increasing COVcu2 under any consideration of β. Notably, the influence of COVcu2 on μNc is more significant for a small slope angle (e.g., β = 1:2), and a large slope angle causes slope μNc to be less sensitive to changes in COVcu2. The divergence of COVNc for these three curves is not pronounced, showing a lower sensitivity to β with different COVcu2. The relationship of Pf of various β with FS = 1, 2 and 3 is presented in Fig. 14. With different β, a similar probability of design failure is captured when the values of FS are the same. For FS = 1, the failure probability increases from 55 to 80% when COVcu1 increases from 0.5 to 2, indicating a similar risk of failure. In contrast, the effect of COVcu2 could be neglected. When FS = 2 and 3, a significant reduced Pf is captured for various COVcu1 and COVcu2.

Fig. 13
figure 13

Variation in μNc and COVNc with COVcu2 for different slope gradients, β (β = 1:1 is the baseline case): a mean of Nc the b COV of Nc

Full size image
Fig. 14
figure 14

Relationship between Pf = P (Nc,i < Nc,det/FS) and β with various FS considering a COVcu1 and b COVcu2

Full size image

5 Discussion

The aforementioned analyses reveal that the coupling effects of the soil spatial correlation parameters (COVcu1, COVcu2, θy/θx), soil properties (cu1/cu2) and geometric parameters (H/B and β) on the ultimate bearing capacity are distinct and complex. Investigations of the sensitivity of each parameter on the mean μNc and coefficient of variation of the bearing capacity factor COVNc are of great importance because they provide practical guidance for the footing placed on a two-layered slope when considering spatial soil variability.

5.1 Sensitivity analysis

In this study, a sensitivity analysis using multivariate adaptive regression splines (MARS) [5, 35, 38, 50, 54] is conducted to quantify the effects of soil properties and geometrical parameters on the bearing capacity factor considering spatial soil variability. MARS is an algorithm for mathematically describing the relationship between a set of input and output variables, which has thus been successfully applied in various geotechnical engineering applications [47–49, 52]. Without undertaking a training process or specific assumptions, a simple model can be produced by a MARS model that can be easily interpreted and analyze the relative importance of each parameter. The end points of the segments (splines), which are called knots or nodes, mark the end of one piecewise set of data and the beginning of another. The resulting piecewise curves, known as basis functions (BFs), allow for bending, thresholds and other nonlinear feature. The data partition of this study is conducted through random approach, 75% of the data were used for training and 25% for testing, the subsets for training and testing are statistically consistent and therefore represent the population. This algorithm can mathematically identify optimal variable transformations and complex interactions between the output and high-dimensional input variables, which could be employed in this study to illustrate the complex response between the bearing capacity and spatial clays.

Six affecting parameters x1 (COVcu1), x2 (COVcu2), x3 (H/B), x4 (β), x5 (cu1/cu2) and x6 (θy/θx), as mentioned above, are selected as input variables, and the output variables are the mean and coefficient of variation of the bearing capacity (μNc and COVNc). Figure 15 shows the relative importance of each input variable estimated by adopting the MARS procedure. The relative importance describes the contribution and the degree of sensitivity of each input variable to μNc and COVNc [47]. Notably, x4 (β) and x1 (COVcu1) are the most important variables for the values of y1 (μNc) and y2 (COVNc), respectively, in which the index of relative importance (IRI) is equal to 1.0. Correspondingly, the following variables for y1 (μNc) are x1 (COVcu1), x3 (H/B), x2 (COVcu2), x5 (cu1/cu2) and x6 (θy/θx), with IRIs of 0.63, 0.55, 0.36, 0.27 and 0.15, respectively. For the coefficient of variation of the bearing capacity COVNc, the descending order is presented with reference to the importance of contributions as follows: x3 (H/B), x2 (COVcu2), x5 (cu1/cu2), x6 (θy/θx) and x4 (β) with IRIs of 0.61, 0.46, 0.40, 0.17 and 0.14, respectively. The results indicate that a noticeable effect of the slope angle β is presented on μNc, and COVcu1 also has an apparent influence on COVNc.

Fig. 15
figure 15

Importance index of each variable: a μNc; b COVNc

Full size image

5.2 Coupled effects

To present the coupled influence of the soil properties and geometrical parameters while considering spatial soil variability, a variance decomposition procedure (ANOVA) is applied [46, 47]. Tables 3 and 4 summarize the ANOVA functions of the proposed MARS model, reflecting the interaction effects of those input variables. A large, generalized cross-validation (GCV) value or a relatively small R2GCV value indicates a significant ability of their interactions to affect the output value (i.e., μNc and COVNc). As shown in Table 3, the most pronounced interaction effect on μNc is captured between the input variables of COVcu2 and H/B. In addition, the COVcu2 coupled effect between COVNc and other determinate input variables (e.g., cu1/cu2 and β) is also emphasized with reference to the GCV value. For COVNc, the most important interaction is between COVcu2 and cu1/cu2. Similar to μNc, COVcu2, coupled with other determinate geometric variables (e.g., H/B and β), has a noticeable effect on COVNc. The coupled effect of COVcu2 summarized in Tables 3 and 4 coincides with the results of parametric analysis in Sect. 4.2.

Table 3 ANOVA decomposition of the MARS model of μNc
Full size table
Table 4 ANOVA decomposition of the MARS model of COVNc
Full size table

As shown in Tables 3 and 4, in addition to COVcu2, the values of μNc and COVNc are also sensitive to the coupled effect between the anisotropic spatial correlation length ratio θy/θx and other variables. Figure 16 plots the coupled effects between x6 (θy/θx) and five parameters (i.e., x1 (COVcu1), x2 (COVcu2), x3 (H/B), x4 (β) and x5 (cu1/cu2)) on the values of y1 (μNc) and y2 (COVNc). As shown in Fig. 16a, b, it can be concluded from the contour lines that the roles of COVcu1 and COVcu2 in governing the values of μNc and COVNc become increasingly important in comparison with that of θy/θx. Specifically, COVNc and μNc are less sensitive to θy/θx for different COVcu1. However, both the values of μNc and COVNc have a greater sensitivity to θy/θx for a large COVcu2 due to the coupled effect between COVcu2 and COVNc. When θy/θx is coupled with soil properties and geometric parameters, the interaction effects between those variables are shown in Fig. 16c–e. Specifically, for H/B and β, the coupled effect with θy/θx induces the highest COVNc, while that of large COVcu2 and small θy/θx is captured with a large value of μNc. When coupled with cu1/cu2, θy/θx noticeably contributes to limiting the values of μNc and COVNc in comparison with that of cu1/cu2.

Fig. 16
figure 16

Variation of μNc and COVNc with the affecting factors for different anisotropic spatial correlation length ratios θy/θx: a COVcu1; b COVcu2; c normalized slope height H/B; d slope angle β; e undrained shear strength ratio cu1/cu2

Full size image

6 Conclusion

In this paper, a RAFELA method is adopted to investigate the effect of soil spatial variability on the ultimate bearing capacity and associated failure mechanisms. The properties of soils are defined by random field theory. The stochastic analysis is carried out using the Monte Carlo simulation technique. On this basis, comprehensive studies on cases with different undrained shear strength ratios, normalized slope heights and slope angles are conducted, offering deeper insight into how the bearing capacity quantitatively changes and couples with variations in slope geometry, soil properties and soil spatial variability. Moreover, the sensitivity of the parameters is discussed through a MARS model. The following conclusions can be drawn:

  1. 1.

    The spatial variability of the soil parameter is taken into consideration for different coefficients of variation (COVs) of two-layered soils. With reference to two-layered soil variability, the soil properties and geometric conditions all affect the variability of the ultimate bearing capacity of rigid footings on two-layered soil slopes. Increasing cu1/cu2, H/B, and β leads to a smaller mean and larger coefficient of variation of the bearing capacity when affecting factors are considered.

  2. 2.

    Soil properties (cu1/cu2) and geometric parameters (e.g., H/B and β) are found to have coupled effects with soil variability (e.g., θy/θx, COVcu1 and COVcu2) on the mean and coefficient of variation of bearing capacity (μNc and COVNc). One notable effect is tied to an increase in the variability of lower layer soils (COVcu2), in which increasing COVcu2 with different H/B, β and cu1/cu2, respectively, leads to a rapid change in μNc and COVNc.

  3. 3.

    A nonlinear relationship between a set of input variables (i.e., COVcu1, COVcu2, H/B, β, cu1/cu2) and output variables (i.e., μNc and COVNc) is captured. The artificial data for the sensitivity analysis are generated through limit analysis considering spatial soil variability. According to the MARS procedure, the slope angle β is the most important variable for the values of μNc, followed by the parameters of COVcu1, H/B, COVcu2, cu1/cu2 and θy/θx. For the effect of these input variables on COVNc, COVcu1, as the most important variable, is followed by H/B, COVcu2, cu1/cu2, θy/θx and β.

  4. 4.

    Design guidance for engineering practice is provided for different anisotropic spatial correlation length ratios θy/θx. Significant COVcu2 H/B and β values are required for ensuring the bearing capacity factors owing to noticeable interaction effects with θy/θx. Furthermore, the coupled effect of θy/θx with the COV of upper layered clay COVcu1 and undrained shear strength ratio cu1/cu2 can be neglected on μNc and COVNc.

The limitation of the work in this paper is that the c–φ soil slope has not been involved. Investigating the influence of various thicknesses of the two layers of soils on the bearing capacity is also beyond the scope of this investigation. They are expected to be discussed in future work. In addition, upper-bound solutions are selected to investigate the influence of the footing distance on the bearing capacity. The investigation is focused on the understanding of the effect of affecting factors rather than an exact quantitative solution.