Load–deflection analysis of laterally loaded piles in unsaturated soils

Abstract

The lateral response of piles is governed by the soil–pile interaction in the shallower layer of surrounding soil, which may be above the water level and thus is unsaturated. There is no comprehensive analytical model for the soil–pile interaction under lateral loads considering both linear and nonlinear behaviors in unsaturated soils. In this study, an analytical solution is proposed to simulate the linear and nonlinear load–displacement variations for laterally loaded piles supported by unsaturated soils. Analytical formulations are developed to determine the stiffness per unit pile length considering the influence of soil suction on the soil modulus of elasticity. Since the current p–y curves available in the literature are unable to adequately address the unsaturated soil reaction to piles, analytical p–y relations for three types of soil are developed regarding the soil suction parameter. In order to expand the scope of application of presented method, the developed solution is extended to step-tapered piles and to piles subjected to simultaneous horizontal and vertical loads. The developed solutions are validated with the results obtained from laterally loaded pile tests reported in the literature. Parametric studies evaluated the effects of pile length and cross-section configuration and applied vertical load on the pile lateral response under various soil unsaturation conditions. The results revealed that the stiffness of the pile–soil system and its load-deformation behavior are improved significantly as the soil suction pressure increases. Furthermore, the lateral pile displacement in unsaturated soil decreases as the pile length and diameter of the upper pile portion increase, and by considering the applied vertical load. Considering the positive effect of soil suction on reducing the lateral response of piles in unsaturated soil (in arid areas) in design may help shorten the pile length or reduce its diameter while achieving a desired force–deflection demand.

1 Introduction

Soils supporting shallow or deep foundation located in arid areas may experience changes of water content throughout their lifespan, but may not be exposed to saturation. The ultimate and serviceability limit states, constructability and cost are the primary considerations for foundation design [68, 79, 80]. In laterally loaded piles, the soil lateral resistance against pile movement is influenced by its effective-stress, regardless of subsoil condition [50]. For unsaturated soil, the degree of saturation or soil suction would significantly impact its effective stress. Accordingly, the effect of soil unsaturation on the pile response should be considered in the analysis of laterally loaded piles. It is well recognized that the soil unsaturation increases the lateral soil resistance resulting in decreasing the pile displacement and improving the pile response to lateral loads [45, 80]. Therefore, ignoring the effects of soil unsaturation in pile design could lead to grossly inefficient foundation design. Thus, it is obvious that considering the effect of soil unsaturation on the lateral behavior of piles would result in a more economical and, in some cases, safer pile foundation design, especially when the soil remains in unsaturated state all the time.

Numerous studies have investigated the static and dynamic lateral and torsional responses of piles installed in saturated or dry soils [5, 12, 13, 15, 19, 23, 28, 41, 44, 56, 59, 63, 81,82,83, 85, 87,88,89,90,91].

Several studies demonstrated that the lateral pile response is governed by the relative pile–soil stiffness ratio and the pile slenderness ratio, i.e., L/d, where L and d are pile length and diameter, respectively [7, 31, 37, 43, 62].

Observing that the displacement and the bending moment along the pile shaft are usually confined to an upper portion of the pile length, Randolph [62] defined a critical length ${L}_{\mathrm{C}}$. This critical length is usually used instead of the true length ($L$) to govern the behavior of the pile for  $L>{L}_{\mathrm{C}}$. Therefore, in some studies, it is suggested to use the critical length more than using the full length ($L$) for the pile [21, 53, 61, 62]. Furthermore, there are also studies that tend to show that the lateral response and the horizontal ultimate capacity of the pile may be considered as strongly dependent by the ultimate lateral pressure (${P}_{\mathrm{ult}}$) profile of the soil [10, 11].

In recent years, limited studies evaluated the effect of soil unsaturation and change in water level on the response of laterally loaded piles, employing empirical, experimental and numerical methods [4, 14, 26, 45,46,47, 84]. Weaver and Grandi [80] evaluated the suitability of existing p–y methods for unsaturated soil by comparing the results of p–y methods to that of three-dimensional finite element analysis. Meanwhile, Mokwa et al. [58] proposed p–y curves for partially saturated soil based on the experimental results they reported.

Almost all studies performed on laterally loaded piles installed in unsaturated soils have considered limited unsaturated soil conditions. Indeed, there is no comprehensive method for investigating the lateral behavior of piles installed in all unsaturated soil types with various matric suction values thus far. In addition, there are no available solutions to calculate the soil stiffness per unit length ($k$), widely used in the design of laterally loaded piles, for unsaturated soil in terms of matric suction. Therefore, this paper addresses these two gaps in the literature for laterally loaded piles installed in unsaturated soils.

An analytical solution is developed to evaluate the lateral response of piles installed in unsaturated soils considering the soil nonlinear behavior, which involves solving the governing differential equation of a beam on an elastoplastic foundation. In addition, equations are derived to calculate k value accounting for soil nonlinearity and degree of unsaturation. Subsequently, an analytical expression is derived to calculate the lateral deflection of step-tapered pile subjected to both lateral load and bending moment. The developed solutions are validated by comparing their predictions with experimental results available in the literature [29] and numerical results obtained using the computer program LPILE [65]. Finally, the developed solutions, along with LPILE, are used to evaluate the effects of soil unsaturation, simultaneous vertical and lateral load application, pile slenderness ratio and variation of the cross section along the shaft on the pile response to lateral loads.

2 Derivation of pile head load–deflection (F–Y) relations

2.1 General load–deflection relation for laterally loaded piles

The differential equation of a beam on an elastoplastic foundation is generally used for the analysis of a laterally loaded pile. Considering a beam element and governing equilibrium equations, the corresponding differential equation is given by Heteny [30]:

$$EI\frac{{\mathrm{d}}^{4}y}{\mathrm{d}{x}^{4}}+ky=0$$

(1)

where E and I are the beam elastic modulus and moment of inertia, respectively, y is the beam deformation at distance x from the origin (left end) and $k$ is the soil stiffness per unit length of the beam [30].

Considering a beam on an elastoplastic foundation as a laterally loaded pile, E is the pile elastic modulus, I is the pile moment of inertia, y is the pile horizontal deflection at distance z from the pile toe, and $k$ is the soil stiffness per unit length of the pile.

By solving the governing differential equation of the pile, the horizontal deflection relationship of any given point along the flexible pile shaft at distance $z$ from the pile tip is given by Heteny [30]:

$${y}_{z}={y}_{0}{F}_{1}\left(\lambda z\right)+\frac{1}{\lambda }{\theta }_{0}{F}_{2}\left(\lambda z\right)-\frac{1}{{\lambda }^{2}EI}{{M}_{0}F}_{3}\left(\lambda z\right)-\frac{1}{{\lambda }^{3}EI}{Q}_{0}{F}_{4}\left(\lambda z\right)$$

(2)

where ${Q}_{0}{, M}_{0}, {\theta }_{0} \mathrm\,{and}\, {y}_{0}$ are, respectively, shear force, bending moment, slope and horizontal deflection of the pile corresponding to the point z = 0 (pile tip). $\lambda$ is defined as $\sqrt[4]{\frac{k}{4EI}}$ and functions ${F}_{1}\left(\lambda z\right)$ to ${F}_{4}\left(\lambda z\right)$ are given by:

$${F}_{1}\left(\lambda z\right)=\mathrm{ cosh}(\lambda z)\mathrm{cos}(\lambda z)$$

(3)

$${F}_{2}\left(\lambda z\right)=\frac{1}{2}(\mathrm{cosh}\left(\lambda z\right)\mathrm{sin}\left(\lambda z\right)+\mathrm{sinh}\left(\lambda z\right)\mathrm{cos}\left(\lambda z\right))$$

(4)

$${F}_{3}\left(\lambda z\right)=\frac{1}{2}(\mathrm{sinh}\left(\lambda z\right)\mathrm{sin}\left(\lambda z\right))$$

(5)

$${F}_{4}\left(\lambda z\right)=\frac{1}{4}(\mathrm{cosh}\left(\lambda z\right)\mathrm{sin}\left(\lambda z\right)-\mathrm{sinh}\left(\lambda z\right)\mathrm{cos}\left(\lambda z\right))$$

(6)

Differentiating Eq. (2) with respect to z gives equations for the determination of the pile slope, moment and shear force at a given point along the pile shaft. Details of calculations are presented in Appendix 1. L, ${F}_{\mathrm{T}}$ and ${M}_{\mathrm{T}}$ are the pile length, lateral load and moment acting at the pile head, respectively. The values of the moment and shear force at the pile tip are zero (${M}_{0}=0$, ${Q}_{0}=0$). However, the deflection (${y}_{0}$) and rotation (${\theta }_{0}$) of the pile tip are two unknowns, which are calculated from ${M}_{\mathrm{l}}={M}_{\mathrm{T}}$ and ${Q}_{\mathrm{l}}={F}_{\mathrm{T}}$. By replacing the values ${y}_{0}, {\theta }_{0},{ M}_{0} \mathrm\,{and}\, { Q}_{0}$ in Eq. (2), the general load–deflection relation of the pile is determined from:

$${y}_{z}=\frac{{\lambda }^{2}{F}_{1}\left(\lambda L\right)}{k}\left[\frac{{M}_{T}}{{F}_{3}(\lambda L)}-\frac{{F}_{T}{F}_{3}\left(\lambda L\right){F}_{4}\left(\lambda L\right)-\lambda {M}_{T}{F}_{2}\left(\lambda L\right){F}_{4}\left(\lambda L\right)}{\lambda {F}_{3}\left(\lambda L\right)\left[{{F}_{3}}^{2}\left(\lambda L\right)-{F}_{2}\left(\lambda L\right){F}_{4}\left(\lambda L\right)\right]}\right]+\frac{{\lambda }^{2}}{k}\left[\frac{{F}_{T}{F}_{3}\left(\lambda L\right)-\lambda {M}_{T}{F}_{2}\left(\lambda L\right)}{{{F}_{3}}^{2}\left(\lambda L\right)-{F}_{2}\left(\lambda L\right){F}_{4}\left(\lambda L\right)}\right]{F}_{2}\left(\lambda L\right)$$

(7)

It should be noted that Eqs. (7), (8) and (33) are for piles that are categorized as flexible or long piles, since the rotation and rigid behavior of short piles are not taken into account in these equations.

In some cases, in which water level or degree of saturation of soil changes during the pile design lifespan, the stiffness of the soil–pile system will change, depending on the magnitude of soil suction changes. Therefore, it should be checked whether the response of the pile is flexible at the minimum and maximum values of the anticipated soil suction range. Based on the criteria proposed by Broms [10, 11], if L > 3.5 $\sqrt[4]{\frac{EI}{k}}$, the pile will be considered to be long (flexible) [10, 11]. In order to examine this condition, Eqs. (19) and (21) for linear soil behavior and Eqs. (30) to (32) for both linear and nonlinear regions of soil are used for the measurement of parameter k required for checking whether the pile is flexible or not. The proposed equations take into account the soil suction stress.

2.2 Load–deflection relation for piles subject to simultaneous lateral and vertical loading

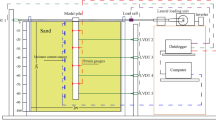
For pile subjected to a vertical load (N) and a lateral load (H) applied at a distance above its head as shown schematically in Fig. 1, the bending moment at the pile head is due to horizontal loads as well as an additional component due to the vertical load times its eccentricity caused by the pile deflection. The load–deflection relation of the pile under such condition is calculated from:

Fig. 1

Schematic of pile subjected to simultaneous vertical and elevated horizontal loads

$$Y\left(L\right)=\frac{ \frac{2\lambda \mathrm{\rm H}}{K}\left[-\frac{\left({F}_{3}(\lambda L\right){F}_{4}(\lambda L){F}_{1}(\lambda L)+{{F}_{3}}^{2}(\lambda L){F}_{2}(\lambda L))}{{2F}_{3}(\lambda L)({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right))}\right]}{1+\left[-\frac{{F}_{1}\left(\lambda L\right)}{{2F}_{3}\left(\lambda L\right)}-\frac{{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right){F}_{1}\left(\lambda L\right)}{2\left({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right)\right){F}_{3}\left(\lambda L\right)}+\frac{4{{F}_{2}}^{2}\left(\lambda L\right)}{8\left({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right)\right)}\right] \frac{2N{\uplambda }^{2}}{K}}+\frac{\frac{2He{\lambda }^{2}}{K}\left[\frac{{F}_{1}\left(\lambda L\right)}{2{F}_{3}\left(\lambda L\right)}+\frac{{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right){F}_{1}\left(\lambda L\right)}{2\left({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right)\right){F}_{3}\left(\lambda L\right)}-\frac{4{{F}_{2}}^{2}\left(\lambda L\right)}{8\left({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right)\right)}\right]}{1+\left[-\frac{{F}_{1}\left(\lambda L\right)}{2{F}_{3}\left(\lambda L\right)}-\frac{{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right){F}_{1}\left(\lambda L\right)}{2\left({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right)\right){F}_{3}\left(\lambda L\right)}+\frac{4{{F}_{2}}^{2}\left(\lambda L\right)}{8\left({{F}_{3}}^{2}\left(\lambda L\right)-{F}_{4}\left(\lambda L\right){F}_{2}\left(\lambda L\right)\right)}\right]\frac{2N{\uplambda }^{2}}{K}}$$

(8)

2.3 Load–deflection relation of step-tapered piles

In some foundation applications, the pile diameter may change with depth. For example, for applications involving large lateral load, the upper segment of the pile may possess larger diameter than the bottom part (Fig. 2a). On the other hand, some end bearing piles are designed with larger diameter of the bottom segment compared to the upper part (Fig. 2b). The excellent performance of step-tapered piles supporting lateral loads motivates construction industry to utilize them in practice to meet the demands for cost-saving and sustainable solutions [6, 35]. Ismael [34, 35] demonstrated that the lateral bearing capacity of step-tapered pile can be increased by 67% if the diameter of the enlarged upper part of pile expands from 0.3 to 0.5 m. Piles with nonuniform cross section have been largely used in recent years [33], particularly in pile foundation of large bridges [20]. However, no research studies have been considered the effect of soil unsaturation and soil matric suction on the lateral response of step-tapered piles. Given their excellent performance in resisting lateral loads and their increased popularity, the load–deflection relation for the step-tapered piles installed in unsaturated soils has been derived in this section. This allows the proposed analytical model to be used for analysis of this type of piles.

Fig. 2

Step-tapered piles: a pile with large-to-small section; b pile with small-to-large section

To derive the load–deflection for step-tapered piles subjected to horizontal load (H) and bending moment (M) at its head, the upper and lower segments are considered as two segments, and the parameters ${Q}_{0}$, ${M}_{0}$, ${\theta }_{0}$ and ${y}_{0}$ are determined for each segment separately. That is ${\lambda }_{1}$, ${L}_{1}$ and ${K}_{1}$ are assigned to the upper pile segment, and ${\lambda }_{2}$, ${L}_{2}$ and ${K}_{2}$ are assigned to the lower segment. Correspondingly, ${\theta }_{n}$ and ${y}_{n}$ are the pile deflection and slope at the section where the pile cross-sections changes.

In the upper pile segment, ${y}_{0}={y}_{n}$ and ${\theta }_{0}={\theta }_{n}$. ${M}_{0}$ and ${Q}_{0}$ are the unknowns which could be calculated from ${Q}_{L1}=H\mathrm\,{ and }\,{M}_{L1}=M$ with respect to the parameters ${y}_{n}$, ${\theta }_{n}$, M and H. In the lower pile segment, ${M}_{0}$ = 0, ${Q}_{0}$ =0, while ${y}_{0}$ and ${\theta }_{0}$ are unknown to be calculated from ${\theta }_{L2}={\theta }_{n}\mathrm\,{ and}\,{ y}_{L2}={y}_{n}$. Consequently, ${Q}_{0}$, ${M}_{0}$, ${\theta }_{0}$ and ${y}_{0}$ are calculated for both upper and lower pile segments using ${y}_{n}$, ${\theta }_{n}$, M and H. In these equations, variables a, b, c, d, g and f are presented in Appendix 2. Finally, substituting parameters ${Q}_{0}$, ${M}_{0}$, ${\theta }_{0}$ and ${y}_{0}$ corresponding to the upper pile segment into Eq. (2), the load–deflection relation of a step-tapered pile may be given as:

$$y(z)={y}_{n}{F}_{1}\left({\Delta }_{1}\right)+\frac{1}{{\lambda }_{1}}{\theta }_{n}{F}_{2}\left({\Delta }_{1}\right)-\frac{4{\lambda }_{1}}{{K}_{1}}\left(\frac{M{\lambda }_{1}-{M}_{0}{\lambda }_{1}{F}_{1}\left({\Delta }_{1}\right)-\frac{{K}_{1}}{{\lambda }_{1}}{y}_{n}{F}_{3}\left({\Delta }_{1}\right)-\frac{{K}_{1}}{{{\lambda }_{1}}^{2}}{\theta }_{n}{F}_{4}({\Delta }_{1})}{{F}_{2}({\Delta }_{1})}\right){F}_{4}\left({\Delta }_{1}\right)-\frac{4{{\lambda }_{1}}^{2}{F}_{3}\left({\Delta }_{1}\right)}{{K}_{1}}\left(\frac{\left[-M{\lambda }_{1}+\frac{{K}_{1}}{{\lambda }_{1}}{y}_{n}{F}_{3}\left({\Delta }_{1}\right)+\frac{{K}_{1}}{{{\lambda }_{1}}^{2}}{\theta }_{n}{F}_{4}\left({\Delta }_{1}\right)\right]{F}_{1}\left({\Delta }_{1}\right)+\left[H-\frac{{K}_{1}}{{\lambda }_{1}}{y}_{n}{F}_{2}\left({\Delta }_{1}\right)-\frac{{K}_{1}}{{{\lambda }_{1}}^{2}}{\theta }_{n}{F}_{3}\left({\Delta }_{1}\right)\right]{F}_{2}\left({\Delta }_{1}\right)}{-\left[{4\lambda }_{1}{F}_{4}\left({\Delta }_{1}\right){F}_{2}\left({\Delta }_{1}\right)+{\lambda }_{1}{{F}_{1}}^{2}\left({\Delta }_{1}\right)\right]}\right)$$

(9)

where ${y}_{n}$ and ${\theta }_{n}$ are to be calculated from ${\left({Q}_{L2}\right)}_{\mathrm{lower segment}}={\left({Q}_{0}\right)}_{\mathrm{upper segment}}$ and ${\left({M}_{L2}\right)}_{\mathrm{lower segment}}={\left({M}_{0}\right)}_{\mathrm{upper segment}}$, which lead to

$${y}_{n}=\frac{{\theta }_{n}d+g}{f}$$

(10)

$${\theta }_{n}=\frac{\left(\frac{b}{c}-\frac{g}{f}\right)}{\left(\frac{d}{f}-\frac{a}{c}\right)}$$

(11)

3 Calculation of k for unsaturated soils

The pile load–deflection relationship is a function of the soil stiffness per unit length of the pile characterized by k. To account for effect of soil unsaturation on the pile deflection, k should be correlated to parameters of soil unsaturation. However, most existing p–y relations ignore the effect of soil unsaturation. In this study, relevant equations are presented to determine k as a function of soil matric suction or degree of saturation for both linear and nonlinear responses.

Soils in real field situations behave nonlinearly, particularly near the top part of the pile. The soil resistance against lateral pile movement is controlled mostly by shallower soil surrounding the pile, which results in a nonlinear pile–soil response. Soil may experience such large strains that exceed the linear limit of the soil medium in offshore structures and earthquake regions [18]. Therefore, Eqs. (30) to (32) in Sect. 3.2 were derived to determine parameter k related to sand, lean clay and glacial till soils for both linear and nonlinear soil behaviors without limitation. However, there are some cases in which soils behave linearly under laterally loaded piles. For instance, in some analytical models, the soil around the pile may be divided into two regions: a nonlinear inner region adjacent to the pile and a linear region for the far field. The soil outside the inner region adjacent to the pile experiences very low strain (< ${10 }^{-5}$) due to pile loading and behaves more or less elastically [18]. The elastic modulus starts degrading at a strain as low as ${10 }^{-5}$ [69, 71]. In order to distinguish between linear and nonlinear regions of soil, Bowles [9] and Hsiung and Chen [32] assumed the soil to be linear elastic up to a certain value of pile deflection and perfectly plastic beyond that value. They considered the soil response to be linear up to a displacement of 12–25 mm [9, 32]. In such cases when soil is under very low strain, in addition to Eqs. (30) to (32) derived in Sect. 3.2, Eqs. (19) and (21) in Sect. 3.1 can be used confidently to determine parameter k.

3.1 Calculating k by using relations ${{\varvec{k}}}_{{\varvec{U}}{\varvec{S}}1}$ and ${{\varvec{k}}}_{{\varvec{U}}{\varvec{S}}2}$

Lu [49] described the elastic modulus ($E$) and shear modulus ($G$) for unsaturated soil as a function of volumetric water content ($\theta$) (Lu [49]), i.e.,

$$E={E}_{\mathrm{d}}+({E}_{\mathrm{w}}-{E}_{\mathrm{d}}){\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\uptheta }_{\mathrm{d}}}\right)}^{m}$$

(12)

$$G={G}_{\mathrm{d}}+({G}_{\mathrm{w}}-{G}_{\mathrm{d}}){\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right)}^{m}$$

(13)

where ${E}_{\mathrm{d}}$ and ${E}_{\mathrm{w}}$ are the elastic moduli corresponding to dry and wet conditions, respectively; ${G}_{\mathrm{d}}$ and ${G}_{\mathrm{w}}$ are the shear moduli corresponding to dry and wet conditions; ${\theta }_{\mathrm{d}}$ and ${\theta }_{\mathrm{w}}$ are the volumetric water contents corresponding to dry and wet conditions; and $\theta$ represents its existing condition.

In Eqs. (12) and (13), parameter m is related to the degree of dependence of soil properties on suction alteration, which may be given by Lu [49] as:

$$m=\frac{\mathrm{log}\left[\frac{{E}_{\mathrm{m}}-{E}_{\mathrm{d}}}{{E}_{\mathrm{w}}-{E}_{\mathrm{d}}}\right]}{\mathrm{log}\left[\frac{{\uptheta }_{\mathrm{m}}-{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right]}$$

(14)

where ${E}_{\mathrm{m}}$ and ${\theta }_{\mathrm{m}}$ are, respectively, the elastic moduli and volumetric water content corresponding to middle point between the two end states, namely dry and wet conditions [49].

The elastic and shear moduli are related to the Poisson’s ratio ($\nu$) as:

$$\nu =\frac{2G}{E}-1$$

(15)

Substituting Eqs. (12) and (13) in Eq. (15) yields:

$$\upnu =\frac{2({G}_{\mathrm{d}}+({G}_{\mathrm{w}}-{G}_{\mathrm{d}}){\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right)}^{m})}{{E}_{\mathrm{d}}+({E}_{\mathrm{w}}-{E}_{\mathrm{d}}){\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right)}^{m}}-1$$

(16)

Based on elastic theory, the relationship between the elastic settlement of a plate resting on elastic medium ($s$) and net effective stress on the soil (${q}_{\mathrm{p}}$) is given by Timoshenko et al. [74] as:

$${K}_{0}=\frac{{q}_{\mathrm{p}}}{s}=\frac{E}{B(1-{\nu }^{2}){I}_{\mathrm{w}}}$$

(17)

where ${q}_{\mathrm{p}}$ is the net effective stress on the soil, s is settlement, B is the plate width, E is the soil elastic modulus, ${K}_{0}$ (kN/m³) is subgrade modulus and ${I}_{\mathrm{w}}$ is a dimensionless influence factor (0.79 for circular plates and 0.88 for rectangular plates) [74]. Since ${k=K}_{0}B$ [30], Eq. (17) can be rewritten as:

$$k=\frac{E}{(1-{\nu }^{2}){I}_{\mathrm{w}}}$$

(18)

Substituting Eqs. (12) and (16) in Eq. (18) gives the unsaturated soil stiffness, ${k}_{\mathrm{US}1}$, as a function of volumetric water content as:

$${k}_{\mathrm{US}1}=\frac{{E}_{\mathrm{d}}+({E}_{\mathrm{w}}-{E}_{\mathrm{d}}){\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right)}^{m}}{\left(1-{\left(\frac{2\left({G}_{\mathrm{d}}+({G}_{\mathrm{w}}-{G}_{\mathrm{d}}) {\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right)}^{m}\right)}{{E}_{\mathrm{d}}+({E}_{\mathrm{w}}-{E}_{\mathrm{d}}){\left(\frac{\theta -{\theta }_{\mathrm{d}}}{{\theta }_{\mathrm{w}}-{\theta }_{\mathrm{d}}}\right)}^{m}}-1\right)}^{2}\right){I}_{\mathrm{w}}}$$

(19)

Vanapalli and Oh [76] described the soil elastic modulus for unsaturated soil, ${E}_{\mathrm{unsat}}$, as a function of the degree of saturation (${S}_{\mathrm{r}}$) and matric suction (${u}_{\mathrm{a}}-{u}_{\mathrm{w}}$), which expresses by:

$$E_{{{\text{unsat}}}} = E_{{\text{w}}} \left( {1 + \alpha \frac{{\left( {u_{{\text{a}}} - u_{{\text{w}}} } \right)}}{{\frac{{P_{a} }}{{101/3}}}}{\text{Sr}}^{\beta } } \right)$$

(20)

where ${P}_{\mathrm{a}}$ is the atmospheric pressure which is considered 101.3 kPa; $\alpha$ and $\beta$ are the fitting parameters ($\beta$ = 1 and 2 for coarse-grained and fine-grained soils, respectively, while $\alpha$ is inversely proportional to the soil plasticity index) [76].

Substituting Eq. (20) in Eq. (18), the unsaturated soil stiffness, ${k}_{\mathrm{US}2}$, may be obtained from:

$${k}_{\mathrm{US}2}=\frac{\left({E}_{\mathrm{w}}\left(1+\alpha \frac{\left({u}_{\mathrm{a}}-{u}_{\mathrm{w}}\right)}{\left(\frac{{P}_{\mathrm{a}}}{101/3}\right)}{Sr}^{\beta }\right)\right)}{\left(1-{\nu }^{2}\right){I}_{\mathrm{w}}}$$

(21)

Vanapalli and Mohamed [77], Rojas et al. [67] and Vanapalli et al. [78] conducted plate load tests on three different soils (Unimin sand, lean clay and compacted glacial till), considering various matric suction values [67, 77, 78]. Unimin sand was classified as a poorly graded sand (SP), according to the USCS. The unsaturated soil parameters interpreted from the plate load test results are presented in Table 1. ${E}_{\mathrm{d}}$, ${E}_{\mathrm{w}}$ and ${E}_{\mathrm{m}}$ were measured by vanapalli (2010) using Eq. (18) and plate load test results. Furthermore, shear modulus corresponding to dry and wet condition $({ G}_{\mathrm{d}}$ and ${G}_{\mathrm{w}})$ and parameter $m$ were calculated using Eqs. (14), (15) and measured values of ${E}_{\mathrm{d}}$, ${E}_{\mathrm{w}}$ and ${E}_{\mathrm{m}}$.

Table 1 Parameters of unsaturated soils, extracted from plate load tests perofomed in [76]

Parameters of Table 1 are used to calculate ${k}_{\mathrm{US}1}$ and ${k}_{\mathrm{US}2}$ for all three aforementioned soil types and for various matric suction values. The soil stiffness, k, could be calculated as the slope of the corresponding p–y curves of tests within the soil elastic response range. Figure 3 shows the results corresponding to relations of ${k}_{\mathrm{US}1}$ and ${k}_{US2}$ and the results of $k$ derived from the plate load tests. As seen, there is a great agreement among results, confirming in turn, the validity of the presented relations. From Fig. 3, it is obvious that the results of both relations for ${k}_{\mathrm{US}1}$ and ${k}_{\mathrm{US}2}$ are very close to the $k$ values derived from plate load tests and the choice between these two relations depends only on the availability of input parameters. It should be mentioned that ${k}_{\mathrm{US}1}$ is used when parameters m, ${E}_{\mathrm{d}}$, ${E}_{\mathrm{w}}$, ${G}_{\mathrm{d}}$, ${ G}_{\mathrm{w}}$, ${\theta }_{\mathrm{d}}$, ${ \theta }_{\mathrm{w}}$ and $\theta$ are available and ${k}_{US2}$ is used when parameters ${S}_{\mathrm{r}}$, ${(u}_{\mathrm{a}}-{u}_{\mathrm{w}})$, $\nu$, $\mathrm{PI}$ and ${E}_{\mathrm{w}}$ are available.

Fig. 3

Comparison of results for ${{\varvec{k}}}_{\mathbf{U}\mathbf{S}1}$ from Eq. (19), ${{\varvec{k}}}_{\mathbf{U}\mathbf{S}2}$ from Eq. (21) and ${\varvec{k}}$ from plate load test for various soils: a Unimin sand, b lean clay and c glacial till

Using $k$ value extracted from plate load test results for calculating the pile–soil structure interaction can be a rational approach. In case of using different sizes for plates and piles, it should be noted that parameter $k$ (stiffness per unit length of pile) which is used in this model is independent of plate width or pile diameter. Results of plate load tests give ${K}_{0}$ which is known as the subgrade reaction modulus and depends on the plate size, as incorporated in ${K}_{0}=\frac{E}{B\left(1-{\nu }^{2}\right){I}_{\mathrm{w}}}$. However, ${k}_{\mathrm{US}1}$ and ${k}_{\mathrm{US}2}$ which are derived in this section are defined as $k=\frac{E}{\left(1-{\nu }^{2}\right){I}_{\mathrm{w}}}$ which are independent of plate width or pile diameter [30]. Therefore, varying the size of the plate or pile will not affect results of ${k}_{\mathrm{US}1}$ and ${k}_{\mathrm{US}2}$.

3.2 Calculating k using p–y relations

The soil around the pile experiences big strains and thus exhibits nonlinear behavior even for the allowable lateral load range. Therefore, the nonlinearity of the soil–pile system should be considered in pile design. For example, for the analysis of laterally loaded piles, nonlinear p–y curves simulating the soil nonlinear behavior are used. Various methods are available in the literature to establish p–y curves for different types of soil such as soft clay [54], stiff clay below water table [64], stiff clay above water table [66] and sand [63]. In addition, Mokwa et al. [58] proposed p–y curves for partly saturated silts and clays [58]. However, there is no method to establish p–y curves for unsaturated soil as a function of saturation degree or matric suction.

As a first step, to establish p–y relationships for unsaturated soils (Unimin sand, lean clay, glacial till) considering matric suction, the results of the plate load tests conducted on Unimin sand [77], lean clay [67] and glacial till [78] for different matric suction values are utilized here to generate corresponding p–y relationships. Mokwa et al. [58] proposed p–y relation for frictional–cohesive soils as:

$$p=0.5{P}_{\mathrm{ult}}{\left(\frac{y}{ A{\varepsilon }_{50}D}\right)}^{n}$$

(22)

where $p$ is the soil resistance per unit pile length, $y$ is the pile horizontal deflection, $n$ is the power coefficient which would be equal to 0.33 for a cubic parabola, $D$ is the pile diameter, ${\varepsilon }_{50}$ is the strain required to mobilize 50% of the soil strength and $A$ is a coefficient which controlling the deflection magnitude which can be evaluated by analyzing results from field lateral load tests or estimated from data available for similar soils [58].

In the current study, values of ${A\varepsilon }_{50}$ were determined using p–y variations obtained from plate load tests. By varying the values of ${A\varepsilon }_{50}$, the p–y curves were established such that they become equal to the p–y curves from the plate load tests for different values of matric suction. ${p}_{\mathrm{ult}}$ is the maximum soil resistance at large deformations. For $\mathrm{c}$-$\mathrm{\varphi }$ soils, the ultimate lateral load carried by a pile is given by Hansen [27]:

$${P}_{\mathrm{ult}}=M{\gamma }_{\mathrm{m}}Dz{K}_{\mathrm{q}}+McD{K}_{\mathrm{c}}$$

(23)

where M is an empirical modification factor, ${\gamma }_{\mathrm{m}}$ is the soil unit weight, $c$ is the soil cohesion, z is the depth from the ground surface, and ${K}_{\mathrm{q}} \mathrm\,{and}\, {K}_{\mathrm{c}}$ are coefficients for the frictional and cohesive components of soil resistance, which depend on the value of $\varphi$ as presented in Appendix 3 [27].

In Eq. (23), the value of ${P}_{\mathrm{ult}}$ is reduced by 15%, as recommended by Helmers et al. [29] to improve the reliability of Brinch–Hansen's theory and preventing from overestimating the ultimate lateral capacity. In the current study, it is assumed $M=0.85$. The value of $M$ can be varied in the analysis if desired.

The p–y curve proposed by Mokwa et al. [58] is calibrated by comparison with p–y curves resulted from plate load tests for different matric suction values. For this purpose, certain parameters, ${A\varepsilon }_{50}$ and $n$, are adjusted until a good match between p–y curves resulted from plate load tests and those resulted from Eq. (22) is achieved. The variation of $A{\varepsilon }_{50}$ for different soils is lower than the variation of $A$ and ${\varepsilon }_{50}$ individually. Accordingly, it is better to use the lumped value of $A{\varepsilon }_{50}$.

Table 2 presents ${A\varepsilon }_{50}$ and $n$ values that result in the best match between p–y curves obtained from plate load tests conducted on aforementioned soil types and those resulted from Eq. (22) for each matric suction value. Having $A{\varepsilon }_{50}$ values corresponding to different matric suction values, the relationship between $A{\varepsilon }_{50}$ and matric suction values is estimated for each of three soil types, which are given by:

Table 2 Properties of considered soils and corresponding p–y curve fitting parameters (${\varvec{n}}$ and ${\varvec{A}}{{\varvec{\varepsilon}}}_{50}$), to match the plate load test results with curves derived from Mokwa’s method [67, 77, 78]

For sand:

$$A{\varepsilon }_{50}=0.0001{({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }^{-0.253}$$

(24)

For lean clay:

$$A{\varepsilon }_{50}=0.0002{\mathrm{e}}^{-0.052({u}_{\mathrm{a}}-{u}_{\mathrm{w}})}$$

(25)

For glacial till:

$$A{\varepsilon }_{50}=0.003{\mathrm{e}}^{-0.022({u}_{\mathrm{a}}-{u}_{\mathrm{w}})}$$

(26)

Substituting each of the above relationships defining $A{\varepsilon }_{50}$ as a function of matric suction given by Eqs. (24) to (26) in Eq. (22), the p–y relations for the three tested unsaturated soil types may be given by:

For sand:

$$p=0.5{P}_{\mathrm{ult}}{\left(\frac{y}{ \left(0.0001{({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }^{-0.253}\right)D}\right)}^{0.8}$$

(27)

For lean clay:

$$p=0.5{P}_{\mathrm{ult}}{\left(\frac{y}{ \left(0.0002{\mathrm{e}}^{-0.052({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }\right)D}\right)}^{0.5}$$

(28)

For glacial till:

$$p=0.5{P}_{\mathrm{ult}}{\left(\frac{y}{ \left(0.003{\mathrm{e}}^{-0.022({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }\right)D}\right)}^{0.35}$$

(29)

By differentiating these p–y relations given by Eqs. (27) to (29) for each soil type with respect to $y$, an equation would be generated for determining parameter $k$ for each soil as a function of matric suction. These equations for three unsaturated soil types are given by:

For sand:

$$k=\frac{{0.4{p}_{\mathrm{ult}}\left(\frac{y}{ \left(0.0001{({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }^{-0.253}\right)D}\right)}^{0.8}}{y}$$

(30)

For lean clay:

$$k=\frac{0.25{p}_{\mathrm{ult}}{\left(\frac{y}{ \left(0.0002{\mathrm{e}}^{-0.052({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }\right)D}\right)}^{0.5}}{y}$$

(31)

For glacial till:

$$k=\frac{0.175{p}_{\mathrm{ult}}{\left(\frac{y}{ \left(0.003{\mathrm{e}}^{-0.022({u}_{\mathrm{a}}-{u}_{\mathrm{w}}) }\right)D}\right)}^{0.35}}{y}$$

(32)

4 Discussion and results

The proposed analytical model includes several lateral load–deflection relations for piles embedded in unsaturated soils and subjected to various loading types. Equation (8) is used for piles subject to simultaneous lateral and vertical loads. Equation (9) is used for step-tapered piles, and Eq. (33) is utilized for piles subject to simultaneous lateral load and bending moment. These equations use expressions for k pertinent to unsaturated soils. In cases which soil is under very low stress level, Eqs. (30) to (32) derived in Sect. 3.2 and Eqs. (19) and (21) in Sect. 3.1. can be used confidently to measure parameter k. If the soil behavior is nonlinear, based on the soil type, one of Eqs. (30), (31) and (32) which is obtained from differentiation of Eqs. (27) to (29) will be selected in analytical solution for substituting it into lateral load–deflection relation. This analytical method helps to analyze the response of piles to lateral loads following the procedure shown step by step in Fig. 4.

Fig. 4

Procedure for using present analytical method for plotting the pile load-deflections variation

The capability of the presented solution is validated by comparing its predictions for laterally loaded piles with the measured data from lateral loading tests on cast-in-place piles installed in partly saturated silty and clayey soils [29] and the results of LPILE [65]. For this purpose, the user-defined p–y curve obtained from Eq. (28) is considered. The effect of soil matric suction on pile lateral performance is investigated. In addition, the effects of loading condition, pile slenderness ratio, and variation of pile cross section on the lateral response of pile in unsaturated soil considering varying matric suction are then evaluated using the developed analytical solution and LPILE by incorporating the user-defined p–y curves obtained from Eq. (28).

4.1 Comparison between calculated and measured pile responses

Helmers [29] conducted lateral loading tests on several cast-in-place-reinforced concrete piles used in supporting sound walls. The piles were installed in partly saturated clay at two locations, namely Prices Fork and Salem. The piles length and diameter were 1.22 m and 203 mm, and their bending stiffness was 2679 kN/m². The soil was unsaturated lean clay (CL) with properties given in Table 2.

For the soil at Prices Fork site, the matric suction and unit weight were 10 kPa and 17.3 kN/m³, respectively. For the soil at Salem site, matric suction and unit weight were 21.4 kPa and 19.9 kN/m³, respectively. Soil parameters of lean clay, including $c$ = 3 kPa, $\varphi$ = 26°, ${\gamma }_{\mathrm{m}}$ and matric suction values, were used in Eq. (31) for calculating the $k$ value for lean clay. To simulate the complex loading scenario of foundations supporting sound walls, the lateral load was applied with an eccentricity of e = 1.22 m which caused a bending moment at the pile head in addition to the lateral load.

The lateral load–deflection responses of the test piles were calculated employing the developed analytical solution represented by Eqs. (31) and (33). The nonlinear soil stiffness, k, corresponding to the level of induced lateral deflections were obtained employing the $k$ relationship for unsaturated lean clay given by Eq. (31). The lateral load–deflection at the pile head was then obtained by substitution the calculated $k$ values into Eq. (33). It should be noted that Eqs. (7) and (33) are the same and are written in two different forms. In Eq. (7), the deflection (y) is a function of force (F) represented by y = f(F) while in Eq. (33), the force (F) is a function of deflection (y) given by F = f(y). The reason for changing Eqs. (7) to (33) is that the $k$ value depends on y, and in fact, it facilitates to determine $k$ value corresponding to a certain deflection. Having such a certain deflection helps to compute the corresponding external force given by Eq. (33).

$$F=\frac{y}{\frac{{\lambda }^{2}{F}_{1}\left(\lambda L\right)}{k}\left[\frac{e}{{F}_{3}(\lambda L)}-\frac{{F}_{3}\left(\lambda L\right){F}_{4}\left(\lambda L\right)-\lambda e{F}_{2}\left(\lambda L\right){F}_{4}\left(\lambda L\right)}{\lambda {F}_{3}\left(\lambda L\right)\left[{{F}_{3}}^{2}\left(\lambda L\right)-{F}_{2}\left(\lambda L\right){F}_{4}\left(\lambda L\right)\right]}\right]+\frac{{\lambda }^{2}}{k}\left[\frac{{F}_{3}\left(\lambda L\right)-\lambda e{F}_{2}\left(\lambda L\right)}{{{F}_{3}}^{2}\left(\lambda L\right)-{F}_{2}\left(\lambda L\right){F}_{4}\left(\lambda L\right)}\right]{F}_{2}\left(\lambda L\right)}$$

(33)

The calculated load–deflection curve is then compared with the range of load–deflection curves obtained from the lateral loading tests performed by Helmers [29]. The load–deflection curve was also calculated employing the program LPILE incorporating user defined p–y curves obtained from Eq. (28) corresponding to lean clay.

Figure 5 compares the calculated pile response using the developed analytical solution based on Eqs. (31) and (33) and the LPILE with the experimental results. Figure 5 shows that the calculated piles responses are in good agreement with the measured response over both the linear and nonlinear regions. This comparison confirms the capability of the developed solution and the proposed p–y relationship for unsaturated clay.

Fig. 5

Comparison among results of lateral loading test [29], those derived from analytical solution given by Eqs. (33) and (31) and those derived from LPILE by incorporating user defined p–y curves obtained from Eq. (28) for: a Prices Fork site; b Salem site

Since the displacement and bending moment along the pile shaft are usually controlled by the upper portion of the pile length [68] and the soil parameters of top 8D (D = pile diameter) govern the pile lateral response [17], the average $k$ value corresponding to soil within the top $8D$ can be assumed to be constant with depth in cohesive soils [51, 86]. Therefore, in this study, the matric suction and also $k$ value which are a function of the degree of saturation are assumed to be constant along the pile length.

4.2 Effect of soil matric suction on pile lateral performance

In this section, the developed analytical solution is used to evaluate the effect of the soil matric suction on the performance of laterally loaded piles embedded in unsaturated soils. A reinforced concrete pile with 500 mm diameter, 12 m length and 108,274 $\mathrm{kN }{\mathrm{m}}^{2}$ bending stiffness is analyzed. The pile is installed in lean clay with properties given in Table 2. Based on the criteria proposed by Broms [10, 11], the pile is categorized as a flexible pile [10, 11]. The applied lateral loads are considered to have 0.5 m eccentricity. Figure 6 shows the pile lateral load–deflection variations obtained from the current analytical solution given by Eq. (33) for various matric suction values of 0, 10, 20, 30, 40, 48, 56, 60 and 63 kPa. It is noted that Eq. (31) was used for calculating k and substituting in Eq. (33). The maximum allowable lateral load (H_allowable) and deflection (y_allowable) for aforementioned pile in saturated soil condition were calculated, respectively, as 170 kN and 48 mm according to the suggestion of Broms [10, 11]. As inferred from Fig. 6, as the soil matric suction increases from 0 to 63 kPa, the pile lateral deflection corresponding to allowable horizontal load decreases from 26.5 to 8 mm, which represents about 69% deflection reduction. It is also observed that as the lateral load increases, the sensitivity degree of lateral deflection of the pile head to changing the matric suction increases dramatically.

Fig. 6

Variation of ratio of lateral load (H) to allowable lateral load (H_allowable) versus pile head deflection for various matric suctions in lean clay soil obtained from analytical solution given by Eqs. (31) and (33)

Figure 7 shows the variation of the lateral load ratio applied to the pile head in unsaturated and saturated soil conditions (H_unsat/H_sat) versus the pile lateral deflection for various values of matric suctions. Figure 7 shows that for a given pile head deflection, as the soil matric suction increases from 0 to 63 kPa, the lateral load tolerated by the pile increases by about 100%. In other word, the required lateral load to create a specified lateral deflection is doubled as the matric suction value increases from 0 to 63 kPa. This stems from the increase in the soil stiffness and resistance against the pile movement due to the soil matric suction.

Fig. 7

Variation of ratio of lateral load in unsaturated (H_unsat) and saturated (H_sat) soil conditions versus pile head deflection for various matric suctions for lean clay soil obtained from analytical solution given by Eqs. (31) and (33)

Figure 8 presents the variation of H_unsat/H_sat with matric suction for a constant pile head lateral deflection of 30 mm. There is a sudden rise in applied lateral load with increasing the matric suction from 48 to 63 kPa. This is because air entry value in the corresponding soil–water characteristic curve for lean clay is 45 kPa. Since the soil shear strength starts to increase nonlinearly after the air entry value [22, 42, 67, 70], the lateral load required for inducing a certain lateral deflection will be subsequently increased.

Fig. 8

Variation of ratio of lateral load in unsaturated (H_unsat) and saturated (H_sat) soil conditions versus soil matric suction for constant deflection of 30 mm obtained from analytical solution given by Eqs. (31) and (33)

To explore the economic advantages of considering the soil matric suction in the design of laterally loaded piles installed in unsaturated soil, the response of a flexible pile 14 m long is analyzed considering cases with different pile diameter using the current developed solution. The pile is installed in lean clay with properties given in Table 2. The applied lateral load is considered to have 0.5 m eccentricity. The lateral design load and deflection are assumed to be 400 kN and 50 mm, respectively. The analytical solution given by Eqs. (31) and (33) is used to evaluate the required diameter of the pile meeting design requirements for different matric suction values of 0, 10, 20, 30, 40, 48, 56, 60 and 63 kPa. Figure 9 shows that for a given lateral design load and deflection, as the soil matric suction increases, the required pile diameter decreases by up to 53%. Correspondingly, as the suction pressure increases from 0 to 63 kPa, the required concrete volume for pile construction decreases by 78%. This is because as the soil suction stress increases, the stiffness of the soil–pile system increases significantly. It is noted that the considered pile with a diameter ranging from 0.7 to 1.5 m is still flexible. The positive soil suction effect may help the designer not to use larger pile diameter unnecessarily while achieving a desired force–deflection demand.

Fig. 9

Variation of required pile diameter and required concrete volume for various matric suctions in lean clay soil obtained from analytical solution given by Eqs. (31) and (33)

4.3 Effect of pile length on its lateral response

In this section, the developed analytical solution and the program LPILE incorporating the developed p–y relationships for unsaturated soil are used to determine the effect of pile length on its head deflection considering the soil suction pressure. The analyses consider reinforced concrete piles with a diameter of 500 mm and bending stiffness of 84,815 N m². The piles are installed in lean clay with properties listed in Table 2. Two pile lengths of 12 and 15 m are considered in the analysis. Based on the criteria proposed by Tomlinson and Woodward [75] and Matlock and Reese [55], both piles are considered to be long (flexible) piles [55, 75]. Two lateral loads of 60 kN and 100 kN with eccentricity of 1 m are also considered. Figure 10 compares the pile head lateral deflection obtained from the analytical solution given by Eq. (33) for obtaining the corresponding load–deflection curve, and Eq. (31) was used for calculating the $k$ value and substituting into Eq. (33) and from LPILE program. This can be done by incorporating the user-defined p–y curves obtained from Eq. (28) due to applying 60 and 100 kN lateral loads. Such curves correspond to various matric suction values of 0, 10, 20, 30, 40, 48, 56, 60 and 63 kPa for both piles with 12 and 15 m lengths.

Fig. 10

Variation of shorter and longer pile head deflections under lateral loads of: a H = 60 kN and b H = 100 kN for various matric suction values in lean clay soil obtained from analytical solution given by Eqs. (31) and (33) and from LPILE program by incorporating user defined p–y curves obtained from Eq. (28)

In order to investigate the effect of matric suction on the pile head deflection, the pile head deflections under lateral loads of 60 and 100 kN for various matric suction values are shown in Fig. 10. As expected, the lateral deflection is much lower for 60 kN applied load compared to that due to 100 kN lateral applied load. The pile head lateral deflection is lower up to 57% for both piles. It is also noted that the difference in pile head deflection for shorter and longer piles is much lower for 60 kN applied load compared to 100 kN lateral applied load.

It is inferred from Fig. 10 that when 100 kN load is applied to heads of both shorter and longer piles, the pile head deflections decrease appreciably as the suction pressure increases. It is also observed that the decrease in pile head deflection is more pronounced for the shorter pile than for the longer pile and the difference accounts for about 28%. As seen in Fig. 10, there is a sudden drop in the pile lateral displacement as the soil matric suction increases from 48 to 63 kPa. This is because the air entry value for the corresponding soil–water characteristic curve of lean clay is about 45 kPa. Since the soil resistance parameters start to increase noticeably after the air entry value [22, 42, 67, 70], the pile lateral displacement will subsequently decrease. Furthermore, as the matric suction increases from 0 to 63 kPa, the difference between the lateral deflection of the longer and shorter piles becomes much smaller. The reason for this is that with increasing the soil suction stress, the stiffness of the soil–pile system significantly increases. The positive soil suction effect may help the designer not to lengthen the pile necessarily for achieving a desired force–deflection demand.

4.4 Effect of vertical load on pile lateral response

The effect of vertical load on the lateral response of piles subjected to combined lateral and vertical loads has been investigated by performing numerical analysis [1,2,3, 38, 39] and analytical solutions [16, 25, 60]. These studies reveal that the vertical load presence results in increasing the pile lateral deflection. However, a number of experimental studies and field investigations have reported contradicting results, suggesting that the vertical load reduces the pile lateral deflection [8, 36, 57, 72, 92]. To explore the effect of the vertical load on the lateral response of piles installed in unsaturated soil and subjected to combined vertical and horizontal loads, the response of the same pile considered in Sect. 4.2 is analyzed considering a vertical load of 200 kN applied at the pile head, in addition to the lateral loads of 60 and 100 kN. The analytical solution given by Eq. (8) for obtaining load–deflection curve and Eq. (31) for calculating k and substituting it into Eq. (8) and the program LPILE incorporating p–y curves obtained from Eq. (28) are used to evaluate the variation of pile head load–deflection response for different matric suction values. According to Figs. 11 and 12, the effect of applying vertical load on the lateral behavior of the pile could be compared for various values of matric suction. As seen, for each shorter or longer pile and for a given soil suction stress, with reducing the horizontal applied load, the sensitivity of the pile lateral behavior to alteration of vertical load (the reduction of lateral displacement of the pile head due to application of the vertical load) decreases by 15% for both piles. This stems from increasing the soil–pile system stiffness, i.e., the rate of change of load with respect to the alteration of lateral deflection induced by the vertical load application.

Fig. 11

Variation of pile head deflection of shorter and longer piles under H = 60 kN lateral load and vertical loads of 0 and 200 kN for various matric suction values in lean clay soil: a analytical solution given by Eqs. (8) and (31); b LPILE program by incorporating user defined p–y curves obtained from Eq. (28)

Fig. 12

Variation of pile head deflection for shorter and longer piles under 100 kN lateral load and vertical loads of N = 0 and 200 kN for various matric suction values in lean clay soil: a analytical solution given by Eqs. (8) and (31); b LPILE program by incorporating user defined p–y curves obtained from Eq. (28)

Figure 12 represents the results for piles tolerated 100 kN lateral and 200 kN vertical loads. As seen, under similar horizontal load and for a given soil suction stress, applying the vertical load leads to decreasing the pile head deflections about 12% and 10% for shorter and longer piles, respectively. This originates from increasing the soil stiffness and resistance against pile movement. It is also observed that under a certain horizontal load, with increasing the matric suction from 0 to 63 kPa, the sensitivity degree of lateral deflection of the pile head to changing the vertical load (the degree of reduction in pile head lateral deflection while increasing the vertical load) decreases by 65% and 98%, respectively, in shorter and longer piles. In fact, for larger soil suction stress values, applying the vertical load would not affect the lateral deflection of the pile head. This is because the effect of increasing the suction stress on increasing the stiffness of the soil–pile system is greater than the effect of increasing the vertical load. In turn, with increasing the suction stress, the effect of the vertical load on the reduction of the lateral deflection of the pile head decreases. In addition, Fig. 12 shows that, for a given nonzero suction stress under a certain horizontal load, the degree of reduction of lateral deflection of the pile head caused by the application of vertical load in the shorter pile is averagely about 23% greater than that for the longer pile. In other words, the sensitivity of the pile lateral deflection to alteration of vertical load in the shorter pile is 23% greater than the longer pile. This is caused by the load dispersion effect: the reduction of the degree of vertical pressure, induced by the vertical load applied on the pile head along the shaft of the longer pile. Such effect would also lead to the reduction in alteration of confining stress at depths along the pile shaft, induced by the application of vertical load. Since the confining stress is directly proportional to the soil resistance, the effect of applying vertical load on the reduction of lateral deflection of the longer pile is lower than its effect on the shorter pile.

4.5 Effect of variation of pile cross section on its lateral response

The effect of nonuniformity of the pile cross section on its lateral behavior is investigated considering different suction pressure. Ismael (2010) performed field tests on piles with top segment of larger cross section than the bottom segment. The piles were installed in sand and subjected to static and lateral loading. It was reported that the increase in pile cross section resulted in better performance under lateral loading and may lead to more economic design. Similar observations were made based on experimental and theoretical studies conducted on step-tapered piles [24, 40, 48, 52, 73]. However, the effect of varying cross section of piles embedded in unsaturated soil has not been investigated.

To investigate the effect of varying the pile cross section on its lateral response, three types of piles are examined. These are a pile with small-to-large cross sections (S–L), a pile with large to small cross sections (L–S) and a pile with uniform cross section (U). The length, diameter and bending stiffness of the segment with small cross section are 3 m, 50 cm and 108,274.5 kN m², respectively. For the segment with large cross section, the length, diameter and bending stiffness are 3 m, 1 m and 1,664,136 kN m², respectively. The piles are embedded in unsaturated lean clay with properties listed in Table 2 and are subjected to lateral load of 100 kN applied with an eccentricity of 1 m. The lateral pile head deflection was analyzed employing the analytical solution given by Eq. (9) for obtaining the corresponding load–deflection curve and Eq. (31) for calculating k and substituting it into Eq. (9). Figure 13 presents the variation of pile head deflection for the different pile considering different values of matric suction obtained from analytical solution. As seen in Fig. 13, for a certain suction stress and under a given lateral load, the maximum lateral deflection of the pile head corresponds to the pile whose upper segment has smaller cross section followed by a larger cross section. This case is called S–L reflecting small-to-large cross sections. Also, L–S stands for the pile whose upper part has larger cross section and its lower part has smaller one. The latter may be more common in practice. Looking in more details, with increasing the diameter of the upper section of the pile by 100%, the lateral deflection of the pile head decreases by 98% on average. This is due to the fact that, in step-tapered piles, the lateral behavior of the whole pile is more significantly affected by the cross section of its upper part rather than that of the lower part. Consequently, with increasing the diameter of the upper part section, the bending stiffness and thus the stiffness of the soil–pile system grow, resulting in the reduction of the lateral deflection of the pile head. Moreover, it is observed that under a given lateral load, the effect of the pile type on the lateral deflection of the pile head decreases by 72% while increasing the matric suction value from 0 to 63 kN. This stems from the fact that with increasing the suction stress, the effect of changing the pile type on alteration of the stiffness of the system rises. Therefore, under a given lateral loading, with increasing the relative stiffness of the system by changing the pile type, the relative lateral deflection would also decrease. Furthermore, it is seen in Fig. 13 that, under the same lateral load, the degree of reduction of lateral deflection of the head of the L–S pile due to increasing the matric suction from 0 to 63 kN is 95% smaller than that of the piles whether with uniform (U) or S–L sections. In other words, under the same horizontal load, with increasing the suction by the same increment, the deflection would not decrease by the same degree in each type of aforementioned piles. Granted that the pile with whether a small-to-large or a uniform cross section possesses considerably smaller initial stiffness of the system with respect to the pile with a large-to-small cross section, increasing the suction could play a decisive role in reducing the deflection of the pile head, while such an issue would be completely reverse for the pile with a large-to-small cross section. The stiffness difference of the system corresponding to various suction conditions increases for the pile with a large-to-small section. As a result, under a specified lateral load, the difference between lateral deflections would decrease for various values of suction stress.

Fig. 13

Variation of pile head lateral deflection corresponding to varying cross sections under: a H = 40 kN and b H = 100 kN lateral loads for various matric suction values in lean clay soil obtained from analytical solution given by Eqs. (9) and (31)

Figure 13 also shows the effect of changing the lateral load on the lateral behavior of different pile types having various cross sections. As seen, with decreasing the horizontal load applied at the pile head, the degree of change in lateral deflection of this spot with respect to the suction change decreases by 90% and 69%, respectively, for the piles with large-to-small and small-to-large sections. That is rooted in stiffness change in the system (the rate of change of the load with respect to lateral deflection) due to the suction alteration. That is, with the decline in lateral load applied on the pile head, the sensitivity of lateral deflection of the pile to alteration of suction decreases. In addition, it is observed that for a given suction value, with decreasing the lateral load, the degree of alteration of the pile deflection with respect to the change of pile type (the impact of the pile type on the lateral deflection of the pile head) decreases by 86% on average. Granted that the stiffness of the system is different for various pile types, the rate of change of the load with respect to lateral deflection is also different. Accordingly, with decreasing the lateral load, the effect of changing the pile type on the alteration of lateral deflection declines.

Since the proposed analytical solution includes some complex equations, a spreadsheet was developed by authors in order to establish the pile head lateral load–deflection curves. The soil properties ($c$, $\varphi$, ${\gamma }_{\mathrm{m}}$ and matric suction) and pile parameters (pile length, diameter and flexural stiffness) were used in spreadsheets as input data. The spreadsheet obtains the nonlinear soil stiffness, $k$, corresponding to the level of induced lateral deflections employing one of Eqs. (30), (31) and (32) for unsaturated sand, lean clay and glacial till soils, respectively. The lateral load–deflection at the pile head was then obtained by substitution the calculated $k$ values into one of Eqs. (8), (9) and (33). Equation (8) was used for calculating the load–deflection curve for piles subject to simultaneous lateral and vertical loads. Equation (9) was used for step-tapered piles, and Eq. (33) was utilized for piles subject to simultaneous lateral load and bending moment.

5 Conclusions

In the present study, an analytical solution is presented for predicting the lateral load–deflection of piles installed in unsaturated soils. This solution includes lateral load–deflection relations and the equations for the determination of the parameter k in unsaturated soil. As shown in the present study, determination of parameter $k$ plays a vital role in unsaturated soils. Therefore, the analytical relations are represented as a function of the degree of saturation, the matric suction or the volumetric water content. The equations of ${k}_{\mathrm{US}1}$ and ${k}_{\mathrm{US}2}$ are the epitome of such relations, which are in conjunction with the elastic domain of the soil. Another method is also represented to determine the parameter k for both linear and nonlinear states of soil. This method is based on differentiating the p–y relations corresponding to Unimin sand, lean clay and glacial till, given, respectively, by Eqs. (27), (28) and (29). In order to evaluate the validity of the present analytical model, the corresponding results are compared with those derived from the lateral loading test performed by Helmers [29] and with the results of the LPILE program. By using the analytical solution and also the LPILE program, the effects of the following phenomena are evaluated on the lateral response of the pile for different values of the soil matric suction: changing the pile type; changing the axial load; and nonuniformity of the cross section of the pile. Therefore, the following results may be mentioned:

• In all pile types under a given lateral load, with increasing the soil suction stress, the pile head deflection decreases due to additional soil resistance originating from the soil suction.

• Under a certain lateral load and a given suction stress, the head deflection of the shorter pile is greater than that of the longer pile.

• For a certain pile, a certain soil matric suction and a certain lateral load, if a vertical load is applied on the pile head, its lateral deflection decreases. This is more pronounced in shorter piles than the longer piles.

• The use of greater cross section in the upper section of the pile with varying cross sections and embedded in unsaturated soils, the lateral deflection of the pile head decreases significantly. This infers that if piles of varying cross sections are of concern, in the presence of unsaturated soils, it is better to have greater cross sections in top segment of piles.

Appendices

Appendix 1

In this section, the equations regarding the slope, moment and shear force are represented for a given point on the beam at the distance x from origin. The relations corresponding to the slope, moment and shear force are given based on Eqs. (34)–(36), respectively.

$${\theta }_{x}={\theta }_{0}{F}_{1}\left(\lambda x\right)-\frac{1}{\lambda EI}{{M}_{0}F}_{2}\left(\lambda x\right)-\frac{1}{{\lambda }^{2}EI}{Q}_{0}{F}_{3}\left(\lambda x\right)-4\lambda {y}_{0}{F}_{4}\left(\lambda x\right)$$

(34)

$$\begin{gathered} M_{x} = M_{0} F_{1} \left( {\lambda x} \right) + \frac{1}{\lambda }Q_{0} F_{2} \left( {\lambda x} \right) \hfill \\ \quad \quad \quad + \frac{k}{{\lambda ^{2} }}y_{0} F_{3} \left( {\lambda x} \right) + \frac{k}{{\lambda ^{3} }}\theta _{0} F_{4} \left( {\lambda x} \right) \hfill \\ \end{gathered}$$

(35)

$$\begin{gathered} Q_{x} = Q_{0} F_{1} \left( {\lambda x} \right) + \frac{k}{\lambda }y_{0} F_{2} \left( {\lambda x} \right) \hfill \\ \quad \quad\;\; + \frac{k}{{\lambda ^{2} }}\theta _{0} F_{3} \left( {\lambda x} \right) - 4\lambda M_{0} F_{4} \left( {\lambda x} \right) \hfill \\ \end{gathered}$$

(36)

Appendix 2

In this section, the relations required for using load-deflection relation of a stepped-piles are represented. The relations corresponding to a, b, c, d, g and f are determined, respectively, from Eqs. (37) to (42).

$$a=\frac{{K}_{2}}{2{\lambda }_{2}^{3}}\left[\frac{4{F}_{2}\left({\Delta }_{2}\right){F}_{3}\left({\Delta }_{2}\right)-4{F}_{1}\left({\Delta }_{2}\right){F}_{4}\left({\Delta }_{2}\right)}{2{{F}_{1}}^{2}\left({\Delta }_{2}\right)+8{F}_{2}\left({\Delta }_{2}\right){F}_{4}\left({\Delta }_{2}\right)}\right]+\frac{{K}_{1}}{{2\lambda }_{1}^{3}}\left[-\frac{4{F}_{1}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)+4{F}_{2}\left({\Delta }_{1}\right){F}_{3}\left({\Delta }_{1}\right)}{2{{F}_{1}}^{2}\left({\Delta }_{1}\right)+8{F}_{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)}\right]$$

(37)

$$b=-\frac{2H{F}_{2}\left({\Delta }_{1}\right)+2{\lambda }_{1}M{F}_{1}\left({\Delta }_{1}\right)}{{\lambda }_{1}\left[2{{F}_{1}}^{2}\left({\Delta }_{1}\right)+8{F}_{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)\right]}$$

(38)

$$c=\frac{{K}_{2}}{{\lambda }_{2}^{2}}\left[\frac{2{F}_{1}\left({\Delta }_{2}\right){F}_{3}\left({\Delta }_{2}\right){F}_{2}\left({\Delta }_{2}\right)-2{{F}_{1}}^{2}\left({\Delta }_{2}\right){F}_{4}\left({\Delta }_{2}\right)}{\left[2{{F}_{1}}^{2}\left({\Delta }_{2}\right)+8{F}_{2}\left({\Delta }_{2}\right){F}_{4}\left({\Delta }_{2}\right)\right]{F}_{2}\left({\Delta }_{2}\right)}+\frac{{F}_{4}\left({\Delta }_{2}\right)}{{F}_{2}\left({\Delta }_{2}\right)}\right]+\frac{{K}_{1}}{{\lambda }_{1}^{2}}\left[\frac{2{F}_{1}\left({\Delta }_{1}\right){F}_{3}\left({\Delta }_{1}\right)-2{{F}_{2}}^{2}\left({\Delta }_{1}\right)}{\left[2{{F}_{1}}^{2}\left({\Delta }_{1}\right)+8{F}_{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)\right]}\right]$$

(39)

$$d =\frac{{K}_{2}}{{\lambda }_{2}^{2}}\left[\frac{2{{F}_{2}}^{2}\left({\Delta }_{2}\right)-2{F}_{1}\left({\Delta }_{2}\right){F}_{3}\left({\Delta }_{2}\right)}{2{{F}_{1}}^{2}\left({\Delta }_{2}\right)+8{F}_{2}\left({\Delta }_{2}\right){F}_{4}\left({\Delta }_{2}\right)}\right]+\frac{{K}_{1}}{{\lambda }_{1}^{2}}\left[\frac{2{{F}_{1}}^{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)-2{F}_{1}\left({\Delta }_{1}\right){F}_{3}\left({\Delta }_{1}\right){F}_{2}\left({\Delta }_{1}\right)}{{F}_{2}\left({\Delta }_{1}\right)\left[2{{F}_{1}}^{2}\left({\Delta }_{1}\right)+8{F}_{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)\right]}-\frac{{F}_{4}\left({\Delta }_{1}\right)}{{F}_{2}\left({\Delta }_{1}\right)}\right]$$

(40)

$$g=\frac{2{\lambda }_{1}M}{{2F}_{2}\left({\Delta }_{1}\right)}+\frac{2H{F}_{1}\left({\Delta }_{1}\right){F}_{2}\left({\Delta }_{1}\right)-2{\lambda }_{1}M{{F}_{1}}^{2}\left({\Delta }_{1}\right)}{\left[2{{F}_{1}}^{2}\left({\Delta }_{1}\right)+8{F}_{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)\right]{F}_{2}\left({\Delta }_{1}\right)}$$

(41)

$$f=\frac{{K}_{2}}{{\lambda }_{2}}\left[\frac{2{F}_{1}\left({\Delta }_{2}\right){{F}_{2}}^{2}\left({\Delta }_{2}\right)-2{{F}_{1}}^{2}\left({\Delta }_{2}\right){F}_{3}\left({\Delta }_{2}\right)}{{F}_{2}\left({\Delta }_{2}\right)\left[{\mathrm{cosh}}^{2}({\Delta }_{2})+{\mathrm{cos}}^{2}({\Delta }_{2})\right]}+\frac{{F}_{3}\left({\Delta }_{2}\right)}{{F}_{2}\left({\Delta }_{2}\right)}\right]+\frac{{K}_{1}}{{\lambda }_{1}}\left[\frac{-2{{F}_{1}}^{2}\left({\Delta }_{1}\right){F}_{3}\left({\Delta }_{1}\right)+2{F}_{1}\left({\Delta }_{1}\right){{F}_{2}}^{2}\left({\Delta }_{1}\right)}{\left[2{{F}_{1}}^{2}\left({\Delta }_{1}\right)+8{F}_{2}\left({\Delta }_{1}\right){F}_{4}\left({\Delta }_{1}\right)\right]{F}_{2}\left({\Delta }_{1}\right)}+\frac{{F}_{3}\left({\Delta }_{1}\right)}{{F}_{2}\left({\Delta }_{1}\right)}\right]$$

(42)

In all above equations, ${\Delta }_{1}$ and ${\Delta }_{2}$ are equal to ${\lambda }_{1}{L}_{1}$ and ${\lambda }_{2}{L}_{2}$, respectively.

Appendix 3

In this section, the relations required for calculating Hansen’s earth pressure coefficients are represented. The relations corresponding to K_q and K_c are represented, respectively, in Eqs. (43) and (48) [27]. Such coefficients would take account the effect of three-dimensional loading of a soil featuring both cohesion and internal friction parameters.

$${K}_{\mathrm{q}}=\frac{{K}_{\mathrm{q}}^{0}+{K}_{\mathrm{q}}^{\infty }{\alpha }_{\mathrm{q}}\frac{z}{D}}{1+{\alpha }_{\mathrm{q}}\frac{z}{D}}$$

(43)

where,

$${K}_{\mathrm{q}}^{0}=\left({\mathrm{e}}^{\left(\frac{\pi }{2}+\varphi \right)\mathrm{tan} \varphi }\mathrm{cos}\left(\varphi \right)\mathrm{tan}\left(45+\frac{\varphi }{2}\right)\right)-\left({\mathrm{e}}^{-\left(\frac{\pi }{2}-\varphi \right)\mathrm{tan}(\varphi )}\mathrm{cos}\left(\varphi \right)\mathrm{tan}\left(45-\frac{\varphi }{2}\right)\right)$$

(44)

$${K}_{\mathrm{q}}^{\infty }={N}_{\mathrm{c}}{d}_{\mathrm{c}}^{\infty }{K}_{0}tg\varphi$$

(45)

$${\alpha }_{\mathrm{q}}=\frac{{K}_{q}^{0}{K}_{0}\mathrm{sin}\varphi }{({K}_{\mathrm{q}}^{\infty }-{K}_{\mathrm{q}}^{0})\mathrm{sin}\left(45+\frac{\varphi }{2}\right)}$$

(46)

$${K}_{0}=1-\mathrm{sin}\varphi$$

(47)

$${K}_{\mathrm{c}}=\frac{{K}_{\mathrm{c}}^{0}+{K}_{\mathrm{c}}^{\infty }{\alpha }_{\mathrm{c}}\frac{z}{D}}{1+{\alpha }_{\mathrm{c}}\frac{z}{D}}$$

(48)

where:

$${K}_{\mathrm{c}}^{0}=\left({\mathrm{e}}^{\left(\frac{\pi }{2}+\varphi \right)\mathrm{tan}(\varphi )}\mathrm{cos}\left(\varphi \right)\mathrm{tan}\left(45+\frac{\varphi }{2}\right)-1\right)\mathrm{cot}(\varphi )$$

(49)

$${K}_{\mathrm{c}}^{\infty }={N}_{\mathrm{c}}{d}_{\mathrm{c}}^{\infty }$$

(50)

$${\alpha }_{\mathrm{c}}=\frac{{K}_{\mathrm{c}}^{0}}{({K}_{\mathrm{c}}^{\infty }-{K}_{\mathrm{c}}^{0})}2\mathrm{sin}\left(45+\frac{\varphi }{2}\right)$$

(51)

$${N}_{\mathrm{c}}=\left[{\mathrm{e}}^{\pi \mathrm{tan}\left(\varphi \right)}{\mathrm{tan}}^{2}\left(45+\frac{\varphi }{2}\right)-1\right]\mathrm{cot}(\varphi )$$

(52)

$${d}_{\mathrm{c}}^{\infty }=1.58+4.09{\mathrm{tan}}^{4}(\varphi )$$

(53)