A general simple method for calculating consolidation settlements of layered clayey soils with vertical drains under staged loadings

Abstract

It is well known that the calculation of consolidation settlements of clayey soils shall consider creep compression in both “primary” consolidation and so-called secondary consolidation periods. Rigorous Hypothesis B method is a coupled method and can consider creep compression in the two periods. But this method needs to solve a set of nonlinear partial differential equations with a proper elastic viscoplastic (EVP) constitutive model so that this method is not easy to be used by engineers. Recently, Yin and his coworkers have proposed a simplified Hypothesis B method for single and two layers of soils. But this method cannot consider complicated loadings such as loading, unloading and reloading. This paper proposes and verifies a general simple method with a new logarithmic function for calculating consolidation settlements of viscous clayey soils without or with vertical drains under staged loadings such as loading, unloading and reloading. This new logarithmic function is suitable to cases of zero or very small initial effective stress. Equations of this simple method are derived for complicated loading conditions. This method is then used to calculate consolidation settlements of clayey soils in three typical cases: Case 1 is a single soil layer without vertical drains under loading only; Case 2 is a two-layered soil profile with vertical drains subjected to loading, unloading and reloading; and Case 3 is a real case of a test embankment on seabed of four soil layers installed with vertical drains under three stages of loading. Settlements of all three cases using the new general simple methods are compared with values calculated using rigorous fully coupled finite element method (FEM) with an elastic viscoplastic (EVP) constitutive model (Cases 1 and 2) and measured data for Case 3. It is found that the calculated settlements are in good agreement with values from FEM and/or measured data. It is concluded that the general simple method is suitable for calculating consolidation settlements of layered viscous clayey soils without or with vertical drains under complicated loading conditions with good accuracy and also easy to use by engineers using spreadsheet calculation.

1 Introduction

In recent decades, many geotechnical structures have been constructed on clayed soil ground, especially on seabed with layered clayey soils and other soil types in many coastal cities in the world. One typical example is two artificial islands (5.10 km² for runway one and 5.45 km² for runway 2) of Kansai International Airport in Osaka, Japan. Runway one was constructed starting in December 1986 and was open in September 1994. Runway two was constructed in May 1999 and was open in August 2007. The excessive settlements have been a problematic issue [1]. In Hong Kong, a total area of 74 km² was reclaimed on seabed since 1887 to 2020. Recently, three large artificial islands were constructed on seabed as part of Hong Kong–Zhuhai–Macao link project. In near future, more marine reclamations will be constructed on seabed in Hong Kong waters. Excessive settlements, especially long-term settlements have been and will be a big concern. It is well known that settlements of saturated clayey soils are caused by dissipation of excessive pore water pressure in voids of soils and also by viscous deformation of soil skeleton. The stress–strain behaviour of the skeleton of clayey soils is time-dependent due to the viscous nature of the skeleton [6, 12, 19, 24]. Methods for calculating settlements of saturated clayey soils shall consider the coupling process of dissipation of excessive pore water pressure and viscous deformation of soil skeleton.

Terzaghi [29] first presented a theory and equations for analysis of the consolidation of soil in one-dimensional (1D) straining (oedometer condition). But this theory cannot consider viscous deformation of soil skeleton. Later, improved methods were proposed, including methods based on Hypothesis A [20, 21] and other methods based on Hypothesis B [2, 3, 6, 10, 11, 19, 15, 16]. Hypothesis A method assumes no creep compression during the “primary” consolidation period, and the creep compression occurs only in the “secondary” compression starting at $t_{\rm EOP}$ which is the time at End-Of-Primary consolidation. Yin and Feng [35] and Feng and Yin [9] pointed out that Hypothesis A method normally underestimates the total settlements due to ignoring creep compression in the “primary” consolidation period.

Hypothesis B is a coupled consolidation analysis using a proper constitutive relationship for the time-dependent stress–strain behaviour of clayey soils. Hypothesis B method needs to solve a set of two partial equations: (i) an equation derived based on mass continuity condition using Darcy’s law and (i) a constitutive equation such Yin and Graham’s [37] 1D elastic viscoplastic model (1D EVP) [38]. Yin and Graham [38] used a finite difference method to solve this set of equations. The computed settlements and excessive pore water pressures were in good agreement with measured data from tests done by Berre and Iversen [5]. Yin and Graham [38] also found that Hypothesis A method underestimated total settlements. Nash and Ryde [22, 23] also used Hypothesis B method adopting 1D EVP model [37] to analyse the consolidation settlement of an embankment on soft ground with vertical drains. Their computed settlements were in good agreement with measured values.

Hypothesis B method needs to solve a set of nonlinear partial different equations, and a computer program is needed. This method is difficult to be used by practicing engineers without such computer program and without a good knowledge of nonlinear constitutive model. To overcome this limitation, Yin and Feng [35] and Feng and Yin [9] proposed a decoupled simplified Hypothesis B method for calculating settlements due to both excessive porewater pressure dissipation and also due to creep compression during and after the “primary” consolidation period. The calculated settlements are in close agreement with measured data and computed values using the fully coupled Hypothesis B method with the aid of computer software. However, this simplified method is neither suitable for complicated loading such as staged unloading and reloading, nor for multiple layers of soils with vertical drains. In this paper, authors propose and verify a general simplified Hypothesis B method (also called a general simple method) for calculating consolidation settlements of layered clayey soils with or without vertical drains under staged loadings including loading, unloading and reloading. Such loading process is commonly used in practice. In addition, a new logarithmic function, which has definition at zero stress, is used in this method for calculating settlements of soils at very small vertical effective stress.

2 Formulation of a general simple method for calculating consolidation settlements of multi-layered soils exhibiting creep under staged loading

2.1 Formulation of a general simplified Hypothesis B method

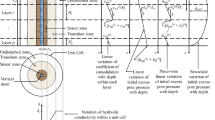
Figure 1 shows a soil profile with n-layers of soils with corresponding thicknesses $(H_{1} ,H_{2} , \ldots H_{n} )$ and depths $(z_{1} ,z_{2} , \ldots z_{n} )$. The total thickness of this profile is $H$. A vertical drain with smear zone is shown in Fig. 1, where $d_{d} = 2r_{d}$ is the diameter of a drain equal to twice radius $r_{d}$ of the drain, $d_{s} = 2r_{s}$ is the diameter of a smear zone equal to twice radius $r_{s}$ of the smear zone, $d_{e} = 2r_{e}$ is the diameter of an equivalent unit cell equal to twice radius $r_{e}$ of the cell. It is noted that vertical drains are installed all in the same triangular pattern or the same square pattern and are subjected a uniform surcharge over all vertical drains. Therefore, deformation of soils in all unit cells is approximately in the vertical direction. Thus, soils in each unit cell are assumed to be in 1D straining on average. 1D straining constitutive models can be used, for example 1D EVP model [36, 37]. If a horizontal soil profile has no vertical drains, then $d_{d} = d_{s} = 0$ and $d_{e} = \infty$ in Fig. 1, which is also suitable for multi-layered soils without vertical drains.

Fig. 1

A soil profile of n-layers with vertical drain subjected to uniform surcharge q(t) with time

Authors propose a general simplified Hypothesis B method for calculating consolidation settlement of multi-layered viscous soils with or without vertical drains under any loading condition for the soil profile under uniform surcharge q(t) in Fig. 1. Formulation of this general simple method is presented below:

$$\begin{aligned} S_{{{\text{total}}B}} & = S_{{{\text{primary}}}} + S_{{{\text{creep}}}} = \sum\limits_{j = 1}^{j = n} {U_{j} S_{fj} } + \sum\limits_{j = 1}^{j = n} {S_{{{\text{creep}}j}} } \\ & {\kern 1pt} = U\sum\limits_{j = 1}^{j = n} {S_{fj} } + \sum\limits_{j = 1}^{j = n} {\left[ {\alpha U_{j}^{\beta } S_{{{\text{creep}},fj}} + \left( {(1 - \alpha U_{j}^{\beta } } \right)S_{{\text{creep,dj}}} } \right]} \\ & \quad {\text{for}}\;{\text{all}}\;t \ge t_{{{\text{EOP}},{\text{lab}}}} \left( {t \ge t_{{{\text{EOP}},{\text{field}}}} {\text{for}}\;S_{{{\text{creep}},dj}} } \right) \\ \end{aligned}$$

(1)

The formulation in Eq. (1) is a de-coupled simplified Hypothesis B method. The “de-coupled” means that “primary” consolidation settlement $S_{{{\text{primary}}}}$ is separated from creep settlement $S_{{{\text{creep}}}}$. The separation of “primary” consolidation from “secondary” compression for a laboratory test is shown in Fig. 2. A normal soil specimen in oedometer test has 20 mm in thickness with double drainage so that the value of $t_{{{\text{EOP}},{\text{lab}}}}$ in Fig. 2 is small with tens of minutes only. $t_{{{\text{EOP}},{\text{field}}}}$ in Eq. (1) is the End-Of-Primary (EOP) time for soil layers in the field. The value of $t_{{{\text{EOP}},{\text{field}}}}$ may vary from a few years to tens of years depending on the thickness and permeability of soils in the field. $t_{{24{\text{hrs}}}}$ in Fig. 2 is the time with duration of 24 h in an oedometer test, normally larger than $t_{{{\text{EOP}},{\text{lab}}}}$ with $t_{{{\text{EOP}},{\text{lab}}}} < t_{{24{\text{hrs}}}} < t_{{{\text{EOP}},{\text{field}}}}$ normally true. In practical application, $t_{{{\text{EOP}},{\text{lab}}}}$ will be replaced by the time $t_{0}$, which is conveniently adopted as 24 h with conventional oedometer tests. The compression indices are calculated using test data from the same duration of 24 h as $t_{0}$. It shall be pointed out that in Eq. (1), the items of $S_{{{\text{creep}},dj}}$ will be zero for $t \le t_{{{\text{EOP}},{\text{field}}}}$ and will become positive $t > t_{{{\text{EOP}},{\text{field}}}}$.

Fig. 2

Curve of void ratio versus log (time) and “secondary” compression coefficient

In Eq. (1), “primary” consolidation settlement $S_{{{\text{primary}}}}$ shall be calculated for multiple soil layers with or without a vertical drain:

$$S_{{{\text{primary}}}} = \sum\limits_{j = 1}^{j = n} {U_{j} S_{fj} } = U\sum\limits_{j = 1}^{j = n} {S_{fj} }$$

(2)

where $U_{j}$ is combined average degree of consolidation for j-layer and $U$ is combined average degree of consolidation for all multiple soil layers with or without a vertical drain:

$$U_{j} = 1 - (1 - U_{vj} )(1 - U_{rj} )$$

(3a)

$$U = 1 - (1 - U_{v} )(1 - U_{r} )$$

(3b)

Equation (3) is called Carrillo’s (1942) formula where $U_{vj} \;{\text{and}}\;U_{rj}$ or $U_{v} \;{\text{and}}\;U_{r}$ are average degree of vertical consolidation and radial consolidation for j-layer or multiple soil layers. If there is no vertical drain, $U_{rj} = U_{r} = 0$, from (3), $U_{j} = U_{vj}$ or $U = U_{v}$. For multiple soil layers, the superposition of the average degree of consolidation for each layer is not valid since the continuation condition at each interface of two layers must be satisfied. $S_{fj}$ is the final “primary” consolidation at End-Of-Primary (EOP) consolidation for j-layer. $S_{fj}$ can be calculated using the coefficient of volume compressibility $m_{v}$ or compression indexes $C_{c}$, $C_{r}$ of j-layer. More details on calculations of $S_{fj}$ and U are presented in the next section.

In Eq. (1), $S_{{{\text{creep}}j}}$ is creep settlement of soil skeleton in j-layer and is equal to:

$$\begin{aligned} S_{{{\text{creep}}j}}\, =\, \alpha U_{j}^{\beta } S_{{{\text{creep}},fj}} + \left( {1 - \alpha U_{j}^{\beta } } \right)S_{{{\text{creep}},dj}} \\ & \quad {\text{for}}\,{\text{all}}\,t \ge t_{{{\text{EOP}},{\text{lab}}}} (t \ge t_{{{\text{EOP}},{\text{field}}}} \,{\text{for}}\;S_{{{\text{creep}},dj}} ) \\ \end{aligned}$$

(4a)

Equation (4a) can also be written as:

$$S_{{{\text{creep}}j}} = \left\{ \begin{gathered} \alpha U_{j}^{\beta } S_{{{\text{creep}},fj}} \quad {\text{for}}\;t \ge t_{{{\text{EOP}},{\text{lab}}}} \hfill \\ \alpha U_{j}^{\beta } S_{{{\text{creep}},fj}} + \left( {1 - \alpha U_{j}^{\beta } } \right)S_{{{\text{creep}},dj}} \;t \ge t_{{{\text{EOP}},{\text{field}}}} \hfill \\ \end{gathered} \right.$$

(4b)

where $U_{j}$ is from Eq. (3a) with value from 0 to 1 only and $\beta$ is a power index with value from 0 to 1. Yin [33] used a parameter $\alpha = 1$ without $U_{j}^{\beta }$. But this over-predicted total consolidation settlement. Yin and Feng [35] and Feng and Yin [9] used $\alpha = 0.8$ without $U_{j}^{\beta }$ and gave results in close agreement with measured data and values from rigorous fully coupled consolidation modelling. In this paper, a general term of $\alpha U_{j}^{\beta }$ is suggested. See more examples later in this paper on more accurate prediction results.

$S_{{{\text{creep}},fj}}$ in Eqs. (1) or (4) is creep settlement of j-layer under the “final” vertical effective stress after load increased, ignoring the excess porewater pressure. $S_{{{\text{creep}},dj}}$ in Eqs. (1) or (4) is “delayed” creep settlement of j-layer under the “final” vertical effective stress ignoring the excess porewater pressure. $S_{{{\text{creep}},dj}}$ starts for $t \ge t_{{{\text{EOP}},{\text{field}}}}$, in other words, is “delayed” by time of $t_{{{\text{EOP}},{\text{field}}}}$ to occur. $t_{{{\text{EOP}},{\text{field}}}}$ is the End-Of-Primary (EOP) of consolidation for field condition of j-layer. More discussion on $S_{{{\text{creep}},fj}}$ and $S_{{{\text{creep}},dj}}$ is in later section.

2.2 Calculation of $S_{fj}$

In Eq. (2), the total primary consolidation settlement $S_{{{\text{primary}}}}$ is sum of settlements $S_{fj}$ of all sub-layers multiplied by an over-all average degree of consolidation $U$. This section presents methods and solutions for calculating $S_{fj}$. In the following calculations, in order to make all equations and text in following paragraphs concise, the layer index “j” is removed, keeping in minds that these equations are for one soil layer.

If the coefficient of volume compressibility $m_{v}$ is used and vertical effective stress increment $\Delta \sigma_{z}^{^{\prime}}$ and thickness H are known for a soil j-layer, $S_{f}$ for j-layer is:

$$S_{f} = m{}_{v}\Delta \sigma_{z}^{^{\prime}} H$$

(5)

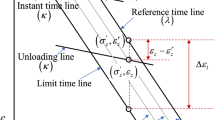
It is noted that $m_{v}$ is not a constant, depending on vertical effective stress, and shall be used with care. For clayey soils or soft soils, it is better to use $C_{c}$ and $C_{r}$ to calculate $S_{f}$ for higher accuracy. An oedometer test is normally done on the same specimen in multi-stages. According to British Standard 1377 [7], the standard duration for each load shall normally last for 24 h. In this paper, the indexes $C_{r} ,\;C_{c}$ and pre-consolidation stress point $(\sigma_{zp}^{^{\prime}} ,\varepsilon_{zp} )\;$ are all determined from the standard oedometer test with duration of 24 h (1 day), that is, $t_{{24{\text{hrs}}}} = 1\;{\text{day}}$, for each load and for each layer. The idealized relationship between the vertical strain and the log (effective stress) is shown in Fig. 3 with loading, unloading and reloading states.

Fig. 3

Relationship of strain (or void ratio) and log(effective stress) with different consolidation states

Yin and Graham [36,37] and Yin [31] pointed out limitations of using a logarithmic function for fitting creep curve of log(time) and strain, when time is zero. In 1D EVP model, Yin and Graham [36,37] introduced a time parameter $t_{o}$ in a logarithmic function to care creep starting from time zero. In many real cases, the vertical effective stress $\sigma_{z}^{^{\prime}}$ is zero or very near zero, for example, $\sigma_{z}^{^{\prime}}$ at surface or near surface of seabed soils or soil ground. If a normal logarithmic function is used for fitting compression curve of log(effective stress) and strain, when the stress is zero, the strain is infinite. To overcome this problem, a unit stress $\sigma_{{{\text{unit}}}}^{\prime }$ is added to the logarithmic function in this paper and was also in Yin’s a nonlinear logarithmic-hyperbolic function in [32]. Adding $\sigma_{{{\text{unit}}}}^{\prime }$ in linear logarithmic stress function is particularly necessary for very soft soils in a soil ground with initial effective stress zero at the top of the surface. For example, the initial vertical effective stress at the top surface in soft Hong Kong Marine Clay (HKMC) in seedbed is zero.

As shown in Fig. 3 and assuming stresses in each layer are uniform, the final settlements $S_{f}$ for j-layer in Eq. (2) for six cases are calculated as follows by adding $\sigma_{{{\text{unit}}1}}^{\prime }$ and $\sigma_{{{\text{unit}}2}}^{\prime }$ in a new logarithmic stress function for elastic compression (OCL) and elastic–plastic (NCL) compression separately.

• (i) Loading from point 1 to point 2 with ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z1}^{^{\prime}}$ and point 2 in OCL:

  $$S_{f,1 - 2} = \varepsilon_{z,1 - 2} H = \frac{{C_{r} }}{{1 + e_{o} }}\log \left( {{{\sigma_{z2}^{\prime } + \sigma_{{{\text{unit}}1}}^{\prime } } \mathord{\left/ {\vphantom {{\sigma_{z2}^{\prime } + \sigma_{{{\text{unit}}1}}^{\prime } } {\sigma_{z1}^{\prime } + \sigma_{{{\text{unit}}1}}^{\prime } }}} \right. \kern-\nulldelimiterspace} {\sigma_{z1}^{\prime } + \sigma_{{{\text{unit}}1}}^{\prime } }}} \right)H$$

  (6a)

  The $\varepsilon_{z,1 - 2}$ is the vertical strain increase due to stress increases from $\sigma_{z1}^{^{\prime}}$ to $\sigma_{z2}^{^{\prime}}$. The OCR is over-consolidation ratio, and OCL is an over-consolidation line. If $\sigma_{{{\text{unit}}1}}^{\prime }$ is zero, (6a) goes back to conventional logarithmic stress function. The value of $\sigma_{{{\text{unit}}1}}^{\prime }$ is from 0.001 kPa to 1 kPa. For very soft soils, $\sigma_{unit1}^{^{\prime}}$ takes values close to 0.01 kPa. Similar strain increase symbols are used in the following equations. Equation (6a) can avoid singularity problem at initial stress zero ($\sigma_{z1}^{^{\prime}} = 0$) and is good for very soft soils, such as slurry under self-weight consolidation.

• (ii) Loading from point 1 to point 4 with ${\text{OCR}} = \sigma_{zp}^{\prime } /\sigma_{z1}^{\prime } > 1$ and point 4 in NCL:

  $$S_{f,1 - 4} = \varepsilon_{z,1 - 4} H = \left[ {{{C_{r} } \mathord{\left/ {\vphantom {{C_{r} } {1 + e_{o} }}} \right. \kern-\nulldelimiterspace} {1 + e_{o} }}\log \left( {{{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } {\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right) + \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {{{\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)} \right]H$$

  (6b)

  NCL is a normal consolidation line. Adding $\sigma_{{{\text{unit}}1}}^{\prime }$ and $\sigma_{{{\text{unit}}2}}^{\prime }$ in Eq. (6b) can avoid singularity problem at initial stress zero ($\sigma_{z1}^{^{\prime}} = \sigma_{zp}^{^{\prime}} = 0$).

• (iii) Loading from point 3 to point 4 with ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z3}^{^{\prime}} = 1$ and point 4 in NCL:

  $$S_{f,3 - 4} = \varepsilon_{z,3 - 4} H = {{C_{c} } \mathord{\left/ {\vphantom {{C_{c} } {1 + e_{o} }}} \right. \kern-\nulldelimiterspace} {1 + e_{o} }}\log \left( {{{\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)H$$

  (6c)

• (iv) Unloading from point 4 to point 6:

  $$S_{f,4 - 6} = \varepsilon_{z,4 - 6} H = {{C_{r} } \mathord{\left/ {\vphantom {{C_{r} } {1 + e_{o} }}} \right. \kern-\nulldelimiterspace} {1 + e_{o} }}\log \left( {{{\sigma_{z6}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z6}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } {\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right)H$$

  (6d)

• (v) Reloading from point 6 to point 5:

  $$S_{f,6 - 5} = \varepsilon_{z,6 - 5} h = {{C_{r} } \mathord{\left/ {\vphantom {{C_{r} } {1 + e_{o} }}} \right. \kern-\nulldelimiterspace} {1 + e_{o} }}\log \left( {{{\sigma_{z5}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z5}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } {\sigma_{z6}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{z6}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right)h$$

  (6e)

• (vi) Reloading from point 6 to point 7:

  $$S_{f,6 - 7} = \varepsilon_{z,6 - 7} H = \left[ {{{C_{r} } \mathord{\left/ {\vphantom {{C_{r} } {1 + e_{o} }}} \right. \kern-\nulldelimiterspace} {1 + e_{o} }}\log \left( {{{\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } {\sigma_{z6}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{z6}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right) + \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {{{\sigma_{z7}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z7}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } {\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{z4}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)} \right]H$$

  (6f)

However, the initial stresses and stress increments in a clayey soil layer are not uniform; Eq. (6) cannot be used. There are two approaches to consider this non-uniform stress as below.

• (a) Dividing j-layer into sub-layers

A general method is to divide this soil layer into sub-layers with smaller thickness, say, 0.25 m to 0.5 m, which has been adopted by previous studies [35, 40]. The stresses and parameters in each sub-layer are considered uniform and constant. The final settlement $S_{f}$ for j-layer is sum of settlements of all sub-layers [9, 35]. For each sub-layer with uniform stresses, equations in Eqs. (6a–6f) can be used depending on the initial and final stress points. This method is flexible and valid for complicated cases in which vertical stress and pre-consolidation pressure may not be uniform.

• (b) Special case of constant parameters $C_{c} ,C_{r}$ and linear changes of initial stresses, stress increments, and pre-consolidation pressure for j-layer

For a clayey soil layer of thickness H, $C_{c} ,C_{r}$ are often constant, but stresses may vary with depth z. Figure 4 shows linear changes of initial vertical effective stress, total vertical effective stress, vertical pre-consolidation stress for a soil layer. Linear changes are in following equations:

$$\sigma_{z1}^{^{\prime}} = \sigma_{z1,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right)$$

(7a)

$$\sigma_{zp}^{^{\prime}} = \sigma_{zp,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{zp,H}^{^{\prime}} - \sigma_{zp,0}^{^{\prime}} } \right)$$

(7b)

$$\sigma_{z}^{^{\prime}} = \sigma_{z4,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right)$$

(7c)

where $\sigma_{z1}^{^{\prime}}$ is the initial vertical effective stress. It is noted that the increase of pre-consolidation stress (or pressure) $\sigma_{zp}^{^{\prime}}$ may not be as fast as the total vertical effective stress $\sigma_{z}^{^{\prime}}$ as shown in Fig. 4. Therefore, there is a point which $\sigma_{zp}^{^{\prime}} = \sigma_{z}^{^{\prime}}$ at depth z_p. Let us consider a general case of loading from point 1 to point 4, the calculation of settlements of j-layer for four different cases are in following.

Fig. 4

Linear changes of initial vertical effective stress ($\sigma_{z1}^{^{\prime}}$), total vertical effective stress ($\sigma_{z}^{^{\prime}}$), vertical pre-consolidation stress ($\sigma_{zp}^{^{\prime}}$) for a soil layer

• (i) Normal consolidation case: ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z1}^{^{\prime}} = 1$.

In this case, initial effective stress $\sigma_{z1}^{^{\prime}}$ and pre-consolidation stress $\sigma_{zp}^{^{\prime}}$ are the same, after the stress increase, $\sigma_{z}^{^{\prime}} > \sigma_{zp}^{^{\prime}} = \sigma_{z1}^{^{\prime}}$. In this case, $S_{f,1 - 4}$ is:

$$S_{f,1 - 4} = \int\limits_{z = 0}^{z = H} {\varepsilon_{z,1 - 4} dz} = \int\limits_{z = 0}^{z = H} {\frac{{C_{c} }}{{1 + e_{o} }}\log \left( {{{\sigma_{z}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \mathord{\left/ {\vphantom {{\sigma_{z}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)dz}$$

(8a)

Substituting Eq. (6) into the above equation:

$$\begin{aligned} S_{f,1 - 4} = & \int\limits_{z = 0}^{z = H} {\frac{{C_{c} }}{{(1 + e_{o} )\ln (10)}}\ln \left[ {\frac{{\sigma_{z4,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right) + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}{{\sigma_{z1,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right) + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right]dz} = \frac{{C_{c} }}{{(1 + e_{o} )\ln (10)}} \\ & \quad \quad \left\{ {\int\limits_{z = 0}^{z = H} {\ln \left[ {\sigma_{z4,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right) + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \right]dz - \int\limits_{z = 0}^{z = H} {\ln \left[ {\sigma_{z1,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right) + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \right]dz} } } \right\} \\ \end{aligned}$$

Let us introduce a new variable $x = \sigma_{z4,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right) + \sigma_{{{\text{unit}}2}}^{^{\prime}}$ and $y = \sigma_{z1,0}^{^{\prime}} + \frac{z}{H}\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right) + \sigma_{{{\text{unit}}2}}^{^{\prime}}$; we have $dz = \left[ {H/\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right)} \right]dx$ and $dz = \left[ {H/\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right)} \right]dy$. Noting that for $z = 0\;{\text{and}}\;H$, we have $x_{z = 0} = \sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}}$ and $x_{z = H} = \sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}}$; $y_{z = 0} = \sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}}$ and $y_{z = H} = \sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}}$. The above equation can be written as:

$$S_{f,1 - 4} = \frac{{C_{c} }}{{(1 + e_{o} )\ln (10)}}\left\{ {\int\limits_{{x = \sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}^{{x = \sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }} {\frac{H}{{\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right)}}\ln xdx} - \int\limits_{{y = \sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}^{{y = \sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }} {\frac{H}{{\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right)}}\ln ydy} } \right\}$$

Since $\int {\ln xdx = x\ln x - x}$ and $\int {\ln ydy = y\ln y - y}$, the above equation becomes:

$$S_{f,1 - 4} = \frac{{C_{c} }}{{(1 + e_{o} )\ln (10)}}\left\{ {\frac{H}{{\left( {\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} } \right)}}\left[ {x\ln x - x} \right]_{{x = \sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}^{{x = \sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }} - \frac{H}{{\left( {\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} } \right)}}\left[ {y\ln y - y} \right]_{{y = \sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}^{{y = \sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }} } \right\}$$

From above, we have:

$$\begin{gathered} S_{f,1 - 4} = \frac{{C_{c} }}{{(1 + e_{o} )\ln (10)}}\left\{ {\frac{H}{{(\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} )}}} \right.[(\sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (\sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - \hfill \\ \quad ((\sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (\sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ))] - \frac{H}{{(\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} )}}[(\sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) \hfill \\ \quad - (\sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - \left. {((\sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (\sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ))]} \right\} \hfill \\ \end{gathered}$$

(8b)

• (ii) Over-consolidation case: ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z1}^{^{\prime}} > 1$ and $\sigma_{z}^{^{\prime}} \ge \sigma_{zp}^{^{\prime}} \;{\text{for}}\;0 \le z \le H$.

Figure 4 shows a case commonly encountered in the field. Initially, the soil is over-consolidated with ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z1}^{^{\prime}} > 1$. After increased loading $\Delta \sigma_{z}^{^{\prime}} = \sigma_{z}^{^{\prime}} - \sigma_{z1}^{^{\prime}} \;$, we have and $\sigma_{z}^{^{\prime}} \ge \sigma_{zp}^{^{\prime}} \;{\text{for}}\;0 \le z \le H$. In this case, we have:

$$S_{f,1 - 4} = \int\limits_{z = 0}^{z = H} {\varepsilon_{z,1 - 4} dz} = \int\limits_{z = 0}^{z = H} {\left[ {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right) + \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)} \right]dz}$$

(8c)

Substituting equations in (6) for $\sigma_{z1}^{^{\prime}} ,\sigma_{zp}^{^{\prime}} ,\sigma_{z}^{^{\prime}}$ into (8c) and using the same method in (i), the integration of above equation is:

$$\begin{gathered} S_{f,1 - 4} = \frac{{C_{r} }}{{(1 + e_{o} )\ln (10)}}\left\{ {\frac{H}{{(\sigma_{zp,H}^{^{\prime}} - \sigma_{zp,0}^{^{\prime}} )}}[(\sigma_{zp,H}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (\sigma_{zp,H}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - (\sigma_{zp,H}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - } \right. \hfill \\ \;((\sigma_{zp,0}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (\sigma_{zp,0}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - (\sigma_{zp,0}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ))] - \frac{H}{{(\sigma_{z1,H}^{^{\prime}} - \sigma_{z1,0}^{^{\prime}} )}}[(\sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (\sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) \hfill \\ \; - (\sigma_{z1,H}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - ((\sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (\sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - (\sigma_{z1,0}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\left. {)]} \right\} + \hfill \\ \;\frac{{C_{c} }}{{(1 + e_{o} )\ln (10)}}\left\{ {\frac{H}{{(\sigma_{z4,H}^{^{\prime}} - \sigma_{z4,0}^{^{\prime}} )}}} \right.[(\sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (\sigma_{z4,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - \hfill \\ \;((\sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (\sigma_{z4,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ))] - \frac{H}{{(\sigma_{zp,H}^{^{\prime}} - \sigma_{zp,0}^{^{\prime}} )}}[(\sigma_{zp,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{zp,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) \hfill \\ \; - (\sigma_{zp,H}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - \left. {((\sigma_{zp,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (\sigma_{zp,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (\sigma_{zp,0}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} ))]} \right\} \hfill \\ \end{gathered}$$

(8d)

• (iii) Over-consolidation case: ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z1}^{^{\prime}} > 1$ and $\sigma_{z}^{^{\prime}} < \sigma_{zp}^{^{\prime}} \;{\text{for}}\;0 \le z \le z_{p}$.

Figure 4 shows a case in which ${\text{OCR}} = \sigma_{zp}^{^{\prime}} /\sigma_{z1}^{^{\prime}} > 1$, but $\sigma_{z}^{^{\prime}} < \sigma_{zp}^{^{\prime}} \;{\text{for}}\;0 \le z \le z_{p}$ and $\sigma_{z}^{^{\prime}} \ge \sigma_{zp}^{^{\prime}} \;{\text{for}}\;z_{p} \le z \le H$. In this case, the settlement calculation shall consider depth $z_{p}$:

$$S_{f,1 - 4} = \int\limits_{z = 0}^{z = H} {\varepsilon_{z,1 - 4} dz} = \left\{ \begin{gathered} \int\limits_{z = 0}^{{z = z_{p} }} {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right)dz\quad {\text{for}}\;0 \le z \le z_{p} } \hfill \\ \int\limits_{{z = z_{p} }}^{z = H} {\left[ {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right) + \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)} \right]dz\quad {\text{for}}\;z_{p} \le z \le H} \hfill \\ \end{gathered} \right.$$

(8e)

Linear equations in Eq. (6) for $\sigma_{z1}^{^{\prime}} ,\sigma_{zp}^{^{\prime}} ,\sigma_{z}^{^{\prime}}$ can be substituted into Eq. (8e). Analytical integration solution can be obtained using the same method in (i) and is not presented here. Equations like Eq. (8) can be obtained for other loading, unloading, and reloading cases with linear changes of stresses and are not discussed here.

In many calculations, $m_{v}$ is needed, for example, in Eq. (5) and $c_{v} = k_{v} /(m_{v} \gamma_{w} )$ and $c_{r} = k_{r} /(\gamma_{w} m_{v} )$ in order to calculate $U_{v}$ and $U_{r}$. If indexes $C_{r} ,\;C_{c}$ and pre-consolidation stress point $(\sigma_{zp}^{^{\prime}} ,\varepsilon_{zp} )\;$ are used to calculate final settlements in Eqs. (6, 7 and 8), the coefficient of vertical volume compressibility $m_{v}$ can be back-calculated as.

• (i) For the case of Eq. (6b) in normal loading:

  $$m_{v,1 - 4} = \frac{{S_{f,1 - 4} }}{{H\left( {\sigma_{z4}^{^{\prime}} - \sigma_{z1}^{^{\prime}} } \right)}}$$

  (9a)

• (ii) For the case of Eq. (6d) in unloading:

  $$m_{v,4 - 6} = \frac{{S_{f,4 - 6} }}{{H\left( {\sigma_{z4}^{^{\prime}} - \sigma_{z6}^{^{\prime}} } \right)}}$$

  (9b)

In Eqs. (9a) and (9b), settlements and stress increments are known so that $m_{v}$ corresponding to the same stress increment can be calculated. In Eq. (9b), $S_{f,4 - 6}$ and $(\sigma_{z4}^{^{\prime}} - \sigma_{z6}^{^{\prime}} )$ are both negative so that $m_{v,4 - 6}$ is positive. The calculation method for $m_{v}$ in Eqs. (9a) and (9b) can be applied to other different loading stages.

2.3 Calculation of $U_{j}$ and $U$

In Eqs. (1) and (2), an average degree of consolidation $U_{j}$ for j-layer or over-all average degree of consolidation $U$ is needed. The basic definition of $U_{j}$ for j-layer is:

$$U_{j} = \frac{{S_{j} (t)}}{{S_{fj} }} = \frac{{\int\limits_{z = 0}^{{z = H_{j} }} {m_{vj} \Delta \sigma_{zj}^{^{\prime}} (t)dz} }}{{\int\limits_{z = 0}^{{z = H_{j} }} {m_{vj} \Delta \sigma_{zjf}^{^{\prime}} dz} }} = \frac{{\int\limits_{z = 0}^{{z = H_{j} }} {[u_{eij} - u_{ej} (t)]dz} }}{{\int\limits_{z = 0}^{{z = H_{j} }} {u_{eij} dz} }} = 1 - \frac{{\int\limits_{z = 0}^{{z = H_{j} }} {u_{ej} (t)dz} }}{{\int\limits_{z = 0}^{{z = H_{j} }} {u_{eij} dz} }}$$

(10a)

where $S_{fj}$ is the final settlement for j-layer using $m_{vj}$ and $\Delta \sigma_{zjf}^{^{\prime}}$, calculated using Eq. (5). It is noted that the final vertical effective stress increment $\Delta \sigma_{zjf}^{^{\prime}}$ is equal to the initial excess pore water pressure $u_{eij}$ for j-layer. $u_{ej} (t)$ is the excess pore water pressure at time t for j-layer. Equation (10a) can be written as:

$$U_{j} = 1 - \frac{{\frac{1}{{H_{j} }}\int\limits_{z = 0}^{{z = H_{j} }} {u_{ej} (t)dz} }}{{\frac{1}{{H_{j} }}\int\limits_{z = 0}^{{z = H_{j} }} {u_{eij} dz} }} = 1 - \frac{{\overline{u}{}_{ej}(t)}}{{\overline{u}{}_{eij}}}$$

(10b)

where $\overline{u}{}_{eij}$ and $\overline{u}{}_{ej}$ are the average initial and current excess porewater pressures, respectively, t for j-layer. The over-all average degree of consolidation $U$ is:

$$U = \frac{{S_{{{\text{primary}}}} }}{{S_{f} }} = \frac{{\sum\nolimits_{j = 1}^{j = n} {S_{j} (t)} }}{{\sum\nolimits_{j = 1}^{j = n} {S_{fj} } }} = \frac{{\sum\nolimits_{j = 1}^{j = n} {\int\nolimits_{z = 0}^{{z = H_{j} }} {m_{vj} \Delta \sigma_{zj}^{^{\prime}} (t)dz} } }}{{\sum\nolimits_{j = 1}^{j = n} {\int\nolimits_{z = 0}^{{z = H_{j} }} {m_{vj} \Delta \sigma_{zjf}^{^{\prime}} dz} } }} = 1 - \frac{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} \int\nolimits_{z = 0}^{{z = H_{j} }} {u_{ej} (t)dz} } }}{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} \int\nolimits_{z = 0}^{{z = H_{j} }} {u_{eij} dz} } }}$$

(11a)

From Eq. (10a), $\overline{u}{}_{ej}(t) = (1 - U_{j} )\overline{u}{}_{eij}$. Using this relation, (11a) can be written:

$$\begin{aligned} U = & 1 - \frac{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} \frac{{H_{j} }}{{H_{j} }}\int\nolimits_{z = 0}^{{z = H_{j} }} {u_{ej} (t)dz} } }}{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} \frac{{H_{j} }}{{H_{j} }}\int\nolimits_{z = 0}^{{z = H_{j} }} {u_{eij} dz} } }} = 1 - \frac{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{ej} (t)} }}{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{eij} } }} = 1 - \frac{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} (1 - U_{j} )\overline{u}_{eij} )} }}{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{eij} } }} \\ & = 1 - \frac{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{eij} - \sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} U_{j} \overline{u}_{eij} } } }}{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{eij} } }} = \frac{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{eij} U_{j} } }}{{\sum\nolimits_{j = 1}^{j = n} {m_{vj} H_{j} \overline{u}_{eij} } }} \\ \end{aligned}$$

(11b)

Attention shall be paid to the definition and differences of $U_{j}$ and $U$. The following paragraphs summarize existing solutions for $U_{v}$, $U_{r}$, $U_{j}$ and $U$.

The early analytical solutions were obtained by Terzaghi [29] for a single soil layer with thickness $H$ under suddenly applied load for 1-D straining. Charts of these solutions can be found in Craig's Soil Mechanics Knappett [17]. For double drainage with linear excess pore water pressure $u_{e}$ distribution or one-way drainage with uniform $u_{e}$ distribution, the following appreciate equation is good and simple to calculate $U_{v}$:

$$\left\{ \begin{gathered} {\text{For}}\;U_{v} < 0.6:\quad T_{v} = \frac{\pi }{4}U_{v}^{2} ,\quad U_{v} = \sqrt {\frac{{4T_{v} }}{\pi }} \hfill \\ {\text{For}}\;U_{v} \ge 0.6:\quad T_{v} = - 0.944\log (1 - U_{v} ) - 0.085,\quad U_{v} = 1 - 10^{{ - \,\,\frac{{T_{v} + 0.085}}{0.933}}} \hfill \\ \end{gathered} \right.$$

(12a)

If we assume that when $U_{v} = 98\%$, $u_{e} \approx 0$; time at $U_{v} = 98\%$ is selected as time at EOP in the field $t_{{{\text{EOP}},{\text{field}}}}$. We have:

$$T_{v} = - 0.944\log (1 - U_{v} ) - 0.085 = 0.150$$

(12b)

$$t_{{{\text{EOP}},{\text{field}}}} = \frac{{T_{v} d^{2} }}{{c_{v} }} = \frac{{1.50d^{2} }}{{c_{v} }}$$

(12c)

where $d$ is the maximum drainage path of a soil layer, if double drainage, $d = H/2$, $c_{v}$ is the coefficient of vertical consolidation.

To consider ramp loading as shown in Fig. 4, a simple correction method for $U_{v}$ proposed by Terzaghi [29] can be used. Solutions to 1-D consolidation under depth-dependent ramp load and to special 1-D consolidation problems can be found in Zhu and Yin [41, 48] Solutions to double soil layers without vertical drains under ramp load can be found in Zhu and Yin [43]. Solutions to 2-D consolidation of a single soil layer with vertical drains under ramp load were obtained by Zhu and Yin [45 , 46 , 47]. Solutions to 2-D consolidation of a single soil layer with vertical drains without well resistance under suddenly applied load were obtained by Barron [4]. Hansbo [14] presented analytical solution to consolidation problem of a soil with vertical drains considering both smear zone and well resistance under suddenly applied load under equal vertical strain assumption.

Solutions to consolidation problem of a stratified soil with vertical and horizontal drainage under ramp loading were obtained by Walker and Indraratna [26] and Walker et al. [27] using a spectral method. The main partial differential equation for the average excess pore water pressure $\overline{u}$ using spectral method is:

$$\frac{{m_{v} }}{{\overline{m}_{v} }}\frac{{\partial \overline{u}}}{\partial t} = - \left[ {dT_{r} \frac{\eta }{{\overline{\eta }}}\overline{u} - dT_{v} \left( {\frac{\partial }{\partial Z}\left( {\frac{{k_{v} }}{{\overline{k}_{v} }}} \right)\frac{{\partial \overline{u}}}{\partial Z} + \frac{{k_{v} }}{{\overline{k}_{v} }}\frac{{\partial^{2} \overline{u}}}{{\partial Z^{2} }}} \right)} \right] + \frac{{m_{v} }}{{\overline{m}_{v} }}\frac{{\partial \overline{\sigma }}}{\partial t} + dT_{r} \frac{\eta }{{\overline{\eta }}}w$$

(13a)

where $\eta = \frac{{k_{r} }}{{r_{e}^{2} \mu }},\;{\text{d}} T_{v} = \frac{{\overline{c}_{v} }}{{H^{2} }},\;{\text{d}} T_{r} = \frac{{2\overline{\eta }}}{{\gamma_{w} \overline{m}_{v} }},\;\overline{c}_{v} { = }\frac{{\overline{k}_{v} }}{{\gamma_{w} \overline{m}_{v} }},\;Z = \frac{z}{H}$. Vertical and horizontal drainages are considered simultaneously in Eq. (13a). All parameters are explained below:

$\overline{u}$: averaged excess pore water pressure (averaged along radial coordinate $r$) at depth Z, a function of time t and Z.

$\overline{\sigma }$: average total stress (averaged along $r$) at depth Z, a function of time t and Z.

w: water pressure applied on the vertical drains, varying with depth Z, which is zero without vacuum pre-loading pressure.

$r_{w}$: unit weight of water.

$k_{r}$: the horizontal permeability coefficient of the undisturbed soil, a function of Z.

$m_{v}$: coefficient of volume compressibility (assumed the same in smear and undisturbed zone), calculated using total incremental strain resulted from primary consolidation under total stress increment, and a function of Z.

Parameters $k_{v}$, $m_{v}$ and $\eta$ can be depth-dependent in a piecewise linear way or kept constant within each layer. $\overline{k}_{v}$, $\overline{m}_{v}$ and $\overline{\eta }$ are convenient reference values at certain depth; for example, values $k_{v,j = 1}$, $m_{v,j = 1}$ and $\eta_{j = 1}$ of layer 1. If so, $\overline{c}_{v} { = }\overline{k}_{v} /\gamma_{w} \overline{m}_{v} = k_{v,j = 1} /\gamma_{w} m_{v,j = 1} = c_{v,j = 1}$. $\overline{\eta } = \overline{k}_{r} /r_{e}^{2} \mu = k_{r,j = 1} /r_{e}^{2} \mu = \eta_{j = 1}$. All the parameters in Eq. (13a) have been normalized and may be different for different soil layers. (No layer index is used here to make presentation concise.) Normalized parameters in Eq. (13a) are: $m_{v} /\overline{m}_{v}$, $\eta /\overline{\eta }$, $k/\overline{k}_{v}$.

The parameter $\eta = k_{r} /(r_{e}^{2} \mu )$ is related to radial permeability $k_{r}$, equivalent radius $r_{e}$ of cylinder cell, and $\mu$. If there is no horizontal drainage in a soil layer, $k_{r} = 0$ to that $\eta = 0$. This is useful for consolidation analysis of soils with partially penetrating vertical drains. All soil layers below vertical drains have $\eta = 0$. Walker and Indraratna [26] and Walker et al. [27] discussed that their method can also simulate the effect of using long and short drains in unison. For example, in lower soil layers where only long drains are installed, $\eta$ shall have smaller value than that of upper soil layers where both short and long drains are present.

$\mu$ inside $\eta$ is a dimensionless drain geometry/smear zone parameter. Expressions for $\mu$ can be taken as the following by considering effects of smear zone, well resistance, or approximation [14]:

$$\begin{aligned} \mu = & \frac{{n^{2} }}{{n^{2} - 1}}\left( {\ln \frac{n}{s} - \frac{3}{4} + \frac{{k_{r} }}{{k_{s} }}\ln s} \right) + \frac{{s^{2} }}{{n^{2} - 1}}\left( {1 - \frac{{s^{2} }}{{4n^{2} }}} \right) \\ & + \frac{{k_{r} }}{{k_{s} }}\frac{1}{{n^{2} - 1}}\left( {\frac{{s^{4} - 1}}{{4n^{2} }} - s^{2} + 1} \right) + \pi z(2l - z)\frac{{k_{r} }}{{q_{w} }}\left( {1 - \frac{1}{{n^{2} }}} \right) \\ \end{aligned}$$

(13b)

In (13b), $T_{r} = \frac{{c_{r} t}}{{r_{e}^{2} }},\;n = \frac{{r{}_{e}}}{{r_{d} }},\;s = \frac{{r{}_{s}}}{{r_{d} }}$. $q_{w} = k_{w} \pi r_{w}^{2}$ is the specific discharge capacity of drain (vertical hydraulic gradient i = 1). z is the vertical coordinate in Fig. 1 and l is the length of drain when closed at bottom or a half of drain when bottom is open. If hydraulic resistance of vertical drains is zero, this means $q_{w} = k_{w} \pi r_{d}^{2} \Rightarrow \infty$. (13b) can be simplified:

$$\mu = \frac{{n^{2} }}{{n^{2} - 1}}\left( {\ln \frac{n}{s} - \frac{3}{4} + \frac{{k_{r} }}{{k_{s} }}\ln s} \right) + \frac{{s^{2} }}{{n^{2} - 1}}\left( {1 - \frac{{s^{2} }}{{4n^{2} }}} \right) + \frac{{k_{r} }}{{k_{s} }}\frac{1}{{n^{2} - 1}}\left( {\frac{{s^{4} - 1}}{{4n^{2} }} - s^{2} + 1} \right)$$

(13c)

Walker and Indraratna [28] also provided an expression for $\mu$ considering parabolic smear zone permeability but ignoring smear zone:

$$\mu = \ln \frac{n}{s} - \frac{3}{4} + \frac{{\kappa \left( {s - 1} \right)^{2} }}{{\left( {s^{2} - 2\kappa s + \kappa } \right)}}\ln \frac{s}{\sqrt \kappa } - \frac{{s\left( {s - 1} \right)\sqrt {\kappa \left( {\kappa - 1} \right)} }}{{2\left( {s^{2} - 2\kappa s + \kappa } \right)}}\ln \left( {\frac{{\sqrt \kappa + \sqrt {\kappa - 1} }}{{\sqrt \kappa - \sqrt {\kappa - 1} }}} \right)$$

(13d)

where $\kappa$ is the ratio of undisturbed horizontal permeability $k_{r}$ to smear zone permeability $k_{so}$ at the drain/soil interface, (at $r = r_{d}$, $k_{s} = k_{s0}$). At $r = r_{s}$, $k_{s} = k_{r}$.

Walker and Indraratna [26] provided an Excel spreadsheet calculation program implemented with VBA program named SPECCON to enable convenient adoption of this method for consolidation analysis of multiple soils layers with or without vertical drains. After inputted all parameters and load $\overline{\sigma }$, this program gives excess pore water pressure at time t $\overline{u}_{ej} (t)$ for j-layer and $\overline{u}_{e} (t)$ for all layers together. The combined average degree of consolidation $U_{j}$ for each j-layer is calculated using Eq. (10a). The overall combined average degree of consolidation $U$ for all layers shall be calculated using Eq. (11a) or Eq. (11b). Once $U_{j}$ and $U$ with time t are known, total “primary” consolidation settlement $S_{{{\text{primary}}}}$ can be calculated using Eq. (2).

2.4 Calculation of $S_{{{\text{creep}}}}$ , $S_{{{\text{creep}}j}}$, $S_{{{\text{creep}},fj}}$ and $S_{{{\text{creep}},dj}}$

In Eqs. (1) or (4b), the total creep settlement $S_{{{\text{creep}}}}$ of all layers together is sum of $S_{{{\text{creep}}j}}$ for all layers. This is a simple superposition. The key items for calculating $S_{{{\text{creep}}j}}$ are $S_{{{\text{creep}},fj}}$ and $S_{{{\text{creep}},dj}}$.

• (a) Calculation of $S_{{{\text{creep}},fj}}$ for different stress–strain states

Creep settlement $S_{{{\text{creep}},fj}}$ of j-layer is calculated as creep compression under the “final” vertical effective stress ignoring coupling of excess porewater pressure nor any ramp loading process. This is an ideal case in order to de-couple this consolidation problem. To consider creep compression occurred in “primary” consolidation starting from time zero, the void ratio $e$ due to creep is [36, 37]:

$$e = e_{o} - C_{\alpha e} \log \frac{{t_{o} + t_{e} }}{{t_{o} }}$$

(14)

where $C_{\alpha e}$ is a creep parameter; $t_{o}$ is another creep parameter; $t_{e}$ is “equivalent time” defined by Yin and Graham [36, 37] and $e_{o}$ is the initial void ratio at $t_{e} = 0.$ In this study, $C_{\alpha e}$ is considered constant as a common practice in engineering. Yin [32] proposed a nonlinear creep model which considers the creep limit with time and the decreasing trend of $C_{\alpha e}$ with effective stress, which shows advantages in very long-term settlement calculations [8]. For settlement calculation of settlements of most soft soils in a normal service life (say 50 years) of a geotechnical structure, it is still reliable and convenient to adopt constant values of $C_{\alpha e}$ to avoid lengthy equations as much as possible [9, 35]. According to the “equivalent time” concept [31, 33, 34, 36, 37], the total strain $\varepsilon_{z}^{{}}$ at any stress–strain state in Fig. 3 can be calculated by the following equation:

$$\varepsilon_{z}^{{}} = \varepsilon_{zp}^{{}} + \frac{{C_{c} }}{V}\log \frac{{\sigma_{z}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }} + \frac{{C_{\alpha e} }}{V}\log \frac{{t_{o} + t_{e} }}{{t_{o} }}$$

(15)

where $\varepsilon_{zp}^{{}} + \frac{{C_{c} }}{V}\log \frac{{\sigma_{z}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}$ is the strain on the normal consolidation line (NCL) under stress $\sigma_{z}^{^{\prime}}$ (also called “reference time line” and noting initial specific volume $V = 1 + e_{o}$) and $\frac{{C_{\alpha e} }}{V}\log \frac{{t_{o} + t_{e} }}{{t_{o} }}$ is the creep strain occurring from the NCL under the same stress $\sigma_{z}^{^{\prime}}$. The above equation is valid for any 1-D loading path. The calculation of $S_{{{\text{creep}},fj}}$ is dependent on the final stress–strain state $(\sigma_{z}^{^{\prime}} ,\varepsilon_{z} )$. To make presentation concise, in the following equations, layer index j_, are removed.

• (i) The final stress–strain point is on an NCL line, for example at point 4

The final creep settlement for any point on NCL line is:

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} }}} \right)H\quad {\text{for}}\;t_{e} \ge 0$$

(16a)

For a suddenly applied load kept for a duration time t, we have $t_{e} = t - t_{o}$. Submitting the above relation into (16a), we have:

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{t}{{t_{o} }}} \right)H\quad {\text{for}}\quad t \ge 1\;{\text{day}}$$

(16b)

Noting $\;t_{o} = 1\;{\text{day}}$ since $\;C_{r} \;{\text{and}}\;C_{c}$ are determined using data with 1-day duration. In (16a), if $t = 1\;{\text{day}}$, from $t_{e} = t - t_{o}$, $t_{e} = 1 - 1 = 0$. This means that at time $\;t = 1\;{\text{day}}$, creep settlement $S_{{{\text{creep}},f}}$ on NCL is zero. According to elastic viscoplastic (EVP) modelling theory [36, 37], the compression strain rate is the sum of elastic strain rate and viscoplastic strain rate. The NCL line in Fig. 3, in fact, has included both elastic strain and viscoplastic strain (or creep strain). The creep settlement in (16a) is additional creep compression starting from 1 day or below NCL.

• (ii) The final stress–strain point is on an OCL line, for example at point 2

Consider a sudden load increase from point 1 to point 2, which is kept unchanged with a duration time t. The final creep settlement for any point, for example point 2, on over-consolidation line (OCL) is:

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} + t_{e2} }}} \right)H\quad {\text{for}}\;t_{e} \ge t_{e2}$$

(16c)

(16c) can be re-written with $\Delta \varepsilon_{{z{\text{creep}}}}$ included:

$$S_{{{\text{creep}},f}} = \left[ {\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} }}} \right) - \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e2} }}{{t_{o} }}} \right)} \right]H = \Delta \varepsilon_{{z{\text{creep}}}} H$$

Referring to Fig. 3, it is seen that $\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{{e{2}}} }}{{t_{o} }}} \right)$ is the strain from point $2^{^{\prime}}$ to point 2, while $\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} }}} \right)$ is the strain from point $2^{^{\prime}}$ to a point below point 2 downward. The increased strain for further creep done from point 2 is $\Delta \varepsilon_{{z{\text{creep}}}}$, which is used to calculate creep settlement $S_{{{\text{creep}},f}}$ under loading at point 2. It is noted that the relationship between $t_{e}$ and the creep duration time t under the stress $\sigma_{z2}^{^{\prime}}$ is $t{}_{e} = t_{e2} + t - t{}_{o}$. $t_{e2}$ here or in (16c) can be calculated below. Using Eq. (15), at point 2 of $(\sigma_{z2}^{^{\prime}} ,\varepsilon_{z2} )$, we have:

$$\varepsilon_{z2}^{{}} = \varepsilon_{zp}^{{}} + \frac{{C_{c} }}{V}\log \frac{{\sigma_{z2}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }} + \frac{{C_{\alpha e} }}{V}\log \frac{{t_{o} + t_{e2} }}{{t_{o} }}$$

From the above, we have:

$$\log \frac{{t_{o} + t_{e2} }}{{t_{o} }} = (\varepsilon_{z2}^{{}} - \varepsilon_{zp}^{{}} )\frac{V}{{C{}_{\alpha e}}} - \frac{{C_{c} }}{{C{}_{\alpha e}}}\log \frac{{\sigma_{z2}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}$$

$$t_{e2} = t_{o} \times 10^{{{(\varepsilon_{z2}{}} - \varepsilon_{zp}^{{}} )\frac{V}{{C{}_{\alpha e}}}}} \left( {\frac{{\sigma_{z2}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}} \right)^{{ - \,\,\frac{{C_{c} }}{{C{}_{\alpha e}}}}} - t_{o}$$

(16d)

It is seen from (16d) that the equivalent time $\;t{}_{e2}$ at point 2 is uniquely related to the stress–strain state point $(\sigma_{z2}^{^{\prime}} ,\varepsilon {}_{z2})$. Substituting $t{}_{e} = t_{e2} + t - t{}_{o}$ into (16c), we have:

$$S_{{\text{creep,f}}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e2} }}{{t_{o} + t_{e2} }}} \right)H\quad t \ge 1\;{\text{day}}$$

(16e)

If we consider unloading from point 4 to point 6 in Fig. 3, using the same approach above, we can derive the following equations:

$$t_{e6} = t_{o} \times 10^{{{(\varepsilon_{z6}{}} - \varepsilon_{zp}^{{}} )\frac{V}{{C_{\alpha e} }}}} \left( {\frac{{\sigma_{z6}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}} \right)^{{ - \,\,\frac{{C_{c} }}{{C_{\alpha e} }}}} - t_{o}$$

(16f)

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} + t_{e6} }}} \right)H = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e6} }}{{t_{o} + t_{e6} }}} \right)H\quad t \ge 1\;{\text{day}}$$

(16g)

Reloading from point 6 to point 5:

$$t_{e5} = t_{o} \times 10^{{{(\varepsilon_{z5}{}} - \varepsilon_{zp}^{{}} )\frac{V}{{C_{\alpha e} }}}} \left( {\frac{{\sigma_{z5}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}} \right)^{{ - \,\,\frac{{C_{c} }}{{C_{\alpha e} }}}} - t_{o}$$

(16h)

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} + t_{e5} }}} \right)H = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e5} }}{{t_{o} + t_{e5} }}} \right)H\quad t \ge 1\;{\text{day}}$$

(16i)

• (b) Calculation of $S_{{{\text{creep}},dj}}$ for different stress–strain states.

$S_{{{\text{creep}},dj}} \,$ is called “delayed” creep settlement of j-layer under the “final” vertical effective stress ignoring the excess porewater pressure. $S_{{{\text{creep}},dj}}$ starts for $\,t \ge \,\,t_{{{\text{EOP}},{\text{field}}}}$, that is, is “delayed” by time of $t_{{{\text{EOP}},{\text{field}}}}$. The selection of time at EOP is subjective since the separation of “primary” consolidation from “secondary” compressions is not scientific and subjective. In the general simple method, the time at $U_{j} = 98\%$ is considered to be the time at EOP, that is, $t_{{{\text{EOP}},{\text{field}}}}$ for field condition for j-layer [35]. Equation (12c) or other solutions for $U_{j}$ can be used to calculate $t_{{{\text{EOP}},{\text{field}}}}$ for a single-layer case. Equations for calculating $S_{{{\text{creep}},dj}} \,$ for different “final” stress–strain state are presented below. The layer index j is removed in following equations.

• (i) The final stress–strain point is on an NCL line, for example at point 4.

Equation (16a) is the final creep settlement for any point on NCL line for $t_{e} \ge 0$ or $t \ge 1\;{\text{day}}$:

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} }}} \right)H\quad t_{e} \ge 0$$

$S_{{{\text{creep}},d}}$ is delayed by $t_{{{\text{EOP}},{\text{field}}}}$:

$$\begin{aligned} S_{{{\text{creep}},d}} = & \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} }}} \right)H - \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{{e,{\text{EOP}},{\text{field}}}} }}{{t_{o} }}} \right)H \\ = & \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{o} + t_{e} }}{{t_{o} + t_{{e,{\text{EOP}},{\text{field}}}} }}} \right)H\quad {\text{for}}\;t_{e} \ge t_{{e,{\text{EOP}},{\text{field}}}} \\ \end{aligned}$$

(17a)

Noting $\because t_{e} = t - t_{o} \quad \therefore t_{{e,{\text{EOP}},{\text{field}}}} = t_{{{\text{EOP}},{\text{field}}}} - t_{o}$. Substituting these time relations into (17a):

$$S_{{{\text{creep}},d}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{t}{{t_{{{\text{EOP}},{\text{field}}}} }}} \right)H\quad {\text{for}}\;t \ge t_{{{\text{EOP}},{\text{field}}}}$$

(17b)

In (17b) $S_{{{\text{creep}},d}}$ is calculated for $t \ge t_{{{\text{EOP}},{\text{field}}}}$, that is, “delayed” by time $t_{{{\text{EOP}},{\text{field}}}}$.

• (ii) The final stress–strain point is on an OCL line, for example at point 2.

The final creep settlement at point 2 is:

$$S_{{{\text{creep}},f}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e2} }}{{t_{o} + t_{e2} }}} \right)H\quad {\text{for}}\;t_{e} \ge t_{e2} \;{\text{or}}\;\,t \ge t_{o} = 1\;{\text{day}}$$

$S_{{{\text{creep}},d}} \,$ is delayed by $t_{{{\text{EOP}},{\text{field}}}}$:

$$\begin{gathered} S_{{{\text{creep}},d}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e2} }}{{t_{o} + t_{e2} }}} \right)H\, - \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t_{{{\text{EOP}},{\text{field}}}} + t_{e2} }}{{t_{o} + t_{e2} }}} \right)H\,\, \hfill \\ S_{{{\text{creep}},d}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e2} }}{{t_{{{\text{EOP}},{\text{field}}}} + t_{e2} }}} \right)H\quad {\text{for}}\;t \ge t_{{{\text{EOP}},{\text{field}}}} \hfill \\ \end{gathered}$$

(18a)

When $t = t_{{{\text{EOP}},{\text{field}}}}$, $S_{{{\text{creep}},d}}$ in (18a) is zero.

Using the same approach, at point 6:

$$S_{{{\text{creep}},d}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e6} }}{{t_{{{\text{EOP}},{\text{field}}}} + t_{e6} }}} \right)H\quad {\text{for}}\;t \ge t_{{{\text{EOP}},{\text{field}}}}$$

(18b)

at point 5:

$$S_{{{\text{creep}},d}} = \frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \left( {\frac{{t + t_{e5} }}{{t_{{{\text{EOP}},{\text{field}}}} + t_{e5} }}} \right)H\quad {\text{for}}\;t \ge t_{{{\text{EOP}},{\text{field}}}}$$

(18c)

3 Consolidation settlements of a clay layer with OCR = 1 or 1.5 from general simple method and fully coupled consolidation analyses

In this section, consolidation settlements of an idealized horizontal layer of Hong Kong Marine Clay (HKMC) are calculated using the simplified Hypothesis B method and two fully coupled finite element (FE) consolidation models. This HKMC layer has 4 m in thickness and is free drained on the top surface and impermeable at the bottom. Over-consolidation ratio (OCR) is OCR = 1 or 1.5. Two FE programs are used for fully coupled consolidation analysis of the HKMC layer: one is software “Consol” developed by Zhu and Yin [42, 44] and the other one is Plaxis software (2D 2015 version) Plaxis [25]. In the “Consol” analysis, a 1D EVP model [36, 37] is used for the consolidation modelling. In Plaxis software (2D 2015 version), a soft soil creep (SSC) model is adopted in the FE simulations. SSC model is in fact a 3D EVP model [30]. The structure and parameters of this SSC model are almost the same as a 3D EVP model proposed by Yin [31] and Yin and Graham [39].

Values of all parameters used in FE consolidation simulation are listed in Table 2. In all FE simulations, a vertical stress of 20 kPa is assumed to be instantly applied on the top surface and kept constant for a period of 18,250 days (50 years). Since HKMC layer is in seabed, the initial vertical effective stress is zero at the top of the HKMC layer surface. Therefore, the unit stress $\sigma_{{{\text{unit}}1}}^{^{\prime}} \;{\text{or}}\;\sigma_{{{\text{unit}}2}}^{^{\prime}}$ in Eq. (6) cannot be zero. The best value of $\sigma_{{{\text{unit}}1}}^{^{\prime}} \;{\text{or}}\;\sigma_{{{\text{unit}}2}}^{^{\prime}}$ shall be determined by oedometer compression test data at very small vertical effective stress. Here we may assume that $\sigma_{{{\text{unit}}1}}^{^{\prime}} \;{\text{or}}\;\sigma_{{{\text{unit}}2}}^{^{\prime}}$ takes values from 0.0 l to 1 kPa and discuss difference of calculated settlement values.

• (a) Normally consolidated HKMC layer with H = 4 m and OCR = 1.

The integrated Eq. (8b) is used to calculate the final “primary” settlement $S_{f,1 - 4}$. The values of all parameters are listed in Table 1. The values of all stresses are $\sigma_{z1,0}^{^{\prime}} = 0,\;\sigma_{z1,H}^{^{\prime}} = 20.76{\text{kPa}},$$\;\sigma_{z4,0}^{^{\prime}} = 20,\;\sigma_{z4,H}^{^{\prime}} = 40.76{\text{kPa}}$. $S_{f,1 - 4}$ is:

$$(40.76 - 20)$$

Table 1 Values of parameters for the upper marine clay of Hong Kong

Using above equation with $\sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.01 kPa, it is found that $S_{f,1 - 4} =$ 0.944 m; if $\sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.1 kPa, $S_{f,1 - 4} =$ 0.928 m; if $\sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.5 kPa, $S_{f,1 - 4} =$ 0.879 m; if $\sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 1 kPa, $S_{f,1 - 4} =$ 0.834 m. This means that the final “primary” settlement $S_{f,1 - 4}$ is sensitive to the value of $\sigma_{{{\text{unit}}2}}^{^{\prime}}$. In this example, we select $\sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.1 kPa so that the final “primary” settlement $S_{f,1 - 4}$ is 0.928 m.

The calculation of average $m_{v}$ and $c_{v}$ is below:

$$\begin{gathered} \Delta \varepsilon_{z,1 - 4} = S_{f,1 - 4} = 0.928/4 = 0.232 \hfill \\ m_{v} = \Delta \varepsilon_{z,1 - 4} /\Delta \sigma_{z,1 - 4}^{^{\prime}} = 0.232/20 = 0.0116\quad (1/{\text{kPa}}) \hfill \\ \end{gathered}$$

$$c_{v} = k/(\gamma_{w} m_{v} ) = 1.9 \times 10^{ - 4} /(9.81 \times 0.0116) = 1.670 \times 10^{ - 3} \;(m^{2} /{\text{day}}) = 0.610\;(m^{2} /{\text{year}})$$

As explained, a thick layer can be divided into small sub-layers. The stresses and values of soil parameters in each sub-layer are assumed be constant. In this case, simple equations in Eq. (6b) can be used to calculate that the final “primary” settlement $S_{f,1 - 4}$ for each sub-layer. This layer of 4 m can be divided into 2, 4, or 8 sub-layers with thickness of 2 m, 1 m, and 0.5 m, respectively. The final “primary” settlement $S_{f,1 - 4}$ calculated is 0.743 m, 0.831 m, 0.881 m and 0.910 m sub-layers with thickness of 4 m, 2 m, 1 m, and 0.5 m, respectively. Values of $S_{f}$, $m_{v}$ and $c_{v}$ for sub-layer thickness of 0.5 m for OCR = 1 are listed in Table 2. $\varepsilon_{zp}$ in Table 2 is the vertical strain in each sub-layer (0.5 m here) from the initial effective stress $\sigma^{\prime }_{zi}$ to pre-consolidation pressure $\sigma^{\prime }_{zp}$ and $\overline{\varepsilon }_{zp}$ is average of all $\varepsilon_{zp}$ values. Since OCR = 1, $\sigma^{\prime }_{zp} = \sigma^{\prime }_{zi}$, the strain $\varepsilon_{zp}$ and $\overline{\varepsilon }_{zp}$ are zero. $\Delta \varepsilon_{z}$ is the strain increase in each sub-layer for loading from $\sigma_{zp}^{^{\prime}}$ to current stress $\sigma_{z}^{^{\prime}}$. $\Delta \overline{\varepsilon }_{z}$ is average of all $\Delta \varepsilon_{z}$ values. $(\overline{\varepsilon }_{zp} + \Delta \overline{\varepsilon }_{z} )$ is total vertical strain. Summary of values of $S_{f}$, $m_{v}$ and $c_{v}$ for different numbers of sub-layers for OCR = 1 is listed in Table 3 including $S_{f}$ obtained by more accurate integration method. It is seen from Table 3 that the more sub-layers (or the smaller thickness of the sub-layers), the more accurate are these $S_{f}$, $m_{v}$ and $c_{v}$. A thickness of 0.5 m is considered as appropriate since the relative error of $S_{f}$ is only $\frac{0.928 - 0.910}{{0.928}} \times 100\% = 1.9\%$ of the integrated one.

Table 2 Calculation of $S_{f}$, $m_{v}$ and $c_{v}$ for sub-layer thickness of 0.5 m for OCR = 1

Table 3 Summary of $S_{f}$, $m_{v}$ and $c_{v}$ for different numbers of sub-layers for OCR = 1

In this example, the general simplified Hypothesis B method in Eq. (1) together with other equations on relevant parameters is used to calculate the total settlement $S_{{{\text{total}}B}}$ using $\alpha = 0.8$ and $\beta = 0$ (denoted B Method 1), $\beta = 0.3$ (denoted B Method 2), and $\beta = 1$(denoted B Method 3). B Method 1 using $\alpha = 0.8$ and $\beta = 0$ is in fact the method published by Yin and Feng [35]. The calculated curves of settlements with log(time) from the simplified Hypothesis B method are shown in Fig. 5a for time up to 100 years. At the same time, Hypothesis A method and two fully coupled finite element models are used to calculate the curves of settlements with log(time), which are also shown in Fig. 5a for comparison. It is seen from Fig. 5a that, when $\alpha = 0.8$ and $\beta = 0.3$ m, B Method 2 gives curves much closer to the curves from the two finite element models of “Consol” by Zhu and Yin [42, 44] and Plaxis software (2D 2015 version). Values of parameters used in Consol software are listed in Table 1b and those of Plaxis in Table 1c. As shown in Fig. 5a, again, Hypothesis A method underestimates the total settlement for the time period.

Fig. 5

Comparison of curves of settlements with log(time) from the simplified Hypothesis B method, Hypothesis A method, and two fully coupled finite element modellings – a h = 4 m and OCR = 1 and b h = 4 m and OCR = 1.5

• (b) Over-consolidated HKMC layer with H = 4 m and OCR = 1.5

Equation (8d) from integration is used to calculate the final “primary” settlement $S_{f,1 - 4}$. Values of all parameters are listed in Table 1. Values of all stresses are $\sigma_{z1,0}^{^{\prime}} = 0,\;\sigma_{z1,H}^{^{\prime}} = 20.76\;{\text{kPa}},\;$$\;\sigma_{zp,0}^{^{\prime}} = 0,\;\sigma_{zp,H}^{^{\prime}} = 31.14\;{\text{kPa}}$$\;\sigma_{z4,0}^{^{\prime}} = 20,\;\sigma_{z4,H}^{^{\prime}} = 40.76\;{\text{kPa}}$. $S_{f,1 - 4}$ is:

$$\begin{gathered} S_{f,1 - 4} = \frac{0.0913}{{3.656\ln (10)}}\left\{ {\frac{4}{(31.14 - 0)}[(31.14 + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (31.14 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - (31.14 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - } \right. \hfill \\ \;((0 + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (0 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - (0 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ))] - \frac{4}{(20.76 - 0)}[(20.76 + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (20.76 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) \hfill \\ \; - (20.76 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - ((0 + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\ln (0 + \sigma_{{{\text{unit}}1}}^{^{\prime}} ) - (0 + \sigma_{{{\text{unit}}1}}^{^{\prime}} )\left. {)]} \right\} + \hfill \\ \;\frac{1.4624}{{3.65\ln (10)}}\left\{ {\frac{4}{(40.76 - 20)}} \right.[(40.76 + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (40.76 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (40.76 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - \hfill \\ \;((20 + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (20 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (20 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ))] - \frac{4}{(40.76 - 0)}[(31.14 + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (31.14 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) \hfill \\ \; - (31.14 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - \left. {((0 + \sigma_{{{\text{unit}}2}}^{^{\prime}} )\ln (0 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ) - (0 + \sigma_{{{\text{unit}}2}}^{^{\prime}} ))]} \right\} \hfill \\ \end{gathered}$$

Using above equation with $\sigma_{{{\text{unit}}1}}^{^{\prime}} = \sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.01 kPa, we find $S_{f,1 - 4} =$ 0.681 m; if $\sigma_{{{\text{unit}}1}}^{^{\prime}} = \sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.1 kPa, $S_{f,1 - 4} =$ 0.669 m; if $\sigma_{{{\text{unit}}1}}^{^{\prime}} = \sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.5 kPa, $S_{f,1 - 4} =$ 0.635 m; if $\sigma_{{{\text{unit}}1}}^{^{\prime}} = \sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 1 kPa, $S_{f,1 - 4} =$ 0.604 m. This means that the final “primary” settlement $S_{f,1 - 4}$ is sensitive to the value of $\sigma_{{{\text{unit}}1}}^{^{\prime}} \;{\text{and}}\;\sigma_{{{\text{unit}}2}}^{^{\prime}}$. In this example, we select $\sigma_{{{\text{unit}}1}}^{^{\prime}} = \sigma_{{{\text{unit}}2}}^{^{\prime}}$ = 0.1 kPa so that the final “primary” settlement $S_{f,1 - 4}$ is 0.669 m. The calculation of average $m_{v}$ and $c_{v}$ is below:

$$\begin{gathered} \Delta \varepsilon_{z,1 - 4} = S_{f,1 - 4} = 0.669/4 = 0.167 \hfill \\ m_{v} = \Delta \varepsilon_{z,1 - 4} /\Delta \sigma_{z,1 - 4}^{^{\prime}} = 0.167/20 = 0.00837\quad (1/{\text{kPa}}) \hfill \\ \end{gathered}$$

$$c_{v} = k/(\gamma_{w} m_{v} ) = 1.9 \times 10^{ - 4} /(9.81 \times 0.00837) = 2.316 \times 10^{ - 3} \;({\text{m}}^{{2}} {\text{/day}}) = 0.845\;({\text{m}}^{{2}} {\text{/year}})$$

This 4-m-thick layer can be divided into small sub-layers. The stresses and values of soil parameters in each sub-layer are assumed be constant. In this case, simple equations in (6b) can be used to calculate that the final “primary” settlement $S_{f,1 - 4}$ in each sub-layer. This layer of 4 m can divided into 2, 4, or 8 sub-layers with thickness of 2 m, 1 m, and 0.5 m, respectively. The final “primary” settlement $S_{f,1 - 4}$ calculated is 0.487 m, 0.573 m, 0.625 m, and 0.646 m sub-layers with thickness of 4 m, 2 m, 1 m, and 0.5 m, respectively. Values of $S_{f}$, $m_{v}$ and $c_{v}$ for sub-layer thickness of 0.5 m for OCR = 1.5 are listed in Table 4. The meanings of $\varepsilon_{zp}$, $\overline{\varepsilon }_{zp}$, $\Delta \varepsilon_{z}$, $\Delta \overline{\varepsilon }_{z}$, and $(\overline{\varepsilon }_{zp} + \Delta \overline{\varepsilon }_{z} )$ are the same as those in Table 2. Summary of values of $S_{f}$, $m_{v}$ and $c_{v}$ for different number of sub-layers for OCR = 1.5 is listed in Table 5 including $S_{f}$ obtained by more accurate integration method. It can be seen that the relative error of $S_{f}$ with sub-layer thickness of 0.5 m is only $\frac{0.669 - 0.646}{{0.669}} \times 100\% = 3.4\%$.

Table 4 Calculation of $S_{f}$, $m_{v}$ and $c_{v}$ for sub-layer thickness of 0.5 m for OCR = 1.5

Table 5 Summary of $S_{f}$, $m_{v}$ and $c_{v}$ for different numbers of sub-layers for OCR = 1.5

The simplified Hypothesis B method in (1) together with other equations on relevant parameters is used to calculate the total settlement $S_{{{\text{total}}B}}$ using $\alpha = 0.8$ and $\beta = 0$ (denoted B Method 1), $\beta = 0.3$ (denoted B Method 2) and $\beta = 1$ (denoted B Method 3) for OCR = 1.5. The calculated curves of settlements with log(time) from the simplified Hypothesis B method are shown in Fig. 5b for time up to 100 years. At the same time, Hypothesis A method and two fully coupled finite element models are used to calculate the curves of settlements with log(time), which are also shown in Fig. 5b for comparison. It is seen from Fig. 5b that when $\alpha = 0.8$ and $\beta = 0.3$ m, B Method 2 gives curves much closer to the curves from the two finite element models of “Consol” by Zhu and Yin [42, 43, 44] and Plaxis software (2D 2015 version). Again, Hypothesis A method underestimates the total settlement.

4 Consolidation settlements of layered soils with vertical drains under staged loading–unloading-reloading from general simple method and fully coupled consolidation analysis

4.1 Description of soil conditions

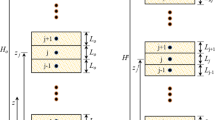
In this section, easy use and accuracy of the general simple method are demonstrated through calculation of consolidation settlements of a multiple-layered soil under multi-staged loadings with comparison with values from fully coupled FE simulations. The soil profile is modified from a real case in Hong Kong [18, 49] as shown in Figs. 6 and 7. This section only studies the first two layers, namely upper marine clay of 6.22 m thick and upper alluvium of 5.80 m thick. To make the consolidation analysis more accurate and to record accumulated settlement at different depths, the upper marine clay layer is divided into two layers by Sondex anchor 3, forming a total of three layers of soils. Properties of upper marine clay and upper alluvium can be found in Table 6.

Fig. 6

Soil profile and settlement monitoring points of a test embankment at Chek Lap Kok for Hong Kong International Airport project in 1980s

Fig. 7

Soil profile including a vertical drain and a smear zone of a test embankment at Chek Lap Kok for Hong Kong International Airport project in 1980s

Table 6 Parameters of soils and vertical drains for HKIA Chek Lap Kok Test Embankment

Prefabricated vertical drains (PVDs) with a spacing of 1.5 m in triangular pattern were inserted in the soils. The radius of influence zone of each PVD was $r_{e} = 0.525d = 0.7875{\text{m}}$ for triangular pattern. The width of PVD was b = 100 mm, thickness was t = 7 mm, and equivalent radius is calculated as $r_{d} = \left( {b + t} \right)/4 + t/10 = 27.45\;{\text{mm}}$ [40]. The installation of PVDs normally causes a smear zone around the vertical drains as shown in Fig. 7. We assume that radius of this smear zone $r_{s} = 5r_{d} = 137.25\;{\text{mm}}$, in which the soils were disturbed and the horizontal permeability $k_{r}$ became $k_{s}$ with values listed in Table 6. Other properties such as OCR and compression indices of the smear zone remain the same as the undisturbed region.

There are four stages of loadings to be applied on top of the soils, including two stages of loading, one stage of unloading and the final stage of reloading. The magnitude of vertical load ($p_{1} ,p_{2} ,p_{3} ,p_{4}$), construction time ($t_{c1} ,t_{c2} ,t_{c3} ,t_{c4}$) and loading stage duration ($t_{1} ,t_{2} ,t_{3} ,t_{4}$) are shown in Fig. 8a. This type of staged loading is very close to the real case of reclamation process from loading (filling to a designed level), increasing loading (surcharging fill), unloading by removing part of surcharging fill, and reloading again due to construction of superstructures on reclaimed land. The final stage of loading (superstructures) may last for 50 years (18,250 days) after completion of reclamation construction. To validate the general simplified Hypothesis B method, a fully coupled finite element (FE) analysis is conducted in Plaxis 2D (2015) for this case. A soft soil creep (SSC) model [30], which is mostly similar to the 3D EVP model by Yin and Graham [39], is adopted as the constitutive model for the two clayey soils in Fig. 7. The parameters used in the FE model for the two soils are the same as those in Table 6. Accumulated settlements at settlement monitoring points 1, 3 and 5 (depths of 0 m, 3 m, and 6 m, respectively) are calculated using the general simple method and the FE model and are plotted with total elapsed time. Excess pore pressures at the centre of each layer and at the middle between $r_{d}$ and $r_{e}$ are calculated by the FE model during the whole consolidation process.

Fig. 8

a Construction time, stage time and vertical pressures of four staged loadings from loading, to unloading and reloading and b state points in vertical strain-log(effective stress) space

4.2 Consolidation settlement calculation by general simple method under staged loadings

This section shows details with steps how to use the general simple method to calculate consolidation settlements of Case 2 under staged loading–unloading–reloading. The total consolidation settlements are summation of “primary” consolidation settlement and creep settlements in Eq. (1). For four stages of loading, details of calculations are presented below.

4.3 Stage 1

As shown in Fig. 8a, for Stage 1 under $p_{1} = 52{\text{kPa}}$, the stress–strain state will move from point i $(\sigma_{zi}^{^{\prime}} ,\varepsilon_{zi} )$ to point 1 $(\sigma_{z1}^{^{\prime}} ,\varepsilon_{z1} )$ as in Fig. 8b. The calculation method of $S_{f}$ is similar to the case of load increment from point 1 to 2 or point 1 to 4 in Fig. 3. Due to the nonlinear strain–stress relationship of soils and non-uniform stress distribution, each j-layer (j = 1, 2, 3 for 3 layers) is divided into several sub-layers (say $N$ sub-layers) with a thickness of $h_{n}$ (0.5 m or less) to calculate $S_{f}$ and $m_{v}$. Within each sub-layer, initial effective stress $\sigma_{zi}^{^{\prime}}$ can be considered as constant. The final vertical effective stress at Stage 1 is calculated as $\sigma_{z1}^{^{\prime}} = \sigma_{zi}^{^{\prime}} + p_{1}^{{}}$ for each sub-layer. The settlement for each j-layer will be the superposition of settlements of all sub-layers ($n = 1 \ldots N$). Therefore, $S_{fj1}$ and $m_{vj1}$ for j-layer with thickness $H_{j}$ in Stage 1 (sub-index “₁” for Stage 1; later “₂”, “₃”, “₄” for Stages 2, 3, and 4) are calculated in the following equations:

$$S_{fj1} = \sum\limits_{n = 1}^{n = N} {\left\{ {\begin{array}{*{20}c} {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{zi}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right)h_{n} {, }\quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{ if }}\sigma_{z1}^{^{\prime}} \le {(}\sigma_{zi}^{^{\prime}} + {\text{POP}})} \\ \begin{gathered} \left[ {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{zi}^{^{\prime}} + POP + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{zi}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right) + \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}{{\sigma_{zi}^{^{\prime}} + POP + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)} \right]h_{n} {, } \hfill \\ \quad \quad \quad \, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,{\text{if }}\sigma_{z1}^{^{\prime}} { > (}\sigma_{zi}^{^{\prime}} + {\text{POP}}) \hfill \\ \end{gathered} \\ \end{array} } \right.}$$

(19a)

$$m_{vj1} = \frac{{\varepsilon_{z1} - \varepsilon_{zi} }}{{p_{1} }} = \frac{{S_{fj1} }}{{H_{j} p_{1} }}$$

(19b)

where n is index for sub-layers within j-layer ($n = 1 \ldots N$), $h_{n}$ is thickness of a sub-layer ($h_{n} \le 0.5{\text{m}}$), POP in Table 6 is called pre-over-consolidation pressure (after [49] and ${\text{POP}} = \sigma_{zp}^{^{\prime}} - \sigma_{zi}^{^{\prime}}$. Equation (19) is valid for the final state $(\sigma_{z1}^{^{\prime}} ,\varepsilon_{z1} )$ in either over-consolidation (OC) state or normal consolidation (NC) state.

Values of $S_{f1}$ and $m_{v1}$ for three layers $(H_{j} ,j = 1,2,3)$ under Stage 1 are calculated using Eq. (19) and listed in Table 7. After this, a Microsoft Excel spreadsheet with macros based on a spectral method developed by Walker and Indraratna [26] is used to calculate the average excess porewater pressure $\overline{u}_{ej}$ for j-layer using known values of $k_{v}$, $k_{r}$, and $k_{s}$ in Table 6 and the calculated $m_{vj1}$ in Table 7. The average degree of consolidation $U_{j1}$ for j-layer for Stage 1 is then calculated using Eq. (10b). Using calculated values of $U_{j1}$ and $S_{fj1}$, the “primary” consolidation settlement $S_{{{\text{primary}}1}}$ in Stage 1 is calculated as:

$$S_{\rm primary} = \sum\limits_{j = 1}^{3} {S_{{{\text{primary}},j}} } = \sum\limits_{j = 1}^{3} {U_{j1} } S_{fj1}$$

(20)

Table 7 Values of $S_{fj}$ and $m_{vj}$ for three soil layers under four stages calculated using the general simple method

To calculate creep settlement $S_{{{\text{creep}}1}}$ during Stage 1, the equivalent time in Yin and Graham’s 1D EVP model should be determined according to the final stress–strain state $(\sigma_{z1}^{^{\prime}} ,\varepsilon_{z1} )$ for each sub-layer. If the soil is in normal consolidation state (i.e. $\sigma_{z1}^{^{\prime}} \ge {(}\sigma_{zi}^{^{\prime}} + {\text{POP}})$), equivalent time $t_{e1}$ at the “final” effective stress $\sigma_{z1}^{^{\prime}}$ in Stage 1 is zero. If the soil is in OC state (i.e. $\sigma_{z1}^{^{\prime}} < (\sigma_{zi}^{^{\prime}} + {\text{POP}})$), $t_{e1}$ should be calculated as:

$$t_{e1} = t_{o} \times 10^{{{(\varepsilon_{z1}{}} - \varepsilon_{zp}^{{}} )\frac{V}{{C{}_{\alpha e}}}}} \left( {\frac{{\sigma_{z1}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}} \right)^{{ - \;\frac{{C_{c} }}{{C{}_{\alpha e}}}}} - t_{o}$$

(21)

where $\varepsilon_{z1} = \varepsilon_{zi} + S_{fj1} /H_{j}$ is the “final” strain without creep at Stage 1. In fact, Eq. (21) is also valid for NC state. The value of $t_{e1}$ is calculated for each sub-layer $h_{n}$. Therefore, $S_{{{\text{creep}},fj1}}$, $S_{{{\text{creep}},dj1}}$, $S_{{{\text{creep}}j1}}$ and total settlement $S_{{{\text{total}}Bj1}}$ for each j-layer, no matter the “final” stress–strain point is in OC or NC state, can be calculated using the following equations:

$$S_{{{\text{creep}},fj1}} = \sum\limits_{n = 1}^{n = N} {\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \frac{{t_{e1} + t}}{{t_{e1} + t_{o} }}h_{n} } {\text{ for }}t_{o} \le t \le t_{1}$$

(22a)

$$S_{{{\text{creep}},dj1}} = \sum\limits_{n = 1}^{n = N} {\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \frac{{t_{e1} + t}}{{t_{e1} + t_{{{\text{EOP}},{\text{field}}}} }}h_{n} } {\text{ for }}t_{{{\text{EOP}},{\text{field}}}} \le t \le t_{1}$$

(22b)

$$S_{{{\text{creep}}j1}} = \alpha U_{j1}^{\beta } S_{{{\text{creep}},fj1}} + \left( {1 - \alpha U_{j1}^{\beta } } \right)S_{{{\text{creep}},dj1}}$$

(22c)

$$S_{{{\text{total}}Bj1}} = U_{j1} S_{fj1} + \left[ {\alpha U_{j1}^{\beta } S_{{{\text{creep}},fj1}} + \left( {1 - \alpha U_{j1}^{\beta } } \right)S_{{{\text{creep}},dj1}} } \right]$$

(22d)

In this case, Eq. (22d) is used to calculate $S_{{{\text{total}}Bj1}}$ for j-layer in Stage 1 with $\alpha = 0.8$ and $\beta = 0.3$. Using Eq. (1), the total settlement $S_{{{\text{total}}B1}}$ of 3 layers in Stage 1 is

$$S_{{{\text{total}}B1}} = \sum\limits_{j = 1}^{j = 3} {S_{{{\text{total}}Bj1}} } = \sum\limits_{j = 1}^{j = 3} {U_{j1} S_{fj1} + \left[ {\alpha U_{j1}^{\beta } S_{{{\text{creep}},fj1}} + \left( {1 - \alpha U_{j1}^{\beta } } \right)S_{{{\text{creep}},dj1}} } \right]}$$

(22e)

4.4 Stage 2

For Stage 2 with $p_{2} = 100{\text{kPa}}$, the final vertical effective stress $\sigma_{z2}^{^{\prime}}$ is $\sigma_{z2}^{^{\prime}} = \sigma_{z1}^{^{\prime}} + p_{2}^{{}} = \sigma_{zi}^{^{\prime}} + p_{1}^{{}} + p_{2}^{{}}$ as in Fig. 8b at point 2 $(\sigma_{z2}^{^{\prime}} ,\varepsilon_{z2} )$. The calculation of $S_{fj}$ is dependent on the soil stress–strain state before and after loading increment as below:

$$S_{fj2} = \sum\limits_{n = 1}^{n = N} {\left\{ {\begin{array}{*{20}c} {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z2}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right)h_{n} {, }\quad \quad \quad \quad \quad \quad \quad {\text{if }}\sigma_{z1}^{^{\prime}} < \sigma_{z2}^{^{\prime}} \le {(}\sigma_{zi}^{^{\prime}} + {\text{POP}}) \, } \\ \begin{gathered} \left[ {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{zi}^{^{\prime}} + POP + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right) + \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z2}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}{{\sigma_{zi}^{^{\prime}} + POP + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}} \right)} \right]h_{n} {, } \hfill \\ \quad \quad \quad \, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,{\text{if }}\sigma_{z1}^{^{\prime}} < {(}\sigma_{zi}^{^{\prime}} + {\text{POP}}) < \sigma_{z2}^{^{\prime}} \hfill \\ \frac{{C_{c} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z2}^{^{\prime}} + \sigma_{unit2}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{unit2}^{^{\prime}} }}} \right)h_{n} , \, \quad \quad \quad \quad \quad \quad \, \quad {\text{if (}}\sigma_{zi}^{^{\prime}} + {\text{POP}}) \le \sigma_{z1}^{^{\prime}} { < }\sigma_{z2}^{^{\prime}} \hfill \\ \end{gathered} \\ \end{array} } \right.}$$

(23a)

$$m_{vj2} = \frac{{\varepsilon_{z2} - \varepsilon_{z1} }}{{p_{2} }} = \frac{{S_{fj2} }}{{H_{j} p_{2} }}$$

(23b)

where $\varepsilon_{z2} = \varepsilon_{z1} + S_{fj2} /H_{j}$ is the final accumulated vertical strain without creep strain at Stage 2. Values of $S_{f2}$ and $m_{v2}$ for three layers $(H_{j} ,j = 1,2,3)$ under Stage 2 are listed in Table 7. In this stage, average degree of consolidation for each layer $U_{j1}$ under $p_{1}$ and $U_{j2}$ under $p_{2}$ should be calculated independently using Walker and Indraratna [26]’s spectral method. For $U_{j1}$, the staged-consolidation time at Stage 2 should be from $t_{1}$ to $(t_{1} + t_{2} )$. For $U_{j2}$, the staged-consolidation time at Stage 2 should be from $0$ to $t_{2}$. Total $S_{{{\text{primary}}}}$ should include the settlements produced by $p_{1}$ and $p_{2}$ with total time below:

$$S_{{{\text{primary}}}} = \sum\limits_{j = 1}^{3} {S_{{{\text{primary}},j}} } = \sum\limits_{j = 1}^{3} {(U_{j1} S_{fj1} + U_{j2} S_{fj2} } )$$

(24)

$S_{{{\text{creep}}j2}}$ only includes the creep settlement at the current loading stage under $p_{2}$ (i.e. $t_{o} < t < t_{2}$ for $S_{{{\text{creep}},f}}$ and $t_{{{\text{EOP}},{\text{field}}}} < t < t_{2}$ for $S_{{{\text{creep}},d}}$). To calculate $S_{creepj2}$, the actual stress–strain state at Stage 2 and its corresponding equivalent time $t_{e2}$ should be determined. First of all, the final creep strain $\varepsilon_{{z,{\text{creep}}1}}$ shown in Fig. 8b and accumulated total strain $\varepsilon_{z1end}$ at the end of Stage 1 (point $1^{\prime \prime }$) should be calculated by the following equations:

$$\varepsilon_{{z,{\text{creep}}1}} = \frac{{S_{{{\text{creep}}j,1}} \left( {t_{1} } \right)}}{{H_{j} }}$$

(25a)

$$\varepsilon_{z1end} = \varepsilon_{z1} + \varepsilon_{{z,{\text{creep}}1}}$$

(25b)

The new apparent pre-consolidation pressure $\sigma_{zp1}^{^{\prime}}$ and the corresponding strain $\varepsilon_{zp1}$ at the end of Stage 1 shown in Fig. 8b due to previous creep (or ageing) should be calculated by solving the following two equations:

$$\varepsilon_{zp1}^{{}} = \varepsilon_{z1end} + \frac{{C_{r} }}{{1 + e_{o} }}\log \frac{{\sigma_{zp1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}$$

(26a)

$$\varepsilon_{zp1}^{{}} = \varepsilon_{zp} + \frac{{C_{c} }}{{1 + e_{o} }}\log \frac{{\sigma_{zp1}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} }}$$

(26b)

From Eqs. (26a, 26b), the apparent pre-consolidation pressure $\sigma_{zp1}^{^{\prime}}$ can be solved as:

$$\sigma_{zp1}^{^{\prime}} = \frac{{\left( {\sigma_{zp}^{^{\prime}} + \sigma_{{{\text{unit}}2}}^{^{\prime}} } \right)^{{\frac{{C_{c} }}{{C_{c} - C_{r} }}}} }}{{\left( {\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} } \right)^{{\frac{{C_{r} }}{{C_{c} - C_{r} }}}} }} \times 10^{{\left( {\varepsilon_{z1end} - \varepsilon_{zp} } \right)\frac{{1 + e_{o} }}{{C_{c} - C_{r} }}}} - \sigma_{{{\text{unit}}1}}^{^{\prime}}$$

(26c)

where $\sigma_{unit1}^{^{\prime}}$ is assumed to be equal to $\sigma_{unit2}^{^{\prime}}$ here. If $\sigma_{zp1}^{^{\prime}}$ is known, $\varepsilon_{zp1}^{{}}$ can be calculated using Eq. (26a) or (26b). With $p_{2}$ applied, if $(\sigma_{z1}^{^{\prime}} + p_{2} ) = \sigma_{z2}^{^{\prime}} \ge \sigma_{zp1}^{^{\prime}}$ (i.e. the soil is in NC state at point $2_{NC}$) as in Fig. 8b, the equivalent time $t_{e2} = 0$. Otherwise, $\sigma_{z2}^{^{\prime}} \le \sigma_{zp1}^{^{\prime}}$, as the case of point $2_{OC}$ in OC state as shown in Fig. 8b ${\text{or}}\;(\sigma_{z2}^{^{\prime}} ,\varepsilon_{z2} )\;{\text{in}}\;{\text{OC}}\;{\text{state}}$, $t_{e2}$ at $\sigma_{z2}^{^{\prime}}$ should be calculated as:${\text{or}}\;(\sigma_{z2}^{^{\prime}} ,\varepsilon_{z2} )\;{\text{in}}\;{\text{OC}}\;{\text{state}}$

$$t_{e2} = t_{o} \times 10^{{{(\varepsilon_{z2}{}} - \varepsilon_{zp}^{{}} )\frac{V}{{C{}_{\alpha e}}}}} \left( {\frac{{\sigma_{z2}^{^{\prime}} }}{{\sigma_{zp}^{^{\prime}} }}} \right)^{{ - \;\frac{{C_{c} }}{{C{}_{\alpha e}}}}} - t_{o}$$

(27)

where $\varepsilon_{z2} = \varepsilon_{{z1{\text{end}}}} + \frac{{C_{r} }}{{1 + e_{o} }}\log \frac{{\sigma_{z2}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z1}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}$ is the vertical strain at point $2_{\rm OC}$ in OC state, before creep at the beginning of Stage 2 loading. The value of $t_{e2}$ is calculated for each sub-layer with thickness $h_{n}$ for the point in either NC state or OC state. Therefore, $S_{{{\text{creep}},fj2}}$ and $S_{{{\text{creep}},dj2}}$ for each j-layer can be calculated using the following equations:

$$S_{{{\text{creep}},fj2}} = \sum\limits_{n = 1}^{n = N} {\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \frac{{t_{e2} + t}}{{t_{e2} + t_{o} }}h_{n} } {\text{ for }}t_{o} \le t \le t_{2}$$

(28a)

$$S_{{{\text{creep}},dj2}} = \sum\limits_{n = 1}^{n = N} {\frac{{C_{\alpha e} }}{{1 + e_{o} }}\log \frac{{t_{e2} + t}}{{t_{e2} + t_{{{\text{EOP}},{\text{field}}}} }}h_{n} } {\text{ for }}t_{{{\text{EOP}},{\text{field}}}} \le t \le t_{2}$$

(28b)

However, since $S_{{{\text{creep}}j2}}$ is calculated from the current stress–strain state under $(p_{1} + p_{2} )$ loading, $U_{j}$ in Eq. (22c) should be replaced by the accumulated average degree of consolidation $U_{{{\text{multi}},j2}}$ for multi-stages of loadings, which is calculated by:

$$U_{{{\text{multi}},j2}} = \frac{{(U_{j2} p_{1} + U_{j2} p_{2} )}}{{p_{1} + p_{2} }}$$

(29)

Finally, the total consolidation settlements for j-layer and for all three layers in the period of Stage 2 are calculated by:

$$S_{{{\text{total}}Bj2}} = U_{{{\text{multi}},j2}} S_{fj2} + \left[ {\alpha U_{{{\text{multi}},j2}}^{\beta } S_{{{\text{creep}},fj2}} + \left( {1 - \alpha U_{{{\text{multi}},j2}}^{\beta } } \right)S_{{{\text{creep}},dj2}} } \right]$$

(30a)

$$S_{{{\text{total}}B2}} = \sum\limits_{j = 1}^{j = 3} {S_{{{\text{total}}Bj2}} = \sum\limits_{j = 1}^{j = 3} {U_{{{\text{multi}},j2}} S_{fj2} + \left[ {\alpha U_{{{\text{multi}},j2}}^{\beta } S_{{{\text{creep}},fj2}} + \left( {1 - \alpha U_{{{\text{multi}},j2}}^{\beta } } \right)S_{{{\text{creep}},dj2}} } \right]} }$$

(30b)

4.5 Stage 3

For Stage 3 of unloading $p_{3} = - 116{\text{kPa}}$, $S_{fj3}$, $m_{vj3}$ and $U_{j3}$ are calculated using the same procedures as Stages 1 and 2. It should be noted that, for this unloading stage, $S_{fj3}$ is simply calculated by:

$$S_{fj3} = \sum\limits_{n = 1}^{n = N} {\frac{{C_{r} }}{{1 + e_{o} }}\log \left( {\frac{{\sigma_{z3}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}{{\sigma_{z2}^{^{\prime}} + \sigma_{{{\text{unit}}1}}^{^{\prime}} }}} \right)h_{n} }$$

(31)

where $\sigma_{z2}^{^{\prime}} = \sigma_{zi}^{^{\prime}} + p_{1} + p_{2}$, $\sigma_{z3}^{^{\prime}} = \sigma_{zi}^{^{\prime}} + p_{1} + p_{2} + p_{3}$, and $\sigma_{z3}^{^{\prime}} < \sigma_{z2}^{^{\prime}}$. As shown in Fig. 8b, point $3_{OC}$ must be in an OC state, but point $3_{OC}$ may be reached from the end of creep at point $2_{NC}$. However, point 2 could be at point $2_{OC}$ in an OC state. If this case, Eq. (31) can still be used. Under unloading condition, as both $S_{fj3}$ and $p_{3}$ are negative, $m_{v3}$ is still positive, and therefore, the spectral method can be normally used to compute the degree of consolidation. The calculation of $S_{{{\text{primary}},j}}$ should contain the settlements produced in the previous stages during the current stage period in the following equation:

$$S_{{{\text{primary}},j}} = U_{j1} S_{fj1} + U_{j2} S_{fj2} + U_{j3} S_{fj3}$$

(32)

where $U_{j1}$, $U_{j2}$ and $U_{j3}$ are the average degree of consolidation under (i)$p_{1}$ from $\left( {t_{1} + t_{2} } \right){\text{ to }}\left( {t_{1} + t_{2} + t_{3} } \right)$, (ii) $p_{2}$ from $t_{2} {\text{ to }}\left( {t_{2} + t_{3} } \right)$, (ii) $p_{3}$ from $0{\text{ to }}t_{3}$, respectively. Calculation of $S_{{{\text{creep}}j3}}$ follows similar procedures as in Stage 2, not be elaborated here. $U_{{{\text{multi}},j3}}$ for calculating creep settlement should be calculated as:

$$U_{{{\text{multi}},j3}} = \frac{{(U_{j1} p_{1} + U_{j2} p_{2} + U_{j3} p_{3} )}}{{p_{1} + p_{2} + p_{3} }}$$

(33)

4.6 Stage 4

For Stage 4 with $p_{4} = 74{\text{kPa}}$, similar procedures as those for Stages 1 and 2 are used for calculations of $S_{fj4}$, $U_{j4}$ and $S_{{{\text{creep}}j4}}$. But $S_{{{\text{primary}},j}}$ and $U_{{{\text{multi}},j4}}$ should be calculated as:

$$S_{{{\text{primary}},j}} = U_{j1} S_{fj1} + U_{j2} S_{fj2} + U_{j3} S_{fj3} + U_{j4} S_{fj4}$$

(34)

$$U_{{{\text{multi}},j4}} = \frac{{(U_{j} p_{1} + U_{j2} p_{2} + U_{j3} p_{3} + U_{j4} p_{4} )}}{{p_{1} + p_{2} + p_{3} + p_{4} }}$$

(35)

where $U_{j1}$,$U_{j2}$, $U_{j3}$, and $U_{j4}$ is the average degree of consolidation under (i)$p_{1}$ from $\left( {t_{1} + t_{2} + t_{3} } \right){\text{ to }}\left( {t_{1} + t_{2} + t_{3} + t_{4} } \right)$, (ii) $p_{2}$ from $\left( {t_{2} + t_{3} } \right){\text{ to }}\left( {t_{2} + t_{3} + t_{4} } \right)$, (iii) $p_{3}$ from $t_{3} {\text{ to }}\left( {t_{3} + t_{4} } \right)$, and (iv) $p_{4}$ from $0{\text{ to }}t_{4}$.

The values of $S_{fj}$ and $m_{vj}$ for Stages 1 to 4 are listed in Tables 7. Using the spectral method and Eqs. (10b), (24), (26) and (28) the average degree of consolidation degree $U_{{\rm multi},j}$ for each layer during four stages is calculated and plotted with time in Fig. 9.

Fig. 9

Calculated curves of $U_{{\rm multi},j}$ and total loading time in logarithmic scale for each j-layer under multi-staged four loadings

4.7 Comparisons of results from the general simple method and fully coupled FE analysis

Figure 10 shows the computed settlements at three measurement points (0, 3 and 6 m) by both simplified Hypothesis B method and FE analysis. It can be found that the settlements at three different depths are close to those computed by FE analysis under four stages of loading, unloading and reloading. The settlements in 50 years in stage 4 are very small. This is because the soils are in over-consolidation state in stage 4 due to the surcharge in stage 2. The results demonstrated that surcharge loading before construction will significantly reduce long-term post-construction settlements.

Fig. 10

Comparison of settlements with accumulated total loading time in logarithmic scale at three settlement monitoring points at z = 0 m, 3 m and 6 m from the simplified Hypothesis B method and fully coupled finite element modelling

$\overline{u}_{j}$ Figure 11 shows the average excess porewater pressure at the centre of each soil layer, compared with the computed excess porewater pressure at the above-mentioned measurement points in the FE model. It is found that excess porewater pressure computed by the spectral method adopted in the general simple method fit well with the one simulated by FE model. In conclusion, the proposed simplified Hypothesis B method is close to fully coupled FE analysis for the case with multiple layered soils under multi-staged loading conditions.

Fig. 11

Comparison of excess porewater pressure with log(total loading time) for three layers from the general simplified Hypothesis B method and fully coupled finite element modelling

5 Consolidation settlements of test embankment on layered soils with vertical drains under staged loading from general simple method, fully coupled consolidation analyses and measurement

5.1 General descriptions of the test embankment

In this section, Test Embankment at Chek Lap Kok for Hong Kong International Airport (HKIA) project in 1980s is used as an example to demonstrate the validity of the new general simple method. Consolidation settlements of this HKIA Chek Lap Kok Test Embankment are calculated using the new general simplified Hypothesis B method and are compared with measured data and values from the simplified finite element (FE) method reported by Zhu et al. [49]. Details of the site conditions, properties of soils, parameters of vertical drains, construction process, parameters used in the FE model can be found in Koutsoftas et al. [18] and Zhu et al. [49]. The calculations of $S_{fj} {, }\Delta \sigma_{z}^{^{\prime}} , \, \Delta \varepsilon_{z} , \, m_{vj} {\text{ and }}c_{vj}$ for each layer under three stages are listed in Table 8.

Table 8 Calculated values of parameters of j-layers for HKIA Chek Lap Kok Test Embankment

Figure 6 shows soil profile and settlement monitoring points of Chek Lap Kok Test Embankment [13, 18]. Elevation in mPD (meter in Principal Datum), depth coordinate, thickness values of four major layers, 8 settlement monitoring points by Sondex anchors, and 9 pore water pressure measurement points are all shown in Fig. 6. In this section, only 4 points at depths 0 m, 3 m, 6 m and 14.5 m are selected to calculate settlements for comparison with measured data.

Figure 7 shows soil profile and vertical drain with smear zone. It is noted that the vertical drain penetrated only 5.1 m into “lower marine clay”. Therefore, “lower marine clay” is divided into two layers: “lower marine clay 1” with thickness of 5.1 m and “lower marine clay 2” with thickness of 0.72 m in order to calculate the average degree of consolidation of each layer better.

Values of parameters of soils and vertical drains for HKIA Chek Lap Kok Test Embankment are listed in Table 6. For more accurate calculation of settlements and the average degree of consolidation, as well as convenient calculation at settlement monitoring points, “upper marine clay” is divided into two main layers of $H_{j} = 3.01\;{\text{m}}\;{\text{and}}\;{3}{\text{.21}}\;{\text{m}}$, “lower marine clay 1” is divided into $H_{j} = 2.47\;{\text{m}}\;{\text{and}}\;2.{63}\;{\text{m}}$, “lower alluvium” is divided into two layers with $H_{j} = 4.165\;{\text{m}}\;{\text{each}}$. There are a total of 8 layers (j = 1…8).

Figure 12 shows construction time ($t_{c1,} \;t_{c2,} \;{\text{or}}\;t_{c3}$), loading stage times ($t_{1,} \;t_{2,} \;{\text{or}}\;t_{3}$), and stage vertical pressures ($p_{1,} \;p_{2,} \;{\text{or}}\;p_{3}$) for each of three staged loadings. It should be noted that in situ monitoring of settlements by Sondex anchors was started 65 days after the construction began. The in situ settlement data from 65 to 909th day of total construction time were recorded and used for comparisons in this study.

Fig. 12

Construction time, stage time and vertical pressures of three staged loadings in HKIA Chek Lap Kok Test Embankment

5.2 Comparisons of results from the general simple method, fully coupled FE analyses, and measurement

In the general simplified Hypothesis B method, calculations of $S_{fj}$, $m_{v}$, $U_{j}$ and $S_{{{\text{creep}}j}}$ for each j-layer under three loading stages are completed in a Microsoft Excel spreadsheet in the same way as that in Sect. 4. In this case, $\alpha = 0.8\;{\text{and}}\;\beta = 0.3$ are used, which is also the same as in previous sections.

The total consolidation settlements $S_{totalB}$ at depths of 0 m, 3 m, 6 m and 14.5 m are calculated using the general simplified Hypothesis B method for three stages of loading. Comparison of curves of settlements with accumulated time at depths of 0 m, 3 m, 6 m and 14.5 m from the general simplified Hypothesis B method, fully coupled finite element modelling and measurement is shown in Fig. 13. It is found that the values from the general simplified Hypothesis B method are in good agreement with measured data and values from fully coupled finite element modelling [49] using a 1-D elastic viscoplastic (1-D EVP) model [36, 37].

Fig. 13

Comparison of curves of settlements with total loading time at depths 0 m, 3 m, 6 m and 14.5 m from the general simplified Hypothesis B method, fully coupled finite element modelling and measurement

6 Summary and Conclusions

A new general simplified Hypothesis B method, also called general simple method, is proposed and verified for calculating consolidation settlements of layered clayey soils exhibiting creep without or with vertical drains under complicated staged loadings. This method is a new un-coupled method compared with fully coupled consolidation methods. Equations of this general simple method incorporating a new logarithmic stress function which avoids singularity problem are rigorously derived. Excess pore water pressure in “primary consolidation” is calculated by using a spectral method implemented in a Microsoft Excel spreadsheet. Two parameters, namely $\alpha$ and $\beta$, are introduced in this method. All other parameters in this method are convectional parameters, which can be easily determined from multi-staged oedometer tests. It is worthy to note that the two creep parameters $C_{\alpha e} \;{\text{and}}\;t_{o}$ are determined from a creep test under a vertical effective stress in a normal consolidation (NC) state. But, using the “equivalent time” ($t_{e}$) concept and theory of Yin and Graham [36, 37], the creep function using $C_{\alpha e} \;{\text{and}}\;t_{o}$ as well $t_{e}$ can be used to calculate creep settlements in OC state and also in unloading/reloading states. Verification studies are carried out by comparing calculated values of settlements by this general simple method with values from fully coupled finite element analysis for Cases 1 and 2 as well as in situ measured data for Case 3. Based on these works, following conclusions can be made.

• (a) From the case study of a single soil layer with OCR = 1 or 1.5 under instantaneous vertical loading, calculated settlements by using the new general simple method agree well with values from fully coupled finite element (FE) analyses by Plaxis and Consol. Selection of $\alpha = 0.8$ and $\beta = 0.3$ is found to have the best performance compared to other selections. It is also clearly revealed that Hypothesis A method underestimates the total settlements.

• (b) From the case study for double layered soils under multi-staged loading–unloading–reloading, consolidation settlements in either short-term or long-term period are very close to values from an FE analysis. It can be concluded that the proposed general simplified Hypothesis B method has a stable performance and good accuracy for layered soils under complicated staged loading schemes.

• (c) The general simple method is applied to calculate consolidation settlements in a real case in HKIA Chek Lap Kok Test Embankment with multi-layered soils and vertical drains under multi-staged loading. Calculated settlements by this new simple method are in good agreement with insitu measured data and also values from an FE analysis.

• (d) Based on the above comparisons and validations, it is found that the new general simple method is accurate and easy to use for calculating consolidation settlements of single or layered soils with and without vertical drains under multi-staged loading, unloading and reloading using parameters from conventional oedometer tests.