1 Introduction

Understanding particle transport in porous media is critical in many engineering problems. For example, suffusion can be defined as a detachment of fine particles induced by hydrodynamic forces applied to the attached fine particles [12, 21, 22, 26]. It has been reported by previous studies for investigating the stability of dams because the seepage-induced detachment and transport of fine particles may cause significant deformation of dams [16, 21, 25]. In addition, retention or detachment of fine particles alters the hydraulic conductivity of coarse-grained soils, which imply that particle transport is critical in the performance of flow-related geotechnical infrastructure [33, 35].

Particles that are transporting through a saturated soil medium can be retained through straining and attachment due to large sizes of particles and attractive interparticle forces or can be detached through hydrodynamic forces. In continuum scale, most studies on investigating particles transporting through the soil, filters, or any geologic media will typically use two or three rate coefficients with advection and dispersion terms to account for mechanisms associated with particle retention or detachment. For example, some studies used attachment and detachment coefficients [7, 15], reversible and irreversible retention of particles with three rate coefficients [8] or straining, attachment, and detachment of particles [4]. In some cases, as many as five rate coefficients have been used to model particle retention at kinetic and equilibrium sites [30]. These modified advection–dispersion-type equations are well suited to explain and fit experimental data obtained in the laboratory for any combination of particle type and porous media. In order to model the retention of particles through saturated porous media and predict the reduction in hydraulic conductivity, it is common practice to use laboratory-measured values of particle transport for determining first-order rate coefficients (attachment or detachment) in the advection–dispersion equation [4].

While laboratory-scale experimental results provide the data (usually retention profiles or breakthrough curves) for evaluating the first-order rate coefficient, it is typically not possible to express those coefficients as a function of the pore size distribution of the porous media, the particle size distribution of the particles, and other microscale parameters such dead pore in water flow. This implies that a single experiment produces one set of back-calculated rate coefficients, which are only valid for corresponding experimental conditions. Therefore, a large experimental matrix would be required to obtain the first-order coefficients at varied size ratios (particle/filtration medium) or different hydrogeochemical conditions (pH, ionic strength, and flow rate) for large-scale simulation of particle transport.

Consequently, it is beneficial to develop an upscaling methodology that can reduce the experimental effort by incorporating the impact of the above-mentioned factors that influence particle retention. Pore network models are computationally less expensive than other pore-scale simulations such as the lattice Boltzmann method and smoothed particle hydrodynamics [27, 34], and they improve on the disadvantages of a macroscopic volume-averaged continuum-scale model (advection–dispersion equation with first-order rate coefficients). The ability to incorporate microscopic features of porous media, as well as properties of the transporting particles, is the main advantages of using pore network models for simulating particle transport in porous media. While it is computationally expensive, pore network models also allow tracking of individual particles during transport and can determine the representative volume of porous media for particle transport within a particular pore size distribution.

This work developed a framework to evaluate attachment coefficients from retention profiles obtained by the pore network model under varied particle size distribution and median size: upscaling from the pore scale to the continuum scale. A three-dimensional cubic pore network was constructed, and particle size distributions of kaolinite particles at three ionic strengths were used to obtain mean and standard deviation values to describe the particle size distribution of the particle. In addition, the impact of the mean and standard deviation of distributions on the retention profiles, breakthrough curves, and the reduction in hydraulic conductivity were examined.

2 Model formulation

2.1 Background: network construction and quantification of fluid flow

The network model was constructed using the open-source project code OpenPNM, which is written in Python. OpenPNM was developed to simulate multiphase flow in porous media [1, 11, 31]. A three-dimensional simple cubic network was constructed to represent the sand medium, which was used for the efficiency of computational work and the effective description of the transport process (easily be obtained through coordination number) [17, 29]. Since all simulations were performed for the case of kaolinite particles transporting through the silica sand, all material-related properties of particles and sand used in pore network simulation were equivalent to kaolinite and Ottawa 20/30 sand.

Because the main purpose of this study was to develop the framework of upscaling the particle transport from the pore scale to continuum scale, the pore network model representing the geometry of the sand medium is not considered here as it requires information on the pore structure of the sand medium (i.e., pore size distribution or X-ray CT image), which may limit the application of the framework. Furthermore, the θ0 value [Eq. (10)] introduced in Sect. 2.3 can be determined by experimental results regardless of types of the pore network model. Therefore, a cubic network model was used to represent the sand medium for this particular application presented in this paper.

In order to more closely emulate Ottawa 20/30 sand packing, the network was modeled using a coordination number (CN) ranging from 5.4–5.5 in all simulations, which was created by randomly eliminating throats from the regular three-dimensional cubic network (CN = 6 for cubic network) [32]. The distance between centers of pores in the network was set equal to the median grain size of the sand (d50), which is equivalent to the throat length of the pore network for uniform sand, based on the geometry of the discrete element model as described in [37]. The shapes of the pores and throats were assumed to be spheres and cylinders, respectively, and the diameters of the pores were initially determined at a given distribution, with the length of throats evaluated as:

$$ L_{ij} = D_{ij} - (d_{{{\text{p}}(i)}} - d_{{{\text{p}}(j)}} )/2 $$
(1)

Because all particle transport simulations in this work were performed in the saturated condition, only single-phase flow was taken into account for the flow calculation in the network model. The Hagen–Poiseuille equation was used for calculating single-phase flow in a cylindrical tube [9], where the hydraulic conductances of throats and half of the pores are expressed as:

$$ g_{{\text{t}}} = \frac{{\pi d_{{\text{t}}}^{4} }}{128L\mu } $$
(2)
$$ g_{{\text{p}}} = \frac{{\pi d_{{\text{p}}}^{4} }}{{128r_{{\text{p}}} \mu }} $$
(3)

Using Eqs. (2) and (3), the hydraulic conductance of fluid between pore i and j (gij) can be obtained by the harmonic mean of three hydraulic conductances:

$$ g_{ij} = \left( {\frac{1}{{g_{{{\text{p}}(i)}} }} + \frac{1}{{g_{{\text{t}}} }} + \frac{1}{{g_{{{\text{p}}(j)}} }}} \right)^{ - 1} $$
(4)

The flow rate between pore i and j (Qij) is obtained successively according to:

$$ Q_{ij} = g_{ij} (P_{i} - P_{j} ) $$
(5)

Pressure values of each pore at given boundary conditions can be determined by solving a system of linear equations based on the mass conservation of fluid at all pores except the boundary pores. To simulate fluid flow from inflow to outflow, Dirichlet-type boundary conditions (pressure difference corresponding to the hydraulic gradient of 0.71) were applied at the top and bottom pores for the calibration of hydraulic conductivity (shown later) before injecting particles into the network. During particle injection, Neumann-type boundary conditions (flow rate was 0.175 cm3 s−1, which corresponds to Darcy velocity of 0.2 cm s−1) were applied at the outflow pores to evaluate the reduction in hydraulic conductivity (k) due to particle retention under the constant flow rate. Particle retention decreased the throat diameter (dt) in Eq. (2), and the hydraulic conductivity of the network in each time step was evaluated using Darcy’s equation from the total pressure drop of the model.

The OpenPNM model was used to construct the pore network model and simulate water flow at a given pressure drop. The original contributions of this work for simulating particle transport can be summarized as follows: (1) generated particles at given particle size distribution to introduce to the model, (2) incorporated theoretical equations for retention of particles into the pore network model, (3) simulated the reduction in hydraulic conductivity, and (4) formatted the large set of data to evaluate particle size distributions of retained and transported particles.

2.2 Particle mass transport: development of sampling methodology

In all simulations, particles were injected at the inflow pores with a constant mass-based concentration. Consequently, the number of particles at the inflow pores, equivalent to the inlet concentration, was determined through unit conversion using the volume and the density of particles, assuming that particles are a sphere. Assuming that the particle size distribution is well described by the lognormal distribution curve, the total number of sampled particles (Nc) is obtained by:

$$ N_{c} = \frac{{V_{{{\text{inlet}}}} C_{0} }}{{4/3\pi \rho_{s} \exp (3\mu_{c} + 4.5\sigma_{c} )}} $$
(6)

Note that exp(3μc + 4.5σc) in Eq. (6) is the expected value of rc3 in a lognormal distribution (the 3rd raw moment). After determining Nc, Latin hypercube sampling, one of the sampling techniques without replacement, was applied at the given particle size distribution. Application of Latin hypercube sampling enabled the sampled rc to more accurately reflect the given particle size distribution regardless of Nc. The cumulative probability of the mth interval (Pm) by Latin hypercube sampling is given as:

$$ p_{m} = \left( {\frac{1}{{N_{c} }}} \right)u_{m} + \left( {\frac{m - 1}{{N_{c} }}} \right) $$
(7)

Using Eq. (7), m sampled rc corresponding to pm values can be obtained by inverting the cumulative distribution function. Note that um is fixed at 0.5 in all simulations to assure reproducibility of sampled rc at given particle size distribution and to eliminate the randomness of sampling for the validity of Nc in Eq. (6). A periodic boundary condition was applied at the inflow pores for the injection of particles, and particles were tracked individually during their transport through the network.

2.3 Particle mass transfer: throat length and deposition

The transport of generated particles from pore to pore was obtained based on the corresponding mass transfer between pores in each time step, with the length of the pore throat included explicitly. The amount of transferred mass from pore i to adjacent pores was calculated using flow rate (Qij) through the corresponding pore throats coupled with a scaled reference length (Lref) to eliminate the error associated with a mass transfer at the pore scale according to:

$$ M_{ij} = C_{i} Q_{ij} \Delta t\left( {\frac{{L_{ij} }}{{L_{{{\text{ref}}}} }}} \right) $$
(8)

Here, Mij is independent of Lij at given Δt with an absence of (Lref/Lij) in Eq. (8). Note that Eq. (8) is valid for pores adjacent to pore i only when Pi > Pj (pore j can be multiple pores). By applying Mij, the number of particles moving from pore i to pore j in each time step was determined through unit conversion. Using Qij in Eq. (8) means that the prediction of the particle movement was analogous to the flow-biased probability model presented in [36], which described the walking direction of particles based on the magnitude of flow rates at the neighboring throats.

Particles were considered retained in the throats if a random number between 0 and 1 for each particle was less than the capture probability (pcap), which is expressed as [13, 28]:

$$ p_{{{\text{cap}}}} = 4\left[ {\left( {\frac{{\theta r_{c} }}{{r_{t} }}} \right)^{2} - \left( {\frac{{\theta r_{c} }}{{r_{t} }}} \right)^{3} } \right] + \left( {\frac{{\theta r_{c} }}{{r_{t} }}} \right)^{4} $$
(9)

To take the effect of water velocity at throats (v) into account, the lumped parameter, θ, is expressed as:

$$ \theta = \theta_{0} \exp ( - v/v_{{\text{c}}} ) $$
(10)

Analytically, vc is given by [23]:

$$ v_{{\text{c}}} = \frac{A}{{61.218\pi \mu h_{0}^{2} }} $$
(11)

The Hamaker constant (= 9.36 × 10−21 J) in silica sand–water–kaolinite system was used in all simulations, which was calculated by refractive indexes and dielectric constants of those materials [18]. In addition, the interaction energy between sand and kaolinite was evaluated based on the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory. The result of the DLVO calculation (Fig. S1 in Supplementary material) revealed that a high energy barrier between sand and kaolinite particles hindered the attachment of particles at the primary minimum, which resulted in the primary attachment at a secondary minimum [5, 19, 20]. Therefore, h0 was set equal to the separation distance corresponding to the secondary minimum (= 5.2 nm). As a result, vc remained constant (= 1.8 × 10−3 m s−1) throughout the simulation.

The retention of particles decreased the radius of throats and increased the pressure drop within the network. The pressure drop at a throat (ΔPp) due to the retention of particles is determined as [14]:

$$ \Delta P_{{\text{p}}} = \frac{{12\mu r_{c} U}}{{r_{t}^{2} }}\left( {1 - \left( {1 - \frac{{r_{c} }}{{r_{t} }}} \right)^{2} } \right)^{2} K_{1} $$
(12)
$$ K_{1} = \frac{{1 - (2/3)(r_{c} /r_{t} )^{2} - 0.202(r_{c} /r_{t} )^{5} }}{{1 - 2.105(r_{c} /r_{t} ) + 2.086(r_{c} /r_{t} )^{3} - 1.707(r_{c} /r_{t} )^{5} + 0.726(r_{c} /r_{t} )^{6} }} $$
(13)

where U is 2·v for laminar pipe flow. The total pressure drop (ΔPtotal) of the throat can be obtained by ΔPtotal = ΔPthroat + Σ ΔPp. The updated effective throat radius (rnew) for the calculation in the next time step after N particles were retained is determined by [28]:

$$ \frac{1}{{r_{{{\text{new}}}}^{4} }} = \frac{1}{{r_{t}^{4} }} + \frac{0.75}{{r_{t}^{4} }}\sum\limits_{i = 1}^{N} {\frac{{r_{c} }}{L}\left( {1 - \left( {1 - \frac{{r_{c} }}{{r_{t} }}} \right)^{2} } \right)^{2} K_{1} } $$
(14)

Note that the retention of particles only occurred in network throats, indicating that the radius of the pores remained constant. In addition, θ decreased as the amount of retained particles increased under constant flow rate due to the increase in v (rt decreases as particles retained). A flowchart of key features used for predicting particle transport/retention is illustrated in Fig. 1.

Fig. 1
figure 1

Flowchart describing key features of the model

Full size image

2.4 Continuum equation for particle transport

The macroscale model used in this work for describing particle transport was an advection–dispersion equation with two first-order coefficients to account for the attachment and detachment of particles [7]:

$$ \frac{\partial (nC)}{{\partial t}} = - \nabla \cdot J_{T} - nk_{{{\text{att}}}} \psi_{{{\text{att}}}} C + \rho_{b} k_{\det } S_{{{\text{att}}}} $$
(15)

where JT is the sum of advective and dispersive fluxes and dispersion coefficient of the particle was calculated by given Reynolds number and Péclet number [10] and ψatt = (1 − Satt)/Smax.

Optimization analysis was performed using the trust-region algorithm to yield optimized first-order attachment and detachment coefficients at a given retention profile (RP) obtained by the pore network model (least square sense as illustrated in Fig. 2). The implicit finite difference method was used to solve Eq. (15) with convergence in each time step. The straining mechanism, which is defined as particle immobilization due to narrow throat sizes [2, 6], was incorporated into the attachment coefficient in Eq. (15). This allowed the use of a single coefficient, katt, to model retention as a function of the input parameters including particle size distribution, the median size of the particle, and throat size distribution.

Fig. 2
figure 2

Examples of optimization analysis: Markers represent the results from pore network simulation, and lines represent the best-fit curves by solving continuum equation [Eq. (15)]

Full size image

2.5 Model calibration and determination of the size of the model

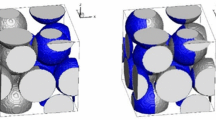
The model was calibrated using the value of the experimentally measured hydraulic conductivity for Ottawa 20/30 sand (0.14 cm s−1) by altering the aspect ratio between pores and throats (diameter of pores/diameter of throats) until the hydraulic conductivity of pore network model converged to the measured hydraulic conductivity (Fig. 3). In addition, in order to avoid boundary effects, the number of modeled pores in the x-, y-, and z-axes was determined as 14, 14, and 40 (Fig. 4). By performing this calibration, the cubic pore network used in this work is hydraulically consistent with the real sand medium. An example visualization of the pore network is illustrated in Fig. 5.

Fig. 3
figure 3

Calibration of the hydraulic conductivity of the network (kpnm) to experimentally measured hydraulic conductivity (kexp)

Full size image
Fig. 4
figure 4

The effect of numbers of pores in x-, y-, and z-axes (Nx, Ny, and Nz) on the hydraulic conductivity (k) of the network. Note that Nx = Ny in this calculation

Full size image
Fig. 5
figure 5

An example visualization of the regular cubic pore network used in this simulation. Colloid suspension was injected at the top of the network, and part of throats were eliminated randomly until CN ~ 5.4. The color of pores indicates pressure values at pores from high (colored in red) to low (colored in blue) (color figure online)

Full size image

2.6 Simulation cases

In total, 72 simulations were performed with the following values for the control variables: mean particle size (µc) = 1.3, 1.8, and 2.2, standard deviation of particle size (σc) = 0.01, 0.1, 0.2, and 0.3, and lumped interparticle force parameter (θ0) = 2, 4, 6, 8, 10, and 12. The mean (µc) values used in the simulation corresponded to the experimental median sizes of kaolinite particles presented in Fig. S2. Retention profiles, breakthrough curves, the reduction in hydraulic conductivity, and size distribution of particles in the retention profiles and the breakthrough curves were evaluated for the 72 cases, with the mass-based concentration C0 in Eq. (6) fixed at 1 g L−1 in all simulations. Note that the sizes of kaolinite particle used here represent the size of kaolinite clusters (aggregated formation of kaolinite particles), which implies that the proposed framework in this work can apply to most of the colloidal particle transport (particles < 10 µm can be defined as colloidal particles [24]. The properties used in this study are summarized in Table 1.

Table 1 Properties of kaolinite and sand used in the simulation
Full size table

3 Results and discussion

3.1 Retention profiles and evaluating attachment coefficients

The retention profiles of 72 cases obtained by the pore network model (some cases are presented in Fig. 6) were fitted in order to determine the attachment coefficient (katt) in Eq. (15) (Fig. 2), which can be used in macroscale simulation (Fig. 7). The value of kdet was fixed to 1 × 10−4/s, by assuming that the detachment coefficient of particles was proportional to the flow rate which was constant in all simulation in this work, and to allow quantitative comparison of katt between each condition. As illustrated in Fig. 7, it is apparent that katt increased as θ0 increased due to the increase in capture probability. In addition, under constant interaction energy (θ0), katt increased as µc and σc increased because increases in the median particle size and in the standard deviation of the particle size resulted in higher capture probability at the column inlet. Physically, θ0 represents the interaction energy between particles and the sand grain, with increasing θ0 values indicating higher attractive energy (i.e., more favorable attachment). In addition, because θ0 is a single parameter that represents both straining and attachment deposition mechanisms, increasing the value of θ0 indicates a high chance for particles to also be retained by straining (reflected in increasing µc and σc). For clay particle transport/retention in a sand medium, large values of θ0 represent the solution chemistry of low ionic strength, which results in more exponential retention profiles due to the large sizes of clay clusters that form in solutions with low electrolyte concentrations [33]. Note that attractive energy between particles and a porous media matrix is a function of mineralogy and solution chemistry.

Fig. 6
figure 6

Retention profiles under a varied θ0 at µc = 2.2 and σc = 0.3, b varied σc at µc = 1.8 and θ0 = 4, c under varied µc = 2.2, 1.8 and 1.3 at θ0 = 8 and σc = 0.3 (c). S + n·C/ρb represents retained particles in the solid phase (S) and aqueous phase (n·C/ρb)

Full size image
Fig. 7
figure 7

Optimized katt under varied θ0 at µc = 2.2, 1.8, 1.3 and σc = 0.01, 0.3. Increasing interparticle attraction, particle size, and particle size standard deviation increased the capture probability, resulting in increased katt (raw data are summarized in Table S1 in supplementary material)

Full size image

The above-mentioned upscaling framework provides the evaluation of katt for the particular particle–porous media system under conditions of variable flow rate and particle sizes (particle and sand), all of which can be evaluated from one experimental retention profile. Because all parameters used in the pore network model except θ0 are available from experimental conditions, θ0 can be back-calculated based on the observed experimental retention profile. (θ0 is not dependent on particle sizes and hydrological conditions.) Using this back-calculated θ0 allows determination of retention profiles at different sizes of particles and pores, as well as a range of hydrological conditions [Eqs. (10), (11)] in the pore network model, which will eventually provide katt at different conditions at given particle–sand medium system for long-term and large-scale simulation. The limitation of not being able to take particle size distribution and hydrological conditions into account in the continuum scale model [Eq. (15)] can be resolved using the proposed framework.

3.2 Effect of parameter θ 0 and particle size distribution of clay particle (μ c and σ c)

The breakthrough curves and reduction in hydraulic conductivity at varied θ0, µc, and σc are presented in Fig. 8. An increase in θ0 resulted in a larger mass of retained particles which lowered particle breakthrough (C/C0) and reduced hydraulic conductivity (K/K0) during 10 pore volumes of flow (Fig. 8), as was anticipated. Essentially no particle breakthrough was observed at values of θ0 > 20 (Fig. 8), and the reduction in hydraulic conductivity was more significant as θ0 increased because of increased particle retention at large values of θ0. Note that the results presented in this work are with an assumption of critical velocity [vc in Eq. (10)] equal to 0.18 cm s−1. (Separation distance is assumed 5.2 × 10−7 cm, corresponding to the distance of kaolinite–water–sand system in 0.1 M monovalent salt solution.) The interparticle attraction forces vary depending on vc, mineralogy of particles, mineralogy of porous material, and solution chemistry used in the vc calculation.

Fig. 8
figure 8

Breakthrough curves and the reduction in hydraulic conductivity during the injection under varied σc at µc = 1.8 and θ0 = 4 (a–c), and under varied µc = 2.2, 1.8 and 1.3 at θ0 = 8 and σc = 0.3 (d–f)

Full size image

As µc and σc increased, less breakthrough and more significant reduction of K/K0 were observed due to the significant surface retention of particles (Fig. 6b, c). The majority of particle transport studies and filtration theories have used the median sizes of the particle (exp(µc) for lognormal distribution) as the representative size in modeling [3]. However, the results presented in Fig. 7 imply that the mean size of the particle size distribution of particles should be used to model particle transport/retention in porous media because the retention profiles and breakthrough curves are dependent on µc as well as σc. (The expected value of particle size distribution is exp(µc + σc2/2) for lognormal distribution.)

3.3 Size distributions of particles in retention profiles and breakthrough curves

The size distributions of retained particles and effluent particles within the network model were illustrated by box plots (Fig. 9). At low values of interparticle attraction (θ0), particles were retained uniformly at all depths in sizes that were slightly larger than the median size of the particle size distribution of the particles; however, crossover points between median sizes of retained particles and the particle size distribution were observed at relatively high values of interparticle forces (θ0). This trend of retained particle size under varied θ0 was comparable for all simulations of mean particle size (µc) and showed that most of the large particles were retained near the injection point (inflow), which led to smaller particles being retained in the bottom part of the sand medium with the impact becoming more significant as θ0 increased. At low values of θ0, the sizes of retained particles were uniformly larger than the median size of the particle size distribution at all depths because of low capture probability. As a result, the median size of effluent particles at θ0 = 2 was roughly identical with the median size of particles in all pore volumes in the network model. At other θ0 values, the median sizes of effluent particles were smaller than the median size of the particle size distribution. The difference between the median sizes of effluent particles and the median (or mean) sizes of the inlet particle distribution was more significant as θ0 increased (Fig. 9).

Fig. 9
figure 9

Size distributions of retained particles and particles in effluent under varied θ0 at µc = 1.8 and σc = 0.3. The edges of the boxes correspond to 25 and 75% coverages, and the red lines in the boxes represent the median value of sizes of retained particles. The whisker line of each box plot indicates 99% coverage for distribution in each depth (color figure online)

Full size image

4 Conclusions

In this work, a pore network model for polydispersed particle transport in porous media was developed to upscale the pore-scale results into the attachment coefficients in the continuum-scale equation. Based on the observed retention profiles, breakthrough curves, and the reduction in hydraulic conductivity from the pore network simulation, the following conclusions can be drawn:

  1. 1.

    The pore network model introduced in this work can be used to reflect particle size distribution of the particles, flow rate, and solution chemistry in the estimation of attachment coefficients in the continuum equation for long-term and large-scale simulation.

  2. 2.

    Larger mean and standard deviation of particle size distribution, and a larger interparticle force led to a more significant reduction in hydraulic conductivity, which is attributed to less breakthrough concentration and a larger amount of retained particles.

  3. 3.

    Low values of interparticle forces resulted in effluent sizes that were similar to the mean of the particle size distribution because the probability of capture (straining or attachment) was low. As the value of the interparticle forces increased, the median sizes of the effluent particles were smaller than the median size of the particle size distribution, with the difference between the median sizes of effluent particles and the median sizes of the particle distribution becoming more significant as θ0 increased.

  4. 4.

    Further development of the pore network model can reflect other pore-scale characteristics of sand medium (pore-scale geometry, the kinetic energy fluctuations of the particle, degree of saturation) into macroscale parameters such as attachment coefficient.