1 Introduction

It is known that the unsaturated sand can exhibit apparent cohesion with a magnitude depending on the variations of suction within the sand. Sandcastle is a good example showing the presence of apparent cohesion within the unsaturated sand. Similarly, the unsaturated soil also exhibits tensile strength with an increase in matric suction. Nearing et al. [27] stated that the tensile strength of soil had a significant effect on the soil erosion and surface sealing. Lu et al. [25] indicated that the tensile stress of the granular soil was commonly adopted as an indication of the soil capability to sustain an external tensile stress without failure. Lu et al. [25] also indicated that tensile strength of sandy soil is dependent on the degree of saturation, particle size, particle size distribution, and porosity. Causarano [5] stated that the water content of a soil had a significant effect on the tensile strength of the soil. In summary, the tensile strength of an unsaturated soil is not constant, but a function of soil suction.

It is believed that for a cohesionless soil, the tensile strength is mainly contributed by two factors, such as (1) capillary force due to matric suction and (2) capillary bonding due to surface tension [14, 22]. Lu et al. [25] presented that most of the existing theories for predicting tensile strength of moist granular soils were derived by considering the intergranular forces between idealized soil particles. These theories are commonly applicable only for a limited range of saturation (i.e., high suction range). Many researchers [1, 4, 7, 14, 18, 21, 25, 26, 31,32,33, 37, 38, 41, 44, 46] developed models for the estimation of the tensile strength of soil. Rumpf [32] proposed a model by upscaling a theorized liquid bridge force for the monosized spherical particles to estimate the tensile strength of moist soil based on the assumption that soil particles are uniformly distributed. Schubert [34, 35] and Pierrat and Caram [30] extended Rumpf’s [32] model by using a normalized degree of saturation to superimpose Rumpf’s [32] interparticle stress in the pendular regime with the stress arising from matric suction in the wet pores. Lu et al. [25] developed the theory for the explanation of tensile strength of sandy soil by adopting the concept of suction stress proposed by Lu and Likos [23]. Yin and Vanapalli [46] proposed a model to estimate the tensile strength of a cohesionless soil from the degree of saturation, using the SWCC as a tool.

Reviewing those models developed by previous researchers, it is observed that the tensile stress of soil can be defined by a general equation as follows:

$${{\sigma}_{\text{t}}}=k{{\sigma}_{\text{tia}}}=kc$$
(1)

where σt is the tensile stress, k is the coefficient which is related to the testing condition (isotropic, uniaxial, or in-between), σtia is the isotropic tensile stress, and c is the total or apparent cohesion of soil as introduced by Fredlund and Rahardjo [9].

Lu et al. [25] stated that the uniaxial conditions could not be maintained for the entire testing process. Therefore, the coefficient of k is dependent on the testing conditions. Lu et al. [25] also pointed out that the isotropic tensile strength was close to the “apparent cohesion” which has the similar definition of the total cohesion as defined by Fredlund and Rahardjo [9]. Different models from various researchers such as [2, 8, 12, 15, 36, 42, 50] were available for the estimation of the total cohesion.

In this paper, the tensile strength of a sandy soil is estimated from its SWCC by adopting the concept of pore-size distribution function (PSDF). Childs and Collis-George [6] were considered as the first researchers who used the PSDF for the estimation of water flow in unsaturated soils. Zhai and Rahardjo [47] and Zhai et al. [49, 51] extended Childs and Collis-George’s [6] method for the estimation of the coefficient of permeability of unsaturated soil. Vanapalli et al. [42] adopted the concept of water area, which defines the effective area of water meniscus, for the estimation of the unsaturated shear strength of soil. Zhai et al. [50] illustrated that the water area from Vanapalli et al. [42] could be calculated from the SWCC by adopting the concept of PSDF. In this paper, the concept of water area is also adopted for the estimation of the tensile strength of the unsaturated soil. Recently, Wen et al. [45] and Kido et al. [16] conducted experiments to investigate the pore water pressure characteristics in soil during the drying and wetting processes. However, the hysteresis of SWCC was not considered in this paper.

It seems that the concept of PSDF has rarely been adopted for the estimation of tensile strength of unsaturated soil. In this paper, the tensile strength of unsaturated sandy soil was estimated from the soil–water characteristic curve (SWCC) based on the concept of PSDF. The estimated results were verified with the experimental data from the published literature. In addition, the effects of the variation in the initial void ratio and fine contents on the estimated tensile strength are also discussed in this paper.

2 Theory

The tensile strength of the unsaturated soil was analyzed in both isotropic and uniaxial conditions. In the analysis, the concept of PSDF was used to estimate the compression stress on the soil structure due to the matric suction. The pulling stresses between soil particles were estimated from the compression stress. Consequently, the tensile strength of the unsaturated soil was estimated from both compression stress and the pulling stress.

2.1 Estimation of the total cohesion, c

Zhai et al. [50] explained that the meniscus between soil particles results in two stresses on the soil structure and soil particles such as (1) the compression stress, σn, on the soil structure, and (2) pulling stress (or capillary bonding), σp, between soil particles. When the soil is in an unsaturated condition, there are various meniscuses created in the pores with different sizes. In each pore, the stresses resulted from the meniscus can be divided into two directions (i.e., x and y directions as shown in Fig. 1). In y-direction, the compression stress can be calculated from the suction times the cross area of the pore (or the cross area of the capillary tube), while the pulling stress between soil particles can be calculated from the suction times cross section of the meniscus as shown in Fig. 1. As shown in Fig. 1, the compression stress and pulling stress resulted from the meniscus in a particular pore are dependent on each other. Once compression stress is generated, pulling stress will be generated simultaneously. In other words, the pulling stress can be calculated from the compression stress based on the ratio between the areas in Fig. 1c, b.

Fig. 1
figure 1

Illustration of stresses resulted from the meniscus in the pore. a Perspective view of the meniscus; b Illustration of compression stress in y-direction; c Illustration of pulling stress in x direction. (ua − uw, is the matric suction, Rs is the radius of meniscus, r is the radius of pore.)

Full size image

The area as shown in Fig. 1b can be calculated from the area of a circle with radius of r as illustrated in Eq. (2), while the area as shown in Fig. 1c can be calculated from the area of the fan (as illustrated in Fig. 1c) with radius of Rs minus the area of triangle as illustrated in Eq. (3).

$${{A}_{{{\sigma}_{\text{ni}}}}}=\pi r_{\text{i}}^{2}$$
(2)

where \(A_{{\sigma_{\text{ni}} }}\) is the effective area for the compression stress resulted from the meniscus in the pore with a radius of ri.

$$A_{{\sigma_{\text{pi}} }} = \alpha R_{\text{s}}^{2} - r_{\text{i}} \sqrt {R_{\text{s}}^{2} - r_{\text{i}}^{2} }$$
(3)

where \(A_{{\sigma_{\text{pi}} }}\) is the effective area for the pulling stress resulted from the meniscus in the pore with radius of ri, sinα = ri/Rs.

The ratio between \(A_{{\sigma_{\text{pi}} }}\) and \(A_{{\sigma_{\text{ni}} }}\) can be defined by a coefficient ηi as illustrated in Eq. (4).

$$\eta_{i} = \frac{{\alpha R_{\text{s}}^{2} - r_{i} \sqrt {R_{\text{s}}^{ 2} - r_{i}^{2} } }}{{\pi r_{i}^{2} }}$$
(4)

As a result, if the compression stress resulted from the meniscus in the pore with ratios of ri is σni, then the pulling stress resulted from the same meniscus is ηiσni.

Zhai et al. [49] stated that the water area corresponding to the pores with radius of ri can be calculated from S(ψi) − S(ψi+1) based on the capillary model. Define the soil suction as ψm, the compression stress and the pulling stress resulted from the meniscus in the pore with radius ri can be calculated as follows:

$$\sigma_{n} \left( {\psi_{m} } \right)_{{r_{i} }} = \left[ {S\left( {\psi_{i} } \right) - S\left( {\psi_{i + 1} } \right)} \right]\psi_{m}$$
(5)
$$\sigma_{p} \left( {\psi_{m} } \right)_{{r_{i} }} = \eta_{i} \sigma_{n} \left( {\psi_{m} } \right)_{{r_{i} }} = \eta_{i} \left[ {S\left( {\psi_{i} } \right) - S\left( {\psi_{i + 1} } \right)} \right]\psi_{m}$$
(6)

Summations of Eqs. (5) and (6) for all the pores in the soil give the compression stress on the soil structure and pulling stress between soil particles as follows:

$$\sigma_{n} = \sum\limits_{i = m}^{N} {\sigma_{n} \left( {\psi_{m} } \right)_{{r_{i} }} } = \sum\limits_{i = m}^{N} {\left[ {S\left( {\psi_{i} } \right) - S\left( {\psi_{i + 1} } \right)} \right]} \psi_{m}$$
(7)
$$\sigma_{p} = \sum\limits_{i = m}^{N} {\sigma_{p} \left( {\psi_{m} } \right)_{{r_{i} }} } = \frac{{\psi_{m} }}{\pi }\sum\limits_{i = m}^{N} {\left\{ {\left[ {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} \alpha_{i} - \sqrt {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} - 1} } \right]\left[ {S(\psi_{i + 1} ) - S(\psi_{i} )} \right]} \right\}}$$
(8)

Vanapalli et al. [42] adopted a normalized degree of saturation, Sn, as illustrated in Eq. (9) to calculate the water area for the estimation of the unsaturated shear strength.

$$S_{\text{n}} = \frac{{S - S_{\text{r}} }}{{1 - S_{\text{r}} }}$$
(9)

where Sn is the normalized degree of saturation, S is the degree of saturation, and Sr is the residual degree of saturation.

Multiplying the water area and the matric suction gives the compression stress on the soil structure due to the meniscus as shown in Eq. (10).

$$\sigma_{n} = \left( {\frac{{S - S_{\text{r}} }}{{1 - S_{\text{r}} }}} \right)\left( {u_{\text{a}} - u_{\text{w}} } \right)$$
(10)

By analyzing the effects of different types of water (i.e., gravity water, capillary water, and hygroscopic water) in soil on the meniscus, Zhai et al. [50] indicated that the hygroscopic water did not contribute to the compression stress and pulling stress because the hygroscopic water is attached to isolated soil particles. Consequently, Zhai et al. [50] recommended that Eq. (10) should be modified as follows:

$$\sigma_{n} = \left( {\frac{{S - S^{\prime }}}{{1 - S^{\prime }}}} \right)\left( {u_{\text{a}} - u_{\text{w}} } \right)$$
(11)

where S′ is the degree of saturation corresponding to the suction of 3100 kPa [3, 29, 50].

Zhai et al. [50] also recommended to replace S with Sn= (S–S′)/(1 − S′) in the plotting of SWCC-S. If the revised SWCC-Sn is used for the calculation of the water area, then Eq. (7) will be consistent with Eq. (11). Consequently, the total cohesion of the soil with soil suction of ψm can be obtained from Eq. (12) as follows:

$$\begin{aligned} c & = c^{\prime} + \left( {\frac{{S - S^{\prime }}}{{1 - S^{\prime }}}} \right)\left( {u_{a} - u_{w} } \right)\tan \phi ^{\prime } \\ & \quad + \frac{{\psi_{m} }}{\pi }\sum\limits_{i = m}^{N} {\left\{ {\left[ {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} \alpha_{i} - \sqrt {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} - 1} } \right]\left[ {S(\psi_{i + 1} ) - S(\psi_{i} )} \right]} \right\}} \\ \end{aligned}$$
(12)

The calculated total cohesion from the third term in Eq. (12) is much less than that from first two terms. Therefore, there is no correction made for the third term in Eq. (12).

It should be noted that Zhou et al. [55] had proposed the capillary water retention curve (CWRC) and the adsorptive water retention curve (AWRC) for the estimation of shear strength of unsaturated soil. The SWCC-Sn in this paper is similar as the CWRC from Zhou et al. [55]. In this study, the effects of the capillary water and the adsorptive water on the tensile strength of the sandy soil are considered to be insignificant. Therefore, the SWCC-Sn is limited to 3100 kPa for the estimation of tensile strength of the unsaturated sandy soil.

2.2 Determination of the coefficient k for the soil subjected to the external tensile stress in one direction

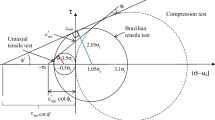
Mohr–Coulomb (M–C) failure criterion (as illustrated in Fig. 2) is commonly used to explain the tensile strength of soil under isotropic and uniaxial conditions. If there is no shear stress in the soil, which is illustrated as point A in Fig. 2, then the obtained tensile stress is named as isotropic tensile stress, σtia. However, if the soil specimen is subjected to the external tensile stress in one direction, then the soil may fail before σtia is reached. The obtained tensile strength in this condition is commonly named as uniaxial tensile stress, σtua. The relationship between σtia and σtua is illustrated in Fig. 2.

Fig. 2
figure 2

(Modified from Lu et al. [25])

Conceptual illustration of isotropic tensile stress, σtia, uniaxial tensile stress, σtua using the M–C failure criterion.

Full size image

In the triangle ABO, the sinϕ′ can be defined by OB dividing by OA. It is noted that OB is equal to the half magnitude of σtua, while OA is equal to the magnitude of (σtia − 0.5σtua). As a result, σtia and σtua can be defined using the following equation:

$$\sin \phi^{\prime} = \frac{{\text{OB}}}{{\text{OA}}} = \frac{{\sigma_{\text{tua}} }}{{2\left( {\sigma_{\text{tia}} - {\raise0.7ex\hbox{${\sigma_{\text{tua}} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\text{tua}} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right)}}$$
(13)

Rearranging Eq. (13) gives Eq.(14) as follows:

$$\sigma_{\text{tua}} = 2\sigma_{\text{tia}} \frac{{\sin \phi^{\prime}}}{{1 + \sin \phi^{\prime}}}$$
(14)

Expressing ϕ′ = 2(ϕ′/2) and Eq. (14) can be rearranged as follows:

$$\sigma_{\text{tua}} = 2\sigma_{\text{tia}} \frac{{2\sin \frac{{\phi^{\prime}}}{2}\cos \frac{{\phi^{\prime}}}{2}}}{{\left( {\sin \frac{{\phi^{\prime}}}{2} + \cos \frac{{\phi^{\prime}}}{2}} \right)^{2} }} = 2\sigma_{tia} \frac{{2\tan \frac{{\phi^{\prime}}}{2}}}{{\left( {1 + \tan \frac{{\phi^{\prime}}}{2}} \right)^{2} }}$$
(15)

Equation (15) can be further rearranged as follows:

$$\sigma_{\text{tua}} = 2\sigma_{\text{tia}} \frac{{2\tan \frac{{\phi^{\prime}}}{2}\left( {1 - \tan \frac{{\phi^{\prime}}}{2}} \right)}}{{\left( {1 + \tan \frac{{\phi^{\prime}}}{2}} \right)^{2} \left( {1 - \tan \frac{{\phi^{\prime}}}{2}} \right)}}{ = }2\sigma_{\text{tia}} \tan \phi^{\prime}\tan \left( {\frac{\pi }{4} - \frac{{\phi^{\prime}}}{2}} \right)$$
(16)

Equation (16) is the same as the equations reported by Lu et al. [25] and Yin and Vanapalli [46].

Consequently, the uniaxial tensile stress, σtua, of soil can be calculated from the isotropic tensile stress, σtia, using Eq. (14) or (16). As shown in Eqs. (14) and (16), the coefficient k for a soil specimen subjected to the external stress in one direction can be defined by \(k = \frac{2\sin \phi '}{1 + \sin \phi '}\) or \(k = 2\tan \phi^{\prime}\tan \left( {\frac{\pi }{4} - \frac{{\phi^{\prime}}}{2}} \right)\).

Substituting Eq. (12) into Eqs. (14) and (16), the uniaxial tensile stress, σtua, of soil can be estimated using Eq. (17) or (18) as follows:

$$\sigma_{\text{tua}} = 2\left\{ \begin{array}{ll} \frac{{S - S^{\prime }}}{{1 - S^{\prime }}}\left( {u_{\text{a}} - u_{\text{w}} } \right){ \tan }\phi^ {\prime }{ + } \hfill \\ \sum\limits_{i = m}^{N} {\frac{{\psi_{m} }}{\pi }\left[ {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} \alpha_{i} - \sqrt {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} - 1} } \right]\left[ {S(\psi_{i + 1} ) - S(\psi_{i} )} \right]} \hfill \\ \end{array} \right\}\frac{{\sin \phi ^{\prime }}}{{1 + \sin \phi ^{\prime }}}$$
(17)
$$\sigma_{\text{tua}} = 2\left\{ \begin{array}{ll} \frac{{S - S^{\prime }}}{{1 - S^{\prime }}}\left( {u_{\text{a}} - u_{\text{w}} } \right){ \tan }\phi ^{\prime }{ + } \hfill \\ \sum\limits_{i = m}^{N} {\frac{{\psi_{m} }}{\pi }\left[ {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} \alpha_{i} - \sqrt {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} - 1} } \right]\left[ {S(\psi_{i + 1} ) - S(\psi_{i} )} \right]} \hfill \\ \end{array} \right\}\tan \left( {\phi ^{\prime }} \right)\tan \left( {\frac{\pi }{4} - \frac{{\phi ^{\prime }}}{2}} \right)$$
(18)

As Fredlund and Xing [10] and van Genuchten [43] equations are commonly used by researchers, both equations are substituted into Eq. (17). Consequently, electronic spreadsheets can be created to estimate the tensile strength of sandy soil from the fitting parameters such as af, nf, and mf in Fredlund and Xing’s [10] equation using Eq. (19) and av, bv, and cv in van Genuchten’s [43] equation using Eq. (22).

$$\sigma = 2\left\{ \begin{array}{ll} \frac{{C\left( \psi \right)\left\{ {\frac{1}{A\left( \psi \right)} - \frac{1}{{A\left( {\psi^{\prime}} \right)}}} \right\}}}{{1 - C\left( \psi \right)\frac{1}{{A\left( {\psi^{\prime}} \right)}}}}\psi { \tan }\phi^{\prime}{ + } \hfill \\ \sum\limits_{i = m}^{N} {\frac{{\psi_{m} }}{\pi }\left[ \begin{aligned} \left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} \alpha_{i} - \hfill \\ \sqrt {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} - 1} \hfill \\ \end{aligned} \right]\left[ {C\left( {\psi_{i + 1} } \right)\frac{1}{{A\left( {\psi_{i + 1} } \right)}} - C\left( {\psi_{i} } \right)\frac{1}{{A\left( {\psi_{i} } \right)}}} \right]} \hfill \\ \end{array} \right\}\frac{{\sin \phi^{\prime}}}{{1 + \sin \phi^{\prime}}}$$
(19)
$$A\left( x \right) = \frac{1}{{\left\{ {\ln \left[ {e + \left( {\frac{x}{{a_{\text{f}} }}} \right)^{{n_{\text{f}} }} } \right]} \right\}^{{m_{\text{f}} }} }}$$
(20)
$$C\left( x \right) = 1 - \frac{{\ln \left( {1 + \frac{x}{{C_{\text{r}} }}} \right)}}{{\ln \left( {1 + \frac{{10^{6} }}{{C_{\text{r}} }}} \right)}}$$
(21)

where af, nf, and mf are fitting parameters in Fredlund and Xing’s [10] equation  and Cr is  the input parameter, a rough estimation of the residual suction. ψ′ is the suction when most of the capillary water in the sandy soil has been drained out and ψ′ could be approximately to be equal to 3100 kPa as recommended by Zhai et al. [50]

$$\sigma = 2\left\{ \begin{array}{ll} \frac{{\frac{1}{{\left\{ {1 + \left( {a_{\text{v}} \psi } \right)^{{b_{\text{v}} }} } \right\}^{{c_{\text{v}} }} }} - \frac{1}{{\left\{ {1 + \left( {a_{\text{v}} \psi^{\prime}} \right)^{{b_{\text{v}} }} } \right\}^{{c_{\text{v}} }} }}}}{{1 - \frac{1}{{\left\{ {1 + \left( {a_{\text{v}} \psi^{\prime}} \right)^{{b_{v} }} } \right\}^{{c_{v} }} }}}}\psi { \tan }\phi^{\prime}{ + } \hfill \\ \sum\limits_{i = m}^{N} {\frac{\psi }{\pi }\left[ {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} \alpha_{i} - \sqrt {\left( {\frac{{\psi_{i} }}{{\psi_{m} }}} \right)^{2} - 1} } \right]\left[ {\frac{1}{{\left\{ {1 + \left( {a_{\text{v}} \psi_{i + 1} } \right)^{{b_{\text{v}} }} } \right\}^{{c_{\text{v}} }} }} - \frac{1}{{\left\{ {1 + \left( {a_{\text{v}} \psi_{i} } \right)^{{b_{\text{v}} }} } \right\}^{{c_{\text{v}} }} }}} \right]} \hfill \\ \end{array} \right\}\frac{{\sin \phi^{\prime}}}{{1 + \sin \phi^{\prime}}}$$
(22)

where av, bv, and cv are fitting parameters in van Genuchten’s [43] equation.

3 Validations and discussions

The comparisons between the estimated results from the proposed equation and the experimental data reported from the published literature are presented in this section. In addition, the effects of variations in the initial void ratio and fine contents on the estimated tensile strengths are investigated and discussed in this section.

3.1 Validations

The experimental data with both information of tensile stress and SWCC are selected for the verification of the proposed equation. By searching the literature, five sets of data were selected such as Esperance sand with porosity of 0.4 and 0.45 from Lu et al. [25], Perth Silty sand from Lu et al. [24], and Ottawa sand without fines and 2% fines from Hwang [13], Perkins [28] and Kim [17]. Only measured data of SWCC for Esperance sand with porosity of 0.4 and Ottawa sand with no fines are reported; therefore, the SWCCs for these two types of soil are also used to estimate their tensile strengths. The measured and best-fitted SWCCs for these soils are illustrated in Fig. 3. Lu et al. [25] indicated that the ratio of the shear stress to the normal stress typically increased drastically as the normal stress decreased. Sture et al. [39] reported that the friction angle could be as high as 70° for clean sand at small normal stress level. In this study, the friction angles for Esperance sand and Perth silty sand, as reported by Lu et al. [25], were adopted as 50 degrees and 48 degrees, respectively. Meanwhile, the friction angle for Ottawa sand was adopted as 55 degrees as reported by Kim [17]. Same friction angles have been adopted by Lu et al. [25] and Yin and Vanapalli [46]. It should be noted that some experimental data of tensile strength were measured at a low degree of saturation, but there was no measured data of SWCC at this low degree of saturation. To avoid the misinterpretation of the data, the tensile strength at a low degree of saturation was not adopted in this study.

Fig. 3
figure 3

Measured and best fitted SWCCs for Esperance sand, Perth Silty Sand, and Ottawa sand

Full size image

Best fitting the experimental data with the Fredlund and Xing’s [10] equation resulted in the fitting parameters (af, nf, and mf) for these soils as illustrated in Table 1. These fitting parameters were subsequently used to estimate the tensile strength for these soils using Eq. (19) with the created electronic spreadsheet. The estimated and measured tensile strengths for those soils are illustrated in Fig. 4.

Table 1 Fitting parameters of the best-fitted SWCCs and friction angles
Full size table
Fig. 4
figure 4

Comparison between estimated and measured tensile stresses for the soils. a For Esperance sand with porosity of 0.4; b for Esperance sand with porosity of 0.45; c for Perth silty sand; d for Ottawa sand with no fines; e Ottawa sand with 2% fines

Full size image

Figure 4 indicates that the trends of the estimated results for these sandy soils agree well with the measured tensile strengths. It is also noted that the estimated results for the Perth silty sand are less accurate than those for Esperance sand and Ottawa sand. Zhai et al. [50] indicated that the soil volume change may occur at low suction range (i.e., less than the air-entry value). Li et al. [19] illustrated that the soil volume change was insignificant beyond the inflection point. In the proposed equation, it is assumed that the soil volume change is negligible. To remove the possible effect of the soil volume change on the estimated results, the measured data of the tensile strength beyond the suction corresponding to the inflection point on the SWCC were selected for comparison with the estimated results as shown in Fig. 5. The suction corresponding to the inflection point, ψin, on the SWCC is computed following the method proposed by Zhai et al. [48]. The computed suctions corresponding the inflection points for Esperance sand, Perth Silty sand, and Ottawa sand were 1.05 kPa, 4.56 kPa, and 2.15 kPa, respectively. The coefficient of determination, R2, which defines the goodness of fitting between the estimated results and measured data are computed for these three types of soil and illustrated in Fig. 5.

Fig. 5
figure 5

Illustration of the R2 of the estimated tensile strength for the suction beyond the inflection points. a For Esperance sand with porosity of 0.4; b for Esperance sand with porosity of 0.45; c for Perth silty sand; d for Ottawa sand with no fines; e Ottawa sand with 2% fines

Full size image

Figure 5 indicates that the values of R2 for Esperance sand with porosity of 0.4, Perth silty sand, and Ottawa sand with no fines are high. However, the values of R2 for Esperance sand with porosity of 0.45 and Ottawa sand with 2% fines are still low. It should be noted that void ratio of soil specimen used in the SWCC testing for Esperance sand is 0.4, while the void ratio of the soil specimen used in the tensile strength measurement is 0.45, as shown in Fig. 5b. The soil specimen used in the SWCC testing for Ottawa sand has no fines, while the specimen used in the tensile strength measurement has 2% fines, as illustrated in Fig. 5e. In other words, the conditions of the soil specimens prepared for SWCC measurement are different from those prepared for tensile strength measurement as illustrated in Fig. 5b, e.

3.2 Effect of variation in the initial void ratio on the estimated tensile strength

The works from [11, 40, 53, 54] indicated that the SWCC varied with a change in the void ratio of the soil. Zhou et al. [53] proposed a model to simulate the variations of the SWCC for the soil with different void ratios, as illustrated in Fig. 6. Zhai et al. [52] indicated that the uncertainty of SWCC due to different void ratios could significantly affect the estimated shear strength of unsaturated soils. Similarly, this uncertainty of SWCC may also affect the estimated tensile strength for the unsaturated soil.

Fig. 6
figure 6

(From Zhou et al. [53])

Illustration of the variation of SWCC with different initial void ratios.

Full size image

Based on the works from Zhou et al. [53], the variation of SWCC was simulated by considering changes in void ratios for Esperance sand. The SWCC for the Esperance and with void ratio of 0.4 can be defined as SWCC0, and the SWCCs for the soil with void ratios of e1, e2, and e3 (e3 > e2 > e1 > 0.4) can be defined as SWCC1, SWCC2, and SWCC3, respectively, as illustrated in Fig. 7a. Either e1, e2, or e3 may represent the porosity of 0.45 which is the void ratio that used for the tensile strength measurement in Fig. 4b. The tensile strengths of Esperance sand are re-calculated by using different SWCCs (i.e., SWCC0, SWCC1, SWCC2, and SWCC3) and illustrated in Fig. 7b.

Fig. 7
figure 7

Illustration of the estimated tensile strength for Esperance sand with different initial void ratios. a Estimated SWCCs for the Esperance sand with different void ratios, b Estimated tensile strength by incorporating different SWCCs

Full size image

Figure 7b indicates that the value of R2 of the estimated tensile strength for Esperance sand increases by using the SWCC from SWCC0 to SWCC3, which means that the uncertainty of SWCC due to the changes in initial void ratio can significantly affect the estimated tensile strength.

3.3 Effect of variation in the percentage of fines on the estimated tensile strength

Indrawan et al. [20] mixed the medium sand with different percentages of fines and observed that the SWCC of the medium sand could be modified by increase in the percentage of the fines, as illustrated in Fig. 8. The works from Indrawan et al. [20] indicated that variation in the percentage of fines could change the shape of SWCC.

Fig. 8
figure 8

(Modified from [20])

SWCCs for the medium sand with different percentages of fines.

Full size image

Following the trends of the SWCC for the sandy soil with different percentages of fines from Indrawan et al. [20], the SWCC for the Ottawa sand with no fines is defined as SWCC0, and the SWCCs for the Ottawas sand with different percentages of fines, f4, f3, f2, f1, (f4 > f3 > f2 > f1 > 0), are defined as SWCC1, SWCC2, SWCC3, and SWCC4, respectively, as illustrated in Fig. 9a. Either f1, f2, f3 or f4 may represent 2% which was the percentage of fines that was used for the tensile strength measurement in Fig. 4e. The tensile strengths of Ottawa sand are re-calculated by using different SWCCs (i.e., SWCC0, to SWCC4) and illustrated in Fig. 9b.

Fig. 9
figure 9

Illustration of the estimated tensile strength for Ottawa sand with fines contents. a Estimated SWCCs for the Ottawa sand with fines contents and b estimated tensile strength by incorporating different SWCCs

Full size image

Figure 9b indicates that the value of R2 of the estimated tensile strength for Ottawa sand increases by using the SWCC from SWCC0 to SWCC4, which means that the uncertainty of SWCC due to the variation in the percentage of fines in soil can also significantly affect the estimated tensile strength.

4 Conclusions

Mathematical equations for the estimation of tensile stress of sandy soil was proposed by adopting the concept of the pore-size distribution function and verified with the experimental data. The estimation results from the equation proposed in this paper agreed well with the measurement data from published literature. In the proposed equation, there are no empirical parameters and the tensile strength of the unsaturated soil can be directly computed from the fitting parameters in the best fit equation (e.g., [10], or [43]). All the results were obtained based on the assumption that the soil volume change can be ignored with the increase in matric suction. It was also observed that the effects of the variation in the initial void ratio and the percentage of fines could have significant effect on the estimated tensile strength.