1 Introduction

Granular flows, such as rock falls, debris flows, and avalanches, widely occur in the course of natural and industrial processes and can result in risks to human safety and industrial efficiency. The understanding of granular flow characteristics has been an important research subject in geotechnical engineering. In many industrial processes, such as agricultural and pharmaceutical product transfers, understanding such flow behaviours is also important to improve the transfer efficiency. However, granular flow characteristics are difficult to predict because of the texture, size, shape, heterogeneity, and density of the granular materials. Therefore, research on flow behaviours caused by these materials must be conducted so that precautionary measures can be taken to mitigate risks caused by the granular flows and to improve efficiency in industrial processes that involve granular materials.

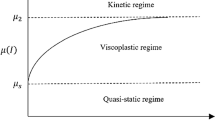
Granular flows are complex and granular materials can appear in both solid-like and liquid-like states [9, 11, 33]. When grains are sufficiently compacted, a fixed and/or stable structure is formed among the grains, which can limit grains’ movement, resulting in a solid-like state. In contrast, when a granular material is dominated by macroscopic deformation and inertia, a fluid-like state can be observed. Previous studies [7, 17, 25] have shown that granular flows can be categorised into three regimes. The first regime is referred to as the quasi-static regime, in which the granular material has low velocity and exhibits a creeping state. The second regime is referred to as the dense regime, in which grains are in close contact with each other, and inertia plays an important role in the movement of the material during macroscopic deformation [25]. The third regime is referred to as the gaseous regime, in which grains have a very high velocity that causes a loss of network structure among the grains. In most cases, granular flows can transition from the gaseous regime to the dense regime and to the quasi-static regime because of energy dissipation, or from the quasi-static regime to gaseous regime. Transitions between the various regimes obfuscate the flow characteristics, involving various phenomena that complicate descriptions of the behaviours.

In describing the granular flows, soil plasticity models can be used to simulate flow characteristics in the quasi-static regime, whereas kinetic theory can be applied to simulate the gaseous regime [17]. For the dense regime, a constitutive law can be developed to account for the flow behaviour. Although many models have been proposed for dense granular flows, most of those models were applicable only to specific scenarios [11, 25, 30]. One constitutive law for granular flows in the dense regime, the μ(I) rheological model, was developed by taking into account both the macroscopic deformation and inertial timescales [17, 25]. That model adopted a yield condition concerning the friction coefficient. The model has a wide range of applications in different configurations [25] and has been successfully implemented in many numerical methods to simulate dense granular flows [4, 5, 17, 20].

Numerical methods offer significant promise to simulate granular flows [3, 15] and can be coupled with rheological models. Calvetti et al. [2] applied the discrete element method (DEM) to investigate the impact force variation over time and the micromechanics of granular masses impacting rigid obstacles. Hu et al. [14] applied the DEM to study micro- and macro-gap-graded and well-graded soils and observed clogging and unclogging events during suffusion. Zhao et al. [42] proposed a coupled approach of applying confining stress to the flexible boundaries in a smoothed particle hydrodynamics (SPH) model while implementing the Mohr–Coulomb model to capture geomechanical deformations. Liang and Zhao [22] coupled the material point method with DEM as a multiscale approach to model geomechanical deformations, and this approach captured the deformation and shear distribution in cases of biaxial compression, rigid footing, soil–pipe interaction, and soil column collapse. Zhang et al. [41] employed the DEM to simulate the deformation of cohesive granular materials and proposed a nonlinear failure criterion for inter-granular interface bonding. Wang et al. [34] coupled a constitutive law with an SPH model to study wet granular flows by introducing a grain-scale capillary interaction. He et al. [12] used an incompressible SPH model to investigate the impact of a granular flow with a Coulomb yield surface on a rigid barrier, and this model captured the many important characteristics, including the flow kinetics, impact force, development of the dead zone and final deposition. Neto and Borja [27] incorporated the multiplicative plasticity approach in the SPH model to investigate granular column collapses and granular flow impacts on a barrier in a sloped channel and predict the runout distance, final deposit height, and impact force of the granular flows. Longo et al. [23] incorporated the μ(I) rheological model into a depth-averaged SPH model to simulate an avalanche and conducted a sensitivity analysis for the rheological parameters to optimise the approximation.

Conventional mesh-based numerical methods such as the finite difference method, finite element method, and finite volume method have also been extensively developed and applied to fluid dynamics. In these methods, a special technique, such as the volume of fluid method, is needed to capture the interface, which may be a free surface [13]. In contrast, mesh-free methods such as the SPH model [8, 26] and moving particle semi-implicit method (MPS) [18, 35] provide a more flexible approach to handling the interface in various flows. In these mesh-free methods, the fluid is discretised into a set of movable points or particles and their movement is traced, and therefore, the free surface can be automatically obtained in the simulations. Shakibaeinia and Jin [31] developed a weakly compressible MPS numerical scheme, referred to as WC-MPS, in which the equation of state is expressed in the form of particle number density and a spatial discretisation is implemented according to the MPS method. The WC-MPS has been successfully applied to model hydraulic jumps, fishway flows, water dam-breaks, water jets, and non-deformable submarine landslides [10, 16, 32, 36]. The μ(I) rheological model can also be coupled to the WC-MPS scheme, and this coupled approach was previously applied to simulate granular column collapses [37, 40].

This study aimed to extend application of the WC-MPS method coupled with rheological model to model granular flows in configurations that have not yet been reported: (1) a granular flow on an inclined plane, (2) instantaneous collapse of a granular column, and (3) a granular dam-break flow. In the simulations conducted using the coupled approach, the pressure, velocity distribution, friction factor, and shear stress of the flows were analysed. These investigations provide multiple insights into these granular flow configurations and demonstrate the potential of the coupled model to solve real geotechnical engineering problems such as those concerning landslides.

2 WC-MPS method coupled with rheological model

2.1 WC-MPS method

The WC-MPS method has been applied to model various open channel flows [10, 16, 32], and this method can also be used to simulate granular flows via a continuum approach [9]. The governing equations are expressed as:

$$\frac{D\rho }{Dt} = 0$$
(1)
$$\rho \frac{Du}{Dt} = - \nabla p + \nabla \cdot {\varvec{\uptau}} + \rho g,$$
(2)

where ρ is the bulk density, u is the velocity, p is the pressure, τ is the deviatoric stress tensor, and g is an external force such as gravity.

The predictor–corrector method is used as the time-splitting scheme to solve the governing equations. In the predictor, an intermediate location and velocity are calculated, and these can be used to calculate the intermediate particle number density <n>* and pressure field. The predictor equations are:

$$u^{*} = u^{k} + \frac{{\nabla \cdot {\varvec{\uptau}}}}{\rho }\Delta t + g\Delta t$$
(3)
$$r^{*} = r^{k} + u^{*}\Delta t,$$
(4)

where u* is the intermediate velocity, uk is the velocity at the previous time step, ∆t is the time step, r* is the intermediate particle location, and rk is the particle location at the previous time step.

According to the results of the predictor, the corrector equations calculate the new velocity and particle location fields. The corrector equations are:

$$u^{k + 1} = u^{*} - \frac{\nabla p}{\rho }\Delta t$$
(5)
$$r^{k + 1} = r^{k} + u^{k + 1}\Delta t,$$
(6)

where uk+1 is the new velocity and rk+1 is the updated particle position.

In the MPS method, a weighting function is applied to the particle interactions. This study adopted a kernel function commonly used in the WC-MPS method [10, 16, 31, 32, 36, 38]:

$$w\left( {r_{ij} ,r_{e} } \right) = \left\{ {\begin{array}{*{20}l} {\left( {1 - \frac{{r_{ij} }}{{r_{e} }}} \right)^{3} } \hfill & {r_{ij} \le r_{e} } \hfill \\ 0 \hfill & {r_{ij} > r_{e} } \hfill \\ \end{array} } \right.,$$
(7)

where re is the search radius, also called the interaction radius, and rij is the distance between the target particle i and surrounding particles j.

In WC-MPS simulations, every target particle interacts with the surrounding particles virtually according to the weighting function. However, including all the particles in the domain for the interaction of each target particle is time-consuming. Therefore, re is defined to reduce the computation time, eliminating contributions from particles beyond the defined circle from the computation of the target particle’s interactions. Because excessively constraining re may reduce the accuracy of the simulation results, an appropriate re value must be selected to balance the time constraints and simulation accuracy. In this study, the selected re was re = 4.0 l, where l is the particle distance; this re has been shown to result in accurate numerical results [38, 40].

With the particle interactions established through the weighting kernel function, the pressure gradient term and viscous term in the governing equations can be discretised according to the following models [19, 31].

The gradient model is

$$\left\langle {\nabla \varPhi } \right\rangle_{i} = \frac{{D_{m} }}{{n_{0} }}\sum\limits_{j \ne i} {\frac{{\varPhi_{j} - \varPhi_{i} }}{{r_{ij}^{2} }}} r_{ij} w\left( {r_{ij} ,r_{e} } \right),$$
(8)

and the Laplacian model is

$$\left\langle {\nabla^{2} \varPhi } \right\rangle_{i} = \frac{{2D_{m} }}{{\lambda n_{0} }}\sum\limits_{j \ne i} {\left( {\varPhi_{j} - \varPhi_{i} } \right)w\left( {r_{ij} ,r_{e} } \right)} ,$$
(9)

where Φ is a scalar, rij is equal to |rj − ri|, Dm is the spatial dimension, and n0 is the initial or average particle number density.

In this study, all simulations were conducted in a 2D coordinate system, and therefore, Dm was equal to 2. The initial particle number density n0 was determined at the initial time as follows:

$$\left\langle n \right\rangle_{i} = \sum\limits_{j \ne i} {w\left( {r_{ij} ,r_{e} } \right)} .$$
(10)

The value \(\lambda\) is defined as [19]:

$$\lambda = \frac{{\int_{V} {r^{2} w\left( {r,r_{e} } \right){\text{d}}V} }}{{\int_{V} {w\left( {r,r_{e} } \right){\text{d}}V} }}.$$
(11)

The equation of state proposed by Batchelor et al. [1] and Monaghan et al. [26] was modified for MPS [31] and applied in this study to obtain the pressure field. In WC-MPS, the fluid is assumed to have very little compressibility (less than 1%), and the equation of state is expressed as:

$$p_{i}^{k + 1} = \frac{{\rho c_{0}^{2} }}{\gamma }\left[ {\left( {\frac{{\left\langle n \right\rangle_{i}^{*} }}{{n_{0} }}} \right) - 1} \right]^{\gamma } ,$$
(12)

where γ is equal to 7 and c0 is the speed of sound. Based on a Mach number of less than 0.1, the density change is smaller than 1%, and c0 = 10Umax, where Umax is the maximum velocity in the problem; therefore, in WC-MPS, the artificial speed of sound is used instead of the real speed of sound [26]. In order to satisfy a stability condition, the maximum time step has to satisfy the Courant–Friedrichs–Lewy [6] condition:

$$\Delta t < \frac{Cl}{{c_{0} }},$$
(13)

where 0 < C < 1 is the Courant number. In this study, the Courant number was equal to 0.25 for every case.

2.2 Boundary conditions

In this study, two types of boundary conditions were considered: a solid boundary condition and a free surface boundary condition. The free surface particles were identified by the following equation [19]:

$$\left\langle n \right\rangle_{i}^{*} < \beta n_{0} .$$
(14)

The pressure on the free surface particles was considered to be zero, and shear stress was calculated according to the rheological model, described below.

In the WC-MPS method, the solid boundary is treated as a combination of wall and ghost particles. Figure 1 illustrates the boundary condition and particle distribution. The black circles in Fig. 1 represent the wall particles, and the grey circles represent the several layers of ghost particles distributed below the wall particles. In this study, because re = 4.0 l, there were four layers of ghost particles beyond the wall particles to compensate for the particle number density close to the boundary. The velocities of the wall and ghost particles were set to be zero to represent the non-slip condition. The pressure and shear stress for the ghost particles were assigned the same values as the closest wall particles [18, 19, 31, 37, 40].

Fig. 1
figure 1

Solid boundary condition and particle types

Full size image

2.3 Rheology model

The μ(I) rheological model has been used to calculate the effective viscosity and stress in granular flows [17], and this model has been implemented in many numerical methods [4, 5, 37, 40]. The model is developed by assuming that the shear stress has the following linear relation with the confining pressure:

$$\tau = \mu p,$$
(15)

where τ is the shear stress, p is the pressure and μ is the friction factor, which is dependent on the inertial number I. The following equation, proposed by Cruz et al. [7], is used to calculate the value of μ:

$$\mu \left( I \right) = \mu_{s} + \frac{{\mu_{2} - \mu_{s} }}{{\frac{{I_{0} }}{I} + 1}},$$
(16)

where I0 is a constant, and μs and μ2 are the minimum and maximum friction values, respectively [17]. When the friction factor is smaller than μs, the flow regime is theoretically a quasi-static regime. When the friction factor begins to increase, the flow regime transitions from a quasi-static regime to a dense regime or even to a gaseous regime.

The inertial number I is defined as [17, 25]:

$$I = \frac{\left| \varepsilon \right|d}{{\left( {\frac{p}{{\rho_{s} }}} \right)^{0.5} }}\;{\text{with}}\;\rho_{s} = \frac{\rho }{\phi },$$
(17)

where |ε| = (0.5εijεij)0.5 is the second invariant of the strain rate tensor \(\varepsilon_{ij} = \frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}\), d is the diameter of the grains, ϕ is the volume fraction, and ρs is the actual density of the granular material.

Extending the constitutive law to a 2D or even 3D problem, the following equation was proposed by Jop et al. [17]:

$$\tau_{ij} = \eta \varepsilon_{ij} \;{\text{with}}\;\eta = \frac{\mu \left( I \right)p}{\left| \varepsilon \right|},$$
(18)

where η is the effective viscosity and τij is the deviatoric stress tensor. This rheological model introduces a yield criterion [17], given as:

$$\left| {\varvec{\uptau}} \right| > \mu_{s} p,$$
(19)

where |τ| = (0.5τijτij)0.5. The granular material flows only when Eq. (19) is satisfied.

However, a very small |ε| leads to an infinitely large value of η, which could be beyond the computation capacity in the simulations. One method of addressing this problem is to constrain the value of η to a very large viscosity. This approach is also described and applied in [4]:

$$\left\{ {\begin{array}{*{20}l} {\tau_{ij} = \eta_{t} \varepsilon_{ij} } \hfill & {{\text{if}}\;\frac{{\mu_{s} p}}{\left| \varepsilon \right|} > \eta_{t} } \hfill \\ {\tau_{ij} = \eta \varepsilon_{ij} } \hfill & {{\text{if}}\;\frac{{\mu_{s} p}}{\left| \varepsilon \right|} < \eta_{t} } \hfill \\ \end{array} ,} \right.$$
(20)

where ηt is the constraining viscosity value; ηt = 500 Pa s was demonstrated to be effective in this study.

In this study, the rheological parameters for the granular material, which was a collection of glass beads, include: μs = tan 20.90°, μ2 = tan 32.76°, the diameter of the granular material d = 2.0 mm, and I0 = 0.279. Additional parameters were introduced for each specific case, as described below.

3 Numerical simulations

Three different cases were simulated by the coupled method described above to illustrate its ability to capture the deformation and dynamics of the granular material. The numerical results were compared to analytical solutions and experimental measurements. Analyses were conducted of the pressure distribution, shear stress, friction factor, velocity, free surface, and runout distance.

The first case investigated the characteristics of a granular flow on a sloped channel. The pressure, shear stress, and velocity of the granular flow were compared with analytical solutions and numerical results. The analytical velocity equation, derived from the Bagnold’s profile, was used to validate the coupled method’s ability to reproduce the velocity extracted from the simulation. The analytical friction factor in the flow can be determined as equal to the ratio of shear stress to pressure. Pressure and shear stress are difficult to obtain in experimental flow measurements. Therefore, this case can verify the coupled model’s pressure and shear stress calculations by comparison with the analytical solutions.

In the second case, the coupled model was used to simulate the flow dynamics of a granular column collapse. The column collapse is an important and ideal configuration to test and validate the coupled model because of the simultaneous occurrence of conditions such as a flowing region and quasi-static regions. The velocity, pressure, and shear stress distribution from the column collapse were investigated using the coupled model. The velocity distribution from the simulation was compared to experimental data, and the simulation shear stress distribution was analysed.

In the last configuration, experimental data from a granular dam-break flow were compared with the numerical results as a further validation of the coupled model’s capability to simulate flow characteristics. The granular dam-break case results in dynamic deformation of the free surface, which contains both flowing and quasi-static regions. In the simulation, the velocity, pressure, shear stress distribution, and friction factor were analysed to illustrate the interrelationships among the different flow regions. The shear stress distribution indicates changes occurring in the different regions of the granular dam-break flow.

The simulations were conducted by solving the governing equations with the predictor–corrector time-splitting scheme, and the spatial discretisation was based on the MPS method. This study did not adopt additional techniques such as numerical viscosity, velocity correction, or damping coefficients. The coupled model was applied to simulate granular flows, and the results were compared to previously reproduced characteristics of granular column collapses, including free surface profiles, runout distances, and velocity distributions [37, 40]. The stress and pressure distributions in granular column collapses as modelled by our method have also been discussed in previous studies [40]. This study aimed to extend the application of the coupled model to additional configurations of granular flows.

3.1 Steady flow down a sloped channel

The coupled model was applied to simulate 2D granular flow on a sloped bed. In the flow, a large amount of the granular material was placed in a tank and the material flowed out through an aperture. With a given distance to the aperture, a uniform steady flow with a constant flow depth can be developed, and analytical solutions for the pressure, velocity, and shear stress for the steady flow can be obtained [4, 28]. Figure 2 presents a schematic of the simulation for the flow on the sloped bed. A 0.25 × 0.25 m2 reservoir filled with sufficient numbers of 2-mm-diameter glass beads was placed upslope of a 2.5-m-long channel at an angle of 24.5°. An aperture of 0.036 m located on the bottom right side of the reservoir allowed the granular material to escape and flow down the sloped channel. Numerically represented fluid particles were placed in a reservoir on the top of the 24.5° slope, and the distance l between the particles was 0.002 m. The initial velocity was zero, and density ρ was set at 2450 kg/m3 (ϕ = 0.6). The Froude number was 0.5, which results in a uniform and steady-flow zone downstream of the aperture, if the slope of the channel is between tan−1 (μs) and tan−1 (μ2) [4].

Fig. 2
figure 2

Schematic of the simulation for granular material flow down a sloped channel

Full size image

The analytical equation used to compute the pressure, shear stress, and velocity distribution was based on two assumptions [4]. The first assumption was that a steady flow on an inclined bed has a velocity in only the x-direction (Fig. 2). Therefore, the shear force is balanced by a gravity force component along the sloped channel bed, whereas the pressure force is balanced with the gravity force component in the y-direction. The second assumption is that the shear stress can be calculated from τ = μ(I)p. The friction coefficient, shear stress, and pressure can then be determined, respectively, as [4]:

$$\tau = \rho g\left( {H - y} \right)\sin \theta ,p = \rho g\left( {H - y} \right)\cos \theta ,\;{\text{and}}\;\mu = \frac{\sin \theta }{\cos \theta },$$
(21)

where θ is the angle of the channel and H is the depth of the flow perpendicular to the channel bed. By applying the definition of the inertial number I, the velocity in the uniform zone yields the following profile [4]:

$$u = \frac{2}{3}I_{\theta } \sqrt {\phi { \cos }\theta } \left( {\frac{H}{d}} \right)^{3/2} \left( {1 - \left( {1 - \frac{y}{H}} \right)^{3/2} } \right)\sqrt {gd} .$$
(22)

The value of the inertial number \(I_{\theta }\) is calculated by [4, 11]:

$$I_{\theta } = I_{0} \frac{{{ \tan }\theta - \mu_{s} }}{{\mu_{s} + \Delta \mu - { \tan }\theta }},$$
(23)

where ∆μ = μ2 − μs is equal to 0.26.

In the simulation using the coupled model, a layer of granular material flowed from the reservoir through the aperture along the channel bed. Over time, the granular flow extended along the bed. Downstream of the aperture, a zone was observed in which the velocity vectors parallel to the channel bed showed less change over time. This layer was observed to have a constant thickness of H ≈ 0.0029 m, which was also observed by Chambon et al. [4] and Pouliquen [28]. Another finding from this simulation was that the length of the uniform zone gradually extended as the wave front moved forward along the bed, and velocity profiles were extracted along the thickness at different locations in this uniform region. The velocity profiles were extracted only when a uniform zone was formed because the flow was neither steady nor uniform in the beginning of the simulations, when the granular material started to flow out the reservoir. Figure 3 compares the numerical and analytical velocity profiles in the uniform region at 4 and 5 s, where the dimensionless velocity Ud = (u2+ v2)0.5/(gH)0.5 was used. The solid line represents the analytical velocity profiles calculated by Eq. (22). Based on the velocity vector parallel to the slope in Fig. 2, the numerical and analytical profiles showed good agreement at both time steps. The velocity component perpendicular to the channel bed in the zone was very small, indicating that a steady uniform region in the flow had developed.

Fig. 3
figure 3

Velocity distribution through the depth (y) in the sloped channel

Full size image

The numerical solution agreed well with the analytical solution, with a linear velocity distribution when y ≤ 0.02 m (Fig. 3). This linear velocity profile in the granular flow was also observed in previous studies [28]. However, for y > 0.02 m, there is a discrepancy between the numerical results and the analytical velocity profiles. This discrepancy could be due to the boundary condition in the coupled method. Grains on the free surface flow with higher velocities than those of other grains can result in the grain interactions becoming dominated by binary collisions, and therefore, the flow close to the free surface may be in the gaseous regime. However, in the simulation with the coupled model, the flow was modelled using a continuum approach rather than by kinematic theory because the granular flow was in the dense regime [9]. With the mesh-free method, the free surface occupies only several particles or points: taking the particle distance l = 0.002 m as an example, the free surface consists of only four particles, compared to 10 particles below the free surface. The comparison shows that the coupled model can capture the velocity information in this steady uniform flow region, with some discrepancy observed on the free surface.

The friction factor was also calculated, and the numerical and analytical results were compared. Figure 4 illustrates the comparison for the friction factor at two time steps (t = 4 s and t = 5 s) along the flow depth y. In this uniform region, the friction μ remains almost constant. Based on Eqs. (16) and (17), the value of the friction factor is related to the pressure, and the values are therefore calculated by using the pressure field in the simulation. The figure shows that the numerical friction factors agreed well with the analytical results below the free surface, with some deviation from the constant friction on the free surface. The maximum fluctuation of the friction factor was approximately ± 0.11.

Fig. 4
figure 4

Distribution of friction factor through the depth at at = 4 s and bt = 5 s

Full size image

The numerically determined distributions of pressure and shear stress were also compared with the analytical results, as shown in Fig. 5. In this case, the analytical shear stress calculated by Eq. (18) was related to pressure multiplying a constant friction factor μ = tan (24.5°). Therefore, the analytical shear stress was linearly distributed because the pressure had a linear distribution. However, fluctuations were observed in the numerical results for the pressure and shear stress. These fluctuations could be due to the equation of state used to calculate the pressure field, which assumed that the flow was weakly compressible. Despite the fluctuations, the numerical results nonetheless showed a linear trend, and the slopes of the fitted lines for both the pressure and shear stress were similar to the analytical solutions. Therefore, the coupled model was able to reflect the pressure and shear stress in the uniform region of the flow down the inclined bed, although fluctuations were also found because of the assumption in the numerical model.

Fig. 5
figure 5

Pressure and shear stress distribution through the depth at t = 5 s

Full size image

3.1.1 2D granular column collapse

This section describes the friction, pressure, and shear stress distributions of a granular column collapse obtained by simulations with the coupled model, in comparison with experimental measurements presented in the study by Xu et al. [40]. The granular column simulated in this study had an initial aspect ratio of a = H/L = 1.25, where H was the height of the column (set at 0.05 m) and 2L was the width of the column. As the granular material collapsed, it was distributed outwards onto a horizontal plate after the gate initially holding the material was lifted. The granular material was a collection of glass beads with diameters of d = 2 mm. The density of the glass beads was ρ = 2500 kg/m3 with a volume fraction of 0.6. The velocity was measured from the side by applying the particle image velocimetry technique [40], and the simulation was conducted in 2D, following the experimental setup. In the simulation, there were 2945 particles with particle distances of l = 0.0025 m to represent the granular column, and this total included fluid particles, ghost particles, and wall particles. The initial velocities of u = 0 and v = 0 were assigned to the fluid particles.

Velocity profiles from the simulation were plotted for different vertical sections (x = ± 0.01, 0.02, 0.03, and 0.04 m from the coordinate origin at the centre of the bottom of the column). Figures 6 and 7 show the velocity distributions with U = (u2 + v2)0.5 at t = 0.129 s and 0.269 s, respectively, in comparison with the experimental measurements. The velocity distribution from the simulation agreed well with the experimental measurements at both time steps. The velocity profiles showed low velocities close to the bottom and greatly increased velocities near the free surface. For the sections close to the column centre, such as x = ± 0.01 m, more of the velocity profiles remained close to zero. At t = 0.129 s, the coupled model slightly overestimated the velocity, perhaps because of the boundary condition set for the simulation and the effect of the gate removal.

Fig. 6
figure 6

Velocity distributions of different vertical sections through the height of the column at t = 0.129 s

Full size image
Fig. 7
figure 7

Velocity distributions of different vertical sections through the height of the column at t = 0.269 s

Full size image

Figures 8 and 9 illustrate the simulated pressure and shear stress distributions through the column height at two time steps. In contrast to the uniform steady flow simulated in the first case, the pressure and shear stress distributions in the granular column collapse were nonlinear in the y-direction. The pressure and shear stress were also larger in the centre of the column. The numerical results for these distributions corresponded to the simulated values and showed a thicker quasi-static layer at the column centre, which increased the pressure and shear stress. The collapse results indicated a highly unsteady non-uniform flow with deformation of the free surface, which produced the nonlinear pressure and shear stress. At t = 0.129 s, the pressure and shear stress were small above the height of y = 0.02 m and increased nonlinearly from y = 0.01 m to the bottom of the column. Similar variations in the pressure and shear stress were observed at t = 0.269 s.

Fig. 8
figure 8

Numerical pressure and shear stress distributions of different vertical sections through the height of the column at t = 0.129 s

Full size image
Fig. 9
figure 9

Numerical pressure and shear stress distributions of different vertical sections through the height of the column at t = 0.269 s

Full size image

With the inertial number I calculated from Eq. (17), the friction coefficient can be obtained by applying Eq. (16) in an analysis of the simulation results. Figure 10 illustrates the friction factor distribution obtained from the simulation, which was in the range of μs and μ2, indicating that the flow of the granular column collapse was in the dense regime. Although the friction factor was very near zero near the bottom of the column, it increased dramatically for y > 0.02 m, close to the free surface, where the particles moved with a larger velocity and therefore encountered significant inertia. Thus, the friction coefficient calculation generated a larger value for the free surface particles.

Fig. 10
figure 10

Distribution of friction factor at at = 0.129 s and bt = 0.269 s

Full size image

3.2 Granular dam-break flow

The dam-break flow is a widely used case for testing mesh-free particle methods. In this study, the granular dam-break flow was simulated by the coupled model and the simulation results were compared to experimental measurements reported by Xu et al. [39]. Figure 11 illustrates the numerical setup, which consisted of a rectangular column of ceramsite particles had diameters d of 5 mm. In the initial condition, a granular column with a height H of 0.18 m and width L of 0.1 m was established on a horizontal plate. The pressure measurements were recorded by a layer of tactile sensors on the bottom of the granular column. The density of the granular material was 2200 kg/m3 with a volume fraction of 0.6. The granular flow was initiated by quickly lifting the baffle, which instantly released the granular material. In the simulation, the particle distance was l = 0.002 m with a total number of 8294 particles. The artificial sound speed used in the coupled model, c0 = 10 m/s, because this was ten times the maximum velocity in the problem. The time step in the simulation Δt was 0.00005 s. The parameters for the rheological model were same as in the previous two cases because the static angle of ceramsite is 22 ± 2°, which is similar to that of glass beads.

Fig. 11
figure 11

Comparisons between numerical results and experimental measurements for the free surface movement in a granular dam-break flow

Full size image

Figure 11 illustrates the movement of the free surface following a dam-break flow, as captured by the simulation and in comparison with the experimental measurements reported by Xu et al. [39]. The simulation results showed good agreement with the experimental measurements at different time steps.

Previous work has shown that the initial aspect ratio a = H/L, where H is the initial height and L is the initial width, plays a very important role in the spread of the granular material [21, 24, 39]: for H/L < 0.7, the collapse of the granular material results in a truncated deposit; for 0.7 < H/L < 3, a conically shaped deposit can be formed; and for H/L ≥ 3, the conically shaped deposit can also be observed. In this simulation, a = 1.8, and a smooth and stretched deposit was observed on the plate. The horizontal extension of the granular pile could be clearly observed at t = 0.08, 0.12, 0.16, 0.24, 0.32, and 0.40 s. As shown in Fig. 11, before t = 0.16 s, the simulated wave front propagated slightly faster than the experimental observation. However, after t = 0.24 s, the runout distance in the simulation agreed well with the experimental results.

Figure 12 compares the pressure distributions of the numerical and experimental results at three different time steps: t = 1.5τc, 2τc, and 3τc, where τc = (H/g)0.5. As shown in the figure, the pressure was not linearly distributed in either the experimental or simulation results. In the experiment [39], the pressure at each position x was averaged over the 20 sensels in the transverse direction to generate the pressure distribution [39]. In contrast, the simulated pressure shown in Fig. 12 was the instantaneous pressure at every time step. The figure shows that the simulated pressure fluctuated around the experimentally determined pressure, and these fluctuations were attributed to the equation of state used in the numerical method. Thus, the proposed method was found to reproduce pressure variation trends that were similar to those of the experimental measurements.

Fig. 12
figure 12

Comparisons between the numerical results and experimental data of the pressures along bottom of the plate over time

Full size image

The velocity contours from the simulations are compared with the experimental observations in Fig. 13. The column failure starts from the initial state (t = 0) while the potential energy of the column transfers to kinetic energy. From t = 0.6 \(\tau_{c}\), three velocity magnitude zones were observed in both the numerical and experimental velocity contours: a high-velocity zone appeared close to the free surface, as marked by the red colour; a quasi-static zone appeared in the left corner; and a zone with intermediate velocity appeared between these two zones. From t = 0 to 1.2τc, the thickness of the high-velocity zone increased, the intermediate-velocity zone decreased, and the area occupied by the quasi-static zone showed minimal change. Between t = 1.2τc to 3.5τc, both the high-velocity and intermediate-velocity zones gradually disappeared because of the energy dissipation, whereas the quasi-static zone became extended along the bottom of the plate. Thus, the simulation results showed good agreement with the experimental measurements in terms of the evolution of the shape of the collapse.

Fig. 13
figure 13

Numerical and experimental [39] velocity contours

Full size image

Figure 14 shows the pressure and shear stress distributions at three time steps and in different vertical sections. The figure clearly shows that the pressure increased with the depth in the flow. The pressures distributions at x = 0.06 m at t = 1.2 τc and 1.8 τc were pseudo-linear. In the flowing region, the pressure distribution appeared to be nonlinear, such as at x = 0.14 m at t = 1.8 τc. The shear stress variation was similar to that of the pressure, and both showed fluctuations. These fluctuations in the simulation were not physical characteristics in the granular flows, but were numerically induced by using the equation of state. Although the numerical model did not capture certain physical fluctuations in the granular flows, such as the granular temperature [29], the pressure fluctuations produced by our method did not affect the kinematics of the granular flows, and the proposed model reproduced the velocity distributions shown in the study by Xu et al. [39].

Fig. 14
figure 14

Numerical results for the pressure and shear stress distributions along the depth of the flow, y

Full size image

The friction factor obtained in the simulation at x = 0.06 m is shown in Fig. 15. The calculated friction factor was between μs and μ2, indicating that the flow was in the dense regime. For y < 0.05 m, the friction factor was very small, although it was still larger than μs, where the low-velocity fields in both the experimental and simulation results indicated a quasi-static region. For y > 0.05 m, the particles moved with considerable velocity, which increased the friction factor but not above μ2. Thus, the flow remained in the dense regime rather than transitioning into the gaseous regime. These characteristics were also observed at other locations and time steps.

Fig. 15
figure 15

a Numerical and experimental [39] velocity contours and b numerical distribution of friction factor

Full size image

4 Summary

In this study, the WC-MPS method was coupled with the μ(I) rheological model and the coupled approach was applied to model three different cases: granular flow down an inclined plate, granular column collapse, and granular dam-break flow. The numerical results were compared with analytical solutions and experimental measurements to validate the coupled model’s capability to simulate granular deformations under various configurations. The velocity and pressure distributions and the friction factor were analysed for each case.

The granular flow down an inclined plate showed a steady uniform flow region. The coupled model captured the dynamics in this region and the numerical results matched well with the analytical solutions. The model reproduced the uniform flow zone, where all velocity vectors were parallel to the sloping plate, and a constant thickness of the flow (H = 0.029 m) was maintained to a considerable distance. The model also captured the linear velocity distribution below the free surface, in good agreement with the analytical solutions. In this flow, the presence of a considerable slope angle of 24.5° accelerated the flow, especially for grains on the free surface, making them behave as in a gaseous regime. This feature of the free surface particles was further confirmed by the calculated friction factor, μ. Some discrepancies in the velocity distributions on the free surface were observed because the coupled model treats the grains on the free surface by applying a continuum approach to the dense granular flow rather than the binary collision applied in the gaseous regime. Although the numerical results displayed fluctuations in the pressure and shear stress distributions, the numerical results nonetheless compared well with the analytical solutions.

A 2D granular column collapse was then modelled by the coupled model, and the resulting velocity distribution was compared with experimental measurements. The simulated velocity profiles agreed well with the measured velocity distribution in the collapse. In this case, the collapse occurred on a horizontal plate such that the free surface grains could not be strongly agitated. The calculated friction factor showed that the flow was in the dense regime where μs < μ < μ2. Because the granular column collapse was a highly unsteady non-uniform flow with large deformation of the free surface, the pressure and shear stress were not linearly distributed, with the pressure and shear stress increasing from the free surface to the bottom of the flow.

These two granular flows showed that the coupled model had the flexibility and robustness to reflect the velocity distribution in comparison with the analytical solutions and experimental measurements. A granular dam-break flow was also modelled to show that the coupled model could calculate the pressure in the flow in comparison with the experimental measurements. First, the surface profiles were plotted and the numerical results showed good agreement with the measurements. By calculating the friction factor, the flow was found to be in the dense regime. The coupled model reproduced the nonlinear pressure distribution of the experimental measurements, and although the modelled pressure exhibited some fluctuations, it nonetheless agreed well with the experimental measurements. The simulated shear stress also showed a nonlinear distribution.

Through the simulation of three different granular flows with different configurations, the coupled WC-MPS and μ(I) rheological models were shown to be able to capture many dynamics of the flows in the dense regime, such as the velocity, pressure, free surface, and shear stress. However, when a flow includes multiple regimes such as the intermediate dense regime and gaseous regime, the coupled model has difficulty reflecting the dynamics beyond the dense regime, and developing a model that can capture these more complex flow dynamics will be the subject of our future work.