1 Introduction

Mathematical modelling and numerical simulations of the mechanical behaviour of naturally occurring materials have enabled the prediction of various environmental phenomena, including geological changes [20]. With these advances in prediction technologies, unstable ground behaviour due to a sudden or temporary main cause, such as a localized torrential downpour and/or an earthquake, becomes predictable to a certain extent [5, 7, 26, 28]. Geo-materials, however, are also subject to particular chemical and biological reactions that affect any related precipitation and weathering processes [31, 52]. Therefore, in considering long-term changes in geo-materials using mathematical prediction techniques, it is also essential to know the future soil conditions.

Soil improvement technologies have been developed experimentally and empirically from a variety of viewpoints, such as geotechnical engineering, geomechanics, chemodynamics, and microbiology [3]. There are more than 40,000 projects worldwide related to soil improvement technologies [18]. Although there are many engineering techniques used in soil improvement technologies [25, 27, 44], the new approach of bio-mediated soil improvement technology deserves special attention. It has been observed through various experimental shearing tests and investigations that the shear strength of microbial-mediated soils can be improved using the process of biochemical cementation [9, 11, 15, 17, 18, 23, 45, 48, 51]. For this reason, this microbial phenomenon is expected to become the focus of innovative techniques for use in next-generation soil improvement technologies.

The biochemical cementation phenomenon may also be observed in a natural environment [39, 42]. The cementation may be fostered in natural environments through the microbially induced cation generation of carbonate dissolution and subsequent carbonate precipitation [36]. Also, the cementation depends on environmental parameters such as temperature and pH values [9, 45]. Thus, microbially induced cementation in geo-materials is of interest from an engineering viewpoint because there is a possibility that this may be applied artificially to natural environments. In contrast, predicting inner structural changes is essential in understanding the cementation mechanism because the reformation of the inner structure of soil directly influences the increase in macroscopic strength of the soil. However, this can be difficult in practice because we may not be able to change certain parameters easily with respect to the microbial activity. Hence, common practice has been to search for different microbes and define the appropriate environmental conditions such as by trial and error through a large number of experiments and observations using microscopes, such as a scanning electron microscope, a transmission electron microscope, and X-ray microtomography. Particularly, X-ray microtomographic investigations have served towards understanding of the evolution of inner microbially induced structures [14, 19, 46, 47]. This technique has permitted direct observation of a real geometry of active calcite bond structures which bridges neighbouring grains and an inactive calcite bond. As a result, this technique has revealed the relevance between micro-organisms in soil and the intrinsic material properties such as void structure and grain distribution [47].

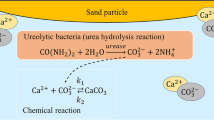
The evolution and inner structures of bio-mediated soil depend on the metabolic pathways of the microbes, bio-mediated changes in the minerals in the soil, and microbial behaviour [17, 51]. In the case of the microbial urea hydrolysis reaction, one of the processes of bio-mediated soil improvement, carbonate precipitations are facilitated by microbial activity in the soil. Various alkalophilic soil bacteria consume urea and decompose it into ammonia and carbon dioxide. Subsequently, the carbon dioxide dissolves into the ground water, carbonate ions in the ground react with calcium ions, and consequently calcite is precipitated at the boundaries of soil particles and on their surfaces [11]. Although there are other pathways for microbial carbonate precipitation (MCP), such as photosynthesis, denitrification, ammonification, sulphate reduction, and methane oxidation [6, 16, 49, 55], the microbial urea hydrolysis reaction is worthy of attention because the reaction occurs efficiently under the influence of natural environmental factors with relatively little time and light/heavy equipment is not needed [10, 15, 18, 38]. That is, this reaction may be suitable for practical application. Nevertheless, studies on the microbial urea hydrolysis reaction have so far relied on experimental and/or observational approaches. In order to understand the long-term effects of MCP and to apply these to natural environments, it is necessary to develop a predictive technique that can determine the future state of the soil when using soil improvement technologies.

Several prediction techniques have been proposed in order to describe the dynamics of granular materials (e.g. [7, 8, 12, 28, 29, 53]). For example, Więckowski [53] formulated the material point method for granular material simulation, in which a large deformation simulation, such as may be used to describe granular flow in a silo, was conducted macroscopically. Additionally, the fracture behaviour of clean sand under biaxial tests was also simulated microscopically using the discrete element method [29]. In contrast, there are very few studies on the simulation of MCP. Fauriel and Laloui [21] proposed a novel mechanical model that considered bio-chemo-hydraulic reactions in order to describe microbial-induced calcium precipitation in soils. Although this kind of model allows the prediction of macroscopic mechanical behaviour, the precipitation process and mechanism related to centralization on soil particles of microbially induced calcium carbonates may not be analysed [1, 21]. This is because the model was formulated from a macroscopic point of view, treating the voids in a soil sample as a variable of its porosity. A bio-cemented simulation based on the discrete element method has also been proposed [22], allowing the simulation of certain MCP granular material fracture behaviours. However, this technique may be not suitable for understanding biochemical precipitation patterns at the soil particle scale as this technique was designed for mechanical strength analysis. A methodology for understanding the patterns and mechanisms related to filling the void structure in sandy soils has not yet been established.

In this work, we attempt to bring a new perspective to the bio-mediated soil improvement technology field, drawing on mathematical modelling and simulation techniques in order to understand the mechanism of microstructural formation and predict the future state of the soil. We describe spatial precipitation patterns obtained using the proposed mathematical model at the soil particle scale and discuss MCP processes on the microscopic level.

2 A mathematical model for microbial urea hydrolysis reaction

2.1 Mathematical formulation

In the field of theoretical biology, it is well known that certain characteristics of bacterial colonies growing on agar plates can be accurately described by a mathematical interaction system based on the reaction–diffusion equation (e.g. [24, 34]). The essential assumption contained in this mathematical model is the introduction of an internal state concept to the reaction–diffusion system [4, 35]. Applying this concept, if the internal state is increased, bacteria actively move and grow, whereas if it is decreased, the bacteria become inactive [35]. Another mathematical model for understanding the bacterial growth on agar pates is the lubricating bacteria model, which explains certain complex colony patterns using the effects of interaction variables defined by their bacterial concentration, the height of the lubrication layer, nutrition, and the presence of stationary bacteria [13, 32]. However, applying these models directly to the urea hydrolysis reaction may be inappropriate as these models do not support phenomena related to MCP. The most important requirement for the urea hydrolysis reaction is that calcium carbonates are precipitated in a metabolic reaction in urea-splitting bacteria [17]. Hence, in formulating a mathematical model to describe the microbial urea hydrolysis reaction, the model must allow for this metabolic reaction.

MCP that is due to the urea hydrolysis reaction corresponds to the following expressions [16]:

$${\text{NH}}_{2} \text{-}{\text{COO}}\text{-}{\text{NH}}_{2} {\text{ + H}}_{2} {\text{O}} \mathop{\leftrightarrows}\limits^{k_1}_{k_2} {\text{CO}}_{3}^{2 - } + 2{\text{NH}}_{ 3}$$
(1)
$${\text{Ca}}^{2 + } + {\text{CO}}_{3}^{2 - } \,\,\mathop{\leftrightarrows}\limits^{k_3}_{k_4}\,\,\,{\text{CaCO}}_{ 3} \downarrow$$
(2)

where k1, k2, k3, and k4 are the reaction rate constants. Eq. (1) relates to the microbial urea hydrolysis reaction, and Eq. (2) relates to the chemical precipitation of calcite particles. In this work, these biochemical equations are formulated in accordance with the reaction–diffusion system [50]. Since 1993, when the processes of ‘birth’ and ‘death’ in living creatures were simulated in a simple system based on a reaction–diffusion system [33, 40], this system has been recognized as a mathematical model that also represents bacterial movements and growth [30, 34]. Hence, a mathematical model that defines microbial urea hydrolysis is an appropriate selection for the present study.

Considering the diffusion and inflow terms in the biochemical reactions [Eqs. (1) and (2)], a mathematical model based on the reaction–diffusion system may be described as follows:

$$\frac{{\partial {\mathbf{A}}}}{\partial t} = \frac{\partial }{{\partial {\mathbf{x}}}}D_{A} \frac{{\partial {\mathbf{A}}}}{{\partial {\mathbf{x}}}} - k_{1} {\mathbf{{\rm A}{\rm B}}} + k_{2} {\mathbf{C}}_{i} {\mathbf{E}}^{2} + {\mathbf{A}}_{\text{in}}$$
(3)
$$\frac{{\partial {\mathbf{B}}}}{\partial t} = \frac{\partial }{{\partial {\mathbf{x}}}}D_{\text{B}} \frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{x}}}} - k_{1} {\mathbf{{\rm A}{\rm B}}} + k_{2} {\mathbf{C}}_{i} {\mathbf{E}}^{2} + {\mathbf{B}}_{\text{in}}$$
(4)
$$\frac{{\partial {\mathbf{C}}_{i} }}{\partial t} = \frac{\partial }{{\partial {\mathbf{x}}}}D_{{{\text{C}}_{i} }} \frac{{\partial {\mathbf{C}}_{i} }}{{\partial {\mathbf{x}}}} + k_{1} {\mathbf{{\rm A}{\rm B}}} - k_{2} {\mathbf{C}}_{i} {\mathbf{E}}^{2} - k_{3} {\mathbf{C}}_{i} {\mathbf{F}}_{i} + k_{4} {\mathbf{P}}$$
(5)
$$\frac{{\partial {\mathbf{E}}}}{\partial t} = \frac{\partial }{{\partial {\mathbf{x}}}}D_{\text{E}} \frac{{\partial {\mathbf{E}}}}{{\partial {\mathbf{x}}}} + k_{1} {\mathbf{{\rm A}{\rm B}}} - k_{2} {\mathbf{C}}_{i} {\mathbf{E}}^{2}$$
(6)
$$\frac{{\partial {\mathbf{F}}_{i} }}{\partial t} = \frac{\partial }{{\partial {\mathbf{x}}}}D_{{{\text{F}}_{i} }} \frac{{\partial {\mathbf{F}}_{i} }}{{\partial {\mathbf{x}}}} - k_{3} {\mathbf{C}}_{i} {\mathbf{F}}_{i} + k_{4} {\mathbf{P}} + \gamma {\mathbf{F}}_{i}$$
(7)
$$\frac{{\partial {\mathbf{P}}}}{\partial t} = k_{3} {\mathbf{C}}_{i} {\mathbf{F}}_{i} - k_{2} {\mathbf{P}}$$
(8)

where A, B, Ci, E, Fi, and P denote the concentrations of \({\text{NH}}_{ 2} \text{-}{\text{COO}}\text{-}{\text{NH}}_{ 2}\), \({\text{H}}_{ 2} {\text{O}}\), \({\text{CO}}_{ 3}^{ 2- }\), \({\text{NH}}_{ 3}\), \({\text{Ca}}^{ 2+ }\), and \({\text{CaCO}}_{ 3}\), respectively. These variables are functions of time and space. \(D_{*}\) is the diffusion coefficient of the related variable *, and these have spatially random values. The inflow terms Ain and Bin are the constant amounts of \({\text{NH}}_{ 2} \text{-}{\text{COO}}\text{-}{\text{NH}}_{ 2}\) and \({\text{H}}_{ 2} {\text{O}}\), respectively. These terms take into account the inflow of and from outside environments. γFi is the inflow term for Ca2+ and is the constant coefficient. It is known that bacteria have extrusion mechanisms called as bacterial Ca2+ pump to maintain low concentrations of intracellular calcium [41]. The Ca2+ adsorption to the cell surface of bacteria by the Ca2+ pump promotes heterogeneous nucleation of calcite, and particularly in the media with high enough concentrations of Ca2+ ions, the bacteria promote the precipitation of calcite [43]. This metabolism may also occur in MICP process because the majority of MICP-related works have used calcium concentrations in the range of 0.1–1 mol/L that are taken for calcium chloride as a source [17]. Hence, this inflow term (γFi) in Eq. (7) aims to capture this extrusion mechanism in the proposed model.

The proposed mathematical model represents a completely open system characterized by the interaction of six elements associated with all variables. The diffusion of CaCO3 is not considered in this model because CaCO3 is a solid material and may not be diffused. If an adequate amount of urea is present in this model, and water and calcium ions are supplied in the analytical region, calcite would be generated constantly at pore space and on surfaces of soil particles. That is, the proposed model has been formulated based on the following hypotheses:

Hypothesis 1:

Precipitation of calcium carbonates occurs randomly in any part of pore space from some nucleation points that remain fixed.

Hypothesis 2:

Precipitation and growth of calcium carbonates occur under constant supersaturation sate.

Whereas particles migration by groundwater advection, adsorption and deposition on the grain surface are not considered in the mathematical formulation. It is noted that the focus in this study is put on precipitation patterns such as bridging neighbouring particles which precipitate randomly in the pore space.

2.2 Discretization

In the current study, the diffusion operators of Eqs. (3)–(8) are discretized using the finite difference scheme. Let us consider the following equation using a variable G and a coefficient D.

$$\frac{\partial G}{\partial t} = \nabla \left( {D\nabla G} \right) = \nabla D\nabla G\, + \,D\nabla^{2} G$$
(9)

Here, the left side may be discretized using the forward Euler integrations, and the first term on the right side is divided into two terms, and each term can be discretized using the forward difference and reverse difference, respectively. That is,

$$\frac{\partial G}{\partial t} = \frac{1}{2}\nabla D\nabla G\, + \,\frac{1}{2}\nabla D\nabla G\, + \,D\nabla^{2} G$$
(10)
$$\begin{aligned} \frac{{G_{i}^{n + 1} - G_{i}^{n} }}{\Delta t} &= \frac{{\left( {D_{i + 1} + D_{i} } \right)G_{i + 1}^{n} - \left( {D_{i + 1} + 2D_{i} + D_{i - 1} } \right)G_{i}^{n} + \left( {D_{i} + D_{i - 1} } \right)G_{i - 1}^{n} }}{{2\Delta x^{2} }} \end{aligned}$$
(11)

where n is the number of the time step, i is the grid number, Δt is the time increment, and Δx is the grid size.

3 Numerical simulation results

3.1 Simulation models

Numerical simulations are conducted for a three-dimensional cuboid. In order to quantitatively obtain the concentration of each element and numerically express MCP in a natural environment, numerous parametric studies may be needed. Thus, each parameter is considered as a dimensionless variable, and the morphological characteristics of the inner sands and the trends of each dimensionless concentration are discussed in the current study.

The system (\(x \times y \times z\)), grid size, and number of grid points are \(2 \times 1 \times 1\), 0.0156, and 545,025, respectively. The time increment (Δt) was set to 0.1, and the diffusion coefficients were randomly chosen to be \(D_{\text{A}} = 5{\text{e}}{-}7\sim5{\text{e}}{-}5\) and \(D_{\text{B}} = D_{{{\text{C}}_{i} }} = D_{\text{E}} = D_{{{\text{F}}_{i} }} = 7{\text{e}}{-}7\sim7{\text{e}}{-}5\). The Neumann boundary conditions were set to all of the surfaces, and two spherical soil particles (radius 0.7 and 0.45), in which the microbial urea hydrolysis reaction does not occur, were arranged as shown in Fig. 1. In the numerical simulations, an adequate amount of urea and water were supplied constantly at the three points in the analytical region (see Fig. 1), \({\mathbf{A}}_{\text{in}} = {\mathbf{B}}_{\text{in}} = 0. 5\sim1.0\) were set in a random manner in Eqs. (3) and (4) throughout the period of analysis. The \(\gamma\) variable in Eq. (7) was set to 0.005.

Fig. 1
figure 1

The numerical simulation model. Two spherical soil particles (radius: 0.7 and 0.45) and three urea and water inflow points are located in the domain

Full size image

The amount of calcite and its precipitation patterns were investigated through various numerical simulations. The entire analytical region was initially placed in the disordered state with a low number of elements, namely \({\mathbf{A}} = {\mathbf{B}} = {\mathbf{C}}_{i} = {\mathbf{E}} = {\mathbf{F}}_{i} = 0. 0\sim0.05\), where the numbers were chosen randomly. Subsequently, the cases with various reactant rate constants on Eqs. (3)–(8) were tested, and the differences in the results determined.

3.2 Simulation results

Figure 2 shows the evolution of a calcite precipitation pattern in the case of \(k_{1} = 25\), \(k_{2} = 0.005\), \(k_{3} = 10\), and \(k_{4} = 0.005\). In the initial stage, the calcite precipitates around the urea and water inflow points and subsequently the calcite particles distribute among the particle boundaries and on the particle surfaces simultaneously. Then, the precipitates eventually connect with each other [see Movies (1a) and (1b)]. The evolution of bond diameter as result of continuous precipitation has also been observed in several experiments [17, 18]. Therefore, the proposed model may be suitable qualitatively for MCP with urea hydrolysis reaction.

Fig. 2
figure 2

The evolution of calcite precipitations by the proposed mathematical model (k1 = 25, k2 = 0.005, k3 = 10, and k4 = 0.005). The times t at which the figures were taken are as follows: at = 1 × 102; bt = 5 × 102; ct = 2 × 103; dt = 5 × 103; et = 1 × 104; and ft = 1 × 104 [zooming of (e)]. The colour bar indicates the calcite concentration; red corresponds to a higher concentration (= 1.0) and light yellow to a lower concentration (= 0.0) (color figure online)

Full size image

Simulations were conducted without using the diffusion terms in Eqs. (3)–(7), that is, by using the reaction equations. Figure 3 shows the evolution of calcite precipitation in the case of a non-diffusion-type model. Calcite precipitation was not observed on the particle surfaces, with only a sparse calcite precipitation present at the urea inflow points [see Movies (2a) and (2b)].

Fig. 3
figure 3

The evolution of calcite precipitations by the non-diffusion model (k1 = 25, k2 = 0.005, k3 = 10, and k4 = 0.005). The times t at which the figures were taken are as follows: at = 1 × 102; bt = 5 × 102; ct = 2 × 103; dt = 5 × 103; et = 1 × 104; and ft = 1 × 104 [zooming of (e)]. The colour bar indicates the calcite concentration; red corresponds to a higher concentration (= 1.0) and light yellow to a lower concentration (= 0.0) (color figure online)

Full size image

Figure 4 shows the variations in calcite concentration in the whole analytical domain for different simulation times. In Fig. 4a, the calcite concentration increased significantly as the value of \(k_{4}\) decreased for \(k_{1} \le k_{3}\). On the other hand, where \(k_{1} > k_{3}\) (see Fig. 4b), the calcite concentration decreased as the value of \(k_{4}\) decreased, and the significant shift in the calcite concentration was not observed.

Fig. 4
figure 4

The variation of calcite concentration with time using the proposed mathematical model. a The case of k1 = 25, k2 = 0.005, and k3 = 10; b the case of k1 = 10, k2 = 0.005, and k3 = 25. In the both cases, the values of k4 are set to 1.0 × 10−2, 0.5 × 10−2, 0.4 × 10−2, 0.3 × 10−2, 0.2 × 10−2, 0.1 × 10−2, and 0.0

Full size image

In addition, Fig. 5 shows the calcite precipitation pattern for \(k_{1} > k_{3}\). The precipitation on the particle surfaces was also observed as well as in the case where \(k_{1} \le k_{3}\) (see Fig. 2), but no precipitation between the soil particles occurred [see Movies (3a) and (3b)]. The calcite concentration variations in the non-diffusion-type model are shown in Fig. 6. Also, several significant shifts were observed in this case.

Fig. 5
figure 5

The evolution of calcite precipitations by the proposed model (k1 = 10, k2 = 0.005, k3 = 25, and k4 = 0.005). The times t at which the figures were taken are as follows: at = 1 × 102; bt = 5 × 102; ct = 2 × 103; dt = 5 × 103; et = 1 × 104; and ft = 1 × 104 [zooming of (e)]. The colour bar indicates the calcite concentration; red corresponds to a higher concentration (= 1.0) and light yellow to a lower concentration (= 0.0) (color figure online)

Full size image
Fig. 6
figure 6

The variation of calcite concentration with time in the non-diffusion type model. a The case of k1 = 25, k2 = 0.005, and k3 = 10; b the case of k1 = 10, k2 = 0.005, and k3 = 25. In the both calculations, the values of k4 were set to 1.0 × 10−2, 0.5 × 10−2, 0.4 × 10−2, 0.3 × 10−2, 0.2 × 10−2, 0.1 × 10−2, and 0.0

Full size image

4 Discussion

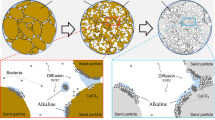
The proposed mathematical model provides microscopic MCP patterns in soil (Figs. 2, 3, and 5). Figure 7 shows the MCP features recently observed in laboratory experiments on sandy soils [17]. From this figure, it may be seen that the precipitation proceeds from the surface of the soil particles and bonds to other particles. In addition, it is known that carbonate precipitation is created at contact points between soil particles taking advantage of urea hydrolysis catalysed by bacteria [11, 17, 37, 54]. From Figs. 2, 5, and 7c, a strong resemblance between the precipitation patterns obtained by the proposed model and MCP features may be observed from the point of view of the morphological process of MCP spreading from soil particle surfaces to voids. The calcite precipitation on particle surfaces was observed in some experiments and in the simulations. It is of note that in these simulations, despite the identical analytical conditions of both the void fraction and particle surfaces, and therefore there were no specific boundary conditions on the particle surfaces, these concentration phenomena still occur. What is the cause of this concentrated calcite precipitation on soil particle surfaces and at soil particle contacts?

Fig. 7
figure 7

Scanning electron microscopy images for microbial-induced solidified sand (modified from DeJong et al. [17]). The calcite cements are produced on the surfaces of sand particles and at void locations

Full size image

As shown in Fig. 3, calcite precipitation concentration was not observed on particle surfaces in the case for which no diffusion terms were used in Eqs. (3)–(8). These results indicate that MCP with the urea hydrolysis reaction may depend on diffusion. The calcium and carbonate ions are diffused into the whole region at the initial stage and remain at the particle boundaries. These ions then bind chemically onto the surface of particles where diffusion stops. Figure 8 shows a conceptual illustration of the MCP process.

Fig. 8
figure 8

Drawing of calcite precipitation after microbial urea hydrolysis. The calcite precipitations occur at void fractions and on the surfaces of grains, and some calcite precipitations are connected to each other. The surface precipitations depend on the diffusion of substances

Full size image

Let us consider the change in the amount of calcite precipitation. From Fig. 4a, we observe that calcite concentration increased as the value of \(k_{4}\) decreased in the case for which \(k_{1} \le k_{3}\). Clearly, there is a transition region between exponentially increasing areas in which the calcite concentration undergoes a significant change. In contrast, in the case for which \(k_{1} > k_{3}\) (see Fig. 4b), calcite concentration decreased as the value of \(k_{4}\) decreased, and no significant shift in the calcite concentration was observed. These results suggest that the significant shift in the calcite concentration may depend on the calcification rate rather than the rate of the urea hydrolysis reaction described in Eq. (1). This implies that chemical inhibitors, the reverse reaction shown in Eq. (2), have a greater impact on these significant shifts than the activity of the microbial urea hydrolysis reaction. In addition, in the case for which \(k_{1} > k_{3}\), where the rate of microbial urea hydrolysis was larger than the calcification rate (see Fig. 6a), although some significant shifts were observed where diffusion terms were used, the gradual increase in calcite concentration observed in laboratory experiments [18] cannot be confirmed. Hence, a value of \(k_{1} \le k_{3}\) is one of the necessary conditions for realizing effective microbial carbonate precipitation. To date, it remained unclear whether or not the significant shifts in calcite concentration are caused by microbial expansion activity. The presented numerical analyses contained in this study have addressed and answered this question.

5 Conclusion

In the current work, a new mathematical model for microbial carbonate precipitation in the case of the urea hydrolysis reaction has been proposed, and a novel numerical simulator developed. Our interpretation of the simulation results may be summarized as follows:

  1. 1.

    The morphology of the precipitation patterns obtained by the proposed model closely resembles the features of MCP.

  2. 2.

    Although there are no specific boundary conditions on the particle surfaces, calcite precipitation on the particle surfaces is observed.

  3. 3.

    In MCP, the diffusion of each ion plays a very important role in the on-particle calcite precipitation.

  4. 4.

    Calcium and carbonate ions are diffused into the whole region, and these ions then bind chemically onto the surface of the particles, at which point diffusion halts.

  5. 5.

    Chemical inhibitors have a larger impact on the significant shifts in the calcite concentration compared to the activity of the microbial urea hydrolysis reaction.

It should be noted that the wide range of physical parameters given in this study should be determined experimentally. Additionally, in the proposed model, the distribution of bacterial population cannot be considered although the distribution may influence to reaction rate constant k1 in Eq. (1). Also, calcium carbonate polymorphisms (calcite, vaterite, and aragonite) cannot be distinguished in the model because metastable transition of calcium carbonates cannot be considered though some complex transitions may be occurred in bio-cementation [2]. Hence, there is room for further improvement in the system. Although the proposed model is not the only possible scheme for understanding soil improvement due to MCP, this work describes a series of techniques that greatly support our understanding of microbial carbonate precipitation at the microscale and provides the details of a novel method that may be applied to other similar processes.