1 Introduction

Cemented granular materials are common in geotechnical engineering, e.g., structured sands [1, 7, 8, 10], gas hydrate bearing sediments [13, 16, 30, 31, 36] and weak rocks [6, 27, 28]. Their macroscopic mechanical behavior has been extensively studied experimentally. There are mainly three categories of constitutive models developed to describe their behavior following different constitutive model frameworks. (1) Modified elasto-plastic constitutive models developed from the remolded soils’ model. These modified models treat cemented granular material as a continuous single-phase material [34]. (2) Binary-mixture-type models where cemented granular material is treated as a composite material consisting of two parts, i.e., structured part and remolded part [12, 14, 47]. (3) Micromechanics-based model that derives the macroscopic behavior of cemented granular material from the collection of contact behavior [15]. These models can capture the general behavior of cemented granular material, but further improvement is required for model capability. However, there is no real progress in these models in the last decade mainly due to, in the authors’ opinion, a lack of understanding in how damage develops inside a sample.

The binary-mixture-type models seem closer to the physical scenario of damage development in cemented granular material than it being treated as a single-phase material. The two parts (structured part and remolded part) in a binary-mixture-type model may be defined in terms of physical entity, e.g., uncemented granular assembly plus cement agent material [14] as shown in Fig. 1a. Alternatively, the two parts can be defined as two sources of shear strength [47] as shown in Fig. 1b or as two reference states [12] as depicted in Fig. 1c. In a general binary-mixture-type model framework, the stresses \(\sigma_{ij}^{{}}\) and strain increments \(d\varepsilon_{ij}^{{}}\) for each part are assembled to obtain the overall constitutive behavior:

$$\sigma_{ij} = \left( {1 - D_{\sigma } } \right)\sigma_{ij}^{\text{s}} + D_{\sigma } \sigma_{ij}^{\text{r}} ,\quad d\varepsilon_{ij} = \left( {1 - D_{\varepsilon } } \right)d\varepsilon_{ij}^{\text{s}} + D_{\varepsilon } d\varepsilon_{ij}^{\text{r}}$$
(1a, b)
$$d\sigma_{ij}^{\text{s}} = D_{ijkl}^{\text{s}} d\varepsilon_{kl}^{\text{s}} ,\quad d\sigma_{ij}^{\text{r}} = D_{ijkl}^{\text{r}} d\varepsilon_{kl}^{\text{r}}$$
(2a, b)

where Dσ and Dε are two weighting variables, the superscripts ‘s’ and ‘r’ represent structured part and remolded part, respectively, and Dijkl is the constitutive matrix.

Fig. 1
figure 1

Conceptualized material components in the binary-mixture-type models: a uncemented granular assembly plus cement agent material [14], b two sources of shear strength [47] and c two reference states [12]

Full size image

The binary-mixture-type models try to respect the granular nature of the material. However, due to the extreme lack of understanding of material behavior at subsample scales (e.g., micro-/particle scale and meso-/particle-group scale), the highly conceptualized models in Fig. 1 and Eqs. (1–2) often cannot satisfactorily reproduce soil behavior in a unified way. A physically meaningful way to partition the two parts has not been proposed, either. Difficulty arises when distributing stresses and strains between the two parts in Eq. (1); it is usually simply assumed that the two parts share the same strain, which is often improper. To fulfill the potential of the physically elegant binary-mixture-type models, it is necessary to investigate the subsample scale behavior of cemented granular material, which is also valuable for the development of micromechanics-based model.

Advanced microscopic experimental techniques have been widely applied to study the responsible microstructures behind the observed macroscopic behavior [6, 9, 16, 17], which facilitates the application of advanced numerical tools, such as discrete element method (DEM), to bridge the scales. In DEM, cemented granular material is regarded as an assembly of particles bonded at contacts. The bond contact behavior has been studied experimentally [11, 21, 22, 25], numerically [39] and analytically [44]. Bond contact models were developed and implemented in DEM [4, 5, 19, 20, 24, 35, 37, 38, 40, 41], including consideration of particle crushing [3]. Particle cluster presence has been reported in experiments [29] and DEM simulations [40, 42, 43]: Bonded particle clusters are naturally formed and subsequently crushed as a result of inter-particle bond breakage, which will be further analyzed in this study. As a significant mesoscale behavior, the evolution of these clusters fundamentally determines the macroscopic behavior which is critically important for constitutive model development. For example, in micromechanics-based model framework, the presence of clusters in cemented granular material requires a granular hexagon description of the mesoscale geometrical and kinematical behavior, such as the H-microdirectional model for clean granular material [32, 33].

Despite these qualitative advancements, quantitative description of particle cluster evolution has not been reported before, which constitutes the motivation of this study. Nondestructive and continuous acquisition of particle cluster configuration is almost impossible with current experimental techniques. With the aid of DEM simulations, this study tracks the evolution of particle clusters in numerical cemented granular materials following various loading paths. Information such as cluster size, shape, position and number is analyzed. The implication of the results for constitutive model development is discussed.

2 Bond contact model and DEM simulations

Structured sand, as a typical cemented granular material, was modeled in this study by applying the bond contact model developed in [40], which has been implemented in PFC3D by the authors [18]. The salient features of this bond contact model are recalled below.

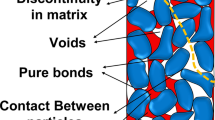
Cemented granular material was idealized as an assembly of bonded spheres. Since grains are simplified as spheres, the bond material between two spheres (with an average diameter of Ds) can be idealized in shape as a short cylinder (referred to as bond cylinder hereafter) with a diameter of Db and a length of Hb, as shown in Fig. 2. The bond cylinder connects two particles’ surfaces and thus has two spherical concave ends. This bond shape is much closer to reality than previous models that assume beam connection of two bonded particles. Two types of bond contacts (thin bond and thick bond) are considered. In a thin bond contact, the bond material deposits at a physical contact (two particles being in contact); in a thick bond contact, the bond material deposits at a virtual contact (two particles being close but not in contact). It is assumed that the bond agent material is sparsely distributed in space at either a thin or a thick contact and there is no interaction between bond materials from any two bond contacts. This assumption best applies to the microscopic structure of low bond content cases in structured sand [40], gas hydrate bearing sediment [38] and some weak rocks [24].

Fig. 2
figure 2

Two types of bond contacts modeled

Full size image

The bond contact model used in this study incorporates complete interactions of two particles in the normal, tangential, rolling and torsion directions. Thus, the bond failure criteria include five basic failure modes (compression, tension, shear, rolling and torsion) and a coupled shear–rolling–torsion failure mode, as shown in Fig. 3.

Fig. 3
figure 3

Bond failure criterion

Full size image

In pure compression failure, a bond is crushed by a compressive force that exceeds the ultimate compressive strength \(R_{\text{nc}}\). In pure tension failure, a bond is pulled apart by a tensile force that exceeds the ultimate tensile strength \(R_{\text{nt}}\). Based on study in [39], we have

$$R_{\text{nc}} = \chi_{\text{c}} \sigma_{\text{c}} \pi \left( {D_{\text{b}} /2} \right)^{2} ,\quad R_{\text{nt}} = \chi_{\text{t}} \sigma_{\text{t}} \pi \left( {D_{\text{b}} /2} \right)^{2}$$
(3a, b)

where \(\sigma_{\text{c}}\) and \(\sigma_{\text{t}}\) are the compressive and tensile strengths of the bond material. The two factors \(\chi_{\text{c}}\) and \(\chi_{\text{t}}\) account for the bond geometry effect on bond strength. According to [39], \(\chi_{\text{c}}\) and \(\chi_{\text{t}}\) can be correlated to two dimensionless geometry factors of the bond cylinder, \(m = H_{\text{b}} /D_{\text{b}}\) and \(n = D_{\text{s}} /D_{\text{b}}\), as

$$\chi_{\text{c}} = C_{1} e^{{C_{2} m}} n^{{C_{3} }} ,\quad \chi_{t} = 1$$
(4a, b)

where \(C_{1}\), \(C_{2}\) and \(C_{3}\) are three fitting parameters.

Apart from pure compressive and tensile failure modes, a bond may fail in shear, rolling or torsion mode under a bond normal force \(F_{{{\rm n},{\rm b}}}\) with \(- R_{\text{nt}} < F_{{{\rm n},{\rm b}}} < R_{\text{nc}}\). The corresponding strength \(R_{i}\) (i = s in shear failure, i = r in rolling failure and i = t in torsion failure) depends on the compression strength \(R_{\text{nc}}\), the tension strength \(R_{\text{nt}}\) and the bond diameter \(D_{\text{b}}\),

$$R_{\text{s}} = S_{\text{s}} \left( {R_{\text{nc}} + R_{\text{nt}} } \right)$$
(5)
$$R_{\text{r}} = S_{\text{r}} \left( {R_{\text{nc}} + R_{\text{nt}} } \right)D_{\text{b}} /2$$
(6)
$$R_{\text{t}} = S_{\text{t}} \left( {R_{\text{nc}} + R_{\text{nt}} } \right)D_{\text{b}} /2$$
(7)

The parameter \(S_{i}\) is a quantity capturing the effect of normal force on strength,

$$S_{i} = m_{i1} f_{\text{n}} + m_{i2} f_{\text{n}} \left[ {\ln \left( {f_{\text{n}}^{ - 1} } \right)} \right]^{{m_{i3} }}$$
(8)

where \(m_{i1}\), \(m_{i2}\), \(m_{i3}\) (i = s, r, t) are fitting parameters and fn is a normalized bond normal force that can be expressed as

$$f_{\text{n}} = \left( {F_{{{\rm n},{\rm b}}} + R_{\text{nt}} } \right) /\left( {R_{\text{nc}} + R_{\text{nt}} } \right)$$
(9)

The strength envelopes are shown in Fig. 3.

Note that Eqs. (5–7) give the bond strength when only shear or rolling or torsional load is acting on the bond cylinder in addition to the normal force. In a general case, the shear force \(F_{{{\rm s},{\rm b}}}\), rolling moment \(M_{{{\rm r},{\rm b}}}\) and torque \(M_{{{\rm t},{\rm b}}}\) together bring a bond to breakage in a coupled way. A coupled failure criterion can be practically described by

$$f_{\text{s}}^{2} + f_{\text{r}}^{2} + f_{\text{t}}^{2} \left\{ {\begin{array}{*{20}c} { < 1} & {\text{intact}} \\ { \ge 1} & {\text{broken}} \\ \end{array} } \right.$$
(10)

where the normalized loads are \(f_{\text{s}} = F_{{{\text{s}},{\text{b}}}} /R_{\text{s}}\), \(f_{\text{r}} = M_{{{\text{r}},{\text{b}}}} /R_{\text{r}}\), and \(f_{\text{t}} = M_{{{\text{t}},{\text{b}}}} /R_{\text{t}}\). This coupled failure criterion is visualized in Fig. 3.

It should be noted that the bond geometry effects described in Eq. (4) and the failure criteria in shear, rolling and torsion described in Eqs. (5–10) have been proposed based on experiments on glued aluminum rod/sphere pairs [21, 22] and numerical simulations [39]. The parallel bond model in PFC [18] can be used as well if a simple model is desired.

For bond installation, only bond cylinder with a slenderness ratio Hb/Db less than a threshold (m0) is allowed to be implemented. A slim bond is not allowed since it is rarely observed in real cemented granular material and it is also mechanically fragile, thus contributing little to the macroscopic strength. The threshold m0 is assumed the same for different bond contents. Db is assumed to follow a normal distribution. For DEM sample with a higher bond content, the bond cylinder diameter Db is greater, and thus, Hb is greater, allowing particles with a larger distance to be bonded. Therefore, higher bond content means more bonded contact and greater bond cylinder size at each contact, leading to a greater bond strength according to Eqs. (5–7). This bond installation methodology is qualitatively based on SEM observations of structured sands [6, 9, 16, 17].

The contact after bond breakage behaves in an unbonded way as described by [23]. The contact behavior after bond breakage is described by a 3D unbonded contact model with rolling and twisting resistances [23]. For a thick bond, after bond breaks, the bond material can bridge the gap between the two previously cemented particles so that the two particles can interact as if they were enlarged in size. This is captured in the model by modifying the contact detection threshold so that the two previously bonded particles can interact even if there is a gap between them. This modification is not implemented for a thin bond. For a post-breakage unbonded contact, the attached bond material on grain surface can increase particle angularity and this is captured in the model by increasing the peak rolling and twisting resistances. The above two modifications in unbonded contact behavior are not implemented for a newly created unbonded contact. See details of the post-breakage unbonded contact in [40]. Capturing such transition has only a very small effect on the quasi-static simulations in this paper. But the authors believe that it would be important for dynamic problem.

The failure of a bonded contact is brittle and can be accompanied by plastic-like sliding/rolling/twisting, contact splitting (in purely tensile failure) or bond crushing (in purely compressive failure) and local adjustment of structure. In our simulations with a low loading rate (axial strain rate = 1%/min), local damping in PFC3D [18] with a damping coefficient of 0.7 was used. The energy release event due to bond breakage was temporally and spatially sparse. Since the bonding effects are weak, the released energy was timely damped so that the overall damage process evolved in a smooth way, unlike concentrated energy release in events like rock burst. Changing the damping coefficient to a lower value (0.4) would only slightly change the numerical results (less than 2% in the stress–strain curve). The very little effect of damping is a result of the very slow loading.

The model parameters are listed in Table 1. See details about their physical meanings and a parametric study in [40]. It is emphasized that this study is based on the widely accepted notion that realistic structured sand and the idealized “DEM material” share common bond effects and granular nature. Therefore, it is practical to choose parameters within common ranges, instead of against a specific structured sand.

Table 1 Contact model parameters
Full size table

Cubic samples with Np = 40,000 spherical particles were simulated in this study. The particle size distribution is shown in Fig. 4. Samples were generated by radius expansion method in a box of six rigid frictionless walls to achieve a uniform and isotropic microstructure. An isotropic stress state of 50 kPa was reached before the bond contact model installation. Four samples were modeled to study the effects of sample density (void ratio e0) and bond content (denoted by c, the ratio of all bond material volume over all particle volume): S1 (e0 = 0.80, c = 1.0%), S2 (e0 = 0.80, c = 3.0%), S3 (e0 = 0.92, c = 1.0%) and S4 (e0 = 0.92, c = 3.0%).

Fig. 4
figure 4

Particle size distribution

Full size image

Note that the bonds do not take any load when it is first installed under the isotropic stress of 50 kPa. This corresponds to the formation of bonding materials possibly through a depositional process after the ground soil skeleton has reached a stable state. Subsequent numerical tests try to mimic geotechnical engineering activities following some simple, idealized loading paths. Complex stress and initial bond conditions reproducing reality can be implemented as well, although the simplest conditions were simulated here.

The boundary walls were rigid and frictionless throughout the sample generation and subsequent loading stages. It has been checked that the samples showed a spatial void ratio fluctuation within 10%, which was assessed by measuring local void ratios across a sample. Judging from the particle cluster configuration to be discussed below, there is no tendency of less or more bond breakage near the boundary. Therefore, the boundary effects are negligible.

The test conditions are shown in Table 2. All the four samples were tested under true triaxial compression (TTC) conditions with a mean stress p = 400 kPa and an intermediate principal stress ratio b = (σ2 − σ3)/(σ1 − σ3) = 0.0, i.e., σ2 = σ3. Besides, TTC tests on S1 were also simulated to investigate the effects of the intermediate principal stress ratio value (b). Conventional triaxial compression (CTC) tests on S1 under four different confining pressures (100–800 kPa) were simulated to study the effects of stress level.

Table 2 Numerical samples and test conditions in DEM simulations
Full size table

3 Macroscopic behavior

Figure 5 presents the macroscopic behavior of the simulated structured sands. Figure 5a shows that increased stress level (confining pressure σ3) can reduce the peak deviator stress ratio η (= q/p) and suppress the volumetric dilation (decrease of void ratio e). Figure 5b shows that an increase in b-value leads to a decrease in peak strength but an increase in dilation. Under non-axisymmetric stress conditions (b = 0.25, 0.5, 0.75), the rapid softening is a result of persistent strain localization, which leads to the premature plateau in void ratio. Figure 5c shows that increase in sample density (decrease in void ratio) and bond content can increase the peak strength and dilation. The softening behavior of sample S3 is accompanied with contraction in Fig. 5c, which is a feature of loose weakly cemented soil. Note that the observed steady void ratio for samples S2 sand S4 in Fig. 5c is transient. Further loading will lead to its decrease to the steady-state void ratio of clean sand. Our DEM simulations covered a wide range of sample density and bond content and replicated typical behavior of structured sand. Therefore, the following discussions on bond breakage and particle clusters should be widely representative. Note that under axisymmetric stress condition, the rigid wall is successful to impose overall uniform deformation, thus facilitating the study of particle cluster evolutions.

Fig. 5
figure 5

Macroscopic behavior of simulated structured sands

Full size image

Bond breakage ratio ω is defined as the ratio of broken bond number over total initial bond number. Figure 6 presents the evolutions of ω in all the simulated samples. The increase in stress level and decrease in b-value can increase the bond breakage ratio at the same deviator strain. Bond breaks more rapidly in samples with lower bond content, and sample density only slightly affects the bond breakage rate. Strain localization slows down the overall bond breakage rate because breakage concentrates in the shear band.

Fig. 6
figure 6

Evolutions of bond breakage ratio ω

Full size image

4 Mesoscale deformation and cluster formation mechanism

Due to the heterogeneous nature of granular material, the macroscopic uniform deformation never means uniform deformation at mesoscale. The local incremental displacement gradient dHloc introduced in [2] was used to evaluate the displacement gradient response in a void cell so that structured deformation pattern at mesoscale (including transient and developing persistent strain localizations) can be visualized. Each void cell was a tetrahedron constructed using the Delaunay tessellation method. The four vertices of a tetrahedron are particles whose incremental displacements were used to calculate each dHloc. To view the spatial distribution of dHloc in an assembly, a dimensionless quotient eloc defined in [26] was calculated for each tetrahedron:

$$e^{\text{loc}} = \frac{{dH_{ij}^{\text{loc}} d\varepsilon_{ij}^{\text{avr}} }}{{d\varepsilon_{ij}^{\text{avr}} d\varepsilon_{ij}^{\text{avr}} }}$$
(11)

where dεavr is the uniform incremental displacement gradient imposed on the boundary walls.

The deviation magnitude of eloc from unit describes the degree of deviation of void cell incremental displacement gradient from the average. Figure 7 presents the spatial distributions of eloc calculated within an incremental axial strain of dεa = 0.06%. For b = 0.0 case in Fig. 7a–c, the incremental displacement gradient is not uniform but concentrates into some seemingly random regions/microbands; such localization is transient, and therefore, no shear band is recognized even when εd reaches 41.5%. For b = 0.25 case, the incremental displacement gradient is localized into two distinctive shear bands with a width of about 10 tetrahedral cells. The deformation patterns in Fig. 7 are typical for axisymmetric and non-axisymmetric loading conditions.

Fig. 7
figure 7

Spatial distributions of dimensionless quotient eloc at different deviator strains (S1, TTC, p = 400 kPa)

Full size image

To explore the link between local displacement and bond breakage, two datasets are prepared: (1) non-weighted set including eloc of all tetrahedron cells, and (2) weighted set including eloc of all tetrahedron cells but eloc of each cell is counted n times where n (≥ 0) is the number of edges that experience bond breakage in a cell during an incremental deformation. The authors think that the n-value can represent the degree of involvement of a cell in bond breakage and particle cluster formation. Therefore, the weighted dataset can be a proper quantitative descriptor of mesoscale behavior of cemented granular material. Figure 8 presents the probability densities of both datasets. In Fig. 8, the non-weighted set exhibits a symmetric distribution about eloc = 1. The weighting manipulation leads to a rightward (positive) shift of the peak density position. The area under the shifted curve is greater on the eloc > 1 side than on the eloc < 1 side. Therefore, the large cell-level deformation rate is a consequence of bond breakage. The spatially non-uniform distribution of eloc indicates non-uniform bond breakage across the sample. The presence of clusters was confirmed in experiments, where structured sands were immersed in deaired water after triaxial compression tests and were found to form a “cohesionless heap” with grain clusters and blocks [29].

Fig. 8
figure 8

Probability densities of eloc in non-weighted and weighted datasets

Full size image

Initially (before deviator loading), all particles are bonded and the whole sample can be viewed as one cluster. Figure 9 presents a typical spatial configuration of particle clusters when the deviator strain reaches 14.3%. Particle clusters were identified by particle labeling method. In this method, all particles are first labeled with number ‘0.’ A traversal of all particles is executed to modify the labels so that particles with the same label belong to the same cluster. For each traversed particle Pi in an outer loop, all particles connected with Pi through bond contacts are traversed in an inner loop. The labels of Pi and its bonded neighbors are sorted from the minimum Lmin to Lmax and denote Lmin+1 the second minimum of their label numbers.

Fig. 9
figure 9

Spatial configuration of bonded particle clusters (sample S1, TTC, b = 0.0, p = 400 kPa, deviator strain εd = 14.3%, bond breakage ω = 75.5%)

Full size image
  1. 1.

    If Lmin = Lmax = 0, Pi and its bonded neighbors have not been assigned to a cluster before, and therefore, they are labeled with a number Qc. Then, Qc is updated to Qc + 1. Initially, Qc equals to 1.

  2. 2.

    If Lmin = Lmax ≠ 0, Pi and its bonded neighbors have already been assigned to the same cluster, and therefore, their labels will not be modified.

  3. 3.

    If 0 < Lmin < Lmax, Pi and its bonded neighbors are assigned to different clusters, but they should belong to the same cluster. Therefore, particles in the sample with a label between [Lmin, Lmax] are re-labeled with Lmin.

  4. 4.

    If 0 = Lmin < Lmax, some particles among Pi and its bonded neighbors have already been assigned to one or more clusters while the rests have not. Therefore, particles in the sample with a label between [Lmin+1, Lmax] are re-labeled with Lmin+1. Particles among Pi and its bonded neighbors with a label of ‘0’ are also assigned with a label of Lmin+1.

The above procedures are repeated for each traversed particle Pi. Finally, the clusters are distinguished by colors according to their number label.

In Fig. 9, there are totally 17, 966 clusters, including single-particle clusters. Clusters are grouped by their sizes, denoted by Dclt (the number of member particles in a cluster). The number of clusters in a size group is denoted by Nclt. In each view of Fig. 9, one or more groups of clusters are shown while other groups are set transparent for nice visualization. Note that clusters are generally randomly distributed in the sample domain, resulting from the overall uniform deformation under axisymmetric loading. Under non-axisymmetric loading, for example b = 0.25 in TTC test as shown in Fig. 10, the largest three wedge-shaped clusters span across the sample and they are separated by two shear bands. Bond breakage mainly occurs within the shear band while bond breakage percent outside the shear band is very small. The focus of this study is put on the uniform deformation conditions.

Fig. 10
figure 10

Spatial configuration of particle clusters under non-axisymmetric loading (sample S1, TTC, b = 0.25, deviator strain εd = 16.3%, bond breakage ω = 71.3%): a perspective view and b plane view (major–minor principal stress plane). Only the largest three clusters are shown

Full size image

Figure 9 shows that clusters are featured by highly angular shapes and the angularity tends to decrease as clusters become small in size. To quantitatively investigate the evolution of cluster features, cluster angularity and integrity indices are introduced. Cluster angularity is defined as ρ = dmax/(2Req) − 1, where dmax is the maximum dimension of a cluster, obtained by searching the maximum value of the distance between any two member particles’ centroids in a cluster plus the sum of their radii. Req is the equivalent radius of the cluster defined as

$$R_{\text{eq}} = \left( {\frac{3}{4\pi }\sum\limits_{i = 1}^{{D_{\text{clt}} }} {V_{i} } } \right)^{1/3}$$
(12)

where Vi is the volume of the ith member particle in a cluster.

By definition, ρ equals to 0 for sphere. Although particles in a cluster are connected through bonds, there can be unbonded contacts between them as well, which act as weak points inside a cluster. Cluster integrity index I is thus defined as the ratio of bond contact number over total contact number in a cluster. Figure 11 presents typical relationships between cluster size and volume-weighted average angularity and integrity (ρavr and Iavr) of clusters in a size group, which are defined as

$$\rho_{\text{avr}} = \frac{{\sum\limits_{i = 1}^{{n_{g} }} {\rho_{i} V_{i} } }}{{\sum\limits_{i = 1}^{{n_{g} }} {V_{i} } }},\quad I_{\text{avr}} = \frac{{\sum\limits_{i = 1}^{{n_{g} }} {I_{i} V_{i} } }}{{\sum\limits_{i = 1}^{{n_{g} }} {V_{i} } }}$$
(13a, b)

where ρi and Ii, respectively, are angularity and integrity, respectively, of cluster i with a volume of Vi and ng is the number of clusters in the size group.

Fig. 11
figure 11

Relationships between a average cluster angularity ρavr and normalized cluster size Dclt/Np, and b average cluster integrity Iavr and normalized cluster size Dclt/Np (sample S1, TTC, b = 0.0, p = 400 kPa)

Full size image

Figure 9 only provides a snapshot in the whole loading process while Fig. 11 offers an evolving view at various values of ω from 0.039 to 94.5%. Figure 11 shows that smaller clusters have lower angularity and greater integrity compared with larger clusters.

5 Cluster evolution

To examine the dynamic process of cluster formation and crushing, Fig. 12 presents the evolutions of cluster number, size and angularity throughout the loading process. As a result of the successive crushing of larger clusters into smaller ones, in Fig. 12a, the total cluster number (Ntot) increases with bond breakage ratio ω at a constant rate in the range of (0, 0.3) and (0.7, 1.0) and the rate keeps increasing in the range of (0.3, 0.7). Similar variation is observed for single-particle cluster number (Nsgl) in Fig. 12b. In Fig. 12c, the maximum cluster size (Dclt,max) decreases with ω in a sigmoidal pattern: Dclt,max first decreases slowly when ω is less than 0.3, followed by a sharp drop before ω exceeds 0.7, and then, again Dclt,max decreases at a very low rate. In Fig. 12d, the volume-weighted average cluster angularity of all clusters (\(\rho_{\text{avr}}^{*}\)) shows a unimodal variation pattern with ω and reaches a peak at ω = 0.7. When ω is less than 0.3, \(\rho_{\text{avr}}^{*}\) changes only slightly. In Fig. 12, all the simulated samples exhibit almost the same evolution process except for under non-axisymmetric loading conditions where localization occurs.

Fig. 12
figure 12

Evolutions of a total cluster number, b single-particle cluster number, c maximum cluster size and d cluster angularity

Full size image

In Fig. 9, with reduction in cluster size, the number of clusters in that size group increases significantly. A plot of (Dclt, Nclt) would give a complete view of the cluster family, similar to the function of particle size distribution curve. In Fig. 13a, Dclt is normalized by Np and Nclt is normalized by Nsgl. Figure 13a shows that in a double-logarithmic plot, cluster number decreases linearly with the increase in cluster size; this trend can be fitted by a linear function (see the lines for ω = 0.31 and 0.76 in Fig. 13a as examples). The fitted lines are forced to pass a specific point (2.5e − 5, 1) that represents single-particle cluster, i.e., Dclt/Np = 1/40,000, Nclt/Nsgl = 1. Note that in Fig. 12b the way Nsgl increases with ω is unique, independent of all factors examined in this study. Therefore, Nsgl acts as a perfect reference point for the fitting purpose in Fig. 13a. The fitting relationship between Dclt and Nclt is

$$\log \left( {\frac{{N_{\text{clt}} }}{{N_{\text{sgl}} }}} \right) = A\left[ {\log \left( {\frac{{D_{\text{clt}} }}{{N_{\text{p}} }}} \right) - \log \left( {\frac{1}{{N_{\text{p}} }}} \right)} \right]$$
(14)

where Np = 40, 000 is constant in this study while Nsgl is a function of ω as shown in Fig. 12b.

Fig. 13
figure 13

Evolutions of a cluster size distribution in effective cluster group, b fitting parameter A, c threshold cluster size and d total and single-particle cluster numbers

Full size image

In Eq. (14), parameter A is determined by curve fitting. Figure 13b shows that A is a unimodal function of ω, slightly influenced by sample void ratio, bond content, stress level and loading path. The general trend (dash curve in Fig. 13b presents an initial increase in A with ω, reaching the maximum of − 2.3 at ω = 0.7, and then, A decreases rapidly toward the theoretical negative infinite. For non-axisymmetric loading cases (TTC tests, b = 0.25, 0.50, 0.75), a premature decrease in A is observed (the ‘line + symbol’ data in Fig. 13b).

The value of Dclt when Nclt = 1 (denoted by \(D_{\text{clt}}^{ *}\)) is of special interest because it represents a threshold size of cluster below which the quantity of clusters can be well described in a statistic way by Eq. (14). Clusters larger than \(D_{\text{clt}}^{ *}\) are so sparsely distributed along Dclt axis and are so small in quantity that they can hardly be described statistically. Hereafter, clusters larger than \(D_{\text{clt}}^{ *}\) are named disperse clusters, while clusters smaller than \(D_{\text{clt}}^{ *}\) are named effective clusters. The spatial configuration of clusters in Fig. 9 can be viewed as disperse clusters embedded in the matrix of effective clusters. From the fitted parameter A, \(D_{\text{clt}}^{ *}\) can be back-calculated and shows a unimodal variation pattern with ω in Fig. 13c.

Figures 12 and 13 show that the quantities describing cluster evolution process are similar among samples of different void ratios and bond contents and under different loading conditions. This implies the existence of a general law governing the cluster evolution and the potential application of the observed mesoscale behavior to constitutive model development is discussed below.

6 Cluster evolution stages and implications for constitutive modeling

The observations in Figs. 12 and 13 imply that cluster evolution roughly has three distinct stages that can be delimited by bond breakage ratio ω = 0.3 and 0.7. Figure 14 presents typical variations of threshold cluster size and the size and number of disperse clusters. Each hollow triangle represents one disperse cluster in the upper plot of Fig. 14.

Fig. 14
figure 14

Evolutions of disperse cluster size and number (sample S1, TTC, b = 0.0, p = 400 kPa)

Full size image

Stage I (ω between 0 and 0.3). The initial intact cemented assembly can be viewed as a single cluster, named mother cluster (the largest cluster in a sample) hereafter. In this stage, the Mother cluster is the only disperse cluster and its size (Dclt,max) only decreases slightly as shown in Fig. 14. In Fig. 13d, the cluster number Ntot and single-particle cluster number Nsgl are very close in this stage, implying that bond breakage mainly leads to detachment of single particles from the mother cluster. In this stage, the mother cluster acts as a skeleton to bear external load, but it is gradually deteriorated due to the ongoing detachment of single particles. To quantitatively examine this feature, the average stress σij of a granular assembly is expressed as

$$\sigma_{ij} = \frac{1}{V}\sum\limits_{k = 1}^{{N_{\text{p}} }} {\sum\limits_{m = 1}^{{N_{c,k} }} {f_{j} l_{i} } } = \underbrace {{\frac{1}{V}\sum\limits_{k = 1}^{{D_{{{\text{clt}},\max }} }}{{\ }{\ }\sum\limits_{m = 1}^{{N_{c,k} }} {f_{j} l_{i} } } }}_{{\sigma_{{ij,{\text{s}}}} }} + \underbrace {{\frac{1}{V}\sum\limits_{k = 1}^{{N_{\text{p}} - D_{{{\text{clt,}}\max }} }}{{\ }{\ }\sum\limits_{m = 1}^{{N_{c,k} }} {f_{j} l_{i} } } }}_{{\sigma_{ij,d} }} = \sigma_{{ij,{\text{s}}}} + \sigma_{{ij,{\text{d}}}}$$
(15)

where V is the sample volume, fj is the contact force, li is a vector pointing from particle centroid to contact center and Nc,k is the number of contacts around particle k. The stress can be partitioned into two parts, representing stresses in the mother cluster skeleton (σij,s) and detached particles σij,d, respectively.

Figure 15 presents the contribution of detached particles to the overall stress. The very little contribution of σi,d (less than 0.5%) indicates that the detached particles actually float in the mother cluster skeleton voids. This observation agrees with the assumption in traditional continuum damage mechanics that microcracks behave like voids, i.e., taking no load. (Note that traditional continuum damage mechanics can be viewed as a special case in the binary-mixture-type model framework.) As shown in Fig. 5, at the end of this stage, the structured sand either has just passed the peak state in a softening response or is in the hardening process but with a deviator stress close to the peak. In a geotechnical problem where failure initiation is the major concern and post-failure response is not the issue, traditional continuum damage mechanics framework (or binary-mixture-type model framework with no contribution from the remolded part) is physically proper to describe the behavior of structured sand in this stage.

Fig. 15
figure 15

Contribution of detached particles to the overall stress (sample S1, TTC, b = 0.0, p = 400 kPa)

Full size image

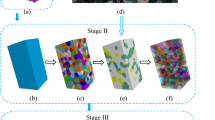
Stage II (ω between 0.3 and 0.7). With increasing bond breakage, the mother cluster is crushed into pieces, which are then further crushed into smaller clusters, forming a continuously distributed effective cluster group as shown in Fig. 13a. This leads to a quick increase in the numbers of total and single-particle clusters and their difference (Ntot − Nsgl) in Fig. 13d. The rapid increase in threshold cluster size \(D_{\text{clt}}^{ *}\) and the number of disperse clusters in Fig. 14 indicates a growing diversity of cluster size in both effective and disperse cluster groups. Figure 14 also indicates that the size span in disperse cluster group reduces significantly as bonds break. This stage ends up with a spatial cluster configuration shown in Fig. 9 where clusters of various sizes and shapes are interwoven.

In this stage, clusters of all sizes are taking load. A smooth and continuous transition from continuum to granular material is observed in this stage. The binary-mixture-type models treat structured sand as a composite material consisting of structured part and remolded part [12, 14, 47], which is physically consistent with the scenario numerically observed in this stage. Therefore, physical fidelity is well respected if the binary-mixture-type model framework could be adopted to develop a constitutive model of structured sand in this stage.

Stage III (ω between 0.7 and 1.0). In this stage, the threshold cluster size decreases rapidly, indicating a decaying diversity in particle size, but both Ntot and Nsgl increase at the largest rates ever as shown in Fig. 13. Figure 14 shows the decrease in both diversity and number of disperse cluster group. Finally, all the bonds are broken and the cemented assembly is totally disturbed.

In this stage, there is no cluster as large as the assembly dimension. The external load is transmitted through contacts within and between clusters. The assembly’s granular feature prevails over its continuum feature. The binary-mixture-type framework is physically reliable as explained above. Besides, the assembly can be viewed as a special clean sand with crushable particles (clusters being regarded as particles). Therefore, crushable sand models [45, 46] may be borrowed for constitutive description of the heavily disturbed structured sand in this stage.

In summary, the elasto-plastic soil models must be highly phenomenological for cemented granular material due to its highly conceptualized yielding, plastic flow and hardening/softening that cannot reflect the mesoscale cluster behavior. Micromechanics-based model should somehow consider the cluster evolution in its derivation from contact behavior to macroscopic behavior to achieve physical fidelity. The binary-mixture-type model framework is the closest to the numerically observed physical scenario among the three categories of constitutive models. The focus would be put on partitioning the cemented granular assembly into two parts in the binary-mixture-type model framework, and one promising solution is inter-cluster contacts being one part and intra-cluster contacts being the other part.

7 Conclusions

This study focuses on the formation and evolution of bonded particle clusters, a salient mesoscale feature of cemented granular material, such as structured sand in geomechanics. DEM simulation results on structured sand show that the macroscopic stress–strain behavior and bond breakage rate are influenced by stress conditions, sample density and bond content. The heterogeneous nature of granular material leads to highly non-uniform deformation at local cell level. The large cell-level deformation rate is a consequence of bond breakage.

Bonded particle clusters are angular in shape and have various sizes. Clusters with different sizes and shapes are interwoven in microstructure. Statistically, smaller clusters are less angular in shape and have less weak points.

The externally applied stress/strain drives the evolutions of cluster size, number and angularity. DEM simulation results suggest three stages in the cluster formation and crushing process. In stage I (bond breakage ratio ω between 0 and 0.3), single particles are spatially randomly detached from the initial intact assembly (mother cluster); the mother cluster bears external load while the detached single particles mainly float in the voids. In stage II (ω between 0.3 and 0.7), a family of clusters with growing size diversity are formed; the cluster size and cluster number follow a linear relationship in a double-logarithmic plot. In stage III (ω between 0.7 and 1.0), the cluster size diversity drops quickly, and finally, all clusters are crushed into single particles.

The purpose of this paper is not to establish a specific constitutive model for cemented granular material. Instead, the applicability and future development of three constitutive model frameworks for cemented granular material are discussed based on the numerical simulation results. From the view of physical fidelity, the binary-mixture-type model framework is very promising to capture the complete mesoscale structure evolution of cemented granular material.

Experimental verification of the simulated cluster evolution is greatly desired in future work. This study focuses on cluster evolution at a sample scale. How clusters form and evolve at field scale and whether sample scale observations are alike field-scale observations deserve further study.