The compression and collapse behaviour of intact loess in suction-monitored triaxial apparatus

Abstract

Loess is susceptible to large and sudden volume reduction induced by loading or wetting. The work in this paper focused on compression and collapse behaviour of the intact loess under isotropic stress condition. To this purpose, an improved technique was introduced for the unsaturated triaxial apparatus that was capable of precise injecting know the amounts of water into the specimen, while continuously monitoring the suction. Tests were performed under two separate hydro-mechanical paths: isotropic compression at various suctions and wetting in steps at various net isotropic stresses. Experimental measurements indicated that the compression behaviour of the intact loess was highly affected by the extent of the level of the suction. The wetting-induced collapse behaviour depended on both the extent of applied net isotropic stress and the hydro-mechanical path. The collapse potential reached a maximum when the specimen was wetted at the initial yield stress. No unique of yield curve was identified from loading and wetting paths in a suction–net mean stress plane. For the same plastic volumetric strain, the suction decrease yield curve identified from wetting path appeared under the loading–collapse yield curve identified from loading path. Interestingly, the uniqueness of the yield curve was identified from loading and wetting paths in a suction–mean effective stress plane. An elastoplastic model of the intact loess under isotropic stress condition incorporating soil water retention behaviour was proposed, using the mean effective stress as constitutive stress. This model is able to reproduce the volumetric behaviour of the intact loess along constant suction paths and wetting paths quite well, using a single-valued compressibility index.

1 Introduction

Loess with interparticle bonds and large voids is widespread in Northwestern China [6, 19, 20, 22]. There are many engineering problems ascribe to the collapsible behaviour of loess such as widely distributed ground fissures, loess landslides induced by rain or irrigation and large deformation problems in metropolitan constructions and high-speed transportations [23, 25, 34, 42].

The loess in situ is often wetted to a certain water content but not fully saturated. Thus, in addition to the total collapsible deformation at saturation, the wetting-induced collapse deformation as a function of water content or matric suction (referred to as suction) before reaching saturation is also important [13]. The wetting-induced deformation of loess has been investigated by means of loading tests at various water contents or suctions [7, 9, 13, 17] or wetting tests at various stresses [2, 7, 13, 18, 41, 44, 48]. The first point to be addressed is whether the wetting-induced deformation of loess remains the same irrespective of the different types of hydro-mechanical path followed, that is, wetting–loading (i.e. first wetting and then loading, referred to as WL test) or loading–wetting (i.e. first loading and then wetting, referred to as LW test). This point is of importance when modelling unsaturated soil behaviour within elastoplastic frameworks. Zhang [46] and Zhang et al. [47] showed that wetting-induced deformation was hydro-mechanical path dependent for intact loess under laterally restrained condition. Nevertheless, Jiang et al. [13] showed that total collapsible deformation was hydro-mechanical path independent for artificial loess under laterally restrained condition. Despite this, test results for wetting-induced collapsible behaviour of loess remain relatively scarce and are still required to validate such uniqueness or independence through WL and LW tests, especially for intact loess.

The second point to be addressed is how to model the wetting-induced deformation of loess. The models of wetting-induced deformation of unsaturated soils in terms of suction as a state variable have been primarily divided into two approaches. The first approach seeks to establish a relationship between wetting-induced deformation and suction directly. For example, the data of wetting tests at various stresses were analysed to define volume change constitutive relationships for the metastable-structured residual gneiss soil [28] and the compacted laterite [36]. The second approach is the elastoplastic framework proposed by Alonso et al. [1] (i.e. the BBM model) and further developed through subsequent researches conducted by authors such as Wheeler and Sivakumar [39], Maatouk et al. [24], Cui and Delage [3], Sun et al. [33, 35], Jotisankasa et al. [15] and Sheng et al. [30]. The central idea of this framework lies in the existence of loading–collapse (LC) yield curves, which can be identified from WL test, in the two-dimensional space of net mean stress and suction. A fundamental assumption associated with the LC yield curve is that plastic deformation due to collapse and loading is similar processes and thus can be described by a single unique curve. Wetting-induced collapse deformation is determined based on the expansion of LC yield curve. Although this approach has been applied widely thus far, few data are available to support the assumption of a unique initial or subsequent yield curve except for the tests reported by Jotisankasa et al. [14, 15]; moreover, limited attention has been paid to collapsible loess.

The objective of this paper is to model the compression and collapsible behaviour of intact loess within elastoplastic frameworks. The loading tests at various suctions and wetting tests at various stresses under isotropic stress condition were performed, using a suction-monitored triaxial apparatus, which is capable of precisely controlling suction or the amount of water injected into the specimen. The influence of suction on the deformation and yielding during loading was investigated. The effect of net isotropic stress on deformation and yielding upon wetting was analysed. These results were used with the aim of validating whether the wetting-induced volumetric deformation and LC yield curve depended on the hydro-mechanical path. A new elastoplastic model was proposed to describe the volume change behaviour of compression and collapse for intact loess, using the mean skeleton stress, or referred to as “mean effective stress”, as constitutive stress.

2 Stress and strain variables

Houlsby [12] presented a clear demonstration that different variables can be conveniently adopted in the description of the constitutive behaviour, provided that the variables chosen were work conjugate with the strain variable increments. All the experimental data presented herein refer to isotropic stress condition. In the experimental programme presented, the total stress and the pore water pressure may be controlled or measured, and the pore air pressure is held constant throughout the tests, and hence, the net stress is the more natural choice to represent the experimental data. In the following, net isotropic stress, p = σ₃ − u_a, and suction, s = u_a − u_w, will be adopted in the presentation of the experimental data. σ₃ stands for the confining pressure, and u_a and u_w stand for pore air and water pressures, respectively. Besides, to identify the hydraulic and mechanical behaviour of an unsaturated soil properly, a measure of the average stress acting on the soil skeleton may provide some advantages in the development of constitutive models (e.g. [10, 26, 29, 31, 40]). Hence, in the formulation of the model presented herein, the volumetric strain, ε_v, is adopted as the strain variable, and the mean skeleton stress, or referred to as “mean effective stress”, p′ = p + S_rs, is adopted as constitutive stress. S_r stands for the degree of saturation. For the description of the amount of pore water, degree of saturation, S_r, will be adopted in the development of models for the water retention curve.

3 Experimental equipment

The apparatus used was a triaxial apparatus of unsaturated soil modified so that the suction was reduced incrementally via the direct addition of small amounts of water into the specimen at a constant net stress (Fig. 1). Using this apparatus, loading tests at various suctions and wetting tests at various net stresses could be performed. In this apparatus, the axis translation method was used to measure the suction of the specimen using a 5-bar high-air-entry ceramic disc. The spiral (0.2 cm in deep) was created the pedestal, for flushing diffused air from the spiral (Fig. 1).

Fig. 1

Schematic diagram of suction-monitored triaxial apparatus

The triaxial cell was lucid acrylic double cell to minimize the change in volume of the inner cell. The inner cell was connected to the volume change tube withstood a certain pressure (< 1 MPa). During a test, a change in the overall volume of the specimen induces the change in water volume inside the inner cell and thus that of water level within the volume change tube. The change in water level within the tube monitored by a different pressure transducer (range 6 kPa, precision 0.01 kPa) was switched to volume change (the precision was 0.01 cm³).

The wetting (drain) water tube with double Plexiglas cylinder was implemented to monitor the inflowing or outflowing of pore water in the specimen. When three-way valve No. 1 (Fig.1) was opened to connect the inner tube and the spiral, the water volume change of the specimen during loading was monitored. When it was opened to link the inner tube and the top cap, the addition of the amounts of non-aerated water into the specimen during wetting was measured directly. The change in water level within the inner tube monitored by a different pressure transducer was switched to volume change (the precision was 0.01 cm³).

The air pressure line was connected to valve No. 3 (Fig. 1) to apply pore air pressure when controlling or measuring the suction. The basic burette or the reservoir was connected to the wetting (drain) water tube for removing the air bubbles from the spiral after a stabilization of each loading or each wetting step. For flushing after a stabilization of each loading step, i.e. to accurately measure the amounts of water outflowing in the specimen, the initial water level within the basic burette was first recorded. Then, three-way valves Nos. 1 and 4 (Fig. 1) were opened to link the basic burette and the wetting (drain) water tube through the two ends of the spiral. The diffused air from the spiral was removed by a water head at both ends of the spiral. After flushing, the water level within the basic burette was returned to the initial value and three-way valve No. 4 was closed. For flushing after a stabilization of each wetting step, i.e. to accurately measure the pore water pressure of the specimen, three-way valves Nos. 1 and 4 should remain closed firstly. The reservoir was subjected to the same pressure as recorded in the base plate. The air backpressure in the wetting (drain) water tube should be adjusted to a pressure slightly lower than the recorded pore water pressure. Then, three-way valves Nos. 1 and 4 were opened to connect the reservoir and wetting (drain) water tube. The air bubbles were removed by the water pressure difference at both ends of the spiral. After flushing, the three-way valves Nos. 1 and 4 were closed. The pore water pressure was then returned to the value existing prior to the flushing process.

The axial loading system included strain- and stress-controlled loading devices. The strain-controlled loading device was the same as the conventional triaxial apparatus. The stress-controlled loading device consisted of pneumatic cylinder, loading ram and load transducer. The axial force and axial deformation were measured using the load transducer (range 5 kN, precision 1 N) and displacement transducer (range 50 mm, precision 0.01 mm), respectively. More details about this apparatus can be found in Zhang [45].

4 Materials and specimen preparation

The intact Q₃ loess used in this experimental study was taken from the slope in Xi’an, China, as indicated in Fig. 2. Exploration works were made by manual cutting in order to keep the natural structure of loess (Fig. 2a), considering its high fragility. High-quality undisturbed block samples (0.25 m × 0.25 m × 0.25 m in size) were collected at a depth of 3–4 m (Fig. 2b). Samples were immediately wrapped in a thick plastic membrane (Fig. 2c), for preserving the in situ water content and soil structure. The sample cubes were carefully transported to the laboratory. To prevent disturbance during cutting, the preparation of an intact block sample first involved cutting a small soil block with an appropriate size. The ends of the specimen were trimmed with a wire saw and then carefully trimmed to be a triaxial specimen, with diameter of 39.1 mm and height of 40 mm (Fig. 2d), using a special cutting apparatus. The desired triaxial specimen size was used to reduce the suction equilibrium time. The intact specimen had a number of voids at the scale visible to the naked eye (Fig. 2d). Scanning electron microscope (SEM) micrographs taken from the intact specimen indicate that the silt particles connected to each other by clay bridges tend to be clustered into loose aggregates, and there are open structures between the aggregates (Fig. 3), similar to the observation reported by Wang et al. [38]. After completing the specimen preparation, the initial suction value of an intact specimen determined was 175 kPa via the null-type axis translation technique. The main physical indices of the intact loess are illustrated in Table 1.

Fig. 2

Pictures from the intact block sample to trimmed specimen. a Exploration works by manual cutting; b high-quality undisturbed block sample; c the wrapped sample in a thick plastic membrane; d trimmed specimen

Fig. 3

Original SEM micrographs on the intact loess structure at different scales: a Zoom X1000 and b Zoom X10000

Table 1 Geotechnical behaviours of the intact Q₃ loess

5 Experimental programme and procedure

Two groups of experiments were conducted to investigate compression and collapsible behaviour of the intact loess under isotropic stress condition, as summarized in Table 2. Each specimen from these tests was prepared at natural water content (w_n = 15.2%), and initial suction value for this specimen was 175 kPa.

Table 2 Testing programme for two groups

The wetting–loading (WL) tests involved isotropic compression at various suctions to study the effect of suction on deformation and yielding induced by loading (Fig. 4a). The natural specimens were first subjected to a sufficiently low value of seating pressure p (= 25 kPa) to avoid any significant compression or collapse. The specimens were then wetted to different target water contents w₀ (= 15.2%, 17.0%, 18.5%, 21.8% and 41.3%) by the direct addition of amounts of water, and the corresponding suction values measured were 175, 100, 75, 50 and 0 kPa, respectively. After reaching an equilibrium state at the desired suction values, the step loading was performed with net isotropic stresses p up to 400 kPa (p = 25, 50, 100, 200, 300 and 400 kPa), at five suctions (s = 175, 100, 75, 50 and 0 kPa). During testing, the overall volume and water volume changes of the specimen were measured. A stabilization period was allowed until all of these values reached the stable standard. Based on the overall volume change–time and the water volume change–time curves (Fig. 5 in the following section), the rates of both overall volume and water volume changes decreased to less than 0.01 cm³/(2 h) during loading, which was taken as the stabilization criteria. The diffused air bubbles from the spiral subsequently were removed before starting the next stage.

Fig. 4

Stress paths for two groups of tests a isotropic compression tests at various suctions and b wetting tests at various net isotropic stresses

Fig. 5

Variations of confining pressure, pore air and water pressures, overall volume change and water volume change over time for WL tests; a WL2; b WL4

The loading–wetting (LW) tests involved wetting in steps at various net isotropic stresses to investigate the effect of the stress on deformation and yielding induced by wetting (Fig. 4b). Each natural specimen was loaded at a suction of 175 kPa to different target net isotropic stresses (p = 0, 25, 60, 100, 150, 178, 200, 300 and 400 kPa), which was then followed by wetting in steps at constant net isotropic stresses. During each step of wetting stage, the value of the pore air pressure u_a (= 175 kPa) and the net isotropic stress remained unchanged, and three-way valve No. 1 was closed. Subsequently, the air backpressure slightly greater than the u_a was applied to the wetting (drain) tube, and then, three-way valve No. 1 was opened at a tiny angle to link the wetting (drain) tube and the top cap. Water was gradually added into the specimen, and the amount was measured by the differential pressure transducer. Three-way valve No. 1 was closed once the amount of water reached the target water content. Referring to the soil water retention curve of the intact loess under zero external stress condition, the wetting criterion was proposed, i.e. the wetting series was at least six or the water content increment was no less than 2%. The target water contents were further determined sequentially, using the initial water content and the wetting criterion. The overall volume change and the pore water pressure of the specimen were measured. Between each wetting increment, a stabilization period was allowed until all of these values reached the stable standard. According to the overall volume change–time and the pore water pressure–time curves (Fig. 6 in the following section), the rates of both overall volume change and water pore pressure decreased to less than 0.01 cm³/(2 h) and 1 kPa/(2 h) during wetting, which were taken as the stabilization criteria. The diffused air bubbles from the spiral subsequently were removed before starting the next stage.

Fig. 6

Variations of confining pressure, pore air and water pressures, overall volume change and water volume change over time for LW tests; a LW3; b LW8

6 Experimental results

6.1 Response of overall volume and water volume changes as well as pore water pressure from WL and LW tests

6.1.1 WL tests

Figure 5 shows the typical variations of the confining pressure, the pore air and water pressures, the overall volume and water volume changes over time, for WL2 and WL4. A negative value of ∆V_w means a decrease in the water content of the specimen, while a positive value of ΔV means a decrease in the overall volume of the specimen. In suction balance (marked by “①”), the confining pressure σ₃ and the pore air pressure u_a were applied to the same value (i.e. 175 kPa), and the pore water pressure u_w recorded was zero. The measured water volume change ΔV_w increased slightly (more negative). To avoid any significant compression or collapse of the specimen, the specimen was subjected to a low value of seating pressure (p = 25 kPa), with slight changes in the measured ΔV and ΔV_w. Following this process (marked by “②”), the value of the u_a (= 175 kPa) remained unchanged, and the specimens were wetted to different target water contents w₀ (17.0% and 21.8%) by the addition of amounts of water under the undrained condition. An increase in the ΔV_w resulted in the increases in both the ΔV and the u_w. After stabilization, the measured pore water pressures were 75 and 125 kPa, i.e. the suction values were 100 and 50 kPa, respectively.

Following the wetting in steps (marked by “③”), the pore air pressure and confining pressure were decreased to the target values simultaneously, to maintain constant suction and net isotropic stress. When the pore water pressure decreased to a value near zero, three-way valve No. 1 was opened, i.e. under the drained condition (marked by “④”). After reaching an equilibrium state at the desired suction value, the step loading was performed with net isotropic stresses p (marked by “⑤”). Owing to the applied net isotropic stress, the measured overall volume change ΔV increased, while the measured water volume change ΔV_w decreased. From these data, the void ratio e and the water content w of the specimen consolidated can be obtained, i.e. e = e₀ − (1 + e₀)ΔV/V₀ and w = w_n − ρ_wΔV_w/M_s, where V₀ and M_s are initial overall volume and solid mass of the specimen, respectively. The degree of saturation, S_r (= G_sw/e, where G_s is specific gravity), of the specimen consolidated can be determined. The compressibility behaviour at different suctions was subsequently discussed in detail.

6.1.2 LW tests

Figure 6 shows the typical variations of the confining pressure, the pore air and water pressures, the overall volume and water volume changes over time, for LW3 and LW8. In suction balance and isotropic compression stages (marked by “① and ②”), the pore water pressure u_w recorded was zero. Owing to the applied net isotropic stress, the measured overall volume change ΔV increased, as well as the measured water volume change ΔV_w (more negative). From these data, the void ratio e, water content w and the degree of saturation S_r of the specimen consolidated can be obtained.

Following the isotropic compression, the water within the wetting (drain) twin tube was added in steps into the specimen under the undrained condition. For each wetting step, the ΔV and the u_w of the specimen increased gradually and tended to stabilize. As wetting to near saturation, the value of u_w was close to that of u_a, i.e. the suction value was close to zero. The void ratio, the degree of saturation S_r and the suction s of the specimen after each wetting stabilization step could be obtained. The water retention and wetting-induced collapse behaviour can be obtained and were subsequently discussed in detail.

6.2 Soil water retention curves

Based on the data of LW tests, the representative soil water retention curve (SWRC) in terms of degree of saturation during wetting is presented in Fig. 7a. The SWRC obtained from WL tests is shown in Fig. 7b for comparison. The degree of saturation S_r exhibited a rapid increase firstly and followed by a slight change, as the suction s decreased from initial value of 175 kPa. The S_r–s curves moved to the upper right with the increase in the net isotropic stress. This finding indicates that the SWRC of the intact loess is strongly dependent on the net isotropic stress. Furthermore, as presented in Fig. 7b, a small evolution in the SWRC of the loess was noted with respect to the hydro-mechanical path. It could be argued as an approximation that both sets of SWRC have similar effects.

Fig. 7

SWRC in terms of degree of saturation. a SWRC from LW tests; b SWRC from LW and WL tests

van Genuchten [37] proposed the water retention model (VG model) written in terms of the degree of saturation S_r for drying path.

$$S_{\text{r}} = \left[ {1 + \left( {\alpha s} \right)^{n} } \right]^{ - m}$$

(1)

where α, n and m are determined as best-fit parameters using the least squares method (it was assumed m = 1 − 1/n). The intersection point of the asymptote for the log S_r–log s curve with the log S_r = 0 axis is equal to the air-entry value s_c (= 1/α), and the slope of the asymptote is equal to mn (= n − l) [8]. In wetting path, the degree of saturation at zero suction was usually less than that for the drying path (i.e. 1.0). For example, the degree of saturation of compacted Pearl clay at zero suction can only reach 0.88 [35]. Therefore, the form of the VG model for wetting path was represented as:

$$S_{\text{r}} = S_{\text{r}}^{0} \left[ {1 + \left( {\alpha s} \right)^{n} } \right]^{ - m}$$

(2)

where $S_{\text{r}}^{0}$ is the degree of saturation at zero suction.

The VG model [Eq. (2)] was employed to interpret the present results of the measured SWRC during wetting under constant net isotropic stresses. The best fitting curves are shown in Fig. 7a, and the parameters are presented in Table 3. The VG model provided an excellent fit to the experimental data over the entire range. Regression values of degree of saturation S_r0 all were about 0.97. The parameter n seemed reasonably independent of the net isotropic stress, and the average value of 1.323 was approximately taken. The parameter α, however, was stress dependent, manifesting that the higher the stress, the smaller the parameter α. In other words, the air-entry value s_c (= 1/α) increased with the net isotropic stress. It is evident that the influence of the net isotropic stress on water retention properties is modelled primarily by focusing on the evolution of the air-entry value, similar to the observation reported by Gallipoli [8].

Table 3 Soil parameters of the VG model for LW tests

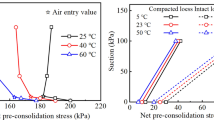
The air-entry value s_c was determined by means of the data of the α, as shown in Table 3. The air-entry value s_c is plotted against the net isotropic stress p in Fig. 8, which could be represented by an empirical formula below:

$$s_{\text{c}} = s_{{{\text{c}}0}} { + }\beta p$$

(3)

where s_c0 (kPa) is the air-entry value at null stress, equal to 9.2 kPa, and β is the soil parameter representing the influence of net isotropic stress on the air-entry value. Regression of the data gave the β = 0.033. Substituting Eq. (3) in Eq. (2) leads to

Fig. 8

Air-entry value as a function of the net isotropic stress

$$S_{\text{r}} = S_{\text{r}}^{ 0} \left\{ {1 + \left[ {{s \mathord{\left/ {\vphantom {s {\left( {s_{{{\text{c}}0}} { + }\beta p} \right)}}} \right. \kern-0pt} {\left( {s_{{{\text{c}}0}} { + }\beta p} \right)}}} \right]^{n} } \right\}^{ - (1 - 1/n)}$$

(4)

Equation (4) indicates that the variation of the degree of saturation S_r with the suction ratio s/s_c (the ratio of suction s to air-entry value s_c) was nearly independent of the net isotropic stress. This may significantly reduce the data set that is necessary to determine the model parameters. In addition, it is worth mentioning that Eq. (4) is based on the fact that the SWRC is obtained under constant stresses.

6.3 Compressibility of intact loess at the WL path

The results of WL tests are shown on a e–ln p diagram in Fig. 9a. Void ratio e exhibited first slight and then rapid decrease with the increase in net isotropic stress p. All e–ln p curves were approximately composed of two intersecting lines. The intersections defined isotropic yield points, and the corresponding yield stress and void ratio were denoted by $p_{\text{y}}^{*}$ and e_y, respectively.

Fig. 9

Compression curves from the WL tests: ae–ln p; be–ln p′

The values of yield stress $p_{\text{y}}^{*}$, slope κ_vs before yielding and slope λ_vs after yielding for WL tests were determined, as shown in Table 4. Plotting yield stress $p_{\text{y}}^{*}$ as a function of suction s allows the determination of the initial LC₀ yield curve presented in Fig. 4. The yield stress $p_{\text{y}}^{*}$ and the slope λ_vs both increased with suction s. The slope κ_vs, however, decreased with the increase in suction s. This finding is similar to test results of the λ_vs from Wheeler and Sivakumar [39] and Sun et al. [35], but is not consistent with the proposal of Alonso et al. [1] or Kohgo et al. [16]. In fact, the tendency of the λ_vs change with the s depended on soil type [33, 16].

Table 4 Soil parameters for WL tests

Using the yield point ($p_{\text{y}}^{*}$, e_y) and the slope λ_vs, the e–lnp curve equation after yielding at various suctions can be obtained, and then, the intersection points N (p_n, e_n) of those curves in the saturated and unsaturated states could be determined. For suction values of 50, 75, 100 and 175 kPa, the values of the p_n were 730, 732, 742 and 750 kPa and the corresponding values of the e_n were 0.700, 0.700, 0.698 and 0.697, respectively. The intersection points slightly dropped with the increase in suction. It means that the compression curves after yielding for intact loess with various suctions gathered to the point N (Fig. 9a). Namely, no collapse occurred at the state of the point N, similar to the test results for the collapsible silty clay by [4, 5].

The results shown in Fig. 9a are re-plotted in Fig. 9b in terms of the mean effective stress, p′ = p + S_rs. The dashed lines in Fig. 9b show the seating load and wetting stages before isotropic compression. As shown, for the specimens subjected to isotropic compression, the changes of the e–ln p′ curves were similar to these of the e–ln p curves, and the void ratio exhibited a slight decrease firstly and followed by a rapid change with increase in the mean effective stress. The stress corresponding to turning points defined effective yield stress $p_{\text{y}}^{{{\prime }*}}$, and these values and the logarithmic elastic and elastic–plastic compliances (i.e. $\kappa_{\text{vs}}^{{\prime }}$ and $\lambda_{\text{vs}}^{{\prime }}$) are shown in Table 4. The $p_{\text{y}}^{{{\prime }*}}$ and the $\lambda_{\text{vs}}^{{\prime }}$ increased with the s. The $\kappa_{\text{vs}}^{{\prime }}$, however, fluctuated in a small range with the change of the suction and could be assumed to be independent of the suction. Thus, the $\kappa_{\text{vs}}^{{\prime }}$ was expressed by $\kappa_{\text{v}}^{{\prime }}$, and the average value of $\kappa_{\text{v}}^{{\prime }}$ = 0.033 was approximately taken.

The $p_{{{\text{y}}0}}^{*}$ and λ_v0 are the yield stress and the slope after yielding for saturated specimen (i.e. WL5), and the values of these are presented in Table 4. The λ_vs or $\lambda_{\text{vs}}^{{\prime }}$ as a function of suction is presented in Fig. 10a. The quantity λ_vs and $\lambda_{\text{vs}}^{{\prime }}$ were represented as:

$$\lambda_{\text{vs}} = \lambda_{\text{v0}} + \frac{s}{a + bs}$$

(5a)

$$\lambda_{\text{vs}}^{{\prime }} = \lambda_{\text{v0}} + \frac{s}{{a_{1} + b_{1} s}}$$

(5b)

where a, b, a₁ and b₁ are soil parameters. a and b are equal to the intercept and the slope of the s/(λ_vs − λ_v0) − s linear, respectively; a₁ and b₁ are equal to the intercept and the slope of the s/($\lambda_{\text{vs}}^{{\prime }}$ − λ_v0) − s linear, respectively. Regression of the data to those functions resulted in a = 950, b = 2.00, a₁= 495 and b₁ = 0.82.

Fig. 10

Variations of λ_vs, $\lambda_{\text{vs}}^{{\prime }}$ and N(s) with suction

In addition, for obtaining the equation of the LC yield curve, it is necessary to determine the intercept N(s) of the isotropic normal compression line on a e–ln($p^{{\prime }} /p_{\text{ref}}^{{\prime }}$) plane, with $p_{\text{ref}}^{{\prime }}$ denoting the arbitrary reference stress (taken as 100 kPa in this study). The values of the N(s) at various suctions were determined by means of the data presented above (Fig. 9b), and these values are shown in Table 4. The N(s) decreased with s (Fig. 10b), which could be described by an empirical formula as follows.

$$N(s) = N( 0) + \frac{s}{{c_{1} + d_{1} s}}$$

(6)

where N(0) is the value of N(s) at s = 0; c₁ and d₁ are the soil parameters, representing the intercept and the slope of the s/[N(s)–N(0)] − s linear, respectively. Regression of the data to this function resulted in c₁= 307 and d₁ = 0.21.

6.4 Wetting-induced collapse behaviour of intact loess at the LW path

Based on the volume change of the specimen during isotropic compression at a constant suction s₀ (= 175 kPa) and wetting in steps at constant net isotropic stress p, the void ratio e induced by the hydro-mechanical coupling was calculated. The suction s was calculated by subtracting pore water pressure u_w from pore air pressure u_a (= 175 kPa) after each step wetting stabilization. The loss of suction was calculated by subtracting suction s from initial suction s₀ and was abbreviated as loss suction $s^{*}$ [36].

The results of LW tests are shown on a e–ln $s^{*}$ diagram in Fig. 11. The e–ln $s^{*}$curve at zero external net stress was an approximately horizontal line (LW1; A₀B₀ path in Fig. 4b), suggesting that no variation was found in the volumetric deformation with the increase in loss suction. This may be explained by the fact that even under application of zero external net stress and just by wetting the intact soil specimen with high resistance, the mean effective stress changes and no-collapse behaviour in this case could be attributed to the interparticle bond strength. This finding is consistent with the results regarding disturbed loess under laterally restrained condition [44, 48] and compacted gneiss soil under isotropic stress condition [27, 28].

Fig. 11

Wetting-induced deformation curves from the LW tests

Figure 11 also indicates that the e–ln $s^{*}$ curve shapes depend on the extent of applied net isotropic stress p. For p ≤ $p_{{{\text{y}}0}}^{*}$, the void ratio e exhibited a slight decrease with the increase in loss suction $s^{*}$. These test points appeared to coincide with a line (LW2; A₁B₁ path in Fig. 4b). Namely, the metastable-structured intact loess studied can be saturated without plastic collapse of its structure under a low net isotropic stress [27]. For p > $p_{{{\text{y}}0}}^{*}$, the void ratio e exhibited first slight and then rapid decrease with the increase in loss suction $s^{*}$. These test points appeared to coincide with two intersecting lines (LW3, LW4, …, LW9; A₂B₂, A₃B₃, …, A₈B₈ paths in Fig. 4b). These intersections were defined the collapse loss suction $s_{\text{y}}^{*}$, and the corresponding suctions were the collapse suctions s_y (= s₀ − $s_{\text{y}}^{*}$), similar to that employed by Rojas et al. [29]. For suctions above this value, the pre-collapse behaviour occurs and the soil behaves elastically without grain slippage. This elastic response can be visualized as the cementing effect provided to the soil microstructure by the suction. However, for smaller values, collapse behaviour occurs and the soil behaves elastoplastically. This elastoplastic response can be visualized as the combination of further structural rearrangements and by the occurrence of local shearing of both the connecting bonds and clay aggregations due to the reduction in the suction. The collapse continues until a new equilibrium configuration is reached. Under a given net stress, the new equilibrium configuration does not require the total destruction of all connecting bonds in the clay aggregations in response to an incremental decrease in suction. This finding is consistent with the results regarding the collapsible compacted gneiss soil [28] and the loessial soil [7, 10, 11] obtained via the wetting tests under constant net stresses.

Inspection of Fig. 11 also reveals that void ratios of the specimens such as LW2, LW3, LW4 and LW5 decreased upon wetting to saturation. This result shows that shrinking is produced if the specimen is wetted from a point that located “inside” the LC₀ yield curve (such as a point A₁, A₂, A₃ or A₄ presented in Fig. 4b). It is not consistent with prediction of the BBM model. According to the model formulation, if the state of the material is at a point such as point A₁, the stress path during wetting lies completely in the elastic domain, and only a small elastic swelling will ensue. However, if a specimen is wetted at a point such as point A₂ or A₄, it should exhibit swelling deformation initially, followed by larger collapsible deformation as the LC yield curve is crossed. This phenomenon might be explained by that the intact loess experienced firstly a small decrease in void ratio as a function of the applied mean effective stress, and the soil state at the beginning of the wetting phase was well inside the initial elastic domain. A decrease in the suction during wetting implied both a reduction in the mean effective stress acting on the soil skeleton (i.e. unloading of the macrostructure formed by the aggregates) and the destruction of the connecting bonds in the clay aggregations (i.e. the collapse of the macrostructure formed by the aggregates). The magnitude of pore collapse caused by the latter was larger than that of swelling caused by the former, resulting in a decrease in the specimen volume [43].

When the specimen was wetted from a point that located “outside” the LC₀ yield curve (such as a point A₅, A₆, A₇ or A₈ presented in Fig. 4b), the void ratio e also exhibited first slight and then rapid decreased with the increase in loss suction $s^{*}$ (such as result of LW6, LW7, LW8 or LW9 presented in Fig. 11). In other words, it exhibited elastic deformation initially upon wetting until reaching a collapse suction value where the larger irreversible collapsible deformation (or plastic deformation) ensued. Sun et al. [32] also obtained consistent results regarding the compacted soil. However, it is not consistent with the assumptions of the BBM model that irreversible collapsible deformation ensued at the beginning of wetting. This phenomenon might be explained by the fact that the collapsible behaviour involved the current void ratio of the specimen. A load was applied to produce the hardening of the specimen and the combination of original structural rearrangements. Then, following a wetting path a reduction in suction was accompanied by a decrease in the mean effective stress (i.e. unloading) and the progressive destruction of the connecting bonds in the rearrangements clay aggregations, with a consequent elastic volumetric shrinking, until the collapse suction value. Afterwards, the total volumetric strains were the sum of elastic shrinking and plastic collapse.

The collapse loss suction $s_{\text{y}}^{*}$ (or collapse suction s_y), slope κ_vp before collapse and slope λ_vp after collapse were determined, as shown in Table 5. No appreciable effects of net isotropic stress p on the slope κ_vp were observed, and the average value (= 0.004) under different net isotropic stresses was taken. The slope λ_vp, however, was net isotropic stress dependent. Figure 12 shows the λ_vp against p/p_sh (where p_sh is the initial collapse pressure determined by the LW tests shown in Fig. 14; the value of that is equal to 55 kPa). The λ_vp–p/p_sh curve showed a nonlinear decreasing trend and could be described using a power function. The quantity λ_vp is represented as:

$$\lambda_{\text{vp}} = C_{1} (p/p_{\text{sh}} )^{{ - C_{2} }}$$

(7)

where C₁ and C₂ are soil parameters. C₁ is equal to the slope λ_vp for p = p_sh, and C₂ represents the effect of net isotropic stress p on slope λ_vp. Regression of the data to this function resulted in C₁= 0.368 and C₂ = 0.446.

Table 5 Soil parameters for LW tests

Fig. 12

Variation in λ_vp with p/p_sh

The variation of collapse loss suction $s_{\text{y}}^{*}$ with net isotropic stress p is shown in Fig. 13. Collapse loss suction first decreased and then increased with the increase in net isotropic stress. The net isotropic stress value of the turning point (= 183 kPa) was close to the yield stress $p_{\text{y}}^{*}$ value of the natural specimen (= 178 kPa). This result was relevant to the higher resistance in the intact specimen due to the contribution of the cementation. The cementation was highly affected by loading or wetting. At a low level of the net isotropic stress, much of the cementation was not destroyed by loading (i.e. mechanical disturbance). The higher the net isotropic stress applied, that is, the larger the mean effective stress acting on the soil skeleton. The cementations were higher sensitive to the wetting-induced collapse. A reduction in collapse loss suction with the increase in the net isotropic stress was thus detected. At a high level of the net isotropic stress, an increase in the mean effective stress acting on the soil skeleton resulted in the combination of structural rearrangements and thus a denser specimen, decreasing the effect of disturbance on the wetting-induced collapse. An increase in collapse loss suction was thus observed as the net isotropic stress increased.

Fig. 13

Relationship between collapse loss suction $s_{\text{y}}^{*}$ and net isotropic stress p

6.5 The hydro-mechanical path dependency of the wetting-induced deformation

The wetting-induced volumetric strain ε_vs was defined as:

$$\varepsilon_{\text{vs}} { = }\frac{{ - \Delta e_{\text{s}} }}{{1{ + }e_{0} }}$$

(8)

where Δe_s is the difference in the void ratios between the natural state suction s₀ (= 175 kPa) and a given suction s_i. The ε_vs at saturation (s_i = 0 kPa) was the total collapsible volumetric strain.

Based on the e–ln p curves of WL tests (Fig. 9a), the wetting-induced volumetric strain ε_vs was determined using double-triaxial equipment technique. Based on the e–ln $s^{*}$ curves of LW tests (Fig. 11), the ε_vs was also determined using the single-triaxial equipment technique. The variations of wetting-induced volumetric strain ε_vs with net isotropic stress p are shown in Fig. 14. The ε_vs–p curves from two methods showed a similar trend. The ε_vs first increased and then decreased with the increase in net isotropic stress. In other words, the wetting-induced deformation of the intact loess did not increase monotonically, with obvious peak points. The net isotropic stress and wetting-induced volumetric strain of the peak point were denoted by p_m and ε_vsm, respectively. The values of the p_m (= 178–200 kPa) obtained via the two methods were independent of loss suction, and close to the yield stress of the natural intact loess. The finding indicates that the maximum wetting-induced deformation for an identical specimen occurs when the wetting takes place at a net isotropic stress close to the yield stress. This phenomenon might be explained by that the destructuration of the original structure in the soil occurred, the specimen became denser, and hence, the collapse due to the suction reduction became smaller. The similar observations are reported by Sun et al. [35], Jiang et al. [13] and Zhang et al. [44].

Fig. 14

Wetting-induced volumetric strain as a function of net isotropic stress

Inspection of Fig. 14 also suggests that the ε_vs obtained by the double-triaxial equipment technique was larger than that obtained by the single-triaxial equipment technique at the same s_i; furthermore, the difference decreased with the s_i. At a high level of the s_i, a clear difference was observed between the single- and double-triaxial equipment techniques. For example, the maximum difference in ε_vs at the s_i of 100 kPa was approximately 2.6%, and the difference in ε_vsm was approximately 2%. This result was primarily because of the different hydro-mechanical path of the two methods, resulting in the difference in the formation and development of the wetting-induced deformation. This finding shows that the wetting-induced deformation of the intact loess turned out to hydro-mechanical path dependent. When wetting to saturation, the maximum difference in ε_vs was approximately 0.9%, and the difference in ε_vsm was approximately 0.3%, indicating that the total collapsible deformation of the two methods yielded similar results, i.e. the final state of the soils subjected to wetting to saturation lies on, or very close to, the virgin consolidation line of the saturated soil. This result agrees with findings of previous researches [13, 25, 35].

The stress at ε_vs = 1.5% was the initial wetting collapse pressure p_sh [21]. The intersection of the ε_vs = 1.5% line and the ε_vs–p curve was the p_sh (Fig. 14). For the same s_i, a larger p_sh was obtained using the single-triaxial equipment technique compared with the double-triaxial equipment technique, and this value decreased with the s_i. The values of p_sh at s_i = 0 kPa were 55 and 30 kPa using the single- and double-triaxial equipment techniques, respectively.

6.6 The hydro-mechanical path dependency of the yielding

The different treatment given so far to the plastic deformations induced by suction or stress changes has only a formal meaning, which has been useful to derive the appropriate relationships. It could be argued as an approximation that both sets of plastic deformations have similar effects [1]. In this manner, a simple way to couple both yield curves results if their position is controlled by the total plastic volumetric strain, $\varepsilon_{\text{v}}^{\text{p}}$ = $\varepsilon_{\text{vp}}^{\text{p}}$ + $\varepsilon_{\text{vs}}^{\text{p}}$, where $\varepsilon_{\text{vp}}^{\text{p}}$ and $\varepsilon_{\text{vs}}^{\text{p}}$ were the plastic volumetric strain induced by loading and wetting, respectively.

The p_y–s curves (LC yield curves) identified from WL tests (Fig. 9a) and the p–s_y curves (SD yield curves) identified from LW tests (Fig. 11) are plotted in a s–p plane, as shown in Fig. 15a, for different plastic volumetric strains ($\varepsilon_{\text{v}}^{\text{p}}$ ≥ 0). The SD yield curves lay under the LC yield curves at the same plastic volumetric strain $\varepsilon_{\text{v}}^{\text{p}}$, suggesting that no unique yield curve in a s–p plane was identified from the loading and wetting paths. At a high level of the net isotropic stress, the phenomenon of plastic collapse did not appear until the suction decreased to the collapse suction s_y, where appreciable hydro-mechanical path effect was observed. At a low level of the stress, the SD and LC yield curves almost coincided, suggesting that the phenomenon of plastic collapse appeared once the suction decreased to the intersection of the LC yield curve, where no appreciable hydro-mechanical path effects were observed. It is not consistent with the assumption of the BBM model proposed by Alonso et al. [1], which showed that a single unique yield curve was identified from the loading and wetting paths.

Fig. 15

Yield curves determined from WL and LW tests. as–p plane; bs–p′ plane

Figure 15a also suggests that the LC yield curve expanded with the increase in the loading- or wetting-induced plastic volumetric strain, which produced the coupled outward movement of the SD curve. For example, from point A₅ loading to point A₇ or from point C wetting to point D, the plastic volumetric strains of 5.14% commenced, and the LC₀ and SD₀ yield curves were thus coupled extended to LC₁ and SD₁, respectively. Moreover, because of the hardening of the specimen, the collapse suction decreased with the increase in the total plastic volumetric due to loading, and SD yield curve tilts further.

The yield points identified from WL tests (Fig. 9b) and LW tests (Fig. 11) are plotted in a s–p′ plane, as shown in Fig. 15b, for different plastic volumetric strains ($\varepsilon_{\text{v}}^{\text{p}}$ ≥ 0). It can be seen that the yield points from the two sets of experiments were approximately on a single curve at the same $\varepsilon_{\text{v}}^{\text{p}}$, indicating that the LC yield curve and their hardening parameters are unique in a s–p′ plane, regardless of the different types of path followed wetting or loading. Further illustrating the LC yield curve has significant differences using different stress variables.

6.7 Formulation of the constitutive model for isotropic stress state

As mentioned above, the wetting-induced deformation of the intact loess first increased and then decreased with the increase in the net isotropic stress. No uniqueness of the yield curve in a s–p plane was identified from loading and wetting paths, which differed from the assumption of the BBM model. Interestingly, the uniqueness of the loading–collapse yield curve in a s–p′ plane was identified from loading and wetting paths. Thus, a new elastoplastic model to describe the compression and collapse behaviour of the intact loess needed to be proposed, using the mean effective stress p′ as constitutive stress.

6.7.1 LC yield curve

The assumed path consists of increasing arbitrarily net stress and decreasing suction, starting from point A in Fig. 16. Under a given wetting or loading path, the stress state of the soil shifts from point B to points C and D on a LC yield curve, and the plastic volumetric strains of two points were equal, corresponding to saturated and unsaturated states, respectively. The normal compression hyperline relationships are given below.

Fig. 16

Derivation of LC yield curve equation

$$e_{\text{C}} = N(0) - \lambda_{\text{v0}} \ln \frac{{p_{\text{y0}} }}{{p_{\text{ref}}^{{\prime }} }}$$

(9)

$$e_{\text{D}} = N({\text{s}}) - \lambda_{\text{vs}}^{{\prime }} \ln \frac{{p_{\text{y}}^{{\prime }} }}{{p_{\text{ref}}^{{\prime }} }}$$

(10)

Summing up these two equations yields

$$N(s) - \left( {\lambda_{\text{vs}}^{{\prime }} - \kappa_{\text{v}}^{{\prime }} } \right)\ln \frac{{p_{\text{y}}^{{\prime }} }}{{p_{\text{ref}}^{{\prime }} }} = N( 0) - \left( {\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} } \right)\ln \frac{{p_{\text{y0}} }}{{p_{\text{ref}}^{{\prime }} }}$$

(11)

Substitution of Eq. (11) yields the result

$$\frac{{p_{\text{y}}^{{\prime }} }}{{p_{{{\text{y}}0}} }} = \exp \left[ {\frac{{N({\text{s}}) - N( 0)}}{{\lambda_{\text{vs}}^{{\prime }} - \kappa_{\text{v}}^{{\prime }} }} + \frac{{\lambda_{\text{v0}} - \lambda_{\text{vs}}^{{\prime }} }}{{\lambda_{\text{vs}}^{{\prime }} - \kappa_{\text{v}}^{{\prime }} }}\ln \frac{{p_{\text{y0}} }}{{p_{\text{ref}}^{{\prime }} }}} \right]$$

(12)

The LC yield curves can be obtained via Eqs. (5b), (6) and (12)

$$\frac{{p_{\text{y}}^{{\prime }} }}{{p_{{{\text{y}}0}} }} = \exp \left[ {\frac{s}{{\lambda_{\text{v0}} + {s \mathord{\left/ {\vphantom {s {\left( {a_{1} + b_{1} s} \right) - \kappa_{\text{v}}^{{\prime }} }}} \right. \kern-0pt} {\left( {a_{1} + b_{1} s} \right) - \kappa_{\text{v}}^{{\prime }} }}}}\left( {\frac{1}{{c_{1} + d_{1} s}} - \frac{1}{{a_{1} + b_{1} s}}\ln \frac{{p_{\text{y0}} }}{{p_{\text{ref}}^{{\prime }} }}} \right)} \right]$$

(13)

This is the equation of LC yield curve. Note that when p_y0 = $p_{{{\text{y}}0}}^{*}$, the p′_y = $p_{\text{y}}^{{{\prime }*}}$ and the LC yield curve becomes an initial LC₀ yield curve.

6.7.2 Hardening laws

Based on Eq. (13), the mean effective stress increment dp′_y is given by

$${\text{d}}p_{\text{y}}^{{\prime }} = \frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}{\text{d}}p_{y0} + \frac{{\partial p_{\text{y}}^{{\prime }} }}{\partial s}{\text{d}}s$$

(14)

where

$$\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }} = \frac{{\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} }}{{\lambda_{\text{v0}} + {s \mathord{\left/ {\vphantom {s {\left( {a_{1} + b_{1} s} \right)}}} \right. \kern-0pt} {\left( {a_{1} + b_{1} s} \right)}} - \kappa_{\text{v}}^{{\prime }} }}\frac{{p_{\text{y}}^{{\prime }} }}{{p_{\text{y0}} }}$$

(15)

$$\frac{{\partial p_{\text{y}}^{{\prime }} }}{\partial s} = p_{{{\text{y}}0}} \left( {A - B\ln \frac{{p_{y0} }}{{p_{\text{ref}}^{{\prime }} }}} \right)$$

(16)

with

$$\left\{ \begin{array}{*{20}l} A = \frac{1}{{\left[ {\lambda _{{{\text{v0}}}} + s/s\left( {a_{1} + b_{1} s} \right) - \kappa _{{\text{v}}}^{\prime } } \right]^{2} }} {\left\{ {\frac{{c_{1} \left[ {\lambda _{{{\text{v0}}}} + s/s\left( {a_{1} + b_{1} s} \right) - \kappa _{{\text{v}}}^{\prime } } \right]}}{{\left( {c_{1} + d_{1} s} \right)^{2} }}} - {\frac{{a_{1} s}}{{\left( {a_{1} + b_{1} s} \right)^{2} \left( {c_{1} + d_{1} s} \right)}}} \right\} } \hfill \\ {B = \frac{{\lambda _{{{\text{v0}}}}^{\prime } - \kappa ^{\prime } }}{{\left[ {\lambda _{{{\text{v0}}}} + s/s\left( {a_{1} + b_{1} s} \right) - \kappa _{{\text{v}}}^{\prime } } \right]^{2} }}\frac{{a_{1} }}{{\left( {a_{1} + b_{1} s} \right)^{2} }}} \hfill\\ \end{array} \right.$$

(17)

When the stress state is on the LC yield curve, the hardening law during loading at a constant suction (e.g. DE path in Fig. 16b) can be obtained by Eq. (14).

$${\text{d}}p_{\text{y0}} = {{{\text{d}}p_{\text{y}}^{{\prime }} } \mathord{\left/ {\vphantom {{{\text{d}}p_{\text{y}}^{{\prime }} } {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}} \right. \kern-0pt} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}$$

(18)

When the stress state is on the LC yield curve, the hardening law during wetting at a constant net isotropic stress (e.g. DF path in Fig. 16b) can be obtained by Eq. (14).

$${\text{d}}p_{\text{y0}} = {{\left( {{\text{d}}p_{\text{y}}^{{\prime }} - \frac{{\partial p_{\text{y}}^{{\prime }} }}{\partial s}{\text{d}}s} \right)} \mathord{\left/ {\vphantom {{\left( {{\text{d}}p_{\text{y}}^{{\prime }} - \frac{{\partial p_{\text{y}}^{{\prime }} }}{\partial s}{\text{d}}s} \right)} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}} \right. \kern-0pt} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}$$

(19)

6.7.3 Volumetric behaviour

An increase in net isotropic stress during loading in the elastic region will be accompanied by an increase in the mean effective stress, with a consequent elastic compressive volumetric strain. Therefore, the elastic volumetric strain increment ${\text{d}}\varepsilon_{\text{v}}^{\text{e}}$ is given by

$${\text{d}}\varepsilon_{\text{v}}^{\text{e}} = \frac{{\kappa_{\text{v}}^{{\prime }} }}{{1 + e_{0} }}\frac{{{\text{d}}p^{{\prime }} }}{{p^{{\prime }} }}$$

(20)

When the stress state is on the LC yield curve and its increment vector points to the yield side of the LC yield curve, the plastic volume strain increment at saturated state is given by

$${\text{d}}\varepsilon_{\text{v}}^{\text{p}} = \frac{{\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} }}{{1 + e_{0} }}\frac{{{\text{d}}p_{\text{y0}} }}{{p_{\text{y0}} }}$$

(21)

Based on Eqs. (18) and (21), once the stress p′ reaches the yield stress value $p_{\text{y}}^{{{\prime }*}}$, the plastic volumetric strain ${\text{d}}\varepsilon_{\text{v}}^{\text{p}}$ at unsaturated state following a loading path is given by

$${\text{d}}\varepsilon_{\text{v}}^{\text{p}} = {{\frac{{\left( {\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} } \right)}}{{1 + e_{0} }}\frac{{{\text{d}}p_{\text{y}}^{{\prime }} }}{{p_{\text{y0}} }}} \mathord{\left/ {\vphantom {{\frac{{\left( {\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} } \right)}}{{1 + e_{0} }}\frac{{{\text{d}}p_{\text{y}}^{{\prime }} }}{{p_{\text{y0}} }}} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}} \right. \kern-0pt} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}$$

(22)

Therefore, the total volume strain is obtained by the combination of the elastic volume strain [i.e. Equation (20)] and plastic volumetric strain [i.e. Equation (22)] during loading at a constant suction.

According to the results of LW tests (Fig. 11), a reduction in suction during wetting in the elastic region will be accompanied by a reduction in the mean effective stress p′, with a consequent elastic shrinkage volumetric strain. Therefore, the elastic volumetric strain increment ${\text{d}}\varepsilon_{\text{v}}^{\text{e}}$ is given by

$${\text{d}}\varepsilon_{\text{v}}^{\text{e}} = \frac{{ - \kappa_{\text{v}}^{{\prime }} }}{{1 + e_{0} }}\frac{{{\text{d}}p^{{\prime }} }}{{p^{{\prime }} }}$$

(23)

Based on Eqs. (19) and (21), once the suction decreased to the intersection of the LC yield curve, the plastic volumetric strain ${\text{d}}\varepsilon_{\text{v}}^{\text{p}}$ at unsaturated state following a wetting path is given by

$${\text{d}}\varepsilon_{\text{v}}^{\text{p}} = {{\frac{{\left( {\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} } \right)}}{{1 + e_{0} }}\frac{1}{{p_{\text{y0}} }}\left( {{\text{d}}p_{\text{y}}^{{\prime }} - \frac{{\partial p_{\text{y}}^{{\prime }} }}{\partial s}{\text{d}}s} \right)} \mathord{\left/ {\vphantom {{\frac{{\left( {\lambda_{\text{v0}} - \kappa_{\text{v}}^{{\prime }} } \right)}}{{1 + e_{0} }}\frac{1}{{p_{\text{y0}} }}\left( {{\text{d}}p_{\text{y}}^{{\prime }} - \frac{{\partial p_{\text{y}}^{{\prime }} }}{\partial s}{\text{d}}s} \right)} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}} \right. \kern-0pt} {\frac{{\partial p_{\text{y}}^{{\prime }} }}{{\partial p_{\text{y0}} }}}}$$

(24)

Therefore, the total volume strain is obtained by the combination of the elastic volume strain [i.e. Equation (23)] and plastic volumetric strain [i.e. Equation (24)] during wetting at a constant net isotropic stress.

6.7.4 Model predictions compared with test results

As commented above, the model requires three parameters (i.e. s_c0, β and n) to describe the water retention behaviour and six parameters (i.e. λ_v0, κ_v, a₁, b₂, c₁ and d₁) to describe the volumetric deformation behaviour under isotropic stress condition. In detail, the parameter of s_c0 was the air-entry value at null net stress; the parameter of β was the gradient of the air-entry value s_c increase with the net isotropic stress; the parameter of n − 1 was the slope of the asymptote for the log S_r–log s curve. The parameters of λ_v0 and $\kappa_{\text{v}}^{{\prime }}$ were the slopes of e–ln p′ curves before and after yielding for saturated soil, respectively; the parameters of a₁ and b₁ were the intercept and the slope of the s/($\lambda_{\text{vs}}^{{\prime }}$–λ_v0) − s linear, respectively; the parameters of c₁ and d₁ were the intercept and the slope of the s/[N(s)–N(0)] − s linear, respectively. Moreover, it is necessary to determine the initial state values e₀, $p_{{{\text{y}}0}}^{*}$ and $p_{\text{ref}}^{{\prime }}$. Regarding the intact loess discussed in this paper, Table 6 shows the values of the model parameters and initial state used for the predictions.

Table 6 Model parameter values and initial state for predictions

Figure 17 shows typical comparisons between the predicted and measured results of WL tests. The stress paths are in a s–p′ plane, as shown in Fig. 17a. According to the model formulation, the initial state of the specimen was at a point such as A₀, and the stress path A₀A₁ lays completely in the elastic domain (Fig. 17a). An increase in effective mean stress (i.e. A₀A₁ path) was therefore accompanied with a small increase in the degree of saturation (Fig. 17b) and a small decrease in void ratio (Fig. 17c). Due to the collapsibility of the intact loess, subsequently an increase in degree of saturation at constant net stress such as A₁G or A₁I path (Fig. 17b) was accompanied by a reduction in suction, which resulted in a decrease in mean effective stress, with a consequent elastic volumetric shrinkage and thus a small decrease in the void ratio (Fig. 17c). Next, an increase in net stress at constant suction, GH or IL path in Fig. 17a, corresponded to an increase in mean effective stress. An increase in the degree of saturation would be expected (Fig. 17b). It exhibited irreversible plastic deformation as the LC yield curve was crossed, with a significant reduction in void ratio (Fig. 17c). The comparison demonstrates that the predicted values agree well with the measured values. The proposed model was able to describe the mechanical and hydraulic behaviour of the intact loess following wetting–loading path quite well.

Fig. 17

Comparison of predicted and measured results of WL tests: as–p′; bS_r–ln p′; (c) e–ln p′

Figure 18 shows typical comparisons between the predicted and measured results of LW tests. The stress paths are in a s–p′ plane, as shown in Fig. 18a. According to the model formulation, the stress state of the specimen at beginning of wetting phase such as a point A₅ located “inside” the initial LC yield curve (Fig. 18a). As degree of saturation increased (Fig. 18b), the suction decreased and the elastic domain shrinks, but the stress state still remained inside it for a while. Due to the collapsibility of the intact loess, a small elastic shrinking would ensue, and thus, a small decrease in void ratio occurred (Fig. 18c), until a predicted suction value of about s = 88 kPa. Afterwards, it should exhibit irreversible collapsible deformation. In addition, the stress state of the specimen at beginning of wetting phase such as a point A₇ located “outside” the initial LC yield curve (Fig. 18a). Since the slope of the subsequent LC yield curve was lower than that of wetting path (A₇B₇), the wetting path was observed to cross the LC yield curve, and an initial elastic shrinking can be observed followed by the collapse of the specimen. The proposed model was able to describe the mechanical and hydraulic behaviour of the intact loess following wetting–loading path quite well, using the effective stress approach.

Fig. 18

Comparison of predicted and measured results of LW tests: as–p′; bS_r–ln p′; ce–ln $s^{*}$

7 Conclusions

This paper presented a new technique for investigating compression and collapse behaviour of intact loess, using a suction-monitored triaxial apparatus. The wetting–loading (WL) and loading–wetting (LW) tests were performed. The conclusions drawn from this study are as follows.

The e–ln p and e–ln p′ curves of WL tests exhibited two approximately linear segments, which could determine the net yield stress and the effective yield stress, respectively. Before yielding, the slope of the former increased with the decrease in the suction, while that of the latter seem to be independent of the suction. After yielding, the slopes of both decreased with the suction. The e–ln $s^{*}$ curves of LW tests also exhibited two approximately linear segments, which could determine the collapse loss suction (or collapse suction). Before yielding, the slope was independent of the net isotropic stress. After yielding, the slope decreased with the increase in the net isotropic stress.

The shrinking was produced during wetting at a constant net isotropic stress. When the specimen was wetted from a point that located “outside” the LC₀ yield curve, it exhibited elastic deformation initially upon wetting until reaching a loss suction value where the larger irreversible collapse deformation (or plastic deformation) ensued.

The wetting-induced volumetric strain was mainly dependent on the net isotropic stress, and a maximum of that occurred when the wetting took place at a net isotropic stress close to the yield stress. It was also dependent on hydro-mechanical path, which was larger using the double-triaxial equipment technique than the single-triaxial equipment technique at the same suction. The difference decreased with the suction, and the total collapsible deformation at saturation from the two methods yielded similar results.

No uniqueness of the yield curve in a s–p plane was identified from the loading and wetting paths. For the same plastic volumetric strain, the SD yield curve due to wetting was located under the LC yield curve induced by loading. The deviation degree decreased with suction, and the two curves completely coincided at a suction of zero. A coupled outwards movement of the LC and SD yield curves were observed with the increase in the plastic volumetric strain. Interestingly, the uniqueness of the yield curve in a s–p′ plane was identified from loading and wetting paths.

Based on the above test results, an elastoplastic model of the intact loess under isotropic stress condition incorporating water retention behaviour was proposed, using the mean effective stress as constitutive stress. The effects of the suction and the hydro-mechanical path on the deformation behaviour, and the influence of the net isotropic stress on water retention behaviour were considered in the proposed model. The model was able to reproduce the hydraulic and mechanical behaviour of the intact loess along constant suction paths and wetting paths quite well. The model parameters can be determined via laboratory tests.