Shear deformation and strength of the interphase between the soil–rock mixture and the benched bedrock slope surface

Abstract

A series of benched excavations were typically carried out on the bedrock slope surface to improve the stability of the soil–rock mixture (S–RM) fill slope. It is difficult to devise an in situ, large-scale direct shear test for the interphase between the S–RM fill and the benched bedrock slope surface. This study introduced a comprehensive approach to investigate the shear deformation and strength of the interphase. First the soil–rock distribution characteristics were analyzed by test pitting, image analysis, and sieve test. Then the PFC2D random structure models with different rock block size distributions were built, and large-scale numerical shear tests for the interphase were performed after calibrating model parameters through laboratory tests. The stress evolution, damage evolution and failure, deformation localization (based on a principle proposed in this paper), rotation of rock blocks, and shear strength were systematically investigated. It was found that as the rock block proportion and rock block size (rock block proportion of 50 %) increase, the fluctuations of the post-peak shear stress–displacement curves of the interphase become more obvious, and the shear band/localized failure path network becomes wider. Generally, smaller rock blocks are of greater rotation angles in the shear band. The peak shear stress and internal friction angle of the interphase increase, while the cohesion decreases with growth of the rock block proportion. However, all these three parameters increase as the rock block size (rock block proportion of 50 %) increases.

1 Introduction

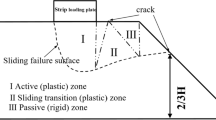
Soil–rock mixtures (S–RMs), such as colluvium, eluvium, and diluvium, are composed of rock blocks and soil, which commonly exist in the earth’s surface [13, 24, 27, 48–50]. Artificially selected S–RM is often utilized as fill in hydropower engineering, road engineering, and foundation engineering applications [49]. The S–RMs with high rock block proportion are typically used to fill slopes in mountainous cities throughout Southwest China, such as in the airport foundation engineering (Fig. 1). The stability of the foundation slope is significantly influenced by the exact characteristics of the S–RM fill, as well as the contact between the fill and the bedrock slope surface where the benched excavation (Fig. 2) is usually carried out to provide more resistance against the fill slope sliding.

Fig. 1

Aerial view of the designed S–RM fill foundation in the expansion project of the Chongqing Jiangbei International Airport (in China) in a mountainous area

Fig. 2

A typical cross section showing the benched excavation scheme of bedrock slope surface for S–RM fill slopes in the expansion project of the Chongqing Jiangbei International Airport, China

To date, numerous investigations have been dedicated to understanding the mechanisms responsible for shear resistance developed within the interphase region between a granular material and a rough solid material surface [12, 15, 19, 42, 43, 45, 46]. Wang et al. [42, 43] described that the interphase consists of the solid surface with its asperities and a variable thickness of granular material directly adjacent to the surface. The interphase approximately corresponds to the intense shear deformation zone (shear band), as shown in Fig. 2. Most previous studies were performed using only small-scale laboratory tests or numerical modeling. However, there are limited applications to the actual, large-scale projects. Considering the negative scale effects of previous experimental and numerical studies, it is essential to study the shear deformation and strength of the interphase between the S–RM fill and the excavated benched bedrock slope surface in the same scale in engineering practice.

Due to the complexity of in situ S–RMs, accurately identifying soil–rock distribution characteristics is a prerequisite for successfully analyzing the stability and deformation of high fill slopes. In the previous studies, Medley [33] estimated the volumetric proportion of rock blocks in an S–RM by measuring the lineal proportion of chord intercepts recovered in a drill core. Xu et al. [50] proposed the digital image processing (DIP) technique to investigate the granulometric characteristics, surface characteristics, directional and shape characteristics of rock blocks in S–RMs. Casagli et al. [5] analyzed the grain size distribution of landslide dams comprised of S–RM in the Northern Apennines using two sampling methods: volumetric sieve analysis and grid by number analysis. Sass and Krautblatter [39] applied the ground-penetrating radar (GPR) to gain insight into the internal sediment structures of 23 alpine scree slopes. More information about the identification of soil–rock distribution in S–RMs was discussed in the literatures reported by Xu et al. [49], Harris and Prick [14], Sass [38], and Coli et al. [10].

Within the past two decades, investigation into the mechanical behavior of S–RMs has increased considerably, in view of the material’s theoretical significance and potential engineering application. Laboratory tests, including triaxial tests [25], consolidation tests [41], and direct shear tests [40], have been conducted to study the influence of the rock block proportion, porosity, and grain size distribution on the deformation and strength of small specimens of S–RMs. To investigate the deformation and failure mechanisms of S–RMs, the organic glass was used as the visually sides of the shear box by Xu et al. [49]. They found that as the rock block proportion increases, the shear zone grows wider. Nevertheless, the S–RM specimens used in above studies were artificial. Consequently, the test results provided little guidelines with regard to the realistic engineering designs. Other researchers have performed in situ, non-conventional shear tests [9, 10, 24, 48] in order to study the shear strength, deformation, and failure mechanisms of natural S–RMs.

Numerical simulations based on the conventional finite element method (FEM) have been widely conducted to investigate the deformation mechanisms of S–RMs, typically in combination with the random structure modeling technique [2, 23, 24, 50, 51]. Recently, the Particle Flow Code (PFC), which is based on the principle of the discrete element method (DEM) and able to model both soil-like and rock-like materials [3, 7, 8, 11, 20, 21, 28, 31, 37], has also been proved to be capable of analyzing complex deformation and failure of binary mediums such as S–RMs [30, 47] and asphalt concrete [6, 29]. PFC regards soil/rock as an assemblage of bonded, rigid circular particles. The mechanical behavior of the particles in this assemblage is described by their movement, which obeys Newton’s second law, and the force and the moment acting at each contact bond between particles obey the force–displacement law [17].

This study introduced a method of numerical shear test on the interphase between the S–RM fill and the benched bedrock slope surface in the scale of actual engineering practice. First, the grain size distribution of the S–RM fill was analyzed by test pitting (in-site measurement, photography, and sampling), image analysis, and sieve test. Random structure models of the S–RM fill, with different rock block size distributions, were then built using PFC^2D. After calibrating model parameters, the numerical modeling with regard to the shear deformation mechanisms of the interphase was investigated from different aspects. And the shear strength parameters were also obtained. The proposed method can not only facilitate the similar designs of S–RM fill slopes, but also enrich the basic theoretical understanding of interphase shear properties.

2 Engineering background

2.1 Description of S–RM fill slope in an airport construction project

The extension project of Jiangbei International Airport examined in this study is located in Chongqing, a mountainous city in China in urgent need of topographic intervention at its airport construction. According to the construction design scheme, the surrounding mountain ridges, which are higher than the designed elevation (403.5 m), must be excavated and filled into the low areas, forming many high fill slopes at the edges of the filled valley (also called “gully zones”) as shown in Fig. 1. The height of the high fill slopes ranges from 50 to 90 m, with the maximum of 130 m. The vertical thickness of the S–RM fill covering the bedrock slope surface varies generally from 20 to 40 m (Fig. 2). The S–RM fill is composed of sandstone, sandy mudstone, mudstone, and soil. The maximum diameter of rock blocks in the S–RM fill is generally smaller than 100 cm. Dynamic compaction with 3000 kN m energy tamping was conducted per 4 m filling thickness as the ground improvement measure. The mudstone mainly breaks into coarse- and fine-grained soil under dynamic compaction. The interphase between the S–RM fill and the bedrock slope surface is the potential sliding surface/band in the fill slope when the bedrock slope angle exceeds a certain value. Therefore, the benched excavation was designed on the bedrock slope surface of which the slope ratio exceeds 1:5, to improve the shear resistance along the bedrock surface (Fig. 2). The bench width was no <200 cm, and the ratio of its height to width was no more than 1:2. The table facet of each bench had a reverse gradient of 2 %.

2.2 Soil/rock threshold of S–RM

It should be noted that the concepts “soil” and “rock” in an S–RM are relative. Here, “soil” refers to material with a finer matrix than rock blocks, such as fine-grained or gravel soil and soil-like weak matrix rocks. There exists a threshold size distinguishing “soil matrix” from “rock blocks.” Grains greater than the threshold size are considered as “rock blocks,” having considerable scale effect on the macro-mechanical behavior of the S–RMs, while grains smaller than the threshold size are defined as “soil matrix,” showing negligible scale effect on the macro-mechanical behavior of the S–RMs [26, 32–34, 47, 49, 50]. Soil matrix and rock block fractions of the S–RMs are judged using the following expression:

$$f = \left\{ \begin{aligned} S \, (d < d_{\text{thr}} ) \hfill \\ R \, (d \ge d_{\text{thr}} ) \hfill \\ \end{aligned} \right.$$

(1)

where S is soil matrix, R is rock blocks, d is grain diameter, and d _thr is the soil/rock threshold of the S–RMs.

Based on the above principle and studies by Xu et al. [49], Medley [32, 33], Lindquist and Goodman [26], and Medley and Lindquist [34], the soil/rock threshold is dependent on the scale of the research object, which can be defined as follows:

$$d_{\rm {thr}} \le 0.05L_{c}$$

(2)

where L _c is the characteristic engineering dimension for S–RMs, such as the height of a landslide, the diameter of a tunnel, the width of a foundation, or the dimension of a laboratory specimen. It changes as scales of interest change on a project.

For the fill slope project in this study, bench width is one of governing factors and has a major influence on the slope stability in the event of sliding along the interphase. The designed minimum bench width of 200 cm is thus the characteristic engineering dimension. Based on Eq. (2), the corresponding soil/rock threshold should not be more than 10 cm. In this study, 6 cm, a typical limit in engineering classification of soil [35], was selected as the soil/rock threshold, leading to more precise simulation results for the following numerical modeling than the use of 10 cm.

2.3 Soil–rock distribution characteristics of S–RM fill

Sieve analysis is a conventional method for obtaining the grain size distribution of soil. However, it is inapplicable to large blocks. In order to study the distribution characteristics of rock blocks in S–RMs, image analysis is commonly utilized [5, 10, 33, 34, 49, 50]. The primary advantages of image analysis are twofold: (1) images can be obtained conveniently by photographic techniques and analyzed in parts using multiple computers, requiring less field work compared to direct measurements from an in situ cross section itself and (2) images can accurately record the original distribution characteristics of rock blocks. More information about rock blocks can be extracted, such as the size, area, geometry, and direction of the long axis, based on these types of images.

In this study, the grain size distribution and directional characteristics of rock blocks (d > 6 cm) were analyzed by image analysis, and the grain size distribution of the soil matrix (d < 6 cm) was analyzed by sieve analysis. The application of this procedure follows three main steps:

• (1) Test pitting. To obtain the cross sections of subsurface S–RMs, five test pits with a length of 11.5 m, width of 3.5 m, and maximum depth of 4.0 m were excavated in different sites (Fig. 3a–b). Locating rods were set every other meter along the upper edges of cross sections, and a measuring tape was hung on each rod (Fig. 3c). Photographs were then taken on the cross sections facing the camera directly, and the soil matrix was sampled.

  Fig. 3

  

  Procedures for obtaining the rock block size distribution and directional characteristics: a, b excavated test pit; c arranging the locating rods and measuring tapes; d taking photographs of the cross section; e recognizing the rock block edges/boundaries and determining the block size, area, and direction of the long axis

• (2) Image analysis. The edges/boundaries of rock blocks (d > 6 cm) were recognized from these photographs using AutoCAD (Fig. 3d–e). Then the 2D block size, area, and direction of the long axis (represented by the inclination angle (α) counterclockwise from the horizontal direction, with a range from 0° to 180°) were determined for each rock block. The total statistical area of cross sections was about 150 m².

• (3) Sieve analysis. Standard sieve analyses were conducted on the soil matrix samples (d < 6 cm). Customary geotechnical sieve series (ASTM standards) were utilized for this task.

Based on the field and laboratory tests, the density of the rock blocks and the grain density of the soil matrix were determined as about 2700 and 2500 kg/m³, respectively. Figure 4a shows the grain size distribution of the S–RM fill. The rock block proportion (weight percentage) is about 65 %. Figure 4b shows the rock block size frequency distribution to the total rock blocks in the S–RMs. The frequency significantly increases from the group of 10–20 cm to that of 20–30 cm and then begins to stabilize. Figure 4c shows the directional frequency distribution of rock blocks, which expresses the frequency of the inclination angle (α) of the rock blocks in each angle range. The frequency histogram shows a “V” shape, as a whole, indicating that during filling with S–RMs, the inclination angles of the rock blocks tend to be in the mechanical stability direction (horizontal) due to gravitational and dynamic compaction.

Fig. 4

Rock block distribution of the S–RM fill: a grain size distribution; b rock block size frequency distribution; c rock block directional frequency distribution

It should be noted that the use of 2D images to estimate 3D geometrical properties of rock blocks inevitably introduces cross-sectional sampling bias. The shape and orientation of the rock blocks relative to the cross-sectional exposure determine whether 2D image analysis either underestimates or overestimates the actual 3D geometrical parameters of the blocks [10]. However, considering the random spatial distribution of the rock blocks, the results of the large-sample 2D image statistics can approximately represent the in situ 3D geometrical characteristics of the blocks to some extent [49]. In the previous study, Xu et al. [50] found that rock block size distribution demonstrates clear statistical self-similarity and 2D fractal dimension is close to that of actual 3D fractal dimension obtained through field sieve tests.

3 Numerical modeling of interphase shear tests

3.1 Model and test setup

3.1.1 Model setup

It is difficult to devise an in situ, large-scale direct shear test for S–RMs due to the obvious scale effect and significant disturbance introduced while preparing the test specimens, particularly the inclined interphase between the S–RM fill and the benched bedrock slope surface (Fig. 2). In this study, PFC^2D was used to model the shear test for the interphase of the high fill slope of Chongqing Jiangbei International Airport. Figure 5 shows the numerical model, in which the bench is 200 cm in width and 100 cm in height with a reverse gradient of 2 % of the table facet (the least favorable of all the design schemes mentioned above). The shear box, composed of smooth rigid walls 1–3, is 300 cm in height and about 1118 cm in length.

Fig. 5

PFC^2D simulation scheme of direct shear test for the interphase

In general, due to the substantial differences in material strength and stiffness between rock blocks and soil matrix, rock blocks do not typically fracture and failure instead occurs primarily at the soil matrix and soil–rock interfaces during shearing [50], particularly for the case in relatively low geostress. According to the observations from the in situ fill of Jiangbei International Airport, in fact few breakages of rock blocks (sandstone) caused by shear deformation were found. In light of this, clump logic [7, 17] was applied to model the rock blocks. A clump is a group of slaved particles which behaves as a rigid body (with a deformable boundary) that cannot be broken apart, regardless of the forces acting upon it. The contacts internal to the clump are skipped during the calculation cycle in order to save the computing time. This study proposed an S–RM modeling approach in which rock blocks, represented by clumps, are randomly created first; then, bonded particles are filled into the spaces to represent the soil matrix.

The random generation process of arbitrary polygonal rock blocks (clumps) is shown in Fig. 6. In PFC, circular particles with specified radii can be randomly generated with no overlaps using the GENERATE command, which can be used as the initial “basic blocks” for generating polygons (Fig. 6a). It effectively averts the complicated and time-consuming judgments of vertex and edge invasions by some other methods [30, 47, 51]. The vertexes of a polygon were connected by walls. Small particles fill into the enclosed region, forming a clump (Fig. 6b). The walls were then removed and a representation of the surface “skin” of particles forming the clump was added (Fig. 6c). The vertex (V _i ) coordinates and area (A) of the random arbitrary polygonal rock block are expressed as follows:

$$\left\{ \begin{aligned} x_{i} = x_{0} + r\cos (\alpha + \sum {\delta_{i} } ) \hfill \\ y_{i} = y_{0} + r\sin (\alpha + \sum {\delta_{i} } ) \hfill \\ \end{aligned} \right.$$

(3)

$$A = \sum\limits_{i = 1}^{n} {\frac{1}{2}r^{2} \sin \delta_{i} }$$

(4)

where (x _i , y _i ) is the coordinate of the ith vertex of the rock block, (x ₀, y ₀) is the center coordinate of the initial basic block, r = d/2, is the radius of the initial basic block, α is the inclination angle of the rock block, δ _i is the ith central angle, and n is the number of vertexes or sides (n = 4, 5, 6, 7, or 8).

Fig. 6

Random generation process of an arbitrary polygonal rock block: a determining the polygon center coordinate and vertexes based on the randomly generated circular basic block; b connecting the vertexes by walls to form the clump filled with some small particles; c removing the walls and adding a representation of the surface “skin” of particles forming the clump

In this study, five different rock block size distributions (represented by RBSDs 1–5) were used (Fig. 7). RBSDs 1–3 are of the same rock block size frequency distribution (Fig. 4b) within size range of 6–100 cm, but different rock block proportions (weight percentages) of 35, 50, and 65 %, respectively. RBSDs 4 and 5 are of the same rock block proportion of 50 %, but different rock block size frequency distributions. RBSD 4 is in size range of 6–40 cm only, while RBSD 5 is in size range of 40–100 cm only. The ratio of the shear box height to the averaged rock block size d ₅₀ is about 7.7 for RBSDs 1–3 (d ₅₀ = 39 cm), 12.0 for RBSD 4 (d ₅₀ = 25 cm), and 4.2 for RBSD 5 (d ₅₀ = 71 cm). The directional frequency distribution of rock blocks in each model is in accordance with the actual distribution shown in Fig. 4c. To avoid over-producing particles (or excessive computing time), a rock block in the size range of 6–10 cm was replaced by single circular particle of the same size. The soil matrix was represented by an assemblage of bonded particles (with shear mechanical properties equivalent to that of the soil matrix) within size range of 3.6–6 cm, without considering the actual grain size distribution characteristics.

Fig. 7

Five different rock block size distributions (RBSDs) used for the interphase direct shear tests

3.1.2 Test setup

As shown in Fig. 5, the shear stress was applied by moving wall 1 and wall 3 at the same velocity. To prevent the S–RMs from spilling in the shear box (composed of walls 1–3) during the shear test, wall 4 was enforced the same velocity as wall 1 in the shear direction, while wall 5 remained fixed. Normal stress was applied and kept constant by instantaneously adjusting the velocity of wall 2, based on the servo mechanism [17]. A constant shear velocity of 0.02 m/s was selected to obtain approximately static loading conditions in PFC. As the thickness of the S–RM fill covering the bedrock slope surface is generally from 20 to 40 m (Fig. 2), normal stresses of 200, 400, and 800 kPa were applied on each model (RBSDs 1–5), respectively. Shear stress (τ) and normal stress (σ _n) can be expressed as follows:

$$\tau = \frac{{F_{\text{wall 1}} - F_{\text{wall 3}} + W\sin \beta }}{l - s}$$

(5)

$$\sigma_{\text{n}} = \frac{{F_{\text{wall 2}} + W\cos \beta }}{l - s}$$

(6)

where F _{wall 1}, F _{wall 2}, and F _{wall 3} are the forces acting on walls 1, 2, and 3, respectively, W is the weight of the tested S–RM fill, l is the length of the shear box, s is the shear displacement, and β is the inclination angle of the benched bedrock slope surface.

3.2 Contact constitutive models and parameter determination

3.2.1 Contact constitutive models

In this study, the constitutive model acting at a particular contact includes three parts: the linear contact stiffness model (defined according to the normal and shear stiffness k _n and k _s of the two contacting particles, where k _n is associated with the particle contact Young’s modulus E _c based on the elastic beam assumption [37]), the slip model (defined according to the friction coefficient μ at the contact, where μ is the smaller friction coefficient of the two contacting particles), and the contact bond model (defined by the normal contact bond strength F _n and shear contact bond strength F _s). Different from the parallel bond model used to model rock-like material with high strength and stiffness [37], the contact bond model is more appropriate for a soil matrix that has a certain extent of cohesion [47].

3.2.2 Parameter determination

Since the micro-parameters of a real material are very difficult to be obtained directly from laboratory tests, and there is as yet no straightforward theoretical solution to transform the macro-parameters into the corresponding micro-parameters, a calibration process making the particle assembly reflect the macro-properties of the real material is essential. Micro-parameters are typically derived through comparing the results of numerical and laboratory tests [7, 8, 21, 30, 37, 47]. If the results of numerical tests do not accurately represent the macro-properties of the material, the micro-parameters are adjusted until satisfactory results are obtained.

In this study, a series of laboratory direct shear tests and corresponding numerical tests were performed to determine the micro-parameters of the contact constitutive models for the soil matrix. Figure 8 shows the test apparatus. The remolded specimen was of the same grain size distribution as the in situ soil matrix (see the curve of d < 6 cm in Fig. 4a), with the density of 2130 kg/m³ and the moisture content of 1.24 %. The dimensions of the specimen were 30 cm in length, 30 cm in width, and 40 cm in height. To eliminate the size effect, quiet a few standards propose the approaches to determine the allowable maximum grain size d _max for direct shear tests in terms of the specimen height H: such as (1/6)H [1], (1/7–1/5)H [18, 22], and (1/8–1/4)H [16]. The d _max of 6 cm (about (1/6.7)H) in this study meets these standards. Actually, the large grain percentage is low as shown in Fig. 4a, and the majority of grains (about 84 %) are smaller than 1/6 of the upper or lower shear box height, i.e., smaller than 3.3 cm. The lower shear box was pushed with a velocity of 0.02 mm/min to realize the shear deformation under constant normal stress (200, 400, or 800 kPa). According to the observations from the laboratory direct shear tests, few breakages of grains were found in shear band due to the existence of fine grains. The grain breakage was not directly modeled in the numerical shear tests, and the soil matrix is represented by an assemblage of bonded rigid particles. Figure 9 shows the shear stress–displacement curves of the soil matrix obtained from both the numerical and laboratory tests. These curves are very similar each other under the same normal stress, indicating that the shear mechanical properties of the soil matrix in the laboratory and numerical tests are consistent. The micro-parameters used for the numerical modeling are listed in Table 1. Detailed description of the corresponding numerical shear test procedure is beyond the scope of this paper and further information can be found elsewhere [8, 47].

Fig. 8

Laboratory direct shear test apparatus for soil matrix

Fig. 9

Shear stress–displacement curves of soil matrix obtained from the numerical and laboratory tests

Table 1 Micro-parameters used for the PFC^2D models

As mentioned above, the clump behaves as a rigid body with a deformable boundary. Therefore, the contacts internal to the clump remain unchanged and are skipped during the calculation cycle. Only the elastic parameters and friction coefficient of particles lying at the boundary of the clump need to be determined. The particle contact Young’s modulus E _c of rock blocks (clumps) was determined as the same value of rock Young’s modulus E, about 13.4 GPa. Other micro-parameters (k _n/k _s, μ) were assumed to be the same as those of the soil matrix, as listed in Table 1. In addition, the bond strength of the contacts with particles external to the clump (i.e., soil–rock interface cementation strength) was assumed to be one-tenth of that of the soil matrix (i.e., F _n = F _s = 0.7 kN). The reliability of the assumed k _n/k _s and μ of rock blocks (clumps) and soil–rock interface cementation strength were discussed in Sect. 4.6.

4 Numerical simulation results and analysis

4.1 Stress evolution

4.1.1 Shear stress–displacement curves

Figure 10 shows the shear stress–displacement curves derived through shear modeling under three different normal stresses. The symbols of M-RBSDs 1–5 represent models are of five different rock block size distributions of RBSDs 1–5, respectively (Fig. 7). The shear stress–displacement curves can be roughly divided into four stages: the rapid stress rise stage (OA), yield stage (continuous reduction in stiffness) (AB), stress drop stage (BC), and residual stress stage (CD), as shown in Fig. 10a. The initial compaction stage observed by Wang et al. [48] in the in situ shear tests of diluvium is not observed during this study, due to the dynamic compaction conducted on the simulated S–RM fill. Curves of M-RBSDs 1–3 with different rock block proportions (35, 50, and 65 %) and same rock block size frequency distribution (rock block size of 6–100 cm), and M-RBSDs 4–5 with different rock block size frequency distributions (rock block size of 6–40 cm for M-RBSD 4 and rock block size of 40–100 cm for M-RBSD 5) but the same rock block proportion (50 %) show the following most notable characteristics:

Fig. 10

Shear stress–displacement curves of M-RBSDs 1–5 under three different normal stresses. Note that M-RBSD 1 is a numerical modeling with the rock block size distribution of RBSD 1 shown in Fig. 7, and M-RBSDs 2–5 are defined based on analogy

• (1) The post-peak shear stress–displacement curves show obvious fluctuations (which are less obvious in pre-peak curves), and with the increases in rock block proportion, rock block size, and normal stress, the fluctuations become more significant due to stronger interactions among the rock blocks in the interphase (shear zone). During the shearing process, in particular the post-peak stage, rock blocks continuously move and rotate. The interactive bitting and disturbing of rock blocks causes the strain energy to accumulate and dissipate, accordingly, which makes the corresponding shear stress increase and decrease, respectively. Greater rock block proportion, rock block size, and normal stress intensify the interactions between rock blocks.

• (2) Generally, for the interphase between S–RM and benched bedrock slope surface, with the increases in rock block proportion and rock block size, the magnitude of the stress drop (∆τ) from peak stress to average residual stress decreases, and the ratio of that to peak stress (∆τ/τ _peak) also declines (Table 2). This is attributed to the enhanced residual shearing resistance of shear band due to increased interactive contacts and biting between rock blocks for the S–RM with greater rock block proportion and rock block size (Fig. 10).

  Table 2 Magnitude of the stress drop (∆τ) from peak stress to the average residual stress, and ratio of that to peak stress (∆τ/τ _peak)

• (3) In general, as rock block proportion, rock block size, and normal stress go up, the shear displacement at peak stress state (s _peak) and increment of shear displacement (∆s) with respect to the stress drop stage (from the peak stress state to the initial state of residual stress) increase (Table 3). There also exists a relatively obvious yield stage near the peak stress as rock block proportion and rock block size increase. Thus, the interphase with greater rock block proportion and rock block size in the S–RM fill presents larger displacement at the pre-peak yield stage and post-peak stress drop stage.

  Table 3 Shear displacement in peak stress state (s _peak) and increment of shear displacement (∆s) associated with the stress drop stage

4.1.2 Contact force distribution

Figure 11 shows the contact force distributions between particles at initial, peak stress, and residual stress states of M-RBSD 3 subjected to 200 kPa normal stress. The black lines represent the compressive forces, while the red lines denote the tensile forces. The thickness of the line is directly proportional to the magnitude of force, and line orientation corresponds to the force direction. Thus, the line segments are thicker and denser in regions where the stress concentration is stronger. At the initial state, the contact force distribution is uniform, without obvious force concentration regions (Fig. 11a). Nevertheless, at the peak stress state, force concentration is quite obvious (Fig. 11b). Contact forces transfer from the shear box to each bench through the rock blocks, resulting in various long and thick force chains. The principal direction of these force chains is controlled by the direction of the resultant force of the shear push force and the normal force acting on the S–RM fill. In peak stress state, shear push force reaches its maximum, and the force chains are strongly inclined toward the shear direction. At this time, the accumulative magnitude of strain energy is largest, which subsequently destroys the interphase. In the residual stress state, under considerable shear displacement of 65 cm, the contact forces between particles are significantly released because the abundant force chains fail (Fig. 11c). Several short and thin force chains remain in the shear zone, maintaining fluctuations of shear stress–displacement curves in the residual stress stage.

Fig. 11

Contact force distributions at a initial state, b peak stress state, and c residual stress state (s = 65 cm) of M-RBSD 3 subjected to the normal stress of 200 kPa

To quantifiably analyze the contact force distribution and evolution, the average contact force tensor R _ij (a second-order density distribution tensor) is calculated from the discrete simulation data [42, 43, 46] as follows:

$$R_{ij} = \frac{1}{2\pi }\int\limits_{0}^{2\pi } {\frac{{\bar{f}_{r} (\theta )}}{{\bar{f}_{r0} }}} m_{i} m_{j} d\theta = \frac{1}{{N_{\text{c}} }}\sum\limits_{k = 1}^{{N_{\text{c}} }} {\frac{{f_{r}^{k} }}{{\bar{f}_{r0} }}} m_{i}^{k} m_{j}^{k}$$

(7)

where $\bar{f}_{r} (\theta )$ is the density distribution function of the average contact force, f ^k _r is the contact force, N _c is the total number of contacts, m = (cos γ, sin γ) is the unit vector in the direction of contact force, and $\bar{f}_{r0}$ is the average contact force over all contacts calculated as follows:

$$\bar{f}_{r0} = \frac{1}{2\pi }\int\limits_{0}^{2\pi } {\bar{f}_{r} (\theta )d\theta } = \frac{1}{{N_{\text{c}} }}\sum\limits_{k = 1}^{{N_{\text{c}} }} {f_{r}^{k} }$$

(8)

$\bar{f}_{r} (\theta )$ can be approximated using the following second-order Fourier series expression:

$$\bar{f}_{r} (\theta ) = \bar{f}_{r0} \left[ {1 + a_{r} \cos 2(\theta - \theta_{r} )} \right]$$

(9)

where a _r is the coefficient of average contact force anisotropies and θ _r is the corresponding principal direction.

Figure 12 shows that a _r rapidly increases in the pre-peak stage and then decreases in the stress drop stage. However, it increases again to a certain extent in the residual stress stage. This observation suggests that the degree of the average contact force anisotropy is greatest in the peak stress state. The principal direction of average contact force anisotropy deviates from a practically vertical direction (basically gravitational direction) to the shear direction in the pre-peak stage, and the maximum angle of deviation is about 33° in the peak stress state. However, the principal direction turns back in the stress drop stage, and comes to the vertical direction in the residual stress stage. These results are consistent with the findings in Fig. 11.

Fig. 12

Average contact force distribution and evolution of M-RBSD 3 subjected to 200 kPa normal stress: a near initial state; b rapid stress rise stage (s = 1 cm); c yield stage (s = 6 cm); d peak stress state (s = 9 cm); e stress drop stage (s = 15 cm); f residual stress stage (s = 65 cm)

4.2 Damage evolution and failure

4.2.1 Damage evolution

In the PFC bond model, if the maximum tensile normal contact force exceeds the normal contact bond strength or the maximum shear contact force exceeds the shear contact bond strength, the bond breaks, and a micro-crack or damage occurs. Figure 13 shows the damage evolution of M-RBSD 1 subjected to 200 kPa normal stress. The black lines represent the tensile micro-cracks, while the red lines denote the shear micro-cracks. Numerous micro-cracks formed and coalesced into macroscopic cracks, as is shown in Fig. 13c–f. According to Fig. 13, the damage evolution process can be detailed as follows.

Fig. 13

Damage evolution of M-RBSD 1 subjected to 200 kPa normal stress: a rapid stress rise stage (s = 1 cm); b yield stage (s = 5 cm); c peak stress state (s = 7 cm); d stress drop stage (s = 15 cm); e residual stress stage (s = 45 cm); f residual stress stage (s = 70 cm)

In the rapid stress rise stage (Fig. 13a, s = 1 cm), due to the substantial differences in material stiffness between rock blocks and soil matrix, micro-cracks first form at the boundaries of some rock blocks (soil–rock interfaces), instead of the soil matrix. These micro-cracks are sporadically distributed and not yet able to cut through the soil–rock interfaces. The deformation behavior of the interphase is almost unaffected at this stage, and the shear stress–displacement curve rises rapidly.

In the yield stage (Fig. 13b, s = 5 cm), many rock blocks, especially in the interphase, are surrounded by micro-cracks where soil–rock interfaces were cut through. Micro-cracks begin to form and partially coalesce in the soil matrix of the interphase, which then gradually develop into a narrow and non-through-going shear band in the peak stress state (Fig. 13c, s = 7 cm). As such, the shear stress–displacement curve becomes relatively flat due to the S–RM stiffness reduction in the interphase, even showing slight fluctuations in the later yield stage near peak stress.

In the stress drop stage (Fig. 13d, s = 15 cm), micro-cracks dramatically develop in the interphase and finally coalesce into a wide and through-going shear band. This phenomenon defines the ultimate failure stage of the interphase.

In the residual stress stage (Fig. 13e, s = 45 cm; Fig. 13f, s = 70 cm), the growth of micro-cracks slows and the development of the shear band comes to be more stable. For shear displacement from 45 to 70 cm (Fig. 13e–f), the shear band almost does not widen.

4.2.2 Failure

Figure 14 shows the failure characteristics of M-RBSDs 1, 3, 4, and 5 under normal stresses of 200 and 800 kPa in 70 cm shear displacement state (an adequately stable state close to the end of numerical computation, with complete interphase failure). To analyze the spatial distribution characteristics of micro-cracks, the domain is discretized into rectangular grids along shear direction (grid spacing is 1 m) and normal direction (grid spacing is 0.2–0.5 m). The ratio of the broken contacts to total contacts (the contacts inside the clumps are skipped) in a grid is defined as the density of micro-cracks. According to the density change along the direction of the arrow as shown in Fig. 14a, the outer contour line (the dotted line in Fig. 14) of shear band can be determined, where the absolute value of the density gradient is maximum. The density significantly decreases outside the line and the soil matrix is almost undamaged.

Fig. 14

Failure characteristics of M-RBSDs 1, 3, 4, and 5 under normal stresses of 200 and 800 kPa in 70 cm shear displacement state

Shear band distribution is significantly influenced by rock block proportion, rock block size, and normal stress. The shear band is wider and its outer contour line undulates widely in M-RBSD 3 (Fig. 14b) than those in M-RBSD 1 (Fig. 14a) under 200 kPa normal stress, due to the higher rock block proportion of M-RBSD 3 than that of M-RBSD 1. Similar patterns of the influences of rock block size can be observed when comparing Fig. 14d with Fig. 14c. When the normal stress is 800 kPa, the shear band is wider and its outer contour line is relatively straight compared to samples under normal stress of 200 kPa. The influences of rock block proportion and rock block size on the outer contour line of the shear band become less significant under the relatively high normal stress condition.

4.3 Deformation localization

4.3.1 A simple principle for identifying localized deformation

The spatial discretization approaches, which first discretize a domain by constructing a nodal graph and then interpolate between adjacent nodes to calculate displacement and strain fields, are generally utilized to identify localized deformation in discrete systems [4, 36, 44, 45]. However, there is as yet no consensus on the optimal approach to calculate strain [36, 45]. For examples, linear, local interpolation approaches produce substantial variations in the strain values in localized zone, and higher-order, non-local interpolation approaches may overly smooth the erratic displacements in localized zone, hindering the clear visualization of the deformation localization as it evolves. In addition, the constructed nodal spacing has a direct control on the precision of the calculated strain values.

In this study, the above spatial discretization approaches were skipped and a simple principle is used for identifying localized deformation. As shown in Fig. 15, the relative displacement of the two contact points of an initial contact can be considered as a contact deformation (micro-deformation), the degree of which can be defined as follows:

$$\xi = \frac{{l_{AB} }}{{r_{m} + r_{n} }} = \frac{{\sqrt {\left( {x_{B} - x_{A} } \right)^{2} + \left( {y_{B} - y_{A} } \right)^{2} } }}{{r_{m} + r_{n} }}$$

(10)

where ξ is the normalized indicator of the contact deformation degree, l _AB is the maximum relative displacement of contact points A and B in the whole computing process, r _m and r _n are the radii of particles m and n, respectively, and (x _A, y _A) and (x _B, y _B) are the current coordinates of points A and B, which can be calculated as follows:

$$\left\{ \begin{aligned} x_{A} = x_{m}^{{\prime }} + r_{m} \cos (\lambda_{m} + \omega_{m} ) = x_{m}^{{\prime }} + r_{m} (\cos \lambda_{m} \cos \omega_{m} - \sin \lambda_{m} \sin \omega_{m} ) \hfill \\ y_{A} = y_{m}^{\prime } + r_{m} \sin (\lambda_{m} + \omega_{m} ) = y_{m}^{{\prime }} + r_{m} (\sin \lambda_{m} \cos \omega_{m} + \cos \lambda_{m} \sin \omega_{m} ) \hfill \\ x_{B} = x_{n}^{{\prime }} + r_{n} \cos (\lambda_{n} + \omega_{n} ) = x_{n}^{{\prime }} + r_{n} (\cos \lambda_{n} \cos \omega_{n} - \sin \lambda_{n} \sin \omega_{n} ) \hfill \\ y_{B} = y_{n}^{{\prime }} + r_{n} \sin (\lambda_{n} + \omega_{n} ) = y_{n}^{{\prime }} + r_{n} (\sin \lambda_{n} \cos \omega_{n} + \cos \lambda_{n} \sin \omega_{n} ) \hfill \\ \end{aligned} \right.$$

(11)

$$\left\{ \begin{aligned} \cos \lambda_{m} = \frac{{x_{n} - x_{m} }}{{\sqrt {\left( {x_{n} - x_{m} } \right)^{2} + \left( {y_{n} - y_{m} } \right)^{2} } }} \hfill \\ \sin \lambda_{m} = \frac{{y_{n} - y_{m} }}{{\sqrt {\left( {x_{n} - x_{m} } \right)^{2} + \left( {y_{n} - y_{m} } \right)^{2} } }} \hfill \\ \cos \lambda_{n} = \frac{{x_{m} - x_{n} }}{{\sqrt {\left( {x_{n} - x_{m} } \right)^{2} + \left( {y_{n} - y_{m} } \right)^{2} } }} \hfill \\ \sin \lambda_{n} = \frac{{y_{m} - y_{n} }}{{\sqrt {\left( {x_{n} - x_{m} } \right)^{2} + \left( {y_{n} - y_{m} } \right)^{2} } }} \hfill \\ \end{aligned} \right.$$

(12)

$$\left\{ \begin{aligned} \omega_{m} = \sum {v_{m,i} \Delta t_{i} } \hfill \\ \omega_{n} = \sum {v_{n,i} \Delta t_{i} } \hfill \\ \end{aligned} \right.$$

(13)

where (x _m , y _m ) and (x _n , y _n ), and (x _m ′, y _m ′) and (x _n ′, y _n ′) are the initial and current center coordinates of particles m and n, respectively, λ _m and λ _n are initial phase angles, ω _m and ω _n are rotation angles (counterclockwise rotation is positive), v _m,i and v _n,i are the angular velocities in ith time step, and ∆t _i is the time of ith time step.

Fig. 15

Schematic diagram of the proposed localization deformation principle

It should be noted that the proposed equations are for calculating the contact deformation (micro-deformation) between two basic cells (spherical particles). The equations are for the boundary particles when calculating the contact deformation between two rock blocks (clumps) or between the soil matrix and rock blocks (clumps). The spatial distribution of many micro-deformations occurring in soil matrix, soil/rock block interfaces, and the contacts between rock blocks reflects the macro-deformation of S–RM.

4.3.2 Visualization of shear band

Based on the principle defined above, the deformation fields of M-RBSDs 1, 3, 4, and 5 under normal stress of 200 kPa in 70 cm shear displacement state are shown in Fig. 16, where the different colors represent the different magnitudes of contact deformation. Figure 17 shows variations in N _ξ /N _tot (where N _ξ is the number of contacts whose deformations are larger than ξ, and N _tot is the total initial contact number) with ξ. All curves have obvious turning points (where curvature is maximum) with respect to ξ = 0.1, as shown in Fig. 17. Therefore, ξ = 0.1 is defined as the threshold value that can be utilized to distinguish the relatively large deformation region (shear band) from the small deformation region (non-shear band) during numerical modeling. Figure 16 clearly shows that the relatively large deformation regions/shear bands (ξ > 0.1) are in accordance with those identified by the micro-crack distribution in Fig. 14a–d. Further, even more localized deformation regions are to be identified, such as the region of ξ > 1.0 shown in Fig. 16.

Fig. 16

Deformation fields of M-RBSDs 1, 3, 4, and 5 under the normal stress of 200 kPa in 70 cm shear displacement state based on the proposed principle

Fig. 17

N _ξ /N _tot versus ξ of M-RBSDs 1, 3, 4, and 5 under the normal stress of 200 kPa in 70 cm shear displacement state

The localized deformation region reflects the major failure paths in the shear band. The failure path circles around one side or both sides of the rock block, as shown in Fig. 18. Similar results were observed in the study by Xu et al. [50] through FEM simulations of direct shear tests on an S–RM. In the first mode (Fig. 18a, b), the failure path deviates from the previous direction, while in the second mode (Fig. 18c, d), the failure zone widens or branches off (forming a failure path network, for example), and thus, multilevel sliding surfaces occur in the shear band. As shown in Fig. 16, as rock block proportion and rock block size increase, the second type of failure path network becomes more obvious.

Fig. 18

Potential failure paths of S–RM: a, b failure path going round through one side of the rock block; c, d failure path going round through both sides of the rock block

4.4 Rotation of rock blocks

To better understand the shear deformation mechanism of the interphase, the instantaneous rotation velocities and cumulative rotation angles of rock blocks of d > 10 cm were measured throughout the entire shearing process. Figure 19 shows the spatial distributions of rock block rotation angles of M-RBSDs 1, 3, 4, and 5 under normal stress of 200 kPa in 70 cm shear displacement state. Comparing counter- and clockwise rotation angles (represented by ω ⁺ and ω ⁻ respectively) for each rock block with average rotation angle $\omega_{\text{ave}}$ of the rock blocks in full size range, it is obvious that rotation angles of the rock blocks in the shear band, as expected, are much greater than those in other regions. It should be noted that all rotation angles were treated as positive/absolute values regardless of clockwise or counterclockwise rotation, in order to perform quantitative comparison. As shown in Fig. 19a, b, most rock blocks rotate clockwise, implying that the main rotation direction is controlled by the shearing direction. However, the percentage of rock blocks with clockwise rotation decreases in the model with higher rock block proportion, i.e., the internal motion becomes disordered and complicated, due to the enhanced interactions between rock blocks by contacting directly or transferring through soil matrix. Comparison between M-RBSDs 4 and 5, as shown in Fig. 19c, d, suggests that the percentage of the rock blocks with clockwise rotation was not significantly affected by the rock block size.

Fig. 19

Spatial distributions of rock block rotation angles of M-RBSD 1, 3, 4, and 5 under the normal stress of 200 kPa in 70 cm shear displacement state. M ⁻ is the number of rock blocks by clockwise rotation, and M is the total number of rock blocks (d > 10 cm)

To analyze the influences of rock block proportion and rock block size on rock block rotation, the average counterclockwise and clockwise rotation angles of the rock blocks in each size range (represented by $\omega_{\text{ave}}^{ + }$ and $\omega_{\text{ave}}^{ - }$, respectively) were calculated. Figure 20 shows the ratios of $\omega_{\text{ave}}^{ + } /\omega_{\text{ave}}$ and $\omega_{\text{ave}}^{ - } /\omega_{\text{ave}}$ of each rock block size range in M-RBSDs 1, 3, 4, and 5 under normal stress of 200 kPa in 70 cm shear displacement state. In general, the ratios of both $\omega_{\text{ave}}^{ + } /\omega_{\text{ave}}$ and $\omega_{\text{ave}}^{ - } /\omega_{\text{ave}}$ decrease as the rock block size increases; in other words, smaller rock blocks have greater rotation angle in a model. The value of $\omega_{\text{ave}}^{ - } /\omega_{\text{ave}}$ (more than 1.0, in particular, when rock block size is <30 cm) is much greater than that of $\omega_{\text{ave}}^{ + } /\omega_{\text{ave}}$ (much <1.0). Figure 20a–b show that the $\omega_{\text{ave}}^{ + } /\omega_{\text{ave}}$ and $\omega_{\text{ave}}^{ - } /\omega_{\text{ave}}$ of M-RBSD 3 are much closer to 1.0 than those of M-RBSD 1, indicating that rotation angle distribution of the models with relatively higher rock block proportions is more uniform. Similar patterns for the impact of rock block size on rotation angle distribution are also observed in Fig. 20c–d.

Fig. 20

Ratios of $\omega_{\text{ave}}^{ + } /\omega_{\text{ave}}$ and $\omega_{\text{ave}}^{ - } /\omega_{\text{ave}}$ of each rock block size range of M-RBSDs 1, 3, 4, and 5 under the normal stress of 200 kPa in 70 cm shear displacement state

4.5 Shear strength

As shown in Fig. 10, the peak shear stress of the interphase increases with growth of rock block proportion and rock block size. To obtain the shear strength parameters of the interphases in M-RBSDs 1–5, linear Coulomb strength envelopes were drawn as shown in Fig. 21. In general, the internal friction angles (φ) vary from 37° to 44° for all five M-RBSDs, and the cohesions (c) are below 40 kPa. The internal friction angle φ increases with increase in rock block proportion (from 35 to 65 % for M-RBSDs 1–3) and rock block size (from size range of 6–40 to 40–100 cm for M-RBSD 4–5). Cohesion c decreases with increase in rock block proportion, while increases as the rock block size increases. It should be noted that the results relevant to rock block size are concluded only based on the contrast of the simulation results from M-RBSDs 4–5 with rock block proportion of 50 %.

Fig. 21

Relationship curves between peak shear stress and normal stress of M-RBSDs 1–5

Xu et al. [49] provided a summary of the relationship between rock block proportion and internal friction angle of S–RMs in a previous study. They suggested that the internal friction angle φ of S–RMs changes only little and approximately equals to that of the soil matrix at rock block proportion below 25 %; when the rock block proportion increases from 25 to 70 %, φ approximately linearly increases with the proportion of rock blocks for compacted S–RMs; and at rock block proportion over 70 %, φ negligibly changes. Direct shear test results in Xu’s study [49] indicated that cohesion c decreases slowly with the increase in rock block proportion from 30 to 70 %, i.e., the reduced quantity of c is very small. The results obtained from the numerical analysis in this study (for dynamic compacted S–RMs) are in accordance with Xu’s summary (for natural depositional S–RMs).

4.6 Discussions of the assumed micro-parameters reliability

As discussed in Sect. 3.2.2, the micro-parameters of the soil matrix were obtained through calibration; however, the soil–rock interface cementation strength F _n(F _s) was assumed to be one-tenth of that of the soil matrix, and the particle stiffness ratio k _n/k _s and friction coefficient μ of rock blocks (clumps) were assumed to be the same as those of the soil matrix—basically, these micro-parameters were obtained without calibration. To confirm the reliability of these micro-parameters adopted, their influences on the shear strength and deformation of the interphase were examined, using M-RBSDs 1 and 3 as examples with rock block proportion of 35 and 65 %, respectively.

As listed in Table 4, three different soil–rock interface cementation strengths were analyzed. The soil–rock interface cementation strength marginally affects the peak shear stress and internal friction angle of the interphase, though it impacts the cohesion significantly. From cementation strength of zero (where interfaces were uncemented, i.e., F _n = F _s = 0) up to the same cementation strength of the soil matrix (where interfaces were adequately cemented, i.e., F _n = F _s = 7 kN), cohesion increases by 6.12 % for M-RBSD 1 and 16.46 % for M-RBSD 3. Though this increment is relatively large, the maximum cohesion is only 41.6 kPa for M-RBSD 1 and 36.8 kPa for M-RBSD 3. Thus, cohesion can be ignored during engineering design where the internal friction angle contributes most to the shear strength. Comparison between Fig. 22a (Fig. 22e) and Fig. 22b (Fig. 22f) shows that the soil–rock interface cementation strength (F _n = F _s = 0.7 and 7 kN are considered here) has only marginal influence on shear band width. For the reasons above, the assumed soil–rock interface cementation strength in the previous sections, one-tenth of that of the soil matrix (i.e., F _n = F _s = 0.7 kN), is reasonable.

Table 4 Influences of soil–rock interface cementation strength on the shear strength of the interphase for M-RBSDs 1 and 3

Fig. 22

Deformation fields of M-RBSDs 1 (a–d) and 3 (e–h) with different micro-parameters of soil–rock interface, under the normal stress of 200 kPa in 70 cm shear displacement state

The internal friction angle of rock is greater than that of soil, and it is positively related to the particle friction coefficient in PFC. Therefore, the adopted particle friction coefficient μ of rock is no less than that of soil (μ = 0.7 in this study) during PFC simulation [27, 30, 47]. In addition, μ is the smaller friction coefficient of the two contacting particles. For these reasons, the particle friction coefficient of rock blocks (clumps) was assumed to be the same as that of the soil matrix. As listed in Table 5, for μ = 0.5 and 0.7, the increase in internal friction angle is 1.37 % for M-RBSD 1 and 3.06 % for M-RBSD 3, and the increase in cohesion is 8.29 % for M-RBSD 1 and 20.45 % for M-RBSD 3. For μ = 0.7 and 1.2, despite the increased peak shear stress, internal friction angle increases only by 0.54 % for M-RBSD 1 and 2.51 % for M-RBSD 3, and cohesion increases only by 3.83 % for M-RBSD 1 and 5.35 % for M-RBSD 3. And the shear band width changes little for μ = 0.7 and 1.2, comparing Fig. 22a (Fig. 22e) with Fig. 22c (Fig. 22g). The assumed particle friction coefficient (μ = 0.7) of rock blocks (clumps) in the previous sections is thus reasonable.

Table 5 Influences of particle friction coefficient of rock blocks (clumps) on the shear strength of the interphase for M-RBSDs 1 and 3

Three particle stiffness ratios (k _n/k _s = 1.0, 2.5, and 5.0) of rock blocks (clumps) were also considered. Table 6 shows that the particle stiffness ratio marginally affects the peak shear stress, internal friction angle, and cohesion. And it as well marginally affects the shear band width, as shown in Fig. 22a (Fig. 22e) and Fig. 22d (Fig. 22h) for k _n/k _s = 2.5 and 5.0, respectively. Consequently, the assumed particle stiffness ratio (k _n/k _s = 2.5) of rock blocks (clumps) in the previous sections is also reasonable.

Table 6 Influences of particle stiffness ratio k _n/k _s of rock blocks (clumps) on the shear strength of the interphase for M-RBSDs 1 and 3

5 Conclusions

This paper provides an effective, comprehensive approach based on the soil–rock distribution characteristics analysis and the large-scale PFC2D numerical modeling toward studying the shear deformation and strength of the interphase between the S–RM fill and the benched bedrock slope surface, since the devising of in situ, large-scale direct shear tests is difficult. The following conclusions can be drawn from the numerical shear tests:

• 1. Post-peak shear stress–displacement curves of the interphase show obvious fluctuations. As rock block proportion and rock block size increase, fluctuations become more significant. The degree of average contact force anisotropy is greatest in the peak stress state.

• 2. Firstly the micro-cracks form at the boundaries of some rock blocks (soil–rock interfaces) due to the substantial differences in material stiffness between rock blocks and soil matrix. Later they begin to develop and partially coalesce in the soil matrix of the interphase in the pre-peak yield stage and finally coalesce into the through-going shear band in the post-peak stage. The shear band becomes wider as the both rock block proportion and rock block size increase.

• 3. A simple principle for identifying localized deformation was proposed. Based on it, the shear band as well as the localized failure paths can be identified. The failure path network in the shear band is considerably affected by rock block proportion and rock block size.

• 4. The rotation angles of the rock blocks in the shear band are much greater than those in other regions. Generally, smaller rock blocks are of greater rotation angles in the shear band. The percentage of rock blocks that move clockwise or counterclockwise is affected significantly by rock block proportion, while slightly by rock block size.

• 5. The peak shear stress and internal friction angle of the interphase go up with increase in rock block proportion and rock block size. The cohesion decreases with increase in rock block proportion, while increases as the rock block size increases.

It should be noted that the rock block size is maintained the same (6–100 cm) while study the effect of rock block proportion, or the rock block proportion is maintained the same (50 %) while study the effect of rock block size. According to the above conclusions, the effect of rock block proportion and rock block size may be counteracted or enhanced in a certain extent if these two factors change simultaneously. For example, the fluctuations of shear stress–displacement curve, the width of shear band, and the internal friction angle of the interphase may change little or do not change if the rock block proportion increases while the rock block size decreases. In addition, the conclusions relevant to rock block size may not be always correct for other rock block proportion, particularly for rock block proportion of smaller than 50 %. The future work will aim at the issue in detail.

In this study, the geometric dimensions of benches were selected as the least favorable among all available design schemes. The impact of design scheme on shear deformation and strength will be discussed in subsequent research. Generally, direct shear tests can be regarded as plane strain tests due to the two-sided displacement constraints by the rigid shear box, i.e., the horizontal deformation perpendicular to the shear direction is limited; thus, only 2D numerical modeling was performed. This study will be extended to consider the 3D effects.