Coordination in the El Farol Bar problem: The role of social preferences and social networks

Abstract

In this paper, we continue the pursuit of the self-coordination mechanism as studied in the El Farol Bar problem. However, in addition to efficiency (the optimal use of the public facility), we are also interested in the distribution of the public resources among all agents. Hence, we consider variants of the El Farol Bar problem, to be distinguished from many early studies in which efficiency is the only concern. We ask whether self-coordinating solutions can exist in some variants of the El Farol Bar problem so that public resources can be optimally used with neither idle capacity nor congestion being incurred and, in the meantime, the resources can be well distributed among all agents. We consider this ideal situation an El Farol version of a “good society”. This paper shows the existence of a positive answer to this inquiry, but the variants involve two elements, which were largely left out in the conventional literature on the El Farol Bar problem. They are social networks and social preferences. We first show, through cellular automata, that social networks can contribute to the emergence of a “good society”. We then show that the addition of some inequity-averse agents can even guarantee the emergence of the “good society”.

1 Introduction

The El Farol Bar problem, introduced by Arthur (1994), has over the years become the prototypical model of a system in which agents, competing for scarce resources, inductively adapt their belief models (or hypotheses) to the aggregate environment they jointly create. The bar’s capacity is basically a resource subject to congestion, making the El Farol Bar problem a stylized version of the central problem in public economics represented by the efficient exploitation of common-pool resources. Real-world examples of this problem include traffic congestion and the congestion of computer networks. On the one hand, we hope that the resources can be utilized without too much idle capacity left; on the other hand, we do not want them to be overused which leads to congestion. When, for some reasons, solving this problem by means of central intervention is either infeasible or undesirable, then it has to be solved in a bottom-up manner as the El Farol problem describes.

1.1 El Farol Bar problem: from efficiency to equity

In the literature, most of the studies addressed this problem from the perspective of learning; hence, the answers depend on how agents learn. Briefly put, there are two kinds of learning mechanism being studied in the literature. The first one is best-response learning (Arthur 1994; Edmonds 1999; Fogel et al. 1999; Challet et al. 2004; Atilgan et al. 2008) and the second one is reinforcement learning (Bell and Sethares 1999; Franke 2003; Zambrano 2004; Whitehead 2008).¹ The typical results are as follows. The best-response learning model tends to have fluctuations, sometimes quite severe, around the threshold (switching between the idle and congestion states), but the steady state where the aggregate bar’s attendance is always equal to the bar’s maximum capacity is very hard to reach. The reinforcement learning model, however, shows that perfect coordination is possible and that it is, indeed, the long-run behavior to which the system asymptotically converges (Whitehead 2008). However, it is an equilibrium characterized by complete segregation (a bimodal distribution of participation): the population split into a group of agents who always go or frequently go (filling the bar up to its capacity at all times) and another group of agents who seldom go or never go.

This latter result has led to a new problem which has rarely been addressed in the literature, namely, the inequity issue. The group of people who have been discouraged by previous unsuccessful attempts and decide to quit obviously share very little or none of the public resources, which may further make them the disadvantaged class in the society. In fact, if we consider attending a bar as a social-engagement opportunity to gain more information and social connections, then the quitting can imply social exclusion or isolation. Therefore, the El Farol Bar problem is not narrowly just an economic distribution problem, it may become a social segregation problem characterized by a group of people who fully occupy the available public resource and a group of people who are discouraged, ignored and completely marginalized.²

In this paper, we continue the pursuit of the self-coordination mechanism of the El Farol Bar problem. However, in addition to the efficiency concern (the optimal use of the public facility), we are also interested in the distribution of the public resources among citizens. Hence, we study two variants of the El Farol Bar problem, which are distinguished from many earlier studies that are only concerned with efficiency. We ask whether self-coordinating solutions can exist in these variants of the El Farol Bar problem so that the public resources can be optimally used with neither idle capacity nor congestion being incurred and, in the meantime, the resources can be well distributed among all agents. We may call this ideal situation with both efficiency and equity the El Farol version of a “good society”.³

1.2 Social networks and social preferences

Through agent-based simulation, we shall show in this paper that the answer is surprisingly yes,⁴ but the likelihood of the emergence of a good society, in addition to learning, also depends on two other elements which have not yet been incorporated in the El Farol Bar literature. These two additional elements are social networks and social preferences. Before we move further, let us first make one remark on these two elements. It should come to us as no surprise that these two elements can be significant in agent-based modeling. In fact, more and more agent-based models have taken these two elements explicitly into account, realizing their importance in emergent dynamics. The former one, social networks, is obvious because agent-based modeling relies heavily on interactions, and social network topologies are what underpin these interactions.⁵ The latter one, social preference, is less obvious but can be well expected when agent-based modeling is extended to the areas involving various pro-social behaviors, which have been examined under intensive interdisciplinary studies across evolutionary biology, the humanities and the social sciences (Chen 2008; Xianyu 2010).

Nevertheless, recognizing their potential significance does not automatically imply that we can predict what will happen. In the vein of the “new kind of science” or computational irreducibility (Wolfram 2002), we can probably only learn the rest from computer simulation, and it is this part where surprise may show up. In this paper, it is the combined force of social networks and social preferences which can solve the even harder efficiency-and-equity El Farol problem that surprises us.

1.2.1 Social networks

In this paper, we sequentially introduce two variants of the original El Farol Bar model, both of which represent a step towards the development of a ‘socially oriented’ version of the El Farol Bar problem. Through a series of simulations, we assess the effect of these socially-grounded assumptions on the macro-dynamics of the El Farol Bar problem and on the kind of equilibria that the system eventually reaches.

The first of these variants concerns the structure of the agents’ interaction and is represented by the introduction of a social network connecting the agents and through which the agents can access the information regarding their neighbors’ choices and strategies. Therefore, in addition to the bar’s aggregate attendance, in this variant, agents can also obtain access to local information. While in the original setup the agents base their decisions on global information, represented by the bar’s aggregate attendance, a feature that is likely to cause herding behavior, making it very difficult for them to coordinate their activities, we may wonder whether coordination will be improved if, instead, the agents base their decisions on only local information, represented by the attendance of their closest neighbors.⁶ As we shall see later, this alteration motivates the simulations of bar attendance dynamics through cellular automata.

It is found that the introduction of social networks coupled with neighbor-based decision rules, in a form of cellular automata, allows the system to always reach an equilibrium characterized by perfect coordination, that is, a state where the bar’s attendance is always equal to the bar’s capacity, but there is a great diversity of these equilibria. The one of most interest to us, the “good society” (all the agents going to the bar with equal accessibility), is one of them. The one normally found with reinforcement learning (a group of agents always going and another group always staying at home) is also one of them. These two, however, are not exhaustive; as we shall see, there are many others, which, to the best of our knowledge, have never been found in the literature before. The effect of social networks can then be concisely represented by the resultant empirical distribution over these equilibria.

1.2.2 Social preferences

After having assessed the effect of this first variant, we introduce a second variant concerning the agents’ preferences for fairness. In the original version of the El Farol Bar problem the agents did not care about their attendance frequency (that is, how often they were going to the bar). The only thing that mattered to them was to make the right choice, even if it implied staying all the time at home. In this paper we assume, instead, that some or all agents are characterized by a preference for fairness or inequity aversion. With this fairness or inequity-averse preference, agents expect a fair share or a minimum attendance frequency and take it as one of their satisfying criteria. If their decision rule does not lead to this fair share, they will react upon it and search for changes.

The inequity-averse preference is one of the essential ideas in the recent literature on the study of pro-social behavior. The agent with the inequity-averse preference does not only care about his own payoff, but also cares about the distribution of payoffs among agents. This idea originated from the attempt to have a coherent framework which can explain the co-existence of selfish behavior in some games but other-regarding behavior in some other games, as repeatedly demonstrated in human-subject experiments.

Our answer to this question is affirmative if one is willing to assume that, in addition to purely self-interested people, there are a fraction of people who are also motivated by fairness consideration$\ldots$ We show that in the presence of some inequity-averse people “fair” and “cooperative” as well as “competitive” and “noncooperative” behavioral patterns can be explained in a coherent framework. (Fehr and Schmidt (1999), pp. 818–819.)

The economic model of the inequity-averse preference was initiated by Bolton (1991), and was refined and established by Fehr and Schmidt (1999) and Bolton and Qckenfels (2000).⁷ There is still a heated discussion on the reconciliation between inequity preference and the conventional rational choice theory, but that is beyond the scope of the paper.⁸ In this paper, we simply take this preference either as exogenously given or as endogenously evolving. For the former case, the inequity-averse agents are characterized by a parameter, called the minimum attendance threshold; for the latter case, the awareness of inequity is endogenously formed through interactions with neighbors in the familiar ‘keeping-up-with-the-Joneses’ manner, i.e., the agents’ minimum attendance threshold is represented by the average of their neighbors’ attendance frequencies.

The incorporation of social preference significantly increases the likelihood of the emergence of the “good society” to the extent that its appearance is always the most likely outcome. The likelihood increases with the size (number) of inequity-averse agents and the degree of their inequity-aversion. However, the emergence of the “good society” does not require all agents to be sensitive to inequity. Our simulation shows that for even a minority of them, up to 20 or 25 %, having this kind of awareness, the emergence of the good society is already guaranteed.

The remainder of the present paper is organized as follows. In Sect. 2, we will present a brief review of the literature on the El Farol Bar problem. Section 3 describes our locally-interacted El Farol Bar model, a model with two-dimensional cellular automata, and the resultant adaptive behavior of agents. Section 4 presents the simulation results with respect to different settings of social networks and social preferences. Section 5 provides a simple analysis and a detailed look at the formation of the perfect coordination in light of our simulation results. Section 6 then concludes the paper with remarks on its current limitations, implications and future work.

2 Literature review

In this section, after introducing the original versions of the El Farol Bar problem and of the closely related minority game (Sect. 2.1), we will consider some of the papers that have extended these two seminal models in various directions. In particular, we will focus on introducing different learning models to the El Farol Bar problem (Sect. 2.2) and local interaction (Sect. 2.3) in the Minority Game.⁹ In the first case, our aim is to provide a review of the macro-dynamics emerging from the models introduced so far, in order to have a background against which to compare the results obtained with the model we introduce in this paper. On the other hand, the papers that consider local interaction in the Minority Game show how the introduction of novel interaction structures has received considerable attention in previous works and, at the same time, allow us to see the crucial importance of the interaction structure to the macro-dynamics generated by these kinds of models.

2.1 The seminal models

In the original El Farol Bar problem (Arthur 1994), $N$ people decide independently, without collusion or prior communication, whether to go to a bar. Going is enjoyable only if the bar is not crowded, otherwise the agents would prefer to stay home. The bar is crowded if more than $B$ people show up, whereas it is not crowded, and thus enjoyable, if attendees are $B$ or fewer. If we denote the agent’s decision “to go” by “1” and “not to go” by “0”, and the actual number of attendees by $n\,(n \le N)$, then the agent’s payoff function has the general form (1).

$$\begin{aligned} U(x,n)=\left\{ \begin{array}{ll} u_{1}, &{} \quad \text{ if }\quad x=0\quad \hbox {and}\quad n \ge B,\\ u_{2}, &{} \quad \text{ if }\quad x=0\quad \hbox {and}\quad n < B,\\ u_{3}, &{} \quad \text{ if }\quad x=1\quad \hbox {and}\quad n > B, \\ u_{4}, &{} \quad \text{ if }\quad x=1\quad \hbox {and}\quad n \le B. \\ \end{array}\right. \end{aligned}$$

(1)

The payoffs have either the order $u_{4} = u_{1} > u_{2} = u_{3}$ or the order $u_{4} > u_{1} = u_{2} > u_{3}$.¹⁰

Arthur assumes that all the agents know the attendance figures in the past $m$ periods and each of them has a set of $k$ predictors or hypotheses, in the form of functions that map the past $m$ periods’ attendance figures into next week’s attendance. After each period, the predictors’ performance indexes are updated according to the accuracy with which the various predictors forecasted the bar’s attendance. Then, the agent selects the most accurate predictor and uses the relative forecast to decide whether to go to the bar or to stay at home the next period. Although the competitive process among predictors never comes to rest, it still produces a remarkable statistical regularity: at the macro level, the number of attendees fluctuates around the threshold level $B$ , while, at the micro level, each agent goes $B/N$ percent of the times, in the long run.

Challet and Zhang (1997) proposed an alternative version of the El Farol Bar problem, known as the minority game (MG). The minority game has a very similar structure to the El Farol Bar problem. There is a binary choice: “go” (1) or “not go” $(-1)$. The three key parameters, namely, the number of agents $(N)$, the memory size $(m)$ and the size of the strategy pool $(k)$, are carried on. The maintenance of performance scores of the strategies in the agent’s pool and the use of them is also carried out in a similar manner. The basic finding is that the attendance frequency or the size of the winners fluctuate around the threshold, in this case, $50\%$. Further studies have shown that the degree of the fluctuation, widely used as a measure of efficiency, can further depend on the three parameters collectively.

Despite their similarity, the El Farol Bar problem and the minority game differ on one fundamental point. The minority games always assign the winners to the less crowded side (those who make a less popular choice) and the losers to the more crowded side. Hence, there is always a majority side that makes the wrong choice, while, in the El Farol Bar problem, there is the possibility of hitting exactly the target $B$, a situation where all the agents, no matter what they decided, made the right choice.¹¹

Compared to the reception of the El Farol Bar problem in economics, the minority game is much better received in econophysics (Challet et al. 2005; Coolen 2005). It has been further extended into a model of financial markets (Challet et al. 2005); in particular, when the financial market is considered from its gambling feature, some can be winners only conditional on others being losers. However, as stated in the introductory section, the kind of problem that concerns us is coordination, and good coordination can lead to a win-win situation. Therefore, we keep this feature of the payoff structure of the original El Farol problem in our model (see Sect. 3.2 for the details). Nonetheless, given the similarity between the two, some studies on the minority game can certainly shed light on the study of the El Farol Bar problem. As we shall see in Sect. 2.3, the inclusion of social networks and the use of cellular automata is actually borrowed from what we learn from the minority game.

2.2 Learning in the El Farol Bar problem

Among the studies introducing novel learning mechanisms in the El Farol Bar problem, we can distinguish two lines of development: those that retain the best-response behavior of Arthur’s El Farol Bar problem and those introducing reinforcement learning mechanisms. While one essential difference between the two is that the latter attempts to reduce the agents’ cognitive loading of the former, there is an addition concern to distinguish the two, which is pertinent to the information requirement and hence to payoff inequalities (Eq. 1).

Two different payoff inequalities have been, implicitly or explicitly, considered in the literature. Based on Eq. (1), these two are (a) $u_{4} = u_{1} > u_{2} = u_{3}$ and (b) $u_{4} > u_{1} = u_{2} > u_{3}$. The choice of the payoff structure (a) implies that that the agents who did not go to the bar can still ascertain whether the bar was crowded or not, since it clearly distinguishes the payoff to the right decisions (forecasts) ($u_{4}$ and $u_{1}$) from that to the wrong decisions (forecasts) ($u_{2}$ and $u_{3}$). This is the typical setting of works adopting the best-response behavioral model. The payoff, in these models, is represented by the amount by which the strategies’ fitness is increased (decreased) after a right (wrong) forecast. To be precise, in some of these models (as the one proposed by Arthur) the strategy fitness is updated by an amount that is inversely proportional to the difference between the strategy’s forecast and the actual aggregate attendance. On the other hand, the choice of the payoff structure (b) implies that those agents staying at home have no possibility of ascertaining whether the bar was too crowded or not, and the payoff as a result of staying at home is independent of the bar attendance $(u_{1} = u_{2})$. This is the typical payoff setting of works adopting reinforcement learning.

In the first line of development, Edmonds (1999) proposes an extension of the El Farol Bar problem where agents can change their strategies set by means of genetic programming and are given the chance to communicate with other agents before making their decision as to whether to go to the El Farol Bar. Simulations show that, as in the original model, the attendance at the bar fluctuates around the threshold level, and does not seem to settle down into any regular pattern. Another work where the agents’ strategies are allowed to co-evolve is that of Fogel et al. (1999). In the model they propose, the agents are endowed with 10 predictors that take the form of autoregressive models with the number of lag terms and the relative coefficients being the variables that evolve over time using evolutionary programming. Their simulations show that the system demonstrates a similar pattern to the original model (Arthur 1994), except with a larger fluctuation. Other more technical aspects of managing a pool of strategies have been studied by Atilgan et al. (2008). Specifically, the differential effects of a kind of slow learning (sticky learning) and a fast learning upon the convergence to the threshold have been found.

Partially due to its computational demands, the other line of this research has abandoned best-response behavior to adopt the more basic reinforcement learning framework. One of the first works where the best-response behavior of Arthur’s original model has been replaced by reinforcement learning is that of Bell and Sethares (1999). In this paper, the authors present an agent-based model where the agents’ strategies are represented by an integer $c$ determining the agents’ attendance frequency: if $c = 2$ the agent goes to the bar once every 2 periods; if $c = 3$ he goes once every 3 periods, and so on. Every time an agent goes to the bar and has a good time (because the bar was not too crowded), he decreases $c$ and goes more often, whereas, in the opposite case, he increases $c$ and goes less often. No change in the attendance frequency takes place if the agent stays at home, as it is assumed that he cannot assess whether he made the right choice or not.

Subsequently, Franke (2003) proposed a reinforcement learning model in which each agent goes to the bar with a probability $p$. If the bar is not crowded he increases $p$, while if the bar turns out to be too crowded, he decreases $p$. If the agent stays at home, a parameter $u$ determines the extent to which the attendance probability is updated according to the bar’s aggregate attendance.

In both Bell and Sethares (1999) and Franke (2003), simulations show that the populations tend to be split in two groups: a group of frequent bar-goers and a group of agents who very seldom go to the bar. This result has been analytically obtained by Whitehead (2008). By applying the Erev and Roth (1998) model of reinforcement learning to the El Farol Bar framework, he shows that the long-run behavior converges asymptotically to the set of pure strategy Nash equilibria of the El Farol stage game.

To sum up, in the best-response models, the aggregate attendance fluctuates around an average value that falls between $B/N$ and a lower bound represented by the mixed strategy that maximizes the aggregate payoff. The point within this range where the average aggregate attendance falls depends on the values assigned to the many parameters characterizing the best-response behavior and induction process. On the other hand, in the reinforcement learning model, two classes of agents emerge: those who often go and those who seldom go. The learning process will asymptotically lead to a state of perfect coordination with complete segregation, where a fraction $B/N$ of the population will always go and the fraction $1-B/N$ will always stay at home.

2.3 Local interaction in the minority game

While the literature on the El Farol Bar problem focused on the effect of the introduction of various learning mechanisms by retaining the interaction structure of the original model, within the literature on the minority game some works have analyzed the effect of different interaction structures, and in particular local interaction, on the system’s macro-dynamics.

The literature on the MG with explicit local interactions or social networks can be divided in two strands characterized by two alternative ways in which the agents make use of local information.¹² In the models of the first strand (Kalinowski et al. 2000; Paczuski et al. 2000; Galstyan and Lerman 2002; Chau et al. 2004; Caridi and Ceva 2004), the agents make their decision on the basis of the best strategy in the set of strategies with which they are endowed, as in the standard MG setup. However, differently from the latter, the input is not represented by the past aggregate outcomes but by the action taken by the agents’ neighbors in the past period. In other words, the variable $m$, which in the traditional MG represents the number of the past global outcomes, in these models represents the number of agents each agent looks at in order to make a decision (i.e., the network degree). The general result of this setup is that the system can reach levels of coordination higher than the coordination obtained in the standard MG.

In the models characterizing the second strand (Slanina 2000; Anghel et al. 2004; Lo et al. 2004; Lavicka and Slanina 2007; Shang and Wang 2007) each agent can decide whether to follow his own strategies, as in the standard MG setup, or imitate the action of one of his neighbors. Of course he will decide to imitate if the performance of the best performing agent among his neighbors is better than his own performance. Also in this case, these works show that through imitation it is possible to reduce the system’s variance to a level lower than the lowest variance reachable with the standard MG and that the best coordination is reached with networks characterized by small degrees (usually, in the order of 2).

In the model we present in this paper, we develop a behavioral model which integrates these two approaches: in our model, the agents’ strategies are represented by lookup tables defining the agents’ actions for every combination of their neighbors’ past choices (like the works in the first strand), but these strategies change over time as the strategies of the best performing agents are imitated (with mutation) by the other agents in the population (like the works in the second strand). As we shall see in the subsequent sections, this way of introducing social networks and local interaction to the model turns out to have an equally, if not more, dramatic effect in the case of the El Farol Bar problem. Not only does the efficiency (coordination) reached by the system depend on the interaction structure, but local interaction leads to new phenomena such as the emergence of attractors of various lengths and the emergence of different clusters of agents.

3 The model

3.1 Model sketch

The review above has pretty much motivated the model to be presented in this section. Let us first give a quick sketch of it. Briefly, in this model, we shall introduce the spatial structure or social networks from the literature on minority games, as reviewed in Sect. 2.3, to the El Farol Bar problem. As already mentioned in the introductory section, this is our first step to explore the effect of social network topologies on the coordination problem. Hence, we do not consider just one social network, but two as a minimum for comparison purposes. Again, as a starting point, we do not complicate the situation with those state-of-the-art networks, but the standard regular network (circular network) and von Neumann networks.

This choice brings us closer to the beginning of agent-based modeling, namely, cellular automata, which are rather locally-based. In our applications, that means agents acquire information and learn, mainly, from their neighbors. This locally-based social learning, like general social learning, significantly reduces the cognitive loading of each individual for maintaining a pool of strategies as assumed by most best-response models reviewed in Sect. 2.2. In fact, in our setting, the pool of strategies is widely shared and maintained by the entire society of agents, and each agent only holds one for his own sake at each point in time.

With this reduction in cognitive loading, we do not further consider individual-style reinforcement learning since our setting already facilitates social learning. We, however, do allow for the individual’s learning but in the usual discovery manner through mutation. The rest of his learning is then through imitation from neighbors. Hence, it is a simple imitation-plus-mutation model for learning. While the agents’ motive for imitating and mutating is driven, as usual, by the fitness of their held strategies, we shall later on further differentiate this motive by their preference for equity, and then complete our agent-based El Farol Bar model with both social networks and social preferences.

3.2 The model

3.2.1 Utility and information

As reviewed in Sects. 2.1 and 2.2, early models which characterize the El Farol Bar problem as a prediction game implicitly assume the inequality $u_{4}=u_{1}>u_{2}=u_{3}$ for Eq. (1). However, in our case the El Farol Bar game is not just a prediction game, but more a congestion game or a coordination game, as it has been motivated in Sect. 1. In fact, in his original version of the ELB game, Arthur (1994) states the following:

The problem was inspired by the bar El Farol in Santa Fe which offers Irish music on Thursday nights; but the reader may recognize it as applying to noontime lunch-room crowding, and to other commons or coordination problems with limits to desired coordination. (Ibid, p. 408; Italics added)

In this aspect of the game, even though the agents’ prediction still matters, that does not mean that they have no demand for food, sociality, the Internet, and easy transportation. In all these situations, the agent wants to avoid congestion, but at the same time he prefers to ‘go to the bar’ instead of ‘staying at home’. Therefore, an appropriate payoff inequality for Equality (1) to reflect this feature of the game is $u_{4} > u_{1} > u_{2} = u_{3},$ which is the one applied in this paper.¹³

Furthermore, we modify the standard settings by adopting the informational structure introduced by the works on the MG with local interaction; more specifically, we study a game in which agents know what their neighbors did on earlier days and make their current decisions based on this information. As in the original El Farol Bar problem, we consider a population composed of $N=100$ agents and set the attendance threshold $B/N=0.6$. Each agent, in addition to the bar’s aggregate attendance (global information), can ‘see’ the actions, the strategies and the strategic performances of their neighbors (local information), which are determined by the given social network.

Fig. 1

Circular (a) and von Neumann (b) neighborhoods

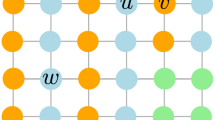
In this paper, we investigate two network typologies as shown in Fig. 1: the circular network (circular neighborhood), where each agent is connected to the two agents to his left and the two agents to his right, and the von Neumann network (von Neumann neighborhood), with the agents occupying a cell in a bi-dimensional grid covering the surface of a torus. Hence, in each of the two networks, the agent is connected to four neighbors, denoted by $N1$, $N2$, $N3$ and $N4$.

The reason why we start with the circular network and the von Neumann network rather than the typical social networks is because these chosen networks have a topology that is very similar to those of the elementary cellular automata studied by Wolfram (Wolfram 2002; Zenil 2013). It therefore endows us with a basic theoretical underpinning which may make it easier to recast the classical El Farol Bar problem into a familiar environment of cellular automata, as a step toward more complex situations.¹⁴

3.2.2 Strategy representation

Contrary to the prototypical El Farol Bar problem and MG settings, each agent is assigned, at the beginning of the simulation, only one strategy $z$, randomly chosen from the whole strategy space. Our representation of the strategy is based on the binary string as normally used in cellular automata. The idea is that each agent will first look at what his four neighbors did in the previous period and only then decide what he will do in the current period, i.e., a mapping from the neighbors’ previous decisions to his current decision. Denote the action “going to the bar” by 1 and “staying at home” by 0. Then there are $2^{4}$ possible states, each corresponding to one combination of the decision “1” or “0” made by the four neighbors. Each strategy is composed of 16 rules specifying the action $D$ the agent has to take in the current period, one rule for each state, as is shown in Fig. 2. Each strategy can then be represented by a 16-bit long string. If we fix the numbering order of the 16 states as indicated in Fig. 2, then the corresponding 16-bit representation for the strategy exemplified there is simply “0010001110101110”, i.e., an array of the decisions corresponding to each of the sixteen states, respectively. All together, there are $2^{16}$ possible strategies in the strategy space.

Fig. 2

The agents’ strategy (example)

3.2.3 Decision accuracy and attendance frequency

We define the variable $d_{i}(t)$ as the action taken by agent $i$ in period $t$: it takes the value 1 if the agent goes to the bar and the value 0 otherwise. Moreover, we define the variable $s_{i}(t)$ as the outcome of agent $i$’s decision in period $t$: it takes the value 1 if the agent took the right decision (that is, if he went to the bar and the bar was not crowded or if he stayed at home and the bar was too crowded) and it takes the value 0 if the agent took the wrong decision (that is, if he went to the bar and the bar was too crowded or if he stayed at home and the bar was not crowded). The agents are endowed with a memory of length $m$. This means that they store in two vectors, ${\mathbf {d}}$ and ${\mathbf {s}}$ of length $m$, the last $m$ values of $d$ and $s$, respectively. So, at the end of any given period $t$, agent $i$’s vectors ${\mathbf {d}}_{i}$ and ${\mathbf {s}}_{i}$, are composed, respectively, of $d_{i}(t),d_{i}(t-1), \ldots ,d_{i}(t+1-m)$, and of $s_{i}(t),s_{i}(t-1), \ldots ,s_{i}(t+1-m)$.

Agent $i$’s attendance frequency over the most recent $m$ periods, $a_{i}$, is defined by (2):

$$\begin{aligned} a_{i} = \frac{1}{m}\sum \limits _{j=t=1-m}^{t}d_{i}(j). \end{aligned}$$

(2)

The attendance frequency’s value can go from 1, if the agent always went to the bar, to 0, if the agent never went to the bar, in the last $m$ periods. Moreover, agent $i$’s decision accuracy rate, $f_{i}$, is given by (3):

$$\begin{aligned} f_{i} = \frac{1}{m}\sum \limits _{j=t+1-m}^{t}s_{i}(j). \end{aligned}$$

(3)

The decision accuracy rate can go from 1, if the agent always made the right decision, to 0, if the agent always made the wrong decision, in the last $m$ periods. We define the duration of agent $i$’s current strategy (the number of periods the agent is using his current strategy) as $r_{i}$. In order for the average attendance and the decision accuracy associated with any strategy to be computed, it has to be adopted for a number of periods equal to the agents’ memory size $m$: so, we can think of $m$ as the trial period of a strategy. We will set this value to 10 for all the agents in all our simulations.

3.2.4 Inequity-averse preference

As mentioned in the introductory section, agents in our model may have an inequity-averse preference, which is characterized by a parameter called the minimum attendance threshold, denoted by $\alpha _{i}$, that is, a fair share of the access to the pubic resources or a fair attendance frequency expected by the agent. It can take any value from 0, if the agents do not care about their attendance frequency, to $0.6$. We do not consider a higher value than $0.6$ because these agents with equity concern do not claim to go with an attendance frequency higher than the threshold $B/N (=0.6)$.

The inclusion of the inequity-averse preference can change the original payoff structure of the game (Eq. 1). Let $U_{\alpha }(x,n,\alpha _{i})$ be the utility function of agent $i$, who has the inequity-averse preference. Then $U_{\alpha }(x,n,\alpha _{i})$ can be formally modified as follows.

$$\begin{aligned} U_{\alpha }(x,n,\alpha _{i})=U(x,n) - \varepsilon , \end{aligned}$$

(4)

where

$$\begin{aligned} \varepsilon =\left\{ \begin{array}{ll} 0, &{} \quad \text{ if }\quad a_{i} \ge \alpha _{i}, \\ \varepsilon ^{+}, &{} \quad \text{ if }\quad a_{i} < \alpha _{i}. \end{array}\right. \end{aligned}$$

(5)

$\varepsilon ^{+}$ is positive and satisfies the inequality $u_{1} > u_{4}- \varepsilon ^{+} > u_{1}-\varepsilon ^{+} > u_{2}$. The agent with the inequity-averse preference has the same utility function as the agent without it when his ‘fair-share’ attendance is satisfied $(a_{i} \ge \alpha _{i})$; otherwise, a displeasure with inequity, $\varepsilon ^{+}$, is subtracted from the regular utility function.

3.2.5 Learning and search heuristics

Differing from the traditional El Farol Bar problem setup, the agents’ strategies are not fixed, but they evolve through both social learning (imitation) and individual learning (mutation). So, the social network plays a role both in the agents’ decision process, allowing the agents to gather information regarding their neighbors’ choices, and, in the agents’ learning process, allowing the agents to imitate their neighbors’ strategies. In any given period, an agent $i$ imitates the strategy of one of his neighbors if the following six conditions are met:

• (a) $f_{i} < 1$ and/or $a_{i} < \alpha _{i}$

• (b) $r_{i} \ge m_{i}$

and the agent has at least one neighbor $j$ for which the following conditions are verified:

• (c) $f_{j} > f_{i}$

• (d) $a_{j} \ge \alpha _{i}$

• (e) $r_{j} \ge m_{j}$

• (f) $z_{j} \ne z_{i}$

Condition (a) is quite obvious. It simply states that the agent will have the tendency to imitate if he is not satisfied with his current situation (strategy). There are two possibilities which may cause this dissatisfaction. First, there are errors in his decision $(f_{i} < 1)$ so there is room for an improvement, and, second, he is not satisfied with his attendance frequency $(a_{i} < \alpha _{i})$. Notice that, by this later qualification, the agent may still look for change even though all his decisions are accurate $(f_{i} = 1)$. Condition (b) shows that the agent will not change his strategy frequently and will consider doing so only if the strategy has been tested long enough, i.e., after or upon the completion of the trial period with a given duration of $m_{i}$. When imitating neighbors, agent $i$ will only consider those strategies which not only lead to more accurate outcomes, but also lead to a satisfactory attendance frequency (Condition (c) and (d)). The above promising strategy should be based on long testing, with a duration of $m_{j}$ periods, rather than sheer luck (Condition (e)). Finally, agent $i$ will not imitate the same strategy which he is currently using. Condition (f) is to avoid this repetition.

If the first two conditions are met but at least one of the last four is not, or, alternatively put, if the agent has not yet reached the optimal strategy and in the current period he cannot imitate any of his neighbors, then the agent, with a probability $p\,(p << 1)$, will mutate a randomly chosen rule on its strategy while with probability $1-p$ he will keep using his present strategy. While the imitation process ensures that the most successful strategies are spread in the population, the mutation process ensures that new, eventually better, strategies are introduced over time. Once the agent has adopted a new strategy (either through imitation or mutation) he will reset his memory to zero and will start keeping track of the new strategy’s fitness. The agent stops both the imitation and the mutation processes if the following two conditions are met:

• (a) $f_{i} = 1$

• (b) $a_{i} \ge \alpha _{i}$

When these two conditions are verified for all the agents, the system reaches the equilibrium: no further change in the agents’ behavior takes place after this point as the agents always make the right decision and go to the bar with a satisfying attendance frequency.

Under the influence of Simon’s notion of bounded rationality, behavioral economists characterize each decision process with three main stays, namely, a search rule, a stopping rule, and a decision rule (Gigerenzer and Gaissmaier 2011). The proposed learning process above can basically be read with this Simonian framework. Conditions (b)–(f) give the search rule, including when to start searching, (a) gives the stopping criteria, and the rest give the decision rule. Notice that the inequity-averse preference, together with the forecasting accuracy, in this model plays exactly the role of the stopping criteria. Hence, agents in our model are bounded rational in the sense of the Simonian satisfying agents, rather than the expected-utility maximizing agents.

3.3 Simulation settings

In the next section, we will show the results of simulations based on two variants of the El Farol Bar problem. In the first version (Sect. 4.1) we introduce the social network only but no inequity-averse preference. In this version, the agents, as in the original model, do not care about their attendance frequency. In this case, the same learning mechanism applies but with the minimum attendance threshold set to 0 $(\alpha _{i}=0, \forall i)$. Accordingly, the agents decide whether or not to imitate their neighbors only on the basis of the strategies’ accuracy rates. In this way, we are able to assess how the outcomes are affected by the introduction of social networks and, in particular, the effect of different network structures on the kinds of equilibria reached by the system, the equilibrium distribution, and, in particular, the emerging likelihood of a ‘good society’.

Then, in Sect. 4.2, we introduce a second variant where all or some agents are inequity averse, in the context of a network structure represented by the von Neumann neighborhood.¹⁵ This version is further differentiated into three scenarios. We first start with a homogeneous population of agents (Sect. 4.2.1) where all agents are inequity averse with the same threshold, i.e., $\alpha _{i}=\alpha , \forall i$ . We then consider a heterogeneous case (Sect. 4.2.2) where only a fixed number of agents are inequity averse with a threshold of 0.6. Denote this parameter by $N_{\alpha ,0.6}$, and the rest of the population are not inequity averse at all. The last scenario (Sect. 4.3) is the same as the second except that the thresholds of the inequity-averse agents are determined endogenously and socially in a ‘keep-up-with-the-Joneses’ (KUJ) manner. Denote this number of agents by $N_{KUJ}$. Step by step we are moving toward a more natural setting to address the question: what is the minimum degree of inequity aversion, in terms of $\alpha , N_{\alpha ,0.6}, N_{KUJ}$ , required for the emergence of the “good society” equilibrium?

4 Results of simulations

Simulation results are presented in this section. The first series of simulations show the contribution of the social network and local interactions to the emergence of the “good society” equilibrium (Sect. 4.1), and the second series of simulations show the significance of social preference in the form of inequity aversion (Sect. 4.2). They will both be presented in histograms (distributions) based on multiple runs.

4.1 Social networks without inequity aversion

We begin with the simulation of the El Farol Bar system with both the circular neighborhood and the von Neumann neighborhood. Each setting is run 1000 times. The results show that each simulation of both settings always reaches perfect coordination, that is, the state where the bar attendance is always equal to the threshold and, consequently, the agents never make the wrong choice. Figure 3 shows the attendances for a typical run with the von Neumann neighborhood. We can see that, in this example, the equilibrium is reached at around period 5000.¹⁶

Fig. 3

The attendances dynamics in a typical run (with the von Neumann neighborhood)

While the El Farol Bar in both networks eventually converges to the same aggregate outcome (a 60 % attendance rate all the time), from the mesoscopic viewpoint, they differ from run to run. To effectively characterize these equilibria at the mesoscopic level, we shall focus on the attendance frequency of agents when the perfect coordination is formed, $a_{i}^{*}$. In this way, our equilibrium can be represented by the heterogeneity in this attendance frequency over all agents. More precisely, the perfect coordinating equilibrium of the El Farol Bar problem is given by the set which shows the observed attending frequencies, $b_{j}^{*}$, and the share of the agents with $b_{j}^{*}$, $\pi _{j}^{*}$.

$$\begin{aligned} \varXi \equiv \left\{ \left( b_{j}^{*}, \pi _{j}^{*}\right) \right\} _{j=1}^{c} \equiv \left\{ \left( b_{1}^{*}, \pi _{1}^{*}\right) , \left( b_{2}^{*}, \pi _{2}^{*}\right) , \ldots \left( b_{c}^{*}, \pi _{c}^{*}\right) \right\} , \end{aligned}$$

(6)

where $b_{1}^{*} > b_{2}^{*} > \cdots > b_{c}^{*}$.

In (6), “$c$” refers to the number of clusters, and $\pi _{j}^{*}$ is the size of the corresponding cluster. Taking the bimodal perfect coordination equilibrium as an example, we have two clusters of agents, one which always goes $(b_{1}^{*} =1)$ and one that never goes $(b_{2}^{*} =0)$; 60 % of agents are of the first kind, and 40 % agents are of the second kind. Hence, this equilibrium is characterized by

$$\begin{aligned} \varXi _{Bi} \equiv \left\{ (1, 0.6), (0, 0.4) \right\} \end{aligned}$$

(7)

Alternatively, the “good society” is an equilibrium characterized as

$$\begin{aligned} \varXi _{G} \equiv \left\{ (0.6, 1) \right\} \end{aligned}$$

(8)

For convenience, we shall call these equilibria, based on the number of emerging clusters, $1C$ equilibrium, $2C$ equilibrium, etc. Hence the “good society” equilibrium, $\varXi _{G}$, is a $1C$ equilibrium, and the segregated equilibrium, $\varXi _{Bi}$, is a $2C$ equilibrium. Then one way to present our simulation result is to show the histogram of each of these $C$ equilibria over our 1000 runs.¹⁷ Figure 4 shows the histogram of the $C$ equilibria from $C=1,2,\ldots ,8$ for both the circular network (CN) and the von Neumann network (vNN).¹⁸

Fig. 4

Histogram of the $C$ equilibria with the circular (CN) and the von Neumann (vNN) neighborhoods

From Fig. 4 we can see that, while the literature on the El Farol Bar problem had identified only one kind of equilibrium, that is, $\varXi _{Bi}$ in (7), the introduction of social networks associated with the use of local information leads to the emergence of many different kinds of equilibria. While the $2C$ equilibria remain the most likely outcome in both networks, with the von Neumann network the system has a non-negligible probability $(18\,\%)$ of reaching the $1C$ equilibrium (the “good society” equilibrium), $\varXi _{G}$. The fact that the system has relatively good chances to reach the perfectly equitable equilibrium is a quite interesting result considering that, in this version, agents have no minimum attendance thresholds; yet, it is the second most likely equilibrium, with a probability up to almost one third of the probability of the $2C$ equilibria. Different network structures are, however, characterized by different equilibria distributions: for example, the probability of reaching $\varXi _{G}$ declines to only $2\,\%$ in the circular network.

A finer look at the results further shows that, within the equilibria characterized by the emergence of two clusters $(2C)$, the great majority (over $90\,\%$) are represented by the $\varXi _{Bi}$. The rest (less than $10\,\%$) are represented by $\varXi _{2}$ (see footnote 17). The great majority of the $3C$ equilibria are represented by an equilibrium where some agents never go to the bar, some always go and the rest go with an attendance frequency of $0.5$, i.e., $\varXi _{3-2}$ in (11). Another relatively frequent outcome is the emergence of the $5C$ equilibria. Within this case, the great majority is represented by a configuration where, besides the three clusters mentioned for the $3C$ case, two more groups of clusters, going to the bar respectively with a frequency of $0.4$ and $0.6$, emerge, such as

$$\begin{aligned} \varXi _{5} \equiv \left\{ (1, 0.58), (0.6, 0.01), (0.5, 0.02), (0.4, 0.01), (0, 0.38)\right\} . \end{aligned}$$

(13)

4.2 Introducing inequity-averse preference: exogenous settings

After seeing the significance of social networks in the emergence of the “good society” equilibrium, in the following sections, we shall examine the effects of the inequity-averse preference. To have a focus, here we only consider the von Neumann network. Hence, in the following sections, agents expect a minimum bar attendance frequency, and, if their actual attendance is below the threshold, they will find a way to change their original decision rule. Within this framework, we further consider two versions of this kind of inequity-averse preference: an absolute one which is given exogenously (Sect. 4.2) and a relative one which is determined endogenously in a “keep-up-with-the-Joneses” manner (Sect. 4.3).

4.2.1 Homogeneous population

For the exogenous settings, we further distinguish the case of a homogeneous population from the case of a heterogeneous population by addressing two different but related questions on the role of inequity aversion in the emergence of the “good society”. For the homogeneous setting, since all agents are given the same minimum attendance threshold $(\alpha _{i} = \alpha , \forall i)$, we then look at the relationship between the likelihood of the “good society” emerging and the degree of inequity aversion (the threshold) in this homogeneous setting.

Fig. 5

Histograms of the C equilibria for six different homogeneous thresholds: $\alpha = 0.1, 0.2,\ldots ,0.6$

We simulate the El Farol Bar dynamics by assuming $\alpha =0.1, 0.2, \ldots , 0.6$. For each parameter value of $\alpha$, an El Farol Bar dynamics with the von Neumann network is run 100 times. Figure 5 shows the distribution over various $C$ equilibria as the counterpart of Fig. 4. To show how this distribution may change with the increase in $\alpha$, the diagram is demonstrated in a three-dimensional version by including the minimum attendance threshold as one of the axes.

From Fig. 5, we can see that if all agents have the same threshold of $0.1$ (that is, the agents are satisfied if their attendance frequency is equal to or above $0.1$), the $1C$ equilibrium (the “good society”) is already the most likely outcome (around $40\,\%$), followed by the $2C$ equilibrium (around $30\,\%$). As we increase the minimum attendance threshold, the frequency of the $1C$ equilibrium increases while the frequencies of all the others decrease, at different rates. Then, with a minimum threshold level of $0.6$, the system reaches the $1C$ equilibrium $100\,\%$ of the time, as it is the only equilibrium compatible with this satisfying level.

Hence, as we can see from this simulation, the early bimodal segregation as obtained in many models using reinforcement learning can be significantly changed within a society of agents with a minimal degree of inequity aversion. Presumably, one might have thought that the addition of this inequity aversion might cause the use of the public resource to become harder to coordinate, but this is not necessarily the case. In fact, a more equitable but still well-coordinated outcome emerges. Therefore, in this sense, citizens with the awareness of their rights and striving for that does indeed facilitate the realization of the good society.

4.2.2 Heterogeneous population

From the previous simulation results, we know that if all the agents have the minimum attendance threshold of $0.6$, the system will surely converge towards the “good society”. Nonetheless, making all agents have identically strong or weak inequity-averse preferences is a strong assumption. Therefore, it would be interesting to know whether the good society will emerge in a more “natural” setting. In the next simulation, we no longer assume that all agents are inequity averse: some are, but some are not. Without losing generality, we further assume that those agents with inequity-averse preferences all have a threshold of 0.6. In this setting, we ask a different question: what would be the minimum number of inequity-averse agents required for the emergence of the “good society”?

Fig. 6

Evolution of the distribution over $1C, 2C$ and other equilibria with the increase in the number of inequity-averse agents

We want, then, to see how the likelihood of the “good society” equilibrium changes when starting from a population entirely composed of agents with no minimum attendance thresholds, then followed by increasing the number of agents with an $\alpha$ of $0.6$. In this simulation, the number of agents with a threshold of 0.6, $N_{\alpha , 0.6}$, is the key parameter, and, we run each of the parameter settings $(N_{\alpha , 0.6}=0, 1, 2,\ldots )$ 100 times so as to approximate the distribution by the respective histogram. Figure 6 shows the evolution of the distribution over various $C$ equilibria. To make this diagram easy to see, we group all equilibria with more than two clusters of agents together, called the more-than-2C ($>$2C) equilibria, and hence only present the distribution over the three major equilibria, i.e., the $1C$, $2C$ and $>$2C.

From Fig. 6, as expected, when the number of agents with inequity aversion is small, the bimodal segregation equilibria dominates, but already with just 10 inequity-adverse agents, the $1C$ equilibria (“good society”) becomes the most likely outcome and that it indeed becomes the unique absorbing state when the population contains at least 20 inequity-adverse agents. In other words, it takes only a small minority of the society (around $20\,\%$) to lead the system to the perfectly equitable outcome.¹⁹

The two sequences of simulations above demonstrate two different approaches to manipulate the degree of inequity-aversion, one directly through the threshold $(\alpha )$, and one through the number of agents with a threshold of 0.6 $(N_{\alpha ,0.6})$. Both show that the “good society” can be the most likely result with only a small degree of inequity aversion: $\alpha$ is only required to be 0.1 in the first case, and $N_{\alpha ,0.6}$ is only required to be 10 in the second case. The latter case further shows that, to surely have the “good society” outcome, there is no need to have all agents with strong inequity-averse preferences $(N_{\alpha ,0.6}=100)$, for it is sufficient for only one fifth of the population to have them. This latter result denotes the positive externality of inequity-averse preferences, and hence makes the realization of the “good society” easier than what we thought in the beginning.

4.3 Introducing the ‘Keeping-up-with-the Joneses’ behavior

Regarding the significance of the inequity-averse preference, the result will be more convincing if it can emerge endogenously, instead of being imposed exogenously. In the next simulation, we propose an alternative way of forming this inequity-averse preference. The social behavior coined as “keeping up with the Joneses” (KUJ) has recently caught the attention of many economists. It has been extensively incorporated into consumption, asset pricing and macroeconomic models (Gali 1994; Ljungqvist and Uhlig 2000). We find that the same idea can be straightforwardly applied to our model, in which agents’ decisions very much depend on those of their neighbors.

Hence, instead of the exogenously given threshold $(\alpha )$, agents will now find their own reference based on the attendance frequency averaged over their neighbors, and use that as their own minimum attendance threshold. In other words, the agents characterized by the “keeping-up-with-the-Joneses” behavior do not want, among those in their neighborhood, those going to the bar with a frequency lower than the average. Since neighbors’ attendance frequencies change over time, this threshold, unlike the previous two settings, is no longer fixed. We call agents in this new setting the KUJ agents.

Like what we have done in Sects. 4.2.1 and 4.2.2, we could further distinguish the case with a homogeneous population from the case with a heterogeneous population; in the former, all agents are KUJ agents, whereas in the latter only part of them are KUJ agents. For the former case, it is relatively easy to see that if all the agents in the population try to ‘keep-up-with-the-Joneses’, the system will inevitably end up reaching the “good society” equilibrium, equivalent to the case where all agents have an $\alpha$ of 0.6 (Sect. 4.2.1). This is the only state where no agent goes to the bar with a frequency lower than the average (that is, where all the agents go to the bar with the same frequency). So, we will only be interested in the heterogeneous case and pose the same question as the one in Sect. 4.2.2, i.e., where we inquire about the minimum number of KUJ agents required for the emergence of the “good society”. Therefore, we set the number of KUJ agents as a parameter, $N_{KUJ}$, and simulate the El Farol Bar dynamics with $N_{KUJ}= 0, 1, 2,\ldots$ We run each $N_{KUJ}$ 100 times so as to show the histogram over different $C$ equilibria.

Figure 7 shows the evolution of the distribution over the $1C$, $2C$ and more-than-2C equilibria with the increase in the number of KUJ agents. We can see that, by and large, the evolution of the distribution is similar to the case with a different number of $N_{\alpha ,0.6}$ (Sect. 4.2.2): in this case, with more than 11 KUJ agents, the $1C$ equilibrium (“good society”) becomes the most likely outcome. Moreover, it takes only around $25\,\%$ of the KUJ agents to lead the system to the perfectly equitable outcome, slightly more than the minimum number required for $N_{\alpha ,0.6}$, but still a small minority.

Fig. 7

Evolution of the distribution over the $1C, 2C$ and other equilibria with the change in the number of KUJ agents

5 Looking into the $1C$ equilibrium

5.1 Consistency between macro and micro emergence

We have shown that perfect coordination, which is not necessarily equitable, can be always achieved in our limited explorations of social networks and social preferences. This result is very atypical with respect to what has been found in the existing literature; therefore, it is worth examining the unique dynamics which we experienced in the simulations.

Fig. 8

Emergent strategies characterizing the $1C$ equilibrium of the von Neumann neighborhood

Without losing generality, we shall focus on the case of the $1C$ equilibrium (“good society”) under the von Neumann network and give an intuitive description of the underlying dynamics leading to it. As we described earlier, our agent-based model is a kind of two-dimensional cellular automata (Wolfram 2002). The slight difference here is that, instead of being homogeneous, our agents initially follow different strategies, but the subsequent social learning through imitation helps increase the homogeneity among them, and makes them eventually follow the same strategy. In other words, a single strategy becomes the attractor under our learning dynamics. This final strategy (attractor) then helps coordinate agents’ attendance in a way that in each single day there are always 60 % of agents attending the bar $((\frac{n}{N})_{t}=0.6, \forall t \ge T^{*})$, and for each agent the attending frequency is 60 % of the time $(r_{i,t}=0.6, \forall i, t \ge T^{*})$. Fully specifying these attractors can be a daunting task; however, our simulations suggest that the number of the attractors with a non-trivial domain of attraction can be rather limited; as a matter of fact, throughout our simulations only four of this kind have been found and they are all shown in Fig. 8.

These four strategies are presented in their effective version, i.e., the one keeping only the active states. This is so because many states are idle when perfect coordination is achieved with the emergence of rather well-structured social patterns (see Fig. 9). The four strategies, as exemplified in Fig. 8, all have only three active states left and three corresponding if-then rules. These three rules together do not require the agent to look at the actions of all four of his neighbors. Take Strategy One as an example. This strategy essentially requires the agent to look at neighbors $N1$ or $N3$ (shown in bold in Fig. 8). If $N1 (N3)$ attended the bar in the previous period, he will then decide to go (rules 11 and 16); otherwise, he will stay home (rule 6).²⁰ Alternatively put, the strategy is simply “do what your neighbors $N1$ or $N3$ did in the last period”. The similar simple interpretation applies to the three other strategies.

These simple rules echo well with the emergent well-structured patterns of bar attendance as the joint force of the upward and downward causation. To see this, Fig. 9 presents the snapshot of the social pattern of bar attendance for a typical run at the $1C$ (“good society”) equilibrium. The specific $1C$ equilibrium shown in Fig. 9 is characterized by Strategy Four (Fig. 8). The effective version of Strategy Four bases the decision upon only one of the four neighbors, either $N2$ or $N3$. Basically, it imitates what $N2$ or $N3$ did in the last period. With everyone following this same strategy, in equilibrium each individual will be presented with a periodic cycle involving only three input states, i.e., 0-1-1-0, 1-0-0-1, and 1-1-1-1. They are, respectively, the three antecedents of Rules 7, 10, and 16.²¹ The left panel of Fig. 9 shows the spatial distribution of the activated rules over the 100 agents for a typical run, and the right panel shows the corresponding attendance distribution.

Fig. 9

A snapshot of the rules adopted (left) and the actions taken (right) by the 100 agents once the equilibrium has been reached. In the simulation we would see the diagonals ‘move’ one step eastward in every period

From the left panel, one can clearly observe the diagonals of the three activated rules, each extending from northeast to southwest, and they are aligned together like a wave which moves one step eastward for each iteration.²² The right panel demonstrates the same pattern in terms of a wave of diagonals of “0” and “1”. The diagonals of 0 correspond to the diagonals of Rule 10 in the left panel, whereas the diagonals of 1 correspond to those of Rules 7 or 16 there. As these diagonals of rules move eastward, the diagonals of 0 and 1 also move eastward accordingly, and at any point in time only 60 % of the agents (gray shaded area in the right panel) attend the bar. At the aggregate level, the bar is then fully utilized.

At the micro level, let us look at the attendance behavior of each individual under the $1C$ equilibrium. We will continue assuming the equilibrium characterized by Strategy Four as an illustration. Given the fact that each individual will encounter a periodic cycle of his environment (the input states), his bar attendance becomes quite regular. In this specific case, each individual will also follow a 10-period cycle as follows: 1-1-1-1-0-0-1-1-0-0 as we can easily see either from the last row (imitating N2) or the last column (imitating N3) of Fig. 9. Hence, each individual attends the bar six times every 10 days, and not only is the bar fully utilized, but it is also equally accessible for each individual.²³

5.2 Analysis: out-of-equilibrium

The analysis above rests upon the equilibrium only. One more interesting feature of agent-based modeling is out-of-equilibrium analysis. This section, therefore, extends the previous analysis into transition dynamics. We continue the previous example, but now examine how the $1C$ equilibrium characterized by Strategy 4 is achieved. One can perceive that in this case we initialize the system in the domain of attraction of Strategy 4;²⁴ hence, one natural thing to look at is the population of agents who actually follow Strategy 4. The solid line of Fig. 10 plots the percentage of this population. This figure increases over time but with some degree of fluctuation. Before it becomes steady, it experiences a significant drop around period 500. Then it comes back and eventually climbs up, and, around period 1200, it almost successfully drives out all other strategies. At this point, agents are becoming homogeneous by following the same strategy.

Fig. 10

The dynamics of the number of agents adopting the optimal strategy (strategy 4) and of the number of ’optimal’ agents actually adopting one of the three rules of the optimal strategy (in this case, rules 7, 10 and 16)

However, adopting the same strategy is not sufficient for, when the perfect coordination is reached, many input states will become transient, and there are only three recurrent states left. In Fig. 10, we, therefore, also plot the number of agents, shown by the dotted line, who not only adopt the optimal strategy, but actually fire one of the three rules characterizing it, that is, Rule 7, Rule 10 and Rule 16. The number of these agents also rises, but remains far from the number of agents who had adopted Strategy Four (the solid line), and that distance has no clear tendency to be shortened until coming to period 1,500, right before the system suddenly reaches the equilibrium. This means that the inputs of the agents are different from those characterizing the equilibrium. Consequently, even if they are already adopting Strategy 4, their behavior is only incidentally determined by the three rules characterizing this strategy as in many periods they end up firing other rules apart from rules 7, 10 and 16. Then, suddenly, after period 1500, the system reaches the equilibrium, a state where not only do all the agents adopt Strategy 4, but they also use the rules characterizing this strategy.

From Fig. 10 we can see that the process leading to the equilibrium is characterized by a stage (in this case lasting up to period 1200) in which the necessary condition for the system to reach the equilibrium (that is, the adoption of Strategy 4 by all the agents) is gradually established by means of a ‘subterranean’ process having no immediate effect on the population’s coordination level. However, once this process comes to an end, the system is ‘ripe’ for the equilibrium: sooner or later, a minor event, such as a mutation, triggers the emergence of coordination that, as we can see from Fig. 10, is a very fast process occurring in less than 100 periods, looking much like spontaneous self-ordering (Kauffman 1993).

5.3 Networks and information efficiency

Earlier in Sect. 4.1, we have seen the different performance in the likelihood of achieving the $1C$ equilibrium (the ‘good society’) between the circular network and the von Neumann network (Fig. 4). Using the analysis provided in Sect. 5.1, in particular, the emergent strategies characterizing the $1C$ equilibrium (Fig. 8), we attempt to provide an intuitive explanation for this observed difference. In parallel to Fig. 8, the $1C$ equilibrium in the case of the circular neighborhood is characterized by the emergence of four different strategies, which are shown in Fig. 11.

Fig. 11

Emergent strategies characterizing the $1C$ equilibrium of the circular neighborhood

We can see that, in this case, the strategies are characterized by five rules, instead of the three rules of the strategies emerging in the von Neumann neighborhood (Fig. 8). Moreover, each of the four strategies corresponds to the actions of just one neighbor rather than two. For example, Strategy 1 in Fig. 11 corresponds to the actions of N1 only (shown in bold characters). We can say that the bi-dimensional structure of the von Neumann neighborhood allows for a more efficient use of the information, compared to the one-dimensional structure of the circular neighborhood. This is reflected in the lower complexity of the strategies emerging in the former neighborhood structure (Fig. 8) as opposed to those in the latter (Fig. 11). The different complexities between the strategies are, in all likelihood, related to the fact that it is more difficult to reach the $1C$ equilibrium with the circular neighborhood than with the von Neumann neighborhood (Fig. 4), as the number of rules the agent needs to get right is higher in the first case compared to the latter.

6 Concluding remarks

The El Farol Bar problem is a highly abstract model suitable for addressing the fundamental issue of the use and the distribution of public resources. Early studies on this problem have only centered on the efficiency aspect of this issue. The equity part of the issue has been ignored. The contribution of this paper is that we integrate these two aspects. While coordination in the El Farol Bar problem when taking both efficiency and equity into consideration can be harder than when only efficiency is considered, it still can be solved bottom-up.

However, to do so, our simulations have shown that under the specified circumstances both social networks and social preferences can play contributing roles. We first show that social network topologies matter for the emergence of a “good society” ($1C$ equilibrium), a state where the bar attendance is always equal to its capacity and all the agents go to the bar with the same frequency. This is exemplified by the comparison made between the von Neumann network and the circular network. It is found that it is much easier for the “good society” to emerge under the former (18 %) as opposed to the latter (only 2 %).

We then show how the introduction of the social preference can further facilitate the emergence of the good society. This depends on a specific group of people who are sensitive to inequity or who have inequity-averse preferences. The emergence of the good society can become increasingly likely with the increase in the degree of inequity aversion. Various simulations, however, show that to surely have the “good society” equilibrium the requirement for inequity aversion is rather mild. For example, even a minority group of agents, like 20–25 % of the whole population, who are inequity averse, is sufficient.

Is the result surprising? Leaving this issue temporally aside, we have to admit that how to find the behavioral rules for each individual so that they can collectively generate the desirable aggregate pattern is in general a very challenging issue for both the sciences and social sciences. This issue has long been studied in various agent-based models, in particular, cellular automata. In this paper, the choice of the social network for the society and the representation of the decision rules for the individuals recast the classical El Farol Bar problem into a familiar environment of cellular automata. When the central planner (model builder) has no single slice of the idea as to what these rules should be, they are then left for the members of society (cellular automata) to find out among themselves. The question, now posed bottom-up, is actually a cruel test for the limit of self-coordination. Despite the possible inherent difficulties, the self-coordination problem may become less hard to solve under some social network topologies and some cultures. This general feature should not be a surprise, but any concretization of it to see how it actually happens is not immediately obvious. While in this paper we have started setting the social preference exogenously, that preference can be generated through a culture of “keeping up with the Joneses” under the given network. In essence, it is the KUJ culture and the network that together facilitate the social search for the “right codes” for a “good society”.

To what extent, can the findings be generalized? An abstract model like the one presented here, being far from any realistic settings, certainly has its limitations. The specific analysis and answers which we obtain in this paper may no longer be applicable in other general and realistic settings. For example, as we have demonstrated in “Dominance of efficient but inequitable outcomes” of Appendix 2, achieving the ‘good society’ equilibrium becomes increasingly difficult when the population size becomes larger. Nonetheless, the wonder prompted by this paper remains, i.e., the potential of using social networks, social preferences or cultures to enhance the self-coordination of a society of agents with simple behavioral rules. Hence, from a comparative study viewpoint, one can imagine that, in the case of societies (towns, countries,...) or societies in different times with very different human interaction webs, social preferences and culture, their self-coordination capabilities to solve some “tragedies of the commons” may be different, although the “tragedies” may often be solved or institutionalized in a top-down manner, too.

Appendices

Appendix 1: Heterogeneous strategies in the multiple clustering equilibria

In Sect. 5, we have provided a simple analysis of the selected strategies in the $1C$ equilibrium. When the $1C$ equilibrium emerges, all the agents adopt the same strategy. However, for equilibria with multiple clusters of agents, normally, agents will be heterogeneous in the strategies adopted when the equilibrium is achieved. A brief account of the heterogeneity is given in this Appendix.

When the $2C$ equilibrium emerges, agents are frozen in their state (1 or 0). This means that they only use one rule from their set of 16 rules, as they face the same situation period after period. In general, the equilibrium is characterized by the presence of many different strategies; for example, in one run the equilibrium was characterized by an ecosystem of 18 different strategies. However, if we consider only the rules which happen to be fired by the population of agents, usually only 4 or 5, we observe the presence of few different strategies, usually from 2 to 5 or 6. The vast majority of the agents have the same strategy. As a concrete example, in one run where the equilibrium was characterized by 5 strategies, the number of agents adopting each of these strategies was 83, 10, 4, 2 and 1.

With the number of agents going to the bar in equilibrium equal to 60, this means that in some cases the different behavior observed between the agents going to the bar and those not going was not caused by different strategies, but by different environments which led them to fire different rules of the same strategy. Conversely, agents with the same behavior may have different strategies. However they either fire a different rule because of their different surroundings, or they fire the same rule because they have the same surroundings, prescribing the same action (in the latter case it means that their strategies differ because of differences in the other rules).

When the $3C$ equilibrium emerges, there are agents going with a frequency of 0.5. However, the general picture is similar to that described for the $2C$ equilibrium. Although we have agents with a different strategy, the vast majority of agents share the same strategy, but they have different behavior because of their different environment, i.e., their neighbors’ behavior.

Appendix 2: Sensitivity analysis

In this Appendix, we shall examine how our fundamental results, as demonstrated in Sects. 4.1 and 4.2, are robust to some of the parameters used in the model. There are basically two results to be examined under this sensitivity analysis. The first result is the dominance of the efficient but inequitable outcomes under the von Neumann network. As shown in Sect. 4.1, under the von Neumann network one can always have perfect coordination. The probability of having a good-society $(1C)$ equilibrium is relatively minor. The dominating equilibria are the ones with many clusters, in particular, the $2C$ equilibria, indicating that public resources are not equally shared by all community members (some members dominate the use of the public resources, but some are excluded). The second result is that the emergence of the $1C$ equilibrium is ensured if there are a sufficient number of agents with social preferences in the community.²⁵

In this section, we test the two aforementioned results with three size-related parameters, namely, the network size (the number of agents), the neighborhood size (the number of neighbors), and the memory size (the length of memory). Each of these parameters can have its significance in economic modeling. First, for the network size $(N)$, it is already known in agent-based computational economics that some simulation results are not scale-free or cannot be scaled-up (Lux and Schornstein 2005). Second, the number of neighbors $(R)$ or the range of interactions can also matter because it can affect the flow and the spread of the information (Lo et al. 2004). Third, memory capacity has constantly been an important parameter in various models of learning. It determines how frequently a strategy will be reviewed and revised, which may affect the results obtained (LeBaron 2001; Chen et al. 2008). Specifically, the neighborhood size and the memory size can have effects on the complexity of strategies $(2^{R})$, the size of the strategy pool $(2^{2^{R}})$, and, through the conditions of learning, (a) to (f), can have effects on the activation and the frequency of learning. The combined effect of this multi-faceted operation is hard to know a priori. We, therefore, design and run a simulation to estimate the results.

1.1 Dominance of efficient but inequitable outcomes

To examine the robustness of the first result, what we plan to do is to take the original values of parameters as a baseline, i.e., $N=100$, $R=4$, and $m=10$, and then perturb each of them with both a downward direction, i.e., $N=5 \times 5$, $R=3$ and $m=5$, and an upward direction, i.e., $N=15 \times 15$, $R=5$ and $m=20$. When we perturb, we do it one parameter at a time. As before, each setting is run 1000 times, and the histograms of the $C$ equilibria over these 1000 runs are shown in Fig. 12 for $N$, Fig. 13 for $R$, and Fig. 14 for $m$.²⁶

Fig. 12

Histogram of the $C$ equilibria with different network sizes. The above figure is the histogram of the $C$ equilibria, which range from $C=1$ to $C=8$, with respect to three different network sizes $(N\hbox {s})$: from left to right, with different degrees of grayness, these are 25, 100, and 225

Fig. 13

Histogram of the $C$ equilibria with different numbers of neighbors. The above figure is the histogram of the $C$ equilibria, which range from $C=1$ to $C=8$, with respect to three different numbers of neighbors ($R$s): from left to right, with different degrees of grayness, these are 3, 4, and 5

Fig. 14

Histogram of the $C$ equilibria with different lengths of memory. The above figure is the histogram of the $C$ equilibria, which range from $C=1$ to $C=8$, with respect to three different lengths of memories ($m$s): from left to right, with different degrees of grayness, these are 5, 10, and 20

The sensitivity analysis needs to be addressed at three different levels: efficiency, distribution of equilibria, and the emergence of the good society ($1C$ equilibrium). Since the results that we have from the three figures are similar, we shall mainly elaborate on the results of the parameter $N$, and, for $R$ and $m$, we only highlight the observed distinctions.

First, the result with regard to the perfect coordination (efficiency) is robust. For each $N$ ($=$ 25, 100, 225), out of all the 1000 simulations, we always have the perfectly coordinated outcomes in the sense that the attendance rate is equal to the bar’s threshold. In these simulations the society always segregates into different numbers of clusters of agents (from one to eight, as shown in Fig. 12), who self-organize themselves well in their bar attendance schedules and frequencies. Second, while the exact histogram will have some mild changes with respect to different numbers of agents, the $2C$ (two-cluster) equilibria constantly play a dominating role in the histogram, indicating that public resources are not equally shared by all community members. Hence, this inequitable outcome is also robust to the number of agents.

Third, what, however, is not robust is the chance of having the $1C$ (good-society) equilibrium. It is well noted that the chance of observing the $1C$ equilibrium declines with the number of agents. Compared with the benchmark $(N=100)$, the likelihood of the $1C$ equilibrium increases up to 40 % when $N=25$ and decreases down to zero when $N=225$. Therefore, a large population size makes the coordination to the ‘good society’ equilibrium increasingly difficult, indicating that the core result, the emergence of the good-society equilibrium, is not size independent.

Figure 13 shows the simulation result with respect to different $R$s. We can see that the neighborhood size has little qualitative effect. It has no effect on the efficient outcome; all runs lead to perfect coordination, and the $2C$ equilibria remain to be the major type. A smaller and a larger value of $R$ ($R=3, 5$) will lessen the chance of observing the $1C$ equilibrium, and there will be a shift in distribution toward many-cluster equilibria when $R$ increases. For example, when $R=5$, the likelihood of reaching the equilibrium with more than three clusters becomes as high as 20 %.

Finally, Fig. 14 shows the simulation results of varying the length of memory $(m)$. It shows that $m$ has no effect on the efficiency results. The perfect-coordination result can always be achieved, and the $2C$ equilibria are still the dominating equilibria. Furthermore, as in the case of $R$, both a smaller and a larger value of $m$ ($m=5, 20$) will lessen the chance of observing the $1C$ equilibrium, and there is a shift in distribution toward many-cluster equilibria when $m$ decreases. For example, when $m=5$, the chance of having $3C$ equilibria is more than 20 %, and even for the $6C$ equilibria the chance remains as high as 10 %.

In sum, our sensitivity analysis shows the robustness of the perfect-coordination result. While different settings of the parameters may affect the distribution of equilibria with different clusters, the $2C$ equilibria are the dominating type. A small community can facilitate the emergence of the good-society $(1C)$ equilibrium, and a large community does just the opposite. In any case, the good-society $(1C)$ equilibrium can never dominate the segregating equilibria.

1.2 Significance of social preferences

With the robustness of the dominance of the efficient but inequitable equilibria, one may find it easier to acknowledge the significance of the presence of agents with social preferences. In this section, we continue to apply the previous sensitivity analysis to the second result that the emergence of the $1C$ equilibrium is ensured as the number of agents with social preferences is sufficiently large. As was the case in Sect. 4.2.2, we vary the number of agents with the inequity-averse preference $(N_{\alpha ,0.6})$ from 1 to 40 with an increment of one, and now test their effect on the emergence of the $1C$ equilibrium with the parameter values of $N$, $R$ and $m$ set in “Dominance of efficient but inequitable outcomes” of Appendix 2. We then do the same thing using $N_{KUJ}$, the number of agents with the KUJ preference, instead. We shall first present the results under different values of $R$ and $m$, which is more evident, and then move to the case of $N$, which is not.

Figure 15 presents the results. The upper left panels show the effect of $N_{\alpha , 0.6}$ on the emergence likelihood of the $1C$ equilibrium, whereas the upper right panel shows the effect of $N_{KUJ}$. As we can see from these two sub-figures, the empirical probability of having the $1C$ equilibrium increases with $N_{\alpha , 0.6}$ and $N_{KUJ}$, and tends to converge to one. This pattern is also consistently observed in the lower left and right panels, which show the effect of $N_{\alpha , 0.6}$ and $N_{KUJ}$ on the emergence likelihood of the $1C$ equilibrium, respectively. Hence, from these four sub-figures, the second result is also robust to these two size-related parameters.

Fig. 15

Social preferences and emergence of the good society. The three lines in the upper left panel show the frequency of achieving the $1C$ equilibrium when $N_{\alpha ,0.6}$ increases from 1 to 40 under three different neighborhood sizes: $R=3$ (blue line), 4 (red), and 5 (green). The three lines in the upper right panel show the same frequency except that $N_{\alpha ,0.6}$ on the $x$-axis is replaced by $N_{KUJ}$. The three lines in the lower left panel show the frequency of achieving the $1C$ equilibrium when $N_{0.6}$ increases from 1 to 40 under three different lengths of memory: $m=5$ (blue line), 10 (red), and 20 (green). The three lines in the lower right panel show the same frequency except that $N_{\alpha ,0.6}$ on the $x$-axis is replaced by $N_{KUJ}$(color figure online)

However, when we come to the parameter $N$, we no longer have this second result characterized by the increasingly converging pattern. Under the scenario $N=225$, the likelihood of emergence of the $1C$ equilibrium continues to be zero and does not increase with $N_{\alpha ,0.6}$ or $N_{KUJ}$. Hence, the presence of the inequity-averse and the KUJ agents can no longer ensure a convergence to the $1C$ equilibrium when the network size is large.

To sum up, the two fundamental results obtained in the main text are robust to the neighborhood size $(R)$ and the memory size $(m)$. The first result is largely robust to the network size $(N)$, except that the empirical probability of the emergence of the $1C$ equilibrium degenerates to 0 when the network size is large. The second result, however, no longer holds when $N$ is large. Putting them together, when $N$ is large, convergence to the $1C$ equilibrium can become extremely difficult even with the presence of agents with social preferences.