The research on a novel multivariate grey model and its application in carbon dioxide emissions prediction

Abstract

Accurate small-sample prediction is an urgent, very difficult, and challenging task due to the quality of data storage restricted in most realistic situations, especially in developing countries. The grey model performs well in small-sample prediction. Therefore, a novel multivariate grey model is proposed in this study, called FBNGM (1, N, r), with a fractional order operator, which can increase the impact of new information and background value coefficient to achieve high prediction accuracy. The utilization of an intelligence optimization algorithm to tune the parameters of the multivariate grey model is an improvement over the conventional method, as it leads to superior accuracy. This study conducts two sets of numerical experiments on CO₂ emissions to evaluate the effectiveness of the proposed FBNGM (1, N, r) model. The FBNGM (1, N, r) model has been shown through experiments to effectively leverage all available data and avoid the problem of overfitting. Moreover, it can not only obtain higher prediction accuracy than comparison models but also further confirm the indispensable importance of various influencing factors in CO₂ emissions prediction. Additionally, the proposed FBNGM (1, N, r) model is employed to forecast CO₂ emissions in the future, which can be taken as a reference for relevant departments to formulate policies.

Introduction

Background

In recent years, climate warming has emerged as one of the most significant environmental challenges faced by countries worldwide. The continuous rise in carbon dioxide (CO₂) emissions is considered a major contributor to increased greenhouse gas emissions and subsequent global warming (Li et al. 2022). Global CO₂ emissions have experienced a sharp increase over the past few decades, nearly doubling to alarming levels, as reported by the International Energy Agency (IEA) (Ding and Zhang 2023). This surge is primarily attributed to the combustion of fossil fuels such as coal, oil, and natural gas to meet energy demands and industrial production (Liu et al. 2022). Consequently, the international community has increasingly recognized the importance of reducing CO₂ emissions and addressing climate change. Under the Paris Agreement, which aims to contain the increase in global average temperature to below 2 °C above pre-industrial levels and strives to limit warming to 1.5 °C to reduce the impact of climate change on the ecosystem, the economy, and human societies, each country sets its emission reduction targets and adopts corresponding emission reduction measures (Ding and Zhang 2023).

According to the World Bank, the top three emitters in terms of CO₂ emissions in 2020 are China (109,446,686.2 kT), the USA (43,205,532.5 kT), and India (22,008,360.3 kT) (as shown in Fig. 1). Only three of the top 10 countries in terms of CO₂ emissions are below the world average in terms of CO₂ emissions per capita, with Canada (13.6 T) ranking first among these 10 countries. Statistically, China accounts for 32.6% of global CO₂ emissions, ranking first in the world. As the world’s largest carbon emitter, China is committed to making efforts to reduce global carbon emissions, and in the general debate of the 75th session of the United Nations General Assembly, China explicitly proposed that it would strive to achieve the goal of “carbon peaking” by 2030 and “carbon neutrality” by 2060 (Wei et al. 2023).

Fig. 1

CO₂ emissions in 2020

Subsequently, China has taken a series of measures to accelerate the realization of the “dual-carbon” goal (Ding et al. 2023a). To promote the adoption of low-carbon technologies and sustainable practices among enterprises, China has set up the world’s largest carbon trading market, which provides economic incentives and benefits to businesses (Zeraibi et al. 2022). In addition, China is promoting the transformation of its energy structure (He et al. 2022), phasing out highly polluting and energy-consuming traditional energy industries and increasing the proportion of renewable energy (Xin-Gang et al. 2022). However, China, being a developing country, continues to grapple with the significant challenge of striking a balance between rapid economic growth and reducing carbon emissions (Huang et al. 2022a; Li et al. 2021a). As the economy expands, the environment faces mounting pressures, and the contradiction between sustainable development and carbon emission reduction becomes increasingly pronounced (Wang et al. 2021; Umar et al. 2021). Consequently, it becomes crucial to accurately predict CO₂ emissions to aid decision-makers in promptly responding to climate change, adjusting existing energy-saving and emission-reduction policies, and formulating feasible programs to promote low-carbon sustainable development (Ye et al. 2022).

To respond to climate change and environmental pollution promptly, it is necessary to accurately predict CO₂ emissions by taking into account a combination of factors. However, due to the small amount of data for some factors, the current popular big data methods are not applicable, so there is an urgent need for a small-sample prediction method to cope with this situation.

As a result, this study proposes a fractional-order multivariate grey prediction model with optimized background values that can accurately predict CO₂ emissions per capita,especially because the model effectively integrates numerous relevant influencing factors and obtains the highest accuracy in both cases. The superior prediction accuracy of the model is attributed to the ability of the fractional-order cumulative operator to make full use of the new information and the optimization of the background value coefficient, which can be used to obtain accurate and stable prediction results. Therefore, the model can be used to predict future CO₂ emission projections per capita, thus providing a reliable basis for policymakers.

Contributions and organizational structure

In summary, this study makes the following key contributions:

• Proposing an improved multivariate grey prediction model. To maximize the information obtained from data, a more enhanced multivariate grey model called FBNGM (1, N, r) is introduced. This upgraded model incorporates the use of a whale optimization algorithm to optimize both the fractional operator and the background value coefficient. As a result, it is expected to enhance the impact of novel information and improve the accuracy of predictions.

• Adequate introduction of various influences to construct CO₂ emissions prediction models. Different from previous CO₂ emission prediction models, this study not only introduces economic, energy, industrial, and other factors, but also establishes three univariate, three multivariate models, and three non-grey multivariate prediction models to predict CO₂ emissions, and eventually confirms the inseparable relationship between CO₂ emissions and the various influencing factors, as well as the outstanding forecasting accuracy demonstrated by the proposed model.

• Performing two numerical cases, results analysis, and future forecasting. To assess the effectiveness and robustness of the proposed model, this study employs two numerical cases of CO₂ emissions per capita obtained from the World Bank and calculated based on energy consumption. This study not only compares the mean absolute error (MAE), absolute percentage error (APE), mean absolute percentage error (MAPE), and root mean square error (RMSE) of the nine models, but also predicts the CO₂ emissions per capita by 2030 according to the established FBNGM (1, N, r) model and finally puts forward relevant suggestions for relevant decision-makers to refer.

Other organizational structures of this study are as follows: “Literature research” provides a review of the relevant studies that have projected CO₂. “Methods” introduces and validates the FBNGM (1, N, r) model proposed by this study. Afterwards, “Model application” presents and discusses the numerical simulation results obtained from applying the FBNGM (1, N, r) model. Based on the forecasting results, “Discussion and policy suggestions” provides several recommendations. Finally, concluding remarks are given in “Conclusion.”

Literature research

Many researchers have proposed a wide range of CO₂ emission forecasting models to enhance the accuracy of predictions. These models can be broadly classified into three categories: statistical models (Weng et al. 2020), artificial intelligence models (Weng et al. 2022; Delanoë et al. 2023), and grey prediction models. In order to further enhance the predictive capabilities of these models, researchers have incorporated relevant factors such as economic, social, and demographic variables.

Factors affecting carbon dioxide emissions

The selection of influencing factors is critical to accurately forecasting CO₂ emissions. It is important to rely on reliable data and scientific methods, consider causality and correlation, and ensure the observability and availability of factors (Jian et al. 2021).

CO₂ emissions are often influenced by economic, demographic, and social factors. Economic development plays a vital role in determining CO₂ emissions. Generally, as the economy develops, there is an increased demand for energy, particularly fossil fuels, which leads to a rise in CO₂ emissions (He et al. 2022). Continuous population growth has led to a corresponding increase in industrial production, transportation, and agricultural activities, further contributing to CO₂ emissions (Huo et al. 2023). Income levels also strongly correlate with CO₂ emissions, as higher-income countries and individuals are more capable of implementing measures that help reduce CO₂ emissions. Conversely, low-income levels often face greater economic pressures and development needs, posing challenges in reducing CO₂ emissions. Energy and industrial infrastructure also contribute significantly to CO₂ emissions. As sustainable energy sources such as solar and wind become more common, the energy mix will gradually shift toward low-carbon solutions (Mohsin et al. 2022). Similarly, the industrial structure is shifting from high-emission to low-emission sectors, resulting in lower CO₂ emissions (He et al. 2022). In addition, the pace of urbanization greatly impacts CO₂ emissions. As urban areas expand, the population in cities increases, leading to greater demand for infrastructure and transportation, subsequently driving up energy consumption and CO₂ emissions (Mohsin et al. 2019).

Statistical models

Statistical modeling is a well-known method to extrapolate future CO₂ emission trends based on historical data and relevant factors. This helps to understand the changing patterns of CO₂ emissions, assess the effectiveness of environmental policies, and formulate sustainable development strategies (Ding and Zhang 2023).

The linear regression model is a widely used statistical approach that relies on a linear equation. In this model, the dependent variable is CO₂ emissions, while the independent variables represent the associated factors. By analyzing historical data and fitting the model, researchers can assess the extent to which each independent variable affects CO₂ emissions. Moreover, this model facilitates the prediction of future emissions by leveraging these established relationships. Meng and Niu (2011) employed a logistic regression model to predict CO₂ emissions from various industries, such as industry, agriculture, and transportation. Xu et al. (2019) discussed the problem of the nonlinear auto regressive model with exogenous inputs (NARX). According to their predictions, China’s CO₂ emissions are expected to peak in 2029, 2031, and 2035 under low growth, moderate benchmark growth, and high growth scenarios, respectively. Karakurt and Aydin (2023) used regression models to project fossil fuel-related CO₂ emissions for the BRICS and MINT countries alone, and the results show that emissions will increase significantly in the future for both groups of countries.

In addition to linear regression models, several other statistical models can be used to predict CO₂ emissions. For example, time series analysis models can capture seasonal, trend, and cyclical variations in emissions. These models can be adjusted for different data characteristics to improve the accuracy of the forecast. In a study conducted by Chen et al. (2022a), the STRPAT method was employed to identify factors influencing CO₂ emissions from energy consumption in 30 regions in China. They combined this approach with an ARIMA model to predict the trend of CO₂ emissions in 2023, revealing a continued increase in China’s emissions and a widening disparity in CO₂ emissions per capita among provinces.

However, the statistical analysis model can produce accurate prediction results heavily depending on sufficient data input for parameter estimation (Wu et al. 2015). These models make inferences based on historical data and known factors, but they may not fully capture all the complexities and uncertainties of the future. Therefore, when using statistical models for CO₂ emission forecasting, it is imperative to exercise caution when interpreting the results and to complement them with insights from other disciplines and expert judgment.

Artificial intelligence models

The use of artificial intelligence (AI) models in predicting CO₂ emissions is becoming more common. As the amount of data increases and computational power improves, AI models can deal with complex nonlinear relationships to provide more accurate CO₂ emission predictions.

In real-world problems, single or hybrid AI models are usually used for prediction. Ren and Long (2021) predicted the carbon emissions of Guangdong Province from 2020 to 2060 using a fast-learning network (FLN) improved by the chicken swarm optimization (CSO) algorithm, verified the superiority of the model by three indicators, MAE, MAPE, and RMSE, and set up nine scenarios to explore the low-carbon development path. To ensure precise forecasting of Turkey’s transportation-related CO₂ emissions, Ağbulut (2022) employed three artificial intelligence techniques for prediction. There is also an interaction between the price fluctuation of fossil energy and CO₂ emissions. Kassouri et al. (2022) analyzed the coordinated movement between the US oil shock and the intensity of CO₂ emissions through a wavelet model. The study found that the rise in oil prices caused by the impact of oil demand and global economic activities cannot replace environmental policies aimed at reducing carbon emissions. Kong et al. (2022) assembled ensemble empirical mode decomposition (EEMD) and variational mode decomposition (VMD) to decompose the original data twice, applied partial autocorrelation function to select the optimal model inputs, and finally predicted the carbon emissions by long and short-term memory (LSTM) neural networks. The results show that the quadratic decomposition technique can improve the accuracy of the model, and the proposed model exhibits excellent accuracy compared with 12 other models.

It is important to note that AI models still face some challenges in predicting CO₂ emissions. The quality and quantity of data are critical for AI models to predict CO₂ emissions, and large-scale, high-quality datasets can provide more accurate model training and prediction results. As a result, incomplete data, uncertainty, and non-linear relationships may affect the accuracy of the models.

Grey prediction models

Artificial intelligence methods typically focus on big data and large samples, requiring a large amount of historical data, and statistical models rely on data for parameter estimation. However, predicting CO₂ emissions is a complex and dynamic issue influenced by various factors, including economic and social aspects. As society continues to evolve, it becomes increasingly important to consider the impact of new information. In situations characterized by limited or incomplete information, the grey prediction model has emerged as a valuable and effective technique (Liu et al. 2012). In recent decades, numerous researchers have introduced a range of extensible and innovative models built upon the foundation of the GM (1, 1) model, which serves as the fundamental grey model (Liu and Deng 2000). The GM (1, 1) model has undergone advancements and enhancements, which can be observed primarily in three aspects: optimization of model parameters (Yu et al. 2021), expansion of model structure (Zeng and Li 2021), and construction of combined models (Chen et al. 2021).

For the univariate grey prediction model, Wu et al. (2020) used a conformable fractional non-homogeneous grey model (CFNGM (1, 1, k, c)) to study the CO₂ emissions of the BRICS countries and predicted the emissions from 2019 to 2025 based on the model. The results demonstrated that the CFNGM (1, 1, k, c) model outperformed other models in prediction accuracy. Xie et al. (2021) introduced a continuous consistent fractional nonlinear grey Bernoulli model (CCFNGBM (1, 1)) for predicting CO₂ emissions resulting from fuel combustion in China. The parameters of the model are optimized by the Grey Wolf optimization (GWO) algorithm, and the experimental results showed that the prediction accuracy of the newly proposed optimized model was better than that of other benchmark models. Gao et al. (2022) created a fractional cumulative grey Gompertz model (FAGGM (1, 1)) based on Gompertz differential equations, which was validated on six carbon emission datasets, and the proposed model achieved the best predictions in all cases.

To conduct a comprehensive analysis of the factors that impact carbon emissions, building on the traditional multivariable model GM (1, N) (Tien 2012), Zeng et al. (2016) incorporated a linear correction term and the grey action quantity to enhance its structure, culminating in the development of the NGM (1, N) model. Experimental results verify that the model with improved structure yields higher prediction accuracy. Ding et al. (2020) identified the relevant influencing factors and established their strong nonlinear effects through grey relational analysis. Subsequently, they devised the discrete grey power model (DGPM (1, N)), capable of accounting for these nonlinear factors. Ye et al. (2021) introduced a new multivariate grey model with time delay, known as ATGM (1, N), for assessing the cumulative effects of CO₂ emissions in China’s transportation industry. Findings demonstrated that the model surpasses six competing models, which included DGM (1, N), GMC (1, N), DDGM (1, N), CDGM (1, N), MDL, and SVR. Wan et al. (2022) developed a grey multivariate prediction model based on dummy variables and their interactions for predicting CO₂ emissions from primary energy consumption in Guangdong Province, and the prediction accuracies of the new model were 2.87% and 0.86% in the simulation and prediction phases, respectively, which were significantly better than those of the other three competing models. Ding et al. (2023b) developed a new grey multivariate coupled model (CTGM (1, N)) for carbon emission prediction to fit the CO₂ emissions of three countries, namely, China, the USA, and Japan, which introduced Choquet fuzzy integrals and grey multivariate delays and was compared with six reference models. The results of the performance tests demonstrated that the CTGM (1, N) model exhibits remarkable stability in predicting carbon emissions.

The grey prediction model described above has shown promising results in predicting CO₂ emissions. However, to further enhance the accuracy of the predictions, it is suggested to incorporate fractional-order cumulative operators and optimized background value coefficients. By introducing these elements, the model has the potential to enhance the precision of its predictions. Furthermore, by optimizing the relevant parameters through the use of optimization algorithms, the effectiveness of the model can be greatly improved.

Although much academic attention has been devoted to CO₂ emissions, previous studies on CO₂ emission projections have primarily focused on specific countries or regions, rather than considering per capita emissions, and have led to differences in projection results due to different data and influencing factors. And it is still a difficult research problem to synthesize the various factors and obtain accurate predictions. Therefore, this study proposes a novel multivariate grey prediction model, which optimizes fractional order and background value coefficients to predict CO₂ emissions per capita. The model considers the contribution of human activities to CO₂ emissions, acknowledging the significant role of humans in driving carbon emissions. Moreover, the study incorporates various factors that impact carbon emissions into the prediction model, aiming to enhance its accuracy and reliability.

Methods

This section primarily introduces the proposed FBNGM (1, N, r) model and its related properties, along with the utilization of the whale optimization algorithm (WOA) (Mirjalili and Lewis 2016). Building on the NGM (1, N) model, initially introduced by Zeng et al. (2016), this study incorporates fractional order operators, background value coefficient, and the WOA algorithm to enhance the predictive accuracy of the NGM (1, N) model. In particular, through the utilization of the WOA algorithm, the fractional operator and background value of the FBNGM (1, N, r) model are optimized with effectiveness.

FBNGM (1, N, r) model

Definition 1. Assume ${{\varvec{Y}}}^{\left(0\right)}=\left({y}^{\left(0\right)}\left(1\right),{y}^{\left(0\right)}\left(2\right),\cdots ,{y}^{\left(0\right)}\left(n\right)\right)$ is a characteristic variable sequence, ${{\varvec{X}}}_{k}^{{}^{\left(0\right)}}=\left({x}_{k}^{\left(0\right)}\left(1\right),{x}_{k}^{\left(0\right)}\left(2\right),\cdots ,{x}_{k}^{\left(0\right)}\left(n\right)\right),k=\mathrm{2,3},\cdots N$ is the sequence of driving variable. ${{\varvec{Y}}}^{\left(1\right)}=\left({{\varvec{y}}}^{\left(1\right)}\left(1\right),{{\varvec{y}}}^{\left(1\right)}\left(2\right),\cdots ,{{\varvec{y}}}^{\left(1\right)}\left(n\right)\right)$ and ${{\varvec{X}}}_{k}^{{}^{\left(1\right)}}=\left({{\varvec{x}}}_{k}^{\left(1\right)}\left(1\right),{{\varvec{x}}}_{k}^{\left(1\right)}\left(2\right),\cdots ,{{\varvec{x}}}_{k}^{\left(1\right)}\left(n\right)\right),k=\mathrm{2,3},\cdots ,N$ are called first-order accumulated generating operation (1-AGO) sequences of ${{\varvec{Y}}}^{\left(0\right)}$ and ${{\varvec{X}}}_{k}^{\left(0\right)}$, respectively.where

$${{\varvec{y}}}^{\left(1\right)}\left(i\right)=\sum_{t=1}^{i}{y}^{\left(0\right)}\left(t\right),i=\mathrm{1,2},\cdots ,n$$

(1)

$${{\varvec{x}}}_{k}^{\left(1\right)}\left(i\right)=\sum_{t=1}^{i}{x}_{k}^{\left(0\right)}\left(t\right),i=\mathrm{1,2},\cdots ,n$$

(2)

Definition 2. Assume ${{\varvec{Y}}}^{\left(0\right)}$ and ${{\varvec{X}}}_{k}^{{}^{\left(0\right)}}$ are the initial sequence, ${{\varvec{Y}}}^{\left(r\right)}=\left({{\varvec{y}}}^{\left(r\right)}\left(1\right),{{\varvec{y}}}^{\left(r\right)}\left(2\right),\cdots {{\varvec{y}}}^{\left(r\right)}\left(n\right)\right)$ and ${{\varvec{X}}}_{k}^{{}^{\left(r\right)}}=\left({{\varvec{x}}}_{k}^{\left(r\right)}\left(1\right),{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right),\cdots ,{{\varvec{x}}}_{k}^{\left(r\right)}\left(n\right)\right)$ are called r-order accumulating generation (r-AGO) sequences of ${{\varvec{Y}}}^{\left(0\right)}$ and ${{\varvec{X}}}_{k}^{{}^{\left(0\right)}}$, respectively.where

$${{\varvec{y}}}^{\left(r\right)}\left(i\right)=\sum_{t=1}^{i}\frac{\boldsymbol{\Gamma }\left(r+i-t\right)}{\boldsymbol{\Gamma }\left(i-t+1\right)\boldsymbol{\Gamma }\left(r\right)}{y}^{\left(0\right)}\left(t\right),i=\mathrm{1,2},\cdots ,n$$

(3)

$${{\varvec{x}}}_{k}^{\left(r\right)}\left(i\right)=\sum_{t=1}^{i}\frac{\boldsymbol{\Gamma }\left({r}_{k}+i-t\right)}{\boldsymbol{\Gamma }\left(i-t+1\right)\boldsymbol{\Gamma }\left({r}_{k}\right)}{x}_{k}^{\left(0\right)}\left(t\right),i=\mathrm{1,2},\cdots ,n$$

(4)

${{\varvec{Y}}}^{\left(r-1\right)}=\left({{\varvec{y}}}^{\left(r-1\right)}\left(1\right),{{\varvec{y}}}^{\left(r-1\right)}\left(2\right),\cdots {{\varvec{y}}}^{\left(r-1\right)}\left(n\right)\right)$ is a sequence of (r − 1)-order accumulating generation ((r − 1)-AGO) sequences obtained through a transformation of the sequence ${{\varvec{Y}}}^{\left(0\right)}$.where

$${{\varvec{y}}}^{\left(r-1\right)}\left(i\right)=\sum_{t=1}^{i}\frac{\boldsymbol{\Gamma }\left(r-1+i-t\right)}{\boldsymbol{\Gamma }\left(i-t+1\right)\boldsymbol{\Gamma }\left(r-1\right)}{y}^{\left(0\right)}\left(t\right),i=\mathrm{1,2},\cdots ,n$$

(5)

${{\varvec{Z}}}^{\left(r\right)}=\left({z}^{\left(r\right)}\left(1\right),{z}^{\left(r\right)}\left(2\right),\cdots ,{z}^{\left(r\right)}\left(n\right)\right)$ is a background value sequence generated by the neighboring elements of ${{\varvec{Y}}}^{\left(r\right)}$,where

$${{\varvec{z}}}^{\left(r\right)}\left(i\right)=\xi \times {{\varvec{y}}}^{\left(r\right)}\left(i\right)+\left(1-\xi \right)\times {{\varvec{y}}}^{\left(r\right)}\left(i-1\right),\xi \in \left(\mathrm{0,1}\right),i=\mathrm{2,3},\cdots ,n$$

(6)

Theorem 1. Suppose ${{\varvec{Y}}}^{\left(r\right)}$, ${{\varvec{X}}}_{k}^{{}^{\left(r\right)}}$, and ${{\varvec{Z}}}^{\left(r\right)}$ are defined as Definitions 1 and 2, the FBNGM (1, N, r) model, which is a fractional multivariable grey prediction model with background value optimization, can be mathematically represented as follows:

$${{\varvec{y}}}^{\left(r-1\right)}\left(i\right)+p{z}^{\left(r\right)}\left(i\right)=\sum_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(i\right)+{q}_{1}\left(i-1\right)+{q}_{2},i=\mathrm{1,2},\cdots ,n$$

(7)

where p is the system development coefficient, ${m}_{k}{x}_{k}^{\left(r\right)}\left(i\right)$ is the driving term, and ${q}_{1}\left(i-1\right)$ and ${q}_{2}$ are the linear correction term and the grey action quantity term, respectively.

Definition 3. Assume ${{\varvec{Y}}}^{\left(0\right)}$ is the initial sequence, ${{\varvec{Y}}}^{\left(-r\right)}=\left({{\varvec{y}}}^{\left(-r\right)}\left(1\right),{{\varvec{y}}}^{\left(-r\right)}\left(2\right),\cdots {{\varvec{y}}}^{\left(-r\right)}\left(n\right)\right)$ is the r-order inverse accumulating generation (r-IAGO) sequence of ${{\varvec{Y}}}^{\left(0\right)}$,where

$${{\varvec{y}}}^{\left(-r\right)}\left(i\right)=\sum_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(r+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(r-t+1\right)}{y}^{\left(0\right)}\left(i-t\right),i=\mathrm{1,2},\cdots ,n$$

(8)

Theorem 2. Let ${{\varvec{Y}}}^{\left(r-1\right)}=\left({{\varvec{y}}}^{\left(r-1\right)}\left(1\right),{{\varvec{y}}}^{\left(r-1\right)}\left(2\right),\cdots ,{{\varvec{y}}}^{\left(r-1\right)}\left(n\right)\right)$ be the (r − 1)-order accumulating generation sequence of ${Y}^{\left(0\right)}$. Assume that ${{\varvec{Y}}}^{\left(0\right)}$, ${{\varvec{X}}}_{k}^{\left(r\right)}$, and ${{\varvec{Z}}}^{\left(r\right)}$ have been defined in Definitions 1 and 2. Then, the estimated parameter vector, i.e., $\widehat{{\varvec{g}}}={\left[{m}_{2},{m}_{3},\cdots ,{m}_{N},p,{q}_{1},{q}_{2}\right]}^{T}$, of FBNGM (1, N, r) satisfies:

• (i) if $n=N+3$ and $\left|{\varvec{M}}\right|\ne 0$ then $\widehat{{\varvec{g}}}={{\varvec{M}}}^{-1}{\varvec{W}}$;

• (ii) if $n>N+3$ and $\left|{{\varvec{M}}}^{T}{\varvec{M}}\right|\ne 0$ then $\widehat{{\varvec{g}}}={\left({{\varvec{M}}}^{T}{\varvec{M}}\right)}^{-1}{{\varvec{M}}}^{T}{\varvec{W}}$;

• (iii) if $n<N+3$ and $\left|{\varvec{M}}{{\varvec{M}}}^{T}\right|\ne 0$ then $\widehat{{\varvec{g}}}={{\varvec{M}}}^{T}{\left({\varvec{M}}{{\varvec{M}}}^{T}\right)}^{-1}{\varvec{W}}$

where

$$\begin{array}{cc}{\varvec{M}}=\left(\begin{array}{ccccccc}{{\varvec{x}}}_{2}^{\left(r\right)}\left(2\right)& {{\varvec{x}}}_{3}^{\left(r\right)}\left(2\right)& \cdots & {{\varvec{x}}}_{N}^{\left(r\right)}\left(2\right)& -{z}^{\left(r\right)}\left(2\right)& 1& 1\\ {{\varvec{x}}}_{2}^{\left(r\right)}\left(3\right)& {{\varvec{x}}}_{3}^{\left(r\right)}\left(3\right)& \cdots & {{\varvec{x}}}_{N}^{\left(r\right)}\left(3\right)& -{z}^{\left(r\right)}\left(3\right)& 2& 1\\ \vdots & \vdots & & \vdots & \vdots & \vdots & \vdots \\ {{\varvec{x}}}_{2}^{\left(r\right)}\left(n\right)& {{\varvec{x}}}_{3}^{\left(r\right)}\left(n\right)& \cdots & {{\varvec{x}}}_{N}^{\left(r\right)}\left(n\right)& -{z}^{\left(r\right)}\left(n\right)& n-1& 1\end{array}\right),& {\varvec{W}}=\left(\begin{array}{c}{{\varvec{y}}}^{\left(r-1\right)}\left(2\right)\\ \begin{array}{c}{{\varvec{y}}}^{\left(r-1\right)}\left(3\right)\\ \vdots \end{array}\\ {{\varvec{y}}}^{\left(r-1\right)}\left(n\right)\end{array}\right)\end{array}$$

Proof. Substitute $i=\mathrm{2,3},\cdots n$ into Eq. (7), we can obtain

$$\left\{\begin{array}{l}{{\varvec{y}}}^{\left(r-1\right)}\left(2\right)=\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)-p{z}^{\left(r\right)}\left(2\right)+{q}_{1}+{q}_{2}\\ {{\varvec{y}}}^{\left(r-1\right)}\left(3\right)=\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(3\right)-p{z}^{\left(r\right)}\left(3\right)+2{q}_{1}+{q}_{2}\\ \vdots \\ {{\varvec{y}}}^{\left(r-1\right)}\left(n\right)=\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(n\right)-p{z}^{\left(r\right)}\left(n\right)+\left(n-1\right){q}_{1}+{q}_{2}\end{array}\right.$$

(9)

The matrix form of Eq. (9) is

$${\varvec{W}}={\varvec{M}}\widehat{{\varvec{g}}}$$

(10)

• (i) When $n=N+3$ and $\left|{\varvec{M}}\right|\ne 0$, then M is an invertible matrix; Eq. (10) has a unique solution.

• (ii) When $n>N+3$, M is a column full rank matrix and $\left|{{\varvec{M}}}^{T}{\varvec{M}}\right|\ne 0$, then M can be discomposed into the product of a $\left(n-1\right)\times \left(N+2\right)$ matrix B and a $\left(N+2\right)\times \left(N+2\right)$ matrix C, i.e., ${\varvec{M}}={\varvec{B}}{\varvec{C}}$. Therefore, the generalized inverse matrix ${{\varvec{M}}}^{\dagger}$ of M can be given by

  $${{\varvec{M}}}^{\dagger}={{\varvec{C}}}^{T}{\left({\varvec{C}}{{\varvec{C}}}^{T}\right)}^{-1}{\left({{\varvec{B}}}^{T}{\varvec{B}}\right)}^{-1}{{\varvec{B}}}^{T}$$

  (11)

  Then, the estimated parameter vector: $\widehat{{\varvec{g}}}$ can be expressed as follows:

  $$\widehat{{\varvec{g}}}={{\varvec{C}}}^{T}{\left({\varvec{C}}{{\varvec{C}}}^{T}\right)}^{-1}{\left({{\varvec{B}}}^{T}{\varvec{B}}\right)}^{-1}{{\varvec{B}}}^{T}{\varvec{W}}$$

  (12)

  Since M is a column full-rank matrix, let ${\varvec{C}}={{\varvec{I}}}_{N+2}$, we have

  $${\varvec{M}}={\varvec{B}}{\varvec{C}}={\varvec{B}}{{\varvec{I}}}_{N+2}={\varvec{B}}$$

  (13)

  then

  $$\begin{array}{l}\widehat{{\varvec{g}}}={{\varvec{C}}}^{T}{\left({\varvec{C}}{{\varvec{C}}}^{T}\right)}^{-1}{\left({{\varvec{B}}}^{T}{\varvec{B}}\right)}^{-1}{{\varvec{B}}}^{T}W\\ ={{\varvec{I}}}_{N+2}^{T}{\left({{\varvec{I}}}_{N+2}{{\varvec{I}}}_{N+2}^{T}\right)}^{-1}{\left({{\varvec{M}}}^{T}{\varvec{M}}\right)}^{-1}{{\varvec{M}}}^{T}W={\left({{\varvec{M}}}^{T}{\varvec{M}}\right)}^{-1}{{\varvec{M}}}^{T}W\end{array}$$

  (14)

• (iii) When $n<N+3$, M is a row full-rank matrix and $\left|{{\varvec{M}}}^{T}{\varvec{M}}\right|\ne 0$, then M can be discomposed into

  $${\varvec{M}}={{\varvec{I}}}_{m-1}{\varvec{C}}$$

  (15)

Similar to point (ii), we can rewrite Eq. (12) as

$$\begin{array}{l}\widehat{{\varvec{g}}}={{\varvec{C}}}^{T}{\left({\varvec{C}}{{\varvec{C}}}^{T}\right)}^{-1}{\left({{\varvec{B}}}^{T}{\varvec{B}}\right)}^{-1}{{\varvec{B}}}^{T}W\\ ={{\varvec{M}}}^{T}{\left({\varvec{M}}{{\varvec{M}}}^{T}\right)}^{-1}{\left({{\varvec{I}}}_{m-1}^{T}{{\varvec{I}}}_{m-1}\right)}^{-1}{{\varvec{I}}}_{m-1}^{T}W={{\varvec{M}}}^{T}{\left({{\varvec{M}}}^{T}{\varvec{M}}\right)}^{-1}W\end{array}$$

(16)

End of proof.

Theorem 3. Given M, W, and $\widehat{{\varvec{g}}}$ as stated in Theorem 2, then.

• (i) Expressed below is the time-response equation for the model in Eq. (7)

  $$\begin{array}{cc}\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(r\right)}(i)=\sum\limits_{u=1}^{i-1}\left[{{\varvec{\eta}}}_{1}\sum\limits_{k=2}^{N}{{\varvec{\eta}}}_{2}^{u-1}{{\varvec{m}}}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}(i-u+1)\right]\\ +{{\varvec{\eta}}}_{2}^{i-1}{\widehat{{\varvec{y}}}}^{\left(r\right)}(1)+\sum\limits_{j=0}^{i-2}{{\varvec{\eta}}}_{2}^{j}\left[(i-j){{\varvec{\eta}}}_{3}+{{\varvec{\eta}}}_{4}\right]\end{array}& i=\mathrm{1,2},\cdots ,n\end{array},$$

  (17)

• (ii) Below is the final restored form of the FBNGM (1, N, r) model:

  $$\begin{array}{cc}\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(0\right)}\left(i\right)=\sum\limits_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(r+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(r-t+1\right)}\left\{\sum\limits_{u=1}^{i-1}\left[{{\varvec{\eta}}}_{1}\sum\limits_{k=2}^{N}{{\varvec{\eta}}}_{2}^{u-1}{{\varvec{m}}}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}(i-u+1)\right]\right.\\ \left.+{{\varvec{\eta}}}_{2}^{i-1}{\widehat{{\varvec{y}}}}^{\left(r\right)}(1)+\sum\limits_{j=0}^{i-2}{{\varvec{\eta}}}_{2}^{j}\left[(i-j){{\varvec{\eta}}}_{3}+{{\varvec{\eta}}}_{4}\right]\right\}\end{array}& i=\mathrm{1,2},\cdots ,n\end{array}$$

  (18)

where

${\widehat{{\varvec{y}}}}^{\left(r\right)}\left(1\right)={y}^{\left(0\right)}\left(1\right)$, ${\eta }_{1}=\frac{1}{1+p\xi }$, ${\eta }_{2}=\frac{1-p+p\xi }{1+p\xi }$, ${\eta }_{3}=\frac{{q}_{1}}{1+p\xi }$, ${\eta }_{4}=\frac{{q}_{2}}{1+p\xi }$

The proof of (i). According to Definition 2 and Theorem 1, we have

$${{\varvec{y}}}^{\left(r-1\right)}\left(i\right)=\sum_{k=2}^{N}{{\varvec{m}}}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(i\right)-p{z}^{\left(r\right)}\left(i\right)+{q}_{1}\left(i-1\right)+{q}_{2}$$

(19)

$${{\varvec{z}}}^{\left(r\right)}\left(i\right)=\xi \times {{\varvec{y}}}^{\left(r\right)}\left(i\right)+\left(1-\xi \right)\times {{\varvec{y}}}^{\left(r\right)}\left(i-1\right)$$

(20)

Since

$${{\varvec{y}}}^{\left(r-1\right)}\left(i\right)={{\varvec{y}}}^{\left(r\right)}\left(i\right)-{{\varvec{y}}}^{\left(r\right)}\left(i-1\right)$$

(21)

Substituting Eqs. (21) and (20) into Eq. (19), we have

$$\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i\right)-{\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i-1\right)\\ =\sum\limits_{k=2}^{N}{{\varvec{m}}}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(i\right)-p\left[\xi \times {\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i\right)+\left(1-\xi \right)\times {\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i-1\right)\right]+{q}_{1}\left(i-1\right)+{q}_{2}\end{array}$$

(22)

Then, we can obtain

$${\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i\right)=\frac{1}{1+p\xi }\sum_{k=2}^{N}{{\varvec{m}}}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(i\right)+\frac{1-p+p\xi }{1+p\xi }\widehat{{\varvec{y}}}\left(i-1\right)+\frac{{q}_{1}}{1+p\xi }\left(i-1\right)+\frac{{q}_{2}-{q}_{1}}{1+p\xi }$$

(23)

Let

${\eta }_{1}=\frac{1}{1+p\xi }$, ${\eta }_{2}=\frac{1-p+p\xi }{1+p\xi }$, ${\eta }_{3}=\frac{{q}_{1}}{1+p\xi }$, ${\eta }_{4}=\frac{{q}_{2}-{q}_{1}}{1+p\xi }$

Then, Eq. (23) becomes

$${\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i\right)={\eta }_{1}\sum_{k=2}^{N}{{\varvec{m}}}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(i\right)+{\eta }_{2}\widehat{{\varvec{y}}}\left(i-1\right)+{\eta }_{3}i+{\eta }_{4}$$

(24)

According to Eq. (24), when i = 2, we get

$${\widehat{{\varvec{y}}}}^{\left(r\right)}\left(2\right)={\eta }_{1}\sum_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)+{\eta }_{2}\widehat{{\varvec{y}}}\left(1\right)+2{\eta }_{3}+{\eta }_{4}$$

(25)

When i = 3, we have

$${\widehat{{\varvec{y}}}}^{\left(r\right)}\left(3\right)={\eta }_{1}\sum_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(3\right)+{\eta }_{2}\widehat{{\varvec{y}}}\left(2\right)+3{\eta }_{3}+{\eta }_{4}$$

(26)

Substituting Eq. (25) into Eq. (26), we obtain

$$\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(r\right)}\left(3\right)={\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(3\right)+{\eta }_{2}\left[{\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)+{\eta }_{2}\widehat{{\varvec{y}}}\left(1\right)+2{\eta }_{3}+{\eta }_{4}\right]+3{\eta }_{3}+{\eta }_{4}\\ ={\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(3\right)+{\eta }_{2}{\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)+{\eta }_{2}^{2}\widehat{{\varvec{y}}}\left(1\right)+2{\eta }_{2}{\eta }_{3}+{\eta }_{2}{\eta }_{4}+3{\eta }_{3}+{\eta }_{4}\end{array}$$

(27)

No general expression can be found from Eq. (27), so we need to continue to so the derivation.

When i = 4, we can get

$${\widehat{{\varvec{y}}}}^{\left(r\right)}\left(4\right)={\eta }_{1}\sum_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(4\right)+{\eta }_{2}\widehat{{\varvec{y}}}\left(3\right)+4{\eta }_{3}+{\eta }_{4}$$

(28)

By substituting Eq. (27) into Eq. (28), we can derive

$$\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(r\right)}\left(4\right)={\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(4\right)+{\eta }_{1}{\eta }_{2}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(3\right)+{\eta }_{1}{\eta }_{2}^{2}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)\\ +{\eta }_{2}^{3}\widehat{{\varvec{y}}}\left(1\right)+2{\eta }_{2}^{2}{\eta }_{3}+{\eta }_{2}^{2}{\eta }_{4}+3{\eta }_{2}{\eta }_{3}+{\eta }_{2}{\eta }_{4}+4{\eta }_{3}+{\eta }_{4}\end{array}$$

(29)

$$\vdots$$

When i = v, we can get

$$\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(r\right)}\left(v\right)={\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(v\right)+{\eta }_{1}{\eta }_{2}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(v-1\right)+\cdots +{\eta }_{1}{\eta }_{2}^{v-2}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)\\ +{\eta }_{2}^{v-1}\widehat{{\varvec{y}}}\left(1\right)+2{\eta }_{2}^{v-2}{\eta }_{3}+{\eta }_{2}^{v-2}{\eta }_{4}+3{\eta }_{2}^{v-3}{\eta }_{3}+{\eta }_{2}^{v-3}{\eta }_{4}+\cdots +v{\eta }_{3}+{\eta }_{4}\end{array}$$

(30)

In Eq. (30), let

$$\begin{array}{c}E={\eta }_{1}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(v\right)+{\eta }_{1}{\eta }_{2}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(v-1\right)+\cdots +{\eta }_{1}{\eta }_{2}^{v-2}\sum\limits_{k=2}^{N}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(2\right)\\ =\sum\limits_{u=1}^{v-1}\left[{\eta }_{1}\sum\limits_{k=2}^{N}{\eta }_{2}^{u-2}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}\left(v-u+1\right)\right]\end{array}$$

$$\begin{array}{c}F=2{\eta }_{2}^{v-2}{\eta }_{3}+{\eta }_{2}^{v-2}{\eta }_{4}+3{\eta }_{2}^{v-3}{\eta }_{3}+{\eta }_{2}^{v-3}{\eta }_{4}+\cdots +v{\eta }_{3}+{\eta }_{4}\\ =\sum\limits_{j=0}^{v-2}{\eta }_{2}^{j}\left[\left(v-j\right){\eta }_{3}+{\eta }_{4}\right]\end{array}$$

By substituting E and F into Eq. (30), then Eq. (30) can be simplified as

$$\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(r\right)}(i)=\sum\limits_{u=1}^{i-1}\left[{\eta }_{1}\sum\limits_{k=2}^{N}{\eta }_{2}^{u-1}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}(i-u+1)\right]\\ +{\eta }_{2}^{i-1}{\widehat{{\varvec{y}}}}^{\left(r\right)}(1)+\sum\limits_{j=0}^{i-2}{\eta }_{2}^{j}\left[(i-j){\eta }_{3}+{\eta }_{4}\right]\end{array}$$

(31)

The proof of (ii). According to the Definition 3

$${{\varvec{y}}}^{\left(-r\right)}\left(i\right)=\sum_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(r+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(r-t+1\right)}{y}^{\left(0\right)}\left(i-t\right),i=\mathrm{1,2},\cdots ,n$$

Then, we have

$${\widehat{{\varvec{y}}}}^{\left(0\right)}\left(i\right)=\sum_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(r+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(r-t+1\right)}{\widehat{{\varvec{y}}}}^{\left(r\right)}\left(i\right),i=\mathrm{1,2},\cdots ,n$$

(32)

By substituting Eq. (31) into Eq. (32), we can obtain the ultimate prediction equation for the FBNGM (1, N, r) model, which is presented below:

$$\begin{array}{c}{\widehat{{\varvec{y}}}}^{\left(0\right)}\left(i\right)=\sum\limits_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(r+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(r-t+1\right)}\left\{\sum\limits_{u=1}^{i-1}\left[{\eta }_{1}\sum\limits_{k=2}^{N}{\eta }_{2}^{u-1}{m}_{k}{{\varvec{x}}}_{k}^{\left(r\right)}(i-u+1)\right]\right.\\ \left.+{\eta }_{2}^{i-1}{\widehat{{\varvec{y}}}}^{\left(r\right)}(1)+\sum\limits_{j=0}^{i-2}{\eta }_{2}^{j}\left[(i-j){\eta }_{3}+{\eta }_{4}\right]\right\}\end{array}$$

(33)

where $i=\mathrm{1,2},\cdots ,n$.

End of proof.

Therefore, Eq. (33) can be used to calculate the simulated and predicted values.

Whale optimization algorithm

Basic idea

The whale optimization algorithm (WOA) was introduced by Mirjalili and Lewis (2016), inspired by the hunting tactics of whales in their natural environment. The main goal of developing the WOA algorithm was to replicate the effective hunting strategies used by whales to solve complex optimization problems more efficiently. When a group of whales hunts together, one whale will inevitably find the prey first. When this happens, other whales will swim towards the successful whale to compete for the prey.

The WOA algorithm stands out due to its ability to mimic the hunting behavior of humpback whales, achieved by combining both optimal and random individuals. It also emulates the spiral movement patterns observed in humpback whales during bubble net attacks. The three phases of whales’ predatory behavior, which include encircling prey, bubble-net attacking, and active search for food, are all integrated into the WOA algorithm.

Mathematical model

This section delineates how the WOA algorithm models the three distinct predatory behaviors utilized by humpback whales: encircling prey, bubble-net attacking, and actively searching for prey, all expressed mathematically.

Encircling prey

Consider an optimization problem in a d-dimensional space, which has the position vector ${\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)$ of the optimal whale individual and the position vector $\overrightarrow{{\varvec{P}}}\left(t\right)$ of a whale individual at iteration t. At the (t + 1)-th iteration, the position vector of a whale individual, denoted as $\overrightarrow{{\varvec{P}}}\left(t+1\right)$, is affected by the presence of an optimal whale individual. The iterative formulas are as follows:

$$\overrightarrow{{\varvec{P}}}\left(t+1\right)={\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)-\overrightarrow{{\varvec{M}}}\cdot \overrightarrow{{\varvec{N}}}$$

(34)

$$\overrightarrow{{\varvec{N}}}=|\overrightarrow{{\varvec{R}}}\cdot {\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)-\overrightarrow{{\varvec{P}}}\left(t\right)|$$

(35)

$$\overrightarrow{{\varvec{M}}}=2\overrightarrow{{\varvec{c}}}\cdot {\overrightarrow{{\varvec{s}}}}_{1}-\overrightarrow{{\varvec{c}}}$$

(36)

$$\overrightarrow{{\varvec{R}}}=2\cdot{\overrightarrow{{\varvec{s}}}}_{2}$$

(37)

where || and $\cdot$ in the calculation formula of $\overrightarrow{{\varvec{N}}}$ represent the absolute value and element by element multiplication, respectively. As the iteration progresses, the vector $\overrightarrow{{\varvec{c}}}$ decreases steadily from an initial value of 2 to a final value of 0, following a linear pattern. ${\overrightarrow{{\varvec{s}}}}_{1}$ and ${\overrightarrow{{\varvec{s}}}}_{2}$ are random vectors in[0,1].

Figure 2 illustrates the principle of Eq. (35) for the 2D problem. By adjusting the values of $\overrightarrow{{\varvec{M}}}$ and $\overrightarrow{{\varvec{R}}}$, you can get the best position around the agent. Furthermore, the position of a search agent can be ascertained by making a comparison with the location of the optimal agent.

Fig. 2

Position vector and possible next location of the whale (Mirjalili and Lewis 2016)

Bubble-net attacking

One of the distinctive hunting techniques employed by humpback whales is bubble-net attacking. To mimic this behavior, two mathematical equations have been developed:

• a) Shrinking encircling mechanism

  The mathematical model for the bubble-net attacking behavior closely resembles the previous model used to simulate the behavior of prey, with the primary difference being the range of values for $\overrightarrow{{\varvec{M}}}$ used in the equations. This behavior is achieved by decreasing $\overrightarrow{{\varvec{c}}}$ in Eq. (36). From Eq. (36), it can be seen that $\overrightarrow{{\varvec{M}}}$ will also decrease when $\overrightarrow{{\varvec{c}}}$ decreases. During each iteration, the vector $\overrightarrow{{\varvec{M}}}$ is a random value between − c and c, where $\overrightarrow{{\varvec{c}}}$ linearly decreases from 2 to 0. That is, the range of $\overrightarrow{{\varvec{M}}}$ is $\left[-\mathrm{2,2}\right]$. Assuming that $\overrightarrow{{\varvec{M}}}$ is a random vector within the range of [− 1, 1], any point lying between the initial position and optimal position will serve as the new position for the whale. When $0\le M\le 1$, all potential locations in 2D space that can be obtained by moving from point $\left({\varvec{P}},{\varvec{Q}}\right)$ to point $\left({{\varvec{P}}}^{*},{{\varvec{Q}}}^{*}\right)$ are considered.

• b) Spiral updating position

  The process of this mechanism can be represented as shown in Fig. 3(b). In this way, the distance between the whale located at $\left({\varvec{P}},{\varvec{Q}}\right)$ and prey located at $\left({{\varvec{P}}}^{*},{{\varvec{Q}}}^{*}\right)$ can be calculated. The spiral position update equation is as follows:

  $$\overrightarrow{{\varvec{X}}}\left(t+1\right)={\overrightarrow{{\varvec{N}}}}^{\prime}\cdot {e}^{bl}\cdot {\text{cos}}\left(2\pi l\right)+{\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)$$

  (38)

  In the above equation, ${\overrightarrow{{\varvec{N}}}}^{\prime}=\left|{\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)-\overrightarrow{{\varvec{P}}}\left(t\right)\right|$ represents the distance between the whale and prey, b is a constant, l is a random number in $\left[-\mathrm{1,1}\right]$.

Fig. 3

Bubble-net search mechanism implemented in WOA: (a) shrinking encircling mechanism and (b) spiral updating position (Mirjalili and Lewis 2016)

As humpback whales pursue their prey, they navigate along a spiral path, progressively tightening their movements into an encircling motion. To replicate this behavior, the simulation involves a 50% chance of employing the contraction mechanism or spiral model to adjust the whale’s position during optimization. The mathematical representation of this model is as follows:

$$\overrightarrow{{\varvec{P}}}\left(t+1\right)=\left\{\begin{array}{c}{\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)-\overrightarrow{{\varvec{M}}}\cdot \overrightarrow{{\varvec{N}}}ifp<0.5\\ {\overrightarrow{{\varvec{N}}}}^{\prime}\cdot {e}^{bl}\cdot cos\left(2\pi l\right)+{\overrightarrow{{\varvec{P}}}}^{*}\left(t\right)ifp>0.5\end{array}\right.$$

(39)

In Eq. (39), p is a random value in 0 to 1.

Search for prey

In the prey predation stage, the random value of $\left|\overrightarrow{{\varvec{M}}}\right|\ge 1$ is used to force the whale to expand the search range. During this process, the whale’s position is updated via a random position. The corresponding mathematical model is as follows:

$$\overrightarrow{{\varvec{K}}}=\left|\overrightarrow{{\varvec{R}}}\cdot {\overrightarrow{{\varvec{P}}}}_{\text{rand}}-\overrightarrow{{\varvec{P}}}\right|$$

(40)

$$\overrightarrow{{\varvec{P}}}\left(t+1\right)={\overrightarrow{{\varvec{P}}}}_{\text{rand}}-\overrightarrow{{\varvec{M}}}\cdot \overrightarrow{{\varvec{K}}}$$

(41)

where ${\overrightarrow{{\varvec{P}}}}_{\text{rand}}$ represents the whale position vector randomly determined in the current population. Figure 4 illustrates the feasible positions that can be achieved with varying $\left|\overrightarrow{{\varvec{M}}}\right|\ge 1$ values.

Fig. 4

Exploration mechanism implemented in WOA (Mirjalili and Lewis 2016)

A set of initial solutions is randomly generated to initiate the WOA algorithm. In each iteration, the whale updates its position according to the randomly selected solution or the current optimal solution. That is, when $\left|\overrightarrow{{\varvec{M}}}\right|\ge 1$, randomly select a solution to update the whale’s position; when $\left|\overrightarrow{{\varvec{M}}}\right|<1$, the new location of whales is selected by the current best solution. Meanwhile, WOA switches freely between the two mechanisms of spiral position update and shrinking encircling mechanism according to the value of p.

The flowchart of WOA algorithm is shown in Fig. 5(b).

Fig. 5

The flowchart of the proposed grey model in this study

Modeling process of the proposed model

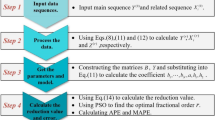
To optimize the background value parameter α and order r in the proposed FBNGM (1, N, r) model, the WOA algorithm is employed. The modeling process of the resulting optimized FBNGM (1, N, r) model is shown in Fig. 5, and further elaborated as follows:

• Step 1: Select the characteristic variable sequence and driving variable sequence.

• Step 2: Eqs. (3) and (4) are used to calculate the r-AGO sequences ${{\varvec{Y}}}^{\left(r\right)}$ and ${{\varvec{X}}}_{k}^{\left(r\right)},k=\mathrm{2,3},\cdots ,N$ with unknown orders r, using Eqs. (5) and (6) to calculate the $\left(r-1\right)$-AGO sequences ${{\varvec{Y}}}^{\left(r-1\right)}$ and background value sequence ${{\varvec{Z}}}^{\left(r\right)}$ with unknown fractional order r and background value parameter α.

• Step 3: Based on the sequences ${{\varvec{Y}}}^{\left(r\right)}$, ${{\varvec{X}}}_{k}^{\left(r\right)},k=\mathrm{2,3},\cdots ,N$, ${{\varvec{Y}}}^{\left(r-1\right)}$, and ${{\varvec{Z}}}^{\left(r\right)}$, the parameter matrices M and W for the FBNGM (1, N, r) model are constructed. Subsequently, the values of each parameter in the parameter vector $\widehat{{\varvec{g}}}={\left[{m}_{2},{m}_{3},\cdots ,{m}_{N},p,{q}_{1},{q}_{2}\right]}^{T}$ for the FBNGM (1, N, r) model is estimated given an unknown order r and background value parameter α.

• Step 4: Utilizing the WOA algorithm, the parameters r and α are optimized. Based on the obtained optimal values of r and α, the estimated value of each parameter in the parameter vector $\widehat{{\varvec{g}}}={\left[{m}_{2},{m}_{3},\cdots ,{m}_{N},p,{q}_{1},{q}_{2}\right]}^{T}$ is calculated, thereby establishing the FBNGM (1, N, r) model.

• Step 5: The performance of the FBNGM (1, N, r) model is evaluated in both the training and test sets by calculating metrics such as mean absolute error (MAE), absolute percentage error (APE), mean absolute percentage error (MAPE), and root mean square error (RMSE).

• Step 6: If the performance of the FBNGM (1, N, r) model meets the accuracy requirements, the model is used to predict future values. The predicted future values are then analyzed, and relevant policy recommendations and suggestions that can be implemented are proposed based on the analysis.

Model application

In this section, two numerical case studies are performed to assess the efficacy of the newly developed FBNGM (1, N, r) model in predicting CO₂ emissions per capita. To further assess the effectiveness of the FBNGM (1, N, r) model, three univariate grey models (NGM (1, 1), FNGM (1, 1), and FBNGM (1, 1)), two multivariable grey models (NGM (1, N) and FNGM (1, N)), a statistical model MLR, a machine learning model SVR, and a neural network model BPNN are compared the model proposed in this study. Furthermore, APE, MAE, RMSE, and MAPE introduced in “Evaluation criteria” are also utilized to analyze the errors of the nine models established in each case. Additionally, the specific experimental data, model evaluation criteria, and analysis and discussion of the experimental results are described in detail as follows.

Data description

Case 1 adopts CO₂ emissions per capita data collected from the World Bank for model training and testing, and case 2 uses CO₂ emissions per capita data (see Table 1) calculated based on fossil energy consumption data obtained from the China Statistical Yearbook 2021 and carbon emission factor coefficients and carbon emission factors obtained from a combination of research institutes (see Table 2).

Table 1 Actual value of total energy consumption, the proportion of coal, petroleum, and natural gas, population, and CO₂ emissions per capita from 1990 to 2022

Table 2 Carbon emission factor coefficients from the consumption of three fossil energy sources

According to the setup of the multivariate model of this study, six factors affecting CO₂ emissions are introduced:

• (1) Economic: Sustained economic growth is usually accompanied by a high level of energy consumption and extensive resource utilization, which leads to an increase in the emission of large quantities of greenhouse gases, such as CO₂ (Jian et al. 2021). This study selects GDP per capita as the economic factor, referencing existing studies.

• (2) Income: In general, as the economic development and per capita income level of a country or region increase, carbon emissions usually increase (Ehigiamusoe and Dogan 2022). Therefore, this study uses the disposable income of residents as an income indicator to introduce the model.

• (3) Transportation: With population growth, accelerated urbanization, and economic activities, the demand for transportation is increasing, and transportation involves the use of large amounts of energy, which in turn contributes to the generation of carbon emissions (Jiang et al. 2022). In this study, the volume of goods transported is used as an indicator to reflect transportation.

• (4) Urbanization rate: Since urbanization is associated with increased energy demand, transport development, and industrialization, an increase in the rate of urbanization tends to be associated with an increase in carbon emissions (Xiaomin and Chuanglin 2023).

• (5) Energy structure: an irrational energy structure will bring great harm to the ecological environment and the physical and mental health of the people, as well as pose a potential threat to the sustainable development of China’s economy, therefore, it is crucial to transition to cleaner energy sources and to reduce dependence on fossil fuels (Li et al. 2021b). The proportion of clean energy is selected in this study as an indicator of energy structure.

• (6) Industrial structure: China’s industrialization is accelerating, and the secondary industry, which is high in energy consumption and pollution, is the main source of CO₂ emissions, and the adjustment of industrial structure has an important impact on emission reduction (Wang et al. 2019). In this study, the proportion of added value of the secondary industry in GDP is included in the prediction model of CO₂ emission as an influential factor to measure the industrial structure.

Except for the CO₂ data, all the other data have been obtained from the National Bureau of Statistics of China. For the first case study, annual CO₂ emissions per capita data from 1990 to 2020 are collected and divided into two sets: the training set (1990–2016) and the test set (2017–2020). The training set is used to build the model, and its performance is evaluated by applying the model to the test set. The training set for the second case study is the years 1990 to 2015, while the data as the test set used to evaluate performance in the model spans the years 2016 to 2022.

Data processing

This study converts fossil fuel consumption into CO₂ emissions per capita, as CO₂ emissions are closely linked to the consumption of fossil fuels. To achieve this, the consumption of each fossil fuel type is calculated by considering the total energy consumption and the proportion of different fossil fuel sources. Specifically, the consumptions of coal, oil, and natural gas are determined using the following formula:

$${\varvec{E}}{{\varvec{C}}}_{i}={\varvec{E}}\times {k}_{i},i=\mathrm{1,2},3$$

(42)

where E is the total energy consumption. ${\varvec{E}}{{\varvec{C}}}_{i}\left(i=\mathrm{1,2},3\right)$ represents the corresponding consumption of coal, oil, and natural gas, respectively. ${k}_{i}\left(i=\mathrm{1,2},3\right)$ represents the proportion of coal, oil, and natural gas, respectively. All data are listed in Table 1.

Second, the CO₂ emissions are determined using the calculation formula from the Intergovernmental Panel on Climate Change (IPCC). The equation used for this calculation is as follows:

$${\varvec{C}}{\varvec{E}}=\sum {\varvec{E}}{{\varvec{C}}}_{i}\times {\varvec{E}}{{\varvec{F}}}_{i}\times \frac{44}{12}$$

(43)

In Eq. (43), CE means CO₂ emissions, ${\varvec{E}}{{\varvec{F}}}_{1},{\varvec{E}}{{\varvec{F}}}_{2},{\varvec{E}}{{\varvec{F}}}_{3}$ represent the CO₂ emissions factors corresponding to coal, oil, and natural gas, respectively. Among them, the value of ${\varvec{E}}{{\varvec{C}}}_{i}\left(i=\mathrm{1,2},3\right)$ determined by studying the literature. Then, the CO₂ emissions coefficients measured by the six institutions are averaged, as shown in Table 2.

Then, the CO₂ emissions per capita can be calculated according to the following equation.

$${\varvec{P}}{\varvec{C}}{\varvec{E}}={\varvec{C}}{\varvec{E}}/{\varvec{P}}$$

(44)

where, ${\varvec{P}}{\varvec{C}}{\varvec{E}}$ is CO₂ emissions per capita, and the P is the number of permanent residents at the end of the year. See Table 1 for calculation results. A visualization of the data trends for CO₂ emissions per capita and all influencing factors for both cases is shown in Fig. 6.

Fig. 6

All data visualizations

Finally, the CO₂ emissions per capita and all influencing factors data in the two cases are standardized by the following formula to eliminate their different dimensions.

$${{\varvec{y}}}_{1}^{\left(0\right)}\left(i\right)=\frac{{y}^{\left(0\right)}\left(i\right)}{{y}^{\left(0\right)}\left(1\right)},i=\mathrm{1,2},\cdots ,n$$

(45)

$${{\varvec{x}}}_{k1}^{\left(0\right)}\left(i\right)=\frac{{x}_{k}^{\left(0\right)}\left(i\right)}{{x}_{k}^{\left(0\right)}\left(1\right)},i=\mathrm{1,2},\cdots ,n,k=\mathrm{2,3},\cdots ,N$$

(46)

Evaluation criteria

To appraise the precision of the proposed model’s predictions, this study employs four criteria: mean absolute error (MAE) (Yang et al. 2024), absolute percentage error (APE), mean absolute percentage error (MAPE) (Cai et al. 2023), and root mean square error (RMSE) (Zhao et al. 2022). Table 3 provides a breakdown of each of these criteria and their associated abbreviations. Additionally, Table 4 outlines the classification system used for the model grade based on the MAPE.

Table 3 The evaluation criteria for model performance

Table 4 Benchmark of modelling accuracy evaluation level about MAPE (Zhou et al. 2020)

Case study 1 — China’s CO₂ emissions per capita from the World Bank

For this subsection, CO₂ emissions per capita data from the World Bank spanning the decade of 1990 to 2020 is used. Specifically, data from 1990 to 2017 is utilized to construct the model, while data from 2018 to 2020 is reserved for testing the model’s performance.

Empirical calculation and results

According to the modeling steps and flowchart introduced in “Modeling process of the proposed model”, the CO₂ emissions per capita (${{\varvec{Y}}}^{\left(0\right)}$) of the research object and the influencing factors GDP per capita (${{\varvec{X}}}_{2}^{\left(0\right)}$), volume of goods transported (${{\varvec{X}}}_{3}^{\left(0\right)}$), disposable income of residents (${{\varvec{X}}}_{4}^{\left(0\right)}$), urbanization rate (${{\varvec{X}}}_{5}^{\left(0\right)}$), proportion of clean energy (${{\varvec{X}}}_{6}^{\left(0\right)}$), and proportion of added value of the secondary industry (${{\varvec{X}}}_{7}^{\left(0\right)}$) are brought into the optimized FBNGM (1, N, r) model, and the optimized fractional order and background value coefficients are obtained as follows:

$$\begin{array}{c}r=0.7730,{r}_{2}=0.9246,{r}_{3}=0.1460,{r}_{4}=0.8579,\\ {r}_{5}=0.0212,{r}_{6}=0.7449,{r}_{7}=0.9492,\xi =0.5113\end{array}$$

Thus, the parameter vector $\widehat{{\varvec{g}}}$ of the model can be obtained and further the time response equation of the FBNGM (1, N, r) model can be obtained:

$$\widehat{{\varvec{g}}}={\left[0.1267,-0.0579,-\mathrm{0.1318,21.6486},-\mathrm{0.2111,1.8964,0.5457},-2.3449,-22.1811\right]}^{T} \begin{array}{c}{\widehat{y}}^{\left(0\right)}\left(i\right)={{y}^{\left(0\right)}\left(1\right)}\times\sum\limits_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(0.7730+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(0.7730-t+1\right)}\left\{\sum\limits_{u=1}^{i-1}\left[0.7818\times \sum\limits_{k=2}^{N}{0.5733}^{u-1}\times \right.\right.\\ \left(0.1267\times {x}_{2}^{\left(r\right)}(i-u+1)\right.-0.0579\times {x}_{3}^{\left(r\right)}(i-u+1)-0.1318\times {x}_{4}^{\left(r\right)}(i-u+1)\\ \left.\left.+21.6486\times {x}_{5}^{\left(r\right)}(i-u+1)-0.2111\times {x}_{6}^{\left(r\right)}(i-u+1)+1.8964\times {x}_{7}^{\left(r\right)}(i-u+1)\right)\right]\\ \left.+{0.5733}^{i-1}{\widehat{y}}^{\left(r\right)}(1)+\sum\limits_{j=0}^{i-2}{0.5733}^{j}\left[-1.8333(i-j)-15.5088\right]\right\}\end{array}$$

Forecasting performance evaluation

To illustrate the efficacy of the proposed model, this has been evaluated by comparing with two multivariate models (NGM (1, N), FNGM (1, N)), three univariate models (NGM (1, 1), FNGM (1, 1), and FBNGM (1, 1)), a statistical model (MLR), a machine learning model (SVR), and a neural network model (BPNN). The findings for each evaluation criterion are presented in Table 5, which is based on the assessment of the accuracy and performance of all nine models using the criteria in the “Evaluation criteria.” An intuitive way to assess the performance and accuracy of various approaches is to create bar charts. Figure 7 displays the comparison chart. Figure 8 shows a box plot of the APE indicator. Additionally, Fig. 9 shows the curves produced by the various models that represent the expected values and matching observed values. In addition, the experimental data will undergo three comparisons: (1) a comparison between the proposed model and univariate grey models; (2) a comparison between the proposed model and multivariate grey models; and (3) a comparison between the proposed model and non-grey models.

Table 5 Comparison of the prediction accuracies of the six models

Fig. 7

Comparison of evaluation criteria for case 1

Fig. 8

Comparison of APE results for the nine models in case 1

Fig. 9

Comparison of the observed and simulated values of the nine models for case 1

(1). For the univariate grey prediction model, the original model, NGM (1, 1), obtained the worst prediction results in both the training and test stages (10.81% and 15.27%, respectively). Although its MAE and RMSE values in the training stage are lower than the other two univariate grey prediction models, the MAPE value is the highest and the NGM (1, 1) model is the only univariate model with a MAPE value higher than 10% in the test stage. The FBNGM (1, 1) model is the only model with a MAPE value lower than 10% in the training stage (MAPE = 9.46%) and achieved the best prediction results in the test stage (MAPE = 1.94%). In addition, the accuracy of the NGM (1, 1) model in the training phase is higher than the accuracy in the test phase, suggesting that the model produced an overfitting phenomenon, which is avoided by the model proposed in this study.

In terms of APE value distribution, as shown in Fig. 8, the APE values of the NGM (1, 1), FNGM (1, 1), and FBNGM (1, 1) models in the training phase span from 0.45 to 26.35%, 0.00 to 29.24%, and 0.00 to 23.10%, respectively. The APE values of the three models in the testing phase span from 12.08 to 18.56%, 1.33 to 5.28%, and 0 to 3.87%, and it is clear that the FBNGM (1, 1) model proposed in this study performs best on case 1.

The results show that the fractional order model FBNGM (1, 1) proposed in this study with optimized background value coefficients fits and predicts best for case 1 in the univariate model.

(2). For the multivariate grey prediction models, it can be obtained from Table 5 and Fig. 7 that the accuracies of the three multivariate grey prediction models are higher than the univariate grey prediction models in the training stage, which indicates that the influences added in this study are effective and enhance the prediction effect of the models. For the evaluation index MAPE, FBNGM (1, N, r) has a value of 1.29% in the training stage, which is 2.9% higher than the NGM (1, N) model and 0.04% higher than the FNGM (1, N) model, while in the testing stage, the prediction accuracy of the FBNGM (1, N, r) model is 0.61%, which is 7.97% and 25.86% higher than the other two multivariate grey prediction models, respectively. For the indicators MAE and RMSE, although the FBNGM (1, N, r) model and the FNGM (1, N) model have the same results in the testing stage, the FBNGM (1, N, r) model reflects a clear advantage in the testing stage.

For the APE metrics that respond to the distribution of errors, according to the box-and-line diagram in Fig. 8, it can be obtained that in the training stage, the distributions of the FNGM (1, N) and FBNGM (1, N, r) models are the same, while the error fluctuation of the NGM (1, N) model is more drastic. However, it is clear that the FBNGM (1, N, r) model has the smallest error fluctuation in the testing phase, and the accuracy of the model is significantly better than that of the FNGM (1, N) and NGM (1, N) models.

It follows that effective influences improve the accuracy of the model. The fractional order cumulative operator can better mine the data trend, and the optimized background value coefficient can further improve the accuracy of the model.

(3). For the non-grey models (MLR, SVR, and BPNN), it can be seen from Table 5 and Fig. 7 that all three models achieved superior prediction accuracy in the training phase, whereas only the MLR model had a prediction accuracy of less than 10% in the testing phase. BPNN is the best-performing non-grey model in the training phase (MAPE = 2.29%) and MLR is the best-performing non-grey model in the testing phase (MAPE = 5.13%). However, the non-grey model accuracy is significantly lower compared to the 1.29% and 0.61% of the FBNGM (1, N, r) model proposed in this study. The low accuracy of the machine learning model SVR and the neural network model BPNN can be attributed to the small amount of data, which is insufficient for model training. Although the amount of data may satisfy the requirements of statistical modeling, the accuracy is still not as good as the model proposed in this study.

In terms of error distribution, the accuracy of the non-grey model, which integrates multiple influencing factors, is higher than that of the non-grey model in the training phase despite the sparser data. The accuracies of the multivariate grey prediction models, except for the NGM (1, N) model, are higher than those of the machine learning model SVR and the neural network model BPNN in the testing stage. The accuracy of the non-grey model is not as good as most of the grey prediction models in the testing stage, but in general, the model proposed in this study achieves the highest accuracy.

Based on the above analysis, it can be concluded that the FBNGM (1, N, r) model proposed in this study can fully mine the data information and avoid the phenomenon of overfitting. In addition, from the prediction results in Fig. 9, the fitting and prediction effects of the FBNGM (1, N, r) model are closer to the real data.

Case study two — CO₂ emissions per capita calculated from the energy data

For this section, the statistics on energy and influencing factors from 1990 to 2022 are chosen, and the CO₂ emissions per capita from energy are computed using the technique described in “Data processing.” The data between 1990 and 2015 are used for modeling, while the data between 2016 and 2022 are kept for testing.

Empirical calculation and results

According to the procedure in “Modeling process of the proposed model,” the fractional order for the study object and each influencing factor and background value coefficient of the FBNGM (1, N, r) model in case two are as follows:

$$\begin{array}{c}r=0.8650,{r}_{2}=0.9871,{r}_{3}=0.7953,{r}_{4}=0.5114,\\ {r}_{5}=0.9898,{r}_{6}=0.5955,{r}_{7}=0.6531,\xi =0.4931\end{array}$$

Then, the parameter vector $\widehat{{\varvec{g}}}$ can be received:

$$\widehat{{\varvec{g}}}={\left[-0.0751,-\mathrm{0.0319,0.2388,3.0528},-\mathrm{0.5238,3.0247,0.8787},-4.0098,-4.3738\right]}^{T}$$

The time-response expression of the FBNGM (1, N, r) can be expressed by

$$\begin{array}{c}{\widehat{y}}^{\left(0\right)}\left(i\right)={{y}^{\left(0\right)}\left(1\right)}\times\sum\limits_{t=0}^{i-1}{\left(-1\right)}^{t}\frac{\boldsymbol{\Gamma }\left(0.8650+1\right)}{\boldsymbol{\Gamma }\left(t+1\right)\boldsymbol{\Gamma }\left(0.8650-t+1\right)}\left\{\sum\limits_{u=1}^{i-1}\left[1.0400\times \sum\limits_{k=2}^{N}{1.3800}^{u-1}\times \right.\right.\\ \left(-0.0751\times {x}_{2}^{\left(r\right)}(i-u+1)\right.-0.0319\times {x}_{3}^{\left(r\right)}(i-u+1)-0.2388\times {x}_{4}^{\left(r\right)}(i-u+1)\\ \left.\left.+3.0528\times {x}_{5}^{\left(r\right)}(i-u+1)-0.5238\times {x}_{6}^{\left(r\right)}(i-u+1)+3.0247\times {x}_{7}^{\left(r\right)}(i-u+1)\right)\right]\\ \left.+{1.3800}^{i-1}{\widehat{y}}^{\left(r\right)}(1)+\sum\limits_{j=0}^{i-2}{1.3800}^{j}\left[-2.7976(i-j)-0.2540\right]\right\}\end{array}$$

Table 6 presents the calculated evaluation metrics for the MAE, MAPE, and RMSE indexes. Correspondingly, Fig. 10 visualizes the results of the evaluation indicators.

Table 6 Comparison of the prediction accuracies of the six models

Forecasting performance evaluation

To thoroughly investigate the applicability of the proposed model FBNGM (1, N, r), several other prediction models are included in the comparison. These models consist of three univariate grey prediction models, two multivariate grey prediction models, and three non-grey prediction models. The performance of all nine models is assessed using the metrics described in “Evaluation criteria.” Histograms of the evaluation metrics are plotted for both the training and test phases, as shown in Fig. 10. Additionally, box plots of the APE values are generated to examine error fluctuations (Fig. 11), and comparisons between simulated and actual values are shown in the form of curves (Fig. 12). The following discussion will provide an analysis of the results obtained from both the training and test phases.

Fig. 10

Comparison of evaluation criteria for case 2. Note: The NGM (1, N) model is not shown in this figure because the error fluctuations are too large

Fig. 11

Comparison of APE results for the nine models in case 2

Fig. 12

Comparison of observed and simulated values of the six models

Regarding the training phase, the NGM (1, N) model demonstrated the poorest performance, with a MAPE value of 64.19%. This value is 63.15% higher than the model proposed in this study, which exhibited the highest accuracy. The performance in the metrics MAE and RMSE is still the worst for the NGM (1, N) model. And for the multivariate grey prediction model with added influencing factors and non-grey prediction model except NGM (1, N) have higher accuracy than the univariate grey prediction model, which indicates that the NGM (1, N) model fails to mine all the information of the data. From Fig. 10, the FBNGM (1, N, r) model proposed in this study performs better than the other two multivariate models and the non-grey prediction model in three indicators. In addition, from Fig. 11, the largest error fluctuations are univariate prediction models in addition to the NGM (1, N) model, which suggests that the influencing factors chosen in this study enhance the prediction accuracy of the model.

As for the discussion of the test stage, only four models, FNGM (1, N), FBNGM (1, N, r), MLR, and BPNN, have MAPE values below 10%, which are 2.49%, 1.38%, 5.32%, and 6.32%, respectively. The MAPE values for the univariate models all exceeded 10%, indicating the crucial role of the influencing factors in predicting CO₂ emissions per capita. From Fig. 10, the best-performing model in terms of MAPE, MAE, and RMSE is the FBNGM (1, N, r) model proposed in this study. Further, from Fig. 11, we can conclude that except for the worst-performing NGM (1, N) model, the NGM (1, 1) model has the largest error fluctuation, which leads to the conclusion that the NGM (1, N) model performs poorly in both univariate and multivariate prediction. The SVR model also displayed suboptimal performance, which may be attributed to the sparse data.

Based on the above comparison of the accuracy of the models in the training and test phases and the comparison curves between the predicted and observed values in Fig. 11, it can be concluded that the FBNGM (1, N, r) model proposed in this study performs optimally among all the models, including univariate grey prediction model, multivariate grey prediction model, and non-grey prediction model.

Forecasting the future CO₂ emissions

After conducting a thorough analysis and rigorous comparison, the FBNGM (1, N, r) model developed in this study has emerged as the most effective tool for predicting CO₂ emissions per capita. Utilizing the FBNGM (1, 1) model, we forecast the influencing factors from 2022 to 2030 and employed Eq. (33) to predict the CO₂ emissions per capita for case 1 from 2021 to 2030 and case 2 from 2022 to 2030. The results of these projections are presented in Table 7.

Table 7 The predicted CO₂ emissions per capita from 2021 to 2030 in case 1 and from 2023 to 2030 in case 2 (unit: t)

The prediction results given in Table 7, and the future emission trends shown in Fig. 13 indicate that based on World Bank data, CO₂ emissions per capita are expected to continue to show an upward trend in the coming years. However, emission projections based on energy data from the National Bureau of Statistics of China show a downward trend in CO₂ emissions per capita from energy. The results of this projection can guide the relevant authorities in formulating effective planning.

Fig. 13

Future trends in CO₂ emissions per capita

Discussion and policy suggestions

As people’s consumption level continues to grow, CO₂ emissions are gradually becoming a major contributor to the acceleration of global warming. First of all, according to the Kuznets Environmental Curve (EKC) hypothesis, GDP per capita is closely related to CO₂ emissions (Aslam et al. 2021). The IPCC has implied in the early years that one of the effective ways to reduce the rate of global warming is to change the consumption level of the people (Luo et al. 2023). Secondly, China’s growing economic level is closely related to the consumption of large amounts of fossil energy. According to statistics, more than 80% of China’s primary energy consumption relies on fossil energy, which directly or indirectly emits large amounts of greenhouse gases (Li and Haneklaus 2021). More importantly, in the context of China’s coal-based economy, this has important implications for national development, environmental improvement, and energy security (Lin and Zhu 2019).

According to the proposed FBNGM (1, N, r) model, the CO₂ emissions per capita of the two cases by 2030 can be obtained. Based on the projected CO₂ emissions per capita by 2030 as demonstrated in Table 7 and Fig. 13, the following conclusions can be drawn: first, CO₂ emissions per capita from energy will start to decline from 2023, indicating that China’s policy measures in promoting clean energy use and reducing fossil energy consumption have been effective; second, although CO₂ emissions per capita from energy will decline in the future, the combined CO₂ emissions per capita will continue to rise, making it difficult to reach the peak in 2030. The study by Wang et al. (2019) also suggests that current energy efficiency and emission reduction measures and policies may not be sufficient to support the goal of peaking carbon emissions by 2030. Wu and Xu’s (2022) study also argues that some regions will not reach the peak by 2030. The study also suggests that China’s energy efficiency and emission reduction policies may not be sufficient to support the goal of peaking carbon emissions by 2030. The reason for this situation is that, in addition to CO₂ emissions from energy, CO₂ emissions from transportation, industrial production, and other sources have not been effectively controlled. Therefore, more relevant national and local emission reduction policies need to be put in place to achieve the target. Here are some suggestions given in this study:

• (1) Improving the low-carbon development policy system (Wang et al. 2021). The government should exercise its leading role in driving progress towards a greener future. This can be achieved by enhancing the existing green system, which encompasses energy conservation, environment protection, and low-carbon standards, in addition to establishing low-carbon entities such as hospitals, campuses, and institutions (Dalla Longa et al. 2022). In order to promote energy conservation and emission reduction, regulations must be put in place to gradually phase out energy consumption patterns that are detrimental to these goals. Policies relating to energy conservation and emission reduction should also be improved, to foster a more environmentally friendly development paradigm (Huang et al. 2022b).

• (2) In order to reduce carbon emissions, it is imperative that we encourage the greater adoption of clean energy sources in place of coal consumption (Gyamfi et al. 2021). As such, we must expedite the development of non-fossil energy and promote the widespread use of clean energy alternatives like wind and solar power. At present, China’s main energy consumption is still concentrated in non-clean energy such as coal and oil (Li et al. 2020). Relevant policy makers should pay close attention to it and formulate appropriate policies.

• (3) The optimal restructuring of industry represents a crucial means of achieving energy conservation and emission reduction goals. Carbon emissions and industrial structure interact with each other (Zhang et al. 2020). Manufacturing, industry and construction are the main areas that generate carbon emissions (Shan et al. 2020). To achieve our energy conservation and emission reduction objectives, we must undertake efforts to promote the low-carbon transformation of conventional industries and work towards the development of a new green, low-carbon economy. This can be accomplished through industrial restructuring and upgrading, wherein clean energy solutions progressively supplant fossil fuels. By reducing industrial energy consumption and carbon emissions, we can accelerate our transition towards a greener and more sustainable future.

• (4) Reducing carbon emissions in human consumption. On the premise of not lowering the living standard, there is a huge space for saving energy for residents (Wang et al. 2020). People are encouraged to travel low-carbon, take more public transport, and reduce the number of private cars. To conserve energy and reduce emissions, we must mindfully utilize electricity, fuel, and solar energy in our daily lives.

• (5) The recovery and reuse of renewable resources during the initial production process have the potential to significantly decrease carbon emissions (Chen et al. 2022b). For example, waste iron, battery recycling, garbage classification, and solid waste treatment are all effective ways to reduce carbon emissions.

Conclusion

Reducing CO₂ emissions is an urgent need for China to reach peak carbon emissions. Accurate prediction of CO₂ emissions will help China to formulate relevant policies and implement feasible measures to reduce CO₂ emissions. Several factors affect CO₂ emissions, among which population growth, economic expansion, urbanization, transportation, energy, and industrial structure have non-negligible correlations with CO₂ emissions. In this context, this study proposes a novel grey prediction model. By considering the influence of various aspects, two numerical cases of CO₂ emissions per capita are selected for modeling in this study, and the proposed model considers the influence of various aspects such as GDP per capita and urbanization rate, to improve the accuracy of prediction.

The theoretical framework of this study incorporates a fractional order operator in the NGM (1, N) model to enhance the impact of recent information and an optimized background value coefficient to improve prediction accuracy. Thus, the FNBGM (1, N, r) model is proposed. In addition, the WOA algorithm is utilized instead of the traditional technique of selecting coefficients to optimize the fractional order and background value coefficient. In addition, the least squares method is used to calculate the model parameters and derive the time response equation as a reliable tool for predicting future trends.

The empirical analysis of this study demonstrated the validity and accuracy of the proposed FBNGM (1, N, r) model, which is used to model the World Bank’s CO₂ emissions per capita data for the years 1990 to 2020, as well as the CO₂ emissions per capita data from energy calculated from the China Statistical Yearbook’s energy data for the years 1990 to 2022. In addition, this study conducts a comparative analysis to verify the validity of the FBNGM (1, N, r) model proposed in this paper. Specifically, univariate grey prediction models NGM (1, 1), FNGM (1, 1), FBNGM (1, 1), multivariate grey prediction models NGM (1, N) and FNGM (1, N) models and non-grey prediction models MLR, SVR, and BPNN were developed in this study using two numerical cases. On the training and test sets, using RMSE, MSE, APE, and MAPE to compare the accuracy of these models with the FBNGM (1, N, r) model. Based on the results of the comparative analysis, it can be concluded that the FBNGM (1, N, r) model proposed in this study has the highest accuracy compared to other models. The MAPE values for the training and test sets of case 1 are 1.29% and 0.61%, respectively. Meanwhile, the MAPE values for the training and test sets of case 2 are 1.04% and 1.38%, respectively. Based on the evaluation criteria listed in Table 3, it is evident that the proposed model performs well on both the training and test sets in the two specific cases studied.

Furthermore, this study utilizes the high-accuracy model proposed to predict future CO₂ emissions per capita for the two numerical cases. The results indicate that CO₂ emissions per capita from the energy sector are expected to continue decreasing from 2023 onwards, while the combined CO₂ emissions per capita will continue to increase. Based on the projections of this study, China has now achieved initial results in energy structure transformation, i.e., reducing fossil energy consumption and increasing clean energy consumption, and will need to further strengthen its carbon reduction efforts in transportation, industrial production, and other areas in the future. In addition, this study proposes a series of recommendations aimed at reducing CO₂ emissions per capita.

The results of the numerical case study convincingly demonstrate that the FBNGM (1, N, r) model proposed in this study accurately predicts CO₂ emissions per capita. However, there is still considerable work to be done to conduct a more comprehensive analysis of the characteristics of CO₂ emissions per capita. In future studies, it would be beneficial to investigate the differences in CO₂ emissions among countries with varying income levels and development situations. Moreover, the model can be enhanced in terms of its structure and other relevant aspects to attain an even higher level of accuracy.