Breakthrough modeling and experimental design for o-xylene dynamic adsorption onto clay material

Abstract

The adsorption of o-xylene onto raw clay material in a fixed bed using a thermal conductivity detector gas chromatography was investigated. Experimental and theoretical studies were established to evaluate the removal efficiency of o-xylene by adsorption on clay materials and to predict kinetic parameters. Column data were describing at different conditions using Bohart–Adams, Wolborska, Thomas, Yoon and Nelson, dose–response, and bed depth service time models. All used models were satisfactory to predict the breakthrough curves. A suitable advection–dispersion–sorption (ADS) model has been also developed to simulate the measured data, based on the nature of the various equilibrium relationships of solid–gas and diverse descriptions of the mass transfer processes within of the adsorbent particle. The experiments can be fitted with high correlated coefficient R ² = 0.996.

Introduction

Volatile organic compounds (VOCs) which have some toxicity have been contributing in some scale to atmospheric pollution (Pires et al. 2001). Therefore and due to the increasing attention on the environmental protection, there is growing public concern about the widespread contamination of air in order to reduce the emissions (Lin and Cheng 2002; Dammak et al. 2015).

Therefore, industries require cheap and effective technologies to reduce the concentration of these gases and vapor to accepted levels. Adsorption which is becoming a more and more popular technique for removal of pollutants has been found to be effective at low concentration (Gupta and Verma 2002). Among VOC, o-xylene is generally considered to be one of the organic pollutants discharged into the environment causing toxic effects on humans (Jones 1999).

The effectiveness of a clay adsorbent can be evaluated from the S-shaped breakthrough curves (Chu 2004; Muhamad et al. 2010; Dammak et al. 2013).

The aim of the present work is to investigate the effects of flow rate, bed depth, and the o-xylene inlet concentration on adsorption capacity by a fixed-bed column. In general, the models proposed for the recovery of gaseous pollutants assume that the adsorption mechanism is governed by mass transfer monitoring followed by the adsorption equilibrium and the kinetics of adsorption (Malek and Farooq 1997). In order to visualize the relationship between the various parameters influencing the mass transfer and the adsorption in the adsorbent bed of clay material, Bohart–Adams, Wolborska, Thomas, Yoon–Nelson, Clark, dose–response, bed depth service time (BDST), and mass transfer models were used to fit the experimental adsorption results. The results of coefficients obtained with modeling the continuous process can be scaled to an actual industrial column.

Materials and methods

Adsorbate and adsorbent

Clay material with average particle diameter of 0.85 mm was supplied from Jebel Sbih located in south of Tunisia in the region of Skhira. O-xylene (C₈H₁₀, 98%) was purchased from Fluka Analytical. The chemical composition of adsorbent was determined by X-ray fluorescence with an ARL1 9800 XP spectrometer. The mineralogical composition was determined by a Rigakud-Max 2200 model X-ray diffractometer. The specific area was determined by ASAP 2010 V5.02 H Unit 1 Serial # 844 apparatus.

Adsorption in continuous fixed-bed column

The column adsorption tests were applied in stainless steel column of 0.4-m height and 0.01-m inner diameter. Clay material was packed into the column. A certain amount of clay material (0.1, 0.15, 0.2 m) was loaded into the column. All the experiments were carried out at 20 °C using mixed gas of o-xylene and nitrogen as a gas carrier. The saturated vapor pressure of o-xylene was used to produce the desired concentrations by diluting with pure nitrogen gas in a flow of 0.27–0.63 × 10⁻³ m³ min⁻¹ to obtain o-xylene inlet concentration (C ₀) of 6.4–11.11 g m⁻³. Comparable operator conditions are used in similar researches (Lee et al. 1990; Minceva and Rodrigues 2004; Chafik et al. 2009; Huang et al. 2009).

The outlet concentrations were monitored using a gas chromatography (Shimadzu GC-2014) equipped with a thermal conductivity detector (TCD) and a packed column using a N₂ carried gas. The adsorption data were taken at 3-min sampling interval to monitor the adsorbent breakthrough until the adsorbent was saturated.

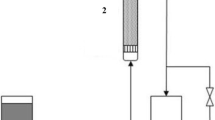
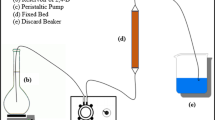
Then, the breakthrough curves with the form of variations of C/C ₀ versus time were obtained. Figure 1 illustrates the experimental configuration used for adsorption of o-xylene on a fixed bed.

Fig. 1

Experimental apparatus of o-xylene vapor sorption

Experimental design

A nonlinear model of degree 2 is sufficient to translate the relation cause and effect between the density (X ₁), Langmuir constant (X ₂), and the axial dispersion (X ₃) on one hand and the breakthrough time as studied answer (Ŷ) on the other hand. The calculation was performed with the statistical software “New Methodology for Efficient Research using Optimal Design (NEMROD)” to estimate the response in the predefined area.

$$ \widehat{\mathit{\mathsf{Y}}}={\mathit{\mathsf{b}}}_{\mathsf{0}}+\sum_{\mathit{\mathsf{i}}=\mathsf{1}}^{\mathsf{3}}{\mathit{\mathsf{b}}}_{\mathit{\mathsf{i}}}{\mathit{\mathsf{X}}}_{\mathit{\mathsf{i}}}+\sum_{\mathit{\mathsf{i}}=\mathsf{1}}^{\mathsf{3}}{\mathit{\mathsf{b}}}_{\mathit{\mathsf{i}\mathsf{i}}}{\mathit{\mathsf{X}}}_{\mathit{\mathsf{i}}}^{\mathsf{2}}+\sum_{\mathit{\mathsf{i}}\prec \mathit{\mathsf{j}}}^{\mathsf{3}}{\mathit{\mathsf{b}}}_{\mathit{\mathsf{i}\mathsf{j}}}{\mathit{\mathsf{X}}}_{\mathit{\mathsf{i}}}{\mathit{\mathsf{X}}}_{\mathit{\mathsf{j}}} $$

(1)

where Ŷ is the predicted response for breakthrough time, b ₀ the offset term, b _i the linear effect, b _ii the squared effect, and b _ij is the interaction effect.

The test factors were coded according to the following equation:

$$ {\mathit{\mathsf{X}}}_{\mathit{\mathsf{i}}}=\frac{{\mathit{\mathsf{Z}}}_{\mathit{\mathsf{i}}}-{\mathit{\mathsf{Z}}}_{\mathsf{0}}}{\Delta \mathit{\mathsf{Z}}} $$

(2)

where Z _i is the value of the independent variables, Z ₀ is the natural value of the independent variables at the center point, and ΔZ is the step change value.

Results and discussions

Clay characterization

The clay material composition is presented in Table 1. SiO₂ and Al₂O₃ are the major constituents of the clay with trace amounts of other oxides. The percentage of iron is relatively high which is typical of Tunisian clays. The mineralogical study by X-ray diffraction of clay material adsorbent presented in Fig. 2 shows that this material is mainly composed of 67% of the smectite (S), 9% of kaolinite (K), and a percentage of 11 and 13% of quartz (Q) and calcite (C), respectively. The specific surface area of clay adsorbent was 67 m² g⁻¹. More details of clay characterization are presented in previous paper (Dammak et al. 2015).

Table 1 Chemical composition of clay material

Fig. 2

X-ray diffraction patterns of clay material (S smectite, K kaolinite, Ph phyllosilicate, Q quartz, C calcite)

Dynamic adsorption

The effect of bed depth on the o-xylene adsorption in continuous packed bed was examined by varying the bed depth from 0.1 to 0.2 m where the inlet concentration and flow rate were constant at 6.4 g m⁻³ and 0.63 × 10⁻³ m³ min⁻¹, respectively. Figure 3 shows that the breakthrough time increased with the increase of bed depth. An increase in the bed height rises the distance for the mass transfer zone to reach the end of column and therefore an increase in the breakthrough time. O-xylene adsorption capacity increased (Table 2) when bed depth decreases as well as the breakthrough curve becomes steeper due to the increase of the mass transfer coefficient. The adsorption along the bed height is highest at the front face of column and decreases gradually in the bed exit. For adsorbents loaded as a random packing in column, a particle can be obstructed by another one in front of it. Thus, exposure time between particle and adsorbate molecules is reduced as well as adsorbed amount (Lua and Jandia 2009; Leyva-Ramos et al. 2007).

Fig. 3

Experimental and initial part of breakthrough model curves for o-xylene onto clay material at different flow rates, bed heights, and inlet o-xylene concentrations. 0.63 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (diamonds); 0.63 × 10⁻³ m³ min⁻¹, 0.15 m, 6.4 g m⁻³ (filled squares); 0.63 × 10⁻³ m³ min⁻¹, 0.2 m, 6.4 g m⁻³ (filled triangles); 0.63 × 10⁻³ m³ min⁻¹, 0.1 m, 8.77 g m⁻³ (filled circles); 0.63 × 10⁻³ m³ min⁻¹, 0.1 m, 11.11 g m⁻³ (empty squares); 0.45 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (empty triangles); 0.27 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (empty circles)

Table 2 Column data and parameters obtained at diverse flow rates, bed heights, and inlet o-xylene concentrations

Experiments were also led at different inlet o-xylene concentrations to observe the continuous adsorption performance of clay material. The breakthrough curves resulted by varying inlet o-xylene concentration from 6.4 to 11.11 g m⁻³ at 0.63 × 10⁻³ m³ min⁻¹ flow rate and 0.1-m bed height are shown in Fig. 3. With high inlet o-xylene concentrations, adsorbent is more quickly saturated and breakthrough curves were delayed. Taking the column adsorption performance into account, lowest inlet o-xylene concentration leads to better o-xylene removal (Table 2).

Figure 3 shows the breakthrough curves obtained at different flow rates (0.63–11.11 × 10⁻³ m³ min⁻¹), while bed height and inlet o-xylene concentration were held constant at 0.1 m and 6.4 g m⁻³, respectively. When the flow rate was reduced, breakthrough time increased and retained o-xylene decreased. This could be due to insufficient residence time of gas molecules in column in the case of high flow rate. At low flow rates, the thickness of the mass transfer boundary layer around the clay will raise, leading to enhanced external mass transfer resistance. These results are similar to those obtained by other researchers in fixed-bed adsorption studies for different VOC and different adsorbent materials (Huang et al. 2003; Yaneva et al. 2008; Zhang et al. 2010).

Models for the initial part of breakthrough curve

A satisfactory design of a column adsorption process demands prediction of the breakthrough curve for effluents (Han et al. 2009). Over the years, several simple mathematical models have been developed for describing and analyzing the practical size column studies for the purpose of industrial applications (Kumar and Chakraborty 2009; Vinodhini and Das 2010).

Several models were developed to predict the breakthrough performance and to determine the adsorption capacity and kinetic constants of fixed-bed columns (Hasan et al. 2010; Rao et al. 2011).

Bohart–Adams model

In 1920, Bohart and Adams (Bohart and Adams 1920) derived an equation to describe vapor profiles in adsorbent filter beds, by reporting experimental data for chlorine transmission through charcoal filters. They showed qualitative agreement with the experimental vapor profiles. Many workers (Aksu and Gönen 2006; Hamdaoui 2006; Calero et al. 2009; Vijayaraghavan and Prabu 2006) have subsequently extended the model to describe and quantify other types of systems. This model does not take into account the external film resistance and the intraparticle mass transfer resistance and assumes that the adsorption is done directly on the adsorbent surface (Ko et al. 2000). The original equation was given in the form:

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}=\frac{ \exp \left(\tau \right)}{ \exp \left(\tau \right)+ \exp \left(\xi \right)-\mathsf{1}}\ \mathsf{with}\ \left\{\begin{array}{l}\tau ={\mathit{\mathsf{K}}}_{\mathsf{BA}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}\times \left(\mathit{\mathsf{t}}-\frac{\mathit{\mathsf{Z}}}{\mathit{\mathsf{v}}}\right)\\ {}\xi =\frac{{\mathit{\mathsf{K}}}_{\mathsf{BA}}\times {\mathit{\mathsf{N}}}_{\mathsf{0}}\times \mathit{\mathsf{Z}}}{\mathit{\mathsf{v}}}\left(\frac{\mathsf{1}-\varepsilon}{\varepsilon}\right)\end{array}\right. $$

(3)

where τ and ξ are dimensionless time and distance coefficient, respectively, C ₀ is the initial o-xylene concentration, C is the concentration at time t, K _BA is the kinetic constant of Bohart–Adams model, N ₀ is the maximum volumetric adsorption capacity of bed, Z is the bed depth, v is the o-xylene velocity and ε is the void fraction of the bed.

To apply the Bohart–Adams model in order to design adsorbent beds requires precise knowledge of K _BA and N ₀ parameters. To predict these parameters’ effects of mass transfer, kinetics and equilibrium of adsorption should be determined. This fact is not easy, and Eq. (3) was fitted to the breakthrough data to determine these two parameters.

Bohart–Adams model is going to be applied to describe the primary part of the breakthrough curve, with concentration values lower than 0.15C ₀ (Sarin et al. 2006).

To facilitate Eq. (3), it can be written as

$$ \frac{{\mathit{\mathsf{C}}}_{\mathsf{0}}}{\mathit{\mathsf{C}}}-\mathsf{1}= \exp \left(\xi -\tau \right)- \exp \left(-\tau \right) $$

(4)

The term exp(τ) is usually small and can be neglected. For long times, the term Z/ν can be also neglected. Insert logarithms in Eq. (4):

$$ \ln \left(\frac{{\mathit{\mathsf{C}}}_{\mathsf{0}}}{\mathit{\mathsf{C}}}-\mathsf{1}\right)=\frac{{\mathit{\mathsf{K}}}_{\mathsf{BA}}\times {\mathit{\mathsf{N}}}_{\mathsf{0}}\times \mathit{\mathsf{Z}}}{\mathit{\mathsf{v}}}\left(\frac{\mathsf{1}-\varepsilon}{\varepsilon}\right)-{\mathit{\mathsf{K}}}_{\mathsf{BA}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}\times \mathit{\mathsf{t}} $$

(5)

To predict the value of K _BA and N ₀ from early breakthrough points using plots of C/C ₀ against t at a given inlet concentration, bed depth and flow rate are likely using the nonlinear regression.

Wolborska model

Wolborska model (1989) is used to describe the dynamic adsorption for low concentrations breakthrough using mass transfer equations. It is given by the following equation:

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}= \exp \left(\frac{\beta_{\mathit{\mathsf{a}}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}\times \mathit{\mathsf{t}}}{{\mathit{\mathsf{N}}}_{\mathsf{0}}}-\frac{\beta_{\mathit{\mathsf{a}}}\times \mathit{\mathsf{Z}}}{\mathit{\mathsf{u}}}\right) $$

(6)

where β _a the kinetic coefficient of the external mass transfer and N ₀ the maximum volumetric adsorption capacity of bed.

The expression of the Wolborska solution is equivalent to the Bohart–Adams relation if the coefficient k _BA is equal to β _a/N ₀ (Guibal et al. 1995).

When Bohart–Adams and Wolborska models were fitted to the full part of the breakthrough curves, they showed low fitness for all the breakthrough curves (not shown). That is why these models were applied only for the initial part of the curves (C/C ₀ < 0.5) (Fig. 3).

Parameters of these models are summarized in Table 3. The saturation concentration N ₀ decreased with increasing bed depth. Kinetic constants k _BA and β _a are generally not affected by the variation of bed depth, inlet o-xylene concentration, or flow rate.

Table 3 Bohart–Adams and Wolborska model parameters

Models for the total breakthrough curve

Thomas model

Thomas model (1944) is the most used model for describing breakthrough curves in the case of a fixed-bed adsorption. This model assumes that the axial dispersion is negligible in the column and the adsorption kinetics follows the Langmuir model (Morales Futulan et al. 2011). It is given by the following relation:

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}=\frac{\mathsf{1}}{\mathsf{1}+ \exp \left[\left(\frac{{\mathit{\mathsf{K}}}_{\mathsf{Th}}}{\mathit{\mathsf{Q}}}\right)\left({\mathit{\mathsf{q}}}_{\mathsf{0}}\times \mathit{\mathsf{m}}-{\mathit{\mathsf{C}}}_{\mathsf{0}}\times \mathit{\mathsf{Q}}\times \mathit{\mathsf{t}}\right)\right]} $$

(7)

where K _Th is the Thomas rate constant, q ₀ is the maximum concentration of the o-xylene in the solid phase, m is amount of adsorbent in the column, and Q is the flow rate of o-xylene.

Yoon–Nelson model

The Yoon–Nelson model (1984) is a relatively simple model developed for the first time to the adsorption of gases on activated charcoal. This model assumes that the rate of diminution in adsorption for every adsorbate molecule is relative to the probability of solute breakthrough on the adsorbent (Calero de Hoces et al. 2010). The equation for this model is

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}=\frac{\mathsf{1}}{\mathsf{1}+ \exp \left({\mathit{\mathsf{K}}}_{\mathsf{YN}}\left({\mathit{\mathsf{t}}}_{\mathsf{50}}-\mathit{\mathsf{t}}\right)\right)} $$

(8)

where K _YN is the Yoon–Nelson constant and t ₅₀ is the time required for retaining 50% of the initial adsorbate.

Clark model

A simulation was described by Clark (1987) for breakthrough curves. The model defined was based on mass transfer theory and the nonlinear equation of Freundlich (Hamdaoui 2006):

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}={\left(\frac{\mathsf{1}}{\mathsf{1}+\mathit{\mathsf{A}}\times {\mathit{\mathsf{e}}}^{-\mathit{\mathsf{r}}\times \mathit{\mathsf{t}}}}\right)}^{\mathsf{1}/\left(\mathit{\mathsf{n}}-\mathsf{1}\right)}\ \mathsf{with}\ \left\{\begin{array}{l}\mathit{\mathsf{A}}= \exp \left(\frac{{\mathit{\mathsf{K}}}_{\mathit{\mathsf{C}}}\times {\mathit{\mathsf{N}}}_{\mathsf{0}}\times \mathit{\mathsf{Z}}}{\mathit{\mathsf{u}}}\right)\\ {}\mathit{\mathsf{r}}={\mathit{\mathsf{K}}}_{\mathit{\mathsf{C}}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}\end{array}\right. $$

(9)

K _C is Clark constant and n is Freundlich constant.

Values of A and r can be determined via plot of C/C ₀ versus t at a given bed height and flow rate involving nonlinear regressive resolution.

Dose–response model

The dose–response model has been frequently used to describe different types of processes in biology such as biosorption in columns (Calero et al. 2009; Aksu and Gönen 2006; Yan et al. 2001). The dose–response model is represented by the equation

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}=\mathsf{1}-\frac{\mathsf{1}}{\mathsf{1}+{\left(\frac{{\mathit{\mathsf{C}}}_{\mathsf{0}}\times \mathit{\mathsf{Q}}\times \mathit{\mathsf{t}}}{{\mathit{\mathsf{q}}}_{\mathsf{0}}\times \mathit{\mathsf{m}}}\right)}^{\mathit{\mathsf{a}}}} $$

(10)

where a is a constant.

Bed depth service time model

It is one of the most widely used models that describe heavy metal adsorption using a fixed-bed column. BDST is a simple model to estimate the relation between the breakthrough time and bed height according to different sorption parameters as inlet concentration of process. In this model, the adsorption capacity of the bed is founded on experimental measuring at different breakthrough times. This model does not take into account the external film resistance and the intraparticle mass transfer resistance, and the solute is adsorbed onto the adsorbent surface (Qaiser et al. 2009). The BDST model can be used to estimate the required bed depth for a given service time. It is given by equation

$$ \frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}=\frac{\mathsf{1}}{\mathsf{1}+ \exp \left[{\mathit{\mathsf{K}}}_{\mathsf{BDST}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}\left(\frac{{\mathit{\mathsf{N}}}_{\mathsf{0}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}\times \mathit{\mathsf{u}}}\mathit{\mathsf{Z}}-\mathit{\mathsf{t}}\right)\right]} $$

(11)

where K _BDST is the adsorption rate constant that describes the mass transfer from fluid to the solid phase.

Table 4 lists the calculated Thomas, Yoon–Nelson, Clark, dose–response, and BDST model parameters from the experimental column data when inlet concentration, bed depth, and flow rate were varied. These parameters correspond to the best results of adsorption capacity obtained at a flow rate of 0.63 × 10⁻³ m³ min⁻¹, inlet concentration of 6.4 g m⁻³, and a bed depth of 0.1 m.

Table 4 Thomas, Yoon–Nelson, Clark, dose–response, and BDST model parameters

The Thomas, Yoon–Nelson, Clark, dose–response, and BDST models were modeled using Oakdale Engineering Data Fit 8.1 software.

The correlation coefficient values ranged from 0.994 to 0.999, indicating that all models were suitable for the description of the adsorption mechanisms for the total breakthrough curves (Table 4). Figure 4 shows the predicted and experimental breakthrough curves at different conditions and validates the correlation coefficient cited.

Fig. 4

Experimental and total breakthrough model curves for o-xylene onto clay material at different flow rates, bed heights, and inlet o-xylene concentrations. 0.3 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (diamonds); 0.63 × 10⁻³ m³ min⁻¹, 0.15 m, 6.4 g m⁻³ (filled squares); 0.63 × 10⁻³ m³ min⁻¹, 0.2 m, 6.4 g m⁻³ (filled triangles); 0.63 × 10⁻³ m³ min⁻¹, 0.1 m, 8.77 g m⁻³ (filled circles); 0.63 × 10⁻³ m³ min⁻¹, 0.1 m, 11.11 g m⁻³ (empty squares); 0.45 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (empty triangles); 0.27 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (empty circles)

For Thomas and dose–response, the predicted maximum adsorption capacities (q ₀) were in agreement and did not show a larger deviation (1.54%) using these two models.

Adsorption capacity increases with the decrease of initial concentration, which may be attributed to a slower saturation of adsorbent in fixed bed at low inlet concentration. A low inlet concentration causes slow transport of o-xylene from the film layer to the surface of adsorbent. This implies a decreased diffusion coefficient and decreased mass transfer driving force (Tor et al. 2009).

Thomas and dose–response models are suitable for adsorption processes (Calero et al. 2009; Han et al. 2008). The constant K _Th that characterized the ratio of adsorbate transfer from the fluid to the solid phase increased with flow rate. Thus, at higher flow rate, adsorbates did not have enough time to diffuse into the adsorbent material, and they passed the column fast before equilibrium occurred. High flow rates will moderate the thickness of the mass transfer boundary layer around the clay, leading to reduce external mass transfer resistance. Similar observation was shown in similar research (Chen et al. 2011; Lua and Jandia 2009; Acheampong et al. 2013).

The Yoon–Nelson model adequately describes the experimental data. The constant k _YN of Yoon–Nelson model increased with increasing initial concentration. The time necessary to reach 50% of the retention, t ₅₀, decreases significantly when the inlet concentration increased. The highest inlet concentration saturated the adsorption column more rapidly (Calero de Hoces et al. 2010). The calculated t ₅₀ values are similar to those acquired experimentally.

By analyzing the parameters of BDST model, the volumetric adsorption capacity, N ₀, decreases with increasing flow rate and bed depth (Muhamad et al. 2010).

In previous study (Dammak et al. 2014), Freundlich model was found to be valid for the adsorption of o-xylene, so the Freundlich constant obtained (n = 2.128) was used as parameter in Clark model. As seen in Table 4, as inlet o-xylene concentration increased, the values of r increased.

For all cited models, the correlation between the experimental and calculated data is not affected by the variation of parameters.

Advection–dispersion–sorption model

The simple models for adsorption in the columns (BDST, Thomas, Yoon–Nelson, etc.) fit experimental results fairly well. However, in order to obtain the transport parameters, another model based on the mass transfer has been developed. The mass balance led to the following second-order partial differential equation:

$$ \underset{\mathsf{I}}{\underbrace{-{\mathit{\mathsf{D}}}_{\mathsf{ax}}\frac{\partial^{\mathsf{2}}\mathit{\mathsf{C}}}{\partial {\mathit{\mathsf{Z}}}^{\mathsf{2}}}}}+\underset{\mathsf{I}\mathsf{I}}{\underbrace{\ \mathit{\mathsf{v}}\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{Z}}}\ }}+\underset{\mathsf{I}\mathsf{I}\mathsf{I}}{\underbrace{\kern0.5em \frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{t}}}\kern0.5em }}+\underset{\mathsf{I}\mathsf{V}}{\underbrace{\frac{\left(\mathsf{1}-\varepsilon \right)}{\varepsilon}\rho \frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}}}=\mathsf{0} $$

(12)

The initial conditions are $\mathsf{at}\ \mathit{\mathsf{t}}=\mathsf{0}\left\{\begin{array}{l}\mathit{\mathsf{C}}\left(\mathit{\mathsf{Z}},\mathsf{0}\right)=\mathsf{0}\\ {}\mathit{\mathsf{q}}\left(\mathit{\mathsf{Z}},\mathsf{0}\right)=\mathsf{0}\end{array}\right.$ _.

The boundary conditions are $\left\{\begin{array}{l}\mathit{\mathsf{Z}}=\mathsf{0}\Rightarrow \mathit{\mathsf{C}}\left(\mathsf{0},\mathit{\mathsf{t}}\right)={\mathit{\mathsf{C}}}_{\mathsf{0}}\\ {}\mathit{\mathsf{Z}}=\mathit{\mathsf{L}}\Rightarrow \frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{Z}}}=\mathsf{0}\end{array}\right.$.

Equation (12) is composed of four terms: the first describes axial dispersion, the second is an advection term, the third depicts the accumulation in fluid phase, and the fourth represents the accumulation in the solid phase. The resolution of Eq. (12), with initial and boundary conditions, leads to the solution of the problem of the fixed-bed adsorption.

Solution 1

Assuming a plug flow, we can neglect the axial dispersion (Simo et al. 2008). Modeling transport equations in a packed column depends greatly on the mechanism by which the mass transfer of solid–fluid occurs. External mass transfer is the diffusion of the solute through the boundary layer surrounding the adsorbent particle, whereas internal mass transfer is the diffusion within the porous network. Therefore, in the modeling of a column, the effects of mass transfer resistance, between the fluid and the particle on one hand and within the particle on the other hand, should be considered (Rutherford and Do 2000a, 2000b; Afzal et al. 2010; Leinekugel-le-Cocq et al. 2007). Glueckauf law is used to describe the internal mass transfer. Linear model was used to describe the adsorption isotherm.

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{1}}\right)\left\{\begin{array}{ll}\mathit{\mathsf{v}}\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{Z}}}+\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{t}}}+\frac{\left(\mathsf{1}-\varepsilon \right)}{\varepsilon}\rho \frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\mathsf{0}\hfill & \mathrm{Mass}\kern0.24em \mathrm{transfer}\kern0.24em \mathrm{balance}\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\frac{{\mathit{\mathsf{k}}}_{\mathit{\mathsf{f}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}}{\rho}\times \left(\mathit{\mathsf{C}}-{\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}\right)\;\hfill & \mathrm{External}\kern0.24em \mathrm{diffusion}\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}\times \left({\mathit{\mathsf{q}}}_{\mathit{\mathsf{i}}}-\mathit{\mathsf{q}}\right)\hfill & \mathrm{Internal}\kern0.24em \mathrm{diffusion}\kern0.24em \left(\mathrm{Gleuckauf}\right)\hfill \\ {}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{i}}}=\mathit{\mathsf{k}}\times \mathit{\mathsf{C}}{}_{\mathit{\mathsf{i}}}\hfill & \mathrm{Adsorption}\kern0.24em \mathrm{isotherm}\kern0.24em \left(\mathrm{Linear}\right)\hfill \end{array}\right. $$

(13)

with ${\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}=\frac{\mathsf{6}\left(\mathsf{1}-\varepsilon \right)}{{\mathit{\mathsf{d}}}_{\mathit{\mathsf{p}}}}$ and ${\mathit{\mathsf{K}}}_{\mathit{\mathsf{S}}}={\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}=\frac{\mathsf{60}\times {\mathit{\mathsf{D}}}_{\mathsf{eff}}}{{\mathit{\mathsf{d}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}$.

To solve Eq. (3), the term $\left(\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}\right)$ must be calculated by combining equations of the system (S ₁). We assume that the adsorption kinetics is controlled by both external and internal diffusion.

Posing $\mathit{\mathsf{x}}=\frac{\mathit{\mathsf{C}}}{{\mathit{\mathsf{C}}}_{\mathsf{0}}}$; $\mathit{\mathsf{z}}=\frac{\mathit{\mathsf{Z}}}{\mathit{\mathsf{L}}}$; ${\mathsf{A}}_{\mathsf{1}}=\frac{\mathsf{v}}{\mathsf{L}}=\frac{\mathsf{u}}{\mathsf{L}\times \kern0ex \epsilon}$; ${\mathit{\mathsf{A}}}_{\mathsf{2}}=\frac{\rho \times \left(\mathsf{1}-\varepsilon \right)}{\varepsilon \times {\mathit{\mathsf{C}}}_{\mathsf{0}}}$; ${\mathit{\mathsf{K}}}_{\mathit{\mathsf{G}}}=\frac{{\mathit{\mathsf{k}}}_{\mathit{\mathsf{f}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}}{\rho}$; ${\mathit{\mathsf{K}}}_{\mathit{\mathsf{s}}}={\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}=\frac{\mathsf{15}\times {\mathit{\mathsf{D}}}_{\mathsf{eff}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}$and $\mathit{\mathsf{K}}=\mathit{\mathsf{k}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}$, the system of equations (S ₁) becomes

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{1}}\right)\left\{\begin{array}{l}\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{t}}}=-{\mathit{\mathsf{A}}}_{\mathsf{1}}\left(\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{z}}}\right)-{\mathit{\mathsf{A}}}_{\mathsf{2}}\left(\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}\right)\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{K}}}_{\mathit{\mathsf{G}}}\times \left(\mathit{\mathsf{x}}-\left(\frac{{\mathit{\mathsf{K}}}_{\mathit{\mathsf{G}}}\times \mathit{\mathsf{x}}+{\mathit{\mathsf{K}}}_{\mathit{\mathsf{S}}}\times \mathit{\mathsf{q}}}{{\mathit{\mathsf{K}}}_{\mathit{\mathsf{S}}}\times \mathit{\mathsf{K}}+{\mathit{\mathsf{K}}}_{\mathit{\mathsf{G}}}}\right)\right)\hfill \end{array}\right. $$

(14)

Initial conditions $\left\{\begin{array}{l}\mathit{\mathsf{t}}=\mathsf{0}\\ {}\mathit{\mathsf{x}}\left(\mathit{\mathsf{z}},\mathsf{0}\right)=\mathsf{0}\\ {}\mathit{\mathsf{q}}\left(\mathit{\mathsf{z}},\mathsf{0}\right)=\mathsf{0}\end{array}\right.$.

Boundary conditions $\left\{\begin{array}{l}\mathit{\mathsf{z}}=\mathsf{0}\Rightarrow \mathit{\mathsf{x}}\left(\mathsf{0},\mathit{\mathsf{t}}\right)=\mathsf{1}\\ {}\mathit{\mathsf{z}}=\mathsf{1}\Rightarrow \frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{z}}}=\mathsf{0}\end{array}\right.$.

The mass transfer models were modeled using COMSOL 4.2 software. The solution 1, described in Fig. 5, shows a deviation from the experimental data (R ² = 0.203). The parameters obtained from mathematical modeling of this solution are given in Table 5. The use of a linear isotherm does not describe the experience properly. Therefore, adsorption isotherm of clay and o-xylene is nonlinear. Improved analytic solution for the system can be obtained using Langmuir isotherm.

Fig. 5

The four solutions for the mass transfer model breakthrough curves for o-xylene onto clay material; 0.63 × 10⁻³ m³ min⁻¹, 0.1 m, 6.4 g m⁻³ (diamonds)

Table 5 Mass transfer model parameters

Solution 2

For this solution, the differential equation system (S ₂) is composed of the same equations than those of (S ₁); only the adsorption isotherm equation becomes the nonlinear equation of Lagmuir.

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{2}}\right)\left\{\begin{array}{ll}\mathit{\mathsf{v}}\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{Z}}}+\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{t}}}+\frac{\left(\mathsf{1}-\varepsilon \right)}{\varepsilon}\rho \frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\mathsf{0}\hfill & \mathrm{Mass}\kern0.24em \mathrm{transfer}\kern0.24em \mathrm{balance}\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\frac{{\mathit{\mathsf{k}}}_{\mathit{\mathsf{f}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}}{\rho}\times \left(\mathit{\mathsf{C}}-{\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}\right)\hfill & \mathrm{External}\kern0.24em \mathrm{diffusion}\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{k}}}_{\mathit{\mathsf{s}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}\times \left({\mathit{\mathsf{q}}}_{\mathit{\mathsf{i}}}-\mathit{\mathsf{q}}\right)\hfill &\;\mathrm{Internal}\kern0.24em \mathrm{diffusion}\kern0.24em \left(\mathrm{Gleuckauf}\right)\hfill \\ {}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{i}}}=\frac{{\mathit{\mathsf{q}}}_{\mathsf{0}}\times {\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}}{\mathsf{1}+{\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}}\;\hfill & \mathrm{Adsorption}\kern0.24em \mathrm{isotherm}\kern0.24em \left(\mathrm{Langmuir}\right)\hfill \end{array}\right. $$

(15)

Posing $\mathit{\mathsf{a}}={\mathit{\mathsf{q}}}_{\mathsf{0}}\times {\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}$; $\mathit{\mathsf{b}}={\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathsf{0}}$; ${\mathit{\mathsf{a}}}_{\mathsf{0}}=\frac{{\mathit{\mathsf{K}}}_{\mathit{\mathsf{G}}}}{{\mathit{\mathsf{K}}}_{\mathit{\mathsf{S}}}}$; ${\mathsf{a}}_{\mathsf{1}}=\frac{\mathsf{a}}{\mathsf{2}\times \mathsf{b}\times {\mathsf{a}}_{\mathsf{0}}}+\frac{\mathsf{1}}{\mathsf{2}\times \mathsf{b}}$; ${\mathit{\mathsf{a}}}_{\mathsf{2}}=\frac{\mathsf{1}}{\mathsf{2}\times \mathit{\mathsf{b}}\times \mathit{\mathsf{a}}{}_{\mathsf{0}}}$and ${\mathit{\mathsf{a}}}_{\mathsf{3}}=\mathit{\mathsf{a}}+{\mathit{\mathsf{a}}}_{\mathsf{0}}$, the final system (S ₂) of differential equations to be solved, using the nonlinear Langmuir isotherm, is the following:

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{2}}\right)\left\{\begin{array}{l}\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{t}}}=-{\mathit{\mathsf{A}}}_{\mathsf{1}}\left(\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{z}}}\right)-{\mathit{\mathsf{A}}}_{\mathsf{2}}\left(\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}\right)\\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{K}}}_{\mathit{\mathsf{G}}}\left[\frac{\mathit{\mathsf{x}}}{\mathsf{2}}-\frac{\mathit{\mathsf{q}}}{\mathsf{2}\times {\mathit{\mathsf{a}}}_{\mathsf{0}}}+{\mathit{\mathsf{a}}}_{\mathsf{1}}-{\mathit{\mathsf{a}}}_{\mathsf{2}}\sqrt{{\left({\mathit{\mathsf{a}}}_{\mathsf{3}}-\mathit{\mathsf{b}}\left({\mathit{\mathsf{a}}}_{\mathsf{0}}\times \mathit{\mathsf{x}}+\mathit{\mathsf{q}}\right)\right)}^{\mathsf{2}}+\mathsf{4}\times \mathit{\mathsf{b}}\times {\mathit{\mathsf{a}}}_{\mathsf{0}}\left(\mathit{\mathsf{q}}+{\mathit{\mathsf{a}}}_{\mathsf{0}}\times \mathit{\mathsf{x}}\right)}\right]\end{array}\right. $$

(16)

Initial conditions $\left\{\begin{array}{l}\mathit{\mathsf{t}}=\mathsf{0}\\ {}\mathit{\mathsf{x}}\left(\mathit{\mathsf{z}},\mathsf{0}\right)=\mathsf{0}\\ {}\mathit{\mathsf{q}}\left(\mathit{\mathsf{z}},\mathsf{0}\right)=\mathsf{0}\end{array}\right.$.

Boundary conditions $\left\{\begin{array}{l}\mathit{\mathsf{z}}=\mathsf{0}\Rightarrow \mathit{\mathsf{x}}\left(\mathsf{0},\mathit{\mathsf{t}}\right)=\mathsf{1}\\ {}\mathit{\mathsf{z}}=\mathsf{1}\Rightarrow \frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{z}}}=\mathsf{0}\end{array}\right.$.

The second solution is approaching the experience and describes it with a correlation coefficient value R ² = 0.972 (Fig. 5). According to this figure, the deviation between experimental and simulated breakthrough is observed in this range, which is specific to our experiments. To further improve the internal transfer model, Rosen law was used to describe the transfer within the means radius of particle R _p .

Solution 3

The differential equation system of solution 3 consists of the mass balance, the external mass transfer equation, the internal mass transfer equation (Rosen law), and the adsorption isotherm (Lagmuir model).

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{3}}\right)\left\{\begin{array}{ll}\mathit{\mathsf{v}}\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{Z}}}+\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{t}}}+\frac{\left(\mathsf{1}-\varepsilon \right)}{\varepsilon}\rho \frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\mathsf{0}\hfill & \mathrm{Mass}\ \mathrm{transfer}\ \mathrm{balance}\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\frac{{\mathit{\mathsf{k}}}_{\mathit{\mathsf{f}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}}{\rho}\times \left(\mathit{\mathsf{C}}-{\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}\right)\hfill & \mathrm{External}\ \mathrm{diffusion}\hfill \\ {}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{D}}}_{\mathsf{eff}}\left(\frac{\partial^{\mathsf{2}}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial {\mathit{\mathsf{r}}}^{\mathsf{2}}}+\frac{\mathsf{2}}{\mathit{\mathsf{r}}}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \mathit{\mathsf{r}}}\right)\hfill & \mathrm{Internal}\ \mathrm{diffusion}\ \left(\mathrm{Rosen}\right)\hfill \\ {}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{i}}}=\frac{{\mathit{\mathsf{q}}}_{\mathsf{0}}\times {\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}}{\mathsf{1}+{\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}}\hfill & \mathrm{Adsorption}\ \mathrm{isotherm}\ \left(\mathrm{Langmuir}\right)\hfill \end{array}\right. $$

(17)

The description of the adsorption phenomenon within the particle is described by the Rosen model.

Posing $\xi =\frac{\mathit{\mathsf{r}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}}$;${\mathit{\mathsf{k}}}_{\mathsf{1}}=\frac{\mathsf{3}\times {\mathit{\mathsf{D}}}_{\mathsf{eff}}\times {\mathit{\mathsf{A}}}_{\mathsf{2}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}$; ${\mathit{\mathsf{k}}}_{\mathsf{2}}=\frac{{\mathit{\mathsf{D}}}_{\mathsf{eff}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}\times {\mathit{\mathsf{k}}}_{\mathit{\mathsf{f}}}}$, the final system (S ₃) of differential equations to be solved, is the following:

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{3}}\right)\left\{\begin{array}{l}\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{t}}}=-{\mathit{\mathsf{A}}}_{\mathsf{1}}\left(\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{z}}}\right)-\frac{\mathsf{3}\times {\mathit{\mathsf{D}}}_{\mathsf{eff}}\times {\mathit{\mathsf{A}}}_{\mathsf{2}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}{\left.\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \xi}\right|}_{\xi =\mathsf{1}}\hfill \\ {}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \mathit{\mathsf{t}}}=\frac{{\mathit{\mathsf{D}}}_{\mathsf{eff}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}\left(\frac{\partial^{\mathsf{2}}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial {\xi}^{\mathsf{2}}}+\frac{\mathsf{2}}{\xi}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \xi}\right)\hfill \end{array}\right. $$

(18)

with

$$ \left\{\begin{array}{l}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}\left(\mathit{\mathsf{z}},\xi, \mathsf{0}\right)=\mathsf{0}\hfill \\ {}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}\left(\mathit{\mathsf{z}},\mathsf{1},\mathsf{t}\right)=\frac{\mathit{\mathsf{a}}\times \mathit{\mathsf{x}}\left(\mathit{\mathsf{z}},\mathit{\mathsf{t}}\right)-\mathit{\mathsf{a}}\times {\mathit{\mathsf{k}}}_{\mathsf{2}}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}\left(\mathit{\mathsf{z}},\mathsf{1},\mathit{\mathsf{t}}\right)}{\partial \xi}}{\mathsf{1}+\mathit{\mathsf{b}}\times \mathit{\mathsf{x}}\left(\mathit{\mathsf{z}},\mathit{\mathsf{t}}\right)-\mathit{\mathsf{b}}\times {\mathit{\mathsf{k}}}_{\mathsf{2}}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}\left(\mathit{\mathsf{z}},\mathsf{1},\mathit{\mathsf{t}}\right)}{\partial \xi}}\hfill \\ {}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}\left(\mathsf{z},\mathsf{0},\mathit{\mathsf{t}}\right)}{\partial \xi}=\mathsf{0}\hfill \end{array}\right. $$

(19)

The model coincides with experience (Fig. 5); the theory balance revealed a narrow gap with the experimental data (R ² = 0.988). In addition, the staggering of breakthrough fronts, which corresponds to kinetic effects of mass transfer, is also well represented by theoretical calculations. The simulation shows a difference in concentration of o-xylene at the outlet of the column which can be attributed to the dispersion term. Therefore, we will take action in solution 4 for quite satisfactory results.

Solution 4

In an attempt to build a theoretical representation that approximates as closely as possible to a real process, we took into account the effects of the axial dispersion. This is necessary when the ratio (length bed/particle diameter) is greater than 30 (Cloirec 2003). In our case, the minimum bed length is 100 mm and the diameter of the particle is 0.85 mm (L _c /d _p  = 117). The axial dispersion coefficient is calculated using Eq. (20) (Ho and Webb 2006; Edward and Richardson 1968).

$$ {\mathit{\mathsf{D}}}_{\mathsf{ax}}=\mathsf{0.73}\times {\mathit{\mathsf{D}}}_{\mathit{\mathsf{m}}}+\frac{\mathit{\mathsf{v}}\times {\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}}{\mathsf{1}+\frac{\mathsf{9.7}\times {\mathit{\mathsf{D}}}_{\mathit{\mathsf{m}}}}{\mathsf{2}\times \mathit{\mathsf{v}}\times {\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}}} $$

(20)

Differential equation system then is composed from the mass balance taking into account the axial dispersion, the external mass transfer equation, the internal mass transfer equation (Rosen law), and the adsorption isotherm (Lagmuir model).

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{4}}\right)\left\{\begin{array}{ll}-{\mathit{\mathsf{D}}}_{\mathsf{a}\mathsf{x}}\frac{\partial^{\mathsf{2}}\mathit{\mathsf{C}}}{\partial {\mathit{\mathsf{Z}}}^{\mathsf{2}}}+\mathit{\mathsf{v}}\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{Z}}}+\frac{\partial \mathit{\mathsf{C}}}{\partial \mathit{\mathsf{t}}}+\frac{\left(\mathsf{1}-\varepsilon \right)}{\varepsilon}\rho \frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\mathsf{0}\hfill & \mathrm{Mass}\ \mathrm{transfer}\ \mathrm{balance}\hfill \\ {}\frac{\partial \mathit{\mathsf{q}}}{\partial \mathit{\mathsf{t}}}=\frac{{\mathit{\mathsf{k}}}_{\mathit{\mathsf{f}}}\times {\mathit{\mathsf{a}}}_{\mathit{\mathsf{p}}}}{\rho}\times \left(\mathit{\mathsf{C}}-{\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}\right)\hfill & \mathrm{External}\ \mathrm{diffusion}\hfill \\ {}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{D}}}_{\mathsf{eff}}\left(\frac{\partial^{\mathsf{2}}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial {\mathit{\mathsf{r}}}^{\mathsf{2}}}+\frac{\mathsf{2}}{\mathit{\mathsf{r}}}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \mathit{\mathsf{r}}}\right)\hfill & \mathrm{Internal}\ \mathrm{diffusion}\ \left(\mathrm{Rosen}\right)\hfill \\ {}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{i}}}=\frac{{\mathit{\mathsf{q}}}_{\mathsf{0}}\times {\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}}{\mathsf{1}+{\mathit{\mathsf{K}}}_{\mathit{\mathsf{L}}}\times {\mathit{\mathsf{C}}}_{\mathit{\mathsf{i}}}}\hfill & \mathrm{Adsorption}\ \mathrm{isotherm}\ \left(\mathrm{Langmuir}\right)\hfill \end{array}\right. $$

(21)

Posing ${\mathit{\mathsf{A}}}_{\mathsf{3}}=\frac{{\mathit{\mathsf{D}}}_{\mathsf{ax}}}{{\mathit{\mathsf{L}}}^{\mathsf{2}}}$, the final system (S ₄) of differential equations to be solved is the following:

$$ \left({\mathit{\mathsf{S}}}_{\mathsf{4}}\right)\left\{\begin{array}{l}\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{t}}}={\mathit{\mathsf{A}}}_{\mathsf{3}}\left(\frac{\partial^{\mathsf{2}}\mathit{\mathsf{x}}}{\partial {\mathit{\mathsf{z}}}^{\mathsf{2}}}\right)-{\mathit{\mathsf{A}}}_{\mathsf{1}}\left(\frac{\partial \mathit{\mathsf{x}}}{\partial \mathit{\mathsf{z}}}\right)-\frac{\mathsf{3}\times {\mathit{\mathsf{D}}}_{\mathsf{eff}}\times {\mathit{\mathsf{A}}}_{\mathsf{2}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}{\left.\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \xi}\right|}_{\xi =\mathsf{1}}\hfill \\ {}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \mathit{\mathsf{t}}}=\frac{{\mathit{\mathsf{D}}}_{\mathsf{eff}}}{{\mathit{\mathsf{R}}}_{\mathit{\mathsf{p}}}^{\mathsf{2}}}\left(\frac{\partial^{\mathsf{2}}{\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial {\xi}^{\mathsf{2}}}+\frac{\mathsf{2}}{\xi}\frac{\partial {\mathit{\mathsf{q}}}_{\mathit{\mathsf{j}}}}{\partial \xi}\right)\hfill \end{array}\right. $$

(22)

Taking into account the term of axial dispersion, the mass transfer model is close to the experience and describes well the breakthrough (R ² = 0.996). This is favorable both on the shape of the simulated curves (Fig. 5) and on the numerical results of the adsorbed amounts (Table 5). Experiments that have been conducted in these conditions can be reproduced correctly by simulation. The comparison between the experimental and model predicted curves gives rise to the conclusion that the mass transfer model (solution 4) is able to predict the column behavior with a good degree of accuracy.

Bed depth, inlet concentration, and gas flow variations obtained with COMSOL describe well the experimental results. In addition, the staggering breakthrough curves match at a time kinetic effects of a transfer material, were well represented by the theoretical calculations.

The mass transfer model provides more information than the other models. The rate constant (k _f ) includes both a diffusion term (D _eff) and velocity term (v), which are important in scaling up the size of the column (depth and diameter) and maximizing the flow rate for efficiency. The difference between internal and external surface areas is accounted for using both total surface area (a _p ) and porosity (ε).

It is clear that the model captures the essential physics of mass transfer inside the column. Thus, this model relates more parameters about the column than the other models, which is more useful in optimizing the column size, flow rate, and particle characteristics. The fact that we obtain a good agreement between the proposed model and the experimental data for a large range of configurations is a very strong argument in favor of the theory.

Industrial extrapolation

The aim of this study is to use raw clay material as adsorbent in industry. Laboratory experiments are carried out under special conditions where the majority of parameters are very well controlled.

In an industrial application, some parameters will have a greater range of variation than in the laboratory, since larger quantities will be deployed. Indeed, the density, the particle size (directly affecting K _L), and the axial dispersion are the parameters which are difficult to control.

The objective of the industrial extrapolation section is to simulate the behavior of the adsorption fronts when density (ρ), Langmuir constant (K _L), and axial dispersion (D _ax) are varied. We purposely chose to enlarge the range of variation of each parameter (10, 20, and 30%) probably much more than it is usually tolerated using experimental design.

A central composite matrix was used (Table 6). The adsorption front (response) will be determined by simulation on COMSOL (and not experimentally). A theoretical model will be established according to the three parameters. We develop in this part a study of the experimental error effect, for various experimental parameters on the adsorption breakthrough.

Table 6 Central composite design matrix for three variables and response results

Parameter choice

The density of the clay material is a parameter which greatly influences the breakthrough front time, and it cannot be determined experimentally. We have tolerated ±10% as margin of error.

Physical adsorption of o-xylene on the clay material is exothermic: at high temperature, the slope of the adsorption isotherm is stiff, which reduces the Langmuir constant K _L. We have tolerated ±20% as margin of error.

D _ax is a function of the diameter of the particle, the porosity of the bed, and the adsorption temperature, so these parameters influence the breakthrough time. During the determination of D _ax, we have tolerated a margin of error of ±30%.

In this part, we have to optimize the breakthrough time in order to minimize the number of adsorption/desorption cycles in an industrial application.

Modeling

The response, Ŷ, can be calculated from X ₁, X ₂, and X ₃ by a quadratic regression model.

$$ \widehat{\mathit{\mathsf{Y}}}=\mathsf{618.0}+\mathsf{61.60}{\mathit{\mathsf{X}}}_{\mathsf{1}}+\mathsf{11.60}{\mathit{\mathsf{X}}}_{\mathsf{2}}-\mathsf{28.70}{\mathit{\mathsf{X}}}_{\mathsf{3}}+\mathsf{26.60}{\mathit{\mathsf{X}}}_{\mathsf{1}}^{\mathsf{2}}-\mathsf{17.40}{\mathit{\mathsf{X}}}_{\mathsf{2}}^{\mathsf{2}}-\mathsf{54.90}{\mathit{\mathsf{X}}}_{\mathsf{3}}^{\mathsf{2}}+\mathsf{1.50}{\mathit{\mathsf{X}}}_{\mathsf{1}}{\mathit{\mathsf{X}}}_{\mathsf{2}}-\mathsf{2.70}{\mathit{\mathsf{X}}}_{\mathsf{1}}{\mathit{\mathsf{X}}}_{\mathsf{3}}+\mathsf{0.00}{\mathit{\mathsf{X}}}_{\mathsf{2}}{\mathit{\mathsf{X}}}_{\mathsf{3}} $$

(23)

The simulated values are obtained by simulation of mass balance equation with COMSOL MULTIPHYSICS. These values replace the experimental data in this section. Therefore, predicted values are those determined by NEMROD.

Table 6 shows the simulation design of clay material based on the variables ρ, K _L, and D _ax for breakthrough time response obtained by mass balance equation model. Predicted breakthrough time and residues are also presented in this table.

The significance of each coefficient of quadratic regression model is determined by Student’s t tests, which are listed in the Table 7.

Table 7 Coefficient model estimation for breakthrough time response

The validation of the quadratic regression model was reanalyzed by using residuals. Residuals were distributed normally with mean zero and constant variance.

The correlation coefficient value R ² = 0.913 justifies an excellent relation (Table 6) between the independent variables and good agreement between the simulated and predicted model (Amari et al. 2008).

It was concluded that Eq. (20) was good to fit to the simulated data. In other words, the assumptions regarding the errors are satisfactory.

The coefficients of the suggested model were calculated according to the experimental responses and the iso-response curves (Table 7). To evaluate the response and interpret the results, these coefficients were used. Therefore, it is needed to predict the effect of each factor and their interactions which can be synergistic or antagonistic.

The greater the amplitude of the t value, the greater the corresponding coefficient is important (Akhnazarova and Kafarov 1982; Khuri and Cornell 1996). Thus, the linear effects of density and Langmuir constant are very significant, as is evident from the Student’s t test values (Table 7). The effect of interactions is considered insignificant at the 95% confidence level.

The effect sign marks the breakthrough time. For a response factor, a synergistic effect is designated by a positive sign, whereas an antagonistic effect is designated by a negative sign (Haaland 1989).

As shown in Table 7 and in the model coefficients (18), it was concluded that absolute value of linear effect was more significant than quadratic effects.

The linear effects of ρ and K _L factors are positive (61.6 and 11.6), whereas that of D _ax factor is negative (−28.7): an increase in ρ and K _L during the adsorption is accompanied with an increase in breakthrough time; the same result is obtained for a decrease in D _ax. All quadratic effects, except of density, are negative: the increase in the axial dispersion in the column does not affect breakthrough time generally. The mutual effect (X _i X _j with i ≠ j) was found to be the least significant effect of all the other factor effects. The mutual effect can be seen in an elliptical shape in proportional with its significance in Figs. 6 and 7. To increase the breakthrough time, variable values should be with same sign.

Fig. 6

Variation of breakthrough time versus ρ and D _ax at K _L = 13.281

Fig. 7

Variation of breakthrough time versus K _L and D _ax at ρ = 1390 kg m⁻³

It is easy to note that the breakthrough time can be maximized when the density of clay is maximized, while the effect of the Langmuir constant and the axial dispersion effect are less important.

In order to visualize the relationship between the simulated variables and the response, we represented the 2D iso-response curves and 3D response surface (Figs. 6 and 7). Each area represented by these figures is a combination of two variables; the other parameters are kept constant at the point center.

The desirability function is the relationship between the expected responses of dependent variable and their desirability. It is based on the assignment of values from 0 (not desirable) and 1 (highly desirable) to the expected response. With desirability function, the values of the dependent variables that produce the most desirable responses can be determined. If the combination of answers is optimal, desirability will have a high value.

A study of the desirability function was performed in order to maximize the breakthrough time. In Table 8, optimal independent variables are enumerated. These values show that with a density of 1530 g cm⁻³, Langmuir constant of 14.28, and a dispersion coefficient of 108.8 × 10⁻⁶ m² s⁻¹, there will be a desirability of 0.862 and a breakthrough time of 713 s.

Table 8 Desirability: maximum coordinates

Conclusions

This study verified that the raw clay material can be used as adsorbent for the treatment of volatile organic compounds.

Dynamic experiments marked the importance of bed height, inlet o-xylene concentration, and flow rate. Decreasing bed height and inlet o-xylene concentration enhanced column performance, whereas, the highest flow rate raised adsorption capacity. It has also been demonstrated that column data could be perfectly described by the Thomas, Yoon–Nelson, Clark, dose–response, and BDST models. Moreover, mass transfer model provides a description of the experimental results at different bed heights, flow rate, and inlet o-xylene concentrations.