Introduction

The main pulmonary artery (MPA) passively regulates pulsatile blood flow during ventricular systole [1], while the entire pulmonary arterial vasculature experiences three-dimensional stresses on account of the local pulsatile hemodynamics. However, pulmonary hypertension (PH) patients typically display thickening and stiffening of the proximal pulmonary arteries [2]. Endothelial cells react to the deviant hemodynamics by addition of extracellular matrix (ECM) components such as increase in fibrotic tissues and other cellular debris, which alters the luminal cross-sectional area in pulmonary arteries [3]. Subsequently, the mechanical response of the MPA and the left and right pulmonary arteries (LPA, RPA) lead to a cascade of biochemical changes that can potentially contribute to the pathological development of PH. Several imaging [4,5,6] and simulation-based studies [7,8,9] have documented aberrant changes in pulmonary arterial wall mechanics from which we can infer biomechanics may have a pronounced role in the progression of PH.

Multiple experimental studies have investigated the mechanical characteristics of the MPA using human [10, 11], porcine [12], canine [13,14,15], bovine [16], and ovine [17,18,19] tissue specimens. Fata et al. [17] investigated the biomechanics of ovine MPA in anterior and posterior locations, and found significant mechanical anisotropy in the anterior MPA specimens. Rogers et al. [11] compared the mechanical properties of the proximal MPA and distal fifth-order pulmonary arteries in normal and sickle cell disease (SCD)-associated PH patients, and found a loss of elasticity and an increase in stiffness of the SCD-associated vessels. Mathews et al. [12] and Azadani et al. [10] applied identical protocols for equibiaxial tensile testing of porcine and human pulmonary (and aortic) roots, respectively. However, region-based biomechanical evaluations, particularly those distal to the MPA, are sparse in the literature. Limited data on location-based material characterization of pulmonary arteries is a challenge for the development of high fidelity computational models, which in turn could be used for non-invasive assessment of PH severity.

The primary objective of this work is to perform a thorough characterization of the material properties of porcine pulmonary arteries along a sequence of axial locations ranging from the proximal MPA to the distal LPA and RPA. The outcome is a quantitative assessment of the location-dependent wall thickness, biomechanical, and microstructural properties of porcine pulmonary artery specimens.

Materials and Methods

Tissue Procurement

Ten porcine heart-lung blocks (Mixed Yorkshire breed, 6–9 months, 120–250 lb) were procured from Animal Technologies Inc. (Tyler, TX). The specimens were initially stored at -20 °C and allowed to thaw for 12–24 h prior to testing. Thereafter, the MPA, LPA, and RPA were excised from each heart-lung block, as shown in Fig. 1(a). Any visible fat or loose connective tissues were removed from the specimens. The arteries were further divided into thirds – proximal (P), middle (M), and distal (D), with the exception of the bifurcation (B) region. Therefore, the experimental groups for the study were labeled as follows: MPA-P, MPA-M, MPA-D, B, LPA-P, LPA-M, LPA-D, RPA-P, RPA-M, and RPA-D, as shown schematically in Fig. 1(b). Arterial rings were dissected from each region as shown in Fig. 1(c) and further processed for biomechanical testing and histology.

Fig. 1
figure 1

Schematic of planar biaxial tensile testing protocol. (a) Main, left, and right pulmonary arteries, and porcine heart of an exemplary specimen. (b) Detailed schematic of the ten experimental groups (MPA-P, MPA-M, MPA-D, B, LPA-P, LPA-M, LPA-D, RPA-P, RPA-M, and RPA-D) utilized in the study. (c) Dissection procedure and (d) specimen preparation. (e) Exemplary specimen from the MPA-P group loaded on the biaxial testing machine. The circumferential direction was aligned with the x-axis and the longitudinal direction with the y-axis of the testing frame, respectively

Full size image

Specimen Preparation for Planar Biaxial Tensile Testing

Six square specimens (approx. 5 ± 1 mm) were dissected from each ring (MPA-P, MPA-M, MPA-D, B, LPA-P, LPA-M, LPA-D, RPA-P, RPA-M, and RPA-D), leading to approximately n = 58 specimens per group (see Fig. 1(d)). The top-left corner of each specimen was marked with Shandon tissue-marking dye (ThermoFischer Scientific, Kalamazoo, MI) to identify the specimen orientation. In addition, four fiducial markers were placed in an array on the luminal surface of the specimen for tracking local deformation of the tissue [17, 20]. The thickness of each specimen was recorded in triplicate using digital calipers (Mitutoyo America Corporation, Aurora, IL). The specimens were then loaded on the biaxial testing machine (CellScale BioTester, Waterloo Instruments Inc., Ontario, Canada) using CellScale’s BioRake sample mounting system, leading to an effective testing area of 4 mm × 4 mm. The specimens were oriented such that the circumferential (identified by the subscript C) and longitudinal (identified by the subscript L) directions were aligned with the testing x- and y-directions, respectively, as illustrated in Fig. 1(e). The tensile tester was equipped with two 10 N load cells in each direction and testing was performed at 37 °C in a PBS bath solution (HyClone, GE Healthcare Bio-Sciences, Pittsburgh, PA).

Biaxial Tensile Testing Protocol

The mechanical characterization of the porcine pulmonary artery specimens was performed per previously established protocols [21,22,23]. Briefly, an initial tare load of 5 mN was applied to each specimen, followed by ten preconditioning cycles within 0–5% strain, and subsequently stretched equibiaxially (λC : λL − 1 : 1), up to 55% strain [12, 21, 22] from its reference configuration for 30 s. The aforementioned step was repeated eight times to reduce tissue hysteresis and the final loading/unloading cycle was utilized for further processing. LabJoy® (Waterloo Instruments Inc., Ontario, Canada) was employed to record the data at 30 Hz and images were acquired at a rate of 1 Hz.

Biomechanical Data Analysis

Force and displacement data were exported from LabJoy® to a custom MATLAB script (The MathWorks Inc., Natick, MA), which generated the corresponding stress-strain curves. The specimens were considered incompressible and a plane stress formulation was adopted [24]. Thus, the contribution from shear forces to the planar biaxial deformation was assumed to be negligible [25]. Under the no-load condition, the separation distances between the rakes in the circumferential (C) and longitudinal (L) directions were defined as L0C and L0L, respectively, as shown in Fig. 2(a), and the undeformed specimen thickness as t0. The stretch ratios in the circumferential (λC) and longitudinal (λL) directions were calculated according to Fung [26], as indicated by equation (1),

$$ {\lambda}_C=\frac{L_C}{L_{0C}},\kern0.75em {\lambda}_L=\frac{L_L}{L_{0L}} $$
(1)

where LC and LL are the instantaneous distances between the rakes during the loading cycle. With the aforementioned stretch ratios, the 2nd Piola-Kirchhoff (PK) stresses (SC, SL) and Cauchy stresses (σC, σL) were calculated according to equation (2a and b) [26],

$$ {S}_C=\frac{F_C}{A_{0C}\ {\lambda}_C},\kern0.75em {S}_L=\frac{F_L}{A_{0L}\ {\lambda}_L} $$
(2a)
$$ {\sigma}_C=\frac{F_C}{A_C}, \kern0.75em {\sigma}_L=\frac{F_L}{A_L\ } $$
(2b)

where FC and FL are the forces recorded by the load cells; AC, AL are the instantaneous cross-sectional areas calculated by virtue of the incompressibility assumption; and A0C, A0L are the cross-sectional areas at the no-load condition. All calculations correspond to the final loading cycle. The Green-Lagrange strains, EC and EL, were evaluated using the stretch ratios by means of equation (3),

$$ {E}_C=\frac{1}{2}\kern0.5em \left({\lambda}_C^2-1\right),\kern1.75em {E}_L=\frac{1}{2}\kern0.5em \left({\lambda}_L^2-1\right) $$
(3)
Fig. 2
figure 2

Calculation of biomechanical parameters from the stress-strain curves [23]. (a) Schematic of the initial and deformed configurations of a specimen. Upon application of tensile forces Fθ and FL, the specimens deform from initial lengths, L0θ and L0L, to Lθ and LL, respectively. (b) The average incremental tensile modulus (TM) was calculated for each stress-strain curve between the regions of 0th – 30th, 30th – 60th, 60th – 90th, and 90th – 100th percentile strains (in both tissue orientations). (c) The anisotropy index (AI) was calculated at two reference states, P30 and P60, where P stands for percentile reference 2nd Piola-Kirchoff (PK) stress (S). (d) The stored elastic strain energy for each specimen was derived by calculating the area under the 2nd PK stress (S) – Green strain (E) curve

Full size image

Using the stress-strain data, we evaluated the stress at 55% strain (S55), tensile modulus (TM), anisotropy index (AI), and area under the curve (AUC) [23]. S55 is the 2nd PK stress calculated at the maximum applied strain of 55% and does not reflect the stress prior to failure. The mean TM was calculated within the following strain ranges (E): E0 → E30, E30 → E60, E60 → E90, and E90 → E100, as illustrated in Fig. 2(b). The anisotropy index, AIi, quantifies the differences in stress-strain behavior between the circumferential and longitudinal directions. It was calculated according to equation (4), which was adapted from Langdon et al. [27],

$$ A{I}_i={\left|{E}_L-{E}_C\right|}_{P_i} $$
(4)

where Pi represents the ith percentile value of the 2nd PK stress. AI was evaluated at P30 and P60, as shown in Fig. 2(c). The strain energy was calculated as the area under the curve subtended by the 2nd PK stress - Green strain curve, as shown schematically in Fig. 2(d). The biomechanical parameters TM, S55, and AUC were calculated for both circumferential and longitudinal directions.

Constitutive Modeling

To represent the location-dependent biaxial mechanical behavior, we utilized the force-displacement data from each specimen to calculate the local Cauchy stress and Green Lagrange strain. The arterial wall was modeled as a nonlinear, elastic, thick-walled cylinder comprising two layers, namely intima-media and adventitia. Typically, for such two-layer models, separate strain energy functions are assigned to the intima-media and adventitia [28], which result in eight material parameters (two sets of four parameters). However, the mechanical behavior recorded during biaxial tensile testing was a combined response of the intima-media and adventitia layers. To this end, Badel et al. [29] proposed and validated a simplified Holzapfel–Gasser–Ogden (HGO) material model [28] that assumes identical exponential behavior for the intima-media and adventitia. Consequently, they performed an addition of the individual layers’ strain energy functions, thus yielding the evaluation of only five model parameters. In this work, we fitted Badel et al.’s simplified HGO material model, with five constants, to the experimental stress-strain data using a MATLAB script. Thirugnanasambandam and colleagues [30] also utilized a similar constitutive model for finite element analysis of abdominal aortic aneurysms. We implemented a two-fiber model for each layer, which is composed of the ground matrix (isotropic material) and two families of collagen fibers wound along the longitudinal direction (anisotropic). The assumptions described in the subsequent paragraphs further elaborate on the simplified HGO material model [28, 29]. Holzapfel et al. [28] measured the angles between collagen fiber families in each layer explicitly through histology. Conversely, we applied an optimization algorithm using a simplified strain energy function to evaluate these angles and the other model parameters based on their fit to the experimental data. It may be argued that Badel et al.’s [29] simplification results in a homogenization of the original HGO model [28]. The mathematical formulation was reproduced from Holzapfel et al. [28], where equation (57) in [28] is included as equation (5),

$$ \varPsi ={\varPsi}_{iso}\left(\overline{\mathbf{C}}\right)+{\varPsi}_{aniso}\left(\overline{\mathbf{C}},{\mathbf{a}}_{01},{\mathbf{a}}_{02}\right) $$
(5)

from which Ψ is a Helmholtz free-energy function that, in this context, represents strain energy within the tissue material. Ψ comprises a volumetric or isotropic contribution (Ψiso) and an isochoric or anisotropic (Ψaniso) contribution. The hyperelastic stress response of the arterial wall is described with a set of three second-order tensors. The Cauchy stress tensor \( \left(\overline{\mathbf{C}}\right) \) and the structure tensors are defined as A1 = a01 ⊗ a01 and A2 = a02 ⊗ a02, where a0i, i = 1, 2, with |a0i| = 1 denotes direction vectors that represent the families of collagen fibers. Integrity bases for the three symmetric second-order tensors (\( \overline{\mathbf{C}} \), A1, A2) comprise the invariants in equation (6),

$$ {\displaystyle \begin{array}{c}{I}_1\left(\overline{\mathbf{C}}\right)= tr\ \left(\overline{\mathbf{C}}\right),\kern1em {I}_2\left(\overline{\mathbf{C}}\right)=\frac{\mathbf{1}}{\mathbf{2}}\left[{\left(\mathbf{tr}\ \overline{\mathbf{C}}\right)}^{\mathbf{2}}-\mathbf{tr}{\overline{\mathbf{C}}}^{\mathbf{2}}\ \right],\kern0.5em {I}_3\left(\overline{\mathbf{C}}\right)=\mathbf{\det}\ \left(\overline{\mathbf{C}}\right),\\ {}{I}_4\left(\overline{\mathbf{C}},{\mathbf{a}}_{01}\ \right)=\overline{\mathbf{C}}:{\mathbf{A}}_{\mathbf{1}},\kern0.5em {I}_5\left(\overline{\mathbf{C}},{\mathbf{a}}_{01}\ \right)={\overline{\mathbf{C}}}^{\mathbf{2}}:{\mathbf{A}}_{\mathbf{1}},\kern0.5em {I}_6\left(\overline{\mathbf{C}},{\mathbf{a}}_{02}\ \right)=\overline{\mathbf{C}}:{\mathbf{A}}_{\mathbf{2}}\\ {}\begin{array}{c}\ {I}_7\left(\overline{\mathbf{C}},{\mathbf{a}}_{02}\ \right)={\overline{\mathbf{C}}}^{\mathbf{2}}:{\mathbf{A}}_{\mathbf{2}},\kern0.75em {I}_8\left(\overline{\mathbf{C}},{\mathbf{a}}_{01},{\mathbf{a}}_{02}\ \right)=\left({\mathbf{a}}_{01}\cdotp {\mathbf{a}}_{02}\right){\mathbf{a}}_{01}\cdotp \overline{\mathbf{C}}{\mathbf{a}}_{02}\\ {}\ {I}_9\left({\mathbf{a}}_{01},{\mathbf{a}}_{02}\ \right)={\left({\mathbf{a}}_{01}\cdotp {\mathbf{a}}_{02}\right)}^{\mathbf{2}}\end{array}\end{array}} $$
(6)

where I3 and I9 are constants, which leads to equation (5) rewritten as

$$ \varPsi ={\varPsi}_{iso}\left({I}_1,{I}_2\right)+{\varPsi}_{aniso}\left({I}_1,{I}_2,{I}_4,{I}_5,{I}_6,{I}_7{I}_8\right) $$
(7)

for which I4 and I6 represent the stretch measures for the two families of collagen fibers. To reduce the number of material constants, equation (7) is simplified as

$$ \varPsi ={\varPsi}_{iso}\left({I}_1\right)+{\varPsi}_{aniso}\left(\ {I}_4,{I}_6\right) $$
(8)

The following assumptions were made for the strain energy function [28]:

  1. 1

    A classical neo-Hookean model is assumed to govern the isotropic response in each layer, as in equation (9),

$$ {\varPsi}_{iso}=\frac{c}{2}\left({I}_1-3\right) $$
(9)

where c > 0 is a stress-like material parameter. This equation takes into account the intima-media and adventitia layers, which are obtained from a parametric estimation process, in contrast to the histology-based protocol outlined in [28]. The parameters cM and cA, which characterize the isotropic behavior of the ground matrix in the intima-media and adventitia layers, respectively, are assumed equal to each other, i.e. cM = cA.

  1. 2.

    To characterize the stiffening effect within each layer, equation (10) was used to formulate the anisotropic component,

$$ {\varPsi}_{aniso}=\sum \limits_{layer=M,\kern0.5em A}\sum \limits_{i=4,6}\frac{k_1}{2{k}_2}\left\{\mathit{\exp}\left[{k}_2{\left({I}_i^{layer}-1\right)}^2\right]-1\right\} $$
(10)
  1. 3.

    The components k1A, k1M and k2A, k2M, which characterize the exponential behavior of the collagen fibers in the adventitia and intima-media are also assumed equal to each other, i.e. k1A = k1M = k1, k2A = k2M = k2, and (k1, k2) > 0. \( {I}_i^{layer} \) is the ith invariant of the Cauchy stress tensor per wall layer [28] . The orientation of the collagen fibers is different in each layer, leading to the calculation of two fiber angles. In this formulation, we assume that under normal loading conditions the arterial wall exhibits elastic symmetry in the direction normal to the first principal stress [30]. Therefore, it is assumed that the collagen extensions occur parallel to the direction of the first principal stress. The fourth and sixth invariants represent the fiber directions of the collagen bundles implicitly, which are represented as βM (intima-media) and βA (adventitia), respectively.

For planar biaxial testing with no shear, the deformation gradient, F, is defined according to equation (11),

$$ \boldsymbol{F}=\left[\begin{array}{ccc}{\lambda}_C& 0& 0\\ {}0& {\lambda}_L& 0\\ {}0& 0& {\lambda}_R\end{array}\right] $$
(11)

where λm (m = C, L, R) represent the stretch ratios in the circumferential, longitudinal, and radial directions, respectively. Incompressibility of the tissue specimens is imposed by equation (12),

$$ J=\det \left(\boldsymbol{F}\right)={\lambda}_C{\lambda}_L{\lambda}_R=1 $$
(12)

from which,

$$ {\lambda}_R=\frac{1}{\lambda_C{\lambda}_L} $$
(13)

The Cauchy-Green tensor \( \left(\mathbf{C}\right) \) is defined as \( \mathbf{C}={\boldsymbol{F}}^{\mathbf{T}}\cdot \boldsymbol{F} \), from which the invariants (see equation 6) are written according to equations (14) and (15),

$$ {I}_1={\lambda}_C^2+{\lambda}_L^2+\frac{1}{\lambda_L^2{\lambda}_C^2} $$
(14)
$$ {I}_4={I}_6={\lambda}_C^2{\cos}^2{\beta}_j+{\lambda}_L^2{\sin}^2{\beta}_j,\kern0.5em where\ \left(j=M,A\right) $$
(15)

The Green-Lagrange strain tensor (E) is given by equation (16),

$$ \mathbf{E}=\frac{1}{2}\ \left({\boldsymbol{F}}^T\boldsymbol{F}-I\right)=\frac{1}{2}\left[\begin{array}{ccc}{\lambda}_C^2-1& 0& 0\\ {}0& {\lambda}_L^2-1& 0\\ {}0& 0& \frac{1}{\lambda_L^2{\lambda}_C^2}-1\end{array}\right] $$
(16)

The circumferential (SC, HGO) and longitudinal (SC, HGO) 2nd PK stresses are calculated following equation (17a and b),

$$ {S}_{C, HGO}=\frac{\partial \psi }{\partial {E}_C}=c\left(1-\frac{1}{\lambda_L^2{\lambda}_C^4}\right)+\sum \limits_{j=M,A}4{k}_1{\cos}^2{\beta}_j\left({I}_4-1\right)\ \mathit{\exp}\left[{k}_2{\left({I}_4-1\right)}^2\right] $$
(17a)
$$ {S}_{L, HGO}=\frac{\partial \psi }{\partial {E}_L}=c\left(1-\frac{1}{\lambda_C^2{\lambda}_L^4}\right)+\sum \limits_{j=M,A}4{k}_1{\mathit{\sin}}^2{\beta}_j\left({I}_4-1\right)\ \mathit{\exp}\left[{k}_2{\left({I}_4-1\right)}^2\right] $$
(17b)

which are then substituted into equation (18) to calculate the Cauchy stress tensor (where S represents the 2nd PK stress tensor)

$$ \overline{\mathbf{C}}=\frac{1}{\mathrm{J}}\mathbf{FS}{\mathbf{F}}^{\mathbf{T}} $$
(18)

Finally, the circumferential (CC, HGO) and longitudinal (CC, HGO) Cauchy stresses are calculated by equation (19a and b),

$$ {C}_{C, HGO}=c{\lambda}_C^2\left(1-\frac{1}{\lambda_L^2{\lambda}_C^4}\right)+\sum \limits_{j=M,A}4{k}_1{\lambda}_C^2{\cos}^2{\beta}_j\left({I}_4-1\right)\ \mathit{\exp}\left[{k}_2{\left({I}_4-1\right)}^2\right] $$
(19a)
$$ {C}_{L, HGO}=c{\lambda}_L^2\left(1-\frac{1}{\lambda_C^2{\lambda}_L^4}\right)+\sum \limits_{j=M,A}4{k}_1{\lambda}_L^2{\sin}^2{\beta}_j\left({I}_4-1\right)\ \mathit{\exp}\left[{k}_2{\left({I}_4-1\right)}^2\right] $$
(19b)

We applied both a genetic and the Levenberg–Marquardt (LM) algorithm to identify the optimum set of material model constants for characterizing the tissue response to biaxial stretch. The optimization with the multi-objective genetic algorithm simultaneously minimized two objective functions that are the sum of the squares of the differences between the experimental and model-predicted Cauchy stresses in the circumferential and longitudinal directions, respectively. The mean of the resulting material model vectors that satisfy the additional constraints of c, k1, k2 > 0 were used as the initial guesses for the LM algorithm, which conducted an iterative least square minimization of the cost functions (fC(x), fL(x)) [31] along the longitudinal and circumferential directions, respectively. Equation (20a and b) represents the cost functions in their discrete form enabled in the MATLAB script,

$$ \underset{x\in {\mathfrak{R}}^n}{\min }{f}_C(x)=\sum \limits_{i=1}^m{\left({\sigma}_C\left({E}_C\right)-{C}_{C,\kern0.5em HGO}\left({E}_C\right)\right)}^2 $$
(20a)
$$ \underset{x\in {\mathfrak{R}}^n}{\min }{f}_L(x)=\sum \limits_{i=1}^m{\left({\sigma}_L\left({E}_L\right)-{C}_{L,\kern0.5em HGO}\left({E}_L\right)\right)}^2 $$
(20b)

where m is the number of observations. This strategy yields reproducible, unique specimen-specific material model constants.

Histological Characterization

Ring specimens (n = 10) from each group were fixed with 4% paraformaldehyde (Sigma-Aldrich Inc., St. Louis, MO) for 48 h. Next, the specimens were embedded with paraffin wax and 5 μm sections were mounted on a glass slide. The sections were processed in successive washes with varying concentrations of alcohol and stained for collagen (Picrosirius red, PSR) and elastin fibers (Verhoeff-Van Gieson, VVG). The slides were viewed under a Leica DMI 6000 B Microscope (Leica Microsystems Inc., Buffalo Grove, IL) and images were captured at 10x magnification. Briefly, randomized regions of interest (ROIs) were defined for each cross-section stained with VVG and PSR, and further processed for quantification of elastin and collagen content using ImageJ (National Institutes of Health, Bethesda, MD). The percentage area fractions for collagen and elastin were quantified according to equation (21),

$$ \% Area\ Fraction=100\ast \frac{target\ protein}{target\ protein+ remaining\ constituents} $$
(21)

where the target protein is either elastin or collagen [32]. VVG ROIs were used to calculate total tissue coverage in terms of pixels. Hue-Saturation-Brightness (HSB) thresholding using ImageJ was applied to isolate the elastin fibers (elastin is characterized as the darkest 50% of pixels) from the rest of the constituents [33]. Using equation (21), elastin area fraction was quantified as the ratio of elastin positive pixels to total tissue coverage pixels. This protocol was repeated for multiple ROIs. PSR ROIs were converted to 8-bit grayscale format (0 = black to 255 = white) [34] and a custom threshold of 0 (black) to 135 (slightly modified from [34]) was applied. The background color was inverted using ImageJ, which separated the non-thresholded portion of the ROI. The total coverage (in pixels) of the ROI was calculated and the collagen percentage was calculated using equation (21). This protocol was then repeated for multiple ROIs. Next, we evaluated intima-media thickness (IMT) and adventitial thickness (AT) of each VVG stained arterial cross-section for each group, as described in [35]. Briefly, IMT (the shortest distance between the luminal side to the edge of the elastic fiber band) and AT (the shortest distance between the elastic fiber band edge to the peri-adventitial edge) measurements were taken from undamaged portions of the VVG stained images. We performed eight measurements each for IMT and AT, per image, and reported the mean thicknesses.

Statistical Analysis

For each group, wall thickness (t0), histological quantification parameters (%collagen, %elastin, IMT, and AT), and biomechanical parameters (AI, TM, S55, and AUC) were reported as mean ± standard deviation (approximately n = 58, except histology). Based on the results of Shapiro-Wilk tests (not included in this manuscript), the eligible parameters were examined for inter-region statistical significance by means of a one-way analysis of variance with Tukey’s multiple comparison analysis. A Kruskal-Wallis test with a Dunn’s multiple comparison test were performed on the remaining parameters. We adopted a statistical significance threshold (α) of 0.05 while the analyses were performed using SAS® (SAS Institute, Cary, NC).

Results

Table 1 shows the wall thicknesses and biomechanical parameters for the ten experimental groups. Box-whisker plots for each variable, including their pairwise statistical output, are included in Figs. 3, 4, 5, 6, 7, 8, 9, and 10.

Table 1 Wall thickness and biomechanical parameters (mean ± std. dev.) for the ten experimental groups
Full size table
Fig. 3
figure 3

(a) Wall thickness (t0) distribution across the ten regions of the pulmonary vasculature, which was found to be significantly different across the groups (p < 0.0001), decreasing from the proximal MPA (MPA-P) to the distal vasculature (see Table 1). (b) Significant pairwise differences in t0 across the regions are highlighted (green) in the triangular matrix

Full size image
Fig. 4
figure 4

2nd Piola-Kirchoff stress at 55% strain for the ten regions of the pulmonary vasculature along the (a) circumferential (S55, C) and (c) longitudinal (S55, L) directions. Significant pairwise differences in (b) S55, C and (d) S55, L are highlighted (green) in the triangular matrix

Full size image
Fig. 5
figure 5

Tensile modulus (TM) calculated between the 0th and 30th percentile strain for the ten regions of the pulmonary vasculature along the (a) circumferential (TMC, 0 − 30) and (c) longitudinal (TML, 0 − 30) directions. Significant pairwise differences in (b) TMC, 0 − 30 and (d) TML, 0 − 30 are highlighted (green) in the triangular matrix

Full size image
Fig. 6
figure 6

Tensile modulus (TM) calculated between the 30th and 60th percentile strain for the ten regions of the pulmonary vasculature along the (a) circumferential (TMC, 30 − 60) and (c) longitudinal (TML, 30 − 60) directions. Significant pairwise differences in (b) TMC, 30 − 60 and (d) TML, 30 − 60 are highlighted (green) in the triangular matrix

Full size image
Fig. 7
figure 7

Tensile modulus (TM) calculated between the 60th and 90th percentile strain for the ten regions of the pulmonary vasculature along the (a) circumferential (TMC, 60 − 90) and (c) longitudinal (TML, 60 − 90) directions. Significant pairwise differences in (b) TMC, 60 − 90 and (d) TML, 60 − 90 are highlighted (green) in the triangular matrix

Full size image
Fig. 8
figure 8

Tensile modulus (TM) calculated between the 90th and 100th percentile strain for the ten regions of the pulmonary vasculature along the (a) circumferential (TMC, 90 − 100) and (c) longitudinal (TML, 90 − 100) directions. Significant pairwise differences in (b) TMC, 90 − 100 and (d) TML, 90 − 100 are highlighted (green) in the triangular matrix

Full size image
Fig. 9
figure 9

Anisotropy index (AI) calculated at the (a) 30th percentile (AI30) and (c) 60th percentile (AI60) 2nd Piola-Kirchhoff stress for each region of the pulmonary vasculature. Significant pairwise differences in (b) AI30 and (d) AI60 are highlighted (green) in the triangular matrix

Full size image
Fig. 10
figure 10

Area under the 2nd Piola-Kirchhoff (PK) stress vs. Green-Lagrange strain curve along the (a) circumferential (AUCC) and (c) longitudinal (AUCL) directions. Significant pairwise differences in (b) AUCC and (d) AUCL are highlighted (green) in the triangular matrix. AUCC (kPa) and AUCL (kPa), represent the strain energy stored during the loading cycle for the circumferential and longitudinal orientations, respectively (see Table 1)

Full size image

Arterial Wall Thickness

The wall thickness (t0) was found to be significantly different across the groups (see Fig. 3; Table 1; p < 0.0001). The highest mean t0 was found in the MPA-M region (2.098 ± 0.32 mm), whereas the lowest mean t0 was recorded in the RPA-D region (0.599 ± 0.152 mm). Overall, mean t0 reduced from the MPA-M to the B regions by 21.4% (2.098 ± 0.32 mm vs. 1.650 ± 0.435 mm; p < 0.0001). Furthermore, we observed a 60.1% decrease in mean t0 from the B to the LPA-D regions (1.650 ± 0.435 mm vs. 0.658 ± 0.189 mm; p < 0.0001) and a 63.7% decrease from the B to the RPA-D regions (1.650 ± 0.435 mm vs. 0.599 ± 0.152 mm; p < 0.0001).

Biomechanical Parameters

Stress at the maximum applied strain

S55 was consistently higher in the longitudinal direction relative to its circumferential counterpart (see Table 1). The MPA-D region exhibited the highest tensile stress in both circumferential (S55, C = 62.71 ± 22.00 kPa) and longitudinal (S55, L = 102.9 ± 48.54 kPa) directions. The minimum values of S55 were recorded for the LPA-D region in both directions (S55, C = 32.36 ± 9.56 kPa; S55, L = 37.13 ± 10.14 kPa), which represent 48.6% and 63.9% of the stresses found in the MPA-D region (see Fig. 4). For the circumferential direction, the pairwise analysis revealed significant differences between the MPA and LPA; MPA and RPA; and B with all other regions (p < 0.0001). However, stresses within the three MPA regions were statistically similar. A pairwise comparison analysis of all the tested regions revealed significant differences in S55, L compared to S55, C (p < 0.0001). S55, L decreased concomitantly from the MPA-D to the distal vasculature (LPA-D and RPA-D) (see Fig. 4; p < 0.0001). However, S55, L was similar in the RPA and LPA regions.

Tensile modulus

The tensile modulus, which is an indicator of arterial stiffness, was relatively higher in the longitudinal direction (TML) than in the circumferential direction (TMC) across all groups (Table 1; see Figs. 5, 6, 7, and 8). The MPA-D region exhibited the highest tensile moduli in both the circumferential (TMC, 0 − 30 = 44.59 ± 12.45 kPa, TMC, 30 − 60 = 50.83 ± 16.77 kPa, TMC, 60 − 90 =111.23 ± 45.32 kPa, TMC, 90 − 100 = 265.40 ± 128.00 kPa) and longitudinal (TML, 0 − 30 = 57.45 ± 21.25 kPa, TML, 30 − 60 = 67.99 ± 21.58 kPa, TML, 60 − 90 = 189.60 ± 98.82 kPa, TML, 90 − 100 = 502.90 ± 310.50 kPa) directions (see Figs. 5, 6, 7, and 8, p < 0.0001). The minimum circumferential tensile modulus was observed in the LPA-D (TMC, 0 − 30 = 32.66 ± 13.33 kPa, TMC, 30 − 60 = 41.02 ± 15.81 kPa, TMC, 60 − 90 = 46.98 ± 16.20 kPa) and RPA-D regions (TMC, 90 − 100 = 93.29 ± 59.59 kPa). This represented a decrease in mean circumferential tensile moduli of 29.0%, 26.9%, 57.8%, and 64.9% for the strain intervals E0 → E30, E30 → E60, E60 → E90, and E90 → E100, respectively, compared to MPA-D. The minimum longitudinal tensile modulus was also observed in the LPA-D region: TML, 0 − 30 = 39.66 ± 15.95 kPa, TML, 30 − 90 = 48.81 ± 18.12 kPa, TML, 60 − 90 = 58.71 ± 19.45 kPa, TML, 90 − 100 = 85.15 ± 23.35 kPa. To this end, the mean longitudinal tensile modulus decreased by 34.4%, 33.8%, 69.0%, and 83.1% for the strain intervals E0 → E30, E30 → E60, E60 → E90, and E90 → E100, respectively, compared to MPA-D.

Anisotropy index

Anisotropy indices calculated at the 60th percentile of the 2nd PK stress (AI60) were greater than those at the 30th percentile (AI30) (see Fig. 9). Furthermore, AI30 did not exhibit any significant pairwise relationships among the different regions. The maximum AI was found in the B region (AI30 = 0.087 ± 0.056, AI60 = 0.113 ± 0.072), while the minimum was observed in the RPA-M and LPA-M regions for AI30 (0.058 ± 0.043) and AI60 (0.071 ± 0.05), respectively. Both AI30 and AI60 were significantly different across all regions (Fig. 9(a), p = 0.00237 and Fig. 9(c), p = 0.0151, respectively).

Area under the curve

The area under the 2nd PK stress – Green-Lagrange strain curve in the circumferential and longitudinal directions are denoted as AUCC and AUCL, respectively. These metrics represent the energies stored in the specimens undergoing tensile loading. Across the pulmonary vasculature, the AUC in the longitudinal direction was found to be higher than its equivalent in the circumferential direction (see Table 1, Fig. 10). The mean AUCL in the MPA-P region (15.62 ± 6.54 kPa) was lower by 28.0% compared to the B region (20.00 ± 8.58 kPa). This was followed by a 43.6% and 32.4% decrease from the B region to the LPA-D (11.28 ± 3.23 kPa) and RPA-D (13.53 ± 4.34 kPa) regions, respectively (see Table 1; p < 0.0001). The MPA-D region exhibited the highest mean AUCC, whereas the LPA-D region had the lowest mean AUCC (13.99 ± 3.86 kPa vs. 9.19 ± 9.28 kPa). The bifurcation region exhibited the highest mean AUC in either tissue orientation (see Fig. 10; Table 1).

Constitutive Modeling

The mean constants for the HGO model are listed in Table 2 for each group. Good agreement (average R2 > 0.989) between experimental and theoretical data was observed for each region of the pulmonary vasculature. Figure 11 shows the mean stress-strain curve for the B region, illustrating the agreement between the experimental data and the HGO multilayer material model.

Table 2 Constants obtained of the Holzapfel-Gasser-Ogden (HGO) multilayer material model for each region of the pulmonary vasculature
Full size table
Fig. 11
figure 11

Cauchy stress vs. Green-Lagrange strain obtained from the Holzapfel-Gasser-Ogden (HGO) multilayer constitutive model compared to the corresponding mean experimental stress-strain curves for the bifurcation (B) region in the circumferential and longitudinal directions (R2 = 0.989 for both curves)

Full size image

Histological Characterization

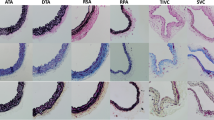
Representative cross-sectional histology images (PSR and VVG staining) for each experimental group are shown in Fig. 12 (elastin stains black in VVG and collagen appears red in PSR). Collagen content (p < 0.0001), elastin content (p < 0.0001), and IMT (p < 0.0001) were found to be significantly different across the regions; the respective statistical analysis can be found in Figs. 13 and 14. AT was not significantly different across the groups (p = 0.3442).

Fig. 12
figure 12

Histological characterization of the porcine pulmonary vasculature. The cross-sections from each experimental group in the top panel were stained with Picrosirius Red for collagen and in the bottom panel with Verhoeff-Van Gieson for elastin, respectively. The scale bar for each image is 1.5 mm

Full size image
Fig. 13
figure 13

Area fraction distribution of the (a) collagen and (c) elastin for the ten regions of the pulmonary vasculature obtained from the histological analysis of the specimens. Significant pairwise differences in (b) collagen and (d) elastin are highlighted (green) in the triangular matrix

Full size image
Fig. 14
figure 14

(a) Intima-media thickness (IMT, in mm) for the ten regions of the pulmonary vasculature obtained from the histological analysis of the specimens. (b) Significant pairwise differences in IMT are highlighted (green) in the triangular matrix

Full size image

Collagen Distribution

Collagen distribution across the different regions revealed that the MPA-P and LPA-D regions had the highest (39.8 ± 5.6% of tissue coverage) and lowest (19.9 ± 6.0% of tissue coverage) collagen content, respectively, as shown in Fig. 13(a). Noteworthy is that the collagen content of the B region was found to be similar to the MPA regions; 38.0 ± 4.2% (B) vs. 39.8 ± 5.6% (MPA-P) vs. 38.7 ± 1.4% (MPA-M) vs. 37.8 ± 5.5% (MPA-D). Collagen content was significantly lower in the distal regions (RPA and LPA, see Fig. 13(a)) compared to the MPA and B regions. In addition, it was found to be similar across all distal regions: LPA-P (25.0 ± 7.3%), LPA-M (22.2 ± 2.3%), RPA-D (22.8 ± 3.8%), RPA-M (21.1 ± 3.8%), RPA-P (20.6 ± 5.1%), and LPA-D (19.9 ± 6.0%).

Elastin distribution

In contrast to the collagen distribution, the elastin content did not exhibit drastic differences between the MPA and distal vasculature regions. The elastin content was highest in the MPA-P regions and lowest in the RPA-M region (68.3 ± 3.1% vs. 46.8 ± 7.6%), as illustrated in Fig. 13(c). Comparable to collagen, the elastin distribution was similar in the MPA-P, MPA-M, MPA-D, and B regions (68.3 ± 3.1% vs. 66.5 ± 2.9% vs. 64.7 ± 2.5% vs. 60.1 ± 5.6%). The elastin content in the LPA and RPA regions were found to be similar: 50.5 ± 9.3% (LPA-P), 51.6 ± 3.4% (LPA-M), 47.9 ± 4.9% (LPA-D), 49.7 ± 1.5% (RPA-P), 46.8 ± 7.6% (RPA-M), and 47.3 ± 6.3% (RPA-D).

IMT and AT

IMT was found to be highest in the MPA regions, as follows: MPA-M (1.39 ± 0.22 mm), MPA-P (1.2 ± 0.36 mm), and MPA-D (1.19 ± 0.52 mm), as shown in Fig. 14. Conversely, LPA-D exhibited the lowest IMT (0.31 ± 0.09 mm). The B region (0.81 ± 0.18 mm) yielded a mean IMT 1.48 times smaller than MPA-M and 0.39 times greater than the LPA-D region. IMT for the other regions was as follows: LPA-M (0.44 ± 0.04 mm), LPA-P (0.43 ± 0.11 mm), RPA-M (0.42 ± 0.11 mm), RPA-D (0.36 ± 0.12 mm), RPA-P (0.35 ± 0.08 mm), and LPA-D (0.31 ± 0.09 mm). AT ranged from 0.15 mm to 0.29 mm and was statistically similar across all regions (p = 0.2844).

Discussion

In this work, we examined the location-dependent structure-function relationship of porcine pulmonary arteries. Our proximity-based categorization formed a locational basis for evaluating differences in the biomechanical properties. There is a void in the literature pertaining to studies that report detailed regional pulmonary arterial mechanical behavior beyond the MPA and our investigation contributes to fill that void. The experimental data were well represented by the anisotropic HGO multilayer material model [28], the suitability of which is widely known for large artery wall mechanics [18, 30].

The MPA Is Thicker than the Remaining Pulmonary Vasculature

A comparative account of the pulmonary artery wall thickness measured in MPA-P region is presented in Table 3 with the thickness of the porcine pulmonary sinus [12], canine MPA [15], ovine MPA [18], and human pulmonary roots [22]. This represents a 27.1% higher wall thickness for the porcine pulmonary sinus in contrast with the MPA-P region. Such difference likely has an effect on the ensuing biomechanical characteristics, as evident from Table 4. The ovine MPA [18] is nearly 1.4 times thicker than the porcine MPA, while the human pulmonary root [22] is nearly 27% thinner than the porcine MPA-P region. Based on the regional wall thickness differences seen in porcine model, the human MPA can be inferred to be considerably thinner than the porcine MPA. In the present work, the MPA exhibited significantly higher wall thickness compared to the LPA and RPA (Fig. 3; p < 0.0001). Matthews et al. [12] and Lammers et al. [16] report on a comparative analysis of wall thickness and elastin fractions in the MPA, LPA, and RPA for control and hypoxic calves. Although not directly comparable to our data, their control groups exhibited a similar trend in mean wall thickness across the locations, i.e. the wall thickness of the MPA is greater than that of the LPA or RPA. Wall thickness changes in the pulmonary arteries are directly related to the proper homeostatic maintenance of the arterial layers – intima, media, and adventitia. A decrease in oxygen level (hypoxic condition) or a pathological insult to these layers leads to severe tissue remodeling, alteration of vascular ECM content, changes in vessel geometry, and eventually yield irregular pulmonary hemodynamics [15, 16, 36]. Hence, the elastin and collagen distributions in the pulmonary arteries play a critical role in maintaining the wall structural integrity and hemodynamics.

Table 3 Pulmonary arterial wall thickness (mean ± std. dev.) for human and animal sources
Full size table
Table 4 Tensile stress calculated at 55% strain (denoted by the subscript 55) along the circumferential and longitudinal directions in the MPA from porcine, canine, ovine, and human sources
Full size table

A significant and abrupt decrease in collagen content was observed when comparing the MPA with the LPA and RPA, suggesting a distinct microarchitectural difference amongst the pulmonary arterial branches. We observed a decrease in elastin from the proximal region of the MPA to the distal regions of the LPA and RPA; however, the elastin content was nearly conserved amongst the LPA and RPA regions. Since these findings can lead to more robust computational PH models, it is imperative to relate them to the intimal thickening characteristics of the pulmonary arteries. For thicker arterial segments such as the MPA regions, the IMT was found to be greater than the thinner, distal vasculatures (Fig. 14). This outcome could be the result of higher wall stresses experienced in the MPA [37]. As PH patients exhibit an increase in intimal thickening, our findings could possibly indicate that the ECM-based pathological damage could be more pronounced in the MPA and B regions, compared to the distal regions.

The MPA Exhibited the Highest Stress

The MPA-D region recorded the highest stress in both circumferential (62.71 ± 22.00 kPa) and longitudinal (102.92 ± 48.54 kPa) directions. Matthews and colleagues [12] reported the only other characterization of the anisotropic biaxial behavior of porcine pulmonary tissues, although their specimens consisted of pulmonary roots. Relative to this work, the circumferential and longitudinal Cauchy stresses in the MPA-P region, which is the closest to the pulmonary root, were different by factors of 1.4 and 0.915, respectively (at 55% Green strain). Evidently, the microstructural dissimilarities between pulmonary roots and pulmonary arteries enabled these differences in biomechanical characteristics [38]. Azadani and co-authors [22] conducted an investigation similar to [12] by using human specimens. Our circumferential and longitudinal Cauchy stresses in the MPA-P region were 1.34 and 0.88 times, respectively, than those reported in [22] (at 55% Green strain). In addition to the microstructural differences, the species of the specimens also influenced the differences in biomechanical properties. The porcine RPA-M region is most similar to the canine RPA samples tested by Debes and Fung [14]. While a direct model to model comparison is thus not feasible, noteworthy is that the circumferential and longitudinal 2nd PK stresses in the RPA-M region were 89.4% and 78.5%, respectively, of the RPA stresses in the canine model (Table 4). We conjecture that the rectangular shape of the test specimens in [15] influenced the inherent biaxial coupling and the ensuing tensile stresses.

The MPA Is the Stiffest Pulmonary Artery

Notably non-linear stress-strain curves with convexity toward the horizontal axis (Fig. 11) were obtained for the MPA-P, MPA-M, MPA-D, and B regions. However, the stress-strain curves for the LPA and RPA regions had significantly less convexity and nonlinearity. All regions registered relatively minor increases between (TMC, 0 − 30, TML, 0 − 30) and (TMC, 30 − 60, TML, 30 − 60) (Figs. 5, 6, 7, and 8), which is a consequence of the quasi-linear stress-strain characteristics up to 45% Green strain. This observation is in reasonable agreement with Mathews et al. [12], who reported linear stress-strain behavior for porcine pulmonary roots (up to 55% Green strain). To this end, the tensile moduli of our porcine pulmonary regions was consistently lower than that of the porcine pulmonary roots [12] in both circumferential and longitudinal directions (Table 5). The tensile moduli of the different regions signify relatively higher stiffness in the longitudinal direction compared to the circumferential direction (Figs. 5, 6, 7, and 8, Table 1). This finding is similar to the constitutive mechanical behavior of the human aorta undergoing large deformations [39]. Due to higher wall thickness, the MPA was substantially stiffer than the LPA and RPA along both principal orientations. Within the MPA, the mean stiffness increased distally. Conversely, the LPA and RPA exhibited a decrease in stiffness from the proximal to the distal end. The differences between AI60 and AI30 for all regions demonstrate the relatively less isotropic behavior of the pulmonary vasculature at high strains. Such findings of anisotropic characteristics are believed to be within the margin of experimental uncertainty.

Table 5 Tensile moduli (TM) along the circumferential and longitudinal orientations (mean ± std. dev.) in the MPA at different strain levels
Full size table

The Elastic Energy Is Higher in the MPA and B Regions

The inter-region variation in AUC revealed an increase of 23.3% (circumferential) and 28.0% (longitudinal) from the proximal MPA to the bifurcation region. This is followed by a concomitant decrease in AUC from the bifurcation to the distal LPA and RPA. This finding highlights a prominent relationship between the structure and function of the pulmonary vasculature. The considerable elasticity of the MPA is critical for passive regulation of the incoming pulsatile blood flow. The MPA transports nearly one-third of the stroke volume during systole, leading to the significant attenuation of blood flow pulsatility distal to the RPA and LPA [40].

Limitations

The primary outcome of the present work is bounded by several important limitations. The arterial specimens utilized in this study were frozen (−20oC) until tensile testing was performed and this may have damaged the specimens’ ECM. However, previous studies [23, 41] have shown that freezing at −20oC has minimal effect on the biomechanical properties of arterial tissues. The relatively small number of animal subjects (n = 10) and young age of the animals (6–9 months) is another important limitation of the study. It is unknown if the any of the animal subjects exhibited a cardiovascular condition as all were assumed to be healthy. During tensile testing, a plane stress condition was assumed for data collection and calculation of all subsequent biomechanical parameters. It is possible that some shear induced deformation occurred, inadvertently, during testing of the specimens. The HGO model assumes that the media and adventitial layers are divided into distinct thirds and presumed to be uniform throughout the wall. Our histological analysis shows that the extent of ECM proteins varies with location with elastin being predominant in the media of most regions.

Conclusions

We performed ex vivo planar equibiaxial tensile testing of porcine pulmonary arteries to evaluate the mechanical characteristics of ten different regions from the proximal MPA to the distal RPA and LPA. The MPA had a significantly higher wall thickness compared to the bifurcation, LPA and RPA, and exhibited the highest mean wall stress and tensile moduli in the longitudinal and circumferential directions. The bifurcation region yielded the highest values of anisotropy index and strain energy. All regions exhibited a higher stiffness in the longitudinal direction compared to the circumferential direction, although the ensuing degree of anisotropy is believed to be within the margin of experimental uncertainty. Following histological analysis of a sample of the specimen cross-sections, the collagen content was found to be the highest in the MPA and decreased significantly at the bifurcation, LPA and RPA. The elastin area fraction did not yield such significant differences amongst the ten regions. Regional differences in intima-media thickness were observed with the MPA having the highest thickness, which decreased concomitantly to the distal LPA and RPA. No significant differences were found in the adventitial thickness amongst the ten regions. The region-based evaluation of the HGO material constants derived from the experimental data can be used in future studies of high fidelity finite element models.