Introduction

The split Hopkinson pressure bar (SHPB) [1] has for some time been the most common technique for dynamic characterization of high-impedance materials (metals or ceramics and many polymers) in compression. Unlike these materials, the use of this technique for dynamic tests on rubbers presents several technical difficulties due to the low mechanical impedance of the specimens. The significant impedance mismatch between a soft specimen and stiff metallic Hopkinson bars causes a noisy, small amplitude force signal in the transmitted bar [2]. This impedance difference can be reduced by adopting viscoelastic bars [3, 4] so that the transmitted signal is large. Alternatively, a quartz-crystal force transducer installed on a metallic bar has been used for direct force measurement at the specimen-bar interface [5]. Another important issue is the long duration of the initial non-equilibrium deformation state due to the low wave speed in rubbers. This non-homogeneity invalidates the usual analysis procedure for Hopkinson bar tests in which stress equilibrium is assumed. A reduction in the time to reach the equilibrium state is necessary and this is usually achieved by using a specimen with a large radius to thickness ratio [4, 6]. Although this specimen design minimizes the wave propagation effect to a certain degree, pulse shaping techniques should also be utilized in order to increase the rise time of the incident pulse [7].

Dynamic tension tests on rubbers have similar technical problems to those mentioned above, but it is even more difficult to obtain the stress equilibrium state due to the inherently long specimen design. Many efforts have been made to ensure stress equilibrium: short specimens with a pulse shaping technique [8], applying dynamic loading simultaneously at both ends of the specimen [9] and thin tubular-shape specimen design for a very short gauge length [10]. However, it still seems that attainment of stress equilibrium is challenging, especially during the initial loading period and, moreover, the non-equilibrium period can be longer as higher strain rates and softer specimens are adopted. Also, the reduction of specimen length needs caution because a low length to width ratio can produce planar or biaxial stress states which exhibit stiffer behaviour than a uniaxial state. In order to overcome this limitation, a recent study has directly used the non-uniform deformation state caused by wave propagation in a specimen, to obtain a dynamic strain stress curve using the nonlinear one-dimensional wave equation and jump conditions [11, 12]. However, in these papers, the material motion only along a central line of the specimen is considered, due to the one dimensional assumption, neglecting the lateral contraction. For many soft materials, such as rubbers, this assumption can lead to the overestimation of the stress-strain curve measurement due to high incompressibility.

Recently, an inverse method, the Virtual Fields Method (VFM), has been actively used to study various linear, nonlinear and anisotropic materials with the aid of full-field displacement measurement techniques [13]. Traditionally, experimental characterization of materials requires an assumption of loading modes in their constitutive model according to specimen shapes and experimental configurations. As an example, for biaxial testing of rubbers, a suitable hyperelastic model is generally converted into the biaxial mode with assumptions of homogeneous biaxial strain states. However, in a real test there is a mixture of several strain states and their distribution varies with the amount of deformation. Using the VFM, these heterogeneous strain states can be considered simultaneously, as constitutive relations are directly involved without the modification for a specific state of strain. The VFM has been applied to the characterization of rubbers under static loading conditions: uniaxial and planar [14] and equi-biaxial states [15]. In these studies, the use of the nonlinear VFM in which hyperelastic models are involved in the VFM procedure enables researchers to successfully identify the model parameters considering the complete heterogeneous strain fields.

The main framework of the VFM is the mathematical manipulation of the principle of virtual work (PVW), and this can offer a choice of experimental data to be used. In the case of VFM application to dynamic tests, virtual displacement fields can be made in order to mathematically nullify the traction force term, representing the applied forces on the specimen, and retain the acceleration term (inertial force) in the PVW equation; thus, there is virtually no need to involve dynamic force measurements or to assume a state of stress equilibrium. This method has been successfully applied to dynamic tests with a conventional Hopkinson bar system on glass [16] & carbon [17] fibre reinforced epoxy composites, aluminium [18] and concrete [19]. The use of acceleration fields in the VFM is particularly advantageous for dynamic tests on rubbers because their low wave speed allows use of a lower imaging speed and higher image resolutions can be obtained. Recently, two of the current authors (S-HY and CRS) studied the application of the VFM to the dynamic tests on pure silicone rubber with a strain rate of the order of 100 s−1 [20]. In this study, a drop-weight test apparatus was used to introduce a small dynamic strain of amplitude about 0.05 in tension and the dynamic deformation fields were recorded by a high-speed camera. The linear elastic constitutive relation was adopted in the PVW equation in order to inversely obtain Young’s modulus and Poisson’s ratio based on the dynamic strain and acceleration fields within the initial wave propagation period. This procedure was repeated at a number of different static pre-stretches with a static force measurement before each dynamic loading. The series of calculated Young’s moduli were assumed to be tangent moduli of the one-term uniaxial Ogden model [21] at each pre-strain. Then, the Young’s modulus values and the differential form of the Ogden equation were optimized to calculate the two material parameters: μ and α. The main reason for this pre-stretching instead of a continuous dynamic deformation was to overcome the experimental limitation that it is difficult to achieve a large strain amplitude and, simultaneously, ensure a constant medium strain rate.

In the present study, the nonlinear VFM applied to experiments on high-speed gas gun apparatus is introduced for a dynamic test on EPDM rubbers in order to achieve a higher strain rate of the order 500 s−1. Unlike the linear VFM used for the drop-weight test, in the nonlinear VFM a hyperelastic nonlinear model is directly involved in the principle of virtual work equation. Here, the PVW equation was combined with the one-term Ogden model and applied to the continuous deformation and acceleration field history until the moment when cracks in the specimen were observed. The set of the nonlinear PVW equations produced by the full-field data at each loading time was then solved by an iterative method to identify the Ogden parameters. This paper first gives a theoretical description of the nonlinear VFM system. The second section shows a finite element simulation of the gas-gun experiment with given Ogden parameters in order to validate the capability of the nonlinear VFM. In the third section, firstly, simple quasi-static experiments are explained showing uniaxial stress-strain curves with three different low rates; secondly, the parameter identification procedure of the drop-weight tests by using the linear VFM is described; and thirdly, the actual gas-gun experiment data are discussed with regard to the identification procedure of the nonlinear VFM. At the end of this third section, all true stress-strain curves are provided together for comparison. The fourth section gives a brief discussion of advantages and disadvantages of the linear and nonlinear VFM. Then, the final section concludes with a summary of the present research.

Virtual Fields Method

The starting point of the VFM is to set up the PVW equation and define a proper constitutive relation. The PVW equation for a dynamic test in two-dimensional plane stress can be written in a component form as [17]

$$ -{\displaystyle \underset{s}{\int }}\ {\sigma}_{ij}{\varepsilon}_{ij}^{*}\ ds = {\displaystyle \underset{s}{\int }}\ \rho {a}_i{u}_i^{*}\ ds $$
(1)

when the following special virtual displacement and strain fields are applied in order to cancel the actual loading term and satisfy kinematic admissibility [16]:

$$ \begin{array}{ll}\left\{\begin{array}{c}\hfill {u}_x^{*,(1)}={x}_1\left({x}_1-L\right)\hfill \\ {}\hfill {u}_y^{*,(1)}=0\hfill \end{array}\right.\hfill & \left\{\begin{array}{c}\hfill\ {\varepsilon}_x^{*,(1)}=2{x}_1-L\hfill \\ {}\hfill {\varepsilon}_y^{*,(1)}=0\kern2.75em \hfill \\ {}\hfill {\varepsilon}_{xy}^{*,(1)}=0\kern2.75em \hfill \end{array}\right.\hfill \\ {}\left\{\begin{array}{l}{u}_x^{*,(2)}=0\hfill \\ {}{u}_y^{*,(2)}={x}_1\left({x}_1-L\right){x}_2\hfill \end{array}\right.\hfill & \left\{\begin{array}{c}\hfill {\varepsilon}_x^{*,(2)}=0\kern4.5em \hfill \\ {}\hfill {\varepsilon}_y^{*,(2)}={x}_1\left({x}_1-L\right)\hfill \\ {}\hfill {\varepsilon}_{xy}^{*,(2)}=\left(2{x}_1-L\right){x}_2\hfill \end{array}\right.\hfill \end{array} $$
(2)

where

σ :

Cauchy stress tensor

u * :

virtual displacement vector

ε * :

virtual strain tensor (the spatial derivative of u*)

s :

current surface area of a solid

ρ :

density

a :

acceleration vector

x 1, x 2 :

current longitudinal (loading) and transverse direction coordinate

Defining the isotropic linear elastic relation to the Cauchy stress term, σ, the true strain and acceleration fields from a dynamic experiment are applied to equation (1) in order to obtain the Young’s modulus E and Poisson’s ratio v. The VFM with the linear elastic relation is defined as the linear VFM in this study. The simple analytical procedure for this PVW is described in the previous drop-weight test study [20]. For the current drop-weight test on EPDM rubber specimens, the same PVW for the linear VFM was used as described in this previous study. It should be noted that the Cauchy stress is adopted; the PVW is based on the current (deformed) configuration so the virtual displacement fields need to be constructed based on the deformed coordinates. In the present study, piecewise virtual fields were adopted instead of the constant virtual fields in equation (2). It was found in the previous study that, compared to equation (2), the use of piecewise virtual fields provided a reduction in the standard deviation of the Young’s modulus estimations of a simulation material with artificially added noises. A full description of the piecewise virtual fields can be found in [13].

As a second method, the nonlinear VFM in conjunction with a hyperelastic model is introduced for application to the gas-gun experiment. The PVW for the nonlinear VFM is modified to be based on the first Piola-Kirchoff (PK1) stress as presented in previous researches [15, 22], the new PVW for the current dynamic case is written as:

$$ -{\displaystyle \underset{S}{\int }}{\Pi}_{ij}\frac{\partial {U}_i^{*}}{\partial {X}_j}dS={\displaystyle \underset{S}{\int }}\rho {a}_i{U}_i^{*}\ dS $$
(3)

where

Π :

the first Piola-Kirchoff stress tensor

U * :

virtual displacement vector defined on the reference configuration

S :

initial surface area

X 1, X 2 :

reference longitudinal (loading) and transverse direction coordinate

This new VFM also requires the special virtual fields for the cancellation of the traction term. However, unlike the linear VFM in which the two material parameters E and v are linearly solved with the two PVW equations (provided by the two sets of the virtual fields, equation (2)), for the new nonlinear PVW, only the first set of virtual fields was implemented because many PVW equations can be produced by using an entire loading history. In other words, a history of E and v estimations was obtained at each time point by setting up two linear PVW equations in the drop-weight test; one set of the Ogden parameters, μ and α, is calculated by solving this nonlinear PVW equation set considering the whole loading history.

The nonlinear PVW equation set can be solved by building up and minimizing a cost function written as

$$ \Phi ={\displaystyle \sum_{k=1}^N}{\left[{\displaystyle \underset{S}{\int }}{\Pi}_{ij}\left({t}_k\right)\frac{\partial {U}_i^{*}}{\partial {X}_j}dS+{\displaystyle \underset{S}{\int }}\rho {a}_i\left({t}_k\right){U}_i^{*}\ dS\right]}^2 $$
(4)

Here, N indicates the total number of the field data produced during a dynamic loading period. In order to minimize this cost function, the MATLAB fmincon was used with a lower boundary of 1 × 10−3 to find positive values of the Ogden parameters.

The PK1 stress fields in the cost function are reproduced at each loading step through a nonlinear constitutive relation defined as the one-term Ogden model. The strain energy form of the one-term (incompressible) Ogden model adopted in the finite element software ABAQUS [23] is given as

$$ W=\frac{2\mu }{\alpha^2}\left({\lambda}_1^{\alpha }+{\lambda}_2^{\alpha }+{\lambda}_3^{\alpha }-3\right) $$
(5)

As the Ogden model is a function of the principal stretch ratio λ i , it is convenient to express the PK1 stress in terms of the principal direction. The PK1 stress in the principal direction with the assumption of plane stress, Π3 = 0, is

$$ \begin{array}{c}\hfill {\Pi}_1=-\frac{1}{\lambda_1}\frac{2\mu }{\alpha^2}\left(\alpha {\lambda}_3^{\alpha}\right)+\frac{2\mu }{\alpha^2}\left(\alpha {\lambda}_1^{\alpha -1}\right)\hfill \\ {}\hfill {\Pi}_2=-\frac{1}{\lambda_2}\frac{2\mu }{\alpha^2}\left(\alpha {\lambda}_3^{\alpha}\right)+\frac{2\mu }{\alpha^2}\left(\alpha {\lambda}_2^{\alpha -1}\right)\hfill \end{array} $$
(6)

These principal PK1 stresses are then transformed into \( {\Pi}_{{\mathrm{X}}_1} \) and \( {\Pi}_{{\mathrm{X}}_2} \) which are based on the experiment coordinate, X 1 and X 2. These transformed PK1 stresses are applied to the cost function. A similar procedure is presented in previous works [14, 15].

Simulation Work

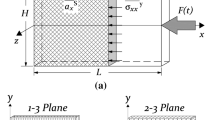
Numerical simulations were performed and analysed to simulate the actual gas-gun experiment and illustrate the nonlinear VFM introduced above. A finite element simulation was conducted in ABAQUS/explicit for the two-dimensional specimen geometry shown in Fig. 1. The dimensions here are similar to the actual specimen design in the gas-gun experiment. The CPS4R element type with a size of 0.5 was used. The fixed boundary condition was applied to the left end and the transversely fixed boundary condition to the right end of the specimen. For the dynamic loading applied to the right end, the velocity boundary condition, which peaked at 14 m s−1, obtained from one of the actual gas-gun experiments was adopted. The total loading time period was 1.4 ms and 140 output steps were given in order to simulate the imaging speed of 100,000 fps used in the gas-gun experiment.

Fig. 1
figure 1

Two dimensional simulation geometry and dimensions

Full size image

The one-term Ogden model was chosen; for its parameters μ (MPa) and α, 3 to 6 and 1 to 4 were respectively used with an interval of 1 so there were in total 16 simulations. This parameter range is chosen such that at least one stress wave reflection occurs within the total simulation time; in addition the parameters obtained from the nonlinear VFM on the gas-gun experiment are within this range. A high bulk modulus of 40 GPa was used in order to make the assumption of incompressibility, i.e., v ≈ 0.5. The density was set to 1370 kg m−3 which was measured from the EPDM specimen by weighing a sample. From each set of simulation data, the true strain, acceleration fields and initial coordinate were extracted and applied to the nonlinear VFM procedure for the prediction of this given parameter set. The predicted parameter results are shown in Fig. 2; it can be found that the parameter set (cross symbol) obtained from the VFM is well matched with the given values (intersected points of dashed lines).

Fig. 2
figure 2

Given parameters (intersected points of dashed lines) and VFM parameter predictions (cross symbol)

Full size image

The quality of the parameter extraction from the current VFM depends on the amount of the loading history involved in the PVW. The history of the parameter prediction produced by the simulation work with μ = 5 MPa and α = 1 can be seen in Fig. 3. The acceleration profile is an averaged value over the specimen surface at each time; the sign change of the acceleration indicates the moment of the wave reflection. Each predicted parameter is obtained by solving the nonlinear PVW with the simulation data history up to each time point; for example, the μ and α at 0.8 ms are obtained using the strain and acceleration field data from 0.0 to 0.8 ms. During the incident wave period (0.0–0.6 ms), it can be seen that the prediction of μ and α is not satisfactory with about 3 and 70 % differences respectively from the given values. However, after the first wave reflection (after around 0.6 ms), the calculated parameters become close to the given parameters in a stepwise way. The jump in this parameter estimation is due to the fact that the strain amplitude in the stress wave is approximately doubled after the stress wave reflection from the rigid end.

Fig. 3
figure 3

Averaged acceleration profile and the history of μ and α prediction

Full size image

Using the same simulation configuration, simple visco-hyperelastic simulations were conducted with a one-term Prony series. The normalized shear constant was given at 0.3 so that the instantaneous and long-term μ respectively were given as 5 and 3.5 MPa for the one-term Ogden model. In order to produce a different Ogden behaviour with the same velocity boundary condition, four different relaxation time constants τ were given at 0.20, 0.15, 0.10 and 0.05 ms. These constants were chosen so that the four Ogden stress-strain curves are located between the instantaneous and long-term curves for the given applied loading rate. The simulation data produced by the four relaxation constants were analysed by the same nonlinear VFM procedure. The four calculated parameter sets are listed in Table 1. These parameters are used to reconstruct the Ogden uniaxial curves as shown in Fig. 4 (left) with the given instantaneous and long-term curves. It can be seen that the longer relaxation time produces the Ogden curve which is closer to the instantaneous one. This observation gives confidence that the present nonlinear VFM procedure is able to capture the stiffer behaviour due to the longer relaxation time. Figure 4 (right) presents the estimation history of μ and α and the averaged acceleration profile from the simulation with τ = 0.05 ms. The μ (3.67 MPa) and α (0.91) given in Table 1 are obtained from the values at the end of the period (at 1.4 ms) of their profiles. The initial averaged acceleration amplitude of Fig. 4 (right) is similar to that shown in Fig. 3 of the pure hyperelastic simulation work. After this incident wave period, it can be observed that the acceleration profile in Fig. 4 (right) is attenuated by about 50 % due to the viscoelastic term whereas no significant attenuation is observed in Fig. 3. This attenuation is the main factor causing the variation of the Ogden parameters with the different relaxation time constants for the same velocity boundary condition.

Table 1 Four Ogden parameter sets obtained from the nonlinear VFM analysis on the visco-hyperelastic simulation
Full size table
Fig. 4
figure 4

(left) Ogden curves reconstructed from the parameters give in Table 1 and the given instantaneous & long-term curves; (right) averaged acceleration profile and the history of μ and α prediction from the visco-hyperelastic simulation with τ = 0.05 ms

Full size image

Experimental Procedure and Results

Quasi-static Experiment

A sheet of commercial EPDM rubber (Amarin Rubber & Plastics Ltd) was used in the present study. For comparison with the gas-gun experiment, tensile quasi-static experiments were conducted. The uniaxial specimens were prepared with dimensions of gauge length = 60 mm, width = 20 mm and thickness = 2 mm. True strain rate control was employed with three strain rates: 0.01, 0.001 and 0.0001 s−1. While testing the specimens, a USB camera (Grasshopper3 USB 3.0 Digital Camera, Point Grey Research, Inc.) was used to capture displacement fields (at 5 fps) on the specimen surfaces (215 × 684 pixels) where a white spray was applied to make a fine speckle pattern. The full-field measurements were then analysed by commercial digital image correlation software (Davis 8.2.0, LaVIsion) with cross-correlation mode [24] and a correlation window of size 16 × 16 each of which includes about three dots of the spray pattern. This subset size was the smallest able to produce high data resolution with a reasonable noise level (spatially averaged standard deviation: 0.1 %) in the axial strain fields obtained from the five static images before loading.

The engineering uniaxial stress was calculated by the load measured from a tensile test machine; the engineering uniaxial strain was obtained from the DIC analysis and interpolated to be matched with the time of the force measurement. The stress and strain values of the four tensile tests were fitted to the one-term uniaxial Ogden model written as follow:

$$ {\sigma}_{eng} = \frac{2\mu }{\alpha}\left({\lambda}^{\upalpha -1}-{\lambda}^{-0.5\upalpha -1}\right) $$
(7)

where λ and σ eng denotes the uniaxial stretch ratio and engineering stress. The one-term Ogden parameters from this fitting are listed in Table 2 and their fitted and experiment curves are presented in Fig. 5.

Table 2 One-term Ogden model parameters obtained from the quasi-static uniaxial tests
Full size table
Fig. 5
figure 5

Uniaxial true strain-stress curves from the experiment (filled symbol) and fitting (open symbol)

Full size image

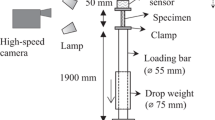
Medium Strain-Rate Test (Drop-Weight Test)

The drop-weight test was adopted for the VFM with the linear elastic constitutive relation. EPDM specimens were prepared with the following dimensions: gauge length = 37 mm, width = 11 mm and thickness = 2 mm. For these specimens, the experimental setting and procedure presented in the previous work [20] were applied to obtain a series of the dynamic full-field measurement at a number of different pre-stretching by means of a high-speed camera (FASTCAM SA5, Photron) at 50,000 fps with the image size of about 420 × 170 pixels. The static force was measured just after pre-stretching and then applied to the PVW with the strain and acceleration fields obtained from the DIC analysis on the dynamic displacement fields. The piecewise virtual fields were automatically produced by considering kinematic admissibility, special virtual fields and noise minimization [25, 26] and the cancellation of the traction force term. A series of the E estimation profiles from two drop-weight tests is shown in Fig. 6 in which the hatched area indicates the period where the E, v and strain rate fields are averaged; the values are listed in Table 3. This hatched area is made so that, for each profile, the E predictions are stable and the v values are bounded between 0.45 and 0.5 for reasonable incompressibility. The legend in Fig. 6 denotes the pre-true strain values and its subscript x for the loading direction. The strain rate \( {\overset{\cdot }{\varepsilon}}_x^{dynamic} \) for each time was obtained by averaging only over the deformed area during the incident wave period; after the wave reflection, the strain rate fields over the whole specimen surface were averaged.

Fig. 6
figure 6

Young’s moduli obtained from the linear VFM and drop-weight tests with pre-stretching; the shaded area indicates the values used to obtain the averaged Young’s moduli

Full size image
Table 3 Averaged young’s modulus, longitudinal strain rate and Poisson’s ratio
Full size table

These E values from the test of SET 1 and 2 were assumed to be the tangent moduli E i tangent at each i th pre-strain location of a uniaxial true strain-stress curve of the one-term Ogden model. Then, the following system of nonlinear equations is established using the differentiated form of the one-term uniaxial Ogden model, equation (7).

$$ \left\{\begin{array}{c}\hfill \frac{d{\sigma}_{true}^{Ogden}}{d\varepsilon}\left(\mu, \alpha,\ {\varepsilon}_x^1\right)-{E}_{tangent}^1=0\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \frac{d{\sigma}_{true}^{Ogden}}{d\varepsilon}\left(\mu, \alpha,\ {\varepsilon}_x^{15}\right)-{E}_{tangent}^{15}=0\hfill \end{array}\right. $$
(8)

This system of nonlinear equations was optimized by using the MATLAB fsolve with Levenberg-Marquardt algorithm. The optimized Ogden parameters were obtained as μ = 4.39 MPa and α = 1.71. The true stress-strain curve for this parameter set is presented in the next section with the results of the gas-gun experiment.

Gas-Gun Experiment and Comparison of Data

The idea of the present gas-gun experiment is based on the high strain rate experiment for testing a yarn of polymeric fibres developed by Russell et al. [27]. Here, eight uniaxial type EPDM specimens (length = 100 mm, width = 11 mm, thickness = 2 mm) were prepared. In each experiment, one end of each of two specimens was fixed on one side of a rectangular aluminium block: the specimens were superglued into a clamp. The dimensions of the aluminium block were determined so that oscillations of the specimen end due to flexure of the block were reduced. The other ends of the specimens were similarly clamped to a rigid frame attached to the barrel of a gas gun. An aluminium projectile was accelerated by the gas gun so that it impacted the block at speeds between 50 and 80 m s−1. A schematic representation of the configuration is shown in Fig. 7.

Fig. 7
figure 7

Schematic representation of the gas-gun experiment and a speckle pattern on a part of the specimen surface with a 12 by 12 correlation window (red rectangle)

Full size image

After shooting, the dynamic displacement on the specimen surface, where a random speckle pattern was applied by a white spray, was captured by the high speed camera at 100,000 fps. If two high speed cameras are available, it is possible to obtain two dynamic displacement fields from the two specimens; however, in this study, only one of the specimen surfaces was captured by one camera. The image size over the specimen surface, for example TEST3, is 203 × 69 pixels. The acquired images were then analysed by the DIC software as explained in the quasi-static experiment but with a smaller correlation window size of 12 × 12 (50 % overlap). These window and overlap sizes were chosen for high data resolution with a reasonable noise level (0.06 %) of the axial strain fields of the five static images. It was found that a further reduction in the window or overlap sizes resulted in a steep increment of the noise level. The displacement and strain fields obtained by the DIC were validated by comparing the global displacement and strain manually calculated using the distance between some clear dots among the speckle pattern. For the acceleration fields, the displacement history of each data point was individually fitted by 9-degree polynomial using MATLAB; then, each fitted displacement history curve was double differentiated to obtain the acceleration curve. The acceleration curves were collated to form the spatial data. The axial (loading direction) displacement, true strain and acceleration fields at loading times of 0.34 and 1.14 ms from TEST 3 are shown in Fig. 8 with the initial coordinate.

Fig. 8
figure 8

Axial displacement (upper), true strain (middle) and acceleration fields (bottom) at 0.34 and 1.14 ms of Test 3

Full size image

The axial strain values are plotted along the lengthwise position by averaging them in the lateral direction. The strain plots at several time points are presented in Fig. 9. The strain curve at 0.24 ms shows that the initial incident strain wave is propagated from the right-hand side (loading end). This incident wave starts to be reflected around 0.54 ms. After this time, the reflected wave travels back toward the loading end. The propagation of the next reflected wave is not clear and the strain along the length becomes uniform. This wave attenuation can be caused by the viscoelastic behaviour of the specimen. The strain values around both ends of the specimen are lower than its global behaviour. This stiffer behaviour at both ends could be an artefact from the large thickness change due to the clamping fixture and a superglue layer used to improve the clamping of the specimen in the fixture. The data from this region are excluded in the VFM procedure by simply making a shorter virtual displacement field.

Fig. 9
figure 9

Axial true strain curves (averaged in the lateral direction) along the lengthwise position from Test 3

Full size image

The time that the strain wave reaches the fixed end of the specimen is about 0.34 ms. From this time, it is possible to approximate the wave velocity c as 108 m/s (= 37 mm / 0.34 ms); using the one-dimensional wave theory, \( c=\sqrt{E/\rho } \), the initial Young’s modulus is approximated at 16 MPa. Then, the initial shear modulus is obtained at 5.3 MPa with the assumption of incompressibility, v = 0.5. The μ in the Ogden model, equation (5), represents the initial shear modulus of the material so the μ parameter to be obtained by the nonlinear VFM procedure should be close to this approximated initial shear modulus.

As explained in the section of Virtual Fields Method, the nonlinear VFM procedure was applied to the strain and acceleration field data from the period within which the second reflection of the acceleration wave was included in the VFM analysis; after this period, cracks and voids start to be observed on the specimens. The VFM result of TEST 3 is given in Fig. 10 showing the estimation history of the Ogden parameters and the profiles of the averaged acceleration and (true) strain rate. Unlike the acceleration values obtained by simply averaging all the values, the strain rate profile is obtained by averaging only the deformed region in the specimen during the incident strain wave period and the whole fields after the first wave reflection. Similarly to Fig. 4 (right) of the simulation work, the estimations of μ and α converge to certain values since the second acceleration wave is included in the optimization procedure of the nonlinear VFM. The period where the estimations are stable is chosen to be averaged to obtain the Ogden parameters as indicated by the hatched box in Fig. 10; the final strain rate is obtained by averaging its values along the period of 0.4–1.7 ms. The same procedure was repeated to obtain these parameters from all gas-gun experiments. The parameters obtained from the four gas-gun experiments are summarized in Table 4.

Fig. 10
figure 10

Averaged acceleration and strain rate profiles and the history of μ and α prediction from the gas-gun experiment on an EPDM rubber (TEST 3)

Full size image
Table 4 Four Ogden parameter sets obtained from the nonlinear VFM and the averaged strain rates of the gas-gun experiments
Full size table

These four Ogden parameter sets are applied to the uniaxial Ogden model, equation (7), in order to reconstruct the true stress-strain curves as shown in Fig. 11. For comparison, this figure includes the three quasi-static curves and the Ogden curve reconstructed by the Ogden parameters obtained from the drop-weight test. This figure shows the clear rate dependency of the present EPDM rubber as the stress-strain curve behaves stiffer for the higher strain rates. This stiffer behaviour can be explained by the fact that the μ term becomes higher for the higher strain rates. It seems that the α term also generally increases but is not strongly dependent on the strain rate since the α values for the drop-weight test (101 s−1, α = 1.71) and one of the quasi-static tests (0.01 s−1, α = 1.46) are not significantly different. The four Ogden curves from the gas-gun experiment in Fig. 11 have a solid line with symbol and a dashed line. The end of the symbolic line indicates the maximum averaged true strain of the last loading step used in the VFM; from this end, the dashed line is extend in order to extrapolate the gas-gun Ogden curves up to a true strain of 0.63 which is the maximum true strain of the drop-weight test.

Fig. 11
figure 11

Ogden uniaxial true stress-strain curves reconstructed by the parameters of the gas-gun, drop-weight and quasi-static tests

Full size image

Discussion

The identified parameters given in Table 4 are obtained from the dynamic full-field data produced by each single gas-gun experiment. This experimental expediency is a clear advantage of the gas-gun experiment with the nonlinear VFM compared to the drop-weight experiment with the linear VFM in which multiple experiments are required to introduce the pre-stretches. The identification by the single experiment has another advantage in that complicated effects caused by the pre-stretches such as softening can be avoided. In addition, it is clear that the gas-gun experiment is more suitable for high strain rates (> 300 s−1) as the maximum strain rate of the current drop-weight system is limited by the mass and drop distance of the weight. However, the drop-weight test with the linear VFM and pre-stretching method is still a useful technique to fill the gap between the high strain-rate and quasi-static tests. It is experimentally complicated to introduce a single loading pulse which induces the medium strain rate of order of 100 s−1 whilst at the same time producing a large strain with a constant strain rate, as the final strain is not independent of the strain rate, and both are also affected by the material properties (in particular the stress wave speed). More positively, the fact that the drop-weight test produces a small strain amplitude allows a use of higher resolution imaging and faster imaging speed using high-speed cameras for which the imaging size needs to be reduced for faster imaging. However, the pre-stretching can induce some inelastic effects, e.g., Mullin’s effect. Thus, once a specimen is stretched, the next stretching should be larger than the previous one.

In summary, the combination of the two techniques: drop-weight with preloads and higher speed loading in a gas gun, allows complete stress-strain curves to be calculated to large strains in tension on hyperelastic materials for which standard high rate testing techniques cannot be used. The relatively low wave speed in these materials allows the use of relatively high resolution and low noise high speed cameras, giving high quality measurements of strain and acceleration. In particular, the gas gun experiments, when combined with a non-linear VFM method and making use of the fact that the compressive stress wave reflects from the fixed specimen end in compression, allows large strains to be investigated, which is required to accurately calculate the strain hardening, giving an accurate calculation of the Ogden model parameters from a single experiment.

Conclusions

Drop-weight and gas-gun experiments were performed on EPDM rubbers in order to characterize the mechanical response to loading at medium and high strain rates in tension. The dynamic deformation fields captured by a high speed camera were applied to the Virtual Fields Method (VFM). By using the correct virtual fields, force measurement was not required; instead, the acceleration fields in the specimen were utilized in the principle of virtual work equation. The previously developed linear VFM was applied to a series of the short dynamic deformation fields obtained in a drop-weight apparatus with several given pre-stretches. From this procedure, a series of Young’s moduli were identified at each given pre-strain and used to reconstruct an Ogden true stress-strain curve. In order to produce data at higher strain rates, the nonlinear VFM directly associated with the one-term Ogden constitutive model was applied to the history of large dynamic deformation fields produced by a newly designed gas-gun experiment. The gas-gun experiment design was first simulated by finite element analysis; this simulation shows that the nonlinear VFM application on the continuous dynamic deformation fields with multiple wave reflections can successfully identify given Ogden parameters. The same nonlinear VFM procedure was applied to experimental data and two Ogden parameter sets were identified at different high strain rates. The five dynamic true strain-stress curves were reconstructed by the Ogden parameters obtained from the four gas-gun and one drop-weight tests. These dynamic curves show their clear rate dependency between the dynamic tests and also from comparison to the quasi-static uniaxial experiments.