Asymptotically Correct Person Fit z-Statistics For the Rasch Testlet Model

Abstract

A well-known person fit statistic in the item response theory (IRT) literature is the $l_{z}$ statistic (Drasgow et al. in Br J Math Stat Psychol 38(1):67-86, 1985). Snijders (Psychometrika 66(3):331-342, 2001) derived $l_{z}^{*}$, which is the asymptotically correct version of $l_{z}$ when the ability parameter is estimated. However, both statistics and other extensions later developed concern either only the unidimensional IRT models or multidimensional models that require a joint estimate of latent traits across all the dimensions. Considering a marginalized maximum likelihood ability estimator, this paper proposes $l_{zt}$ and $l_{zt}^{*}$, which are extensions of $l_{z}$ and $l_{z}^{*}$, respectively, for the Rasch testlet model. The computation of $l_{zt}^{*}$ relies on several extensions of the Lord-Wingersky algorithm (1984) that are additional contributions of this paper. Simulation results show that $l_{zt}^{*}$ has close-to-nominal Type I error rates and satisfactory power for detecting aberrant responses. For unidimensional models, $l_{zt}$ and $l_{zt}^{*}$ reduce to $l_{z}$ and $l_{z}^{*}$, respectively, and therefore allows for the evaluation of person fit with a wider range of IRT models. A real data application is presented to show the utility of the proposed statistics for a test with an underlying structure that consists of both the traditional unidimensional component and the Rasch testlet component.

Item response theory (IRT) is ubiquitously used as the underlying statistical model for calibrating items and scoring examinee responses. Establishing that the IRT model adequately fits the data is an important aspect of establishing validity for the intended use of test scores resulting from the assessment. Item statistics, including item fit, are taken into account during the item review process and could indicate that the item should be modified or rejected altogether. Even when all items fit the model, it is possible that the model does not fit for a particular examinee. For example, a person answering all easy items incorrectly but all other items correctly is an unexpected or aberrant response pattern for a given set of item parameters. Aberrant responses refer to a series of answers examinees provided that are unlikely to arise given their true ability and the chosen psychometric model. In other words, there is a lack of fit between response patterns and the model used for scoring. Many test-taking behaviors such as cheating, lack of motivation and random response can cause aberrant responses and lead to a poor person fit.

Various indices have been proposed to capture the degree of person fit (see Meijer and Sijtsma, 2001, or Karabatsos, 2003, for a survey of person fit statistics in the earlier literature. More recently, fit statistics were proposed by, among others, von Davier and Molenaar 2003; Glas and Dagohoy 2007; de la Torre and Deng and Deng, 2008; Sinharay 2015; 2016; Xia and Zheng, 2018. A relatively recent review can be found in Rupp, 2013). Among these statistics, one of the most well-known is the standardized loglikelihood statistic of a response pattern, denoted as $l_{z}$, first developed by (Drasgow et al., 1985). The statistic provides a measure of the degree to which the response pattern is aberrant, given a known value of the true ability $(\theta )$. $l_{z}$ asymptotically follows a standard normal distribution (Drasgow et al., 1985; Snijders, 2001).

In practice however, the true ability is not known but estimated from the same data on which $l_{z}$ is computed. Even though Drasgow et al. (1985) indicated that the effects from the estimated ability $(\hat{\theta })$ were fairly small given the fact that standardization of the response loglikelihood has reduced its dependency on the estimated ability, other researchers have found scenarios where $l_{z}$ deviates from standard normal. Molenaar and Hoijtink (1990) found that in Rasch model for dichotomous items, even when assuming $\hat{\theta }=\theta$ given a raw score, the deviation from normality of $l_{z}$ was particularly evident when $\hat{\theta }$ was far from the mean of the item difficulties, and when the test was short. Negative skewness and heavy tails were observed in the example cases they showed. Several other studies have found that the variance of $l_{z}$ can be considerably smaller than 1 when the true ability $\theta$ is replaced by the estimated ability $(\hat{\theta })$ (e.g., Nering, 1995; Reise, 1995; Seo & Weiss, 2013). Molenaar and Hoijtink (1990) proposed a modified version of the person fit index, by using the result that the sum of the raw scores is a sufficient statistic for $\hat{\theta }$ for the Rasch model. The first few central moments of the proposed statistic were computed and used in deriving a chi-squared distribution-based approximation that accounts for the skewness of the loglikelihood person fit index. Bedrick (1997) used a different approximation that involves the use of Edgeworth expansion for skewness correction. von Davier and Molenaar (2003) extended the work of Molenaar and Hoijtink (1990) to latent class models and mixture distribution IRT models for both dichotomous and polytomous data. They also compared the performance of the two aforementioned approaches to reduce the skewness of the person-fit index. Liou and Chang (1992), on the other hand, used a so-called network algorithm to obtain the exact significance of the loglikelihood person fit index when conditioning on either the maximum likelihood ability estimates or the sum score in Rasch model. Meanwhile, Snijders (2001) derived a framework of asymptotically normal person fit statistics for dichotomous items when the $\hat{\theta }$ is used, among which is the modified version of $l_{z}$ now commonly referred to as the $l_{z}^{*}$ statistic. When $\hat{\theta }$ is the maximum likelihood estimate, the essence of $l_{z}^{*}$ lies in correcting the loglikelihood variance estimate in the original of $l_{z}$. It was shown in Snijders (2001) that $l_{z}^{*}$ produced type I error rates close to the nominal rate. Sinharay (2016) derived $l_{z}^{*}$ for mixed format test, where polytomous items can also be handled along with dichotomous items.

An important limitation of $l_{z}$ and $l_{z}^{*}$, and the other previously mentioned person fit indices in the literature, is that they only address the person fit assessment with a unidimensional latent trait. More recently, there have been some efforts to extend $l_{z}$ and $l_{z}^{*}$ for their uses with multidimensional constructs. Albers et al. (2016) proposed $l_{zm}$ and $l_{zm}^{*}$, which are used for dichotomous items and multiple subscales. Hong et al. (2121) provided more rigorous derivations of these statistics, extensions to mixed item types, and more extensive simulation studies. It should be noted that an implicit requirement to use $l_{zm}$ or $l_{zm}^{*}$ is that person estimates are obtained across all dimensions. In practice, however, one of the important use cases of introducing additional latent variables is to address the local dependencies among items that share a common stimulus or belong to the same testlet. Some popular models developed to this end are the testlet models (Bradlow et al., 1999) and particularly the widely used Rasch testlet model (Wang and Wilson, 2005). In such cases, usually the overarching latent trait is of primary interest, while the other traits are incorporated as so-called “nuisance” dimensions to account for the testlet effects. When examining the person fit with these models, $l_{zm}$ or $l_{zm}^{*}$ cannot be applied unless $\theta$ estimates for all the dimensions are obtained, counter to the idea of introducing testlet effects as nuisance dimensions. On the other hand, a direct application of $l_{z}$ and $l_{z}^{*}$ ignoring the testlet effects is also not a good solution. Chen (2013) investigated the utility of $l_{z}$ on detecting aberrant responses for the testlet model and found that the detection rate was worse when there were more testlet items or the testlet variance was larger. In sum, there is a need to develop a feasible approach of person fit evaluation that works for testlet models.

This paper proposes two new statistics, $l_{zt}$ and $l_{zt}^{*}$, which extend $l_{z}$ and $l_{z}^{\mathrm {*}}$, respectively for the Rasch testlet model when the marginalized maximum likelihood estimation (MMLE) is used for $\theta$ estimation (i.e., the nuisance dimensions are integrated out. More details about MMLE are provided in a later section of this paper). Moreover, with the advances in technology enhanced items and test delivery system, test developers nowadays create novel tests with an underlying latent structure that incorporates both items organized in testlets and unidimensional standalone items (e.g., New Hampshire Department of Education, 2019). It will be shown that $l_{zt}$ and $l_{zt}^{*}$ reduce to $l_{z}$ and $l_{z}^{\mathrm {*}}$, respectively, with unidimensional MLE estimation of $\theta$, and therefore can be considered as a generalized approach to evaluate person fit when the underlying structure includes both a testlet component and observed variables that do not belong to any testlet.

The rest of this paper is organized in the following way. First, we provide some theoretically background on $l_{z}$ and $l_{z}^{*}$, as well as some technical details about the MMLE method for the estimation of the overall $\theta$ under the Rasch testlet model. We then extend the original $l_{z}$ statistics to its form in the Rasch testlet model and illustrate how the variance of the loglikelihood can be corrected when MMLE is used to obtain the new statistics we call $l_{zt}^{*}$. A simulation study follows to evaluate the performance of $l_{zt}^{*}$, including the Type I error rate and power under the Rasch testlet model. We then demonstrate an application of $l_{zt}^{*}$ on a real dataset from a large-scale standardized assessment, to show that $l_{zt}^{*}$ is flexible such that it can be applied to a wider range of models which allow for both the testlet model for some item sets and a traditional unidimensional model for other items. Finally, we discuss practical considerations and future direction of these statistics.

1 Review of the $l _{ z }$ and $l _{ z }^{{*}}$ Statistics for Unidimensional Models

Because the extension of $l_{z}$ and $l_{z}^{*}$ this paper presents mainly concerns the Rasch testlet model for dichotomous item responses, we offer a review of $l_{z}$ and $l_{z}^{*}$ for dichotomous items here to achieve a better connection to the method to be proposed. A didactic presentation of $l_{z}^{*}$ was offered by Magis, Raîche, and Béland (2012). A presentation of $l_{z}$ and $l_{z}^{*}$ for mixed format tests is available from Sinharay (2016) where $l_{z}^{*}$ for dichotomous items was shown as a special case.

Consider an examinee with true ability $\theta$ who responds to a test consists of n items modeled by a unidimensional IRT model (for example, the one-, two-, and three-parameter logistic model). Throughout the paper, item parameters of the IRT models are assumed to be known. Let $Y_{j}$ be the binary response provided by the examinee to item j, $p_{j}\left( \theta \right) =P(Y_{j}=1\vert \theta )$ be the probability of correct response to item j, and $q_{j}\left( \theta \right) =1- p_{j}\left( \theta \right)$. As defined by Snijders (2001), one class of the person fit statistics $W_{j}$ for dichotomous items can be expressed in a centered form as

$$\begin{aligned} W\left( \theta \right) =\mathop {\sum }\limits _{j=1}^n {\left( Y_{j}-p_{j}\left( \theta \right) \right) w_{j}\left( \theta \right) }, \end{aligned}$$

where $w_{j}\left( \theta \right)$ is a suitable weight function. The random variance $W(\theta )$ has expected value

$$\begin{aligned} E\left( W\left( \theta \right) \right) =0 \end{aligned}$$

and variance

$$\begin{aligned} Var\left( W\left( \theta \right) \right) =n\sigma _{n}^{2}\left( \theta \right) =\mathop {\sum }\limits _j^n {w_{j}\left( \theta \right) p_{j}\left( \theta \right) q_{j}\left( \theta \right) }. \end{aligned}$$

Under regularity conditions, the standardized version of $W(\theta )$ which takes the form

$$\begin{aligned} \frac{W\left( \theta \right) }{Var\left( W\left( \theta \right) \right) } \end{aligned}$$

asymptotically follows a standard normal distribution by the Lindeberg-Feller central limit theorem for independent but non-identically distributed random variables. The $l_{z}$ statistics (Drasgow et al., 1985) is defined as

$$\begin{aligned} l_{z}\left( \theta \right) =\frac{l\left( \theta \right) -E\left( l\left( \theta \right) \right) }{Var\left( l\left( \theta \right) \right) } . \end{aligned}$$

(1)

For dichotomous items,

$$\begin{aligned} l\left( \theta \right) =\mathop {\sum }\limits _j^n {Y_{j}\log {p_{j}\left( \theta \right) }+\left( {1-Y}_{j} \right) \log {q_{j}\left( \theta \right) }}, \end{aligned}$$

which is the log-likelihood of the examinee’s item scores. The expected value of $l\left( \theta \right)$ is

$$\begin{aligned} E\left( l\left( \theta \right) \right) =\sum \limits _j^n {p_{j}\left( \theta \right) \log {p_{j}\left( \theta \right) }+q_{j}\left( \theta \right) \log {q_{j}\left( \theta \right) }}, \end{aligned}$$

and the variance of $l\left( \theta \right)$ is

$$\begin{aligned} Var\left( l\left( \theta \right) \right) =p_{j}\left( \theta \right) q_{j}\left( \theta \right) \left( \log \frac{p_{j}\left( \theta \right) }{q_{j}\left( \theta \right) } \right) ^{2}. \end{aligned}$$

$l_{z}\left( \theta \right)$ is a special case of the standardized version of $W(\theta )$ when

$$\begin{aligned} w_{j}\left( \theta \right) =\log \frac{p_{j}\left( \theta \right) }{q_{j}\left( \theta \right) }. \end{aligned}$$

Note that $W\left( \theta \right)$ (or $l_{z}\left( \theta \right)$) is defined in terms of true ability $\theta$. However, when applied to real data, $\theta$ is unknown and must be replaced by the estimated value $\hat{\theta }$. Several research studies have shown that $l_{z}\left( \hat{\theta } \right)$ differs from a standard normal distribution when $\hat{\theta }$ is used and therefore provides an inaccurate assessment of person fit (Molenaar & Hoijtink 1990; Nering, 1995; Reise 1995; Snijders, 2001; van Krimpen-Stoop & Meijer, 1999). Snijders (2001) provided a remedy to this problem. First, using the Taylor expansion on $W\left( \theta \right)$, he showed

$$\begin{aligned} \frac{1}{\sqrt{n} }W\left( \hat{\theta } \right) \approx \frac{1}{\sqrt{n} }W\left( \theta \right) +\sqrt{n} \left( \hat{\theta }-\theta \right) \left[ \frac{1}{n}\sum \limits _{j=1}^n \left( Y_{j}-p_{j}\left( \theta \right) \right) w_{j}^{'}\left( \theta \right) -\frac{1}{n}\sum \limits _{j=1}^n {p_{j}^{'}\left( \theta \right) w_{j}\left( \theta \right) } \right] , \end{aligned}$$

where $w_{j}^{'}\left( \theta \right)$ and $p_{j}^{'}\left( \theta \right)$ are the first derivative of $w_{j}\left( \theta \right)$ and $p_{j}\left( \theta \right)$, respectively. The term $\sqrt{n} \left( \hat{\theta }-\theta \right)$ is bounded assuming it has a non-degenerate distribution when $n\rightarrow \infty$. While the first term in the bracket tends to 0 since it is an average of a random variable with expected value of 0, the second term in the bracket does not. Snijders suggested to replace $w_{j}\left( \theta \right)$ with a $\tilde{w}_{j}\left( \theta \right)$ such that $\sum \nolimits _{j=1}^n {p_{j}^{'}\left( \theta \right) \tilde{w}_{j}\left( \theta \right) } =0$. To be specific, if a $\hat{\theta }$ satisfies the condition that

$$\begin{aligned} r_{0}\left( \hat{\theta } \right) +\sum \limits _{j=1}^n \left( Y_{j}-p_{j}\left( \hat{\theta } \right) \right) r_{j}\left( \hat{\theta } \right) =0. \end{aligned}$$

The modified weight $\tilde{w}_{j}\left( \theta \right)$ can be defined as

$$\begin{aligned} \tilde{w}_{j}\left( \theta \right) =w_{j}\left( \theta \right) -c_{n}\left( \theta \right) r_{j}\left( \theta \right) , \end{aligned}$$

(2)

where

$$\begin{aligned} c_{n}\left( \theta \right) =\frac{\sum \nolimits _{j=1}^n {p_{j}^{'}\left( \theta \right) w_{j}\left( \theta \right) } }{\sum \nolimits _{j=1}^n {p_{j}^{'}\left( \theta \right) r_{j}\left( \theta \right) }}. \end{aligned}$$

Then, the new variable

$$\begin{aligned} W^{*}\left( \hat{\theta } \right) =\frac{W\left( \hat{\theta } \right) +c_{n}\left( \hat{\theta } \right) r_{0}\left( \hat{\theta } \right) }{Var\left( W^{*}\left( \hat{\theta } \right) \right) } \end{aligned}$$

asymptotically follows a standard normal distribution, where

$$\begin{aligned} {Var\left( W^{*}\left( \hat{\theta } \right) \right) =n\tau }_{n}\left( \hat{\theta } \right) =\sum \limits _{j=1}^n {\tilde{w}_{j}^{2}\left( \hat{\theta } \right) } p_{j}\left( \hat{\theta } \right) q_{j}\left( \hat{\theta } \right) . \end{aligned}$$

(3)

For an MLE, $r_{0}\left( \hat{\theta } \right) =0$; For a maximum a posteriori (MAP) estimator, $r_{0}\left( \hat{\theta } \right) =d\textrm{log}\left( f\left( \hat{\theta } \right) \right) /d(\hat{\theta })$, where $f\left( \hat{\theta } \right)$ is a prior distribution of ability; For a weighted likelihood estimator (WLE), $r_{0}\left( \hat{\theta } \right) =J\left( \hat{\theta } \right) /2\left( I\left( \hat{\theta } \right) \right)$, where $J\left( \hat{\theta } \right) =\sum \nolimits _{j=1}^n \frac{p_{j}^{'}\left( \hat{\theta } \right) p_{j}^{''}\left( \hat{\theta } \right) }{p_{j}\left( \hat{\theta } \right) q_{j}\left( \hat{\theta } \right) }$ , $I\left( \hat{\theta } \right) =\sum \nolimits _{j=1}^n \frac{p_{j}^{'}\left( \hat{\theta } \right) ^{2}}{p_{j}\left( \hat{\theta } \right) q_{j}\left( \hat{\theta } \right) }$ and $p_{j}^{''}\left( \theta \right)$ is the second derivative of $p_{j}\left( \theta \right)$. $r_{j}\left( \hat{\theta } \right)$ is given in general by

$$\begin{aligned} r_{j}\left( \hat{\theta } \right) =\frac{p_{j}^{'}\left( \hat{\theta } \right) }{p_{j}\left( \hat{\theta } \right) q_{j}\left( \hat{\theta } \right) } \end{aligned}$$

Consequently,

$$\begin{aligned} l_{z}^{*}\left( \hat{\theta } \right) =\frac{l\left( \hat{\theta } \right) -E\left( l\left( \hat{\theta } \right) \right) +c_{n}\left( \hat{\theta } \right) r_{0}\left( \hat{\theta } \right) }{Var\left( l_{z}^{*}\left( \hat{\theta } \right) \right) }. \end{aligned}$$

(4)

Comparing Eq. (1) with Eq. (4), we see that $l_{z}^{*}\left( \hat{\theta } \right)$ is obtained using the equation of $l_{z}\left( \hat{\theta } \right)$ by adjusting the mean with $c_{n}\left( \hat{\theta } \right) r_{0}\left( \hat{\theta } \right)$ and adjusting the variance by replacing $Var\left( l_{z}\left( \hat{\theta } \right) \right)$ with $Var\left( l_{z}^{*}\left( \hat{\theta } \right) \right)$. Particularly for an MLE, since $r_{0}\left( \hat{\theta } \right) =0$, only the variance needs to be adjusted, and the above formula reduces to

$$\begin{aligned} l_{z}^{*}\left( \hat{\theta } \right) =\frac{l\left( \hat{\theta } \right) -E\left( l\left( \hat{\theta } \right) \right) }{Var\left( l_{z}^{*}\left( \hat{\theta } \right) \right) } . \end{aligned}$$

(5)

As we will show later in the Method section, this adjustment of the variance under MLE is a general strategy on which we relied when adjusting the extended version of $l_{z}$ for the Rasch testlet model under MMLE. To provide a better connection, we shall now take a closer look at $Var\left( l_{z}^{\mathrm {*}}\left( \hat{\theta } \right) \right)$ to see what information is needed to compute it. Omitting $\hat{\theta }$ for simplicity, based on Eqs. (2) and (3), we have

$$\begin{aligned} Var\left( l_{z}^{*} \right) =\sum \limits _{j=1}^n \left( w_{j}-c_{n}r_{j} \right) ^{2} p_{j}q_{j}, \end{aligned}$$

where $c_{n}=\frac{\sum \nolimits _{j=1}^n {p_{j}^{'}w_{j}} }{\sum \nolimits _{j=1}^n p_{j}^{'} r_{j}}$, $r_{j}= \frac{p_{j}^{'}}{p_{j}q_{j}}$ and $w_{j}=\log \frac{p_{j}}{q_{j}}$. Therefore

$$\begin{aligned} Var\left( l_{z}^{*} \right)&=\sum \limits _{j=1}^n {\left( \log {\frac{p_{j}}{q_{j}}-}\left( \frac{\sum \nolimits _{j=1}^n {p_{j}^{'}\log \frac{p_{j}}{q_{j}}} }{\sum \nolimits _{j=1}^n \frac{{p_{j}^{'}}^{2}}{p_{j}q_{j}} } \right) \frac{p_{j}^{'}}{p_{j}q_{j}} \right) ^{2}p_{j}q_{j}} \\&=\sum \limits _{j=1}^n {p_{j}q_{j}\left( \log \frac{p_{j}}{q_{j}} \right) ^{2}} -2\left( \sum \limits _{j=1}^n {p_{j}^{'}\log \frac{p_{j}}{q_{j}}} \right) *\frac{\sum \nolimits _{j=1}^n {p_{j}^{'}\log \frac{p_{j}}{q_{j}}} }{\sum \nolimits _{j=1}^n \frac{{p_{j}^{'}}^{2}}{p_{j}q_{j}} }+\frac{\left( \sum \nolimits _{j=1}^n {p_{j}^{'}\log \frac{p_{j}}{q_{j}}} \right) ^{2}}{\sum \nolimits _{j=1}^n \frac{{p_{j}^{'}}^{2}}{p_{j}q_{j}}} \\&=\sum \limits _{j=1}^n {p_{j}q_{j}\left( \log \frac{p_{j}}{q_{j}} \right) ^{2}} -\frac{\left( \sum \nolimits _{j=1}^n {p_{j}^{'}\log \frac{p_{j}}{q_{j}}} \right) ^{2}}{\sum \nolimits _{j=1}^n \frac{{p_{j}^{'}}^{2}}{p_{j}q_{j}} }. \end{aligned}$$

We should now examine the terms of the final form of $Var\left( l_{z}^{*} \right)$ above. The first term is exactly the original definition of $Var\left( l_{z} \right)$. For the numerator of the second term, if we define $h\left( \hat{\theta } \right) =l\left( \hat{\theta } \right) -E\left( l\left( \hat{\theta } \right) \right)$ (note that this is the numerator of $l_{z}^{*})$, we find it amounts to $\left( h^{'}\left( \hat{\theta } \right) \right) ^{2}$ for an MLE $\hat{\theta }$, where $h^{'}\left( \hat{\theta } \right) =$ $-\sum \nolimits _{j=1}^n \left( p_{j}^{'}\log \frac{p_{j}}{q_{j}} \right)$ is the first derivative of $h\left( \hat{\theta } \right)$. Finally, the denominator of the second term can be recognized as test information at $\theta =\hat{\theta }$ (let’s denote it as $I\left( \hat{\theta } \right) )$. Therefore, we can rewrite the above definition of $Var\left( l_{z}^{*} \right)$ as

$$\begin{aligned} Var\left( l_{z}^{*}\left( \hat{\theta } \right) \right) =Var\left( l_{z}\left( \hat{\theta } \right) \right) -\frac{\left( h^{'}\left( \hat{\theta } \right) \right) ^{2}}{I\left( \hat{\theta } \right) }. \end{aligned}$$

This alternative definition of $Var\left( l_{z}^{*} \right)$, as we shall see in the later section of this paper, holds true when $l_{z}^{*}$ is extended for the Rasch testlet model.

2 Rasch Testlet Model and MMLE $\mathbf {\theta }$ Estimation

Before we describe our extended method, we provide some basic information about the Rasch testlet model and the utility of MMLE estimation of $\theta$. While unidimensional models have been working well with tests that consist of traditional items, it is arguably not the best choice when a test consists of testlets. A testlet, sometime called an item cluster or an item bundle, is a set of items that share a common stimulus. Because of such bundling, an examinee’s responses to items within a testlet are usually interdependent even when conditioned on the examinee ability. That is, the usual local independence assumption does not hold within testlets. Ignoring such dependencies would result in biased item parameter estimates and underestimation of the standard error of measurement (e.g., Sireci et al., 1991; Wainer & Lukhele, 1997; Wainer & Thissen, 1996; Wainer & Wang, 2000; Yen, 1993). A common approach to account for the testlet effect is to include additional dimensions corresponding to the bundling of the items in the IRT model. These additional dimensions incorporated are usually considered “nuisance” dimensions as the true values of examinees’ latent traits on these dimensions are often not of primary interest. One popular example of adopting this approach is the Rasch testlet model. For binary data, the Rasch testlet model is defined as

$$\begin{aligned} p_{jk}\left( \theta \vert u_{k} \right) =P\left( Y_{jk}=1\vert \theta , u_{k} \right) =\frac{\exp \left( \theta +u_{k}-b_{j} \right) }{1+\exp \left( \theta +u_{k}-b_{j} \right) } , \end{aligned}$$

(6)

where $Y_{jk}$ is the response to item j from testlet k and can be either 0 or 1, $\theta$ is the examinee’s overall ability, $u_{k}$ is the latent trait related to testlet k, and $b_{j}$ is the difficulty parameter of item j.

To understand how $l_{z}$ and $l_{z}^{*}$ can be extended for the Rasch testlet model, there is a need to review the methods for the estimation of latent traits in multidimensional IRT (MIRT) models. Two commonly used estimators for the latent traits in MIRT models are the maximum likelihood estimator (MLE) and the expected a posteriori (EAP) estimator. Let y be a vector collecting the observed item scores for all items in all testlets, and u be a vector collecting the latent traits pertain to the nuisance dimensions. The MLE is obtained by maximizing the likelihood of the observed items scores jointly for $\theta$ and u. That is,

$$\begin{aligned} \left( \hat{\theta }, \hat{{{\varvec{u}}}} \right) _{MLE}={\textrm{argmax}}_{\theta ,{\varvec{u}}}l\left( \theta ,{{{\varvec{u}}}}\vert {\varvec{y}} \right) , \end{aligned}$$

where $l\left( \theta ,{\varvec{u}}\vert {\varvec{y}} \right)$ is the log-likelihood of the observed item scores. The EAP estimator is the posterior mean vector of the latent traits, defined as

$$\begin{aligned} \left( \hat{\theta }, \hat{u} \right) _{EAP}=\int _{-\infty }^\infty \left( \theta ,{\varvec{u}} \right) p\left( \theta ,{\varvec{u}}\vert {\varvec{y}} \right) d\left( \theta ,{\varvec{u}} \right) , \end{aligned}$$

where $p\left( \theta ,{\varvec{u}}\vert {\varvec{y}} \right)$ is the joint posterior distribution of $\theta$ and ${\varvec{u}}$, given the observed item score vector. Both estimators are multivariate, i.e., they jointly obtain the estimate of the overall ability $\theta$ and the estimates of the latent traits regarding the testlet effects (${\varvec{u}})$. Therefore, when these two methods are used, the log-likelihood involved in obtaining $l_{z}$ and the corresponding correction involved to obtain $l_{z}^{*}$ can be considerably more difficult to disentangle than those in a unidimensional model.

However, the purpose of introducing the nuisance dimensions ${\varvec{u}}$ is solely to account for the item clustering or testlet effect; Most of the time, only the overall $\theta$ is of primary interest. In this vein, Rijmen et al. (2018) proposed to use the marginalized maximum likelihood estimator (MMLE) for the overall $\theta$ estimation. The MMLE can be obtained in two steps. First, the nuisance dimensions ${\varvec{u}}$ are integrated out in the observed data likelihood to obtain the marginalized likelihood function of $\theta$,

$$\begin{aligned} L\left( \theta \vert {\varvec{y}} \right) =\int _{-\infty }^\infty {p\left( {\varvec{y}}\vert \theta ,{\varvec{u}} \right) p\left( {\varvec{u}} \right) d{\varvec{u}}}. \end{aligned}$$

Second, $\hat{\theta }$ is found by maximizing the resulting marginal (log-)likelihood function,

$$\begin{aligned} \left( \hat{\theta } \right) _{MMLE}={\textrm{argmax}}_{\theta }l_{marginal}\left( \theta \vert {\varvec{y}} \right) , \end{aligned}$$

where $l_{marginal}=Log\left( L\left( \theta \vert {\varvec{y}} \right) \right)$. In a simulation study, Rijmen et al. (2018) found that the MMLE provided a better recovery of the overall ability parameter than the MLE and EAP estimators in the presence of substantial testlet effects, and that only the MMLE accurately took into account the loss of information due the dependencies between items from the same stimulus. The mathematical simplicity of MMLE relative to the other joint estimators offers an opportunity to develop a suitable person fit measure on the basis of $l_{z}$. The next section shows that the original $l_{z}$ statistics can be extended to work for the Rasch testlet model, and an asymptotically corrected version can be derived to produce a new person fit z-statistic when the MMLE $\hat{\theta }$ is used.

3 Method

3.1 Extension of ${l}_{{z}}$ for the Rasch testlet model

Consider a test that consists of K testlets where each item within a testlet is scored either 0 or 1. The probability of getting a score of $y_{jk}$ for item j in testlet k based on the Rasch testlet model is defined as

$$\begin{aligned} p_{y_{jk}}=\hbox {P}\left( Y_{jk}=y_{jk}\vert \theta ,u_{k} \right) =\left( p_{jk}\left( \theta \vert u_{k} \right) \right) ^{y_{jk}}\left( q_{jk}\left( \theta \vert u_{k} \right) \right) ^{1-y_{jk}}, \end{aligned}$$

where $p_{jk}\left( \theta \vert u_{k} \right)$ is as defined in Eq. (6), and $q_{jk}\left( \theta \vert u_{k} \right) =1-p_{jk}\left( \theta \vert u_{k} \right) .$

The likelihood of the overall ability $\theta$ for an MMLE is defined as

$$\begin{aligned} L\left( \theta \vert {\varvec{y}} \right) =\prod \limits _{k=1}^K \int {{\prod \limits _{j=1}^n}_{k} \hbox {P}\left( Y_{jk}=y_{jk}\vert \theta ,u_{k} \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}}, \end{aligned}$$

where $n_{k}$ is the number of items in testlet $k, g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right)$ is the assumed prior distribution of $u_{k}$ with a mean of 0 and a variance of $\sigma _{u_{k}}^{2}$. The log-likelihood statistics is therefore

$$\begin{aligned} l\left( \theta \vert {\varvec{y}} \right)&=\sum \limits _{k=1}^K \textrm{log}\left[ \int \textrm{Exp}\left( \mathop {\sum }\limits _{j\mathrm {=1}}^{n_{k}} \left( y_{jk}\textrm{log}\left( p_{jk}\left( \theta \vert u_{k} \right) \right) \right. \right. \right. \\&\quad \left. \left. \left. +\left( 1-y_{jk} \right) \textrm{log}\left( q_{jk}\left( \theta \vert u_{k} \right) \right) \right) \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k} \right] . \end{aligned}$$

Analogous to what it is in a unidimensional model, the standardized log-likelihood statistics is defined as

$$\begin{aligned} l_{zt}\left( \theta \right) =\frac{l\left( \theta \vert {\varvec{y}} \right) -E\left( l\left( \theta \vert {\varvec{y}} \right) \right) }{\sqrt{Var\left( l\left( \theta \vert {\varvec{y}} \right) \right) } }. \end{aligned}$$

Under regularity conditions, $l_{zt}\left( \theta \right)$ follows a standard normal distribution and can be used for person fit evaluations. The obstacle here is to compute $E\left( l\left( \theta \vert {\varvec{y}} \right) \right)$ and $Var\left( l\left( \theta \vert {\varvec{y}} \right) \right)$. As a model from the Rasch family, a merit of the Rasch testlet model is that a sufficient statistic for $\theta$ exists in a relatively simple form. Similar to the unidimensional Rasch model where the sum of the items score of the entire test is a sufficient statistic for $\theta$, Appendix A shows that the vector $\left\{ r_{1},r_{2},\cdots ,r_{k}, r_{k+1},\cdots ,r_{K} \right\}$ is the sufficient statistic for $\theta$, where $r_{k}$ is the sum of the item scores of testlet k and K is the total number of the testlets. Therefore,

$$\begin{aligned} E\left( l\left( \theta \vert {\varvec{y}} \right) \right) =\sum \limits _{k=1}^K \left[ E\left( l\left( \theta \vert r_{k}\right) \right) \right] . \end{aligned}$$

In the equation above,

$$\begin{aligned} E\left( l\left( \theta \vert r_{k}\right) \right)= & \int {\left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {p_{jk}\left( \theta \mathrm {\vert }u_{k} \right) \left( \theta \mathrm {-}b_{jk} \right) } \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} \nonumber \\ & +\sum \nolimits _{r_{k}\mathrm {=0}}^{n_{k}} \left\{ \textrm{log}\left[ \int {\textrm{Exp}\left( r_{k}u_{k}\mathrm {+}\sum \limits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk}\left( \theta \mathrm {\vert }u_{k} \right) \right) } \right) g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} \right] \right\} \nonumber \\ & p\left( r_{k}\mathrm {\vert }\theta \right) \end{aligned}$$

(7)

under the Rasch testlet model with binary data, where $p\left( r_{k}\mathrm {\vert }\theta \right) =\int p\left( r_{k}\vert \theta ,u_{k} \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}$ is the probability of getting a sum score of $r_{k}$ from testlet k after marginalizing out the nuisance dimension. The calculation of $p\left( r_{k}\vert \theta ,u_{k} \right)$ is described later in this section, where it was carried out by using the Lord-Wingersky algorithm (Lord and Wingersky, 1984).

On the other hand, the variance of the loglikelihood can also be computed for each testlet and summed up as follows:

$$\begin{aligned} Var\left( l\left( \theta \vert {\varvec{y}} \right) \right) \mathrm {=}\sum \limits _{k=1}^K \left[ Var\left( l\left( \theta \vert r_{k}\right) \right) \right] \mathrm {=}\sum \limits _{k\mathrm {=1}}^K \left[ E\left( l^{\textrm{2}}\left( \theta \vert r_{k}\right) \right) \mathrm {-}\left( E\left( l\left( \theta \vert r_{k}\right) \right) \right) ^{\textrm{2}} \right] . \end{aligned}$$

Let ${\varvec{y}}_{k}$ denote the vector of item scores for testlet k, and ${\mathbbm {y}}_{r_{k}}$ denote the set of score patterns that leads to a sum score of $r_{k}$. In the equation above

$$\begin{aligned} E\left( l^{\textrm{2}}\left( \theta \vert r_{k}\right) \right)= & \sum \limits _{r_{k}=0}^{n_{k}} \sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} p\left( {\varvec{y}}_{k}\mathrm {\vert }\theta \right) \left\{ \left( \sum \nolimits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) }\right. \right. \nonumber \\ & \quad \left. \left. + \hbox {log}\left[ \int {Exp\left( u_{k}r_{k}\mathrm {+}\sum \limits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk}\left( \theta \mathrm {\vert }u_{k} \right) \right) } \right) g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} \right] \right) ^{\textrm{2}} \right\} ,\nonumber \\ \end{aligned}$$

(8)

where $p\left( {\varvec{y}}_{k}\mathrm {\vert }\theta \right)$ is the probability of getting a score pattern ${\varvec{y}}_{k}$ after marginalizing out the nuisance dimension. The computational burden of the above formula is driven by the number of possible score pattern ($2^{{n_{k}}})$ and can become substantial when ${n_{k}}$ is large. Therefore, we offer a workaround which is based on the Lord-Wingersky algorithm.

Setting

$$\begin{aligned} L_{r_{k}}=\textrm{log}\left[ \int {\textrm{Exp}\left( u_{k}r_{k}\mathrm {+}\sum \limits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk}\left( \theta \mathrm {\vert }u_{k} \right) \right) } \right) g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} \right] , \end{aligned}$$

we can rewrite (5) as follows:

$$\begin{aligned} E\left( l^{\textrm{2}}\left( \theta \vert r_{k}\right) \right) =\int {\sum \limits _{r_{k}=0}^{n_{k}} \sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\left( \prod \limits _{j=1}^{n_{k}} p_{y_{jk}} \right) \left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \mathrm {+}L_{r_{k}} \right) ^{2}} g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} . \end{aligned}$$

Rewrite

$$\begin{aligned}&\sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\left( \prod \limits _{j=1}^{n_{k}} p_{y_{jk}} \right) \left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \mathrm {+}L_{r_{k}} \right) ^{2}}\\&\quad =\sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\left( \prod \limits _{j=1}^{n_{k}} p_{y_{jk}} \right) \left( \left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \right) ^{2}+2\left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \right) L_{r_{k}}\mathrm {+}L_{r_{k}}^{2} \right) } \\&\quad =\sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\left( \prod \limits _{j=1}^{n_{k}} p_{y_{jk}} \right) \left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \right) ^{2}} +2L_{r_{k}}\sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\left( \prod \limits _{j=1}^{n_{k}} p_{y_{j}} \right) \left( \sum \limits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \right) } \\ &\qquad +L_{r_{k}}^{2}p\left( r_{k}\mathrm {\vert }\theta \right) , \end{aligned}$$

and define

$$\begin{aligned} W_{m}\left( {n_{k}},r_{k} \right) =\sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\left( \prod \limits _{j=1}^{n_{k}} p_{y_{jk}} \right) \left( \sum \nolimits _{j\mathrm {=1}}^{n_{k}} {y_{jk}\left( \theta \mathrm {-}b_{jk} \right) } \right) ^{m}} \end{aligned}$$

if $0\le r_{k}\le {n_{k}}$ and otherwise, we now have

$$\begin{aligned} E\left( l^{\textrm{2}}\left( \theta \vert r_{k}\right) \right) =\int {\sum \limits _{r_{k}=0}^{n_{k}} \left( W_{2}\left( {n_{k}},r_{k} \right) +2L_{r_{k}}W_{1}\left( {n_{k}},r_{k} \right) +L_{r_{k}}^{2}W_{0}({n_{k}},r_{k}) \right) g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} . \end{aligned}$$

(9)

For $m=0$, $W_{0}\left( {n_{k}},r_{k} \right)$ is the probability of obtaining a sum score of $r_{k}$ for a testlet with ${n_{k}}$ items and can be computed recursively using the Lord-Wingersky algorithm. For simplicity, let $p_{jk}=p_{jk}\left( \theta \mathrm {\vert }u_{k} \right)$ and $q_{jk}=q_{jk}\left( \theta \mathrm {\vert }u_{k} \right)$.

For ${n_{k}}=1$,

$$\begin{aligned} W_{0}\left( 1,1 \right)&= p_{jk} , \\ W_{0}\left( 1,0 \right)&= q_{jk} . \end{aligned}$$

For ${n_{k}}=\mathrm {2, 3, 4,\cdots }$

$$\begin{aligned} W_{0}\left( {n_{k}},r_{k} \right) =q_{{n_{k}}k}W_{0}\left( {n_{k}}-1,r_{k} \right) +p_{{n_{k}}k}W_{0}\left( {n_{k}}-1,r_{k}-1 \right) . \end{aligned}$$

Similarly, we can extend the Lord-Wingersky algorithm to compute $W_{1}\left( {n_{k}},r_{k} \right)$ and $W_{2}\left( {n_{k}},r_{k} \right)$ recursively. For testlet k, let ${{\varvec{y}}}_{k}^{\mathbf {'}}$ denote the vector of the first ${n_{k}}-1$ item scores, and $\mathbbm {y}_{r_{k}}^{'}$ denote the set of score patterns for the first ${n_{k}}-1$ items that lead to a sum score of $r_{k}$. Then

This extended version of the Lord-Wingersky algorithm significantly reduced the computational burden $E\left( l^{\textrm{2}}\left( \theta \vert r_{k}\right) \right)$. Also, note that $W_{0}\left( {n_{k}},r_{k} \right) =\sum \limits _{{{\varvec{y}}}_{k}\in y_{r_{k}}} \left( \prod \limits _{j=1}^{n_{k}} p_{y_{jk}} \right) =p\left( r_{k}\vert \theta ,u_{k} \right)$. By marginalizing out $u_{k}$ as follows,

$$\begin{aligned} p\left( r_{k}\vert \theta \right) =\int {p\left( r_{k}\vert \theta ,u_{k} \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}}, \end{aligned}$$

we obtain $p\left( r_{k}\vert \hat{\theta } \right) .$ This is the marginal probability of summed score needed in the computation of Eq. (7). To this point, all the components for computing $l_{zt}(\theta )$ have been derived.

3.2 Variance Correction of ${l}_{{zt}}$

Define the numerator of $l_{zt}$ as $h\left( \theta \vert {{\varvec{y}}} \right)$. When MMLE $\hat{\theta }$ is used,

$$\begin{aligned} h\left( \hat{\theta }\vert {\varvec{y}} \right) =l\left( \hat{\theta }\vert {\varvec{y}} \right) -E\left( l\left( \hat{\theta }\vert {\varvec{y}} \right) \right) . \end{aligned}$$

Based on the Taylor series expansion for $\hat{\theta }$ around $\theta$,

$$\begin{aligned} h\left( \hat{\theta }\vert {\varvec{y}} \right) =h\left( \theta \vert {\varvec{y}} \right) +h^{'}\left( \theta \vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) +r\left( \hat{\theta } \right) , \end{aligned}$$

where $r\left( \hat{\theta } \right)$ is the remainder. In Appendix B, we prove that this remainder is negligible. Therefore, asymptotically

$$\begin{aligned} \frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right) =\frac{1}{\sqrt{K} }h\left( \theta \vert {\varvec{y}} \right) +\frac{1}{\sqrt{K} }h^{'}\left( \theta \vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) \end{aligned}$$

or

$$\begin{aligned} \frac{1}{\sqrt{K} }h\left( \theta \vert {\varvec{y}} \right) =\frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right) -\frac{1}{\sqrt{K} }h^{'}\left( \theta \vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) , \end{aligned}$$

when $K\rightarrow \infty$. $\frac{1}{\sqrt{K} }h\left( \theta \vert {\varvec{y}} \right)$ is asymptotically normal with mean of 0 and variance given by

$$\begin{aligned} Var\left( \frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right) \right) +\frac{1}{K}{h^{'}\left( \theta \vert {\varvec{y}} \right) }^{2}Var\left( \hat{\theta }-\theta \right) +\frac{1}{K} h^{'}\left( \theta \vert {\varvec{y}} \right) *Cov\left( h\left( \hat{\theta }\vert {\varvec{y}} \right) ,\left( \hat{\theta }-\theta \right) \right) . \end{aligned}$$

A side product of the simulation studies presented in the next section is an investigation of the magnitude of the covariance term above. In a nutshell, at each true $\theta$values of {-2, -1, 0, 1, 2}, 10000 test cases were simulated and the correlations between $h\left( \hat{\theta }\vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right)$ were computed for the Rasch testlet model as well as the unidimensional Rasch model. The results, which are presented in Appendix C, indicated that the covariance term is generally very close to 0. Therefore, by omitting the covariance term, we have that the sampling variation of $\frac{1}{\sqrt{K} }h\left( \theta \vert {\varvec{y}} \right)$ is bigger than the sampling variation of $\frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right)$ by the term of $\frac{1}{K}{h^{'}\left( \theta \vert {\varvec{y}} \right) }^{2}Var\left( \hat{\theta }-\theta \right)$, or in other words, $\frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right)$ is asymptotically normal with mean 0 and variance $Var\left( \frac{1}{\sqrt{K} }h\left( \theta \vert {\varvec{y}} \right) \right) -\frac{1}{K}{h^{'}\left( \theta \vert {\varvec{y}} \right) }^{2}Var\left( \hat{\theta }-\theta \right)$. The denominator used for normalization of $\frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right)$ is estimated by the point estimate of the variance, which has the same value asymptotically when replacing $\theta$ by $\hat{\theta }$. That is, the variance of $\frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right)$ is estimated by $Var\left( \frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right) \right) -\frac{1}{K}{h^{'}\left( \hat{\theta }\vert {\varvec{y}} \right) }^{2}Var\left( \hat{\theta }-\theta \right)$. So eventually

$$\begin{aligned} \frac{\frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right) }{\sqrt{Var\left( \frac{1}{\sqrt{K} }h\left( \hat{\theta }\vert {\varvec{y}} \right) \right) -\frac{1}{K}{h^{'}\left( \hat{\theta }\vert {\varvec{y}} \right) }^{2}Var\left( \hat{\theta }-\theta \right) }} \end{aligned}$$

is asymptotically standard normal. Note that $Var\left( \hat{\theta }-\theta \right)$ is in fact the inverse of the expected Fisher information provided by all the items in the test, or in another term, the inverse of the test information. Thus, we can consequently define the new person fit z-statistics as

(10)

where $I\left( \hat{\theta } \right)$ is the test information at $\theta =\hat{\theta }$, defined as

$$\begin{aligned} I\left( \hat{\theta } \right) =\sum \nolimits _{k\mathrm {=1}}^K \left\{ \sum \nolimits _{r_{k}\mathrm {=0}}^{n_{k}} \left[ \left( \frac{\int {\textrm{Exp}\left( r_{k}u_{k}\mathrm {+}\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk}\left( \hat{\theta }\mathrm {\vert }u_{k} \right) \right) } \right) \left( r_{k}\mathrm {-}\sum \nolimits _j^{n_{k}} {p_{jk}\left( \hat{\theta }\mathrm {\vert }u_{k} \right) } \right) g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} }{\int {\textrm{Exp}\left( r_{k}u_{k}\mathrm {+}\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk}\left( \hat{\theta }\mathrm {\vert }u_{k} \right) \right) } \right) g\left( u_{k} \vert {\textrm{0, }\sigma _{u_{k}}^{\textrm{2}}}\right) du_{k}} } \right) ^{\textrm{2}}p\left( r_{k}\mathrm {\vert }\hat{\theta } \right) \right] \right\} . \end{aligned}$$

Appendix D shows how $I\left( \hat{\theta } \right)$ was derived. It can now be recognized that the variance correction applied here for the Rasch testlet model with an MMLE ability estimate has the same form as what was shown earlier (in the review of $l_{z}$ and $l_{z}^{*}$ section) for the unidimensional model when MLE is used. Naturally, $l_{zt}$ and $l_{zt}^{*}$ reduce to $l_{z}$ and $l_{z}^{*}$, respectively when no cluster effect is present. To compute in Eq. (10), note that with MMLE

$$\begin{aligned} h^{'}\left( \hat{\theta }\vert {\varvec{y}} \right) =0-\frac{dE\left( l\left( \hat{\theta }\vert {\varvec{y}} \right) \right) }{d\hat{\theta }}=-\sum \limits _{k=1}^K \frac{dE\left( l\left( \hat{\theta }\vert r_{k} \right) \right) }{d\hat{\theta }} . \end{aligned}$$

(11)

Based on Eq. (7), $\frac{dE\left( l\left( \hat{\theta }\vert r_{k} \right) \right) }{d\hat{\theta }}$ is computed as

The only unknown in the above equation is , i.e., the derivative of $p\left( r_{k}\vert \hat{\theta } \right)$ with respect to $\hat{\theta }$. While $p\left( r_{k}\vert \hat{\theta } \right)$ is computed recursively by our extended Lord-Wingersky algorithm, can also be computed recursively as follows by applying the product rule to $W_{0}\left( {n_{k}},r_{k} \right)$:

for ${n_{k}}=1$,

and for

$$\begin{aligned} W_{0}^{'}\left( {n_{k}},r_{k} \right)&=q_{{n_{k}}k}^{'}W_{0}\left( {n_{k}}-1,r_{k} \right) +q_{{n_{k}}k}W_{0}^{'}\left( {n_{k}}-1,r_{k} \right) +p_{{n_{k}}k}^{'}W_{0}\left( {n_{k}}-1,r_{k}-1 \right) \\&\quad +p_{{n_{k}}k}W_{0}^{'}\left( {n_{k}}-1,r_{k}-1 \right) . \end{aligned}$$

Therefore,

To this point, all components to compute $l_{zt}^{*}\left( \hat{\theta } \right)$ have been derived.

4 Simulation Study

4.1 Type I Error Rates

This section presents the results of a simulation study conducted to investigate the empirical type I error rate of $l_{zt}$ (i.e., before correction) and $l_{zt}^{*}$ (i.e., after correction). Items used in the studies were sampled from an operational item bank of a K-12 standardized assessment in the United States. The test length varied at 6 testlets and 12 testlets. Table 1 presents the summary of items.

All items have been previously calibrated, and their parameters were taken as fixed values. For each test length condition, true $\theta$ values from -2 to 2 with a step of 1 were selected, and 10,000 simulated test datasets were generated at each $\theta$ value. $\hat{\theta }$s were then estimated by the MMLE in each test and used for the calculation of person fit statistics. Critical values were chosen corresponding to nominal error rates of $\upalpha =.05$ and .01 to identify aberrant responses. Occasionally, there were cases where all items were answered correctly or incorrectly. Since these cases do not provide information on how the IRT model fit to the data as the MMLE is not defined (i.e., $\hat{\theta }$ is $\infty$ or $-\infty )$, they were discarded when summarizing the simulation results. The highest value of the discard rate at any given $\theta$ was 0.001 with the 6-testlet test when $\theta =-2$. In addition, to provide a baseline for comparison, instead of using $\hat{\theta }$, $l_{zt}$ was also computed for the simulated responses by plugging in the true $\theta$.

Table 1 Summary of Items Used in the Simulations.

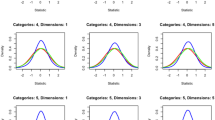
Figure 1 shows the kernel density of $l_{zt}$ and $l_{zt}^{*}$ (both computed with $\hat{\theta })$ overlaid with the standard normal distribution for each condition. When $\theta =0$, both $l_{zt}$ and $l_{zt}^{*}$ were close to a standard normal distribution. However, as $\theta$ became more extreme, the variance of $l_{zt}$ diminished and the distribution of $l_{zt}$ deviated from standard normal, whereas $l_{zt}^{*}$ remained close to standard normal. Consequently, as shown in Table 2, Type I error rates of $l_{zt}$ computed with $\hat{\theta }$ were reasonably close to the nominal rate at $\theta =0$, but were much smaller when $\theta$ became more extreme. On the contrary, the values of $l_{zt}^{*}$ were always close to the nominal rates and were often substantially better than those of $l_{zt}$. It was also found that the baseline Type I error rates of $l_{zt}$ computed with $\theta$ (rows denoted with “true $\theta$” in the table) were somewhat higher than the nominal rates, especially when $\theta$ became more extreme. $l_{zt}^{*}$, which was computed with $\hat{\theta }$, provided Type I error rates that are closer to the nominal rate even when compared to baseline rates provided by $l_{zt}$ computed with $\theta$. Finally, the asymptotic approximation of $l_{zt}^{*}$ became better when test-length increased as one would expect.

Fig. 1

Distributions of $l_{zt}$ and $l_{zt}^{*}$ overlaid with the standard normal distribution for each condition in the simulation study.

Table 2 Type I Error Rate from Simulation.

4.2 Power

To investigate the power of $l_{zt}^{*}$, the data used in the investigation of the Type I error rate were manipulated to reflect aberrant responses. A spuriously-high-score scenario was created where 10% (or 30%) of the most difficult items among the test were assigned responses of 1, and a spuriously-low-score scenario was created where 10% (or 30%) of the easiest items were assigned responses of 0. Similar to what was done in the Type I error rate analysis, cases where the MMLE was not defined were discarded. The highest value of the discard rate at any given $\theta$ was 0.069 with the 6-testlet test when $\theta =-2$ and the data has 30% aberrantly low scores. The overall discard rate across all conditions was 0.003. Tables 3 and 4 indicate that at $\theta$ values where aberrant responses are more likely to arise (i.e., low $\theta$ values for the spuriously-high-score scenario and high $\theta$ values for the spuriously-low-score scenario), $l_{zt}^{*}$ offered sufficiently large power of detection. Although $l_{zt}$ also offered more power at those $\theta$ values than other values, the power of $l_{zt}^{*}$ was always higher than that of $l_{zt}$. For a relatively short test with relatively less aberrant responses, $l_{zt}$ lacked its power even at $\theta$ values where aberrant responses are more likely to arise, whereas $l_{zt}^{*}$ offered decent power. As expected, the power increased as test length and the percentage of aberrant responses increased.

Table 3 Power Under Spuriously-high-score Scenario.

Table 4 Power Under Spuriously-low-score Scenario.

5 Application to Real Data

An advantage of $l_{zt}^{*}$ is that it allows person fit evaluation for not only tests consist of items modeled by either unidimensional models or the Rasch testlet model, but also for novel tests that are modeled by a mixture of these two types of components. This section demonstrates such an application of $l_{zt}^{*}$ to a U.S. statewide test assessing the Next Generation of Science Standards (NGSS). The test is mainly comprised of item clusters. An item cluster represents a series of interrelated examinee interactions directed toward describing, explaining and predicting scientific phenomena. Within each item cluster, a set of explicit assertions were made about examinee’s knowledge or skills according to specific features they’ve demonstrated through their interactions with the item cluster. In this setting, an assertion is analogous to a traditional item, and it was scored as 1 if it was asserted and 0 if it is not asserted. An item cluster is an item bundle (testlet) consists of multiple assertions. To account for the conditional dependency amount assertions within an item cluster, the part of the latent structure that describes the item clusters is the same as the Rasch testlet model. That is, an overall science dimension as well as additional “nuisance” dimensions corresponding to the bundling of the items. On the other hand, the model also allows a subset of assertions to depend only on the overall science dimension. These so-called stand-alone assertions typically pertain to shorter items (typically less than 4 assertions within an item) and were assumed independent given the overall dimension. This part of the latent structure is the same as the unidimensional Rasch model. Figure 2 shows the model graphically.

Fig. 2

Directed graph of the IRT model in the real data analysis.

The item pool of the assessment consisted of 27 item clusters and 24 stand-alone items. The test was administered online using a linear-on-the-fly test design (LOFT) such that each examinee received 6 item clusters and 12 stand-alone items at random that meets the test blueprint. A total of 12,026 examinees who completed all 18 items were included in the analysis. All the items have been previously calibrated. Table 5 presents a summary of the 18 test items an individual would typically receive.

MMLE was used to estimate examinee abilities. Since no examinee answered all items correctly or all items incorrectly, no MMLE estimate was undefined. $l_{zt}^{*}$ values were computed for every examinee. Specifically, using the general definition of $l_{zt}^{*}$ in Eq. (10), each component involved in the computation can be calculated separately for the item clusters and for the stand-alone assertions, and then simply combined (added) to produce the statistics. Examinees were flagged if their $l_{zt}^{*}$ values were below the critical value of the nominal error rates at $\alpha =$.05, and further flagged if below the critical value at $\upalpha =$.01. Three examinee groups were then created based on the flags: No Flag/ Flagged at .05/ Flagged at .01. Within each subset, a “person-total” correlation is computed for each examinee. Analogous to the item-total correlation, the person-total correlation is essentially the correlation between an examinee’s item scores and the average scores of the same items by all examinees. One would expect an examinee to be more likely to fit if his/her item scores agree better with the item scores of other examinees, and therefore less likely to be flagged. The person-total correlation was computed at both item level and the assertion level, where at the assertion level the assertion scores were used, and at the item level the average assertion scores within an item were used. For both levels, the person-total correlation was averaged within each examinee subsets. In addition, the $l_{z}^{*}$ statistics were computed for the same examinees with MLE ability while ignoring the cluster effect. The same procedure of flagging and person-total correlation computation described above were applied. Table 6 presents results for both $l_{zt}^{*}$ and $l_{z}^{*}$. Both methods yielded similar correlations for the group without flag. However, as expected for $l_{zt}^{*}$, the group with no flag has correlations much higher than the flagged groups at both the item and assertion levels, and the lowest correlations were observed with the group flagged at .01. On the other hand, for $l_{z}^{*}$, both flagged groups have relative high correlations that are close to the ones found in the group with no flag.

Table 5 Summary of Items Parameters for an 18-item Test, averaged over all examinees.

Table 6 Average Person-total Correlation among Examinee Subsets.

For each examinee within a subset, a few more detail can be depicted to examine the agreement among the p-value of $l_{zt}^{*}$, person-total correlation, and the pattern of item scores. First, the assertions an examinee received were grouped. The 6 item clusters, together with all the stand-alone assertions naturally formed a total of 7 groups. These groups of assertions were then arranged in a descending order by the average assertion difficulty. The average assertion scores of each group were calculate for the examinee and plotted against the grouping. Figure 3 shows the plots for four examinees. The title of a panel shows the person-total correlation and the p-value of $l_{zt}^{*}$, respectively for an examinee. The examinee on the top-left panel is from the subset with no flags. In general, this examinee’s average item group scores increased as the difficulty of the item group decreased (except for one obvious outlier) and therefore had a moderately high person-total correlation of 0.29. This examinee was not classified as a misfit with a p-value of 0.579. The examinee on the top-right panel is also from the subset with no flags. A strong increasing pattern was observed. This examinee had a correlation of 0.77 and was not classified as misfit with a higher p-value of 0.967 than the examinee on top-left. On the contrary, examinees in the bottom panels are from the flagged subsets. The examinee on the bottom-left had a p-value of 0.028, and a low correlation of 0.1. The pattern of the average item group scores against average item group difficulty seemed to be random. Finally, the examinee on the bottom-right had a p-value of 0.002. A decreasing pattern and a slightly negative person total correlation of $-$0.07 was observed. These figures suggested the flagging of the $l_{zt}^{*}$ agreed with other sources of evidence when assessing the fit for the same person.

Fig. 3

Agreement among the p-value of $l_{zt}^{*}$, person-total correlation, and the pattern of item scores for four examinees in the real data analysis.

6 Conclusion and Discussion

IRT testlet models have been frequently put into practice where the latent trait corresponding to the overall dimensional is usually of primary interest while other dimensions are incorporated as nuisance dimensions only to address the local dependencies between items within clusters. Moreover, unlike a traditional test which usually assumes either a unidimensional or multidimensional latent structure for every item in the test, novel tests (and models) may incorporate both components in their latent structure. Just like it is with unidimensional models, person fit evaluation with these models is an important part of the model-data fit evaluation that facilitates the delivery of reliable and valid test results. However, research on person fit statistics beyond unidimensional model is relatively scarce. The current study embarks on an effort to fill this gap by offering a person fit z-statistics appropriate for the Rasch testlet model, traditional unidimensional models, as well as models that have both components. Under the Rasch testlet model, the proposed person fit indices, $l_{zt}$ and its corrected version $l_{zt}^{*}$, are extensions of the well-known existing indices $l_{z}$ and $l_{z}^{*}$ for unidimensional models. In the simulation study, the Type I error rate and power of the new statistics under the Rasch testlet model were investigated and found to be consistent with the results of their counterparts under unidimensional models in the literature (Sinharay, 2016; Snijders, 2001). $l_{zt}^{*}$ provided close to nominal Type I error rate and good power to detect aberrant response. Furthermore, this method of extension entailed a generalized approach to correct the variance of the loglikelihood when maximum likelihood estimation was used to estimate ability parameters. Under traditional unidimensional model, $l_{zt}$ and $l_{zt}^{*}$ reduce to $l_{z}$ and $l_{z}^{*}$, respectively. This generalization keeps person fit evaluation with both the unidimensional models and the Rasch testlet model under the same framework and allows for person fit evaluation with models that have both components in their latent structure. The real data analysis example shows the utility of $l_{zt}^{*}$ under such a circumstance, which is otherwise not possible with $l_{z}^{*}$ without violating the original model assumption.

While developing $l_{zt}$ and $l_{zt}^{*}$ for their use with Rach testlet model, the Lord-Wingersky algorithm was extended in a few ways to achieve efficient computation. These extensions are considered another important contribution of this article. In a nutshell, three kinds of extensions of the algorithm were presented. First, realizing the fact that the expected value of the entire data loglikelihood under Rasch testlet model can be accumulated testlet by testlet using within testlet sum score loglikelihoods, the Lord-Wingersky algorithm was extended. Note that this straightforward extension is the same as what was described by Cai (2015) in his Equation 16 or 20, which took advantage of the assumed bifactor structure (or more generally, the two-tier structure). Second, the Lord-Wingersky algorithm is further extended for computing components in the variance of the loglikelihood. An implication of this extension is that not only can one use the algorithm to compute the probabilities of sum scores (e.g., $W_{0}({n_{k}}, r_{k}))$, but one can also define other related quantities (e.g., $W_{1}\left( {n_{k}},r_{k} \right)$ and $W_{2}\left( {n_{k}},r_{k} \right) )$ to make use of the recursive nature of the algorithm as needed. The third extension of the Lord-Wingersky algorithm was applied when computing $\frac{dE\left( l\left( \hat{\theta }\vert r_{k} \right) \right) }{d\hat{\theta }}$, where the derivative of the sum score within a testlet was needed. Although the extension was again a straightforward application of the product rule from basic calculus, it avoided doing numerical integration directly on $\frac{dE\left( l\left( \hat{\theta }\vert r_{k} \right) \right) }{d\hat{\theta }}$, and therefore increased the accuracy of the results as well as the speed of computations.

Like most of the person fit statistics in the literature, $l_{zt}^{*}$ is a statistic pertaining to one individual. A statistically significant $l_{zt}^{*}$ does not necessarily mean an examinee had abnormal testing behaviors. Further investigation of the flagged examinees must be conducted, especially when drawing high-stake conclusions such as whether an examinee cheated during the test. Nonetheless, it can serve as a screening mechanism to find individuals with potential testing behavior related issues. How liberal/rigid the screening criteria is would depend on resource available. When an aggregated unit of examinees is of concern, person fit statistics like $l_{zt}^{*}$ can also be useful by either simply checking the percentage of examinees flagged within the aggregated unit or constructing t statistics to flag units statistically.

One limitation of $l_{zt}^{*}$is that the current extension only concerns the Rasch testlet model when $\theta$ is estimated by MMLE. The relatively straightforward derivation of $l_{zt}^{*}$ relied on the fact that a sufficient statistic exists for a given testlet, as well as the fact that the nuisance dimension is marginalized out in MMLE. There could be scenarios where people prefer to use a more complex model such as a bifactor model not belonging to the Rasch family or other multidimensional IRT models where latent trait on multiple dimensions are of interest. There could also be scenarios where EAP, MLE, or MAP (maximum-a-posteriori) estimators are preferred. Under those scenarios, the derivation of $l_{zt}$ and $l_{zt}^{*}$ could become more challenging. In addition, there has also been a recent study that corrects the standardized person-fit statistics regarding both the use of an estimated ability and the use of a finite number of items Gorney et al. (2024). Further study is needed to explore these topics regarding the $l_{zt}$ and $l_{zt}^{*}$ statistics.

Finally, as concluded by Sinharay (2016), among others, the $l_{z}^{*}$ statistics is appropriate when an investigator wants to test against an unspecified general and may not be the most appropriate person-fit statistic for a particular problem, such as for a computer adaptive test. Also, when item parameters are not treated as fixed but need to be estimated, any aberrant response in the data would have impact on the item parameter estimation and in turn affects the person fit statistics. As an extension of shares these same limitations. More research on these topics, as well as the performance of $l_{zt}^{*}$ against other person fit statistics, would be helpful to practitioners.

Appendices

Appendix A: Sufficient Statistic for MMLE ${\theta }$ under the Rasch Testlet Model

For a test consists of K testlets, the likelihood of the MMLE overall ability $\theta$ is defined as

Define , we can see the that the likelihood function of $\theta$ was factored into a product of which does not depend on $\theta$ and the rest of the terms which does depend on $\theta$ but only through $r_{k}$. Therefore, based on the Fisher–Neyman factorization theorem, we can conclude that vector $\left\{ r_{1},r_{2},\cdots ,r_{K} \right\}$ is the sufficient statistic for $\theta$. That is, all the information about $\theta$ available in a response pattern ${\varvec{y}}$ is given by $\left\{ r_{1},r_{2},\cdots ,r_{K} \right\}$.

Appendix B: Proof of the Taylor Expansion Remainder Term Being Negligible

Recall that we defined

$$\begin{aligned} h\left( \hat{\theta }\vert {\varvec{y}} \right) =h\left( \theta \vert {\varvec{y}} \right) +h^{'}\left( \theta \vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) +r\left( \hat{\theta } \right) \end{aligned}$$

By rearranging the above equation,

$$\begin{aligned} r\left( \hat{\theta } \right) =h\left( \hat{\theta }\vert {\varvec{y}} \right) -h\left( \theta \vert {\varvec{y}} \right) -h^{'}\left( \theta \vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) . \end{aligned}$$

Taking derivative of $r\left( \hat{\theta } \right)$ with respect to $\hat{\theta }$ gives

$$\begin{aligned} r^{'}\left( \hat{\theta } \right) =h^{'}\left( \hat{\theta }\vert {\varvec{y}} \right) -h^{'}\left( \theta \vert {\varvec{y}} \right) . \end{aligned}$$

According to the mean value theorem, there exists a point $\tilde{\theta }$ such that

$$\begin{aligned} h^{''}\left( \tilde{\theta }\vert {\varvec{y}} \right) =\frac{h^{'}\left( \hat{\theta }\vert {\varvec{y}} \right) -h^{'}\left( \theta \vert {\varvec{y}} \right) }{\left( \hat{\theta }-\theta \right) } . \end{aligned}$$

Therefore,

$$\begin{aligned} r^{'}\left( \hat{\theta } \right) =h^{'}\left( \hat{\theta }\vert {\varvec{y}} \right) -h^{'}\left( \theta \vert {\varvec{y}} \right) =h^{''}\left( \tilde{\theta }\vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) . \end{aligned}$$

Taking the antiderivative of $r^{'}\left( \hat{\theta } \right)$ and because $r\left( \theta \right) =0$, we obtain

$$\begin{aligned} r\left( \hat{\theta } \right) =\frac{1}{2}h^{''} \left( \tilde{\theta }\vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) ^{2} . \end{aligned}$$

We now provide some property regarding the function h.

• 1. $\frac{h^{'}\left( \theta \vert {\varvec{y}} \right) }{K}$ is bounded for any $\theta$

Proof

The loglikelihood function of a testlet k is defined as

Let $t_{k}=G\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right)$ be the CDF, we then have

And since $u_{k}= G^{-1}\left( t_{k} \vert {0, \sigma _{u_{k}}^{2}}\right)$, we have

Let

Since $f\left( t_{k} \right) \rightarrow 0$ when both $t_{k}\rightarrow 0$ and $t_{k}\rightarrow 1$, we can define $f\left( 0 \right) =0$ and $f\left( 1 \right) =0$, so that $f\left( t_{k} \right)$ is considered continuous in [0,1]. By applying the mean value theorem for integral, there exists a value $c_{k}\in \left( 0,1 \right)$ and at which

Using the above equation, we see

which can be bonded by ${n_{k}}$.

As for the derivatives of the expected loglikelihood, we have

Since , using similar argument, we know there exists $d_{jk}$ that $E\left( y_{jk} \right) =\frac{\textrm{exp}\left( \theta +d_{jk}-b_{j} \right) }{1+\textrm{exp}\left( \theta +d_{jk}-b_{j} \right) }$, hence

$$\begin{aligned} E\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) =\sum \limits _{j\mathrm {=1}}^{n_{k}} \left( p_{jk}\left( \theta \vert d_{jk} \right) \textrm{log}\left( p_{jk}\left( \theta \vert d_{k} \right) \right) +\left( 1-p_{jk}\left( \theta \vert d_{jk} \right) \right) \textrm{log}\left( q_{jk}\left( \theta \vert d_{k} \right) \right) \right) \end{aligned}$$

and

$$\begin{aligned}&\frac{dE\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) }{d\theta }\\ &\quad =\sum \limits _{j\mathrm {=1}}^{n_{k}} \left[ p_{jk}\left( \theta \vert d_{jk} \right) q_{jk}\left( \theta \vert d_{jk} \right) \textrm{log}\left( p_{jk}\left( \theta \vert d_{k} \right) \right) -p_{jk}\left( \theta \vert d_{jk} \right) q_{jk}\left( \theta \vert d_{jk} \right) \textrm{log}\left( q_{jk}\left( \theta \vert d_{k} \right) \right) \right] \end{aligned}$$

Let $s_{1}$ stands for all the terms within the summation operator above. $s_{1}$ is bounded because both addends approach to 0 as $\theta$ goes to $\pm \infty .$ Suppose the absolute value, $\left| s_{1} \right|$, is less than some real number $\mu _{1}$, then $\left| \frac{dE\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) }{d\theta } \right| <u_{1}{n_{k}}$. Therefore,

This proves that $\frac{h^{'}\left( \tilde{\theta } \right) }{ K}$ is bounded for any $\theta$.

• 2. $\frac{h^{''}\left( \theta \vert {\varvec{y}} \right) }{K}$ is bounded for any $\theta$

Proof

Using the earlier results from proof 1, we can find that

$$\begin{aligned} l_{k}^{''}\left( \theta \vert {\varvec{y}} \right) =-\sum \limits _{j\mathrm {=1}}^{n_{k}} \left( p_{jk}\left( \theta \vert d_{k} \right) q_{jk}\left( \theta \vert d_{k} \right) \right) . \end{aligned}$$

Here $p_{jk}\left( \theta \vert d_{k} \right) q_{jk}\left( \theta \vert d_{k} \right)$ is bounded by 1/4 for any value of $\theta$, hence $l_{k}^{''}\left( \theta \vert {\varvec{y}} \right)$ is bounded by $\frac{{n_{k}}}{4}$.

We also have

$$\begin{aligned} \frac{d^{2}E\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) }{d\theta ^{2}}&=\sum \limits _{j\mathrm {=1}}^{n_{k}} \left[ \left( q_{jk}\left( \theta \vert d_{jk} \right) -p_{jk}\left( \theta \vert d_{jk} \right) \right) p_{jk}\left( \theta \vert d_{jk} \right) q_{jk}\left( \theta \vert d_{jk} \right) \textrm{log}\left( p_{jk}\left( \theta \vert d_{k} \right) \right) \right. \\&\quad \left. +\left( p_{jk}\left( \theta \vert d_{jk} \right) -q_{jk} \left( \theta \vert d_{jk} \right) \right) p_{jk}\left( \theta \vert d_{jk} \right) q_{jk}\left( \theta \vert d_{jk} \right) \textrm{log}\left( q_{jk}\left( \theta \vert d_{k} \right) \right) \right. \\&\quad \left. +p_{jk}\left( \theta \vert d_{jk} \right) q_{jk} \left( \theta \vert d_{jk} \right) \right] . \end{aligned}$$

Let $s_{2}$ stands for all the terms within the summation operator above. $s_{2}$ is bounded because all addends approach to 0 as $\theta$ goes to $\pm \infty .$ Suppose the absolute value, $\left| s_{2} \right|$, is less than some real number $\mu _{2}$, then $\left| \frac{d^{2}E\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) }{d\theta ^{2}} \right| <u_{2}{n_{k}}$.

Using the above results, we show that $\left| l_{k}^{''}\left( \theta \vert {\varvec{y}} \right) -\frac{d^{2}E\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) }{d\theta ^{2}} \right| \le \,\left( u_{2}+\frac{1}{4} \right) {n_{k}}$. Therefore,

$$\begin{aligned} \left| \frac{h^{''}\left( \theta \right) }{K} \right|&=\frac{\left| \sum \nolimits _{k=1}^K \left( l_{k}^{''}\left( \theta \vert {\varvec{y}} \right) -\frac{d^{2}E\left( l_{k}\left( \theta \vert {\varvec{y}} \right) \right) }{d\theta ^{2}} \right) \right| }{K}\le \frac{K\left( u_{2}+\frac{1}{4} \right) \textrm{max}\left\{ n_{1},n_{2},\cdots ,n_{K} \right\} }{K}\\ &=\left( u_{2}+\frac{1}{4} \right) \textrm{max}\left\{ n_{1},n_{2},\cdots ,n_{K} \right\} . \end{aligned}$$

This proves that $\frac{h^{''}\left( \tilde{\theta } \right) }{ K}$ is bounded for any $\theta$.

Now recall that the remainder of the Taylor expansion is

$$\begin{aligned} r\left( \hat{\theta } \right) =\frac{1}{2}h^{''}\left( \tilde{\theta }\vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) ^{2} \end{aligned}$$

For $h^{''}\left( \tilde{\theta }\vert {\varvec{y}} \right) \left( \hat{\theta }-\theta \right) ^{2}$, we have

Here, $\sqrt{K} \left( \hat{\theta }-\theta \right)$ is asymptotical normal, $\left( \hat{\theta }-\theta \right)$converges to 0 in probability, and is bounded. Therefore, converges to 0 in probability. This indicates that the remainder is negligible.

Appendix C: Simulation Results of the Correlation Between ${h}\left( \hat{\theta }{\vert y} \right)$ and $\left( \hat{\theta }{-\theta } \right)$

True $\theta$	Correlation between $h\left( \hat{\theta }\vert y \right)$ and $\left( \hat{\theta }-\theta \right)$
	Rasch Testlet Model		Unidimensional Rasch Model*
	6 Testlets	12 Testlets	43 items	96 items
$-$2	0.0276	0.0281	0.0022	0.0073
$-$1	0.0091	0.0100	$-$0.0089	0.0012
$-$0	0.0168	$-$0.0074	$-$0.0074	$-$0.0051
$-$1	0.0005	$-$0.0213	0.0033	0.0026
$-$2	0.0046	$-$0.0327	$-$0.0019	$-$0.0126
*Note. For the unidimensional Rasch model, item difficulty parameter values used in the simulation for the 43-items and 96-items conditions are the same as the ones used in the 6-tetlets and 12-testlets conditions, respectively

Appendix D: Expected Fisher Information Computation

For a testlet k consists of j items, the expected Fisher information is

where $p\left( {\varvec{y}}_{k}\mathrm {\vert }\hat{\theta } \right)$ is the marginal probability of score pattern ${\varvec{y}}_{k}$ after marginalizing out the nuisance dimension, and $l\left( \theta \vert {\varvec{y}}_{k} \right)$ is the log-likelihood of ${\varvec{y}}_{k}$. The right-hand side of the above equation can be written as

$$\begin{aligned} -\sum \limits _{{\varvec{y}}_{k}} \left( \frac{d^{\textrm{2}}l\left( \theta \vert {\varvec{y}}_{k} \right) }{d\theta ^{\textrm{2}}}p\left( {\varvec{y}}_{k}\mathrm {\mathbf {\vert }}\theta \right) \right) =-\sum \limits _{r_{k}=0}^{n_{k}} \sum \limits _{{{\varvec{y}}_{k}}\in \mathbbm {y}_{r_{k}}} {\frac{d^{\textrm{2}}l\left( \theta \vert {\varvec{y}}_{k} \right) }{d\theta ^{\textrm{2}}}p\left( {\varvec{y}}_{k} {\mathbf {\vert }}\theta \right) }, \end{aligned}$$

where ${n_{k}}$ is the number of items in the testlet, and $\mathbbm {y}_{r_{k}}$ is the set of score patterns that leads to a sum score of $r_{k}$. Using the property that the sufficient statistic for $\uptheta$ is the raw score, we have $\frac{d^{\textrm{2}}l\left( \theta \vert {\varvec{y}}_{k} \right) }{d\theta ^{\textrm{2}}}=\frac{d^{\textrm{2}}l\left( \theta \vert r_{k} \right) }{d\theta ^{\textrm{2}}}$ when ${\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}$. Hence

$$\begin{aligned} -\sum \limits _{r_{k}=0}^{n_{k}} \sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} {\frac{d^{\textrm{2}}l\left( \theta \vert {\varvec{y}}_{k} \right) }{d\theta ^{\textrm{2}}}p\left( {\varvec{y}}_{k}\mathrm {\mathbf {\vert }}\theta \right) }&=-\sum \limits _{r_{k}=0}^{n_{k}} \left[ \frac{d^{\textrm{2}}l\left( \theta \vert r_{k} \right) }{d\theta ^{\textrm{2}}}\sum \limits _{{\varvec{y}}_{k}\in \mathbbm {y}_{r_{k}}} \left( p\left( {\varvec{y}}_{k}\mathrm {\mathbf {\vert }}\theta \right) \right) \right] \\ &=-\sum \limits _{r_{k}=0}^{n_{k}} \left[ \frac{d^{\textrm{2}}l\left( \theta \vert r_{k} \right) }{d\theta ^{\textrm{2}}}p\left( r_{k}\mathrm {\mathbf {\vert }}\theta \right) \right] . \end{aligned}$$

The computation of $p\left( r_{k}\mathrm {\mathbf {\vert }}\theta \right)$ is shown in the main body using the Lord-Wingersky algorithm. For $\frac{d^{\textrm{2}}l\left( \theta \vert r_{k} \right) }{d\theta ^{\textrm{2}}}$,

$$\begin{aligned} \frac{d^{\textrm{2}}l\left( \theta \vert r_{k} \right) }{d\theta ^{\textrm{2}}}&= \frac{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) \left( r_{k}-\sum \nolimits _{j\mathrm {=1}}^{n_{k}} p_{jk} \right) ^{2}g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} }{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} } \quad \hbox { A} \\&\quad -\frac{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) \left( \sum \nolimits _{j\mathrm {=1}}^{n_{k}} p_{jk} q_{jk} \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} }{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} } \quad \hbox { B} \\&\quad -\left( \frac{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) \left( r_{k}-\sum \nolimits _{j\mathrm {=1}}^{n_{k}} p_{jk} \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} }{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} } \right) ^{2} \quad \hbox { C} \end{aligned}$$

Define $p\left( u_{k} \vert {\theta ,r}_{k}\right) =\frac{\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) f\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) }{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) f\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} }$, then term A above is (omitting cluster index k)

$$\begin{aligned}&\sum \limits _{r=0}^n {\left\{ \int {p\left( u \vert {\theta ,r}\right) \left( r-\sum \limits _{j\mathrm {=1}}^n p_{j} \right) ^{2}du} \right\} p\left( r \right) } =\int {\left\{ \sum \limits _{r\mathrm {=0}}^n {p\left( u \vert {\theta ,r}\right) p\left( r \right) \left( r-\sum \limits _{j\mathrm {=1}}^n p_{j} \right) ^{2}} \right\} du} \\&\quad =\int {\left\{ \sum \limits _{r\mathrm {=0}}^n {p\left( r,u\vert \theta \right) \left( r-\sum \limits _{j\mathrm {=1}}^n p_{j} \right) ^{2}} \right\} du}\\&\quad =\int {\left\{ \sum \limits _{r\mathrm {=0}}^n {p\left( r \vert {\theta ,u}\right) p\left( u \right) \left( r-\sum \limits _{j\mathrm {=1}}^n p_{j} \right) ^{2}} \right\} du} \\ &\quad =\int {p\left( u \right) \left\{ \sum \nolimits _{r\mathrm {=0}}^n {p\left( r \vert {\theta ,u}\right) \left( r-\sum \nolimits _{j\mathrm {=1}}^n p_{j} \right) ^{2}} \right\} du} \\&\quad =\int {p\left( u \right) E_{r\vert u}\left( r-\sum \nolimits _{j\mathrm {=1}}^n p_{j} \right) ^{2}du} . \end{aligned}$$

Since $E_{r\vert u}\left( r-\sum \nolimits _{j\mathrm {=1}}^n p_{j} \right) ^{2}=\sum \nolimits _{j\mathrm {=1}}^n p_{j} q_{j}$, term A becomes

$$\begin{aligned} \int {p\left( u \right) \left( \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j} \right) du} . \end{aligned}$$

Similarly, term B is,

$$\begin{aligned}&\quad -\sum \limits _{r\mathrm {=0}}^n \left\{ \int {p\left( u \vert {\theta ,r}\right) \left( \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j} \right) du} \right\} p\left( r \right) \\&=-\int {\left\{ \sum \limits _{r\mathrm {=0}}^n {p\left( u \vert {\theta ,r}\right) p\left( r \right) \left( \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j} \right) } \right\} du} \\&=-\int {\left\{ \sum \limits _{r\mathrm {=0}}^n {p\left( r,u\vert \theta \right) \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j}} \right\} du} =-\int {\left\{ \sum \limits _{r\mathrm {=0}}^n {p\left( r\vert \theta ,u \right) p\left( u \right) \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j}} \right\} du}\\&\quad =-\int {p\left( u \right) \left( \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j} \right) \left( \sum \nolimits _{r\mathrm {=0}}^n {p\left( r\vert \theta ,u \right) } \right) du} =-\int {p\left( u \right) \left( \sum \limits _{j\mathrm {=1}}^n p_{j} q_{j} \right) du} . \end{aligned}$$

Therefore, term A and term B canceled out, and $\frac{d^{\textrm{2}}l\left( \theta \vert r_{k} \right) }{d\theta ^{\textrm{2}}}$ is simply provided by term C. Hence,

$$\begin{aligned} I_{k}\left( \theta \right)&=\sum \limits _{r_{k}=0}^{n_{k}} \left[ \left( \frac{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) \left( r_{k}-\sum \nolimits _{j\mathrm {=1}}^{n_{k}} p_{jk} \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} }{\int {\textrm{Exp}\left( r_{k}u_{k}+\sum \nolimits _{j\mathrm {=1}}^{n_{k}} {\textrm{log}\left( q_{jk} \right) } \right) g\left( u_{k} \vert {0, \sigma _{u_{k}}^{2}}\right) du_{k}} } \right) ^{2}p\left( r_{k}\mathrm {\mathbf {\vert }}\theta \right) \right] . \end{aligned}$$

It follows that the test information at $\theta =\hat{\theta }$ for a test with K testlets is

$$\begin{aligned} I\left( \hat{\theta } \right) =\sum \nolimits _{k\mathrm {=1}}^K {I_{k}\left( \hat{\theta } \right) }. \end{aligned}$$