1 Introduction

Cluster analysis is playing an important role in real applications, such as stock data analysis, market segmentation, production supervision, and anomaly detection [28, 39]. In recent years, spectral clustering has been attracting wide attention due to conducting K-mean clustering on the spectral representation rather than original representation [11, 31, 32]. To do this, spectral clustering first obtains the spectral representation of original data by conducting the eigenvalue decomposition of the affinity matrix of original data, and then conducts K-means clustering on the resulted spectral representation [30].

Spectral clustering generates the new representation (i.e., the spectral representation) of original data through matrix spectral analysis theory so that it is simple to implement, and does not easily fall into local optimal solution, compared to other clustering methods [30]. The key step of spectral clustering is the learning of spectral representation, i.e., affinity matrix learning, which is also the key difference between spectral clustering and K-means clustering. Usually, the construction of the affinity matrix includes local representation methods and global representation methods. The global representation methods represent each data point by all of data points [34, 46], while the local representation methods use the local information of original data to construct the affinity matrix between samples, such as local subspace affinity [33] and locally linear manifold clustering [6]. However, previous spectral clustering still has issues to be addressed.

First, cluster performance always suffers from the influences of redundant features and outliers. However, it is very often to find them on original data. Hence, the quality of both the cluster models and the affinity matrix constructed on original data are not guaranteed [25, 37, 40]. In the literature, some studies only focused on avoiding the influence of either redundant features or outliers for constructing clustering model. For example, the literature [16, 38] employed the sparse technique to avoid the influence of redundant features for clustering, while the studies in [5, 19, 45, 46] used the low-rank method to avoid the influence of outliers. A few literature has focused on taking the two issues into account in a unified framework [42]. For example, some studies in [17, 25] proposed avoiding the influence of redundant features by an ℓ2,1- norm regularization as well as reducing the effect of outliers by the robust estimator.

Second, the affinity matrix learning is also affected by the redundant features and outliers. A number of previous literature focus on constructing the affinity matrix from the low-dimensional space of original data rather than the original space used in traditional spectral clustering [20, 27]. To the best of our knowledge, no literature has focused on simultaneously learning clustering models and the affinity matrix from the low-dimensional space of original data by reducing the influence of outliers and redundant features.

Third, many clustering methods (such as K-means clustering and spectral clustering) need to specify the cluster number, which requires prior knowledge. Recently, the literature [25] focuses on automatically learning the cluster number by designing a regularization, but does not taking into account the influence of outliers and redundant features on the affinity matrix learning.

In this paper, we proposed a new clustering algorithm to address above three issues in a unified framework by employing the half-quadratic optimization technique. Specifically, our proposed method employs the sparse regularization and the half-quadratic technique, respectively, to reduce the influence of redundant features and outliers so that our method is available to learn a clustering model and the affinity matrix from the low-dimensional space of high-dimensional original data. Moreover, we employ an ℓ2,1-norm regularization to automatically determine the cluster number. Furthermore, we propose a new alternating optimization strategy to solve the proposed objective function.

Compared to the previous clustering methods, we conclude the contributions of our proposed method as follows:

  • The proposed method jointly conducts the clustering task and feature selection from low-dimensional space of original data in a unified framework. This makes our method reduce the influence of outliers and redundant features. To the best of our knowledge, a few literature has focused on these two issues simultaneously.

  • The proposed method does not need to predefine the cluster number, which is an open issue in the clustering study. Although some studies focused on solving this issue, they did not take into account the influence of outliers and redundant features.

We summarize the rest of this paper as follows. We briefly review the literature related to this paper in Section 2. In Section 3, we give the detailed description of our proposed method as well as list our optimization strategy to the resulted objective function. After that, we present experiment results in Section 4 and finally conclude this paper in Section 5.

2 Related work

In this section, we briefly review existing methods for clustering analysis by the information, such as the clustering definition, the clustering categories, and previous clustering methods for dealing with the noise and redundancy inherent data points.

2.1 Clustering analysis

Cluster analysis pushes data points to be grouped in clusters, helping us to analyze and describe the real-world. Thus it is an important branch in the field of machine learning as well as plays an important role in the real applications, such as psychology, biology, pattern recognition, and data mining [1, 26]. According to the calculation criteria of the similarity between two objects, previous clustering algorithms can be divided into the subcategories, such as partition-based methods, hierarchical method, and density-based method. The partition-based clustering method (e.g., K-Means algorithm and K-modes algorithm) simply divides data points to several non-overlapped subsets such that every data point belongs to only one subset [4]. The hierarchical clustering method is to create a hierarchical tree by calculating the similarity between different types of data points. Moreover, in the clustering tree, original data points with different categories are located in the lowest layer of the tree while the top layer of the tree is located in the root node of a cluster. Traditional methods for a clustering tree generation include the bottom-up merge methods and the top-down split methods [44]. The density-based clustering method is designed to start from the distribution density of data objects, and then connects adjacent regions with enough density to detect clusters with different shapes. Recently, the density-based clustering methods are mainly used for clustering spatial data in the domain of database [36].

2.2 Clustering methods for feature selection

Clustering analysis usually involves high-dimensional data, which contains noise and redundancy to degrade the clustering performance [5, 14]. However, most existing clustering algorithms did not pay attention to this issue. A naive solution to noise and redundancy is to first conduct dimensionality reduction and then conduct clustering analysis on the reduced data. However, such a two-step strategy can not grantee to output significant clustering performance as the goal of the first step (i.e., dimensionality reduction [38, 40]) is focused on reducing the feature number rather than improving the clustering performance [42, 45, 46]. Recently, Volker et al. proposed to combine clustering analysis with feature selection in a unified framework [24]. Martin et al. proposed the concept of feature saliency and introduces the Expectation–Maximization (EM) algorithm for clustering analysis [15]. Zhu et al. proposed a novel one-step spectral clustering algorithm to combine the similarity learning with feature selection in a unified one-step clustering framework to simultaneously conduct feature selection and spectral clustering [41].

2.3 Clustering methods for similarity measurement

Cluster analysis is an unsupervised learning method due to the lack of class labels, so the goal of clustering is to maximize the similarity between two data points within the same category as well as minimize the similarity between two data points in different categories. Hence, the similarity measurement is the key step for clustering analysis [14]. In the literature, Zelnik-Manor proposed to self-adjust the number of the nearest neighbors of data points for conducting spectral clustering [35]. Wang et al. proposed determining the similarity by the density and distance of the data points [23]. Liu et al. proposed adjusting the similarity between data points by the number of shared neighbors between two data points [18].

2.4 Clustering methods for avoiding the influence of outliers

Although many methods have been proposed to improve the robustness of clustering analysis, how to improve the robustness of clustering algorithms is still a challenging problem due to the diversity and complexity of noise. Recently, Wang et al. proposed to assign a scale value to each data point according to the distance between the data point and the corresponding centroid, so as to distinguish normal data points from outliers in the clustering process [29]. Liu et al. proposed to seek the lowest rank representation that can represent the data points as linear combinations of the bases for spectral clustering [7]. Zhu et al. proposed a new robust multi-view clustering method to solve the initialization sensitivity of existing multi-view clustering, and introduce the correlation entropy loss function to estimate the reconstruction error for effectively avoiding the impact of outliers [48].

3 Approach

In this section, we list the notations used in this paper in Section 3.1, and then report the details of our proposed method in Section 3.2. Finally, we describe our optimization method for the proposed objective function in Section 3.3.

3.1 Notations

In this paper, matrices and vectors are denoted as boldface uppercase letters and boldface lowercase letters, respectively. More specifically, given a matrix X = [xij], its i-th row and j-th column are denoted as xi and xj, respectively. We denote the Frobenius norm, ℓ2,p-norm of a matrix X, respectively, as \(||\mathbf {X}|{|_{F}} = \sqrt {\sum \nolimits _{i} {||{\mathbf {x}_{i}}} ||_{2}^{2}} = \sqrt {\sum \nolimits _{j} {||{\mathbf {x}_{j}}||}_{2}^{2}}\) and \(||\mathbf {X}|{|_{2,p}} = {\left (\sum \nolimits _{i} {\sqrt {\sum \nolimits _{j} {x_{ij}^{\frac {p}{2}}} } } \right )^{{\textstyle {1 \over p}}}}\). We further denote the transpose operator and the inverse of a matrix X as XT and X− 1, respectively.

3.2 Proposed method

Finding the internal structure of data is a challenging task in clustering task [13, 37]. Given a data set \( {\textbf {X}} = [{{\textbf {x}}_{1}},{{\textbf {x}}_{2}},...,{{\textbf {x}}_{n}}] \in \mathbb {R}^{n\times d}\) as the data matrix with n samples, where d represents the number of the features, we can use either global representation methods or local representation methods to construct the affinity matrix \(\mathbf {S} \in \mathbb {R}^{n\times n}\). Since the local representation method linearly represents the relationship between the data point and its nearest neighbors [16, 40], it could effectively avoid the influence of outliers, so that it has been proved better than the global representation method [45, 46]. In this paper, the local representation method is used to construct the affinity matrix, using Euclidean distance to measure the similarity between the data points, with the assumption that every data point can be connected to other data in the data set. Specially, letting si,j to represent the similarity between the i-th data point and the j-th data point, a small distance \(||{\textbf {x}}_{i}-{\textbf {x}}_{j}||_{2}^{2}\) should be assigned a large probability sij while a large distance \(||{\textbf {x}}_{i}-{\textbf {x}}_{j}||_{2}^{2}\) should be assigned a small probability si,j. Hence, we can obtain the following objective function based on previous literature [38, 43]

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min \sum\limits_{j = 1}^{n} s_{i,j}{|| \textbf{x}_{i} - \textbf{x}_{j}||}_{2}^{2} \end{array} \end{array} $$
(1)

Previous methods (e.g., [11, 39, 43]) assume that the affinity matrix constructed in the original feature space can accurately represent the true relationship among data points, so the affinity matrix can be used to guide the original feature space for conduct the prediction task. However, such prediction is often inaccurate because both the redundant features and outliers in the data set make the actual distribution of the data set complex. Thus, it is difficult to guarantee that the affinity matrix learnt from the original feature space can effectively guide the clustering process in the intrinsic low-dimensional subspace. This makes that it is very challenging to conduct clustering on high-dimensional data. To address this issue, we explore the optimal subspace in the original feature space and extract the inherent affinity matrix from the optimal low-dimensional subspace, based on the assumption that original data structure actually lies on a low-dimensional space.

More specifically, by denoting \(\textbf {W} \in \mathbb {R}^{d\times c}\) (where c ≤ d is the dimensions of intrinsic space of original high-dimensional data) as the transformation matrix that maps the original data X to its intrinsic subspace spanned by XW, we design to learn an intrinsic affinity matrix \(\textbf {S} \in \mathbb {R}^{n\times n}\) in the intrinsic low-dimensional space via the following objective function

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{\textbf{W,S}} \sum\limits_{j = 1}^{n} s_{i,j}{|| \textbf{x}_{i}\textbf{W} - \textbf{x}_{j}\textbf{W}||}_{2}^{2} + \beta {|| \textbf S||}_{2}^{2}+\lambda{| \textbf W ||}|_{2,1}\\ s.t., \textbf{W}^{T}\textbf{X}^{T}\textbf{X}\textbf{W} = \textbf{I}_{c},\forall i,\textbf{s}_{i}^{T}{\textbf{1}} = 1,0 \le {s_{i,j}} \le 1, \end{array} \end{array} $$
(2)

where λ is a tuning parameter. The penalty \({\left \| \textbf {W} \right \|_{2,1}}\) conducts feature selection by outputting the row sparsity on W to remove redundant features of X. While the orthogonal constraint on the scatter matrix \({{\textbf {W}}^{T}}{{\textbf {X}}^{T}}{\textbf {X}}{\textbf {W}} = {{\textbf {I} }_{c}}\in \mathbb {R}^{c\times c}\) actually conducts subspace learning to transfer original d-dimensional feature space into c-dimensional space. In this way, (2) reduces the influence of redundant features by two kinds of dimensionality reduction methods, i.e., subspace learning and feature selection.

In spectral clustering, the quality of the affinity matrix will affect the effect of clustering. Moreover, the ℓ2-norm regularization is only effective for Gaussian noise processing with independent distribution, and can not effectively handle the abnormal edge of the affinity matrix S, i.e., outliers. In other words, in the process of optimizing W, the abnormal edges will still appear. Given noisy real-world data, heavy contamination of the connectivity structure by connections across different underlying clusters is inevitable. To address this issue, in this paper, our method uses robust estimators to automatically prune spurious inter-cluster connections while maintaining veridical intra-cluster correspondences by the following objective function

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{\textbf{W,S}} {\sum\limits_{i,j=1}^{n} {{s_{i,j}}{\rho }(|| \textbf{x}_{i}\textbf{W} - \textbf{x}_{j}\textbf{W}||}_{2}}) + \beta {|| \textbf S ||}_{2}^{2}+\lambda {||\textbf W ||}_{2,1}\\ s.t., \textbf{W}^{T}\textbf{X}^{T}\textbf{X}\textbf{W} = \textbf{I}_{c},\forall i,\textbf{s}_{i}^{T}\textbf{1} = 1,0 \le s_{i,j} \le 1, \end{array} \end{array} $$
(3)

where ρ(.) is a robust estimator designed by the half-quadratic theory [9, 12, 22] and the ℓ2,1-norm regularization on (xiW −xjW) could automatically output the number of the clusters based on the data distribution [25].

Robust estimators could produce robust estimations that are not unduly influenced by outliers and output significant performance with reducing influence of outliers [12]. Based on the half-quadratic theory, the researchers designed a number of robust estimators, each of which could theoretically reduce the influence of outliers. In this paper, for simplicity, we use the well-known German and Reynolds estimator [3] to replace ρ(.), i.e.,

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \rho (\textbf z) = \frac{ - 1}{{1 + | \textbf z|}}~~\text{with}~~ \varphi(\textbf{z})=\frac{1}{{(1 + \textbf{z})}^{2}} \end{array} \end{array} $$
(4)

where z is a vector or a matrix, φ(z) is a minimization function.

According to the literature [22], the half-quadratic theory usually transfers the robust estimator to its equivalent formulation by introducing an auxiliary variable p, e.g.,\(\rho ({z_{i}}) = \min \limits _{{p_{i}}} \left \{ {p_{i}}{z_{i}^{2}} + \varphi ({p_{i}})\right \}\), where \({p_{i}}{z_{i}^{2}}\) is a quadratic function and φ(pi) is the dual function of the robust estimator. Usually, each robust estimator has a corresponding minimization function, we can assign different weights to each zi by minimization function. Specifically, if zi is an outlier, the value of pi is small or even 0, and vice versa. In this way, the influence of outliers will be reduced.

Based on above analysis, we transfer our objective function in (3) to our final objective function as follows.

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{{\textbf{W}},{\textbf{S}}, \textbf P} \sum\limits_{i,j = 1}^{n} s_{i,j}p_{i,j}|| \textbf{x}_{i}\textbf{W} - \textbf{x}_{j}\textbf{W } ||_{2}^{2} + \varphi (\textbf{P})+ \beta{||\textbf S||}_{2}^{2}+ \lambda || \textbf{W} ||_{2,1}\\ s.t., \textbf{W}^{T}\textbf{X}^{T}\textbf{X}\textbf{W} = \textbf{I}_{c},\forall i,\textbf{s}_{i}^{T}{\textbf{1}} = 1,0 \le s_{i,j} \le 1. \end{array} \end{array} $$
(5)
figure a

3.3 Optimization

Equation (5) is not jointly convex to all the variables (i.e., S, W and P), but is convex for each variable while fixing the others. In this paper, we employ an alternating optimization strategy to optimize (5) and list the details in Algorithm 1.

  • (i)Update P by fixing S and W

According to the literature [2, 22], if the variables S and W are fixed, P can be updated by the following formula:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} {p_{i,j}}=\frac{1}{(1 + {{\| \textbf{x}_{i}\textbf{W} - \textbf{x}_{j}\textbf{W} \|}_{2}})^{2}},i,j=1,...,n. \end{array} \end{array} $$
(6)

  • (ii) Update S by fixing W and P

Given P and W, we obtain the optimization problem with respect to S as follows:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{\mathbf{S}} ~ \sum\limits_{i,j}^{n} s_{i,j}p_{i,j} \|\mathbf{x}_{i}\mathbf{W} - \mathbf{x}_{j}\mathbf{W}\|_{2}^{2} + \beta \|\mathbf{s}_{i}\|_{2}^{2},\\ s.t. \forall i,\textbf{s}_{i}^{T}{\textbf{1}} = 1,0 \le {s_{i,j}} \le 1 \end{array} \end{array} $$
(7)

The optimization of S is independent on each row, so we further change (7) to individually optimize si (i = 1,…,n) as follow:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{\mathbf{s}_{i}^{T}\mathbf{1} = 1, s_{i,j} \ge 0} \sum\limits_{j = 1}^{n} s_{i,j} e_{i,j} + \beta s_{i,j}^{2}, \end{array} \end{array} $$
(8)

where ei = {ei,1,...,ei,n}, \(e_{i,j}=p_{i,j}|| {\textbf {x}_{i}}{\textbf {W}^{T}} -{\textbf {x}_{j}}{\textbf {W}^{T}} ||_{2}^{2}\).

We first calculate k nearest neighbors of each data point, and then set the value of si,j as 0 if the j-th data point is not one of k nearest neighbors of the i-th data point. Otherwise, the value of si,j can be solved by Karush–Kuhn–Tucker (KKT) [47] conditions, i.e.,

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} s_{i,j} = \left\{ {\begin{array}{*{20}{c}} \frac{\hat e_{i,k + 1} - e_{i,j}} {k\hat e_{i,k + 1} - \sum\limits_{j = 1}^{k} e_{i,j} }~~~j \le k\\ ~~~~~0 ~~~~~~~~~~~~~~~~~j > k \end{array}} \right. \end{array} \end{array} $$
(9)

The number of nearest neighbors k can be tuned by cross-validation methods. Moreover, different data points have different numbers of nearest neighbors, base on the constraint “\(\hat e_{i, k + 1} = \hat e_{i, j}\)“ for specific k and j.

  • (iii)Update W by fixing S and P

While fixing P and S, the objective function with respect to W becomes:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \mathop {\min}\limits_{{\textbf{W}}} \sum\limits_{i,j = 1}^{n} s_{i,j}p_{i,j}|| \textbf{x}_{i}\textbf{W} - \textbf{x}_{j}\textbf{W} ||_{2}^{2}+ \lambda || \textbf{W} |_{2,1}\\ s.t.,{\textbf{W}^{T}\textbf{X}^{T}\textbf{X}\textbf{W}}= \textbf{I}_{c},\forall i,\textbf{s}_{i}^{T}{\textbf{1}} = 1,0 \le {s_{i,j}} \le 1 \end{array} \end{array} $$
(10)

By setting \({\tilde s}_{i,j} = s_{i,j}p_{i,j}\) and \(\textbf {L} = \textbf {D} - \tilde {\textbf {S}} \in {{\mathbb R}^{n \times n}}\) as Laplacian matrix, where \(\textbf {D} = diag(\tilde {\textbf {S}}\textbf {1})\), (10) is equivalent to

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{{\textbf{W}}} ~ tr(\textbf{W}^{T}\textbf{X}^{T}\textbf{L}\textbf{X}\textbf{W}) + \lambda || \textbf{W} ||_{2,1}, s.t., {\textbf{W}^{T}\textbf{X}^{T}\textbf{X}\textbf{W}}= {\textbf{I} }_{c} \end{array} \end{array} $$
(11)

Since the ℓ2,1-norm regularization is convex and non-smooth, we employ the framework of iteratively reweighted least squares (IRLS) to optimize S, via changing (11) to the following objective function

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{{\textbf{W}}} ~ tr({\textbf{W}}^{T}{\textbf{X}}^{T}\textbf{LXW }+ \lambda {\textbf{W}}^{T}\textbf{QW)}, s.t., \textbf{W}^{T}\textbf{X }^{T}\textbf{X}\textbf{W} = \textbf{I}_{c} \end{array} \end{array} $$
(12)

where Q is a diagonal matrix with the i-th diagonal element \(q_{i,i} = \frac {1 }{2\|{\mathbf {w}^{i}\|_{2}^{2}}}, {i=1,...d.}\)

In (12), both Q and W are unknown. Moreover, Q depends on W. According to the IRLS framework, we design an iterative algorithm to solve problem (12) by two sequential steps until the algorithm converges: 1) By fixing the value of W, we can obtain the value of Q; 2) By fixing the value of Q, (12) is changed to an eigen-decomposition problem with respect to W.

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} \min\limits_{{\textbf{W}}}~ tr({\textbf{W}^{T}}({{\textbf{X}}^{T}}\textbf{LX} + \lambda {\textbf{Q)W)}}, s.t.,{\textbf{W}^{T}\textbf{X}^{T}\textbf{X}\textbf{W}} = {\textbf{I} }_{c} \end{array} \end{array} $$
(13)

The optimal solution W in (13) is the eigenvectors of \((\textbf {X}^{T}\textbf {X}+\chi \textbf {I}_{d})^{-1}({{\textbf {X}}^{T}}\textbf {LX} + \lambda {\textbf {Q}})\) since\(\textbf {X}^{T}\textbf {X}+\chi \textbf {I}_{d}\) is invertible, where χ is a very small positive value.

3.4 Convergence analysis

This section proves that the objective function value in (6) monotonically decrease in each iteration. Denoting the objective function in (6) as J(W,S,P), according to the properties of half-quadratic theory in [9], if the values of both W and S are fixed, the optimization ofP has a closed-form solution. Hence, we have

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} J({\textbf{W}}^{t+1},{\textbf{S}}^{t+1},{\textbf{P}}^{t + 1}) \le J({\textbf{W}}^{t+1},{\textbf{S}}^{t+1},{\textbf{P}}^{t}) \end{array} \end{array} $$
(14)

When the values of Wt+ 1 and Pt are fixed, the optimization of St+ 1 takes a closed-form solution, so we have

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} J({\textbf{W}}^{t+1},{\textbf{S}}^{t+1},{\textbf{P}}^{t} ) \le J({\textbf{W}}^{t+1},{\textbf{S}}^{t},{\textbf{P}}^{t}) \end{array} \end{array} $$
(15)

Since we conduct the optimization of W by the eigenvalue decomposition method, so we have

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} J({\textbf{W}}^{t+1},{\textbf{S}}^{t},{\textbf{P}}^{t} ) \le J({\textbf{W}}^{t},{\textbf{S}}^{t},{\textbf{P}}^{t}) \end{array} \end{array} $$
(16)

By integrating above three results together, i.e., (14)-(16), we obtain

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} J({\textbf{W}}^{t+1},{\textbf{S}}^{t},{\textbf{P}}^{t} ) \le J({\textbf{W}}^{t},{\textbf{S}}^{t},{\textbf{P}}^{t}) \end{array} \end{array} $$
(17)

By combining (14), (15) with (17), we have:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} J({\textbf{W}}^{t+1},{\textbf{S}}^{t+1},{\textbf{P}}^{t+1} ) \le J({\textbf{W}}^{t},{\textbf{S}}^{t},{\textbf{P}}^{t}) \end{array} \end{array} $$
(18)

4 Experiments

In this section, we evaluated our proposed clustering method, by comparing to seven state-of-the-art clustering methods, on two synthetic data sets and 12 public data sets, in terms of clustering performance.

4.1 Experimental analysis on synthetic data sets

In this subsection, we evaluated the effectiveness of our proposed method on two synthetic data sets with different data distributions.

4.1.1 Experimental analysis on the two-moon data set

The bimonthly data was randomly generated for the first synthesized data set. Specifically, there were two clusters in the data set and they were distributed in the two-moon shape, where each cluster contains 100 data points and the noise ratio was set as 0.13. The aim of this experiment was set to use our proposed method to calculate the affinity matrix by dividing all of the data points into two clusters accurately. In our experiment, we marked these two clusters in the data set as red and blue colors respectively, as shown in Figure 1a. We also denoted the width of the line as the similarity of between two data points, as shown in Figure 1b-c.

Figure 1
figure 1

Visualization of the clustering results of our proposed method on the two-moon synthetic data

Full size image

As shown in Figure 1b, in the original data set, there are connection points from different clusters connected to each other. However, there are no data points connected between the two clusters for our proposed method in Figure 1c. This indicates that our proposed method has successfully divided the data into two clusters by avoiding the influence of outliers.

4.1.2 Experimental analysis on the three-ring data set

In the second synthetic data set, we randomly generated a three-ring data set with five dimensions, where the first two dimensions were distributed in three circles and the left three features are redundant features. Since only the first two dimensions of the data set contain important information, finding a subspace containing important information is very important for clustering. We visualized the original data sets represented by the first two features in Figure 2a.

Figure 2
figure 2

Visualization of the clustering results of our proposed method and two dimensionality reduction methods (e.g., LPP and PCA) on the three-ring data set. We only visualized the first two features of the original data set in Figure 2a

Full size image

In our experiment, we compared the clustering result of our proposed method with two commonly used dimensionality reduction methods, such as principal component analysis (PCA) and local retention prediction (LPP), and then visualized all the results in Figure 2.

From Figure 2, we knew that both LPP and PCA methods (i.e., Figure 2b and c, respectively) did not find an effective low-dimensional subspace to output reasonable clustering results. However, our proposed method finds subspaces correctly as it is almost identical to the subspaces formed by the first two important dimensions. As a result, our proposed method outputs feasible significant clustering results, as shown in Figure 2d. Hence, our proposed is able to deal with the influence of redundant features.

4.1.3 Summarization on two synthetic data sets

Based on the experimental results in Figures 1–2, our proposed method has been shown to be available individually dealing with either redundant features or outliers. In Section 4.2, we showed that our proposed method could deal with both redundant features and outliers on 12 real-world data sets, compared to the state-of-the-art clustering methods.

4.2 Experimental analysis on real benchmark data sets

4.2.1 Data sets

We evaluated our proposed clustering methods and the comparison methods on twelve benchmark data sets, whose details were summarized in Table 1.

Table 1 The details of all data sets used in our experiment
Full size table

4.2.2 Comparison methods

The comparison methods include two classic clustering methods (i.e., NCut and k-means [8]), five state-of-the-art clustering methods (i.e., Low-Rank Representation (LRR) [19], Constrained Laplacian Rank (CLR) [21], Sparse subspace clustering (SSC) [5]), and SMooth Representation (SMR) [10]), and Structured Sparse Subspace Clustering (SSSC) [17].

We listed the details of the comparison methods as follows.

  • k-means partitions all the data points into k groups so that the data points in the same group are with minimal mean.

  • NCut partitions all the data points into k disjoint groups, where the weights of the edges between the groups are minimum.

  • LRR seeks the lowest rank representation to linearly represent the data points.

  • SSC first assumes that each point can be sparsely represented by all other data points, and then groups the data points drawn from multiple linear or affine subspaces of high-dimensional data.

  • SMR makes use of the least square function and the trace norm regularization to enforce the grouping effect among representation coefficients, and then achieves the subspace segmentation.

  • CLR learns the affinity matrix to have exactly k connected components where k is the number of clusters.

  • CSSC integrate the affinity matrix learning with spectral clustering in a unified framework, as well as uses spectral clustering to correct errors in the affinity matrix.

4.2.3 Experimental setting

In the experiment, we employed four evaluation metrics (such as clustering ACCuracy (ACC), Normalized Mutual Information (NMI), F-measure and Adjusted Rand Index (ARI)) to evaluate the clustering performance of all the methods. We set the range of parameters (i.e.,λ and β) in our methods as λ ∈{10− 3,10− 2,...,103} and β ∈{10− 3,10− 2,...,103}, as well as set the parameters in the comparison methods based on the literature so that all comparison methods achieved their best clustering performance in our experiments.

We listed the details of four evaluation metrics as follows:

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} ACC = \frac{N_{correct}}{N}, \end{array} \end{array} $$
(19)

where N represents the total sample number and Ncorrect represents the sample number accurately clustered.

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} ARI = \frac{{TP + TN}}{{TP + FP + FN + TN}} \end{array} \end{array} $$
(20)

where TP means that two samples clustered in a class are correctly classified, TN means that two samples that should not be clustered in a class are correctly separated, FP means that samples that should not be clustered in a class are incorrectly placed in a class, and FN means that samples that should not be clustered in a class are incorrectly separated.

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} F-measure = \frac{({\beta^{2}} + 1)PR}{{{\beta^{2}}P + R}} \end{array} \end{array} $$
(21)

where \(P = \frac {TP}{TP + FP}\) and \(R = \frac {TP}{TP + FN}\).

$$ \begin{array}{@{}rcl@{}} \begin{array}{l} NMI = \frac{{H(A) + H(B)}}{{H(A,B)}} \end{array} \end{array} $$
(22)

where A and B are clustering results, and H(A,B) is the joint entropy of A and B.

4.2.4 Experimental analysis of real-world data sets

We listed the clustering results of all the methods on these real data sets in Tables 2, 3, 4 and 5 and had the following observations.

Table 2 Clustering results on three public data sets, i.e., Wine, Ecoil, and Control
Full size table
Table 3 Clustering results on three public data sets, i.e., Parkinsons, Movement, and Vehicle
Full size table
Table 4 Clustering results on three public data sets, i.e., Jaffe, German, and Usps
Full size table
Table 5 Clustering results on three public data sets, i.e., Isolet, Statlog, and Mfeatures
Full size table

Our proposed method achieved the best performance, followed by CSSC, CLR, SMR, SSC, LRR, NCut, and k-means. For example, the accuracy of our method improved on average by 5.29%, compared to the best comparison methods (i.e., CSSC) on all 12 data sets. It may be that our method uses subspace learning to learn the affinity matrix from the low-dimensional subspace so that our method removes the influence of outliers and redundant features as well as uses robust estimation to avoid the influence of outliers in the data. On the contrary, the comparison algorithm cannot take into account the effects of these two constraints at the same time, so that they could obtain reliable models.

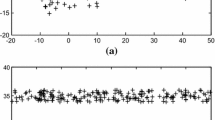
4.3 Parameters sensitivity

Two parameters need to be adjusted in our proposed objective function. In this section, we changed the values of λ and β by setting their ranges as {10− 3,10− 2,...,103} to investigate the variations of the clustering accuracy of our method. We listed the results on all data sets in Figure 3.

Figure 3
figure 3

ACC variations of our method at different parameter settings on 12 data sets

Full size image

The results showed that our method is sensitive to parameters setting. Moreover, different ranges of the parameter values need to be set for different data sets to get the best results. From example, our proposed method easily achieves significant clustering results while setting β ∈{101,102,103}. Moreover, the parameter β is more sensitive than the parameter λ in our objective function.

5 Conclusion

This paper has proposed a new clustering method, which learns the affinity matrix from the low-dimensional space of original data as well as uses the robust estimator to reduce the influence of outliers. Experimental results demonstrate the effectiveness of the method for clustering tasks.