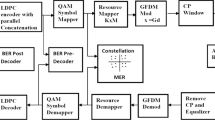
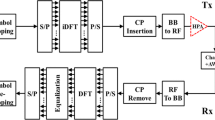
Abstract
Generalized frequency division multiplexing (GFDM) is a flexible block structured multicarrier scheme for next generation wireless systems featuring low out-of-band radiation and high spectrum efficiency. There are various approaches suggested for its analysis via simulations but testing in real time environments is necessary for its standardization. Traditional data aided methods of synchronization avoid the effect of egress noise in pilot preamble destroying its spectral advantage. To safeguard this advantage, preamble needs to be pulse shaped. The main contribution of this paper is the derivation of generalized maximum likelihood estimation of frequency and time offsets for receiver synchronization in GFDM systems, using the modified preamble by the application of matrix inversion lemma. The dependency of the choice of the filter on Cramer–Rao lower bound of frequency offset estimation is also emphasized. The performance of the system is analysed over additive white Gaussian noise and multipath channel environments. The authors carried out real time implementation of GFDM system using IEEE 802.11 short preamble in indoor environments by employing national instruments universal software radio peripheral 2953R boards as hardware platform which is interfaced with LABVIEW for practical validations of the results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Orthogonal frequency division multiplexing (OFDM) has dominated the wireless world over the past two decades as a physical layer multi-carrier (MC) technique mainly because of its easy implementation and single tap equalization [1]. A low complex flexible implementation is attained by using inverse fast Fourier transform (IFFT) at the transmitter, fast Fourier transform (FFT) at the receiver and single tap equalization is achieved by using a redundant cyclic prefix (CP) to mitigate multipath environments [2]. Due to which, it is adopted in many of the wireless standards such as IEEE 802.11, 802.16, 802.22, long term evolution (LTE) etc. In a typical mobile radio environment, the usage of IFFT at the transmitter would result in high peak to average power ratio (PAPR) which requires a costly power amplifier in order to compensate the effect [3]. The utilization of CP, which is included to combat the fading environment leads to decrease in bandwidth efficiency. In addition, the major limitation of OFDM is its inability to fill fragmented spectrum due to spectral leakage.
These demerits of OFDM impose major challenges in the current markets to serve the user needs for next generation mobile communication. There is a common consensus among research community from both academic and industries to replace OFDM [4]. Though numerous physical layer modulation schemes are proposed for 5G, it is worth mentioning that they all inherit the advantages which are present in OFDM and address its limitations [5]. Alternate waveforms like filter bank multi carrier (FBMC) technique use a well localized prototype filter for avoiding ingress, egress noises and in turn reduce out-of-band (OOB) emission. This MC technique requires ramp-up at the start and ramp-down at the end of each data packet which will cause a loss in spectral efficiency, thereby making it inefficient for low latency 5G applications like Internet of Things (IoT) and machine to machine communication (M2M)[6].
To address these issues, generalized frequency division multiplexing (GFDM) a flexible time-frequency block structure was introduced by Fettweis covering OFDM and single-carrier frequency domain equalization (SC-FDE) as corner cases [7]. The concept of circular pulse shaping of individual subcarrier which bears a number of subsymbols is combined with tail biting to obtain a GFDM signal. Tail biting results in high spectral efficiency along with significant reduction in OOB emission but it introduces non orthogonality which in turn will effect the symbol error rate (SER) performance [8]. Successive interference cancellation (SIC) was adopted in [9] in order to achieve an equivalent performance of OFDM system.
Though numerous attempts are imposed for improving orthogonality [10], however, due to its fundamental non orthogonal nature it is still prone to severe inter carrier interference (ICI) and inter symbol interference (ISI) which results in symbol time offset (STO) and carrier frequency offset (CFO)[11]. This makes synchronization the hardest problem in real channel environments [12]. These misalignments are estimated either by using data aided methods or by using the redundant CP. In [13], maximum likelihood (ML) estimate using correlation with CP was proposed, but the main drawback involved with this method is that, it would be difficult to locate actual data because training symbols and actual symbols look alike. Another drawback associated with CP based synchronization methods is that, they rely on channel behaviour and are not ideal for multipath environments. Most popular pilot aided methods estimate STO by searching for two same halves, which present in training signal [14]. However this metric has a plateau shape which causes large STO varience. STO estimation can be further improved by considering different metrics as proposed in [15,16,17]. A similar extensions to GFDM systems are presented in [18, 19], highlighting the performance degradation than traditional OFDM systems [20].
We have implemented the GFDM in perspective PAPR and channel estimation in our previous work [21] where OOB emissions are not given importance. In general, all the mentioned synchronization techniques use rectangle pulse shaping filter for pilot preamble which create non negligible OOB radiations. Further, employing rectangular filtering for standard IEEE 802.11 preamble with multiple identical data leads to spikes and slow decaying of side lobes which in turn leads to destruction of the advantage of GFDM. To circumvent this problem, in this paper the data aided synchronization is performed after limiting the pilot preamble with an arbitrary pulse shape. The main contribution of this paper is deriving an ML estimation algorithm for time and frequency offset estimation for any number of sets of identical data for the preamble after employing pulse shaping. The Cramer–Rao lower bound (CRLB) for CFO is derived and the influence of choice of filters on it is discussed. We conclude that the usage of pulses like Tukey will improve the crucial spectral response with a little increment in estimation error. Another vital contribution is, prototyping GFDM system model for real time environment employing universal software radio peripheral (USRP) as transmitting hardware which is driven by LABVIEW software. Widely accepted IEEE 802.11 short preamble is utilized for adjusting the misalignments which occur due to indoor channel variations. It will be proved in real time results that the suggested procedure provides smooth transitions in the received spectral response.
This paper is organized as follows: Sect. 2 emphasizes on GFDM system model. Section 3 presents the ML algorithm for time and frequency adjustments for the pulse shaped preamble. In Sect. 4, the derivation for CRLB on CFO estimation for an arbitrary pulse shape is performed. Section 5 briefly describes the performance analysis with the modified preamble in simulations and real time environments and finally, Sect. 6 concludes the paper.
2 System Model
GFDM system is a block structured modulation scheme with K subcarriers and M subsymbols in one complete block of length \(N=MK\). The independently generated quadrature amplitude modulation (QAM) data symbols which are to be modulated are represented with \(d_k(m)\), where \(m=0, 1, \ldots M-1\) and \(k=0, 1~ \ldots K-1\) are the indexes corresponding to subsymbol and subcarrier. It is important to note that each subcarrier bears \(d_k=[d_k(0), d_k(1) \ldots d_k(M-1)]\) symbols along its time axis. To perform GFDM modulation, data on every subcarrier is upsampled by an amount of K.
The obtained upsampled data \(p_k=[p_k(0), p_k(1) \ldots p_k(MK-1)]\) is circularly convolved with prototype filter g(n) of length MK to eliminate OOB noise. Finally, summation is performed along the subcarrier index after up converting to corresponding subcarrier frequency to obtain GFDM signal x(n) [22].
Here \(\circledast \) corresponds to the circular convolution operation and the value of \(n =0, 1, \ldots MK-1\). Due to the flexible nature of GFDM system, it simulates the behaviour of pulseshaped OFDM system if \(M =1\) and reduces to SC-FDE when \(K=1\). The choice of filter g(n) and its design strongly influences the error rate and spectral behaviour of the system. In this work, we used root raised cosine (RRC) protyping filter exclusively on GFDM symbol for limiting OOB emissions. On the preamble, both Tukey pulse and well known rectangular pulse are used and their performance has been compared. It has been proved that usage of Tukey filter is showing a better spectral response over rectangular filter with a little compromise on the error floor. The detail description and Meyer auxiliary functions used for generation of filter coefficients can be found in [22]. RRC filters can be characterised by Meyer auxiliary function in its simplified form as,
The auxiliary function \(f(\beta )\) is defined on \(\beta =k/{\alpha K}\) which is used to describe the roll off region by varying \(\alpha \) in frequency domain. Here \(\alpha \) can be seen as a measure of overlap for \(k^{th}\) sub carrier centred around the normalised frequency k/K. The mathematical formulation for the truncated Meyer auxiliary function is [22]
This function is used for RRC pulse generation because of its excellent spectral properties. Alternate matrix representation for GFDM system presented in [23] is given by,
The matrix \(\textbf{A}\) is modulation matrix of size \(N \times N\) representing all the necessary signal processing operations. The data vector \(\textbf{d}= [d_0(0) \ldots d_0(M-1) \ldots d_{K-1}(M-1)]^T\) consists of all the QAM modulated data symbols. Here, T in superscript represents the transpose of a matrix.
3 Maximum Likelihood Estimation
The standard IEEE 802.11 preamble will consist of ten identical symbols which are of short length of 16 and two long symbols. The short symbols are utilized for symbol synchronization and long symbols are used for channel estimation. The traditional and the Tukey pulse shaped preamble with ten short symbols are shown in the Fig. 1. We can clearly observe the suggested modified preamble in frequency domain is having a less amplitude at its start and end. This is the primary reason of reduction of OOB emission in the spectral response of the GFDM system which will discussed in result section. In this section. ML algorithm is derived assuming a non-dispersive channel with AWGN nature for simplicity. An extension for dispersive channels can be done by replacing the \(\textbf{A}\) with \(\textbf{HA}\) in the process of obtaining GFDM signal \(\textbf{x}\) where \(\textbf{H}\) represents the block circulant matrix [21]. The signal model with perfect channel estimation can be given as,
The pilot preamble inserted is at the start of the data packet as shown in Fig. 1, will be utilized to perform ML estimation. The preamble of the received signal r(n) is anticipated to have the pilot preamble which consists of contiguous samples with \(N_p\) sets of identical data of size L. Let the set of data \(I^i=\left\{ \theta +iL\ldots \theta +(i+1)L \right\} \) symbolize all sets of identical data in the pilot preamble which can be indexed with \(I^i, i=0,1,\ldots N_p-1\). To safeguard the spectral advantage, all these sets of data are pulse shaped before transmission. An important note is that even after pulse shaping the samples in \(N_p\) sets i.e., \(r(k), k \in \cup _{i=0}^{N_p-1}I^i \) are pairwise correlated. This is because we have used the same pulse shape filter for all identical parts of the preamble. Then these pulse shaped samples are assembled into a \(L \times 1 \) vector \(\textbf{r}\), defined as \(\textbf{r}=[r(1) ~ r(2) \ldots r(L)]^T\). Hence for \(m,n \in [0, N_p-1]\) and \(m\ge n \) we obtain
In (7), \(\textbf{E}[.]\) represents the expectation operator. So, \(\sigma _s^2 = \textbf{E}[x^2(k)]\) and \(\sigma _n^2 = \textbf{E}[w^2(k)]\) denotes the signal and noise power respectively. \(\sigma _g^2\) represents the energy of pulse shaping filter and \(\epsilon ^{'}=2\pi L \epsilon /N\) is the CFO corresponding to the set \(I^0\). The log likelihood function \(\Lambda (\theta ,\epsilon )\) is expressed as logarithm of the probability density function (PDF) \( f(\textbf{r}|\theta ,\epsilon ) \) with conditioned variables \(\theta \) and \(\epsilon \), since they have to be estimated. The PDF of L observed samples of \(\textbf{r}\) with above conditions can be represented as,
Here the conditioned variables \(\theta \) and \(\epsilon \) are dropped for simplicity. For every k we assume f(r(k)) is one dimensional Gaussian random variable with zero mean, its PDF will be of the form,
In (8), the denominator is multiplication of \(N_p\) complex Gaussian PDF which will be simplified into,
where \(\textbf{z}(k)=[r(k) ~ r(k+L) \ldots ~ r(k+(N_p-1)L)]^T\). The numerator in (8) can be expressed as joint PDF of \(f(\textbf{z}(k))\) given by
where \(\textbf{R}\) denotes the correlation matrix. Then the expectation of \(\textbf{z}\) using (7) will be resulted into,
where I and \(\eta =\sigma _n^2/\sigma _g^2 \) in (11) represents the identity matrix and the ratio of noise power to energy of the pulse shaping filter respectively. The value of normalized \(\sigma _g^2\) is unity for rectangular filter but in the case of other filters its value deteriorates. So, the ratio \(\eta \) is the measure of increase in noise power because of pulse shaping. The vector \(\textbf{q}=[1,e^{j\epsilon ^{'}},\ldots e^{(N_p-1)\epsilon ^{'}}]\) separates the effect of \(\epsilon ^{'}\) for the defined set. The determinant of the matrix \(\textrm{det}(\textbf{R})\) can be obtained as \((\sigma _g^2)^{N_p}\left( \eta ^{N_p}+ N_p \eta ^ {N_p-1} \sigma _s^2 \right) \). Then inverse of the matrix obtained after utilization of lemma proposed in [24] is given by
Then Joint PDF after substituting (12) into (10) results into
By simple manipulation we can solve
where \(\gamma \) is the correlation coefficient given by \(\gamma _m(k)= \sum _{p=m} ^{N_p-1} r(k+(p-m)L)r^*(k+pL)\). Here subscript \(*\) denotes complex conjugate operation and \(\textrm{Re}\) is the real part of the complex number. The log likelihood function becomes,
By simple manipulations the \(\Lambda (\theta ,\epsilon )\) value can be simplified as below,
where \(c_1= \frac{\left( \eta +\sigma _s^2\right) ^{N_p}}{ \eta ^{N_p-1}\left( \eta +N_p\sigma _s^2\right) } \), \(c_2=\frac{ \sigma _s^2}{\sigma _g^2 \eta \left( \eta +N_p\sigma _s^2\right) }\) and \(c_3 =\frac{(N_p-1)\sigma _s^4}{\eta \sigma _g^2 \left( \eta +N_p\sigma _s^2\right) \left( \eta +\sigma _s^2\right) }\). The first term and last term are not considered for estimation since they are independent of \(\theta \) and \(\epsilon \). Then ML estimate results into
The above Eq. (17) is obtained after neglecting the positive multiplication constants and \(\rho =\sigma _s^2/(\sigma _s^2+\eta )\). However, we can observe from (17) that, the estimation is done using ML detection will require \(N_p^2L^3\) multiplication. In the first step the STO is estimated as,
Here, the obtained STO \(\hat{\theta }\) can be used to estimate the CFO \(\epsilon \). The proposed ML algorithm presumes that the CFO estimate makes \(\angle \left[ \sum _{\hat{\theta }}^{\hat{\theta }+L-1} \gamma _m(k)\right] + m \epsilon ^{\prime} =0\) for \(m=1,\ldots N_p-1\) where \(\angle \) represents the angle. Therefore, we can alternatively find the estimate of CFO for a index m as,
All the \(N_p-1\) estimates obtained by varying \(m=1,\ldots N_p-1\) we can find the final estimated CFO can be obtained as,
By simplifying using (20) will require \(N_p^2L^2\) multiplication and thus will result in low complexity.
4 Cramer Rao Lower Bound
In this section CRLB for unbiased CFO estimaion is derived considering STO as a priori. CRLB is defined as sharpness of estimating the unknown parameter. To quantify mathematically we have to determine the peak of the negative second derivative of likelihood function. So, CRLB is
By performing second derivative we obtain
Substituting the constant \(c_2\) as we computed in the previous section into (22) yields
By expansion of the summation in (23) the second derivative will be simplified into
Finally, the CRLB can be given by
The following conclusions can be made after observing the bound:
-
As the energy of the pulse shape filter in the symbol interval decrease we observe raise in \(\eta \) value which inturn increase the bound value. It indirectly inference the increase in the error floor.
-
When data samples in each set or number of sets used i.e., when L, \(N_p\) increase the bound is going to decrease. It is to be remembered that the increase of number of sets requires a trade off in data efficiency.
-
Presence of Multiple sets in the preamble will offer an advantage of increase in range of CFO estimation at the cost of bit error rate (BER) (Fig. 2).
5 Results
This paper validates real time implementation of the GFDM system in indoor room environment using IEEE 802.11 short preamble by employing pulse shaping. For demonstration, the hardware platform used is NI USRP 2953R which is interfaced with LABVIEW software of NI. USRP is capable of operating in frequency range of 1.2–6 GHz with a bandwidth of 120 MHz. These configurations enable us to test all waveform used in today’s mobile communication. PC shown in the Fig. 3 is connected to USRP using a NI PXIe-PCIe8371 which is having a high throughput of 832 MB/sec. The real time demonstrator is having two USRP terminals, one acting as transmitter and other as receiver. Both USRP’s are connected to workstations for baseband processing. Parameters used for demonstration are tabulated in Table 1. The transmitter USRP acquires digital IQ samples via PCIExpress card which performs digital to analog conversion and transmits over air. In receiver, IQ samples captured by USRP are passed to the host PC using another PCI-Express connection for performing baseband operations. Since USRP performs principal operations like decimation, up and down frequency conversion etc in hardware it exhibits real time communication scenario. It is to be noted that after performing all signal processing operations on GFDM symbol, a zero padding sequence of length 8 is added at the start and at the end to a complete packet.
This is done inorder to differentiate the received signals in time. After performing all the required base band operations, RF up-conversion is done and transmitted over the air using the transmit antenna. Initially, based on the simulation parameters which are tabulated in Table 1, the mean square error (MSE) versus SNR analysis for CFO and STO over AWGN as well as dispersive channel conditions for various pulse shaping filters are presented. The choosen dispersive channel is rayleigh with 8 taps linearly varying from 0 to −8 dB.
Figure 4, illustrates the MSE vs SNR of CFO over AWGN and dispersive channel. For pulse shaping, two types of filters are employed namely Rectangular and Tukey. From the figure it is evident that as the SNR increases, a better probability of error is attained for all the cases. The theoretical analysis carried out in Section IV for CRLB is plotted against SNR. It can be viewed that at an SNR of 10 dB, the observed error floor is \(1.7\times 10^{-5}\). Without loss of generality, the bound is plotted by considering the rectangular pulse shape filter. It is obvious that, both the pulse shaping filters yield good performance over AWGN channel. There is a slight degradation in performance over dispersive channel conditions. Over AWGN channel, at an SNR of 10 dB, Rectangular filter attains a MSE of \(2.61\times 10^{-5}\) while Tukey filter has MSE of \(5.87\times 10^{-5}\). In case of dispersive channel environment, the performance deteriorates for Tukey pulse shaping filter when compared with Rectangular pulse shaping filter. This is clearly observed because at an SNR of 10 dB, Tukey attains an error of \(1.28\times 10^{-4}\) while Rectangular achieves \(3.2\times 10^{5}\). The reason behind the accuracy of the result is that among received preamble set, it is easy to prove that the product \( r(k+(p-m)L)r^*(k+pL)\) in (22) results into continuous summation of constant multiplying random variables which follow chi-square distribution with two degrees of freedom and three zero mean Gaussian random variables. So, with the increase in number of preamble data, the real and imaginary part of \( \gamma _m(k)\) by statistical properties converge to \(\textrm{sin}(2\pi m \epsilon ^{'})\) and \(\textrm{cos}(2\pi m \epsilon ^{'})\) receptively. So, at a consistent time offset estimation, varience of each term converges to zero indicating the best possible accuracy for CFO estimation for the proposed scheme.
The MSE for STO vs SNR for both the pulse shaping filters namely Rectangular and Tukey over AWGN as well as dispersive channel is depicted in Fig. 5. Here, it can be observed that a huge amount of error is obtained when Tukey pulse shaping is employed over dispersive channel environment. At an SNR of 5 dB the observed error is 0.22546 while the error decreases progressively as the SNR increases. At an SNR of 10 dB the error attained for Rectangular and Tukey filer is 0.0193286 and 0.0634 respectively over dispersive channel. However, the performance is improved over AWGN channel for both the pulse shaping filters. The peak of likelihood function is broadened by the channel dispersion for multipath environments. This results in high error floor of STO estimation at low SNR.
For the purpose of comparison we considered [18], where the authors have derived the ML estimate for estimating CFO and STO using the available CP. From the simulation results shown in Figs. 6 and 7 it can evidenced that, the aforementioned method results in high error floor when compared with the proposed method. Another interesting aspect to note is that, even though Tukey pulse results in considerable error floor when compared with Rectangular pulse but yields a better performance than the method proposed in [18]. However, the better results are obtained at the cost of data efficiency for the proposed method. Therefore, we can conclude that the block structure of GFDM data is not suitable for direct application of CP-based synchronization.
The usage of tukey filter resulted in high MSE than the traditional rectangular filter because of increase in the value of \(\eta \) as evidenced from Figs. 4 and 5. The exact advantage of using this filter can be depicted in the spectral response of real time results. The IEEE 802.11a standard preamble consists of ten short symbols and two long symbols which are identical with each other. For demonstration simplicity, we have used 10 repeated short symbols for time and frequency estimation. The data is transmitted in IQ representation, but the Quadrature phase data is only shown since it provides enough interpretation. Each short symbol in the preamble extends to a duration 4 micro seconds and hence consists of 16 samples. High amplitude in the data packet occurs because of this preamble as depicted in Fig. 8. For the proposed preamble, each 16 length short sequence is windowed by generating a tukey filter with ramp up and down of 2 bits. The repetition in preamble enables us to enhance the CFO estimation range later in the receiver. The discontinuities in the amplitude of the Quadrature signal in Fig. 8 occurs because of circular prototyping. The advantage of this representation lies in reduction of the energy spending required by the USRP terminal.
The received spectrum is depicted in Fig. 9 where a minimum OOB radiation of \(-46\) dB has been observed. This is achieved because of localization of time and frequency using a prototype filter. So, at every subcarrier we could get reduction in egress noise which was the major concern in OFDM systems. Since we are presenting real time results a more realistic spectrum is shown in Fig. 9. This spectrum is obtained after adding rectangular pulse shaped preamble of length 160 to the GFDM symbol. The zigzag nature of spectrum occurs because of addition of noise. We also observe spikes in the spectrum due to the rectangular filtering of preamble, decreasing its reliability in scrambled spectrum applications. In this figure, half of the subcarriers are disabled intentionally to illustrate the difference in OOB emissions between the conventional and proposed preamble. Figure 10, clearly shows the advantage of enforcing the Tukey pulse shaping in GFDM system. Though there are little spikes but the maximum amplitude of spikes is decreased from −26 to −35 dB. A relatively sharp decay in side lobes is observed due to incorporation of pulse shaping in preamble which in turn leads to reduction of OOB emission. Hence, the advantage of GFDM is maintained.
The observed experimental values in indoor environments are tabulated below in Table 2. Energy detection method incorporated in the receiver not only estimates the the data packet along with misalignments which arises due to channel delay but also includes the time lag introduced by pulse shaping and matched filtering as shown in Fig. 1. The Fig. 8, shows the received IQ signal and its corresponding spectrum is shown in Fig. 10 where both are diminished in amplitude, distorted in time and frequency. These impairments occur due to indoor channel environments. The spectrum after enforcing synchronization algorithms which suggest that the system performance is not destroyed by adding pulse shape to the preamble. GFDM combats the real time environments similar to OFDM despite of its non orthogonal nature. An important point to be observed is that there is a lag in the captured IQ signal by USRP. Indirectly it is a measure of transfer capability, so one wants it to be as minimum as possible. In this regard, we were able to capture the GFDM signal along with the pulse shaped preamble at a value of 3.5 ms as shown in Fig. 8. Lag in the IQ received signal is not only because of transmission wait but also real time processing delay of USRP hardware.
6 Conclusion
In this paper, ML estimation algorithm using pulse shaped multiple sets of identical data for correcting the time and frequency misalignments for GFDM systems is derived. This is done to preserve the spectral advantage of the system. The CRLB for the frequency offset for an arbitrary pulse shape is also obtained. Simulations results obtained by modifying the preamble data in IEEE 802.11a standard, prove a little error floor due to noise enhancement in AWGN and multipath channels. The main advantage of this modified preamble occur in the real time results by reduction of slope and unwanted spikes in the spectrum characteristics. Therefore, the method proposed in this paper can be employed for the modern 5G communication systems.
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Kumar, R. A., & Prasad, K. S. (2021). Performance analysis of GFDM modulation in heterogeneous network for 5G NR. Wireless Personal Communications, 116(3), 2299–2319.
Telagam, N., Lakshmi, S., & Kandasamy, N. (2021). Performance analysis of parallel concatenation of LDPC Coded SISO-GFDM system for distinctive pulse shaping filters using USRP 2901 device and its application to WiMAX. Wireless Personal Communications, 121(4), 3085–3123.
Bandari, S. K., Vakamulla, V. M., & Drosopoulos, A. (2017). PAPR analysis of wavelet based multitaper GFDM system. AEU - International Journal of Electronics and Communications, 76, 166–174.
Chang, Y.-K., & Ueng, F.-B. (2018). A novel turbo GFDM-IM receiver for MIMO communications. AEU - International Journal of Electronics and Communications, 87, 22–32.
Farhang-Boroujeny, B., & Moradi, H. (2016). OFDM inspired waveforms for 5G. IEEE Communications Surveys Tutorials, 18(4), 2474–2492.
Charrada, A., & Samet, A. (2012). Estimation of highly selective channels for OFDM system by complex least squares support vector machines. AEU - International Journal of Electronics and Communications, 66(8), 687–692.
Fettweis, G., Krondorf, M., & Bittner, S. (2009). GFDM–generalized frequency division multiplexing. In VTC Spring 2009—IEEE 69th Vehicular Technology Conference, pp. 1–4.
Bandari, S. K., Vakamulla, V. M., & Drosopoulos, A. (2018). GFDM/OQAM performance analysis under Nakagami fading channels. Physical Communication, 26, 162–169.
Datta, R., Michailow, N., Lentmaier, M., & Fettweis, G. (2012). GFDM interference cancellation for flexible cognitive radio PHY design. In 2012 IEEE Vehicular Technology Conference (VTC Fall), pp. 1–5.
Bandari, S. K., Mani, V. V., & Drosopoulos, A. (2016). Multi-taper implementation of GFDM. In 2016 IEEE Wireless Communications and Networking Conference, pp. 1–5.
Baas, N. J., & Taylor, D. P. (2004). Pulse shaping for wireless communication over time or frequency-selective channels. IEEE Transactions on Communications, 52(9), 1477–1479.
O’Donnell, R. (2007). Prolog to synchronization techniques for orthogonal frequency division multiple access (OFDMA): A tutorial review. Proceedings of the IEEE, 95(7), 1392–1393.
van de Beek, J. J., Sandell, M., & Borjesson, P. O. (1997). ML estimation of time and frequency offset in OFDM systems. IEEE Transactions on Signal Processing, 45(7), 1800–1805.
Schmidl, T. M., & Cox, D. C. (1997). Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications, 45(12), 1613–1621.
Park, B., Cheon, H., Kang, C., & Hong, D. (2003). A novel timing estimation method for OFDM systems. IEEE Communications Letters, 7(5), 239–241.
Minn, H., Bhargava, V. K., & Letaief, K. B. (2003). A robust timing and frequency synchronization for OFDM systems. IEEE Transactions on Wireless Communications, 2(4), 822–839.
Mohammadi-Siahboomi, J., Omidi, M. J., & Saeedi-Sourck, H. (2016). Low-complexity CFO compensation technique for interleaved OFDMA system uplink. AEU - International Journal of Electronics and Communications, 70(5), 718–726.
Wang, P. S., & Lin, D. W. (2016). Maximum-likelihood blind synchronization for GFDM systems. IEEE Signal Processing Letters, 23(6), 790–794.
Gaspar, I., Festag, A., & Fettweis, G. (2015). Synchronization using a pseudo-circular preamble for generalized frequency division multiplexing in vehicular communication. In 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), pp. 1–5.
Lim, B., & Ko, Y. C. (2017). SIR analysis of OFDM and GFDM waveforms with timing offset, CFO, and phase noise. IEEE Transactions on Wireless Communications, 16(10), 6979–6990.
Valluri, S., & Mani, V. V. (2018). Joint channel mitigation and side information estimation for GFDM systems in indoor environments. AEU - International Journal of Electronics and Communications, 95, 146–154.
Michailow, N., Matthé, M., Gaspar, I. S., Caldevilla, A. N., Mendes, L. L., Festag, A., & Fettweis, G. (2014). Generalized frequency division multiplexing for 5th generation cellular networks. IEEE Transactions on Communications, 62(9), 3045–3061.
Farhang, A., Marchetti, N., & Doyle, L. E. (2016). Low-complexity modem design for GFDM. IEEE Transactions on Signal Processing, 64(6), 1507–1518.
Golub, G. H., & Van Loan, C. F. (1989). Matrix computations (2nd ed.). Johns Hopkins University Press.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that the manuscript is original, has not been published before and is not currently being considered for publication elsewhere. We know of no Conflict of interest associated with this publication, and there has been no significant financial support for this work that could have influence this outcome. As a corresponding author, I confirm that the manuscript has been read and approved for submission by all the named authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Siva Prasad, V., Mani Vakamulla, V. & Gunturu, C. Implementation of GFDM System Using USRP. Wireless Pers Commun 137, 1979–1996 (2024). https://doi.org/10.1007/s11277-024-11329-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-024-11329-3