1 Introduction

Multiuser multiple-input multiple-output (MU-MIMO) structures attract much attention from the wireless communication research area, because of their promising improvement in terms of spatial diversity, multiplexing gain, and high spectral efficiency [1]. The characteristics possessed by MU-MIMO techniques, which can increase the data rate, degrees of freedom, and connecting reliabilities of wireless communication systems [2]. Let the MIMO techniques become the essential parts of several foremost communication standards [3], for example, LTE, WiMAX, and IEEE 802.11ac, etc. In addition, the MIMO structure enables massive configurations of antennas to meet the needs of 5G communication systems. Linear precoding technology has been widely used in 4G and the design of transmitters of the MU-MIMO communication in 5G mobile communication systems [4]. The sum-rate capacity of the broadcast channels can be achieved when the MU-MIMO system with space division multiple access (SDMA) techniques has been adopted. Meanwhile, the usages of the multiuser diversity and beforehand multiuser interference eliminating planning on transmitter can improve the system capacities [5, 6].

The MU-MIMO technique utilizes precoding to eliminate the co-channel interference (CCI) beforehand and simplify the complexities of receivers significantly. It is proved that when the knowledge of interferences has been equipped on transmitters beforehand, optimal precoding can be designed for interference compensation based on the theorem of the dirty paper coding (DPC) [7] at the Gaussian MIMO broadcast channel. The channel inversion method adopted some conventional MIMO detecting criteria, for example, zero-forcing (ZF) [8] and minimum mean squared error (MMSE) [9]. The ZF precoding method applied in the transmitter can depress CCI completely, however, the un-normalized precoding vector could magnify noise. It is noted that the MMSE performs better than the ZF. Although the MMSE-based channel inversion method weighs the impact between noise and CCI, the MMSE still cannot achieve good performance. For the purpose to obtain the greatest precoding gain, the singular value decomposition (SVD) [10] has been applied on the channel matrix and exploits the right-singular vectors that corresponding to the maximum singular values to process precoding for good performance.

To enhance the estimate accuracy of the precoding matrix for increasing system capacity, heuristic evolution algorithms have been adopted to deal with many complex optimization tasks. Particle swarm optimization (PSO) [11] is a random global optimization algorithm that simulates the behaviors of a flock of birds. The PSO algorithm is easy to implement and highly computationally efficient due to its low demand for memory and CPU resources. In this paper, the PSO algorithm has been introduced to the precoding design of the MU-MIMO system to conduct optimal searching for maximizing the objective function based on signal to interference plus noise ratio (SINR) to inhibit CCI and increase MU-MIMO system capacity, and the PSO-searching based (PSB) precoder and the improved PSB (IPSB) precoder have been proposed. First, we adopt the PSO algorithm according to the objective function to search for optimal linear precoding vectors. In comparison with SVD precoder and other conventional linear precoders, the system capacity of the MU-MIMO communication system with the proposed PSB precoder is significantly superior to the others. Secondly, this paper also adopted adaptive multiple inertia weights based on the deviation between the current particle position and the optimal global position of the objective function to dynamically calculate the values of inertia weight according to the searching abilities of the particles individually. The IPSB precoder lets every particle can obtain appropriate inertia weights along each dimension of the search space at each searching iteration. According to the situations of each particle, the IPSB precoder utilizes a simple and effective measurement to indicate whether each particle lacks global exploration ability in each dimension, and the fine strategy of dynamically adjusting inertia weights can be built and the promising system capacity can be achieved.

The paper has been organized as follows. Section 2 describes signal model, SVD precoder, and problem formulation. Section 3 presents the PSB precoder and IPSB precoder. Simulation results are given in Sects. 4 and 5 concludes the paper.

2 Signal Model and Problem Formulation

2.1 Signal Model

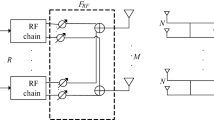
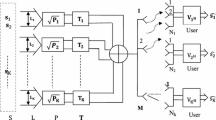
Consider a downlink channel of a MU-MIMO communication system with \(K\) users. The number of transmitting antennas of base station (BS) is denoted by \(M_{T}\), and the number of the receiving antennas of MS for the \(k{\text{th}}\) user is represented as \(M_{{R_{k} }}\), \(k = 1,2, \ldots ,K\). Then, the total receiving antennas of all users is \(M_{R} = \sum\nolimits_{k = 1}^{K} {M_{{R_{k} }} }\). The related system block diagram shows in Fig. 1. The deployment of antennas of the system is described as \(\{M_{{R_{1} }} ,M_{{R_{2} }} ,...,M_{{R_{K} }} \} \times M_{T}\), and the channel is modeled as a Rayleigh fading channel. The MIMO channel of the \(k{\text{th}}\) user is described as \({\mathbf{H}}_{k} \in {\mathbb{C}}^{{M_{{R_{k} }} \times M_{T} }}\), and the entire channel response matrix \({\mathbf{H}}\) can be represented as

$${\mathbf{H}} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}_{1}^{T} } & {{\mathbf{H}}_{2}^{T} } & \cdots & {{\mathbf{H}}_{K}^{T} } \\ \end{array} } \right]^{T} \in {\mathbb{C}}^{{M_{R} \times M_{T} }}$$
(1)

where \(( \bullet )^{T}\) is denoted as the transpose of vector or matrix. The data vector of the \(k{\text{th}}\) user is represented as \({\mathbf{x}}_{k} \in {\mathbb{C}}^{{r_{k} \times 1}}\), and the stack of data vector is \({\mathbf{x}} = [{\mathbf{x}}_{1}^{T} \, {\mathbf{x}}_{2}^{T} \, \cdots \, {\mathbf{x}}_{K}^{T} ]^{T}\). Then, the receiving data vector of the system is given by

$${\mathbf{y}} = {\mathbf{G}}({\mathbf{HWx}} + {\mathbf{n}})$$
(2)

where \({\mathbf{y}} = [{\mathbf{y}}_{1}^{T} \, {\mathbf{y}}_{2}^{T} \, \cdots \, {\mathbf{y}}_{K}^{T} ]^{T} \in {\mathbb{C}}^{r \times 1}\) is the receiving data vector and \({\mathbf{n}} = [{\mathbf{n}}_{1}^{T} \, {\mathbf{n}}_{2}^{T} \, \cdots \, {\mathbf{n}}_{K}^{T} ]^{T}\) is the vector stack of the observed spatially and temporally white additive Gaussian noise with zero mean and variance \(\sigma_{n}^{2}\). The total number of the data streams is represented as \(r = \sum\nolimits_{k = 1}^{K} {r_{k} } \le rank({\mathbf{H}}{)} \le \min (M_{R} ,M_{T} )\), where \(r_{k}\) is the number of data streams of the \(k{\text{th}}\) user. The precoding matrix and linear receiver are denoted by \({\mathbf{W}}\) and \({\mathbf{G}}\), respectively. The precoding matrix \({\mathbf{W}}\) of the transmitter is defined as

$${\mathbf{W}} = [{\mathbf{W}}_{1} \, {\mathbf{W}}_{2} \, \cdots \, {\mathbf{W}}_{K} ]^{T} \in {\mathbb{C}}^{{M_{T} \times r}}$$
(3)

where \({\mathbf{W}}_{k} \in {\mathbb{C}}^{{M_{T} \times r_{k} }}\) is the precoding matrix of the \(k{\text{th}}\) user.

Fig. 1
figure 1

Downlink system block diagram of MU-MIMO communication system

Full size image

The decoding matrix \({\mathbf{G}}\) of linear receiver can be represented as

$${\mathbf{G}} = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{1} } & \cdots & \cdots & 0 \\ \vdots & {{\mathbf{G}}_{2} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\mathbf{G}}_{K} } \\ \end{array} } \right]$$
(4)

where \({\mathbf{G}}_{k} \in {\mathbb{C}}^{{r_{k} \times M_{{R_{k} }} }}\) is the decoding matrix of the \(k{\text{th}}\) user. The linear receiver \({\mathbf{G}}_{k}\) has been used to detect the transmitted signal of the \(k{\text{th}}\) user, and the detected signal is given by

$${\mathbf{s}}_{k} = {\mathbf{G}}_{k} {\mathbf{y}}_{k}$$
(5)

The linear receiver \({\mathbf{G}}_{k} \in {\mathbb{C}}^{{r_{k} \times M_{{R_{k} }} }}\) can be designed via ZF or MMSE criteria. To simplify the analysis, assume that the power distribution is \(\beta = {{p_{k} } \mathord{\left/ {\vphantom {{p_{k} } {\sigma_{n}^{2} }}} \right. \kern-0pt} {\sigma_{n}^{2} }} = {{p_{0} } \mathord{\left/ {\vphantom {{p_{0} } {K\sigma_{n}^{2} }}} \right. \kern-0pt} {K\sigma_{n}^{2} }}\), such that the linear receiver can be represented as

$${\mathbf{G}}_{k} = {\mathbf{P}}_{k}^{H} ({\overline{\mathbf{H}}}_{k} {\overline{\mathbf{H}}}_{k}^{H} + \beta {\mathbf{I}}_{{M_{{R_{k} }} }} )^{ - 1}$$
(6)

where \({\overline{\mathbf{H}}}_{k} = {\mathbf{H}}_{k} {\mathbf{W}}_{k}\), \(( \cdot )^{ - 1}\) denotes the matrix inversion, and \(( \cdot )^{H}\) represents the complex conjugate transpose of matrix. \({\mathbf{I}}_{{M_{{R_{k} }} }}\) is the \(M_{{R_{k} }} \times M_{{R_{k} }}\) identity matrix and \({\mathbf{P}}_{k} = [{\mathbf{H}}_{k} {\mathbf{W}}_{k} ]_{{(r_{k} )}} = [{\overline{\mathbf{H}}}_{k} ]_{{(r_{k} )}}\), where \([ \cdot ]_{{(r_{k} )}}\) represents the \(r_{k}\) column vectors of the matrix. The SINR of the \(k{\text{th}}\) user obtained from linear detection is calculated as

$$\begin{aligned} {\text{SINR}}_{k} &= \frac{{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{k} {||}_{2}^{2} }}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{i} {||}_{2}^{2} } + {||}{\mathbf{G}}_{k} {||}_{2}^{2} }} \hfill \\ &= \frac{{{{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{k} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{k} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}}}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {{{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{i} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{i} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} { + }1}} \hfill \\ \end{aligned}$$
(7)

where \({|| } \bullet { ||}_{2}^{2}\) denotes vector norm, and the matrix \({\mathbf{W}}_{k}\) has to perform normalization to prevent the noise of precoding vector in the receiver has been enlarged. The perfect estimated propagation channel matrix \({\mathbf{H}}_{k}\) leads to the ideal precoder matrix \({\mathbf{W}}_{k}\) that can be obtained. Meanwhile, the maximum SINR can be reached. In the time-division-duplex (TDD) system, due to the reciprocity principle, the channel estimation of uplink can be applied in the down-link transmission to proceed the joint precoding for all user in BS.

2.2 The SVD Precoder

Assume the MIMO channel matrix \({\mathbf{H}}_{k}\) (\(k = 1,2, \ldots ,K\)) is available and perfectly estimated in BS. It can be realized through the property of the reciprocity principle of the TDD model or the feedback of the frequency-division-duplex (FDD) model. So that, the channel matrix \({\mathbf{H}}_{k}\) of the \(k{\text{th}}\) receiver is known via channel estimation. Under the circumstances of equal power distribution, the optimal power distribution can be realized via the water-filling (WP) algorithm [12] according to the SINR of each user. The MIMO channel of the \(k{\text{th}}\) user can be decomposed by SVD as

$${\mathbf{H}}_{k} = {\mathbf{U}}_{k} {{\varvec{\Sigma}}}_{k} {\mathbf{V}}_{k}^{H}$$
(8)

where the matrix \({\mathbf{U}}_{k} \in {\mathbb{C}}^{{M_{{R_{k} }} \times M_{{R_{k} }} }}\) is formed by left singular vectors, the singular value matrix \({{\varvec{\Sigma}}}_{k} \in {\mathbb{C}}^{{M_{{R_{k} }} \times M_{T} }}\), and the matrix \({\mathbf{V}}_{k} \in {\mathbb{C}}^{{M_{T} \times M_{T} }}\) is formed by right singular vectors. If the matrix \({\mathbf{F}}_{{SVD,a_{k} }} = [{\mathbf{V}}_{k} ]_{{(r_{k} )}}\) applied as the precoding vectors of the \(k{\text{th}}\) user, then the greatest precoding gain \({||}{\mathbf{H}}_{k} {\mathbf{W}}_{SVD,k} {||}_{2} = {||}{\mathbf{H}}_{k} [{\mathbf{V}}_{k} ]_{{(r_{k} )}} {||}_{2}\) can be obtained, where \([{\mathbf{V}}_{k} ]_{{(r_{k} )}}\) represents the \(r_{k}\) column vectors corresponding to the \(r_{k}\) largest singular values. Such that, using the right singular vectors which corresponding to the largest singular values to proceed precoding is an idea to obtain fine performance. The design steps of MU-MIMO SVD precoder performs as follows:

  • Step 1. Estimate signal transmission channel \({\mathbf{H}}\).

  • Step 2. Extract the matrix \({\mathbf{H}}_{k}\) of each user from propagation channel matrix \({\mathbf{H}}\).

  • Step 3. Implement the SVD of \({\mathbf{H}}_{k} = {\mathbf{U}}_{k} {{\varvec{\Sigma}}}_{k} {\mathbf{V}}_{k}^{H}\), and let \({\mathbf{F}}_{{SVD,a_{k} }} = [{\mathbf{V}}_{k} ]_{{(r_{k} )}}\), where \({\mathbf{F}}_{{SVD,a_{k} }}\) is the precoding matrix of \(k{\text{th}}\) user, and \({\mathbf{F}}_{SVD,a} = {[}{\mathbf{F}}_{{SVD,a_{1} }} \, {\mathbf{F}}_{{SVD,a_{2} }} \, \cdots \, {\mathbf{F}}_{{SVD,a_{K} }} ] \in {\mathbb{C}}^{{M_{T} \times r}}\) (\(k = 1,2, \ldots ,K\)).

  • Step 4. Perform SVD of matrix \({\mathbf{H}}_{k} {\mathbf{F}}_{{SVD,a_{k} }} = {\tilde{\mathbf{U}}}_{k} {\tilde{\mathbf{\Sigma }}}_{k} {\tilde{\mathbf{V}}}_{k}^{H}\).

  • Step 5. Define diagonal matrix \({{\varvec{\Sigma}}}_{e} = \left[ {\begin{array}{*{20}c} {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{1}^{{(r_{1} )}} } & \cdots & \cdots & 0 \\ \vdots & {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{2}^{{(r_{2} )}} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{K}^{{(r_{K} )}} } \\ \end{array} } \right] \in {\mathbb{R}}^{r \times r}\), \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{k}^{{(r_{k} )}}\) represent the \(r_{k}\) largest singular values of the singular value matrix \({\tilde{\mathbf{\Sigma }}}_{k}\).

  • Step 6. Applied WP algorithm on matrix \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{k}^{{(r_{k} )}}\) to establish matrix \({\mathbf{D}}_{k}\), and implement \({\mathbf{F}}_{SVD,b} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{1} } & \cdots & \cdots & 0 \\ \vdots & {{\mathbf{D}}_{2} } & \vdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\mathbf{D}}_{K} } \\ \end{array} } \right] \in {\mathbb{C}}^{{M_{x} \times r}}\).

  • Step 7. Compute the MU-MIMO SVD precoding matrix \({\mathbf{W}}_{SVD} = \beta {\mathbf{F}}_{SVD,a} \cdot {\mathbf{F}}_{SVD,b}\).

The SINR of the \(k{\text{th}}\) user obtained from linear detection of MU-MIMO system with SVD precoder is given by

$$\begin{aligned} {\text{SINR}}_{SVD,k} &= \frac{{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{SVD,k} {||}_{2}^{2} }}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{SVD,i} {||}_{2}^{2} } + {||}{\mathbf{G}}_{k} {||}_{2}^{2} }} \hfill \\ & = \frac{{{{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{SVD,k} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{SVD,k} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}}}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {{{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{SVD,i} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\mathbf{H}}_{k} {\mathbf{W}}_{SVD,i} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} + 1}} \hfill \\ \end{aligned}$$
(9)

2.3 Problem Formulation

In the reality, the estimation errors of propagation channel are inevitable due to the reciprocity mismatch or delay, and the propagation channel \({\mathbf{H}}_{k}\) of the \(k{\text{th}}\) user can be modeled as \({\mathbf{H}}_{k} = {\hat{\mathbf{H}}}_{k} + {\mathbf{E}}_{k}\), where \({\mathbf{E}}_{k} \in {\mathbb{C}}^{{M_{{R_{k} }} \times M_{T} }}\) is the estimation error matrix which constructed by independent random Gaussian distribution elements with zero mean and variance \(\sigma_{e}^{2}\). The estimation of precoding matrix based on SVD using the estimated propagation channel \({\hat{\mathbf{H}}}_{k}\) denoted as \({\hat{\mathbf{W}}}_{SVD,k}\). The SINR of \(k{\text{th}}\) user with \({\hat{\mathbf{W}}}_{SVD,k}\) can be represented as follow:

$$\begin{aligned} {\text{SINR}}_{SVD,k} & = \frac{{{{\beta {||}{\mathbf{G}}_{k} ({\hat{\mathbf{H}}}_{k} + {\mathbf{E}}_{k} ){\hat{\mathbf{W}}}_{SVD,k} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} ({\hat{\mathbf{H}}}_{k} + {\mathbf{E}}_{k} ){\hat{\mathbf{W}}}_{SVD,k} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}}}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {{{\beta {||}{\mathbf{G}}_{k} ({\hat{\mathbf{H}}}_{k} + {\mathbf{E}}_{k} ){\hat{\mathbf{W}}}_{SVD,i} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} ({\hat{\mathbf{H}}}_{k} + {\mathbf{E}}_{k} ){\hat{\mathbf{W}}}_{SVD,i} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} + 1}} \\ & = \frac{{{{\beta {||}{\mathbf{G}}_{k} {\hat{\mathbf{H}}}_{k} {\hat{\mathbf{W}}}_{SVD,k} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\hat{\mathbf{H}}}_{k} {\hat{\mathbf{W}}}_{SVD,k} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}}}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {{{\beta {||}{\mathbf{G}}_{k} {\hat{\mathbf{H}}}_{k} {\hat{\mathbf{W}}}_{SVD,i} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\hat{\mathbf{H}}}_{k} {\hat{\mathbf{W}}}_{SVD,i} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} + 1}} + e_{k} \\ \end{aligned}$$
(10)

where

$$e_{k} = \frac{{{{\beta {||}{\mathbf{G}}_{k} {\mathbf{E}}_{k} {\hat{\mathbf{W}}}_{SVD,k} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\mathbf{E}}_{k} {\hat{\mathbf{W}}}_{SVD,k} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}}}{{\sum\limits_{{i = 1,i \notin (r_{k} )}}^{K} {{{\beta {||}{\mathbf{G}}_{k} {\mathbf{E}}_{k} {\hat{\mathbf{W}}}_{SVD,i} {||}_{2}^{2} } \mathord{\left/ {\vphantom {{\beta {||}{\mathbf{G}}_{k} {\mathbf{E}}_{k} {\hat{\mathbf{W}}}_{SVD,i} {||}_{2}^{2} } {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} \right. \kern-0pt} {{||}{\mathbf{G}}_{k} {||}_{2}^{2} }}} + 1}}$$
(11)

If apply \({\mathbf{W}}_{SVD} = \beta {\mathbf{F}}_{SVD,a} \cdot {\mathbf{F}}_{SVD,b}\) as precoding matrix to the \(k{\text{th}}\) user, the maximum precoding gain will be obtained and the CCI will reduced to zero, and the maximum SINR of the \(k{\text{th}}\) user can be reached after the MMSE detection has been proceeded. However, it is exited that the actual situation is the transmission channel of users is not orthogonal nor ill. In addition, if using the singular vectors of \({\hat{\mathbf{H}}}_{k}\) as the precoding matrix straightly, the performance will degrade due to the affection of the estimation error of the propagation channel of the \(k{\text{th}}\) user. Such that, the singular vectors are not suitable to adopt as precoding vectors. Suppose that the \({\mathbf{F}}_{{SVD,a_{k} }} \ne [{\mathbf{V}}_{k} ]_{{(r_{k} )}}\) has been applied as the precoding matrix for the \(k{\text{th}}\) user, the SINR of the \(k{\text{th}}\) user can be approximated as the simplified function

$$\begin{aligned} {\text{SINR}}_{SVD,k} & \approx \frac{{\beta {||}{{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} \xi_{k} {||}_{2}^{2} }}{{\sum\limits_{i = 1, \, i \ne k}^{K} {\beta {||}{{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} \rho_{i} {||}_{2}^{2} } + 1}} + e_{k} \\ & = \frac{{{||}({{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} )^{T} ({\hat{\mathbf{W}}}_{SVD,k}^{H} [{\mathbf{V}}_{k} ]_{{(r_{k} )}} ){||}_{2}^{2} }}{{\sum\limits_{i = 1, \, i \ne k}^{K} {{||}({{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} )^{T} ({\hat{\mathbf{W}}}_{SVD,k}^{H} [{\mathbf{V}}_{i} ]_{{(r_{i} )}} ){||}_{2}^{2} } + {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }}} + e_{k} \\ \end{aligned}$$
(12)

where \({{\varvec{\uplambda}}}^{{(r_{k} )\max }}\) denote the \(r_{k}\) largest singular values of \({\hat{\mathbf{H}}}_{k}\), \(\xi_{k} = {||}{\hat{\mathbf{W}}}_{SVD,k}^{H} [{\mathbf{V}}_{k} ]_{{(r_{k} )}} {||}_{2}^{2}\) can be the parameter of the measurement of the precoding gain, and \(\rho_{i} = {||}{\hat{\mathbf{W}}}_{SVD,k}^{H} [{\mathbf{V}}_{i} ]_{{(r_{i} )}} {||}_{2}^{2}\) (\(i = 1,2, \ldots ,K\) and \(i \ne k\)) is the measurable parameter of CCI.

In the study of the matters of precoding of the MU-MIMO system, the influences of CCI, noise, estimation errors of propagation channel and precoding gain is the obvious factors for the performance. However, the traditional linear precoding only considers one of these factors, not all of them simultaneously. Although, literature [13] proposed the maximum processing rate linear precoding, and considered using linear precoding to maximize the sum rate of MU-MIMO system, but the optimization objective function is too complex to compute. Due to the space of the parameters searching possess high dimension properties, so that, these kinds of problems seem to be a fine application domain of swarm intelligence algorithm. In this paper, we propose a simpler method to solve the optimal linear precoding problem of linear MMSE receivers, and deduced the simple version of the objective function to search optimal linear precoding vector.

3 The Optimal Linear Precoder Design Based on PSO Searching

3.1 The PSO-Searching Based (PSB) Precoder

Particle Swarm Optimization has been proposed in 1995 by Eberhart and Kennedy [11], it is an effective searching method in multidimensional problems with a confirmed domain. The system capacities are related to the SINR which is transmitted to the \(k{\text{th}}\) user, so that the system capacities of MU-MIMO system can be expressed as

$$C_{MU} = \sum\limits_{k = 1}^{K} {\log_{2} \left( {1 + {\text{SINR}}_{k} } \right)}$$
(13)

The goal of the PSB precoder is to maximize the system capacities of MU-MIMO system. For the MU-MIMO system, the optimal linear precoding vectors can maximize the SINR in each receiver, and can be represented as

$${\hat{\mathbf{W}}}_{k} = \arg \mathop {\max }\limits_{{{\mathbf{W}}_{k} \in {\mathbf{U}}}} \sum\limits_{k = 1}^{K} {\log_{2} \left\{ {1 + \left( {\frac{{{||}({{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} )^{T} ({\hat{\mathbf{W}}}_{k}^{H} [{\mathbf{V}}_{k} ]_{{(r_{k} )}} ){||}_{2}^{2} }}{{\sum\limits_{l = 1,l \ne k}^{K} {{||}({{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} )^{T} ({\hat{\mathbf{W}}}_{k}^{H} [{\mathbf{V}}_{l} ]_{{(r_{l} )}} ){||}_{2}^{2} } + {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }}}{ + }e_{k} } \right)} \right\}}$$
(14)

where the \({\hat{\mathbf{W}}}_{k}\) is the precoding matrix of the \(k{\text{th}}\) user, \([{\mathbf{V}}_{k} ]_{{(r_{k} )}}\) is the column vectors extracting from the right singular vectors of \({\mathbf{H}}_{k}\) which are corresponding to the \(r_{k}\) maximum singular values. Moreover, the left singular matrix \({\mathbf{U}}\) is a unitary matrix and satisfies \({\mathbf{U}}^{H} {\mathbf{U}} = {\mathbf{I}}\). It can be seen from the above equation, for the purpose of the maximum system capacities, the SINR of each user should be maximized. According to (14), the PSB precoder utilize the swarm intelligence of the PSO algorithm to perform the maximum fitness value searching of fitness function to find the precoding vectors of the \(k{\text{th}}\) user, that is adopting the following fitness function to implement the maximum fitness value measurement:

$$Y({\mathbf{x}}_{i,j}^{t} ) = \frac{{\left\| {({{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} )^{T} {[}({\mathbf{x}}_{i,j}^{t} )^{H} [{\mathbf{V}}_{k} ]_{1} {]}} \right\|_{{2}}^{{2}} }}{{\sum\limits_{l = 1,l \ne k}^{K} {\left\| {({{\varvec{\uplambda}}}_{k}^{{(r_{k} )\max }} )^{T} {[}({\mathbf{x}}_{i,j}^{t} )^{H} [{\mathbf{V}}_{l} ]_{1} {]}} \right\|_{{2}}^{{2}} } + {1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0pt} \beta }}}$$
(15)

Fitness value \(Y({\mathbf{x}}_{i,j}^{t} )\) denotes the acquired SINR from the precoding vector \({\mathbf{x}}_{i,j}^{t} \in {\mathbb{C}}^{{M_{T} \times 1}}\) (position) of the \(i{\text{th}}\) particle of the \(j{\text{th}}\) population in the \(t{\text{th}}\) iteration. The designing steps of MU-MIMO PSB precoder show as follows:

  • Step 1. Estimate signal transmission channel \({\hat{\mathbf{H}}}\).

  • Step 2. Extract the estimation of individual transmitting channel matrix \({\hat{\mathbf{H}}}_{k}\) of each user from \({\hat{\mathbf{H}}}\).

  • Step 3. Perform SVD of \({\hat{\mathbf{H}}}_{k}\) and indicated as \({\hat{\mathbf{H}}}_{k} = {\hat{\mathbf{U}}}_{k} {\hat{\mathbf{\Sigma }}}_{k} {\hat{\mathbf{V}}}_{k}^{H}\) (\(k = 1,2,...,K\)).

  • Step 4. Perform PSO algorithm to obtain \({\mathbf{F}}_{PSB,a} \in {\mathbb{C}}^{{M_{T} \times r}}\).

    1. A.

      Let vector \({\mathbf{x}}_{{{1},j}}^{0} = [x_{{{1},j,1}}^{0} \, x_{{{1},j,2}}^{0} \, \cdots \, x_{1,j,D}^{0} ]^{T} = [{\hat{\mathbf{V}}}_{k} ]_{{(r_{k} )}}\) represent the initial position of the first particle within the population that has \(N_{p}\) (\(i = 1,2,...,N_{p}\)) particles in a \(D\)-dimensional (\(d = 1,2,...,D\)) optimization problem, the rest particles’ initial positions are generated randomly, in which its’ velocity vector \({\mathbf{v}}_{i,j}^{0} = [v_{i,j,1}^{0} \, v_{i,j,2}^{0} \, \cdots \, v_{i,j,D}^{0} ]^{T}\) is initialized randomly, where the zero of the superscript represent the initialization, and the number of populations is \(N_{f}\) (\(j = 1,2,...,N_{f}\)). Calculate the initial fitness value of each particle via substitute the initial position \({\mathbf{x}}_{i,j}^{0}\) into the fitness function, and count the global best solution \({\mathbf{g}}_{j}^{0}\). The best position of the \(i{\text{th}}\) particle of the \(j{\text{th}}\) population is denoted as \({\mathbf{p}}_{i,j}^{0}\).

    2. B.

      Calculate the position \({\mathbf{x}}_{i,j}^{t}\) and velocity \({\mathbf{v}}_{i,j}^{t}\) of each particle at \(t{\text{th}}\) iteration, meanwhile compute the global best solution \({\mathbf{g}}_{j}^{t}\) and the best position of the \(i{\text{th}}\) particle of the \(j{\text{th}}\) population till the current iteration \({\mathbf{p}}_{i,j}^{t}\) via evaluate the fitness value of each particle. The superseding of the position and velocity vectors of the \(i{\text{th}}\) particle of \(j{\text{th}}\) population of the \(t + 1\) times iteration can be represented as follow:

      $${\mathbf{v}}_{i,j}^{t + 1} = w^{t} {\mathbf{v}}_{i,j}^{t} + c_{1} {\mathbf{r}}_{1}^{t} \odot [{\mathbf{p}}_{i,j}^{t} - {\mathbf{x}}_{i,j}^{t} ] + c_{2} {\mathbf{r}}_{2}^{t} \odot [{\mathbf{g}}_{j}^{t} - {\mathbf{x}}_{i,j}^{t} ]$$
      (16)
      $${\mathbf{x}}_{i,j}^{t + 1} = {\mathbf{x}}_{i,j}^{t} + {\mathbf{v}}_{i,j}^{t + 1}$$
      (17)

      where \(\odot\) denote the elements multiplier in the correspondent position of two different vectors. \(w^{t}\) is the inertia weight to maintain the previous movement. \(c_{1} {\mathbf{r}}_{1}^{t}\) and \(c_{2} {\mathbf{r}}_{2}^{t}\) represent the vector of uniform distribution random variable between \(0\) to \(1\) of \(t{\text{th}}\) iteration. Generally, the values of \(c_{1}\) and \(c_{2}\) will be set as integer constants. The position of candidates of the solution space of the precoding matrix of the PSO optimal searching is a complex number. The new position of each particle in next iteration has to calculate the real and the imaginary part of \({\mathbf{x}}_{i,j}^{t + 1}\) with complex number.

    3. C.

      When the termination condition of the iteration process has been reached, the maximum number of iteration times \(N_{s}\) (\(t = 1,2,...,N_{s}\)) has been satisfied, the global best solution of the final iteration \({\mathbf{g}}_{j}^{{N_{s} }}\) can be seem as the optimal solution \({\mathbf{g}}_{j}\) of this multi-dimensional optimization problem, that is \([{\mathbf{F}}_{PSB,a} ]_{{(r_{k} )}} = {\mathbf{g}}_{j}\).

  • Step 5. Perform SVD of matrix \({\mathbf{H}}_{k} {\mathbf{F}}_{{PSB,a_{k} }} = {\tilde{\mathbf{U}}}_{PSB,k} {\tilde{\mathbf{\Sigma }}}_{PSB,k} {\tilde{\mathbf{V}}}_{PSB,k}^{H}\).

  • Step 6. Define diagonal matrix \({{\varvec{\Sigma}}}_{PSB,e} = \left[ {\begin{array}{*{20}c} {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{PSB,1}^{{(r_{1} )}} } & \cdots & \cdots & 0 \\ \vdots & {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{PSB,2}^{{(r_{2} )}} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{PSB,K}^{{(r_{K} )}} } \\ \end{array} } \right] \in {\mathbb{R}}^{r \times r}\), where \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{PSB,k}^{{(r_{k} )}}\) represent the \(r_{k}\) largest singular values of singular matrix \({\tilde{\mathbf{\Sigma }}}_{k}\).

  • Step 7. Apply WP algorithm on matrix \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Sigma } }}_{PSB,k}^{{(r_{k} )}}\) to establish matrix \({\mathbf{D}}_{PSB,k}\), and implement \({\mathbf{F}}_{PSB,b} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{PSB,1} } & \cdots & \cdots & 0 \\ \vdots & {{\mathbf{D}}_{PSB,2} } & \vdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {{\mathbf{D}}_{PSB,K} } \\ \end{array} } \right] \in {\mathbb{C}}^{{M_{x} \times r}}\).

  • Step 8. Calculate the linear precoding matrix \({\mathbf{W}}_{PSB} = \beta {\mathbf{F}}_{PSB,a} \cdot {\mathbf{F}}_{PSB,b}\) of PSB precoder.

3.2 The Improved PSO-Searching Based (IPSB) Precoder

The searching capability of the PSO consists of global exploration and local exploitation abilities. For the convergences of PSO optimal searching the marginal effect of the capability global exploration decrease with the iteration times increase. The inertia weight \(w^{t}\) of the PSO is adopted to control the influence of the previous history of velocities on the current velocities, which balances global exploration and local exploitation abilities of the particle swarm, and affects the trade-off between global and local exploration abilities. Appropriate inertia weight selection will furnish the balancing between global and local exploration abilities causing fewer iteration times on average for the optimal solution finding. The PSO may lack the global search ability at the end of the optimal solution searching iteration procedure, and the required optima of complicated and complex cases maybe fail to be found.

In each iteration, the position of the particle substitute into the fitness function leads to the fitness value of the particle, and to evaluate the best position of the swarm is to find out the position corresponding to the largest fitness value. The fitness value of the global best position of \(j{\text{th}}\) population \({\mathbf{g}}_{j}\) denoted as \(Y({\mathbf{g}}_{j} )\). For the \(i{\text{th}}\) particle, \(Y({\mathbf{g}}_{j} ) = Y({\mathbf{x}}_{i,j}^{t} ) + Y^{\prime}({\mathbf{x}}_{i,j}^{t} )({\mathbf{g}}_{j} - {\mathbf{x}}_{i,j}^{t} )\), where \(Y^{\prime}({\mathbf{x}}_{i,j}^{t} )\) is the first order derivative of the fitness function \(Y({\mathbf{x}}_{i,j}^{t} )\). Let \(Y({\mathbf{g}}_{j} ) = 0\), then the \(\varepsilon_{i,j}^{t + 1} = ({\mathbf{g}}_{j} - {\mathbf{x}}_{i,j}^{t} ) = - [Y^{\prime}({\mathbf{x}}_{i,j}^{t} )]^{ - 1} Y({\mathbf{x}}_{i,j}^{t} )\). Due to particles will move toward the global best position corresponding to the particle \({\mathbf{g}}_{j}\), the marginal effect of the searching capability of each particle in the \((t + 1){\text{th}}\) iteration can be represented as

$$\gamma_{i,j}^{t + 1} = 1/(1 + e^{{ - \varepsilon_{i,j}^{t + 1} }} )$$
(18)

where the parameter \(\varepsilon_{i,j}^{t + 1}\) describes the disparities of the position between the particle and the global best position that implies the moving forward direction and distance of particles at the next iteration. First, the IPSB precoder defines the marginal effect \(\gamma_{i,j}^{t + 1}\) of the searching capability of each particle in the \((t + 1){\text{th}}\) iteration. The marginal effect predicts the searching capability of particles at the next iteration, and it affects the effectiveness degree of inertial velocity in calculations of the particle moving velocity. Second, the parameter \(\varepsilon_{i,j}^{t + 1}\) has been used in calculating the particle moving velocity to assist particles moving toward the global best position, which can increase the accuracy of the searches of the global best position effectively. The modified termination criterion of the IPSB precoder helps the searching procedure of the global best position terminated at reasonable iteration times, which can reduce the unnecessary searching iteration times. For the simplifying of the statement of IPSB precoder, the modified parts which improves the searching performance are described below:

  1. 1.

    Replace the conventional linearly decreasing inertia weight \(w^{t}\) with the marginal effect \(\gamma_{i,j}^{t + 1}\) of searching capability of each particle. In most situations, fitness functions of PSO searching are nonlinear, the nonlinearly changing marginal effects \(\gamma_{i,j}^{t + 1}\) are more suitable to control the search capabilities switches between global exploration and local exploitation abilities than linear decreasing inertia weights \(w^{t}\). The traditional linearly decreasing inertia weight \(w^{t}\) modeled as a real number, however, the candidates of the solution space of precoding matrix of PSO searching is a complex number. The marginal effect \(\gamma_{i,j}^{t + 1}\) of the searching capability of each particle in searching iterations is modeled as a complex number, which can modify the real and imaginary part of the influence of the previous movement synchronously.

  2. 2.

    The modified moving velocity updating calculation equation of each particle is represented as

    $${\mathbf{v}}_{i,j}^{t + 1} = \gamma_{i,j}^{t + 1} \times {\mathbf{v}}_{i,j}^{t} + c_{1} \times rand( \cdot ) \times ({\mathbf{p}}_{i,j} - {\mathbf{x}}_{i,j}^{t} ) + c_{2} \times rand( \cdot ) \times ({\mathbf{g}}_{j} - {\mathbf{x}}_{i,j}^{t} ) + \varepsilon_{i,j}^{t + 1}$$
    (19)

    The parameter \(\varepsilon_{i,j}^{t + 1}\) has been used to help particles of the population distributed on a sufficiently large space to ensure the optimal solution can be explored.

  3. 3.

    Modify the termination criterion that is if the marginal effects of searching capability cannot provide contributions to raise the fitness value, then cease the iteration. The termination criterion of the conventional PSO algorithm is determine the number of iterations in advance for the linear decreasing inertia weight changes from the maximum value to the predefined minimum value. However, it is hard to predefine the number of iterations to find the optimal solution. The modified termination criterion of the improved PSO algorithm consults the variation of fitness value, when the fitness value remains the same level for a time period the iteration of the PSO searching process has to be stopped. The marginal effect \(\gamma_{i,j}^{t + 1}\) of the searching capability of each particle leads to the variable iteration times.

Finally, the steps of the IPSB precoder are according to the steps of the PSB precoder meanwhile utilizing the modification mentioned above to generate the precoding weight matrix as \({\mathbf{W}}_{IPSB}\).

4 Computer Simulation

For illustrating the performance of proposed PSB precoder and IPSB precoder, several simulations are conducted under the perfect and imperfect channel estimation environments. We use a downlink of the MU-MIMO communication system with \(K = 3\) users. The uniform linear array with half-wavelength distance between any two elements has been adopted, and the number deployment of relative array antenna elements is \(\{ M_{{R_{1} }} ,M_{{R_{2} }} ,M_{{R_{{3}} }} \} \times M_{T} = \{ 3, \, 3, \, 3\} \times 8\). The channel response matrix \({\mathbf{H}}_{k}\) of the \(k{\text{th}}\) user is modeled as a Rayleigh fading channel [14] for \(k = 1, \, 2, \, \ldots , \, K\). Moreover, assume that the channel response matrix has been estimated. For analysis simplified, the binary phase shift keying (BPSK) has been utilized to perform simulation. Every simulation result is presented after \(10^{3}\) data bits were processed, assume each user only transmits a single data stream, and it is averaged by \(10^{3}\) times independent Monte Carlo runs with independent noise samples for each run. For comparison, the performance of the proposed PSB precoder and the IPSB precoder is also compared with the ZF precoder [8], MMSE precoder [9], and presented SVD precoder. The parameters of PSO for the simulations are described as follows. The acceleration constants \(c_{1}\) and \(c_{2}\) are equal to 2. The population size is set \(N_{p} = 50\) and the maximum number of iterations is \(N_{s} = 1000\). In addition, the inertia weight \(w^{t + 1} = \alpha w^{t}\), where \(w^{0} = 1\) and \(\alpha = 0.99\). For imperfect propagation channel, the estimation error matrix \({\mathbf{E}}_{k}\) is modeled as the random Gaussian distribution with zero mean and variance \(\sigma_{e}^{2}\), where the value of \(\sigma_{e}^{2}\) is determined from the variation region \([ - 15{\text{dB}}, \, 0{\text{dB}}]\) randomly.

The performance of the proposed PSB precoder and IPSB precoder is compared under various scenarios. Figure 2 plots the bit error rate (BER) versus different signal-to-noise ratio (SNR) under the variation interval of \({\text{SNR}} = [ - 10{\text{ dB}}, \, 20{\text{ dB}}]\). While SNR is lower than \(0{\text{ dB}}\), it depicts that the ZF and MMSE precoders also have poor detection performance even in the perfect channel estimation case. Expect for the proposed precoder, the remaining precoders suffer from severe performance degradation when faced channel estimation error. As expected, the performance improvement of the IPSB precoder is apparent due to it can significantly suppress the perturbation of the estimation error in the imperfect estimation channel. Figure 3 shows the BER versus the number of users, and the variation interval of users \(K = [3, \, 6, \, 9, \, 12, \, 15, \, 20]\). As illustrated in this figure, on the infrastructure which the BS with eight antenna elements, the BER performance of each precoder degrades as the number of users increases. However, the BER performance of the PSB and IPSB precoders is superior to the ZF, MMSE, and SVD precoder. Figure 4 shows the system capacity versus the input SNR of users. The computation of system communication capacity is according to (13). The system communication capacities are relative to the BER of data transmission, the better BER performance, the better system communication capacity. As shown in this figure, the proposed PSB and IPSB precoders respectively have superior performance in the perfect and imperfect channel estimation. Moreover, it can be found that performance of the system communication capacities of the SVD precoder is better than those of the other precoders. According to the results of Fig. 4, Table 1 illustrates the performance improvement of system capacities in terms of percentage under the perfect and imperfect channel estimation. An improved percentage formula of system capability is defined as

Table 1 The performance improvement of system capabilities
Full size table
$${\text{PI(\%) = }}\frac{{C_{a} - C_{b} }}{{C_{b} }} \times 100$$
(20)

where \(C_{a}\) represents the capacity of the proposed precoder (PSB or IPSB) and \(C_{b}\) is the capacity of the other precoders (ZF, MMSE, and SVD). The performance improvement, \({\text{PI}}(\%)\), metric gives the improvement in the system capability of the PSB precoder or the IPSB precoder with respect to that of the ZF, MMSE, and SVD, respectively. A higher positive value of this metric implies a better improve performance. Figure 5 illustrates the system capacity comparison of the cumulative distribution function (CDF) distributions comparison under SNR = 10 dB. The calculation of the CDF is direct at the samples collection of the data transmitting rate of three users under the number of trials is \(10^{3}\) times. It demonstrates the distribution chart of the CDF, and both the performance of BER of the MU-MIMO communication system with PSB and IPSB precoders respectively has superior performances, there are over 90% probabilities the user can reach than \(40{\text{ bps/Hz}}\) data transmitting rate under the situation of perfect estimation of propagation channel. And, under the imperfect estimation of propagation channel, the data transmitting rate of users can reach than \(30{\text{ bps/Hz}}\) over 90% probabilities. Moreover, the system capacity of the IPSB precoder design has better performance than the PSB precoder design. Again, these figures show that the proposed precoders can work with robustness in the presence of imperfect channel estimation.

Fig. 2
figure 2

The BER versus the input SNR of users

Full size image
Fig. 3
figure 3

The BER versus the number of users

Full size image
Fig. 4
figure 4

The system capacity versus the input SNR of users

Full size image
Fig. 5
figure 5

The system capacity CDF distributions comparison under SNR = 10 dB

Full size image

5 Conclusions

The maximum precoding gain can be obtained by the presented SVD precoder under the perfect estimated propagating channel. However, the transmitting channels of users are non-orthogonal in the realities. The SINR of individual users cannot reach the maximum level due to the precoding matrix of users can be affected by CCI easily. Meanwhile, the channel estimation may not be perfect, and the entire system performance of the MU-MIMO communication system will be brought down. In this paper, the design of the PSB and IPSB precoders utilizes the PSO searching approaches of swarm intelligence algorithm to perform the optimal searching of the precoding matrix to maximize the output SINR of individual users. The proposed IPSB precoder by means of changing the calculation method of the moving velocities and inertia weight vectors of each particle from traditional PSO algorithm to obtain the superior performance to the PSB precoder. The simulation results show that the proposed PSB and IPSB precoders have superior effectiveness in defense of the CCI to improve the system capacities of the MU-MIMO communication system.