1 Introduction

GNSS signal acquisition is the first step of the software defined receiver (SDR) [1,2,3]. In this step, bit transition, Doppler frequency, Doppler rate and code phase four-dimension detection should be performed. However, this process requires a lot of calculations.

In order to improve the efficiency of GNSS code phase search, the FFT-based method [4] has been proposed. However, this method still has a slow search speed in multiple satellites, and articles [6, 7] have compressed code phases to expedite the acquisition process. In order to reduce computational complexity even further, the two-dimension compressed search method [8] in both Doppler frequency and code phase domains has been proposed. Nevertheless, the impact of bit transition on the integration peak has been overlooked by the methods outlined in references [6, 8]. In addressing the problem, the proposed solution in article [9] involves employing a weak acquisition method based on semi-bit coherent differential integration process. To minimize the number of Doppler frequency searches, the article [10] has proposed the synthesized Doppler frequency hypothesis testing (SDHT) method. However, the method does not consider the impact of Doppler rate on integration peak in high-dynamic acquisition scenarios. Moreover, the computational burden can be further improved.

When Doppler rate is not equal to 0 Hz/s in high-dynamic environment, bit transition, Doppler frequency, Doppler rate and code phase four-dimension detection is needed [11]. Both Doppler frequency and Doppler rate estimation should be estimated in frequency parameters estimation process. Since these parameters limit the integration time improvement, the differential process [12,13,14,15] has been be used to increase the integration time. However, in high-dynamic and weak signal environments, the computational burden should also be considered, and the article [11] has proposed a block accumulating semi-coherent integration of correlations method (BASIC). For long coherent integration in a high dynamic environment, the articles [16, 17] have used the fractional Fourier transform (FRFT) to estimate and compensate for the Doppler rate in the incoming signal. Moreover, to further improve integration in the case of bit transitions, the probability of bit transitions has been considered in parameters estimation process [18]. Based on the idea that the discrete chirp-Fourier transform (DCFT) can be used to improve the signal detection probability [19], we used DCFT and block zero-padding processes to estimate parameters in weak signals and high dynamic environments [20]. In this way, integration time is improved while bit signs are estimated. Nevertheless, since DCFT requires many computation costs, it is necessary to enhance the efficiency of the parameters estimation.

To further reduce the computational complexity in high-dynamic environments, the low-computation GNSS acquisition method (LGAM) in the high-dynamic environment has been proposed in this paper. Firstly, large Doppler search step is set for SDF hypotheses. In this way, the step compresses the serial Doppler search, and post-correlation signal model is derived in the high-dynamic environments. Then, based on the derived model, double-FFT based detection has been proposed. Finally, LGAM combines SDF process and double-FFT based detection. To the best of our knowledge, the way of double-FFT based detection is the first time to be proposed. Besides, the Doppler rate resolution has been analyzed based on derived post-correlation detection variable in the paper. Mean acquisition computation (MAC) and detection probability of LGAM have been analyzed in this paper. Simulation results show that since LGAM is based on sparse Doppler frequency structure and adopts double-FFT based detection, which leads to reduction of complex multiplications, the computational cost of LGAM is lower than general methods under the moderate SNR.

This paper is organized as follows. Firstly, the high-dynamic signal model has been proposed. Then, based on compressed Doppler frequency search, post-correlation signal has been derived. For estimation of Doppler frequency and Doppler rate with low computational burdens, double-FFT based detection has been proposed. LGAM combines compressed Doppler frequency search with the double-FFT based detection. To illustrate algorithm performance, total MAC and detection probability have been derived. Finally, the tests for acquisition performance comparison have been proposed.

2 Signal Model

In this paper, BPSK modulated L1 frequency GPS coarse/acquisition (C/A) code signal is chosen for explaining the proposed method. However, the proposed method can be directly applicable to other GNSS signals such as BOC signals.

In the absence of noise, the received intermediate frequency (IF) signal through I-Q down conversion process can be modeled as follows:

$${r}_{I}\left({n}_{I}\right)={A}_{I}{C}_{\tau }\left({n}_{I}\right)B({n}_{I})\mathit{exp}\left[j2\pi \left(\left({f}_{I}+{f}_{d}\right){n}_{I}{T}_{I}+{\alpha }_{0}{n}_{I}^{2}{T}_{I}^{2}\right)\right]$$
(1)

where \({n}_{I}=\mathrm{0,1},...,\frac{T}{1000{T}_{I}}-1\). \({T}_{I}\) represents the sampling interval of digital IF in second. \(T\) represents integration time (IT) in millisecond. \({A}_{I}\) represents the amplitude of IF signal, \({C}_{\tau }\left(\right)\) represents pseudorandom code with initial code phase \(\tau \), \(B\left(\right)\) represents bit signs, \({f}_{I}\) represents IF, \({f}_{d}\) represents Doppler frequency, and \({\alpha }_{0}\) represents Doppler rate. The local code can be constructed as follows:

$${L}_{I}\left({n}_{I}\right)=C\left({n}_{I}\right)\mathit{exp}\left[-j2\pi \left({f}_{I}+{f}_{k}{\Delta }_{f}\right){n}_{I}{T}_{I}\right]$$
(2)

where \({\Delta }_{f}\)=\(500/T\) represents the final Doppler resolution of proposed method determined by the influence of Doppler resolution on integration peak [10]. \({f}_{k}\) represents search index. After the code phase correlation and Doppler frequency search, the post-correlation signal \(R\left(n\right)\) can be expressed as

$$R\left(n\right)=\frac{1}{{N}_{t}}{\sum }_{{n}_{I}=n{N}_{t}}^{\left(n+1\right){N}_{t}-1}{r}_{I}\left({n}_{I}\right){L}_{I}\left({n}_{I}\right)$$
(3)

where n = 0, 1,…,T − 1. Ts = NtTI. Nt represents the number of samples per code period.

3 Proposed Method

In this section, IF signal goes through SDF process, which includes compressed Doppler process and parallel code process. Based on SDF process, post-correlation signal model is derived. Then, based on the model, double-FFT based detection has been proposed for parameters estimation. Besides, Doppler rate search step has been derived in this part. Finally, combining SDF process and double-FFT based detection, LGAM has been proposed.

3.1 Sparse Doppler Frequency (SDF) Process

When Doppler search index \({f}_{k}\) =\({k}_{f}{M}_{f}\) where \({k}_{f}=-{K}_{f},-{K}_{f}+1,...,0,...,{K}_{f}\), \({K}_{f}\) represents the maximum of \({k}_{f}\) and \({M}_{f}\) represents the compressed factor of Doppler frequency, the post-correlation signal \(R\left(n\right)\) can be written as:

$$ \begin{aligned} R\left( n \right) & \approx \frac{A_I }{{N_t^2 }}B\left( n \right)\mathop \sum \limits_{n_t = nN_t }^{\left( {n + 1} \right)N_t - 1} C\left( {n_I } \right)C_\tau \left( {n_I } \right) \\ & \quad \mathop \sum \limits_{n_I = nN_t }^{\left( {n + 1} \right)N_t - 1} \exp \left[ {j2\pi \left( {\left( {f_d - k_f M_f \Delta_f } \right)n_I T_I + \alpha_0 n_I^2 T_I^2 } \right)} \right] \\ & \approx \frac{A_I }{{N_t^2 }}B\left( n \right)\mathop \sum \limits_{n_I = nN_t }^{\left( {n + 1} \right)N_t - 1} C\left( {n_I } \right)C_\tau \left( {n_I } \right)\mathop \sum \limits_{n_I = nN_t }^{\left( {n + 1} \right)N_t - 1} \exp \left[ {j2\pi \overline{f}n_I T_I } \right] \\ & = \frac{A_I }{{N_t^2 }}B\left( n \right) \cdot A_\tau \mathop \sum \limits_{n_I = nN_t }^{\left( {n + 1} \right)N_t - 1} \exp \left[ {j2\pi \overline{f}n_I T_I } \right] \\ \end{aligned} $$
(4)

where \({A}_{\tau }\)=\({\sum }_{{n}_{I}=n{N}_{t}}^{\left(n+1\right){N}_{t}-1}C\left({n}_{I}\right){C}_{\tau }\left({n}_{I}\right)\). \(\overline{f}\) represents the average frequency between intervals \(n{N}_{t}{T}_{I}\) and \(\left(\left(n+1\right){N}_{t}-1\right){T}_{I}\), and is equal to \({f}_{0}+{\alpha }_{0}n{N}_{t}{T}_{I}+{\alpha }_{0}\frac{{N}_{t}-1}{2}{T}_{I}\), where \({f}_{0}\)=\({f}_{d}-{k}_{f}{M}_{f}{\Delta }_{f}\) represents residual Doppler frequency. When the local code is aligned with received signal, (3) can be simplified to

$$ \begin{aligned} R\left( n \right) & \approx \frac{A_I }{{N_t }}B\left( n \right)A_\tau \frac{{1 - \exp \left( {j2\pi \overline{f}T_s } \right)}}{{1 - \exp \left( {j2\pi \overline{f}T_I } \right)}}\exp \left[ {j2\pi \overline{f}nT_s } \right] \\ & = B\left( n \right)\frac{A_I }{{N_t }}A_\tau \frac{{\sin \left( {\pi \overline{f}T_s } \right)}}{{\sin \left( {\pi \overline{f}T_I } \right)}}\exp \left[ {j\pi \overline{f}\left( {2n + 1} \right)T_s - j\pi \overline{f}T_I } \right] \\ \end{aligned} $$
(5)

Since \(\pi \overline{f}{T}_{I}\) is really small,

$$R\left(n\right)\approx {A}_{n}B\left(n\right)\mathit{exp}\left[j\pi \overline{f}\left(2n+1\right){T}_{s}\right]$$
(6)

where \({A}_{n}=\frac{{A}_{I}}{{N}_{t}}{N}_{c}{A}_{\tau }\mathit{sin}c\left(\pi \overline{f}{T}_{s}\right)\). Here, when local code is aligned with the received signal, \({A}_{\tau }\)=\(\left(1-\frac{\left|{i}_{c}{T}_{I}-\tau \right|}{{T}_{c}}\right)\) where \({T}_{c}\) is chip duration, and \({i}_{c}\) corresponding to each n may not be the same due to rate of change of code-phase over long integration period in high dynamic environments, and code Doppler compensation method [19] can be used. So \({i}_{c}\) is considered as the same value over long integration period when local code is aligned with the received signal. When local code is not aligned with the received signal, \({A}_{\tau }\approx 0\). Then, when \({f}_{0}\)=\(\left|{f}_{d}-{k}_{f}{M}_{f}{\Delta }_{f}\right|\le \frac{{M}_{f}{\Delta }_{f}}{2}\),

$$\overline{\left|f\right|}{T}_{s}=\left|{f}_{0}+{\alpha }_{0}n{N}_{t}{T}_{I}+{\alpha }_{0}\frac{{N}_{t}-1}{2}{T}_{I}\right|{T}_{s}\le \left({M}_{f}\frac{250}{T}+{\alpha }_{M}T{T}_{s}+{\alpha }_{M}\frac{{T}_{s}}{2}\right){T}_{s}$$
(7)

where\(\left|{\alpha }_{0}\right|\le {\alpha }_{M}\). For GPS L1 CA signal, it is assume that 20 ms \(\le T\le \) 500 ms. When \({\alpha }_{M}\)=500 Hz/s, \(T=\) 500 ms and\({M}_{f}=T\), (7) can be simplified as:

$$\overline{\left|f\right|}{T}_{s}\le \left(250+250+0.25\right){T}_{s}=0.50025$$
(8)

So the maximum loss in sinc() of An is about\(20{\text{lgsinc}}(\uppi \overline{{\text{f}}}{T }_{S}))\approx -3.9{\text{dB}}\), which is ignored in this article based on analysis [11].

Above all, An may not be changed with time variable n. It assumed that A represents An in the following analysis.

3.2 Double-FFT Based Detection in Presence of Bit Signs

Due to the influence of Doppler rate α0, residual Doppler frequency f0, bit signs B(n), and code phase τ on detection peak, there is four-dimension search costing too much computational complexity. α0, B(n), and τ can be estimated based on differential signal by FFT. Then, f0 can be estimated by FFT. So we call it double-FFT based detection.

After differential process, the differential signal db0(nd) can be written as:

$${d}_{{b}_{0}}({n}_{d})={R}^{*}({n}_{d})R({n}_{d}+{N}_{B})={A}^{2}B({n}_{d})B({n}_{d}+{N}_{B})\mathit{exp}\left[j4\pi {n}_{d}{N}_{B}{\alpha }_{0}{T}_{s}^{2}+j{\varphi }_{0}\right]$$
(9)

where \({n}_{d}\)=\({b}_{0}\),\({b}_{0}+1\),…,\({b}_{0}+T-1-{N}_{B}\), \({b}_{0}\)=0,…, \({N}_{B}\)−1, \({N}_{B}\) represents the number of samples per bit period, \({\varphi }_{0}\)=\(j\pi T\left[2{f}_{0}+{\alpha }_{0}\left({N}_{t}-1\right){T}_{I}+{\alpha }_{0}\left({N}_{B}+1\right){T}_{s}\right]\). Then, based on FFT, one-bit integration process can be written as:

$$ \begin{aligned} \varphi_{b_0 } (n_1 ,k_\alpha ) & = \mathop \sum \limits_{n_d = (n_1 - 1)N_B + 1}^{n_1 N_B } d_{b_0 } (n_d )\exp \left[ { - j\frac{2\pi k_\alpha }{{N_{B0} }}n_d } \right] \\ & \approx \frac{A^2 }{{N_B }}\exp \left( {j\varphi_0 } \right)\mathop \sum \limits_{n_d = (n_1 - 1)N_B + 1}^{n_1 N_B } B(n_d )B(n_d + N_B )\mathop \sum \limits_{n_d = (n_1 - 1)N_B + 1}^{n_1 N_B } \exp \left[ {j2\pi \left( {2N_B \alpha_0 T_s^2 - 2N_B \frac{k_\alpha }{{N_{B0} }}T_s } \right)n_d } \right] \\ & = \frac{A^2 }{{N_B }}\exp \left( {j\varphi_0 } \right)B_{b_0 } \left( {n_1 } \right)\frac{{1 - \exp \left( {j2\pi \alpha_k N_B } \right)}}{{1 - \exp \left( {j2\pi \alpha_k } \right)}}\exp \left[ {j2\pi \alpha_k \left( {(n_1 - 1)N_B + 1} \right)} \right] \\ \end{aligned} $$
(10)

where \({n}_{1}\)=1,…, \({N}_{SB}\), \({N}_{SB}=\frac{T}{{N}_{B}}-1\). \({N}_{B0}\) represents the number of FFT points. \({\alpha }_{k}=2{N}_{B}{\alpha }_{0}{T}_{s}^{2}-2{N}_{B}\frac{{k}_{\alpha }}{{N}_{B0}}{T}_{s}\). \({\Delta }_{\alpha }=\frac{1}{{N}_{B0}{T}_{s}}\) represents Doppler rate resolution. When \({b}_{0}\) is the correct bit transition position, \({B}_{{b}_{0}}\left({n}_{1}\right)=\pm {N}_{B}\). Or \(\left|{B}_{{b}_{0}}\left({n}_{1}\right)\right|<{N}_{B}\). To detect the bit transition position, final integration variable \(\varphi \left({B}_{L},{b}_{0},{k}_{\alpha }\right)\) can be written as:

$$ \begin{aligned} \varphi \left( {B_L ,b_0 ,k_\alpha } \right) & = \mathop \sum \limits_{n_1 = 1}^{N_{SB} } \varphi_{b_0 } (n_1 ,k_\alpha )B_L \left( {n_1 } \right) \\ & \approx \frac{A^2 }{{N_B N_{SB} }}\exp \left( {j\varphi_0 } \right)\frac{{1 - \exp \left( {j2\pi \alpha_k N_B } \right)}}{{1 - \exp \left( {j2\pi \alpha_k } \right)}}\mathop \sum \limits_{n_1 = 1}^{N_{SB} } B_{b_0 } \left( {n_1 } \right)B_L \left( {n_1 } \right)\mathop \sum \limits_{n_1 = 1}^{N_{SB} } \exp \left[ {j2\pi \alpha_k \left( {(n_1 - 1)N_B + 1} \right)} \right] \\ & = \frac{A^2 }{{N_B N_{SB} }}\exp \left( {j\varphi_0 } \right)\frac{{1 - \exp \left( {j2\pi \alpha_k N_B } \right)}}{{1 - \exp \left( {j2\pi \alpha_k } \right)}}\frac{{1 - \exp \left[ {j2\pi \alpha_k N_B N_{SB} } \right]}}{{1 - \exp \left[ {j2\pi \alpha_k N_B } \right]}}\mathop \sum \limits_{n_1 = 1}^{N_{SB} } B_{b_0 } \left( {n_1 } \right)B_L \left( {n_1 } \right)\exp \left[ {j2\pi \alpha_k } \right] \\ \end{aligned} $$
(11)

where BL(n1) ∈ {1,-1}. When \({b}_{0}\) is the correct bit transition position, BL(n1) and \({B}_{{b}_{0}}\left({n}_{1}\right)\) have the same bit signs, and \(\varphi \left({B}_{L},{b}_{0},{k}_{\alpha }\right)\) reaches the maximum value. Meanwhile, detection variable \({J}_{\alpha }\) corresponding to different Doppler rate detection units can be written as:

$$ \begin{aligned} J_\alpha \left( {k_\alpha } \right) & = {\mathop {max}\limits_{\tau ,B_L ,b_0 }} \left| {\varphi \left( {B_L ,b_0 ,k_\alpha } \right)} \right|^2 \\ & \approx A^2 \left| {\frac{{1 - \exp \left( {j2\pi \alpha_k N_B } \right)}}{{1 - \exp \left( {j2\pi \alpha_k } \right)}}\frac{{1 - \exp \left[ {j2\pi \alpha_k N_B N_{SB} } \right]}}{{1 - \exp \left[ {j2\pi \alpha_k N_B } \right]}}} \right| \\ & \approx A^2 N_B N_{SB} \left| {\sin c\left( {\pi \alpha_k N_B } \right)\sin c\left( {\pi \alpha_k N_B N_{SB} } \right)} \right| \\ \end{aligned} $$
(12)

Assuming that Tα represents detection threshold for Doppler rate estimation, which can be set based on false alarm probability (FAP). When \({J}_{\alpha }\ge \mathrm{T\alpha }\), the estimated Doppler rate can be obtained. If \({J}_{\alpha }<\mathrm{T\alpha }\), the value of A is so small, and other Doppler frequency units should be performed.

The parameter τ, α0 and bit signs of signal R(n) can be estimated by the process above. Then, the R(n) can be simplified to \({\varphi }_{2}\left(n,{k}_{f}\right)\), which can be modeled as (13) for the residual Doppler frequency estimation:

$${\varphi }_{2}\left(n,{k}_{f}\right)=A\mathit{exp}\left[j\pi {f}_{0}\left(2n+1\right){T}_{s}\right]$$
(13)

Based on FFT, residual Doppler frequency \({f}_{0}\) can be estimated as follows:

$${J}_{f}\left({k}_{f}\right)={\sum }_{n=0}^{{N}_{f}-1}{\varphi }_{2}\left(n,{k}_{f}\right)\mathit{exp}\left(-j2\pi \frac{{k}_{f}}{{N}_{f}}n\right)$$
(14)

where \({N}_{f}\) represents the number of points of FFT. \({\Delta }_{f}=\frac{1}{{N}_{f}{T}_{s}}\) represents Doppler resolution. It is assumed that \({N}_{F}\) represents the number of values that \({k}_{f}\) can take, and \({T}_{f}\) set based on FAP represents detection threshold for residual Doppler frequency estimation. When \({J}_{f}\left({k}_{f}\right)\ge {T}_{f}\), the estimated \({f}_{0}\) can be obtained.

3.3 Low-Computation GNSS Acquisition Method (LGAM)

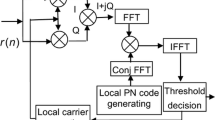
LGAM has been shown in Fig. 1, which combines SDF process and double-FFT based detection. The double-FFT based detection can be realized by the following two-step parameters estimation. In the presence of noise, IF signal \({r}_{I}\left(n\right)\) can be modeled as:

$${r}_{IN}\left(n\right)={r}_{I}\left(n\right)+w\left(n\right)$$
(15)

where both the real part and imaginary part of \(w\left(n\right)\) obey a normal distribution with mean value 0 and variance σ2. LGAM can be depicted with more details as follows:

Fig. 1
figure 1

LGAM diagram

Full size image

Step 1: Code Phase, Bit Signs, and Doppler Rate Estimation

After SDF process, post-correlation signal \(R\left(n\right)\) in presence of noise can be obtained. Due to influence of Doppler rate and residual Doppler on integration peak, detection can not be performed, and Doppler rate and residual Doppler should be estimated. The differential signal can be obtained based on (9). Due to the influence of bit signs, integration process can performed by (10) and (11). The detection variable \({J}_{\alpha }\left({k}_{\alpha }\right)\) consists of the maximum value corresponding to the code phase and bit signs. Based on set threshold Tα, the unit kα corresponding to correct Doppler rate can be obtained. Above all, code phase, Doppler rate and bit signs can be estimated. In this way, the number of Doppler search can be reduced by compressed Doppler search, and step 2 should never be used when \({J}_{\alpha }\left({k}_{\alpha }\right)<{T}_{\alpha }\), which reduces computational burdens.

Step 2: Residual Doppler Frequency Estimation

Based on bit transition positons, Doppler rate, bit signs, and the post-correlation signal obtained from step 1, the post-correlation signal for step 2 \({\varphi }_{2n}\left(n,{k}_{f}\right)\) can be written as:

$${\varphi }_{2n}\left(n,{k}_{f}\right)={\varphi }_{2}\left(n,{k}_{f}\right)+w\left(n\right)$$
(16)

Since Doppler frequency from compressed Doppler search is too large, when \({M}_{f}=T\), residual Doppler frequency ranges from 250 to − 250 Hz, residual Doppler frequency search should be used. Based on (14), the detection variable \({J}_{f}\left({k}_{f}\right)\) for Doppler frequency estimation detection can be obtained. If Jf is bigger than the set threshold Tf, the estimated Doppler frequency can be obtained. Otherwise, it proves that the signal is absent, or acquisition fails.

4 Performance Analysis

In the high-dynamic environment, there may be no Doppler rate, or it means that Doppler rate = 0 Hz/s2. When Doppler rate ≠ 0 Hz/s, SDHT [10] is chosen as compared method for Doppler frequency hypotheses. To compare with method SDHT [10], LGAM1 is proposed when Doppler rate =0 Hz/s, and can be seen as special case of LGAM where FFT operation is removed in (10). To compare with method DCFT [20], LGAM2 is proposed when Doppler rate ≠0 Hz/s, and is the same process as LGAM. Total MAC has been derived based on search state diagram for complexity analysis, and detection probability of proposed methods have been analyzed in this section.

4.1 Complexity Analysis

Figure 2 illustrates the circular search state diagram of LGAM, where an arrow represents code parallel process and double-FFT based detection for a Doppler frequency hypothesis represented by a node. The overall transfer function [10] of Doppler frequency search for the computational complexity can be found as:

$$G(c)=\frac{{G}_{D}(c)\left[1-{G}_{F}^{{D}_{f}}[c]\right]}{{D}_{f}\left[1-{G}_{F}[c]\left[1-{G}_{M}{\left({G}_{\alpha ,F}(c)\right)}^{{D}_{f}-1}\right]\right]}$$
(17)

where

Fig. 2
figure 2

Search state diagram of LGAM for Doppler frequency hypotheses based on compressed Doppler process

Full size image
$${G}_{D}(c)={P}_{D}{c}^{{N}_{c}}$$
(18)
$${G}_{M}(c)={P}_{M}{c}^{{N}_{c}}+{P}_{f}$$
(19)
$${G}_{F}(c)={c}^{{N}_{c}}$$
(20)

For a Doppler frequency hypothesis, Pf represents FAP under an incorrect Doppler frequency hypothesis H0,f, PD represents detection probability, and PM represents miss probability. Df represents the number of search for Doppler frequency. c denotes the unit computational complexity for a complex multiplication. Nc represents the average number of complex multiplications for a Doppler frequency hypothesis. When Doppler rate α0 = 0 in high-dynamic environment [22], FFT operation is removed in (10) for α0 = 0. In this way, the factor \({\text{exp}}[-{\text{j}}\frac{2\uppi \begin{array}{c}{k}_{\alpha }\end{array}}{\begin{array}{c}{N}_{B0}\end{array}}\begin{array}{c}{n}_{d}\end{array}]\) is removed in (10), and Nc can be written as:

$${N}_{c}=\frac{2{K}_{f}+1}{{D}_{f}}\left(\begin{array}{c}T{N}_{t}{\mathit{log}}_{2}{N}_{t}+2T{N}_{t}+\\ {N}_{t}{N}_{B}^{2}\left({N}_{SB}-1\right)+{N}_{f}+2{N}_{f}{\mathit{log}}_{2}{N}_{f}\end{array}\right)$$
(21)

where \(\begin{array}{c}{K}_{f}\begin{array}{c}{M}_{f}{\Delta }_{f}={f}_{dm}\end{array}\end{array}\), \({f}_{dm}\) represents the maximum value of Doppler frequency \({f}_{d}\). \({D}_{f}=2{K}_{f}{M}_{f}+1\). \({TN}_{t}{log}_{2}{N}_{t}+{2TN}_{t}\) is complex multiplications of code phase parallel process.\({N}_{t}{N}_{B}^{2}({N}_{SB}-1)\) is complex multiplications for the step 1 of LGAM based on (10). Nf is complex multiplications obtained from (13). \({N}_{f}{log}_{2}{N}_{f}\) is complex multiplications of (14). However, it is necessary to calculate the positive and negative value of residual Doppler, it costs \(2{N}_{f}{log}_{2}{N}_{f}\) for the step 2 of LGAM. When Doppler rate α0 ≠ 0 in high-dynamic environment, Nc can be written as:

$${N}_{c}=\frac{2{K}_{f}+1}{{D}_{f}}\left(\begin{array}{c}T{N}_{t}{\mathit{log}}_{2}{N}_{t}+2T{N}_{t}+{N}_{t}{N}_{B}^{2}\left({N}_{SB}-1\right)+\\ 2{N}_{t}{N}_{B}\left({N}_{SB}-1\right){N}_{B0}{\mathit{log}}_{2}{N}_{B0}+{N}_{f}+2{N}_{f}{\mathit{log}}_{2}{N}_{f}\end{array}\right)$$
(22)

where \({N}_{t}{N}_{B}\left({N}_{SB}-1\right){N}_{B0}{\mathit{log}}_{2}{N}_{B0}\) represents complex multiplications of (10). However, it is necessary to calculate the positive and negative value of Doppler rate, it costs \(2{N}_{t}{N}_{B}\left({N}_{SB}-1\right){N}_{B0}{\mathit{log}}_{2}{N}_{B0}\) complex multiplications for calculating (10).

Mean acquisition computation (MAC) [10] is the mean complex multiplications cost to detect correct parameters in GNSS acquisition. The total MAC can be written as:

$$\mathit{MAC}={\mu }_{p}+{\mu }_{f}$$
(23)

where \({\mu }_{p}\) represents complex multiplications in preparing process. \({\mu }_{f}\) represents complex multiplications in Doppler search.

In LGAM, FFT of received signal for code phase parallel search costs \(T{N}_{t}{\mathit{log}}_{2}{N}_{t}\) complex multiplications.

In Doppler frequency search of LGAM, \({\mu }_{f}\) can be written as:

$${\mu }_{f}=\frac{dG\left(c\right)}{dc}\left|c=1\right.=\frac{{N}_{c}}{{P}_{D}}+{N}_{c}\left({D}_{f}-1\right)\left(\frac{1}{{P}_{D}}-\frac{1}{2}\right)$$
(24)

When detection probability is high (Pi,D = 1), the low bound of \({\mu }_{f}\) can be written as

$${\mu }_{fL}=0.5({D}_{f}+1){N}_{c}$$
(25)

To compare with CAMDP, SDHT [10] and DCFT [20], called the FFT-based methods, are used. The total number of complex multiplications of the methods can be shown in Table 1.

Table 1 Low bound of total MAC comparison
Full size table

In Table 1, \({N}_{cs}=\frac{2{K}_{f}+1}{{D}_{f}}T\left({N}_{t}{\mathit{log}}_{2}{N}_{t}+2{N}_{t}\right)+\frac{{D}_{f}-2{K}_{f}-1}{{D}_{f}}\left(\frac{T{N}_{t}}{2}\right)\) [10], Nc1 and Nc2 can be obtained from (21) and (22),

For DCFT method, parallel code process needs T(Ntlog2Nt + 2Nt) complex multiplications. Doppler rate search costs Nt(2NB0 − 1)(T + NB) complex multiplications, and residual Doppler frequency search costs NtNB(2NB0 − 1)(2NSBNflog2Nf) complex multiplications. So \({N}_{cd}=\frac{2{K}_{f}+1}{{D}_{f}}\left(T\left({N}_{t}{\mathit{log}}_{2}{N}_{t}+2{N}_{t}\right)+{N}_{t}\left(2{N}_{B0}-1\right)\left(T+{N}_{B}\right)+{N}_{t}{N}_{B}\left(2{N}_{B0}-1\right)\left({N}_{SB}\times 2{N}_{f}{\mathit{log}}_{2}{N}_{f}\right)\right)\). When T = [20,500] ms, NB0 = NSB (see in the “Appendix”), \({D}_{f}=\frac{[-\mathrm{10,10}]{\text{KHz}}}{{\Delta }_{f}}\), Nt = 2046, and \({N}_{f}=\frac{[\mathrm{0,250}]{\text{Hz}}}{{\Delta }_{f}}\), low bound of total MAC comparison can be drawn in Fig. 3

Fig. 3
figure 3

Low bound of total MAC comparison

Full size image

It can be seen from Fig. 3 that the theoretical total number of complex multiplications increase when the signal length increases. Moreover, since (9) and (10) are adopted, the computational cost of LGAM is much lower than that of SDHT or DCFT methods under the same signal length. When IT is 500 ms and Doppler rate is 0 Hz/s in the high-dynamic environment, the computational cost of SDHT is about 15 times as large as that of LGAM1. Moreover, When IT is 500 ms and Doppler rate is not equal to 0 Hz/s in the high-dynamic environment, the computational cost of DCFT is about 780 times as large as that of LGAM2.

4.2 Detection Probability Analysis

Here, we assume that only one correct code phase, Doppler frequency and Doppler rate hypothesis contains useful signal energy. The detection variables of LGAM can be written as:

$${J}_{i,\Gamma ,k}={\left|{\sum }_{n=1}^{{N}_{\Gamma }}\left({x}_{n}+j{y}_{n}\right)\right|}^{2}={\left({\sum }_{n=1}^{{N}_{\Gamma }}{x}_{n}\right)}^{2}+{\left({\sum }_{n=1}^{{N}_{\Gamma }}{y}_{n}\right)}^{2}$$
(26)

where i = 1, 2 represents LGAM1 or LGAM2. \(\Gamma = \alpha ,{\text{F}}\) represents step 1 or step 2. k = 0, 1 represents the incorrect detection unit or correct detection unit. xn and yn are real numbers. The central limit theorem states that if a sufficient number of summed random variables have a finite variance then the sum will be approximately normally distributed [12]. Based on the theory,\({\sum }_{n=0}^{N-1}{x}_{n}\sim N({\mu }_{x},{\sigma }_{x}^{2})\), and\({\sum }_{n=0}^{N-1}{y}_{n}\sim N({\mu }_{y},{\sigma }_{y}^{2})\), where\({\text{E}}\left({\sum }_{n=0}^{N-1}{x}_{n}\right)={\mu }_{x}\),\({\text{E}}\left({\sum }_{n=0}^{N-1}{y}_{n}\right)={\mu }_{y}\),\({\text{D}}\left({\sum }_{n=0}^{N-1}{x}_{n}\right)={\sigma }_{x}^{2}\), and\({\text{D}}\left({\sum }_{n=0}^{N-1}{y}_{n}\right)={\sigma }_{y}^{2}\). When k = 0, \({\mu }_{x}={\mu }_{y}=0\). E() represents expectation operation. D() represents variance operation. N() represents the normal distribution.

Based on the analysis above, \({J}_{i,\Gamma ,k}\) obeys chi-square distribution 2 degrees of freedom [21], the probability density function (PDF) of \({J}_{i,\Gamma ,k}\) can be written as:

$$p\left({J}_{i,\Gamma ,k}\right)=\frac{1}{2{\sigma }_{i,\Gamma ,k}^{2}}\mathit{exp}\left(-\frac{{J}_{i,\Gamma ,k}+{a}_{i,\Gamma ,k}^{2}}{2{\sigma }_{i,\Gamma ,k}^{2}}\right){I}_{0}\left(\sqrt{\frac{{a}_{i,\Gamma ,k}^{2}{J}_{i,\Gamma ,k}}{{\sigma }_{i,\Gamma ,k}^{4}}}\right)$$
(27)

where \({I}_{0}()\) represents the 0-order modified Bessel function with first kind. \({a}_{i,\Gamma ,k}^{2}={\left({\mu }_{x}\right)}^{2}+{\left({\mu }_{y}\right)}^{2}\). \({\sigma }_{i,\Gamma ,k}^{2}={\sigma }_{x}^{2}={\sigma }_{y}^{2}\).

Under an incorrect Doppler frequency hypothesis \({H}_{0,f}\), \({a}_{i,\Gamma ,k}^{2}=0\), and the FAP of \({J}_{i,\Gamma ,0}\) can be written as:

$${P}_{i,\Gamma ,fa}=P\left\{{J}_{i,\Gamma ,0}\ge {T}_{i,\Gamma }|{H}_{0,f}\right\}=1-{\left({\int }_{0}^{{T}_{i,\Gamma }}p\left({J}_{i,\Gamma ,0}\right)d{J}_{i,\Gamma ,0}\right)}^{{N}_{i,\Gamma }{N}_{t,\Gamma }}\approx 1-{\left(1-\mathit{exp}\left(-\frac{{T}_{i,\Gamma }}{2{\sigma }_{i,\Gamma ,0}^{2}}\right)\right)}^{{N}_{\Gamma }{N}_{t,\Gamma }}$$
(28)

where \({N}_{t,\alpha }={N}_{t}\), \({N}_{t,F}\), \({N}_{i,F}\) represents the number of residual Doppler values. \({N}_{i,\alpha }\) represents the number of Doppler rate values. Under a correct Doppler frequency hypothesis \({H}_{1,f}\), detection probability \({P}_{i,\Gamma ,D}=P\left\{{J}_{i,\Gamma ,1}\ge {T}_{i,\Gamma }|{H}_{1,f}\right\}\) can be written as:

$$ \begin{aligned} P_{i,\Gamma ,D} & = P\left\{ {J_{i,\Gamma } \ge T_{i,\Gamma } |H_{1,f} } \right\} = \mathop \smallint \limits_{T_{i,\Gamma } }^{ + \infty } p\left( {J_{i,\Gamma ,1} } \right)\left( {\mathop \smallint \limits_0^{J_{i,\Gamma ,1} } p\left( {J_{i,\Gamma ,0} } \right)dJ_{i,\Gamma ,0} } \right)^{N_{t,\Gamma } N_{i,\alpha } - 1} dJ_{i,\Gamma ,0} \\ & \approx \mathop \sum \limits_{n = 0}^{N_{t,\Gamma } N_{i,\alpha } - 1} \left( {\frac{{\left( { - 1} \right)^n }}{n + 1}\left( {\begin{array}{*{20}c} {N_{t,\Gamma } N_{i,\alpha } - 1} \\ n \\ \end{array} } \right)\exp \left( {\frac{{na_{i,\Gamma ,1}^2 }}{{2\left( {n + 1} \right)\sigma_{i,\Gamma ,0}^2 }}} \right)Q\left( {\frac{{a_{i,\Gamma ,1} }}{{\sigma_{i,\Gamma ,1} \sqrt {n + 1} }},\frac{{\sqrt {{\left( {n + 1} \right)T_{i,\Gamma } }} }}{{\sigma_{i,\Gamma ,1} }}} \right)} \right) \\ \end{aligned} $$
(29)

When \({P}_{i,\Gamma ,fa}<<1\),\({\left({\int }_{0}^{{J}_{i,\Gamma ,1}}p\left({J}_{i,\Gamma ,0}\right)d{J}_{i,\Gamma ,0}\right)}^{{N}_{t,\Gamma }{N}_{i,\alpha }}\approx 1\), and (29) can be simplified further as:

$$ \begin{aligned} P_{i,\Gamma ,D} & = P\left\{ {J_{i,\Gamma } \ge T_{i,\Gamma } |H_{1,f} } \right\} \\ & = \mathop \smallint \limits_{T_{i,\Gamma } }^{ + \infty } p\left( {J_{i,\Gamma ,1} } \right)\left( {\mathop \smallint \limits_0^{J_{i,\Gamma ,1} } p\left( {J_{i,\Gamma ,0} } \right)dJ_{i,\Gamma ,0} } \right)^{N_{t,\Gamma } N_{i,\alpha } - 1} dJ_{i,\Gamma ,0} \approx Q\left( {\frac{{a_{i,\Gamma ,1} }}{{\sigma_{i,\Gamma ,1} }},\frac{{\sqrt {{T_{i,\Gamma } }} }}{{\sigma_{i,\Gamma ,1} }}} \right) \\ \end{aligned} $$
(30)

Under a correct Doppler frequency hypothesis \({H}_{1,f}\), the miss detection probability \({P}_{i,\Gamma ,M}\).

$$ \begin{aligned} P_{i,\Gamma ,M} & = P\left\{ {J_{i,\Gamma } < T_{i,\Gamma } |H_{1,f} } \right\} \\ & = \mathop \smallint \limits_0^{T_{i,\Gamma } } p\left( {J_{i,\Gamma ,1} } \right)dJ_{i,\Gamma ,0} \left( {\mathop \smallint \limits_0^{J_{i,\Gamma ,1} } p\left( {J_{i,\Gamma ,0} } \right)dJ_{i,\Gamma ,0} } \right)^{N_{t,\Gamma } N_{i,\alpha } - 1} \\ & = \left( {1 - Q\left( {\frac{{a_{i,\Gamma ,1} }}{{\sigma_{i,\Gamma ,1} }},\frac{{\sqrt {{T_{i,\Gamma } }} }}{{\sigma_{i,\Gamma ,1} }}} \right)} \right)\left( {1 - \exp \left( { - \frac{{T_{i,\Gamma } }}{{2\sigma_{i,\Gamma ,0}^2 }}} \right)} \right)^{N_\Gamma N_{t,\Gamma } - 1} \\ \end{aligned} $$
(31)

Under a correct Doppler frequency hypothesis \({H}_{1,f}\), the FAP \({P}_{i,\Gamma ,f}=1-{P}_{i,\Gamma ,M}-{P}_{i,\Gamma ,D}\). The detection probability \({P}_{i,D}\) can be written as:

$${P}_{i,D}={P}_{i,\alpha ,D}{P}_{i,F,D}$$
(32)

Let us consider the GPS L1 CA signal with the following parameter settings: \({f}_{I}\)=0, \({f}_{dm}\)=5 kHz, \({\alpha }_{0}\)=500 Hz/s, \({T}_{I}\)=1/2046000 s, \({N}_{t}\)=2046, \({N}_{B0}\)=\({N}_{SB}\), Doppler rate resolution \({\Delta }_{\alpha }=\frac{1}{{N}_{B0}{T}_{s}}\), compression factor of Doppler frequency \({M}_{f}=T\), detection threshold \({T}_{i,\Gamma }\) is set based on \({P}_{i,\Gamma ,fa}\)=0.0002, and the number of Monte Carlo is 10,000. Based on the settings above, LGAM detection probability of Doppler frequency and Doppler rate can be drawn in Fig. 4.

Fig. 4
figure 4

Detection probabilities comparison for LGAM, DCFT and SDHT (T and S represents theoretical detection probabilities and simulated detection probabilities, respectively)

Full size image

In Fig. 4, the longer the integration time, the larger the detection probability under the same SNR. Since the differential process removes the interaction between two variables Doppler and Doppler rate and reduces SNR value, the detection probabilities of LGAM are lower than the detection probabilities of DCFT and SDHT. This is why MAC of LGAM is larger than that of comparison methods in a relatively low SNR. Moreover, the comparison will be analyzed in the following section. Since LGAM2 needs to detect Doppler rate, the detection probability of LGAM2 is lower than that of LGAM1 under the same IT and SNR. By the way, the detection probabilities can be improved by the set FAP and \({T}_{I}\).

5 Simulation Results

To prove that LGAM has a low computational complexity, this section has been conducted by semi-physical simulation. The methods SDHT and DCFT have been chosen as compared methods with the simulated MAC as the computational criterion. The simulated parameters can be written in Table 2 (Fig. 5).

Table 2 Simulation parameters
Full size table
Fig. 5
figure 5

How to obtain IF signal of the GPS L1 C/A signal

Full size image

The GPS L1 CA signal is produced by the signal simulator (HWA-RNSS-7200) and sent by its antenna. Then, the GPS IF sampled data can be obtained by the IF signal collector. Finally, some noise has been added in GPS IF sampled data for the processing of the following compared methods.

MAC can be obtained from (23), where \({\mu }_{p}\) can be obtained from Table 1 and \({\mu }_{f}\) can be obtained from (24). \({P}_{D}\) in (24) can be obtained from simulation or theoretical Eq. (32). The simulated MAC is calculated by simulated \({P}_{D}\), and the simulated MAC is calculated by theoretical \({P}_{D}\). Above all, total MACs under different SNRs have been shown in Fig. 6.

Fig. 6
figure 6

MAC comparison (S stands for simulated curve, and T stands for theoretical curve)

Full size image

Since LGAM1 adopts FFT to estimate the residual Doppler frequency instead of using adjacent Doppler units search by SDHT, LGAM1 costs lower computation than SDHT does. Therefore, the MAC of LGAM1 is lower than that of SDHT when SNR is higher than − 43 dB. However, MAC is also affected by detection probability \({P}_{D}\), and differential process is adopted by LGAM1. So LGAM1 performs not well in low SNR compared with coherent process in SDHT. So due to the influence of detection probability, LGAM1 costs more computation than SDHT when SNR is lower than − 43 dB.

When Doppler rate is not equal to 0 Hz/s in high-dynamic environment, since LGAM2 adopts the differential process for Doppler frequency and Doppler rate estimation instead of using two-dimension search based on Fourier transform, the computational burdens can be reduced and the MAC of LGAM2 is lower than that of DCFT when SNR is higher than − 46 dB. The same reason with analysis above, LGAM1 costs more computation than SDHT when SNR is lower than − 46 dB.

6 Conclusions

To further reduce the computational burden in high-dynamic situation, this paper has proposed a low-computation GNSS acquisition method (LGAM) for sparse Doppler frequency hypotheses. Compressed factors \({M}_{f}\) was adopted for compressed Doppler process. In this way, compared with parallel code search method, searching all possible Doppler frequency units is not needed, and estimation accuracy can be improved based on the double-FFT based detection for residual Doppler frequency search with low computational complexity. Moreover, the differential signal process based on FFT was adopt for fast Doppler rate estimation in the detection, and Doppler rate resolution was derived based on (10) and (12). In addition, the detection and false alarm probabilities of proposed method were derived. Based on the probabilities, the theoretical MAC was derived. In Fig. 3, the total MAC of LGAM was much lower than that of SDHT and DCFT under moderate SNR when integration times are the same. The simulation proved that although LGAM performed not well in low SNR due to influence of detection probability, the simulated MAC of LGAM was lower than that of SDHT and DCFT under a moderate SNR based on Fig. 6.

7 Discussion

In proposed method, compressed Doppler search and FFT-based code phase estimation have been used in coarse acquisition, and Doppler rate and fine Doppler have been estimated based on differential FFT process in fine acquisition. Moreover, Doppler rate resolution was derived based on theoretical format. The proposed method can be further applied in other GNSS signals such as beidou signal.