1 Introduction

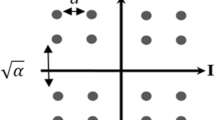
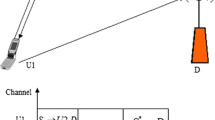
Non-Orthogonal Multiple Access (NOMA) is explored extensively in the literature because of its high spectral efficiency. The uplink communication of NOMA is depicted in Fig. 1. The chief objective of NOMA is that, the users who lie farther from the base-station need more power when compared to the users nearby [1, 2]. Hence, there is a possibility to pair several users on the basis of their channel settings, and allocate them the same time and frequency resources, but differing powers.

Fig. 1
figure 1

NOMA Up Link Communication

Full size image

In the case of switched network systems, packets are considered as the unit of data. The system, in turn, must guarantee that, each packet of data is accurately received for enabling the application which uses the packets for proper functionality. Hence, every packet is safeguarded by 2 defending lines, they are, automatic repeat request (ARQ) and forward error correction coding (FEC). In the receiver end, the channel decoder tries to correct the errors present in the packets received. If the decoding process fails, ARQ is invoked, during which the transmitting unit is requested resend the packets which have errors [3,4,5].

This research work proposes the combination of NOMA and ARQ, to combine the merits of the two and enhance the throughput of the network (Fig. 2).

Fig. 2
figure 2

NOMA Up Link Communications

Full size image

For a greater improvement of uplink communication, we have chosen both cases NOMA and OMA. Practically we observed improvement of channel capacity, throughput, and outage probability.

To improve the throughput of a wireless system as well as reduce the interference among the multiple transmissions, successive interference cancellation helps with the successful decoding of these packets, but it could not achieve the required throughput in [6].

In an orthogonal multiple access technology in [7], author khan discussed OMA plays a vital role in 3G/4G beyond systems. But it is more challenging in the uplink communication systems than downlink communication systems because many to one nature of uplink transmissions and users limit the transmitted power in an uplink transmission. Solutions for this problem need to provide higher spectral efficiency then it becomes more cost expensive.

In OMA interference cancellation is occurred by the perfect orthogonality, it becomes complicated for a greater number of users and also OMA decoding the users based on their signal strength. Hence the capacitance for a far user is declined and outage probability for a far user is increasing [8, 9].

NOMA plays a vital role in 5G communication, like machine-to-machine communication, physical layer security, internet of things, ultra-reliable low latency (URLL), vehicle communication, and higher quality reliable communication, above all are suggested by the author in [10, 11].

According to the author [12], in NOMA power is allocated to users in inverse order, such that maximum power is allocated to the weaker signal strength user and minimum power is allocated to the stronger signal strength user. The rest of the resources are common for all users, such as time, frequency, and spectrum. In NOMA, superimposed users are decoded by the successful interference cancellation technique, such as decoding the weaker signal first, then decoding the rest of the users.

We proposed improving outage probability and throughput [13, 14], and these authors successively lowered outage probability and enhanced throughput. Again, we are focusing on decreasing outages and boosting throughput across many approaches. As well as increasing channel capacity.

The rest of the research paper is organized as follows: In Sect. 2, we discussed the system model for NOMA and OMA on Nakagami and Rician fading channels. Section 3 discussed the improvement of capacity. In Sect. 4, we discussed how NOMA and OMA with ARQ methods may increase throughput and outage probability. Coming to Sect. 5, here we define the outage expression and achievable rate. Define numerical results and comparison between NOMA and OMA schemes in terms of reliability, throughput, and latency. In Sect. 5 Finally, the conclusion was explored.

2 Proposed Model

We consider uplink communications with a limited number of users, which are us1 and us2. Us1 is near the base station and us2 is located farther from the base station. These two users are superimposed by the superposition principle [15]. From this, us1 has greater signal strength, and us2 has weaker signal strength. According to the author, [16] power is allocated to the users in an inverse order [17].

According to the author in [18], in the case of OMA, the base station knows a part of the available resources which are allocated to each user, then users are separated by orthogonality. In the case of NOMA, composite signals are separated (decoded) by the SIC. In NOMA, the base station knows the channel state information of each user. Then, the base station decodes the weakest user signal (us2), hence this decoded signal is separated by the composite signals. In this way, NOMA decodes both users successfully without interference, and the latency of the system is reduced. The information suggested by the author in [18, 19] NOMA performance is better than the OMA in terms of outage probability and throughput. As per the author, the channel capacity of SIC is better than the OMA (Table 1).

Table 1 List of key notations
Full size table

Here, we extend our results by analysing the network throughput for each user when applying the type1 ARQ protocol. According to [20,21,22], type1 ARQ performance is better than hybrid automatic repeat request (HARQ) and chase combined hybrid automatic repeat request (CCHARQ), i.e., lower latency and complexity. In the type-1 ARQ protocol, each user is allowed to retransmit its packet if it receives the NACK feedback from the base station. Which means that packets will not be decoded perfectly. Every user processes an N trail for the transmission of a single packet. It offers high reliability in terms of lower outage probability, especially for the NOMA schemes.

$$\mathrm{X}={\sum }_{j=1}^{L}{h}_{uj}{x}_{uj}$$
(1)

2.1 System Model for NOMA and OMA in Nakagami Channel

Here we study NOMA and OMA for the AWGN channel. Based on the priority, assume the Beata portion of the signal is assigned to the primary user and the rest of the signal is assigned to the second user. In the NOMA case, users can utilize all resources whenever needed. Again, assume that user transmission is uncoordinated. It implies that there will be interference between them. It’s a guarantee that the channel will remain constant for the entire duration of the packet, while our analysis accounts for the short block length effect.

In the general case, y belongs to \({c}^{n}\) consist of n decoded packets, which were transmitted during the coherence interval, then the system model is.

$$\mathrm{Y}={\sum }_{j=1}^{L}{h}_{uj}{x}_{uj}+{w}_{uL}$$
(2)

Here \({h}_{uj}\) is the fading channel effect, for user L, which is used for quasi-static relay fading distributing signals and independent identical packets. \({x}_{uL}\) is the transmitted vector of user L, \({w}_{uL}\) is the additive white gaussian noise vector of user L. Here gaussian channel declared has zero mean circular symmetric gaussian channels and unity variance signals. The OMA scenario implies which part of the received signal is allocated to each user. While in the NOMA scenario which only knows decoding order for SIC [23].

Assume the number of information bits in each transmitted packet is k, thus all the users have the same load. These users are mapped to n number of links for the reduction of transmission delay. For simplicity consider two users with the SIC at the base station, user1 is decoded first and user2 is treated as interference. Afterwards, user1 is removed. The superimposed signal, then user2 can be decoded. Thus, user1 has no interference [24].

In this system, we characterize the individual rates and outage probability for both the users in the NOMA and OMA scenarios. We are proceeding with the Nakagami channel and the Rician fading channel [25].

2.1.1 Nakagami

In the Nakagami channel system model, assume channels have unity gains.

$${\mathrm{Y}=x}_{u1}{h}_{u1}+{x}_{u2}{h}_{u2}+\mathrm{w}$$
(3)

According to the author in [9], the maximum achievable rate ℜ is.

$$\Re = {\text{C}} - \sqrt{\frac{{\boldsymbol{\kappa}}}{n}} Q^{ - 1} \left( {p_{e} } \right)$$
(4)

where the capacity of the network is C, \({\boldsymbol{\kappa}}\) is the characteristics of the channel dispersion and Q is the cumulative Gaussian distribution.

Gaussian function Q(t) is

$$Q\left(t\right)+{\int }_{t}^{\infty }\frac{1}{\sqrt{2\pi }}{e}^{{-s}^{2}}/2ds$$
(5)

Then the channel capacity is C = \({log}_{2}\)(1 + ⍴), \({\boldsymbol{\kappa}}\) (P) is channel dispersion.

$${\boldsymbol{\kappa}}\left( \uprho \right) = \left( {1 - \frac{1}{{\left( {1 + \rho } \right)^{2} }}} \right) log_{2}^{2} {\textit{e}}$$
(6)

The probability of error is

$$p_{e} = \left( {1 + \frac{{g\rho_{s} }}{{\sin^{2} \Theta }}} \right)^{ - 1}$$
(7)

From Shannon Heartly law,

$${\text{C}} = {\text{B}}\log 2\left( {1 + {\text{r}}} \right)$$
(8)

The number of transmission bits is k then the throughput of the system is

$$\eta = \frac{1}{{\left( {\frac{k}{n}(1 - p_{e} )} \right)^{ - 1} }}$$
(9)

The order of the system vanished as n changes hence neglected those order terms. Compute the individual user rates for the OMA scenario. In OMA's successful decoding rate are.

$$\Re_{{{\text{u}}1}} = {\text{C}}\left( \rho \right) - \sqrt {\frac{{\boldsymbol{\kappa}}\left( \rho \right)}{{\beta n}}} Q^{ - 1} \left( {Pe} \right)$$
(10)
$$\Re_{u2} \left( \uprho \right) = 1 - \sqrt {\frac{{\boldsymbol{\kappa}}\left( \rho \right)}{{\left( {1 - \beta } \right)n}}}$$
(11)

From these β refers to the amount of resource that we allocated to the initial user.

The performance of the system is evaluated based on the outage probability transmission, the system outage probabilities are \(p_{e1}\) and \(p_{e2}\) [14].

$$p_{e1} = {\text{Q}}\left( {\frac{{C(P_{u1} ) - k}}{{\sqrt {n\beta {\boldsymbol{\kappa}}\left( {P_{u1} } \right)} }}} \right)$$
(12)
$$p_{e2} = Q\left( {\frac{{C\left( {\rho_{u2} } \right) - k}}{{\sqrt {n\left( {1 - \beta } \right){\boldsymbol{\kappa}}\left( {\rho_{u2} } \right)} }}} \right)$$
(13)

For the NOMA case, it assumed that,

$$\rho_{{u1 = P_{u1} }} \;{\text{and}}\;\rho_{u2} = \frac{{P_{u2} }}{{1 + P_{u1} }}$$
(14)

An outage probability and rates are defined by adjusting the value of β, for the first user \({\beta }_{u1}\)=1 and second user \({\beta }_{u2}\)=0. Now shows those equations are.

$$p_{e} = Q\left( {\frac{{C\left( \uprho \right) + 0.5log_{2 - K}^{n} }}{{\sqrt {n{\boldsymbol{\kappa}}\left( \rho \right)} }}} \right)$$
(15)

The applied modification technique is to a quasi-static Rician fading channel.

2.1.2 Quasi-Static Rician Fading Channel

Channel coefficient h is constant for quasi-static Rician fading channel, then the exponential distributed probability density function is in [26, 27].

$$\mathrm{Y}={x}_{u1}{h}_{u1}+{x}_{u2}{h}_{u2}+\mathrm{w}$$
(16)

The maximum channel rate in the quasi-static Rician fading channel is

$$\Re = log_{2} \left( {1 + \rho_{u1} } \right) - \sqrt{\frac{{\boldsymbol{\kappa}}}{n}} Q^{ - 1} \left( \varepsilon \right) + {\text{O}}\left( {\frac{{log^{n} }}{n}} \right)$$
(17)

where \(O\left( \frac{logn}{n} \right)\) is the remainder term is the number of channels use n increases, the order becomes close to zero Then the capacity of the network is?

$${\text{C}} = log_{2} \left( {1 + \uprho } \right)$$
(18)

The outage capacitance is defined in terms of channel capacitance

$$C_{e} = {\text{super imposed}}\left( {{\text{R}}:log_{2} \left( {1 + \rho } \right)} \right) < \Re < p_{e}$$
(19)

The squared envelope of the coefficient is Z = \(e^{ - z}\).

Rate ℜ = k/n, here several information bits are k, no of the channel used for transmission is n. Then the outage probability of quasi-static Rician fading channel is in [27]

$$p_{e} = \frac{1}{2}\left[ {1 - \sqrt {\frac{{\left( {\beta \rho /\sqrt 2 } \right)^{2} }}{{(\rho + 1)^{2} - \left( {\beta \rho /\sqrt 2 } \right)^{2} }}} \exp - \frac{{\left( {2 - \sqrt 2 } \right)k\rho /2}}{{\left( {\rho + 1} \right)^{2} - \left( {\beta \rho /\sqrt 2 } \right)}}} \right]$$
(20)

From an OMA scenario in [4].

The error probability approximation in [5, 7] OMA scenario is written as Q(f(z)),

$$W\left( z \right) = {\text{Q}}\left( {{\text{f}}\left( {\text{z}} \right)} \right) = \left\{ {\begin{array}{*{20}c} 1 & {if} & {z \le \sigma_{ui} } \\ {0.5 - \frac{{b_{ui} }}{{\sqrt {2\pi } }}b^{m} } & {if} & {\sigma_{i} < z < \delta u_{i} } \\ 1 & {if} & {z \ge \theta_{ui} } \\ \end{array} } \right.$$
(21)

where \({\theta }_{u1}\)=\(\frac{{e}^{\frac{k}{\beta n}-1}}{{\rho }_{u1}}\), \({\theta u}_{2}\)=\(\frac{{e}^{\frac{k}{(1-\beta )}}n}{{\rho }_{u2}}\)

$$b_{u1} = \sqrt {\mathop {\frac{{\beta n\rho_{u1}^{2} }}{{e^{{\frac{2k}{{\beta n}} - 1}} }}}\limits_{1} } ,\;\;b_{u2} = \sqrt {\frac{{\left( {1 - \beta } \right)n\rho_{u2}^{2} }}{{e^{{\frac{2k}{{n\left( {1 - \beta } \right)}} - 1}} }}}$$

By consider the NOMA scenario from the above equation we solve, we set \(\beta\) values 0 and 1 respectively.

In [5] integration of outage probability is Peaverage.

$$P_{eaverage} = \int\limits_{0}^{\infty } {P_{s} (\rho )P_{{\rho_{s} }} \left( {\left( \rho \right)} \right)} d\rho$$
(22)

To find the expression for the outage probability, Pei, each user is assumed to have the same probability.

For (i = 1,2),

$$p_{ei} = 1 - \frac{{b_{ui} }}{{\sqrt {2\pi } }}e^{{ - \theta u_{i} \left( {e^{{\frac{\pi }{{2b_{ui}^{2} }}}} - e^{{\frac{\pi }{{2b_{ui}^{2} }}}} } \right)}}$$
(23)

Appling NOMA with SIC to make the channel interference-free. In this technique, u2 decodes first, hence interference is much larger than noise, thus approximation is given by the author.

$${\rho }_{u2}\left(\mathrm{z}\right)=\frac{{{|h}_{u2}|}^{2}{p}_{u2}}{{{|h}_{u1}|}^{2}{p}_{u1}}$$
(24)

Then the NOMA user2 outage probability is given by [14]

$$\begin{aligned} p_{1} & = \frac{1}{{\left( {\frac{{2\frac{{b_{u2} }}{{\sqrt {2\pi } }}p_{u2}^{2} (\delta_{u2} - \delta_{u1} + 2p_{u1}^{2} \delta_{u2} \rho_{u2} }}{{2(p_{u2} + p_{u1} \delta_{u2} )^{2} }}} \right)^{ - 1} }} \\ p_{2} & = \frac{1}{{\left( {\frac{{2\frac{{b_{u2} }}{{\sqrt {2\pi } }}p_{u2} \log ((p_{u1} \delta_{u2} + \delta_{u1} )/(p_{u1} \delta_{u1} + \delta_{u2} )}}{{p_{u1} }}} \right)^{ - 1} }} \\ p_{3} & = \frac{1}{{\left( {\frac{{p_{u1} p_{u2} (\delta_{u1} + \delta_{u2} )2\frac{{b_{u2} }}{{\sqrt {2\pi } }}\theta_{u2} \delta_{u2} - 2\frac{{b_{u2} }}{{\sqrt {2\pi } }}\theta_{u2} \delta_{u2} }}{{2(p_{u2} + p_{u1} \delta_{u2} )^{2} }}} \right)^{ - 1} }} \\ p_{e2} & = \frac{1}{{(p_{1} + p_{2} + p_{3} ) - 1}} \\ \end{aligned}$$
(25)

2.2 Applying ARQ Technique for Enhancement of Throughput

In a modern wireless system, requiring high data rates and reliability, it is possible through incremental redundancy (IR), redundancy (RR), ARQ, and HARQ. ARQ provides better performance than HARQ and IR. Ultra-reliable low latency communication (URLLC) plays a significant role in wireless communication. But it is a risky task for multiple transmissions. The outage probability for both users is relatively high.

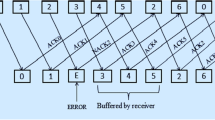
The author explained that in retransmitting the information based on the feedback acknowledgement if a positive acknowledgement is received, no error is detected during the execution. Hence, it sends new information otherwise requested to retransmit the same information until successful decoding of the information. The outage probability for N transmission is \(p_{eN}\).

$$p_{eN} = \prod\limits_{m = 1}^{n} {p_{em} }$$
(26)

In the above equation, \({\in }_{um}\) is represents the outage probability for the \({m}^{th}\) transmission, the outage probability for the first transmission is unity i.e., \({\in }_{0}=1\).

In this system, outage probability is increasing due to the presence of feedback. Hence, the throughput of the system is declining. According to the author, the overall system throughput after applying ARQ is

$$\eta_{ui} = \frac{1}{{(\frac{k}{n}(1 - p_{ei} ))^{ - 1} }}$$
(27)

According to the author, [15] is defined that, for each transmission spectral efficiency is reduced, the result for the \({m}^{th}\) transmission of ARQ round is R=\(\frac{k}{mn}\) then the overall throughput with feedback delay is

$$\tau = {\text{mn}}\mathop \sum \limits_{i = 1}^{m} p_{ei - 1} + {\text{D}}\left( {{\text{m}} - 1} \right) \mathop \sum \limits_{i = 1}^{m - 1} p_{ei - 1}$$
(28)

Here, D is the feedback delay for channel use and the outage probability is equal for all the transmissions, but the packet dropping probability is independent for each transmission.

According to the author [15], for successful transmission without error and boosting system reliability, the order of the system has been chosen so that the power required for the number of information bits transformation is Ƙ = k (1 − \(p_{en}\)). You may know that the throughput is the ratio between the number of information bits transformed to channel uses.

$$\eta_{ui} = \frac{1}{{(k\backslash \tau )^{ - 1} }} = \frac{{k\left( {1 - p_{en} } \right)}}{{{\text{mn}}\mathop \sum \nolimits_{i = 1}^{m} p_{ei - 1} {\text{ + D(m}} - 1{)} \mathop \sum \nolimits_{i = 1}^{m - 1} p_{ei - 1} }}$$
(29)
$$t_{m} = \frac{{k\left( {1 - p_{ei}^{n} } \right)}}{{\left( {1 + \left( {M - 1} \right)p_{ei} } \right)\left( {Nn} \right) + D\left( {N - 1} \right)}}$$
(30)

3 Capacity Improvement

Capacity improvement is a major tool for feature generation communications. There are various ways to improve capacity.

3.1 Network Capacity for TDMA

In TDMA, user1 and user2 transmit alternatively. Assume each user transmits an unequal distance. The author analyses the mathematical capacity of [8, 28].

$$C_{tdma} = {{\text{B}} \mathord{\left/ {\vphantom {{\text{B}} 2}} \right. \kern-0pt} 2}log_{2} \left( {1 + {{s_{u11} } \mathord{\left/ {\vphantom {{s_{u11} } {n_{u1} }}} \right. \kern-0pt} {n_{u1} }}} \right) + {{\text{B}} \mathord{\left/ {\vphantom {{\text{B}} 2}} \right. \kern-0pt} 2}log_{2} \left( {\frac{{s_{u12} }}{{n_{u2} }}} \right)$$
(31)

Here \({n}_{u1}\), \({n}_{u2}\) are noise power levels at ap1, B is the channel bandwidth.

3.2 Network Capacity for NOMA

In NOMA, AP1 perform successive interference cancellation, for successful decoding of user1 and user2.

At AP1 the sum capacity for the user1 is

$$C_{u11} = {\text{B}}log_{2} \left( {1 + {{s_{u11} } \mathord{\left/ {\vphantom {{s_{u11} } {n_{u1} }}} \right. \kern-0pt} {n_{u1} }}} \right) + {\text{B}}log_{2} \left( {\frac{{s_{u12} }}{{n_{u2} }}} \right)$$
(32)

Capacity an AP1 due to the user2 is

$${C}_{u12}=\mathrm{B}{log}_{2}\left(\frac{{s}_{u12}}{{n}_{u2}+{s}_{u11}}\right)$$
(33)

Then the successive interference cancellation at AP1 is \({C}_{sic}\)

The above analysis convey that the capacity of TDMA is overcome by the \({C}_{sic}\).

$$C_{sic} > C_{tdma}$$
(34)

the capacity relation between NOMA and OMA is explained by the author in [17]

$$\begin{aligned} C_{OMA} & = \log_{2} \left( {\uprho \sqrt {\beta_{u1} *\beta_{u2} } } \right) \\ C_{NOMA} & = \log_{2} \left( {\uprho *\beta_{u1} } \right) \\ C_{NOMA\;\& \;OMA} & = \frac{1}{2}\log_{2} \left( {\frac{{\beta_{u1} }}{{\beta_{u2} }}} \right) \\ \end{aligned}$$
(35)

The improved capacity of NOMA over TDMA depends on the RSS of the link. For example, if we pick up su11 = 10db, su12 = 6db, nu1 = nu2 = 5db, B = 0–100 dB, then we achieved = 10 dB, and = 10 dB. Those results increased linearly with the bandwidth.

4 Practical Observations

The experimental results show that NOMA performs better than OMA in both cases, including with ARQ and without ARQ, and the results are compared with [14, 15]. It even proved that the call dropping probability (outage probability) of NOMA is the minimum when compared with OMA. In this scenario, we have considered a limited number of resources for simplicity.

The outage probability of NOMA is minimum compared with OMA. The outage probability is reduced when applying ARQ as shown in Fig. 4

Figure 3. 2 × 2 network with two clients and two APs. The capacitance of TDMA and NOMA increases almost linearly with the bandwidth. Here, AP1 receives the signals from both clients, user1 and user2.

Fig. 3
figure 3

Capacity versus Bandwidth of NOMA and TDMA

Full size image

In the Nakagami channel, we consider a limited number of resources that are block length N = 5000, several users k = 50 to 100, and power supply p = 10 dB. We observed an outage probability for both NOMA and OMA scenarios, and also an individual difference was observed, including with ARQ and excluding with ARQ. From the result, it is clear that the outage probability of OMA is more than NOMA. It also proves that the outage probability of NOMA and OMA has been reduced by applying an ARQ technique. It is depicted in Fig. 4.

Fig. 4
figure 4

2 × 1 network Outage probability for NOMA and OMA with ARQ and without ARQ

Full size image

The throughput graph for the Nakagami channel is observed in Fig. 5, which is the result of NOMA versus OMA without ARQ. The resources used for practical observation are blocked length N = 1, the number of users k = 1 to 4, and power supply p1 = 10db, p2 = 3db. The throughput of NOMA has almost increased, but, in OMA, it is declining rapidly. Overall performance shows that the throughput of NOMA is better than OMA.

Fig. 5
figure 5

NOMA versus OMA without ARQ the throughput of the system reduces rapidly

Full size image

For the Nakagami channel, we examined the throughput of individual multiple access techniques. For this purpose, we chose the number of users k = 2 to 10, block length N = 2, power per each user is 20db, the secondary user is 10db, and the number of retransmissions n = 2. In Fig. 6, we plot the throughput for NOMA and OMA with ARQ as a function of the number of users. It is observed that NOMA versus OMA with ARQ provides better throughput than without ARQ.

Fig. 6
figure 6

NOMA versus OMA with ARQ the throughput of the system increasing approximately linear

Full size image

5 Conclusion

In this paper, we have done a capacity comparison between NOMA and OMA. The capacity of NOMA overcomes OMA. Again, compare NOMA and OMA in various aspects, such as throughput, outage probability, and power with respect to the number of finite blocks length in both relays fading channel and AWGN channel. We have observed a result that shows NOMA allows transmission rates with higher throughput than OMA and thus NOMA overcomes OMA. When Appling NOMA with ARQ does not provide a satisfactory level of throughput for a higher number of transmission levels, but the reliability of the system has been enhanced in terms of throughput optimization. Even though NOMA has provided better performance than OMA in terms of outage probability, throughput optimization, and power domain. Through practical observation, outage probability is rising when an increasing number of information bits while the throughput of the system is reduced. Solutions for this problem cooperative NOMA-ARQ may provide better results for this problem. Machine learning with NOMA provides multiple user transmissions.