1 Introduction

The Internet of Things (IoT) is increasingly applied in diverse fields, improving people's lives and promoting the comprehensive development of society. IoT utilizes collected data for logistics tracking, environmental monitoring, medical analysis and other services. Internet of Medical Things (IoMT) is mainly composed of patients, doctors and medical data collection equipment. In IoMT, the health data of patients is collected in real-time through mobile devices and stored in the network servers for access by legitimate medical personnel to facilitate monitoring, diagnosis and treatment services for patients. Cloud computing is favored by more and more users due to its advantages of low cost, high speed and almost unlimited storage capacity. Likewise, in IoMT, patients are more inclined to store their own data in the cloud in order to share it with healthcare workers. Considering the security aspect [1], it is necessary to guarantee that the collected data is not eavesdropped and leaked. This will be achieved by data encryption. Among them, the receiver and sender of the data share a pair of keys, that is, the sender performs encryption operations through the shared key, and the receiver uses this key to restore the original data.

Group-oriented applications have been developed for various applications to jointly collect data [2,3,4]. As an example, data collected jointly for logistics tracking, environmental monitoring, multi-user interactive computing, etc. The basic function of group-oriented applications is to build a secure communication environment for all group members. Therefore, it is necessary to ensure that the collected data is not eavesdropped or tampered.

Many scholars have conducted research in secure group communication, and they have designed methods for establishing group keys using diverse encryption techniques, such as Shamir's secret sharing [5], homomorphic encryption [6], oblivious [7] or trusted third party [8], etc., for secure communication between group users. At present, security group communications have attracted wide attention [2], and have great progress [9,10,11,12]. For example, at present, secure group communication has been applied to heterogeneous vehicle networking systems, military communication systems, satellite communication systems [3] and other fields.

Based on the method that the key generation center needs to be active all the time, Laih et al. [13] designed the first threshold secret sharing method to broadcast the secret parameter to the members. Subsequently, some researchers made further efforts based on this scheme [14,15,16,17]. The non-interactive nature of the group key establishment scheme makes it more effective than most interactive schemes. For instance, in IEEE 802.11i standard [18], the server generates a secret group key, and uses the paired key shared between it and the mobile device to encrypt this group key to ensure the security. And then each mobile device will receive the ciphertext of the corresponding key sent by the server for secure group communication. Wu et al. [14] used symmetric binary polynomial management to distribute group keys for secure communication across multiple groups. It is more effective than point-to-point communication.

Recently, Cheng et al. [19] applied a multivariate polynomial based on the RSA modulus to present a new inter-group key generation scheme. For m members participating in group communication in this scheme, each needs to store (\(m-1\)) univariate polynomial coefficients, and needs to compute (\(m-1\)) univariate polynomials to recover the group key. Another protocol using asymmetric bivariate polynomials to establish group keys was designed in [20], where two univariate polynomials of order \(t-1\) and \(h-1\) still need to be stored. [21] proposed a new non-interactive scheme for 5G sensor network, which simultaneously realizes the authentication of members and the computational output of group arithmetic. And it used as a group arithmetic computation output scheme.

Mahender et al. [22] provided an aggregated sign encryption scheme for cloud-centric IoMT systems, in order to achieve data transmission security. A secure authentication scheme for medical sensor networks has been proposed in [23], which uses biometric keys to establish secure data transmission between patients and local processing units. In [24], a community cloud-based security and privacy-aware mobile healthcare framework was proposed for application in the IoMT, which provides effective authentication and access control for patients. A data sharing scheme applied to cloud-assisted IoMT system was designed by Hao et al. [25]. This scheme utilizes attribute encryption and proxy re-encryption method to guarantee the data is secure. Zhou et al. [26] designed a novel security proposal suitable for IoMT which mainly uses the authentication handshake protocol to ensure secure communication in medical environment.

The above excellent recent schemes implement group key distribution and arithmetic computation, but there is a problem that the communication cost increases with the number of users. Resource-constrained IoMT devices are always limited by computational, energy, communication or range capabilities. Thus, based on the above communication challenge, a novel proposal of lightweight and fast membership authenticated group key agreement for resource-constrained IoMT devices is presented in this paper. Our proposal simultaneously realizes the authentication of members and the negotiation of group keys. More importantly, it solves the problem that the above-mentioned member-side communication consumption is affected by the number of members in the group.

We apply symmetric binary polynomial and XOR operations to construct this lightweight and fast membership authentication group key agreement. First of all, after generating a univariate polynomial by the Membership Registration Center (MRC), members can get their own token. The role of the token is to distribute pairwise shared secrets and authenticate the identities of members. Then, by using XOR operation functions, except for the initiator member, other members use the shared keys to mask their input and broadcast the masked value directly without encryption. Only the initiator member needs to encrypt his own masked value before transmitting it to other users in group. Finally, the group key is efficiently calculated by each member based on all the published information collected. The designed protocol is potentially attractive for resource-constrained IoMT devices.

The main contributions can be summed up as follows.

  • This paper designs a membership authentication group key protocol for resource-constrained IoMT devices based on a binary polynomial that is used to generate tokens to authenticate members, generate shared secrets, and establish group keys.

  • Our method is effective because there is no need to additionally authenticate members and assign pairwise shared keys. Logic XOR as the main calculation method greatly reduces the calculation overhead, which is the outstanding advantage of this scheme. More importantly, the cost on communication for group members is not affected by the number of members.

  • Our scheme is resistant to both internal and external attacks. Moreover, the security analysis proves that this solution meets all the defined security characteristics.

Organization: We introduce the relevant preliminaries in Sect 2, describe the model of the presented scheme in Sect 3. And this proposal is designed in Sect 4. We demonstrate security and analyze performance in Sect 5. Finally, we summarize this study in Sect 6.

2 Preliminaries

In Shamir’s \((t,n)\) secret sharing [5] scheme, \(s\) is a secret that needs to be protected and it is concealed in the polynomial as a constant term. A \(t-1\) degree polynomial \(f(x)\) is randomly selected by the trusted dealer and used to produce shares, \(f({x}_{i})\mathit{mod}p,\) for shareholders, where \(i=\mathrm{1,2},\dots ,n\), \(f(0)=s\), \(p\) is a prime and \(p>s,\) \({x}_{i}\) refers to the public identifier of shareholder. There are also some researchers using bivariate polynomials to design \((t,n)\) secret sharing protocols [27,28,29,30,31,32], which have been widely used.

\(F(x,y)={\sum }_{i=0}^{t-1}{\sum }_{j=0}^{t-1}{a}_{i,j}{x}^{i}{y}^{j}mod p\) is a bivariate polynomial of order \(t-1\), where \({a}_{i,j}\in GF\left(p\right)\) and \(p\) is a prime. Binary polynomials are divided into two types: symmetric and asymmetric. The coefficients of a symmetric bivariate polynomial satisfy the equation \({a}_{i,j}={a}_{j,i},\forall i,j\in [0,t-1]\). In symmetric case, the dealer randomly picks a \(t-1\) degree symmetric binary polynomial, \(F(x,y),\) where \(F(\mathrm{0,0})=s,\) \(p>s,\) and \(s\) refers to the secret. Each participating shareholder \({U}_{i}\) is allocated a share, \(F({x}_{i},y)\mathit{mod}p,i=\mathrm{1,2},...,n,\) which is a \(t-1\) degree univariate polynomial generated by the dealer. \({x}_{i}\) refers to the public identification information of shareholder, \({U}_{i}.\) It should be noted that the share is generated by a symmetric polynomial, so it satisfies \(F({x}_{i},{x}_{j})=F({x}_{j},{x}_{i}),\) \(\forall i,j\in [0,t-1]\). And then, a pair of shared keys \(F({x}_{i},{x}_{j})=F({x}_{j},{x}_{i})\) can be calculated between shareholders \({U}_{i}\) and \({U}_{j}.\)

This paper designs a novel lightweight and fast membership authenticated group key agreement, which can be effectively applied to resource-constrained IoMT devices. The tokens generated by the scheme are used for the following purposes: (a) authenticate the identity of the user; (b) establish pairwise shared keys; (c) distribute the group secret key. It can also be said that the constructed scheme implements the above three operations. The proposed scheme provides users with the functions of identity verification and group key negotiation. Further, compared with most existing schemes of the same type [33,34,35], our scheme greatly reduces communication and computational overhead. More importantly, the increase in the number of group members does not impose any burden on the members.

3 Model of the Presented Scheme

In this section, we introduce the network model and security model of the proposed scheme in detail.

3.1 Network Model

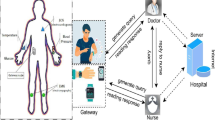
A typical IoMT model contains four types of entities, namely Trusted Authority (TA), patients, Cloud Severs (CS) and users. Here users refer to medical professionals who use privacy-protected data to provide medical diagnostic services to patients, and to conduct public health data mining. In addition, TA plays the role of a Membership Registration Center (MRC), which is fully trusted. In the IoMT, patients, users and other entities and devices connected through the Internet are closely connected to achieve efficient patient-to-user and user-to-user communication. Secure group communications are necessary in a typical IoMT model to realize bioinformatics data analysis (see Fig. 1). The constructed proposal ensures the security of group communication in the IoMT model, where patients, users, and other entities and devices are able to participate in group communications.

Fig. 1
figure 1

A typical IoMT model

Full size image

In the network model for resource-constrained IoMT described by our scheme, there are \(n\) participating users \(\{{U}_{1},{U}_{2},\dots ,{U}_{n}\}\) and a trusted registration center MRC, as shown in Fig. 2. Users who need to obtain group communication services should first register with MRC, including adding new users to the system and deleting logged-out users.

Fig. 2
figure 2

Group communications for resource-constrained IoMT

Full size image

It is critical to negotiate a group key to guarantee secure conversation among members of the group. For instance, a group key is established before a group message exchanged, so that all users can calculate jointly with their secret inputs. The proposed scheme assumes that the members participating in the communication will all abide by the protocol. Hence, before negotiating a secret group key for \(\mathrm{m}\) group members, which m > 2 and m < n, it is necessary to mutually verify the legitimacy of their identities to prove that they belong to the same communication group. To authenticate the identities of the members, it is first necessary to distribute keys for each member.

The designed proposal needs to distribute tokens to members for identity verification. The tokens are obtained secretly from the MRC, and produced using a symmetric binary polynomial.

Before computing the shared secret using its own secret token, each group member requires to broadcast an integer picked at random to other group members. The output value obtained by the hash function operation of the pairwise key is used as the authentication response of each member, which can verify the identity of the member. In other words, by verifying this response, it can be determined whether the member belongs to the same group. After the authentication phase, the identity of each member participating in the group communication is mutually determined. After that, except for the initiator member, other members involved in the communication use shared key to hide their input through XOR operation, and broadcast the masked value directly without encryption. Only the initiator member needs to encrypt the mask value before sending it to other members. Subsequently, members use the collected published data to generate the group key without the interaction of the users participating in the communication. The transmission mode of broadcast enables the presented scheme to effectively complete the authentication of members and the distribution of group keys. Since only lightweight operations such as logical XOR are used, our protocol greatly improves the computational efficiency. Furthermore, the non-interactive nature of the scheme ensures that the communication overhead of the client is not affected by the size of group. The performance evaluation of our program is analyzed in detail in Sect 5.

3.2 Security Model

The security model of the presented scheme is introduced in this subsection, and the detailed analysis is demonstrated in Sect 5.

3.2.1 Type of Attackers

This scheme mainly considers attacks from internal attackers and external attackers. Insider attackers usually refer to legitimate users with tokens. Attackers try to launch internal attacks using their own tokens to obtain secrets. In contrast, external attackers refer to unregistered illegitimate users without tokens. Attacker attempts to produce authentic tokens to impersonate legitimate users.

3.2.2 Security Features

It is crucial to ensure that the following security features are satisfied for secure group communication.

  1. (a)

    Correctness Only if all members of the group follow the rules can group authentication be performed to generate the correct secret group key.

  2. (b)

    Replay attack resistance of authentication response Responses used by group members to authenticate their identities are one-time and cannot be reused.

  3. (c)

    Replay attack resistance of group keys The generated group key is fresh and can only be used once.

  4. (d)

    Replay attack resistance of the group key authentication The message used to verify the group key is one-time.

  5. (e)

    Forward secrecy of group keys Users who participated in previous group communications do not know the current group key.

  6. (f)

    Backward secrecy of group keys The former key is not known to users participating in the current group communication.

4 Our Presented Scheme

In this section, a lightweight and fast membership authenticated group key agreement scheme is presented using a binary symmetric polynomial, which is based on XOR operation. Our proposal is shown in Fig. 3.

Fig. 3
figure 3

the steps of membership authentication and group key agreement

Full size image

5 Analysis

5.1 Security Analysis

First, we analyze how the scheme satisfies the security properties defined in Sect 3. B and how it resists various attacks in this section.

5.1.1 Security Features

  1. (a)

    Correctness:

    Membership authentication- \({k}_{i,j}\) can be calculated in Step 2 only if each member \({U}_{i}\) participating in the group communication has passed the identity authentication. Hence, the response value \({Auth}_{i,j} =h\left({k}_{i,j}\parallel {r}_{j}\right)\) in Step 4 is used to verify the membership of \({U}_{vi}\) to \({U}_{vj}\). Unregistered users cannot pass authentication because they do not possess valid tokens distributed by MRC.

    Group key establishment- The XOR operation rule ensures the correctness of this security feature. Since \({q}_{{{v}_{i}}_{.}}={s}_{i}\oplus {k}_{i,1}\oplus {k}_{i,2}\oplus \dots {\oplus {k}_{i,j}\oplus \dots \oplus k}_{i,m}mod p, \mathrm{where} i,j=\mathrm{1,2},\dots ,m, \mathrm{and} j\ne i\), we can obtain \({q}_{{{v}_{i1}}_{.}}\oplus {q}_{{{v}_{2}}_{.}}\oplus \dots \oplus {q}_{{{v}_{i}}_{.}}\oplus \dots \oplus {q}_{{{v}_{m}}_{.}}mod p={s}_{1}\oplus {s}_{{2}_{.}}\oplus \dots \oplus {s}_{{i}_{.}}\oplus \dots \oplus {s}_{m}mod p={K}_{i}.\)Group key authentication- If the verification \(H({K}_{1}||L)=H({K}_{2}||L)=\cdots H({K}_{i}||L)=\cdots =H({K}_{m}|\left|L\right)\mathit{mod}p\) holds for each group member, \(K\) is confirmed as the group key.

  2. (b)

    Replay attack resistance of authentication response: \({Auth}_{i,j} =h\left({k}_{i,j}\parallel {r}_{j}\right)\) is generated by a hash function, and the shared secret key \({k}_{i,j}\) and the integer \({r}_{j}\) randomly picked by \({U}_{{v}_{j}}\) are used as the input of \(h()\). Since \({r}_{j}\) is randomly selected in each authentication process, the freshness of \({Auth}_{i,j} =h\left({k}_{i,j}\parallel {r}_{j}\right)\) is guaranteed. Therefore, the scheme can resist replay attacks in the authentication stage.

  3. (c)

    Replay attack resistance of group keys: \(K={s}_{1}\oplus {s}_{{2}_{.}}\oplus \dots \oplus {s}_{{i}_{.}}\oplus \dots \oplus {s}_{m}mod p\) is generated by the secret input \({s}_{i}\) of \({U}_{{v}_{i}}\). The randomness of \({s}_{i}\) ensures that the group key \(K\) is fresh in each round of sessions.

  4. (d)

    Replay attack resistance of the group key authentication: \(H({K}_{i}||L)\) is calculated by hashing \({K}_{i}\) and \(L\), where \({K}_{i}\) is the XOR sum of the secret value \({s}_{i}\) and \(L\) is the XOR sum of the integer value \({l}_{i}\). \({K}_{i}\) and \(L\) are randomly generated in each round of sessions, ensuring the freshness of \(H({K}_{i}||L)\). Therefore, the replay attack in the group key authentication process can be resisted

  5. (e)

    Forward secrecy of group keys: The key \(K\) of each round of session is negotiated by the members currently participating in the group communication and is unknown to the former members.

  6. (f)

    Backward secrecy of group keys: The new key \(K\) of each round of session is negotiated by the group members involved in the current communication, and the previous key is unknowable to new users.

5.1.2 Possible Attacks

Theorem 1

Internal Attack- Rebuilding the tokens require at least \(t\) internal attackers to participate in it. The secret polynomial \(F(x,y)\) can resist the joint recovery of at most \(t-1\) colluded members.

Proof

The inside attackers refer to users who have registered with MRC, and have their own valid tokens. The tokens are generated by \(F(x,y)={a}_{\mathrm{0,0}}+{a}_{\mathrm{1,0}}x+{a}_{\mathrm{0,1}}y+{a}_{\mathrm{1,1}}xy+\cdots +{a}_{t-1,t-1}{x}^{t-1}{y}^{t-1}\mathit{mod}p\) with degree \(-1\), which is symmetric and has \(\frac{t(t+1)}{2}\) different coefficients. And, each token \({s}_{i}(y)\) is a \(t-1\) degree univariate polynomial. If \(h\) users with tokens collude together, \(h\cdot t\) equations can be constructed, and \({C}_{2}^{h}\) pairs of shared keys are obtained. Thus, \(h\) colluding users, i.e. insider attackers, can obtain \(h\cdot t-{C}_{2}^{h}\) linear independent equations. It is impossible to recover \(F(x,y)\) when the insider attacker has a number of linear independent equations less than the coefficient of\(F(x,y)\), (i.e.,\(\frac{t(t+1)}{2}>h\cdot t-{C}_{2}^{h}\)). Therefore, they can’t know any information of the secret. From the inequality \(\frac{t(t+1)}{2}>h\cdot t-{C}_{2}^{h}=h\cdot t-\frac{h(h-1)}{2},\) we can get \(h<t\). According to the Lagrange difference polynomial, it can be known that at least \(t\) legal members are required to collude to recover\(F(x,y)\). Therefore, the number of collusion users that the proposed scheme can resist does not exceed\(t-1\). \(t\) can be set by MRC based on how many participants there are in the group session. As an example, when\(n = \left\lfloor {t - 1} \right\rfloor\), it is impossible to recover \(F(x,y)\) even if all members collude. This situation belongs to information-theoretic secure.

In addition, when the group key is generated, the secret input of each member is masked by XOR operations with the corresponding shared key. Since any other member’s valid token is not known to inside attackers for recovering its corresponding shared secret key, the secret information of users is unlikely to be accessible to the insider attacker.□

Theorem 2

External Attack- It is impossible for any secret information to be obtained by an external adversary.

Proof

External attack refers to an adversary trying to pretend to be a legitimate group member to obtain secret key, where the adversary belongs to external attacker. An external attacker is an illegitimate member who is not registered with MRC and does not possess a valid token. During the group key establishment phase, except for the initiator member, the unencrypted information broadcast by other legitimate members is calculated by secret input and shared keys. Since any legitimate token is not known to external attackers for recovering its corresponding shared secret key(include the initiator member’s pairwise shared keys), it is impossible for any secret information to be obtained by the external attacker. At the same time, the initiator member encrypted the masked value using shared keys, and external attacker cannot recover his/her shared secret without knowing the legitimate token of his/her, thus, no secrets are leaked from the broadcast session messages. To sum up, it is impossible for an external attacker to gain the secret input on the member side, nor to successfully impersonate a legitimate member. Therefore, the proposed proposal can withstand external attack.□

5.2 Performance Evaluation

We will discuss the performance of the proposed design in this sub-section. At present, the encryption and decryption operations in most key establishment protocols are complex, resulting in high computational costs. Moreover, most solutions are interactive, which causes a greater computational burden on the user side. At the same time, the communication cost of users is affected by the number of members in group, that is, the increase in the number of members will increase the communication overhead. Based on the above problems, the performance characteristics of the proposed scheme are first explained.

  1. (1)

    Function feature

    Our solution has more functional advantages than other solutions. Firstly, user authentication and group key negotiation are implemented simultaneously in the designed scheme. Secondly, this scheme is non-interactive, which means that users can directly send their own values without communication between them. Thirdly, our protocol only uses lightweight operations such as XOR and hash functions, which significantly increases computing performance and lowers complexity. Moreover, since recovering the masked secret value only requires XOR operation between the secret input values and the shared keys, the communication cost at the user end is no longer influenced by the number of group members, and then, except for the initiator member, each member broadcasts this masked value (that is, no need extra encryption and just broadcast one message, no matter how many group members there are). Only the initiator member needs to encrypt the mask value with the shared key before broadcasting the message to other members. The group key result can be obtained using XOR operation by all members’ masked secret values. This makes the designed scheme faster and more lightweight. In addition, each user's token is utilized for (a) authenticate members; (b) distribute shared keys; (c) negotiate group keys. Hence, our proposal is efficient.

  2. (2)

    Constant-round feature realizing real low communication cost on the group member side

    The number of session rounds is a critical element impacting the complexity of communication when there are more group members [36]. Typically, increased number of rounds comes at the cost of reduced client efficiency. Therefore, the invariance of the number of session rounds is the key to improving the efficiency of the group key generation. However, the number of users has an impact on the communication cost of the client, that is, an increase in group size will result in higher communication costs. To address this issue, we employ a broadcast-masked-value-based method while ensuring that the users’ communication consumption is not affected by the number of group members since except for the initiator member, the communication overhead of other users only contains the broadcast mask value (that is, no need extra encryption and just broadcast one message, no matter how many group members there are). As a result, the constant round feature of the designed scheme significantly reduces the communication expense of the client.

  3. (3)

    Lightweight encryption method

    Symmetric key encryption means that both parties use the same key for encrypting and decrypting the data. Although this method ensures the confidentiality of data, it faces two challenges of key distribution and management, because these two processes will bring huge communication and storage overhead to users. In contrast, asymmetric encryption algorithms must use different keys for encryption and decryption, which guarantees confidentiality, authenticity and non-repudiation of data. Unfortunately, larger computational modulus leads to higher computational cost, such as RSA algorithm with at least 1024-bit modulus. In addition, some state-of-the-art group key establishment protocols [37,38,39,40] using Bilinear map, complexity presumptions, and Computation Diffie–Hellman (CDH) have large computational overhead. Compared with the above encryption methods, the bivariate polynomial based scheme provides effective identity verification and information theory security, while reducing the cost of calculation and communication. Furthermore, the use of logical XOR as the primary calculation method is the outstanding advantage of our group key agreement, which ensures the lightweight of this scheme.

In conclusion, the designed protocol is more lightweight and more fast than other cryptographic protocols. The overhead of calculation, communication and storage of the presented proposal is analyzed as follows.

  1. 1.

    Storage Cost

In the proposed scheme, each registered member owns a token, \({s}_{i}(y),\) which is a \(t-1\) order univariate polynomial generated by MRC. Therefore, each member should store \(t\) coefficients. And then, each member consumes \(t{\mathit{log}}_{2}p\) bits of memory space, where \(p\) is the modulus, which uses much smaller modulus than asymmetric encryption algorithms.

  1. 2.

    Computation Cost

We consider the computational complexity of our proposal to be equal to the computational complexity of the member side. According to Horner’s rule [41], we regard the evaluating of a \(t-1\) degree polynomial as \(t-1\) times of multiplication and \(t\) times of addition. Calculating \(m-1\) pairwise shared keys \({k}_{i,j}={s}_{vi}({x}_{vj})=F({x}_{vi},{x}_{vj})\) for each member is equivalent to evaluating \(m-1\) different polynomials. Additionally, each member executes the hash function \(m\) times, one of which is used to verify his identity to other members, and we use the other \((m-1)\) times to verify the membership of other members. In our scheme, recovering the masked secret value only requires XOR operation between the secret input values and the shared keys, and then, except for the initiator member, other members broadcast their own masked value directly without encryption. Only the initiator member needs to encrypt the mask value with the shared key before broadcasting the message to other members. After each member collects all the published information, the group key can be calculated only by the XOR operation. Eventually, this key can be verified with only a hash function. In general, compared with most public key-based protocols, our proposal greatly reduces the computational complexity. As an example, the computation cost of the RSA [42] algorithm is about \(1.5{\mathit{log}}_{2}N\) modulo multiplications, where \(N\ge 1024\) bits.

  1. 3.

    Communication Cost

During the Membership Authentication phase of our scheme, all communication is done through broadcasting. This process transmits a total of \(m\) random integers, \(\{{r}_{i},i=\mathrm{1,2},\cdots ,m\}\) and \(m(m-1)\) responses. When generating the group key, a total of \(m\) integers \(\{{l}_{i}\}\), \((m-1)\) unencrypted messages and \((m-1)\) encrypted messages are transmitted. Lastly, \(m\) hash outputs are required for group key authentication phase.

The data transmitted by our proposal is computed based on the modulus of the polynomial. Meanwhile, a binary polynomial is used to authenticate the identities of members and distribute shared keys, which greatly reduces the communication overhead. This communication cost is low.

In contrast to most existing related works, the communication overhead of users in our proposal is not affected by the number of members since except for the initiator member, the single user's communication cost just requires to broadcast this masked value. In other words, there is no need extra encryption and broadcast only one message, no matter how many group members there are. It is really constant-round and communication-efficient.

Overall, the proposed scheme is fast, lightweight, and extremely effective.

6 Conclusion

We designed a new construction for lightweight and fast membership authenticated group key agreement for resource-constrained IoMT devices. This protocol provides member authentication and group key agreement, while achieving lightweight computations and fast communications on each group member side. Specifically, the logical XOR operation is used as the main calculation method, and the communication cost of the user is not affected by the number of participants in group communication. Furthermore, this proposal is non-interactive and in a broadcast way. Security analysis proves that our scheme achieves ideal security, and performance evaluation reveals that this proposal is more lightweight and faster in computation and communication. Therefore, the designed secure and effective group key distribution approach is definitely attractive for resource-constrained IoMT devices.