Combinatorial Design Based Key Pre-distribution Scheme with High Scalability and Minimal Storage for Wireless Sensor Networks

Abstract

Given the sensitivity of applications and the sensor node’s resource constraints, key management is an important security concern in Wireless Sensor Networks (WSNs). Combinatorial Design based schemes are used to propose key pre-distribution in WSNs as they have patterns that can be mapped to the WSNs. We employ Combinatorial Designs to pre-distribute the keys to the sensor nodes. The deployment area is divided into equal-sized regions called cells. The network comprises two types of sensor nodes: ordinary sensor nodes and cell masters. The ordinary sensor nodes within a cell can communicate with each other directly. The inter-cell communication is through the cell masters, which have higher resource capabilities than the ordinary sensor nodes. To take into account the Radio Frequency range of cell masters, we use Lee sphere region around each cell (Ruj in ACM Transactions on Sensor Networks (TOSN) 6:4, 2009, Rui Key predistribution using partially balanced designs in wireless sensor networks, 2007). The proposed key pre-distribution scheme for cell masters provides high network scalability with low key storage overhead compared to other schemes. The model’s performance is measured in terms of key storage overhead and the number of sensor nodes supported. A detailed analysis of resiliency in terms of fractions of links disrupted is also presented. Also, the proposed scheme achieved better resiliency and requires much less number of keys to be stored in sensor nodes than the existing schemes.

1 Introduction

WSNs compromises of a huge number of sensor nodes deployed in a physical environment which collect information and send it to a base station. The sensor nodes communicate using wireless links. The sensor nodes have limited battery power, storage, and computational capabilities [3]. They are used to measure conditions of the environment like humidity, temperature, pollution levels, sound etc. They are used in multitude of applications in areas like military, health, industrial and agriculture controls, disaster relief etc. [3,4,5]. The sensor nodes are usually deployed in hostile environments, and it is not reasonable to safeguard each sensor node individually. Securing the communication between the sensor nodes thus becomes very crucial. Therefore, maintaining the confidentiality of the sensed data is one of the major security factors to be taken care of in WSNs. Encryption techniques are used to provide confidentiality by distributing secret keys to the sensor nodes. Asymmetric encryption algorithms have high computation cost and consume more energy. Since the sensor nodes have limited resource capabilities, the symmetric key establishment is preferred over the public key establishment. Due to lack of infrastructure in WSNs, there is no trusted third party that can assign keys to the sensor nodes [6]. Hence, key pre-distribution(KPrD) is widely used in WSNs.

The technique of distributing keys to the sensor nodes prior to deployment in the target area is known as KPrD. Key establishment in sensor network consists of three phases such as KPrD phase, Shared key discovery phase and Path key establishment phase. In KPrD phase sensor nodes are provided with the secret keys. In Shared key discovery phase any pair of sensor nodes can find out the common keys between them using the shared key algorithm. Path key establishment phase is a process wherein the two nodes that do not have a common key identify a set of intermediate sensor nodes that share a common key. Thus, a path is formed by these intermediate sensor nodes to connect the two nodes that do not share a common key.

There are mainly three types of KPrD schemes: Probabilistic, Deterministic, and Hybrid. In a probabilistic scheme, keys are selected from the key pool either randomly or by following a probabilistic distribution and assigned to the sensor nodes. In a deterministic KPrD scheme, a deterministic pattern is employed to draw keys from the key pool. The hybrid KPrD scheme is a combination of random and deterministic schemes. One naive approach is to distribute the same secret key to all the nodes in the sensor network. Though this is easy to implement, it has a significant disadvantage: if an attacker compromises a single node and gets the secret key, the whole network’s security is jeopardized. Another approach is to distribute pairwise keys to each node in the network. Thus, if the total number of sensor nodes in the network is N, each node will store $N -$ 1 keys. This scheme is highly resilient to node compromise attacks, but it is not feasible for a large number of nodes due to high storage overhead. Hence, using combinatorial design for KPrD is the middle ground.

In this article, we propose a novel combinatorial design-based scheme for KPrD for a heterogeneous network comprising ordinary sensor nodes and cell masters differing in their resource capabilities. The cell masters possess higher computational and power capacities than the ordinary sensor nodes. The deployment region is clustered into equal-sized squares known as cells. A different key-pool is used for each cell. This is helpful in battlefields wherein compromise of one of the cells does not affect other cells; thus, providing complete detachment of the compromised cell from the rest of the network. The intra-cell communication is through ordinary sensor nodes, and inter-cell communication is through cell masters. The proposed scheme is designed to minimize the storage overhead while providing good scalability and being resilient against node capture attacks.

The proposed scheme finds its application in smart power grid system that use WSNs. The nodes are usually deployed in hostile areas. The information communicated between the sensor nodes of smart power grid is sensitive and is critical in the operation of the system so that the data is not erroneously modified or deleted which can result in failure of entire power grid system. And also, the compromise of certain part of the WSNs should not affect the other parts. The proposed model can be used in such cases to provide confidentiality of the data transferred between the sensor nodes without consuming more storage and at the same time its highly scalable which is essential for smart grids. WSNs are also essential part of SCADA (Supervisory Control and Data Acquisition) networks to collect the data from sensor nodes and also help in sending commands to actuators. The proposed scheme can be used in such systems so that the information exchanged between the sensor nodes can be secured using lesser key ring size depending upon the size of the network.

1.1 Organization

The rest of the paper is organised as follows. In Sect. 2, we present the recent works in the area of KPrD. In Sect. 3, the preliminaries required to understand this paper are presented. The Residual Design is discussed in Section 4. The new KPrD scheme is proposed in Sect. 5. The detailed analysis of the proposed scheme is presented in Sect. 6. The comparative analysis of our scheme with existing schemes is given in Sect. 7 and finally we conclude our paper in Sect. 8.

2 Literature Survey

Many Combinatorial design based deterministic approach for KPrD are being proposed in the recent times. Blundo et al. [7] suggested a polynomial based KPrD scheme. Liu and Ning [8] proposed a pairwise KPrD scheme which used Blundo et al.’s [7] polynomial-based scheme. Liu and Ning [8] used a pool of polynomials instead of a unique random polynomial. Each node is assigned a subset of polynomial shares from the pool. A common key between the two nodes is found if nodes’ polynomial shares belong to the same polynomial. If yes, then a common key is found. Liu and Ning [9] proposed two random pairwise KPrD schemes that use deployment knowledge. The first scheme, called as closest pairwise scheme, distributes pairwise keys between the sensor nodes that are near to each other. In the second scheme, they use Blundo et al.’s [7] scheme of KPrD using polynomials. Here, the deployment area is divided into equal-sized squares called cell with coordinates. Based on the coordinates, each sensor node is allocated to a cell that is nearest. Each cell is assigned a bivariate t-degree polynomial. The setup server finds out the home cell to which the sensor node belongs and assigns the home cell coordinates. It then assigns the polynomial shares of neighboring cells and its home cell.

Blom [10] proposed a scheme called Symmetric Key generation system for KPrD that makes use of symmetric matrices. The scheme uses two matrices: the public matrix and the private matrix [10]. The public matrix is known to all the nodes. Each node maintains a single row of the private matrix. Whenever a node i wants a shared key between another node j, it multiplies ith row of private matrix with the public matrix. The adversary can get all the keys in the network by capturing only c nodes, where c is the security parameter. Du et al. [11] proposed a multi-space Blom’s [10] scheme. They maintained multiple key spaces instead of a single key space, as in Blom’s [10] scheme. Each node maintained a fixed number of key spaces. Two nodes can then calculate the pairwise keys if they share common key space. This improved the resiliency compared to Blom’s [10] scheme. Huang et al. [12] and Huang and Medhi [13] utilized deployment knowledge along with multi-space Blom’s [10] scheme to put forward a new KPrD scheme.

Combinatorial Design was first used for KPrD in WSNs by Camtepe and Yener [14]. Authors mapped Generalized Quadrangles and Balanced Incomplete Block Design to KPrD. Lee and Stinson [15] formalized the method of using combinatorial design for KPrD. They also proposed the use of Transversal Design (TD) for the KPrD. Two nodes either have 0 or 1 key in common. Simonova et al. [16] proposed a KPrD scheme for a homogeneous network using deployment knowledge. They assigned keys to sensor nodes using Lee and Stinson’s [15] Transversal Design. Simonova et al. [16] also proposed a preliminary framework for KPrD in a heterogeneous network. Ruj and Roy [1] put forward a KPrD scheme using CD. The model consisted of two nodes, namely sensor nodes and cell masters. normal sensor nodes were used for intra-cell communication. Ruj and Roy [1] employed Camtepe and Yener’s [14] scheme for distribution of keys to sensor nodes. The cell masters were assigned keys using Transversal design. This scheme gave connectivity of 1, and the resiliency of the model improved. Mitra et al. [17] articulated a deterministic scheme to distribute keys to the sensor nodes based on pairwise connectivity and projective planes. They employed a rectangular grid structure to place the nodes along the columns and rows such that the nodes along columns having more power than the ones along the rows. Bechkit et al. [6] introduced a new combinatorial design based KPrD scheme that uses Unital Design. This scheme improved the scalability and provided good probability of key sharing. Bag [18] proposed a new combinatorial design-based key distribution scheme mostly motivated by the Ruj and Roy [1] scheme. However, the number of agents per cell in Bag’s [18] scheme depended upon the grid’s size. Bag and Roy [19] proposed a key pre-distribution scheme using SBIBD scheme of [14] and [10] scheme. [20] proposed another combinatorial design scheme that used Residual Design derived from symmetric balanced incomplete block design (SBIBD). Modiri et al. [20] scheme further greatly enhanced the scalability and also reduced the key storage overhead. Kumar and Pais [21] presented a combinatorial design based scheme inspired by Ruj and Roy [1]. Kumar and Pais [21] further improved the resiliency of [1] scheme against the node capture attacks. Kumar and Pais [22] put forward a hybrid scheme to distribute keys, which is a combination of pairwise keys and combinatorial design that reduced heads’ storage overhead. Kumar et al. [23] proposed another novel scheme in which they assigned keys to only 3/4th of the cell masters. The scheme provided by Kumar et al. [23] does not require any location information. They further used this scheme in En-Route filtering for WSNs [24]. Another scheme was proposed by Kittur et al. [25] wherein a combination of SBIBD and cartesian product of two SBIBD was used to propose a KPrD scheme for a heterogeneous network.

3 Preliminaries

3.1 Design

A design [26] is defined as a pair ($X$,$A$) that satisfies the following properties:

• 1. $X$ is called points which is a set of elements.

• 2. $A$ is a multiset of blocks that are nonempty subsets of $X$

$X$ is the point set. $A$ is a multiset because there can be two identical blocks in $A$ and such blocks are called repeated blocks. If the design does not contain repeated blocks then it is called simple design.

3.1.1 Balanced Incomplete Block Design (BIBD) and SBIBD

Consider positive integers $v$, $k$ and $\uplambda$ wherein $v$ > $k$ $\geqslant$ 2. A ($v$, $k$, $\uplambda$)-balanced incomplete block design (abbreviated as ($v$, $k$, $\uplambda$-BIBD) [26] is a design ($X$,$A$) that satisfies the following properties:

• 1. The point set |$X$| $=$ $v$,

• 2. Exactly $k$ points are present in every block, and

• 3. Every pair of distinct points is present in exactly $\uplambda$ blocks.

In a BIBD, $k$ < $v$ and hence it is known as incomplete block design.

There are two basic properties of a ($v$, $k$, $\uplambda$)-BIBD [26]. They are:

• Every point occurs in exactly r blocks where $r = \frac{\uplambda (v-1)}{k-1}$.

• Total b blocks are produced by the design where $b = \frac{vr}{k}$.

For example, conisder a BIBD with total number of points = 7, block size = 3 and $\uplambda$ = 1 where $X$ and $A$ are as follows.

$X$ = {100, 200, 300, 400, 500, 600, 700}, and

$A$ = {(100, 200, 300), (100, 400, 500), (100, 600, 700), (200, 400, 600), (200, 500, 700), (300, 400, 700), (300, 500, 600)}.

A symmetric BIBD abbreviated as SBIBD is a BIBD wherein the total number of blocks (b) is equal to the total number of points (v) i.e $b$ $=$ $v$ (or where $r$ $=$ $k$ or where $\uplambda$($v$ − 1) = $k^2 - k$ [26].

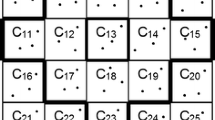
3.2 Lee Sphere Region

Consider the network area cleft into equal-sized square regions called cells. A Lee sphere is a region around a chosen cell that compromises the set of all neighbors that are no more than Lee distance ($\rho$) away from the chosen cell [27]. The distance between the two cells is calculated by taking the sum of horizontal and vertical distances which is called the Manhattan distance [28]. The Fig. 1 depicts the Lee sphere region of a cell.

Fig. 1

A network area consisting of 25 cells. The highlighted region in the figure shows the cells which are within Lee ($\rho$) distance of 2 of cell $C_{13}$

4 Residual Design

Let us consider any block say $B_0$ of balanced design with index $\uplambda$, any two elements (or treatments) that occur together in block $B_0$ must appear together in $\uplambda$ − 1 blocks. If the two elements do not occur in block $B_0$, then they must be present together in $\uplambda$ blocks. Therefore, the blocks B/$B_0$ form a pairwise balanced block design with index as $\uplambda$ when B loops over the remaining blocks. Such a design is called Residual Design.

Theorem 1

The Residual Design [26] of a ($v$, $k$, $\uplambda$)-SBIBD is a BIBD with parameters ($v$ − $k$, $v$ − 1, $k$, $k$ − $\uplambda$, $\uplambda$) such that k $\geqslant$ $\uplambda$ + 2.

If there is a Residual Design [29] with parameters ($v$ − $k$, $v$ − 1, $k$, $k$ − $\uplambda$, $\uplambda$) then a ($v$, $k$, $\uplambda$)-SBIBD exists if $\uplambda$ $=$ 1 or $\uplambda$ $=$ 2.

The Residual Design is a BIBD whose block sizes are least 2, and no more than the total count of points minus one.

Theorem 2

Let (V, B) be a SBIBD with point set V $=$ {$y_1$, $y_2$, $y_3$,...$y_v$} and blocks B $=$ {$B_1$, $B_2$, $B_3$,...$B_v$}. Then for any i from 1 to v $B_1$/$B_i$, $B_2$/$B_i$, $B_3$/$B_i$,..., $B_{i+1}$/$B_i$, $B_{i+2}$/$B_i$,.., $B_v$/$B_i$ are the blocks of (v − k, v − 1, k, k − $\uplambda$, $\uplambda$)

Consider a ($q^2$ + q + 1, q + 1, 1)-Symmetric BIBD then in total there will be $q^2$ + q + 1 Residual Design classes. Each class of Residual Design is ($q^2$, q, 1)-BIBD. Thus, total ($q^2 + q + 1)(q^2 + q)$ blocks are generated. Each block is repeated q times. Each element is repeated $q^2(q+1)$ blocks.

Consider symmetric BIBD of seven points, block size of 3 and $\uplambda$ = 1 with the point set, V $=$ {100, 200, 300, 400, 500, 600, 700}. The blocks are $B_1$ $=$ {100, 200, 400}, $B_2$ $=$ {200, 300, 500}, $B_3$ $=$ {300, 400, 600}, $B_4$ $=$ {400, 500, 700}, $B_5$ $=$ {500, 600, 100}, $B_6$ $=$ {600, 700, 200}, $B_7$ $=$ {700, 100, 300}. Now, the residual blocks can be generated as follows:

Class 1: point set is V/ $B_1$ $=$ {300, 500, 600, 700} which is {4, 2, 1}-BIBD. $B_2$/$B_1$ $=$ {300, 500} $B_3$/$B_1$ $=$ {300, 600} $B_4$/$B_1$ $=$ {500, 700} $B_5$/$B_1$ $=$ {500, 600} $B_6$/$B_1$ $=$ {600, 700} $B_7$/$B_1$ $=$ {700, 300}.

Class 2: point set is V/ $B_2$ $=$ {100, 400, 600, 700} which is {4, 2, 1}-BIBD. $B_1$/$B_2$ $=$ {100, 400} $B_3$/$B_2$ $=$ {400, 600} $B_4$/$B_2$ $=$ {400, 700} $B_5$/$B_2$ $=$ {600, 100} $B_6$/$B_2$ $=$ {600, 700} $B_7$/$B_2$ $=$ {700, 100}.

Similarly, the blocks are generated for class 3, 4, 5, 6, 7 and can be seen in Table 1. The notations utilized in this paper are represented in Table 2.

Table 1 Residual blocks generated from (7, 3, 1)-SBIBD

Table 2 Notations

5 Proposed Scheme

In the proposed scheme, the network is divided into equal-sized regions called cells similar to the scheme of [30]. Therefore, we need two types of KPrD methods- one for the sensor nodes within the cell and the other for cell masters placed in each cell. The sensor nodes within a cell are alloted keyrings through Symmetric BIBD. For inter-cell communication, another kind of sensor nodes called cell masters (CM) situated in each cell are used. The keyrings to cell masters are given by generating blocks of Residual Design. Though SBIBD gives full connectivity, it does not scale well if more nodes are added i.e., it generates only ($q^2$ + q + 1) keyrings each of size (q + 1) for a prime power q. Residual Design can produce ($q^2$ + q + 1)($q^2$ + q) keyrings for the same prime power q with a keyring size q. The communication range of sensor nodes is limited by their Radio Frequency (RF) range. In practical scenarios, cell masters can communicate with only a few other neighboring cell masters. To incorporate this, we consider Lee sphere region around each cell to find the physical neighbors. Two cell masters within the Lee sphere region sharing at least one common key are termed as the key neighbors. In this proposed scheme, each cell contains three cell masters of different types i.e the key pools are derived from three different point sets.

A detailed analysis of key storage overhead, scalability, connectivity and resiliency is discussed in further sections.

5.1 Pre-distributing Keys in a Cell

For the ordinary sensor nodes to communicate intra-cell, the keyrings are generated using a deterministic approach through Symmetric BIBD as proposed in schemes of [14, 21]. The blocks of symmetric design are formed by using Difference sets as in [21] scheme. Let each cell consist of n ordinary sensor nodes. The $q^2$ + q + 1 symmetric BIBD keyrings are generated such that $q^2$ + q + 1 $>=$ n, where q is prime. These keyrings of size q + 1 keys are then assigned to the n ordinary sensor nodes. The sensor nodes exchange their key identities to discover the common key. The ordinary sensor nodes within each cell can communicate with each other directly with connectivity 1. Each cell is alloted keyrings using this approach such that the key-pool is different for each cell.

5.2 KPrD for Cell Master

For inter-cell communications, cell masters are deployed in each cell. Three cell masters are placed in each cell as proposed in [1, 21]. By doing this, the resiliency is enhanced as the compromise of one cell master (CM) does not break the communication link with the other cell masters of other cells. Three different point sets are used to generate three types of key-pools namely Type i, Type ii, Type iii. Each cell master is assigned only one type of keys, no two cell masters within a cell have the same type of keys. Each cell is denoted by C$_{i}$ for 0$\le$i$\le$ $N$ where N is the total number of cells in the network. The three types of cell masters are denoted as CM$_{i1}$, CM$_{i2}$, CM$_{i3}$. The communication between the ordinary sensor nodes and the cell master of a cell is through pairwise keys that is assigned during the pre-distributing keys within a cell phase. In Ruj and Roy’s [1] scheme, the key assignment to cell masters is done using Transversal Design. In Kumar and Pais’s [21] scheme, symmetric BIBD is used to assign keyrings to the cell masters. In this proposed scheme, the keyrings assigned to the cell masters are generated from Residual Design. A Residual Design gives good scalability as it can generate ($q^2$ + q + 1)($q^2$ + q) blocks for a prime power q in contrast to symmetric BIBD that generates only ($q^2$ + q + 1) blocks.

Consider N to be the total number of cells then number of cell masters of each type will be N i.e N cell masters of Type i, N cell masters of Type ii and N cell masters of Type iii. Thus, there will be 3N number of cell masters in the entire network. To assign keyrings of a particular type of keys to N cell masters, the Residual Design is used. As discussed previously, the number of Residual blocks generated for a given prime power q from symmetric BIBD blocks are ($q^2$ + q + 1)($q^2$ + q). Each block in Residual Design is repeated q times. But, this repetition of blocks affects the network’s resiliency. This is because block repetition means that two nodes may get the same keyring. Hence, the compromise of one node causes the compromise of other nodes that have the same keyring as that of the compromised node. To assign unique keyrings to each node in the network, a prime power q should be selected such that N $<=$ ($q^2$ + q + 1)(q + 1) to build ($q^2$ + q + 1, q + 1, 1) - SBIBD. The SBIBD blocks are then used to generate ($q^2$ + q +1)($q^2$ + q) Residual Design blocks. Only unique blocks are chosen to assign as keyrings to the N cell masters from the generated Residual Design blocks. Every two keyrings of cell masters share between 0 to q - 1 keys. The procedure is the same for assignment of keyrings to other types of cell masters, but the key pool for each type will be different. Table 3 shows the mapping from Residual Design to KPrD for cell masters. The algorithm for key assignment to cell masters is summarized in Algorithm 1.

Once, the keyrings are assigned to the cell masters, then each cell master finds the set of physical neighbors within its Lee sphere region and that have the same type of keys. The cell masters then exchange their key identifiers to find the common keys. If the cells share more than one key, then the pairwise key can be found by calculating the hash on the concatenated common keys as proposed in Bechkit et al. [6] scheme. Through this, the network’s resiliency improves as it requires the adversary to compromise all the common keys to disrupt the link of communication. If no common key is shared between the two nodes, then, they can communicate through the secure path formed between them composed of several links.

Table 3 Mapping from Residual Design to KPrD in cell masters

6 Analysis

In this section, analysis of the proposed model with respect to key storage overhead, scalability, connectivity and resiliency is presented.

6.1 Key Storage Overhead

The ordinary sensor nodes in each cell are alloted keyrings using symmetric BIBD of order q. The keyring size of the ordinary sensor nodes depends on the block size, which is q + 1. Thus, the key-storage overhead for ordinary sensor node is l(q + 1) where l is the size of the key. It can also be represented as O($\sqrt{n}$) where the ordinary sensor count per cell is represented by n and n $<=$ $q^2$ +q +1.

The cell masters are assigned keys generated using Residual Design of order q. The size of each block in a Residual Design is q. Thus, memory required for cell masters to store these Residual keys is l(q) where l is the key size. The number of Residual keys stored by cell master is of the order O($\root 3 \of {N}$) where the cell count (N) and ($q^2$ + q +1)(q +1) $>=$ N. Since sensor nodes have minimal resources, any significant reduction in the amount of storage space required to store the keys will be an added advantage. The proposed scheme achieves this by consuming less storage compared to the existing schemes.

6.2 Scalability

Scalability is the maximum number of nodes that can be supported by the network. In the proposed scheme, the intra-cell communication is done through distributing keys produced using SBIBD. Keeping in mind the density of each cell required for future, an appropriate value of q should be chosen to generate the keyrings. In the proposed model, the number of regions decides the count of cell masters required. For a prime power q, the number of Residual blocks that can be generated is ($q^{2}$ + q +1)($q^{2}$ + q). Since each block is repeated q times, the maximum size of network is

$$\begin{aligned} \frac{(q^2+q+1)(q^2+q)}{q} = (q^2+q+1)(q+1) \end{aligned}$$

(1)

.

Thus, the number of cell masters supported is of the order $q^{3}$, where q is a prime power. Figure 2 depicts the number of nodes supported for a given keyring size of proposed scheme that uses Residual Design and Symmetric BIBD (Camtepe and Yener [14], Ruj and Roy [1], Bag and Roy [19], Kumar and Pais [21]). From the graph shown in Fig. 2 it can be seen that for a given keyring size, Residual Design scales better than the SBIBD scheme.

Fig. 2

Scalability in terms of count of nodes supported for a given keyring size of the proposed model which uses Residual Design is compared with the schemes Camtepe and Yener [14], Ruj and Roy [1], Bag and Roy [19], Kumar and Pais [21] that use SBIBD

6.3 Resiliency

Sensor nodes are usually deployed in unattended areas. The adversaries can compromise the nodes and get hold of the keys present in the keyring. Since, combinatorial design is used to generate the keyrings, the keys will be repeated in other keyrings. Thus making the communication links unsafe for communication using the compromised keys. Therefore, we present the resiliency of the proposed model to study the consequence of node compromise on the security of the network. The resiliency of the model can be calculated by measuring the number of links compromised when sensor nodes are attacked randomly. This can be expressed mathematically as follows:

$$\begin{aligned} R(s) = \frac{Number\ of\ links\ disrupted\ when\ s\ nodes\ are\ compromised}{Total\ number\ of\ links\ in\ the\ network} \end{aligned}$$

(2)

where R(s) provides the model’s resiliency when s number of nodes are compromised.

When P ordinary sensor nodes are compromised then only the links within the cell are broken. This is measured in-terms of Local Resiliency (Rl(P)). If K cell masters used for inter-cell communication get attacked, then the links between them are exposed. This can be called as Global Resiliency (Rg(K)).

6.3.1 Assessment of Local Resiliency Rl(P)

In the proposed scheme, Symmetric design is employed to generate the keyrings and thus each key from the key-pool is present in the keyrings of q + 1 sensor nodes. Whenever an attacker gets hold of a key ($P^{'}$), the number of communication links disrupted will be q(q + 1)/2. Compromising a sensor node leads to the compromise of all the q + 1 keys in its keyring. Since combinatorial design is employed, the keys will be repeated in several other keyrings. Whenever more than one node is compromised within a cell, the actual number of unique keys revealed to the attacker may be less, and hence the communication links disrupted by the attack will be less. The local resiliency can be expressed as

$$\begin{aligned} Rl(P) = \frac{P(q(q+1)^{2}/2)}{N(q^{2}+q+1)(q^{2}+q)/2} \end{aligned}$$

(3)

where the cell count in the network is given by N. This can be further simplified as

$$\begin{aligned} Rl(P) = \frac{P(q+1)}{N(q^{2}+q+1)} \end{aligned}$$

(4)

. The lower the value of Rl(P) the better the resiliency. The experimental and theoretical results of Local Resiliency Rl(P) is given in Table 4.

Table 4 Experimental and theoretical values of Local Resiliency Rl(P) where N is the cell count in the entire network, n is the ordinary sensor count per cell, q +1 gives the keyring size, P is the count of ordinary sensor nodes attacked

6.3.2 Assessment of Global Resiliency Rg(K)

In the proposed scheme, cell masters help to perform inter-cell communications. The communication of a cell master is limited to Lee sphere ($\rho$) region only. Thus, a particular cell can have a maximum of 2$\rho (\rho +1)$ cells within its Lee sphere region ($\rho$). These cells are called the physical neighbors of that cell. Each cell consists of three cell masters, one cell master with Type i keys, one of Type ii keys, and one of Type iii keys. Thus, in a given Lee sphere region of a cell, inter-cell communications can happen through any of the three cell masters of that cell. In the estimation of global resiliency, two type of links namely secondary links and primary links are considered. The cell-to-cell communication, i.e., between two neighbors that share common keys, is represented by a primary link. Whereas secondary links represent the connection between cell master to cell master of a particular type. For example, let us consider two cells say Cell 1 ($C_{1}$) and Cell 2 ($C_{2}$) who are within the Lee sphere region sharing common keys then, there will be three secondary links ($CM_{11}$) and ($CM_{21}$), ($CM_{12}$) and ($CM_{22}$), ($CM_{13}$) and ($CM_{23}$) and a single primary link between them. Since multiple connections exist between the two key sharing neighbours, only when all the secondary links between them are vandalized, a primary link between them is broken. If any cell master is attacked, it leads to breaking of only one secondary link between itself and key-sharing neighbors, but the other secondary links can still be utilized for secure communication. Whenever any key i is compromised, then according to Residual Design, this key will be present in the keyrings of q(q +1) cell masters. Thus, all these cell masters cannot use the key i to communicate with their neighbors.

In global resiliency, we estimate the number of primary links disrupted when K cell masters are attacked randomly because only when primary link between two cells is compromised/broken then only the communication between those two cells cannot happen but if a secondary link is compromised/broken between the two cell masters then communication can still happen using the remaining secondary links. The type of keys and the number of unique keys that will be compromised is uncertain and hence determining exactly which secondary links get disrupted is unfeasible. Thus, it is not possible to estimate the exact number of primary links broken. Table 5 shows the experimental values of global resiliency. Lower the value of Rg(K) better is the resiliency. It can be observed that the proposed model is highly resilient to node compromise attacks. The Table 5 gives the global resiliency for different sizes of network, Lee sphere region. It can be seen that the proposed model performs well for increased compromised cell masters also. If two cell masters share more than one key of a particular type, then a hash is calculated on those concatenated common keys to find the pairwise key between them. Thus, this improves the resiliency as the attacker needs to capture all the shared keys to calculate the common key.

Table 5 Estimation of Global resiliency(Rg(K)) where N represents the cell count in the entire network, q is the number of keys for each cell master, $\rho$ is the Lee sphere region, K is the number of cell masters vandalized

6.4 Connectivity

The nodes in each cell can communicate directly with each other. Hence, the connectivity is 1 for intra-cell communication. Cell masters are assigned keyrings using Residual Design. Modiri et al. [20] presents the probability of sharing at least one common key between two nodes which have the keyrings of Residual Design as

$$\begin{aligned} \frac{q^2}{q^2+q}\times Q_{SC} + (\frac{q-1}{q^2+q} \times \frac{q^2+1}{q^2+q} + \frac{q^2}{q^2+q} (\frac{q^2-q+1}{q^2+q}) \times Q_{DC} \end{aligned}$$

(5)

where,

$$\begin{aligned} Q_{SC} = \frac{\left( {\begin{array}{c}q^2+q\\ 2\end{array}}\right) }{\left( {\begin{array}{c}(q^2+q)(q^2+q+1)\\ 2\end{array}}\right) } \quad Q_{DC} = \frac{\left( {\begin{array}{c}q^2+q\\ 1\end{array}}\right) \left( {\begin{array}{c}q^2+q\\ 1\end{array}}\right) }{\left( {\begin{array}{c}(q^2+q)(q^2+q+1)\\ 2\end{array}}\right) } \end{aligned}$$

(6)

In our model, we employ Lee sphere region around each cell, thus the cell master can communicate with other key-sharing cell masters which are within that Lee sphere ($\rho$) region. Now, experimentally it is observed that for Lee sphere distance $\rho$ > 1, any two nodes can always communicate with each other either directly or through secure path.

7 Comparative Analysis

In this section, a comparative study of the proposed scheme with other existing schemes is presented regarding storage overhead, scalability, resiliency. Table 6 purveys an analysis of different schemes in terms of network type, type of deployment, key storage overhead, and resiliency.

Table 6 Comparative analysis of proposed model with the existing schemes

Table 7 Key storage comparison for various schemes

The Huang et al.’s [12] scheme differs from our scheme as it uses multiple space Blom [10] scheme, and the nodes are distributed in groups in a two-dimensional area. All the sensor nodes have the equal storage and power capacities i.e., it is a homogeneous network, whereas our scheme has ordinary sensor nodes and cell masters i.e., it is a heterogeneous network. In the proposed scheme the nodes within a cell can communicate with every other node with a probability of 1 unlike theirs where the probability is > 0.5. The number of keys stored in each node is 68, which is much higher than our scheme as seen in Table 7. Thus our scheme reduces storage and communication delays.

Liu and Ning [8, 30] formulated a scheme to pre-distribute pairwise keys to the sensor nodes using Blundo et al. [7] polynomial based method. Liu and Ning [8] further incorporated deployment knowledge in the scheme to propose a KPrD scheme for grid structure. The whole deployment area was divided into a grid of size $m \times m$ and then generated 2m number of polynomials. Unlike our scheme wherein a set of nodes are deployed in each cell, Liu and Ning [8] placed only one node at each intersections of the grid and assigned them two polynomial shares.

Simonova et al. [16] proposed a KPrD scheme for heterogeneous networks consisting of weak and strong nodes based on Transversal Design [15]. However, the number of strong sensor nodes depends on the size of the network, whereas it is fixed to three in our scheme. In Simonova et al. [16] scheme, the fraction of links broken whenever sensor nodes are compromised is much higher than our scheme.

Ruj and Roy [1] employed Camtepe and Yener’s [14] method of symmetric BIBD for KPrD. The number of keys saved in each cell master in their method is higher than our scheme i.e., it is of the order of $\sqrt{N}$ for their scheme and $\root 3 \of {N}$ for our scheme.

Similar to the scheme of Ruj and Roy [1], Bag [18] proposed a scheme wherein the number of agents in a region i.e., q + 1, depended on deployment size ($q \times q$). This lead to an overhead due to a large number of agents. In our method, the number of agents per cell is set to three.

Bag and Roy [19] proposed a KPrD scheme that is deterministic using combinatorial design. The capture of the special node of a cell by the adversary causes the whole cell to get disconnected from the network as the scheme places only one special node in each cell. In our scheme, to isolate a cell from the network, the attacker has to disrupt all the three cell masters present in a cell.

In Kumar and Pais [21] scheme, combinatorial design based KPrD scheme wherein symmetric BIBD is used for both ordinary sensor nodes and cell masters. However, the key storage overhead is higher than our scheme for cell master. It is of the order of $\sqrt{N}$ for their scheme and $\root 3 \of {N}$ for our scheme. Also, the number of cell masters that can be supported is ($q^{2}$ + q + 1), which is lesser than our scheme ($q^{2} + q + 1$)(q + 1) for a prime power q.

Our proposed scheme has several advantages over the existing ones. The key storage overhead is low. If the number of nodes in a cell is n, then key storage overhead for common sensor node is $\sqrt{n}$. And the key storage overhead for cell masters is of the order $\root 3 \of {N}$ where the cell count in the network is N. Table 7 gives a comparative study of the number of keys stored per ordinary sensor node and cell masters. It can be seen that our scheme has a lower storage overhead than the other schemes. Also, for a given keyring size, the number of cell masters and thus the number of cells supported is (q + 1) times higher than the schemes that use Symmetric BIBD where q is a prime power. Also, our scheme has three cell masters. Thus, to detach a cell from the rest of the network, all the three cell masters of a cell need to be compromised by the adversary. In our scheme, different key pools are employed for key distribution to each cell’s sensor nodes, thus the compromise of one cell does not affect other cells and hence provides better resiliency against node capture attacks. A comparative study of the fraction of links broken when nodes are compromised randomly is given in Fig. 3. It is observable that the proposed scheme has high resiliency than most of the schemes. Bag and Roy [19] scheme adopts that to compromise the super node of a cell, all the other nodes of a cell need to get compromised and hence it provides better resiliency than other schemes. But in real WSNs, this assumption may not always suit. Our scheme has taken equal probability of randomly capturing the ordinary sensor nodes and the cell masters. In Liu and Ning [30] scheme the pairwise keys are pre-distributed to the sensor nodes and hence their scheme has high resiliency.

Fig. 3

Comparison for various schemes Ruj and Roy [1] (k = 12 and Z = 16093), Bag [18] (q = 13 and Z = 16055), Bag and Roy [19] (p = 11, c = 4 and Z = 16093), Simonova et al. [16] (k = 16, p = 11 and Z = 12100), Huang et al. [12] ( $\omega$ = 7, $\alpha$ = 1, $\gamma$ = 8, $\tau$ = 2, $n_{z} = 100$ and Z = 10000), Liu and Ning [30] (m = 60, L = 1, k = 200 and Z = 10000), Kumar and Pais [21] CDKPD (k = 12 and Z = 16093) and Kumar and Pais [21] CD-RKPD ($\rho$ = 4, k = 12 and Z = 16093), proposed scheme ($\rho$ = 4, N = 289, q for ordinary sensor nodes = 7, Z = 16473) (Z = total sensor nodes in a WSN)

8 Conclusion

In the proposed work, a scheme for pre-distributing the keys for a heterogeneous WSNs is presented. The deployment region is split into equal-sized cells, with each cell having ordinary sensor nodes and three cell masters. Since, symmetric design is used to generated keys for the ordinary sensor nodes, the key storage overhead is of the $\sqrt{n}$ where ordinary sensor node count per cell is denoted by n. The cell master’s key storage overhead is of the order $\root 3 \of {N}$ as another combinatorial design known as Residual design is employed to generate the secret keys where N is the cell count. The use of Residual design to distribute the keys to the cell masters proved to be highly scalable as it can support network sizes of the order $q^3$ compared to other schemes like Camtepe and Yener [14], Ruj and Roy [1], Bag and Roy [19], Kumar and Pais [21] that use SBIBD where q is a prime power.

We also presented a detailed analysis of our scheme’s key storage overhead, scalability, connectivity and resiliency. It can be observed that our scheme provides good scalability and reduces key storage overhead. Also it offers better resiliency against the random sensor node attacks by the adversary.