Energy Harvesting for Cooperative Cognitive Radio Networks

Abstract

In this paper, we analyze the performance of cooperative cognitive radio networks where the secondary nodes harvest energy from radio frequency signals. Our analysis takes into interference aspect: the secondary source and relays transmit only when they generate low interference to primary receiver ($P_R$). Besides, we analyze the signal to interference plus noise ratio at secondary relays and destination taking into consideration primary interference. To reach higher data rates, harvesting duration is optimized in this paper.

1 Introduction

In CCRN, secondary and primary nodes transmit over the same channel. There are three transmission strategies: interweave CRN where the secondary nodes perform spectrum sensing and are allowed to transmit only where primary nodes are idle. In underlay CRN, secondary source can transmit only when it generate interference to primary receiver ($P_R$) is lower than threshold I. In overlay CRN, secondary nodes has to relay the primary signal to improve its Quality of Service (QoS). In CCRN, relays can amplify the secondary source packet to secondary destination.

In conventional CCRN, relay nodes have a battery that should be recharged or changed. In many situations, the battery cannot be recharged or changed easily such as wireless sensor networks deployed in the desert or in a mountain. To increase network lifetime, relay nodes can harvest energy from RF signal [1,2,3]. CCRN with energy harvesting is the scope of this paper. Next section gives the literature review.

2 Literature Review

Energy harvesting (EH) can be performed from different sources of energy such as wind, solar or radio frequency (RF) signals. EH form RF signals is the aim of this paper [1,2,3,4,5,6]. Enhanced data rates in EH systems can be obtained by optimizing the power of different nodes [7,8,9,10,11,12,13]. EH allows to enhance the performance of multiple input multiple output (MIMO) systems [14,15,16]. Many researchers considered CRN with EH as a new mean to recharge the battery of CRN nodes [17,18,19]. Security aspects of EH systems has been improved by adding jamming signals so that the packet cannot be decoded by a malicious eavesdropper [20,21,22,23,24]. Optimal Resource allocation for EH systems has been suggested in [25, 26]. The powers allocated to different sub-carriers are optimized to increase data rates. EH for CRN and non CRN has been considered in [27]. The analysis shows that EH allows to increase CRN lifetime. Joint optimization of energy harvesting and sensing process was suggested in [28, 29]. Spectrum sensing detection threshold was optimized in [29] to maximize the throughput.

The contribution of the paper are

• Evaluate the packet error probability (PEP) of CCRN with EH and opportunistic AF (O-AF), O-decode and forward (O-DF), partial and reactive relay selection (PRS and RRS).

• Our analysis takes into account of interference aspect. In fact, secondary source and relays transmit only when they generate interference to $P_R$ less than interference threshold I. Besides, we analyze the SINR by considering interference from primary transmitter $P_T$.

• Optimize harvesting duration to maximize the throughput at secondary destination. A low harvesting duration offers low energy to communicate resulting in low throughput. A large harvesting duration don’t leave time for communication so that the throughput is low. A non-optimized harvesting duration was considered in [28, 29].

The article contains eleven sections. Section 3 provides the system model whereas Sect. 4 gives the cumulative distribution function (CDF) of SINR. Sections 5, 6, 7 and 8 study the CDF of O-AF, PRS, RRS and O-DF. Section 9 derives the PEP and throughput whereas Sect. 10 provides some theoretical and simulation results. Finally, conclusions are presented in last section.

3 System Model

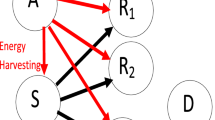
The first part of the frame, with duration $\alpha F$, is dedicated for EH by the secondary source S and secondary relays $R_{i}$. F is the frame duration. They harvest energy from wireless signal transmitted by node A. The second and third parts, with durations $(1-\alpha )F/2$, are dedicated for secondary source and selected relay transmission to the destination. Figure 1 shows that there are a source S, a destination D and L relays $R_{i}$. Primary transmitter $P_T$ is communicating with $P_R$. The source and relays are allowed to transmit only when their generate interference to primary receiver $P_{R}$ less than I. Our analysis takes into account the interference signal at secondary relays and destination emitted by primary transmitter.

Fig. 1

System model

4 SNR Statistics

4.1 Absence of Interference from $P_T$

The harvested energy by S is written as [24]

$$\begin{aligned} E=\beta P_{A}\alpha F|g_{AS}|^{2}=\beta kE_{A}\alpha |g_{AS}|^{2}, \end{aligned}$$

(1)

where $0<\beta <1$ is the efficiency of energy conversion, $P_{A}$ is the power of $A,E_{A}=T_sP_A$, $T_{s}$ is the symbol duration, $g_{XY}$ is the channel coefficient between of link X–Y and $k=F/T_{s}$.

The symbol energy of the source is equal to E divided by the number of symbols transmitted, i.e. $(1-\alpha )k/2$:

$$\begin{aligned} E_{S}=\frac{E}{(1-\alpha )k/2}=2\beta E_{A}\frac{\alpha }{1-\alpha } |g_{AS}|^{2}, \end{aligned}$$

(2)

The SNR at relay $R_{i}$ is written as

$$\begin{aligned} \gamma _{SR_{i}}=\frac{E_{S}}{N_{0}}\left| g_{SR_{i}}\right| ^{2}=2\beta \alpha \frac{ E_{A}}{(1-\alpha )N_{0}}|g_{AS}|^{2}\left| g_{SR_{i}}\right| ^{2}. \end{aligned}$$

(3)

where $N_{0}$ is noise variance.

Similarly, the SNR of link $R_{i}-D$ is written as

$$\begin{aligned} \gamma _{R_{i}D}=2\beta \alpha \frac{E_{A}}{N_{0}(1-\alpha )} \left| g_{AR_{i}}\right| ^{2}\left| g_{R_{i}D}\right| ^{2}. \end{aligned}$$

(4)

For Rayleigh channels, the SNR is the product of two exponential r.v $X=X_{1}X_{2}$. The probability density function (PDF) of X is written as

$$\begin{aligned} f_{X}(x)=2\sigma _{1}\sigma _{2}K_{0}\left( 2\sqrt{\sigma _{1}\sigma _{2}x}\right) , \end{aligned}$$

(5)

where $\sigma _{1}=\frac{1}{E(X_1)}$ and $\sigma _{2}=\frac{1}{E(X_2)}$.

The CDF of X is given by

$$\begin{aligned} F_{X}(x)=1-2\sqrt{\sigma _{1}\sigma _{2}x}K_{1}\left( 2\sqrt{\sigma _{1}\sigma _{2}x}\right) . \end{aligned}$$

(6)

The Proof is given in “Appendix 1”.

Using (5) and (6), the PDF and CDF of $\gamma _{SR_{i}}$ is written as

$$\begin{aligned} F_{\gamma _{SR_{i}}}(x)&= 1-\sqrt{2\sigma _{AS}\sigma _{SR_{i}}\frac{ N_{0}(1-\alpha )}{\alpha \beta E_{A}}x}K_{1}\left( \sqrt{2\sigma _{AS}\sigma _{SR_{i}}\frac{N_{0}(1-\alpha )}{\alpha \beta E_{A}}x}\right) , \end{aligned}$$

(7)

$$\begin{aligned} f_{\gamma _{SR_{i}}}(x)&= 1-\sqrt{\sigma _{AS}\sigma _{SR_{i}}\frac{ N_{0}(1-\alpha )}{\alpha \beta E_{A}}}K_{1}\left( \sqrt{2\sigma _{AS}\sigma _{SR_{i}}\frac{N_{0}(1-\alpha )}{\alpha \beta E_{A}}x}\right) , \end{aligned}$$

(8)

where

$$\begin{aligned} \sigma _{XY}=\frac{1}{E\left( |g_{XY}|^{2}\right) }, \end{aligned}$$

(9)

Similarly, the CDF of $\gamma _{R_{i}D}$ is equal to

$$\begin{aligned} F_{\gamma _{R_{i}D}}(x)&= 1-\sqrt{2\sigma _{AR_i}\sigma _{R_{i}D}\frac{ N_{0}(1-\alpha )}{\alpha \beta E_{A}}x}K_{1}\left( \sqrt{2\sigma _{AR_i}\sigma _{R_{i}D}\frac{N_{0}(1-\alpha )}{\alpha \beta E_{A}}x}\right) , \end{aligned}$$

(10)

$$\begin{aligned} f_{\gamma _{R_{i}D}}(x)&= 1-\sqrt{\sigma _{AR_i}\sigma _{R_{i}D}\frac{ N_{0}(1-\alpha )}{\alpha \beta E_{A}}}K_{1}\left( \sqrt{2\sigma _{AR_i}\sigma _{R_{i}D}\frac{N_{0}(1-\alpha )}{\alpha \beta E_{A}}x}\right) , \end{aligned}$$

(11)

4.2 Analysis of Interference from $P_{T}$

When there is interference from $P_{T}$, the SINR of first hop can be expressed as

$$\begin{aligned} \Gamma _{SR_{k}}=\frac{eX_{5}X_{4}}{f+X_{3}}, \end{aligned}$$

(12)

where $X_{4}=|g_{SR_{k}}|^{2},$$X_{3}=|g_{P_{T}R_{k}}|^{2}$.

$$\begin{aligned} X_{5}&= |g_{AS}|^{2}, \end{aligned}$$

(13)

$$\begin{aligned} e&= \frac{2\beta E_{A}\alpha }{(1-\alpha )E_{P_{T}}}, \end{aligned}$$

(14)

$$\begin{aligned} f&= \frac{N_{0}}{E_{P_{T}}}. \end{aligned}$$

(15)

The CDF of $\Gamma _{SR_{k}}$ is derived in “Appendix 2”. The CDF of the SNR of second hop, $\Gamma _{R_{k}D}$, is expressed similarly.

5 Opportunistic AF

Let U be relays’ indexes that cause interference at $P_R$ lower than T. The CDF of SNR of O-AF is expressed as

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}}(x)=\sum _{u}P(U=u)F_{\Gamma _{SR_{sel}D}|U=u}(x), \end{aligned}$$

(16)

where $P(U=u)$ is the probability that relays in u cause interference to $P_{R}$, $I_{R_{j}P_{R}}$, less than I:

$$\begin{aligned} P(U=u)=\prod _{j\in u}P\left( I_{R_{j}P_{R}}<I\right) \prod _{i\notin u}P\left( I_{R_{i}P_{R}}>I\right) \end{aligned}$$

(17)

and

$$\begin{aligned} P\left( I_{R_{j}P_{R}}<I\right)&= P\left( E_{R_{j}}\left| h_{R_{j}P_{R}}\right| ^{2}<I\right) =P\left( \frac{2E_{A}\beta \alpha }{(1-\alpha )}\left| h_{AR_{j}}\right| ^{2}\left| h_{R_{j}P_{R}}\right| ^{2}<I\right) \nonumber \\&= 1-2\sqrt{\frac{\sigma _{HR_{i}}\sigma _{R_{i}D}I(1-\alpha )}{E_{A}2\alpha \beta }} K_{1}\left( 2\sqrt{\frac{\sigma _{HR_{i}}\sigma _{R_{i}D}I(1-\alpha )}{E_{A}2\alpha \beta }}\right) \end{aligned}$$

(18)

When the set of available relays is $U=u$, we have

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}|U=u}(x)=P\left( \max _{j\in u}\left( \Gamma _{SR_{j}D}\right) \le x\right) >P\left( \max _{j\in u}\left( \Gamma _{SR_{j}D}^{up}\right) \le x\right) , \end{aligned}$$

(19)

where $\Gamma _{SR_{j}D}^{up}$ is an upper bound of SNR [30].

$$\begin{aligned} \Gamma _{SR_{j}D}=\frac{\Gamma _{SR_{j}}\Gamma _{R_{j}D}}{\Gamma _{SR_{j}}+\Gamma _{R_{j}D}+1}<\Gamma _{SR_{j}D}^{up}=\min \left( \Gamma _{SR_{j}},\Gamma _{R_{j}D}\right) . \end{aligned}$$

(20)

We deduce

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}|U=u}(x)>\prod _{j\in u}F_{\Gamma _{SR_{j}D}^{up}}(x) \end{aligned}$$

(21)

If we assume that the SNRs $\Gamma _{SR_{j}}$ and $\Gamma _{R_{j}D}$ are independent, we have

$$\begin{aligned} F_{\Gamma _{SR_{j}D}^{up}}(x)&= P\left( \min \left( \Gamma _{SR_{j}},\Gamma _{R_{j}D}\right) \le x\right) =1-P\left( \min \left( \Gamma _{SR_{j}},\Gamma _{R_{j}D}\right) >x\right) \nonumber \\&= 1-\left( 1-F_{\Gamma _{SR_{j}}}(x)\right) \left( 1-F_{\Gamma _{R_{j}D}}(x)\right) \end{aligned}$$

(22)

The CDF of SINR is computed using (16) and (21)–(22).

6 Partial Relay Selection (PRS)

In PRS, transmission is performed by the relay with the best SINR. We have

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}}(x)=\sum _{u}P(U=u)F_{\Gamma _{SR_{sel}D}|U=u}(x), \end{aligned}$$

(23)

where

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}|U=u}(x)=\sum _{k\in u}p_{k}F_{\Gamma _{SR_{sel}D}|U=u,R_{sel}=R_{k}}(x) \end{aligned}$$

(24)

$p_{k}$ is the probability to select relay $R_{k}$, $R_{sel}$ is the selected relay.

When $R_{k}$ is the selected relay, the SINR is written as

$$\begin{aligned} \Gamma =\frac{\Gamma ^{\max }\Gamma _{R_{k}D}}{\Gamma ^{\max }+\Gamma _{R_{k}D}+1}<\min \left( \Gamma ^{\max },\Gamma _{R_{k}D}\right) \end{aligned}$$

(25)

$\Gamma ^{\max }$ is the SINR at the selected relay which is the maximimum over all available relays in set u:

$$\begin{aligned} \Gamma ^{\max }=\max _{i\in u}\Gamma _{SR_{i}} \end{aligned}$$

(26)

If $\Gamma ^{\max }$ and $\Gamma _{R_{k}D}$ are independent, we have

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}|U=u,R_{sel}=R_{k}}(x)&= 1-P\left( \Gamma ^{\max }>x\right) P\left( \Gamma _{R_{k}D}>x\right) \nonumber \\&= 1-\left( 1-F_{\Gamma _{R_{k}D}}(x)\right) \left( 1-\prod _{i\in u}F_{\Gamma _{SR_{i}}}(x)\right) \end{aligned}$$

(27)

The probability to select relay $R_{k}$ is equal to

$$\begin{aligned} p_{k}=P\left( \Gamma _{SR_{k}}>\max _{j \in u j\ne k}\Gamma _{SR_{j}}\right) \end{aligned}$$

(28)

Let $X=\max _{q \in u q\ne k}\Gamma _{SR_{q}}$, we have

$$\begin{aligned} p_{k}=\int _{0}^{+\infty }P\left( \Gamma _{SR_{k}}>x\right) f_{X}(x)dx=\int _{0}^{+\infty }\left[ 1-F_{\Gamma _{SR_{k}}}(x)\right] f_{X}(x)dx \end{aligned}$$

(29)

We have

$$\begin{aligned} F_{X}(x)=\prod _{q\in u,q\ne k}F_{\Gamma _{SR_{q}}}(x). \end{aligned}$$

(30)

A simple derivative gives the PDF of X

$$\begin{aligned} f_{X}(x)=\sum _{q\in u,q\ne k}f_{\Gamma _{SR_{q}}}(x)\prod _{p\in u ,p\ne k,p\ne q}F_{\Gamma _{SR_{p}}}(x). \end{aligned}$$

(31)

7 Reactive Relay Selection RRS

In RRS, transmission is performed by relay node with the largest SINR of $R_i$-D link. The corresponding CDF of SINR is given by

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}}(x)=\sum _{u}P(U=u)F_{\Gamma _{SR_{sel}D}|U=u}(x), \end{aligned}$$

(32)

where

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}|U=u}(x)=\sum _{k\in u}p_{k}F_{\Gamma _{SR_{sel}D}|U=u,R_{sel}=R_{k}}(x) \end{aligned}$$

(33)

$p_{k}$ is the probability to select relay $R_{k}$.

When $R_{k}$ is the selected relay, the SINR is written as

$$\begin{aligned} \Gamma =\frac{\Gamma ^{\max }\Gamma _{SR_{k}}}{\Gamma ^{\max }+\Gamma _{SR_{k}}+1}<\min \left( \Gamma ^{\max },\Gamma _{SR_{k}}\right) \end{aligned}$$

(34)

$\Gamma ^{\max }$ is the maximum SINR of second hops over all available relays in set u:

$$\begin{aligned} \Gamma ^{\max }=\max _{i\in u}\Gamma _{R_{i}D} \end{aligned}$$

(35)

If $\Gamma ^{\max }$ and $\Gamma _{SR_{k}}$ are independent, we have

$$\begin{aligned} F_{\Gamma _{SR_{sel}D}|U=u,R_{sel}=R_{k}}(x)&= 1-P\left( \Gamma ^{\max }>x\right) P\left( \Gamma _{SR_{k}}>x\right) \nonumber \\&= 1-\left( 1-F_{\Gamma _{SR_{k}}}(x)\right) \left( 1-\prod _{i\in u}F_{\Gamma _{R_{i}D}}(x)\right) \end{aligned}$$

(36)

The probability to select relay $R_{k}$ is equal to

$$\begin{aligned} p_{k}=P\left( \Gamma _{R_{k}D}>\max _{j\in u, j \ne k}\Gamma _{R_{j}D}\right) \end{aligned}$$

(37)

Let $Y=\max _{q\in u, q \ne k}\Gamma _{R_{q}D}$, we have

$$\begin{aligned} p_{k}=\int _{0}^{+\infty }P\left( \Gamma _{R_{k}D}>x\right) f_{Y}(x)dx=\int _{0}^{+\infty }\left[ 1-F_{\Gamma _{R_{k}D}}(x)\right] f_{Y}(x)dx \end{aligned}$$

(38)

The CDF of Y is given by

$$\begin{aligned} F_{Y}(x)=\prod _{q\in u ,q\ne k}F_{\Gamma _{R_{q}D}}(x). \end{aligned}$$

(39)

The PDF of Y is given by

$$\begin{aligned} f_{Y}(x)=\sum _{q \in u ,q\ne k}f_{\Gamma _{R_{q}D}}(x)\prod _{p \in u ,p\ne k,p\ne q}F_{\Gamma _{R_{p}D}}(x). \end{aligned}$$

(40)

8 Opportunistic DF

Let $C=u$ be the relays that have correctly decoded the packet and cause interference at $P_{R}$ less than I, the CDF of SINR can be computed from

$$\begin{aligned} F_{\Gamma _{Rsel}D}(x)=\sum _{u}P(C=u)F_{\Gamma _{Rsel}D|C=u}(x), \end{aligned}$$

(41)

where

$$\begin{aligned} P(C=u)&= \prod _{j\in u}\left( 1-PEP_{SR_{j}}\right) P\left( I_{R_{j}P_{R}}<I\right) \nonumber \\&\times \prod _{i\notin u}\left[ 1-\left( 1-PEP_{SR_{i}}\right) P\left( I_{R_{i}P_{R}} <I\right) \right] \end{aligned}$$

(42)

$PEP_{SR_{j}}$ is the PEP at $R_{j}$ and

$$\begin{aligned} F_{\Gamma _{Rsel}D|C=u}(x)=P\left( \max _{j\in u}\Gamma _{R_{j}D}\le x\right) =\prod _{j\in u}F_{\Gamma _{R_{j}D}}(x). \end{aligned}$$

(43)

9 Throughput Optimization

The PEP is given ny

$$\begin{aligned} PEP=\int _{0}^{+\infty }g(x)f_{\Gamma }(x)dx \end{aligned}$$

(44)

where g(x) is the instantaneous PEP:

$$\begin{aligned} g(x)=1-\left[ 1-2\left( 1-\frac{1}{\sqrt{Q}}\right) erfc\left( \sqrt{x\frac{3\log _2(Q)}{2(Q-1)}}\right) \right] ^{N+n_p} \end{aligned}$$

(45)

Q is the size of QAM modulation, N and $n_p$ are the number of data and error detection symbols.

We have the following upper bound [31]

$$\begin{aligned} PEP \le \int _{0}^{w_{0}}f_{\gamma }(x)dx=F_{\gamma }(w_{0}) \end{aligned}$$

(46)

where $w_0$ is a waterfall threshold [31]

$$\begin{aligned} w_{0}=\int _{0}^{+\infty }g(x)dx \end{aligned}$$

(47)

The number of transmitted bits is given by

$$\begin{aligned} \frac{k}{2}(1-\alpha )\log _2(Q) \end{aligned}$$

(48)

They are correctly receiver with probability, $1-PEP$. We deduce the throughput in bit/s/Hz:

$$\begin{aligned} Thr(\alpha )&= \frac{\frac{k}{2}(1-\alpha )\log _2(Q)(1-PEP)}{kT_sB} P\left( I_{SP_R}<I\right) \nonumber \\&= \frac{(1-\alpha )}{2}\log _2(Q)(1-PEP)P\left( I_{SP_R}<I\right) \end{aligned}$$

(49)

where $B=1/T_s$ is the bandwidth, the term $P(I_{SP_R}<I)$ is due to the fact that the source is allowed to transmit only when it generates interference to $P_R$ less than I.

In this article, harvesting duration, $\alpha T$ is optimized to reach high throughput

$$\begin{aligned} \alpha _{opt}={\mathop {argmax}\limits _{\alpha }} Thr(\alpha ). \end{aligned}$$

(50)

10 Numerical Results

All theoretical curves as well as simulations were performed with MATLAB. Figure 2 shows the PEP of O-AF for different interference threshold I. Let $d_{XY}$ be the distance between nodes X and Y. We have made simulations for $d_{SR_k}=d_{SP_R}=2$, $d_{AS}=d_{AR_k}=d_h=1$. $d_h$ is the harvesting distance. There are 5 relays, $d_{SR_i}=0.3$ and $d_{R_iD}=0.7$. The PEP decreases as I increases due to less severe interference constraints so that there are more available relays. There is a small difference between theoretical and simulation results at low SNR due to the approximation in (20). At high SNR, our theoretical derivations are confirmed with simulation results.

Fig. 2

Effects of interference threshold on PEP of O-AF

Figures 3 and  4 compare the PEP of O-AF, Partial and reactive relay selection when $d_{SR_i}=1-d_{R_iD}=0.3$ or $d_{SR_i}1-d_{R_iD}=0.8$. Figure 3 shows that RRS offers a lower PEP than PRS for $d_{SR_i}=1-d_{R_iD}=0.3$. Figure 4 shows that the PEP of PRS is lower than that of RRS when $d_{SR_i}1-d_{R_iD}=0.8$. O-AF offers the lowest PEP since it uses the end-to-end SINR for relay selection and the best relay is selected.

Fig. 3

PEP of O-AF, RRS and PRS: $d_{SR_i}=1-d_{R_iD}=0.3$

Fig. 4

PEP of O-AF, RRS and PRS : $d_{SR_i}1-d_{R_iD}==0.8$

Figure 5 shows the PEP of O-DF for $I=10$, $d_{R_iP_R}=2$ and $d_{SR_i}=1-d_{R_iD}=0.3$. Our theoretical derivations are confirmed with simulation results as there is no approximation in the analysis. The PEP decreases as we increase the number of relay nodes.

Fig. 5

PEP of O-DF for different number of relays

Figures 6 and 7 show the throughput of O-AF versus harvesting duration. We observe that the proposed optimization of harvesting duration leads to significant throughput enhancement. A small value of $\alpha$ is required at high average SNR. Besides, Fig. 8 shows that optimal harvesting duration allows significant throughput enhancement with respect to $\alpha =1/3$ (same duration allocated to harvesting and source or relay transmission).

Fig. 6

Throughput optimization for BPSK modulation

Fig. 7

Throughput optimization for 64 QAM modualtion

Fig. 8

Throughput of optimal $\alpha$ versus $\alpha =1/3$

Figure 9 shows the PEP of O-AF for $d_{P_TS}=d_{P_TR_k}=1,1.5,2$, $d_{SP_R}=d_{R_kP_R}=2$ and $d_h=1$, $d_{SR_k}=1-d_{R_kD}=0.3$. There are $L=5$ relays. The PEP increases as $d_{P_TS}=d_{P_TR_k}$ decreases due to interference. Interference is an important performance metric to evaluate the performance of CCRN.

Fig. 9

PEP of O-AF for $d_{P_TS}=d_{P_TR_k}=1,1.5,2$

11 Conclusion

In this article, we evaluated the packet error probability of CCRN where secondary nodes harvest energy from RF signal. We have derived the throughput in the presence of primary interference. Secondary source and relays are allowed to transmit only when they generate low interference to primary receiver. To reach higher data rates, harvesting duration was optimized.

Appendices

Appendix 1

Let $X_{1}$ and $X_{2}$ be exponential r.v. The CDF of $X=X_{1}X_{2}$ is given by

$$\begin{aligned} P_{X}(x)=P(X_{1}X_{2}\le x)=\int _{0}^{+\infty }P\left( X_{1}\le \frac{x}{y} \right) \sigma _{2}e^{-\sigma _{2}y}dy. \end{aligned}$$

(51)

We deduce

$$\begin{aligned} P_{X}(x)&= \int _{0}^{+\infty }\left[ 1-e^{-\sigma _{1}\frac{x}{y}}\right] \sigma _{2}e^{-\sigma _{2}y}dy \nonumber \\&= 1-\int _{0}^{+\infty }e^{-\sigma _{1}\frac{x}{y}}\sigma _{2}e^{-\sigma _{2}y}dy \end{aligned}$$

(52)

We have

$$\begin{aligned} \int _{0}^{+\infty }e^{-\frac{c}{y}}e^{-\frac{y}{d}}dy=2\sqrt{\frac{c}{d}} K_{1}\left( 2\sqrt{\frac{c}{d}}\right) . \end{aligned}$$

(53)

We use (52) and (53) with $c=\sigma _{1}x$ and $d=\frac{1}{ \sigma _{2}}$, we obtain

$$\begin{aligned} P_{X}(x)=1-2\sqrt{\sigma _{1}\sigma _{2}x}K_{1}\left( 2\sqrt{\sigma _{1}\sigma _{2}x}\right) . \end{aligned}$$

(54)

We deduce the PDF

$$\begin{aligned} p_{X}(x)=-\frac{\sqrt{\sigma _{1}\sigma _{2}}}{\sqrt{x}}K_{1}\left( 2\sqrt{ \sigma _{1}\sigma _{2}x}\right) -2\sqrt{\sigma _{1}\sigma _{2}x}K_{1}^{{\prime }}\left( 2\sqrt{\sigma _{1}\sigma _{2}x}\right) \frac{\sqrt{\sigma _{1}\sigma _{2}}}{ \sqrt{x}}. \end{aligned}$$

(55)

Using

$$\begin{aligned} K_{1}^{^{\prime }}(z)=-K_{0}(z)-\frac{K_{1}(z)}{z}, \end{aligned}$$

(56)

we obtain

$$\begin{aligned} p_{X}(x)=2\sigma _{1}\sigma _{2}K_{0}\left( 2\sqrt{\sigma _{1}\sigma _{2}x}\right) . \end{aligned}$$

(57)

Appendix 2

$$\begin{aligned} P\left( \Gamma _{SR_{k}}\le x\right) =P\left( \frac{eX_{4}X_{5}}{f+X_{3}}\le x\right) =P\left( X_{4}X_{5}\le x\frac{X_{6}}{e}\right) , \end{aligned}$$

(58)

where

$$\begin{aligned} X_{6}=f+X_{3}. \end{aligned}$$

(59)

Since $X_{3}$ is exponential r.v., the PDF of $X_{6}$ is given by as

$$\begin{aligned} f_{X_{6}}(u)=\alpha _{3}e^{-\alpha _{3}(u-f)},u\ge f \end{aligned}$$

(60)

Therefore, we have

$$\begin{aligned} P\left( \Gamma _{SR_{k}}\le x\right) =\int _{f}^{+\infty }P\left( X_{4}X_{5}\le x\frac{y}{ e}\right) f_{X_{6}}(y)dy, \end{aligned}$$

(61)

Using the results of “Appendix 1”, we have

$$\begin{aligned} P\left( \Gamma _{SR_{k}} \le x\right)&= \int _{f}^{+\infty }\left[ 1-2\sqrt{\alpha _{4}\alpha _{5}x\frac{y}{e}}K_{1}\left( 2\sqrt{\alpha _{4}\alpha _{5}x\frac{y }{e}}\right) \right] \alpha _{3}e^{-\alpha _{3}(y-f)}dy, \nonumber \\&= 1-\alpha _{3}e^{\alpha _{3}f}2\sqrt{\alpha _{4}\alpha _{5}\frac{x}{e}} \int _{f}^{+\infty }\sqrt{y}K_{1}\left( 2\mu \sqrt{y}\right) e^{-\alpha _{3}y}dy \nonumber \\&= 1-\alpha _{3}e^{\alpha _{3}f}2\sqrt{\alpha _{4}\alpha _{5}\frac{x}{e}} \int _{0}^{+\infty }\sqrt{y}K_{1}\left( 2\mu \sqrt{y}\right) e^{-\alpha _{3}y}dy \nonumber \\&+\alpha _{3}e^{\alpha _{3}f}2\sqrt{\alpha _{4}\alpha _{5}\frac{x}{e}} \int _{0}^{f}\sqrt{y}K_{1}\left( 2\mu \sqrt{y}\right) e^{-\alpha _{3}y}dy \end{aligned}$$

(62)

where

$$\begin{aligned} \mu =\sqrt{\frac{\alpha _{4}\alpha _{5}x}{e}} \end{aligned}$$

We have

$$\begin{aligned} \int _{0}^{+\infty }\sqrt{y}K_{1}\left( 2\mu \sqrt{y}\right) e^{-\alpha _{3}y}dy=\frac{e^{ \frac{\mu ^{2}}{2\alpha _{3}}}}{2\mu \alpha _{3}}W_{-1,0.5}\left( \frac{\mu ^{2}}{ \alpha _{3}}\right) , \end{aligned}$$

(63)

where $W_{\mu ,\nu }(x)$ is the Whittaker function.

The CDF of $\Gamma _{SR_{k}}$ is given by

$$\begin{aligned} F_{\Gamma _{SR_{k}}}(x)&= 1-\alpha _{3}e^{\alpha _{3}f}2\sqrt{ \alpha _{4}\alpha _{5}\frac{x}{e}}\frac{e^{\frac{\mu ^{2}}{2\alpha _{3}}}}{ 2\mu \alpha _{3}}W_{-1,0.5}\left( \frac{\mu ^{2}}{\alpha _{3}}\right) \nonumber \\&+\alpha _{3}e^{\alpha _{3}f}2\sqrt{\alpha _{4}\alpha _{5}\frac{x}{e}} \int _{0}^{f}\sqrt{y}K_{1}\left( 2\mu \sqrt{y}\right) e^{-\alpha _{3}y}dy. \end{aligned}$$

(64)