1 Introduction

In the future 5G wireless networks, boosting SE performance is inevitably required to cover the explosive growth of spectrum demands. Bandwidth shrinkage pushes network providers to improve the system capacity via resorting to physical layer techniques wherein, SE can be improved by massive MIMO implementations and/or effective channel estimations [1]. Further capacity enhancements could be achieved through network densification[2, 3], device-to-device (D2D) communications [4], and cloud RANs [5]. According to the facts of spectrum scarcity and progressive growth of data rates, exploiting a new cellular band is envisioned as crucial necessity.

The mmWave bands (30 GHz - 300 GHz) have been considered for supporting high data rate with indoor and outdoor point-to-point communications [6]. Thanks to small wavelength of mmWave, massive array of dipoles can be packed up in a small plate which offers a significant array gain to struggle the huge path loss. Moreover, it provides the capability to synthesize high directive beams which able to convey spatially multiplexing data streams. Further, more privileges of gain and performance can be achieved when communication systems are characterized by the integrity of mmWave, massive MIMO and hybrid precoding. On the other hand, deploying mmWave for 5G backhauling brings critical challenges. For instance, path loss proportionally increases with square of frequency and the propagation loss caused by rain attenuation [7].

Unfortunately, precoding over mmWave massive MIMO communications cannot be accomplished entirely at the digital domain, where it is infeasible to consider one RF chain per antenna element as in conventional MIMO systems. In fact, this limitation leads to an excessive cost of implementation complexity and power consumption. Hence, the hybrid precoding has been considered to break this limitation by reducing the number of RF chains which is responsible for joining the digital precoding stage with the analog one [8]. The circuit of analog precoder is designed without regarding variable voltage amplifiers (VGAs) [9] where, the power loss is reduced at the cost of sacrificing with the ability of controlling the RF magnitude. Although, the circuit design of phase shifter has been concerned in many studies [10,11,12,13], but they didn’t regard designing low complex hybrid precoding algorithms for mmWave massive MIMO systems. The analog beam-formers [10, 12] are implemented for near optimal performance while achieving the full diversity. Authors of [11] proposed an iterative limited-power baseband precoding to handle multi-data streams where, both diversity and multiplexing were addressed at a limited number of the RF chains. Literature [13] discussed the quantized phase control to introduce a precise analog to digital converter (A/D). Although, the studies [10,11,12,13] argued issues of phase quantization and capability of handling data streams, but they didn’t investigate any of performance metrics.

In the other hand, hybrid precoding techniques with mmWave massive MIMO communication systems has been studied extensively [14,15,16,17,18]. Many efforts have been introduced towards hybrid precoding structure [8, 19,20,21,22,23,24,25,26]. Particularly, orthogonal matching pursuit (OMP) is the most vastly used algorithm wherein, the steering angles of analog beam-formers were extracted from eigenvectors of mmWave channel [8, 19, 20]. Hybrid precoding based on OMP was regarded as sparse constrained problem, due to mmWave nature, with capability of matrix reconstruction as being followed in image processing field. However, the used constraints and approximations in OMP solution lead to unavoidable performance loss. Authors of studies [19] and [23] focused on reducing OMP complexity through exploiting the result of matrix inversion in each iteration of their proposed algorithm.

Most of the recent studies argued the optimality of hybrid structure from hardware design perspectives. Authors of [24] studied the optimal hybrid precoder when RF chains number at least double of transmitted data streams. Nonetheless, this design didn’t take into account the solution limits at wide range of RF chains and data streams. On the other hand, authors of [27] investigated the impact of RF chains comparing with both data streams and antenna elements for point-to-point and multi-user scenarios. RF stage was designed without regarding VGAs to reduce power consumption at the analog domain[26]. Further, Alternating optimization algorithm based hybrid prcoding was proposed in pioneering work [28] to reduce design complexity. Wherein, the spectral efficiency of hybrid precoders is directly optimized in Riemannian manifold at cost of overhead time complexity stemmed from nested loops of iterative conjugate gradient algorithm. The authors extended their work to develop a low complex precoders based on alternating optimization but, they neither considered aligning channel directions nor maintained the orthogonality among transmitted streams. Further, the limited resolution of practical phase shifters hasn’t been regarded. Hence, their design aspects still require more investigations.

The majority of aforementioned studies have focused on design aspects to simplify the complexity of hybrid precoders in mmwave massive MIMO systems. This usually leads to performance loss or requires designing complex algorithms. Moreover, These studies didn’t concern the integration between design simplicity and practical aspects without sacrificing performance. As a result, we have been motivated to find a new algorithmic design that comprises low complexity and practical considerations, while maintaining performance approximates the unconstrained precoder.

1.1 Contributions

In this section, we present a novel low complex hybrid precoding algorithm wherein, both analog and digital precoders/combiners are optimized to approach the unconstrained precoder. In more details, our contributions can be listed in the following points:

  • We exploit channel information to initialize analog precoder, where a large array gain can be harvested through aligning channel modes. Then, analog beam-formers are updated by an alternative simple precoder which is derived from tight upper bound of hybrid precodering problem. This will result in low cost processing in the analog domain. Further, we enforce unit modulus constraint for each entity of analog precoding matrix to save energy consumption. As well, the digital precoder will be designed based on the legacy of modified water-filling after some mathematical transformation where, orthogonality among transmitted data streams is guaranteed.

  • With respect to the practical design aspects, we adopt phase quantization for analog beam-formers via minimizing the euclidean distance between original phases and the quantized ones. Hence, our hybrid precoding algorithm can be applied for practical phase shifters that have a limited resolution of precision. So far, simulation results will display SE comparison among quantized analog precoders (for one and two bits of quantization) and the unquantized one. Results will reveal that there is no considerable performance loss. Hence, our proposed approach not only combines low complexity and practical aspects but also, it stands as a benchmark of performance.

  • Furthermore, we consider power consumption model, beside the previous SE evaluations, for the purpose of evaluating overall EE performances. Accordingly, we will debate the interplay between performance loss and capacity improvement.

  • Finally, we fairly compare our proposed hybrid precoders including the quantized versions with state-of-the-art: OMP, unconstrained digital precoder and analog precoder. Results will demonstrate that our proposed design outperform OMP and approach the unconstrained precoder with marginal losses.

1.2 Paper Organization and Notations

The rest of the paper is organised as follows. Section 2 states the system model including the scattering channel model of mmWave, followed by problem formulation. Then, we optimize hybrid precoders and consider practical phase shifters as in Sect. 3. Simulation results reveal the rigidity of proposed hybrid algorithm in Sect. 4. Finally, Sect. 5 will present a brief conclusion which followed by the more relevant references.

Note that, the bold face capital and small letters stand for matrix and vector, respectively. \(\mathbf {X}_{i,j}\) refers to entry on i\({th}\) row and j\({th}\) column of matrix \(\mathbf {X}\). The conjugate, transpose and Hermitian of matrix \(\mathbf {X}\) are represented as \(\mathbf {X}^*\), \(\mathbf {X}^T\) and \(\mathbf {X}^H\); \(Tr( \mathbf {X} )\), and \({{\left\| \mathbf {X} \right\| }_{F}}\) denote trace and Frobenius norm; \({{\mathbf {X}}^{\dagger }}\) and \({{\mathbf {X}}^{-1}}\) express the Moore-Penrose pseudo inverse and the inverse of matrix \(\mathbf {X}\), respectively. \(\mathfrak {R}\{.\}\) represents the real part of complex variable and \(\mathbb {E}[.]\) denotes the expectation of random variable.

2 System Model and Problem Formulations

In this section, we consider single cell downlink mmWave massive MIMO system. Then, hybrid precoding problem will be formulated.

2.1 System Model

Fig. 1
figure 1

Fully connected hybrid precoding transceiver system

Full size image

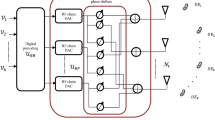
Figure 1 considers hybrid precoding structure wherein, mmWave channel and massive MIMO are taken into account. Base station (BS) is equipped with \(N_t\) transmitting antennas which are stacked as a uniform plane array (UPA) to transmit \(N_s\) data streams. At the receiver side, we assume a single user having \(N_r\) receiving antennas. The number of RF chains, which interfacing the digital precoder with the analog one, at transmitter and receiver are designated by \(N_{RF}^{t}\) and \(N_{RF}^{r}\); such that \({{N}_{s}}\le N_{RF}^{t}\le {{N}_{t}}\) and \({{N}_{s}}\le N_{RF}^{r}\le {{N}_{r}}\), respectively.

The transmitted signal \(N_t \times 1\) vector is mathematically written as \(\mathbf {x}={{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \mathbf {s}\). The average transmitted power of Gaussian data symbol, given by \(N_s \times 1\) vector, can be expressed as \(\mathbb {E}[{{\mathbf {s}}^{H}}\mathbf {s}] =\frac{{{\mathbf {I}}_{{{N}_{S}}}}}{{{N}_{s}}}\). As shown in Fig. 1, the hybrid precoding structure consists of two processing stages: an \(N_{RF}^{t}\times {{N}_{s}}\) low dimensional digital (baseband) precoder \({{\mathbf {F}}_{BB}}\); followed by an \({{N}_{t}}\times N_{RF}^{t}\) high dimensional analog precoder \({{\mathbf {F}}_{RF}}\). It should be noted that the total processing power of hybrid precoders is normalized to satisfy \(\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| _{F}^{2}={{N}_{s}}\). The received signal after decoding processes is denoted by the following expression

$$\begin{aligned} y=\sqrt{\rho }{{\left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) }^{H}} {\mathbf H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}}\mathbf {s} +{{\left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) }^{H}}\mathbf {n}. \end{aligned}$$
(1)

where \(\rho\) refers to the average received power, \(\mathbf {H}\) represents \(N_r \times N_t\) scattering channel matrix. Since decoding process at receiver side resembles the precoding at transmitter then, we have an \(N_{RF}^{r}\times {{N}_{s}}\) digital decoder \({{\mathbf {W}}_{BB}}\) followed by an \({{N}_{r}}\times N_{RF}^{r}\) analog decoder \({{\mathbf {W}}_{RF}}\). \(\mathbf {n}\) denotes \(N_r \times 1\) noise vector which is assumed as independent and identically distributed random variable (i.i.d) with zero mean and average power \(\sigma _{n}^{2}\), i.e. \(\mathbf {n} \sim {\ }\mathcal {C}\mathcal {N}\left( \text {0},\sigma _{n}^{2} \right)\). Further, the channel state information (CSI) is assumed perfectly known for both transceiver sides. In practical scenarios, CSI is estimated firstly at receiver through training sequence and then, it is shared with transmitter using a limited feedback channel as in FDD systems [16, 29]. Based on (1), the SE achieved by hybrid precoding system can be written as

$$\begin{aligned} SE={{\log }_{2}}\left| {{\mathbf {I}}_{{{N}_{s}}}}+SINR \right| \end{aligned}$$
(2)

where, SINR represents the signal-to-noise-plus-interference ratio which is expressed as in (3).

$$\begin{aligned} SINR=\frac{\rho }{\sigma _{n}^{2}{{N}_{s}}}.\left| \frac{{{\left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) }^{H}}\mathbf {H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} {{\left( {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right) }^{H}}{{\mathbf {H}}^{H}}\left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) }{{{\left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) }^{H}} \left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) } \right| \end{aligned}$$
(3)

Let \(\mathbf {A}={{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}}\), then we can rewrite (3) by (4).

$$\begin{aligned} SINR=\frac{\rho }{\sigma _{n}^{2}{{N}_{s}}}. \left| {{\left( {{\mathbf {A}}^{H}}\mathbf {A} \right) }^{-1}} {{\mathbf {A}}^{H}}\mathbf {H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} {{\left( {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right) }^{H}} {{\mathbf {H}}^{H}}\mathbf {A} \right| , \end{aligned}$$
(4)

Then, we substitute both of (4) and the well-known mathematical definition \({{\mathbf {A}}^{\dagger }} ={{\left( {{\mathbf {A}}^{H}}\mathbf {A} \right) }^{-1}}{{\mathbf {A}}^{H}}\) into (2), we can get the final expression of SE in terms of precoding matrices as in (5).

$$\begin{aligned} SE={{\log }_{2}}\left| \left( {\mathbf {I}_{{{N}_{s}}}} +\frac{\rho }{\sigma _{n}^{2}{{N}_{s}}}{{\left( {{\mathbf {W}}_{RF}} {{\mathbf {W}}_{BB}} \right) }^{\dagger }}\mathbf {H}{{\mathbf {F}}_{RF}} {{\mathbf {F}}_{BB}}{{\left( {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right) }^{H}} {{\mathbf {H}}^{H}}\left( {{\mathbf {W}}_{RF}}{{\mathbf {W}}_{BB}} \right) \right) \right| . \end{aligned}$$
(5)

It should be noted that the hybrid structure in Fig. 1 includes connecting each RF chain with each antenna element through a network of phase shifters \({{N}_{p}}={{N}_{t}}N_{RF}^{t}\). This configuration is called fully connected structure which is remarked by full beam-forming gain due to large degree of freedom (DoF). Nevertheless, it has a hardware complexity that can be mitigated by reducing \({{N}_{p}}\) or by replacing this structure with the partially connected configuration [30,31,32,33] at the cost of sacrificing DoF.

2.2 Channel Model

Millimeter wave channel model is characterized by clusters of scatterers (Saleh-Valenzuela model) whereas, the signal propagation is subjected to high free-space path loss. This model can be mathematically represented by the following [9]

$$\begin{aligned} \mathbf {H}=\sqrt{\frac{{{N}_{t}}{{N}_{r}}}{{{N}_{cl}}{{N}_{ray}}}} \sum \limits _{i=1}^{{{N}_{cl}}}{\sum \limits _{l=1}^{{{N}_{ray}}} {{{\alpha }_{il}}{{\mathbf {a}}_{r}}\left( \phi _{il}^{r},\theta _{il}^{r} \right) }}{{\mathbf {a}}_{t}}{{\left( \phi _{il}^{t},\theta _{il}^{t} \right) }^{H}}. \end{aligned}$$
(6)

where \(N_{cl}\) states the number of clusters wherein, an \(N_{ray}\) rays can be described by path gain \(\alpha _{il}\). We assume that \(\alpha _{il} \sim {\ }\mathcal {C}\mathcal {N}\left( \text {0},\sigma _{\alpha ,i}^{2} \right)\), such that the total average power of all clusters is indicated by \(\sum \nolimits _{i=1}^{{{N}_{cl}}}{\sigma _{\alpha ,i}^{2}=\hat{\gamma }}\). This, also, satisfies normalized average channel gain described by \(\mathbb {E}\left[ \left\| \mathbf {H} \right\| _{F}^{2} \right] ={{N}_{t}}{{N}_{r}}\). In addition, \({{\mathbf {a}}_{t}}\left( \phi _{il}^{t},\theta _{il}^{t} \right)\) and \({{\mathbf {a}}_{r}}\left( \phi _{il}^{r},\theta _{il}^{r} \right)\) represent transmit and receive array response vector for given azimuth \(\left[ \phi _{il}^{t},\phi _{il}^{r} \right]\) and elevation angles \(\left[ \theta _{il}^{t},\theta _{il}^{r} \right]\) of departure and arrival, respectively. In this paper, we suppose that massive MIMO elements are installed uniformly in \(y-z\) plane (UPA) where an \(\sqrt{N_t}\times \sqrt{N_t}\) antenna elements are equally spaced. Based on this setting, the array response of \(l{th}\) ray in \(i{th}\) cluster is given as

$$\begin{aligned} \mathbf {a}({{\phi }_{il}},{{\theta }_{il}})=\frac{1}{\sqrt{N}}{{\left[ 1,...,{{e}^{j\frac{2\pi }{\lambda }d\left( p\sin {{\phi }_{il}}\sin {{\theta }_{il}}+q\cos {{\theta }_{il}} \right) }},...,{{e}^{j\frac{2\pi }{\lambda }d \left( (\sqrt{N}-1)\sin {{\phi }_{il}}\sin {{\theta }_{il}} +(\sqrt{N}-1)\cos {{\theta }_{il}} \right) }} \right] }^{T}} \end{aligned}$$
(7)

where p and q are the antenna indexes in 2D which is defined by \(0\le p\le \sqrt{N}\) and \(0\le q\le \sqrt{N}\). Noting that the antenna spacing is denoted by d which is usually scaled by wavelength \(\lambda\).

2.3 Problem Formulation

Inspired by [8] and [19], the design of hybrid precoders/decoders can be decoupled into two individual sub problems: one handles analog precoding/combining problem with a unit modulus constraint of steering angles and the other solves digital precoding/combining problem constrained by an extra power constraint. Generally speaking, The hybrid precoding problem can be described by

$$\begin{aligned} \begin{array}{ll} \underset{{{\mathbf {F}}_{RF}},{{\mathbf {F}}_{BB}} }{\text {minimize}} &{} \quad {{\left\| {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}} {{\mathbf {F}}_{BB}} \right\| }_{F}} \\ \text {subject to} &{} \quad \mathbf {F}_{RF}\in \varPsi , \\ &{} \quad \left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| _{F}^{2}={{N}_{s}}. \end{array} \end{aligned}$$
(8)

where \(\mathbf {F}_{FD}\) stands for an \(N_t \times N_s\) fully digital precoder which is considered as the optimal unconstrained (virtual/digital) precoder. The first constraint emphasizes on the feasibility of analog precoder through feasible set \(\varPsi\) of steering angles, wherein unit modulus constraint of each entity has been regarded, i.e. \(\left| {{({{\mathbf {F}}_{RF}})}_{i,j}} \right| =\left| {{({{\mathbf {W}}_{RF}})}_{i,j}} \right| =1\). It has been proved that the optimization problem in (8) is approximately equivalent to maximization of spectral efficiency in (5). It is intuitive that approaching SE performance of virtual precoder can be achieved by making the hybrid precoders are sufficiently proximate the fully digital precoder. Noting that the unconstrained precoder matrices are directly deduced form the decomposition of channel matrix, i.e. the corresponding \(N_s\) columns of channel eigenvectors.

The formulation in (8) is usually named as “matrix factorization problem” where, we will adopt an iterative low complex algorithm to optimize the precoding matrices, \(\mathbf {F}_{RF}\) and \(\mathbf {F}_{BB}\). In the fact, simultaneous optimization of the precoding matrices appears very complicated task due to aforementioned constraints of both analog and digital precoders. Hence, decoupling the objective in (8) facilitates getting the optimal solution with less complexity.

3 Proposed Hybrid Precoding Algorithm

Since the computational complexity is a crucial factor for practical designs, we have to propose a low complex and efficient hybrid precoding algorithm. In the following section, we demonstrate the main ideas of the proposed precoders, followed by the corresponding pseudo code.

3.1 Digital Precoder Design Concept

Similar to orthogonal columns of the unconstrained/fully digital precoder \(\mathbf {F}_{FD}\), we shall enforce orthogonality constraint on the digital precoder \(\mathbf {F}_{BB}\). This property relieves the experienced interference among the multiplexed data streams. Then, we will deploy the concept of water-filling to maintain this orthogonality depending on the effective channel \({{\mathbf {H}}_{e}}=\mathbf {H}{{\mathbf {F}}_{RF}}\). Let’s assume the condition that satisfies orthogonal property as the following

$$\begin{aligned} \mathbf {F}_{BB}^{H}{{\mathbf {F}}_{BB}}=\beta \mathbf {F}_{D}^{H} \beta {{\mathbf {F}}_{D}}={{\beta }^{2}}{{\mathbf {I}}_{{{N}_{s}}}} \end{aligned}$$
(9)

where \(\mathbf {F}_{D}\) denote unitary matrix with dimension \(N_{RF}^{t}\times {{N}_{s}}\) which is the same of \(\mathbf {F}_{BB}\). The \(\beta\) stands for weight power coefficient or scaling factor that will be discussed in the following section. To optimize the digital precoder,the analog beam-formers are initialized with a suboptimal solution from which, an array gain and channel alignment could be earned. In particular, CSI is exploited to initialize the steering angles as \(\mathbf {F}_{RF}^{(0)}={{e}^{j\angle {{\mathbf {H}}^{H}}}}\). Once those angles have been obtained, it became a temporary solution for evaluating \(\mathbf {F}_{BB}\). Then, hybrid beam-formers are updated as will be shown in the following sections.

3.2 Upper Bound of Hybrid Precoding Problem

In this section, we drive an upper bound of hybrid precoding problem by substituting (9) into (8) and then recast the yielding results as in the following lines

$$\begin{aligned}&{{\left\| {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| }^2_{F}},\nonumber \\&\quad = Tr\left( {{\left( {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right) }^{H}}\left( {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right) \right) , \nonumber \\&\quad = Tr\left( \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{FD}} \right) -Tr\left( \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right) \nonumber \\&\qquad - Tr\left( \mathbf {F}_{BB}^{H}\mathbf {F}_{RF}^{H}{{\mathbf {F}}_{FD}} \right) +Tr\left( \mathbf {F}_{BB}^{H}\mathbf {F}_{RF}^{H}{{\mathbf {F}}_{RF}} {{\mathbf {F}}_{BB}}\right) , \nonumber \\&\quad = Tr\left( \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{FD}} \right) -\beta Tr\left( \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right) \nonumber \\&\qquad - \beta Tr\left( {{\left( {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right) }^{H}} {{\mathbf {F}}_{FD}} \right) +{{\beta }^{2}}Tr\left( {{\left( {{\mathbf {F}}_{RF}} {{\mathbf {F}}_{D}} \right) }^{H}}{{\mathbf {F}}_{D}}{{\mathbf {F}}_{RF}} \right) , \nonumber \\&\quad = Tr\left( \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{FD}} \right) -2\beta Tr \left( \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right) \nonumber \\&\qquad + {{\beta }^{2}}Tr\left( {{\left( {{\mathbf {F}}_{RF}} {{\mathbf {F}}_{D}} \right) }^{H}}{{\mathbf {F}}_{D}}{{\mathbf {F}}_{RF}} \right) ,\nonumber \\&\quad =\left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}-2\beta \mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H} {{\mathbf {F}}_{RF}} \right) \right\} +{{\beta }^{2}} \left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2} \end{aligned}$$
(10)

According to (10), increasing the second term minimizes the objective function of (8). Hence, We can directly find \(\beta\) coefficient which satisfies minimization of the objective function by differentiating (10) with respect to \(\beta\) and equating the result with zero to get the following

$$\begin{aligned} \beta =\frac{\mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}} \right) \right\} }{\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2}}. \end{aligned}$$
(11)

To ensure feasibility of \(\beta\), we substitute (11) into (10) to obtain a new form of the objective function as in the following

$$\begin{aligned} \left\| {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| _{F}^{2}= & {} \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}-\frac{2{{\left( \mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H} {{\mathbf {F}}_{RF}} \right) \right\} \right) }^{2}}}{\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2}}\nonumber \\&+\frac{\mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H} {{\mathbf {F}}_{RF}} \right) \right\} }{{{\left( \left\| {{\mathbf {F}}_{RF}} {{\mathbf {F}}_{D}} \right\| _{F}^{2} \right) }^{2}}}.\left\| {{\mathbf {F}}_{RF}} {{\mathbf {F}}_{D}} \right\| _{F}^{2},\nonumber \\ \left\| {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| _{F}^{2}= & {} \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}-\frac{{{\left( \mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H} {{\mathbf {F}}_{RF}} \right) \right\} \right) }^{2}}}{\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2}}. \end{aligned}$$
(12)

According to the orthogonality constraint of (9), the upper limit of \({\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2}}\) can be mathematically deduced as

$$\begin{aligned}&\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2} = Tr\left( {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}}\mathbf {F}_{D}^{H} \mathbf {F}_{RF}^{H} \right) , \nonumber \\&let \quad {SVD}\left( {{\mathbf {F}}_{D}}\mathbf {F}_{D}^{H} \right) = \mathbf {K}\left( \begin{matrix} {{\mathbf {I}}_{{{N}_{s}}}} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} \\ \end{matrix} \right) {{\mathbf {K}}^{H}}, \nonumber \\&\therefore \left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2} =Tr\left( \left( \begin{matrix} {{\mathbf {I}}_{{{N}_{s}}}} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} \\ \end{matrix} \right) {{\mathbf {K}}^{H}}\mathbf {F}_{RF}^{H}{{\mathbf {F}}_{RF}} \mathbf {K} \right) , \nonumber \\&\quad \le Tr\left( \mathbf {F}_{RF}^{H}{{\mathbf {F}}_{RF}} \right) .\nonumber \\&\therefore \left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2} \le \left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2}. \end{aligned}$$
(13)

where \(\mathbf {K}\) stands for eigenvectors of singular value decomposition (SVD). Noting that the result of this decomposition turns to identity if \(\mathbf {F}_{D}\) is always square matrix, i.e. the inequality in (13) is converted to strict equality if and only if \({{N}_{s}}=N_{RF}^{t}\) . In the following lines, we utilize the result of (13) to get the upper bound of (12)

$$\begin{aligned} {{\left\| {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| }_{F}}\le \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}-\frac{{{\left( \mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}} \right) \right\} \right) }^{2}}}{\left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2}} \end{aligned}$$
(14)

By introducing some algebraic manipulation on the right-hand side of (14), we can get

$$\begin{aligned}&\left[ \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}-\frac{{{\left( \mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}} \right) \right\} \right) }^{2}}}{\left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2}}+\frac{\left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}}{2\left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2}}\right. \\&\qquad -\left. \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2}+\frac{1}{2} \right] \times 2\left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2} \\&\quad =\left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2} -2{{\left( \mathfrak {R}\left\{ Tr\left( {{\mathbf {F}}_{D}} \mathbf {F}_{FD}^{H}{{\mathbf {F}}_{RF}} \right) \right\} \right) }^{2}} +\left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2} \\&\qquad \because \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2} \approx Tr\left( {{\mathbf {F}}_{D}}\mathbf {F}_{FD}^{H} {{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H} \right) \\&\qquad \therefore \left\| {{\mathbf {F}}_{FD}} \right\| _{F}^{2} =\left\| {{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H} \right\| _{F}^{2} \forall {{N}_{s}}=N_{RF}^{t} \end{aligned}$$

Plugging all the previous steps into (14), the final upper bound expression is denoted as

$$\begin{aligned} \left\| {{\mathbf {F}}_{FD}}-{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{BB}} \right\| _{F}^{2}\le \left\| {{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H}-{{\mathbf {F}}_{RF}} \right\| _{F}^{2}. \end{aligned}$$
(15)

3.3 Hybrid Precoder Design

As we mentioned before that directly optimizing the main objective function in (8) incurs an additional computational complexity. Accordingly, we minimize the upper bound (15) instead of the original objective. Whereas, power transmission constraint is satisfied by normalizing the digital precodeing matrix after consecutive updates of the hybrid precoding matrices. In more details, the analog precoding subproblem is firstly solved by considering the upper bound (15) as objective function with temporarily disabled transmit power constraint as described below

$$\begin{aligned} \begin{array}{ll} \underset{{{\mathbf {F}}_{RF}},{{\mathbf {F}}_{D}} }{\text {minimize}} &{} \quad \left\| {{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H} -{{\mathbf {F}}_{RF}} \right\| _{F}^{2}, \\ \text {subject to} &{} \quad \left| {{\left( {{\mathbf {F}}_{RF}} \right) }_{i,j}} \right| =1,\quad \forall i,j , \\ &{} \quad \mathbf {F}_{D}^{H}{{\mathbf {F}}_{D}}={{\mathbf {I}}_{{{N}_{s}}}}. \end{array} \end{aligned}$$
(16)

From optimization subproblem in (16), we note that \(\mathbf {F}_{RF}\) is no longer multiplied with \(\mathbf {F}_{BB}\) as in the main objective. This leads to simplified solution of analog precoder that can be described in the following closed form expression

$$\begin{aligned} \angle {{\mathbf {F}}_{RF}}\approx \angle \left( {{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H} \right) . \end{aligned}$$
(17)

It is cleared from Eq. (17) that, analog precoder has been constructed from the corresponding phases of the equivalent precoder \({{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H}\). The mathematical expression of (17) can be visualized as the projection of \({{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H}\) on the feasible set of analog precoder \(\varPsi\), which is also equivalent to the first constraint in (8).

On the other hand, the digital precoding subproblem can be considered as in the following optimization problem, wherein \(\mathbf {F}_{RF}\) is instantaneously fixed

$$\begin{aligned} \begin{array}{ll} \underset{{{\mathbf {F}}_{D}} }{\text {minimize}} &{} \quad \left\| {{\mathbf {F}}_{FD}}\mathbf {F}_{D}^{H} -{{\mathbf {F}}_{RF}} \right\| _{F}^{2} \\ \text {subject to} &{} \quad \mathbf {F}_{D}^{H}{{\mathbf {F}}_{D}}={{\mathbf {I}}_{{{N}_{s}}}}. \end{array} \end{aligned}$$
(18)

The constraint in (18) denotes power normalization with respect to \(\beta ^2\). Unfortunately, the aforementioned optimization problem is not convex in \(\mathbf {F}_{D}\). Therefore, we can replace (18) with another equivalent form as in the following

$$\begin{aligned} \begin{array}{ll} \underset{{{\mathbf {F}}_{D}} }{\text {maximize}} &{} \quad {{\log }_{2}}\left| {{\mathbf {I}}_{{{N}_{s}}}} +\mathbf {H}{{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \mathbf {F}_{D}^{H}{{\left( \mathbf {H}{{\mathbf {F}}_{RF}} \right) }^{H}} \right| \\ \text {subject to} &{} \quad Tr\left( \mathbf {Q}{{\mathbf {F}}_{D}}\mathbf {F}_{D}^{H} \right) \le P . \end{array} \end{aligned}$$
(19)

Where, P is the total transmit power which is assumed to be uniformly allocated for each data steams. For massive MIMO configurations, we can approximate \(\mathbf {Q}=\mathbf {F}_{RF}^{H}{{\mathbf {F}}_{RF}}\) to \(\mathbf {Q}=N_t \mathbf {I}_{N_t}\) with high probability since, the off-diagonal entries of the product \(\mathbf {F}_{RF}^{H}{\mathbf {F}}_{RF}\) are considered much less than \(N_t\) [8]. Optimization problem and its constraint in (19) are convex with respect to \(\mathbf {F}_{D}\). Problem (19) has water-filling solution. Taking into account that our problem adopts power normalization for the transmitted streams. As a result, the solution is slightly modified to become

$$\begin{aligned} {{\mathbf {F}}_{D}}={{\mathbf {Q}}^{{}^{-1}/{}_{2}}}{{\mathbf {V}}_{1}} {{\mathbf {\Lambda }}_{{{N}_{s}}}}\Rightarrow \frac{1}{\sqrt{{{N}_{t}}}}{{\mathbf {V}}_{1}}{{\mathbf {I}}_{{{N}_{s}}}} \end{aligned}$$
(20)

where \({{\mathbf {\Lambda }}_{{{N}_{s}}}}\) denotes diagonal square matrix of power allocation. Due to power normalization criterion, we can write \({{\mathbf {\Lambda }}_{{{N}_{s}}}}\approx \sqrt{\frac{P}{N_{RF}^{t}}}{{\mathbf {I}}_{{{N}_{s}}}} ={{\mathbf {I}}_{{{N}_{s}}}}\). Also, \(\mathbf {V}_{1}\) represents the first \(N_s\) columns returned from SVD of the effective channel. This can be mathematically interpreted as

$$\begin{aligned} SVD\left( \mathbf {H}{{\mathbf {F}}_{RF}}{{\mathbf {Q}}^{^{-1}{{/}_{2}}}}\right) =SVD\left( \frac{\mathbf {H}{{\mathbf {F}}_{RF}}}{\sqrt{{{N}_{t}}}}\right) =\mathbf {U\Sigma V}_{1}^{H} \end{aligned}$$
(21)

Accordingly, we can briefly draw the design of digital precoder, at any channel realization k, as follows

$$\begin{aligned} SVD\left( \frac{\mathbf {HF}_{RF}^{(k)}}{\sqrt{{{N}_{t}}}} \right)= & {} {{\mathbf {U}}^{(k)}}{{\mathbf {\Sigma }}^{(k)}} {{\left( \mathbf {V}_{1}^{(k)} \right) }^{H}}, \nonumber \\ {{\mathbf {F}}_{D}}= & {} \frac{1}{\sqrt{{{N}_{t}}}}\mathbf {V}_{1}^{(k)} {{\mathbf {I}}_{{{N}_{s}}}}. \end{aligned}$$
(22)

3.4 Quantized Analog Precoder

According to (17), each element in the \(\mathbf {F}_{RF}\) matrix can be continuously generated from infinite resolution phase shifters. But in the fact, this violates the limited capability of the phase shifters that have a finite resolution of their produced steering angles. Hence, and for the practical purpose of implementations, we propose phase control method to quantize steering angles of analog precoder via specified number B bits of precision. Then, we investigate the impact of quantization on the overall performance. Moreover, we will depict the performance gape between quantized solution and the unquantized one. Mainly, the concept of quantization depends on minimizing the Euclidean distance between the quantized and unquantized steering angles. Accordingly, the phase of an entry in the qunatized matrix is represented by

$$\begin{aligned} {{\angle {{\hat{\mathbf {F}}}_{RF}}}}\,={\hat{\phi }} =\frac{2\pi \hat{n} }{{{2}^{B}}} \end{aligned}$$
(23)

where \(\hat{n}\) is chosen to satisfy the following criteria

$$\begin{aligned} \hat{n} = \underset{ n\in \left\{ 0,...,{{2}^{B}}-1 \right\} }{\text {argmin}} \left| \phi -\frac{2\pi n}{{{2}^{B}}} \right| . \end{aligned}$$
(24)

where \(\phi\) refers to the unquantized phases that is obtained from (17). Note that the digital precoding matrix is reevaluated for the quantized analog precoder (23) to evaluate the total quantized performance.

3.5 Energy Efficiency Computation

In this part, we argue one of the most important key performance of networks. We aim to discuss the energy efficiency (EE) of the proposed hybrid precoder. EE is defined by the ratio between a benefit and cost, where the profit refers to the spectral efficiency defined by (5) and the cost denotes power consumption [28] that can be modeled as in the following expression

$$\begin{aligned} PC={{P}_{maj}}+N_{RF}^{t}{{P}_{RF}}+{{N}_{t}}{{P}_{PA}}+{{N}_{p}}{{P}_{s}}. \end{aligned}$$
(25)

The first term, in (25) \(({P}_{maj})\) defines the major power consumption of the main BS circuits. The second term \((N_{RF}^{t}.{P}_{RF})\) accounts for the total power dissipation in RF chains. Further, the third and fourth terms denote the total power loss due to power amplifier and the phase shifters.

According to equations (5) and (25), the total EE can be described as follows

$$\begin{aligned} \eta =\frac{SE}{PC}, \qquad \text {(bits/Hz/J)}. \end{aligned}$$
(26)

In the following lines, we shall introduce our proposed approach for hybrid precoder followed by further remarks which confirm the low complexity of the proposed solution.

figure d

Similarly, the proposed algorithm has been deployed to evaluate decoding/combining matrices \(\mathbf {W}_{RF}\) and \(\mathbf {W}_{BB}\), at receiver side, which are substituted in (5) to return the total SE and EE performance.

Remark 1

Line (1) is inspired by the optimizers which require an initial suboptimal/guess point for fast convergence to final solutions. Therefore, this initialization reduces the overhead-time of running algorithm and brings the benefits of array (beamforming) gain. Also, line (1) can be interpreted as aligning data stream transmission with dominant channel modes.

Remark 2

Updating analog precoder in line (4) is realized simply by extracting phases of alternative precoder whose dimension is \(N_t \times N_{RF}^{t}\). Utilizing the upper bound instead of the original objective simplifies the solution with marginal performance loss comparing with the expected solution of the main optimization problem (8). This loss returns to the gap between \(\left\| {{\mathbf {F}}_{RF}}{{\mathbf {F}}_{D}} \right\| _{F}^{2}\) and \(\left\| {{\mathbf {F}}_{RF}} \right\| _{F}^{2}\) as discussed in (13). In general, this gap varies with the limits of RF chains \({{N}_{s}}\le N_{RF}^{t}\le 2{{N}_{s}}\).

Remark 3

We have noted that line (7) is independent of the \(\beta\) coefficient since, at transmitter, normalizing \({{\mathbf {F}}_{BB}}\) is equivalent to normalizing \({{\mathbf {F}}_{D}}\). On the other hand, at receiver, the digital decoding matrix \(\mathbf {W}_{BB}\) only depends on the received signal and the associated noise. Hence, the SINR in (3) is independent of factor \(\beta\) and this reduce computational complexity of the proposed algorithm.

4 Simulations Results and Discussions

In this part of paper, we exhibit performance of the proposed algorithm. Let’s assume that a number of data streams are sent through an array of antenna elements \(N_t =144\) which have been mounted in a square plate (\(\sqrt{N_t} \times \sqrt{N_t}\)); such that all elements are equally spaced by \(d=0.5\lambda\). Those streams are received by \(N_r=36\) antennas which are similarly installed as in the transmitter side. Further, we consider mmWave (clustered) channel model with \(N_{cl}=5\) clusters, \(N_{ray}=10\) rays and the average power per cluster is \(\sigma _{\alpha , i}^{2}=1\). The distribution of azimuth and elevation angles are assumed Laplacian with mean angular spread of (\(10^o\)) for all arrival and departure angles (AoAs and AoDs) [28]. Noting that the simulation results are averaged over 100 channel realizations.

4.1 Spectral Efficiency Evaluation

Fig. 2
figure 2

Spectral efficiency for different precoding algorithms at case \({{N}_{s}}=N_{RF}^{t}=N_{RF}^{r}=3\). (Color figure online)

Full size image

SE has been plotted against different levels of signal power \((SNR_{dB})\) considering the worst case \({{N}_{s}}=N_{RF}^{t}=N_{RF}^{r}\); as shown in Fig. 2. The proposed algorithm (dotted blue line) displays a significant performance. The magnified scale, at the middle-left, demonstrates very small gap that is evaluated by \(-5 dB\) or 0.31bits / s / HZ of loss comparing with the unconstrained digital precoder (black solid line). This reflects the rigidity of our algorithm and precision of the derived upper bound (15) along all SNR range. Moreover, the proposed hybrid approach outperform the other algorithms such as OMP [8] and the analog beamforming. This superiority comes from not only utilizing effective channel information with modified water-filling to keep the orthogonality criterion but also, extracting the steering angles from low complex (alternative) beamformers. Hence, the proposed approach harvests benefits of both array gain that potentially substitutes experienced losses in mmWave channel and low complexity design.

As well, the SE of quantized hybrid precoders, with one or two bits of precision, approximates the SE performance of unquantized hybrid precoders (dotted blue line). Particularly, the average SE performance of two bits quantized precoder (dotted green line) has been degraded with about \(-1.5 dB\) comparing with the unquantized performance. Meanwhile, the proposed unquantized algorithm achieves gain more than 4.3dB comparing with OMP (sold green line). Therefore, we can firmly conclude that our algorithm (quantized and unquantized) stands as a benchmark for hybrid precoding structure.

It is worth to be mentioned that the study [24] introduced a closed formula of hybrid precoding problem at the special case of \(N_{RF}^{t}\ge 2{{N}_{s}}\), \(N_{RF}^{r}\ge 2{{N}_{s}}\) at which authors’ solution approximates the unconstrained digital precoder. On contrary, our proposed approach investigates a wider range of \(N_{RF}^{t}\) described by \({{N}_{s}}\le N_{RF}^{t}<2{{N}_{s}}\) to check if the proposed approach able to achieve a significant performance or not. Fig. 3 depicts fast saturation of the proposed approach (quantized and unquantized) to fixed levels of SE for the given range of RF chains. It is visualized that the average performance loss between the unqauntized hybrid algorithm and the fully digital precoder is evaluated by \(-5 dB\). Meanwhile, the SE degradation of the two bits quantized precoder is evaluated by about \(-2.2 dB\) comparing with its counterpart of the one bit quantized precoder.

Furthermore, Fig. 3 demonstrates that OMP outperform the one bit qunatized precoder only when \(N_{RF} > 2N_s\) due to available high DoF at reconstructing precoding matrices. On contrary, the qunatized hybrid performance using one bit of precision has a high merit at \(N_{RF} \le 2N_s\) which makes it preferable at the worst cases of performance (i.e. at \(N_{RF}=N_s\)) or at the cases which require more power saving. It worth noted that the same aforementioned discussions, about SE performance behavior, can be deduced with higher number of data streams, as shown in Fig. 4b. Figure 4a remarks a divergence of the one bit quantized approach which slightly increases with \(N_s\) since, the resolution of quantization process may not be sufficient to steer large number of data streams.

Fig. 3
figure 3

Spectral efficiency versus defined range of \(N_{RF}\) when \({{N}_{s}}=2\) and \({SNR=0dB}\)

Full size image
Fig. 4
figure 4

Comparisons of the spectral efficiency performance

Full size image

4.2 Energy Efficiency Performance

Fig. 5
figure 5

Energy efficiency performance at \({{N}_{s}}=3,8\) and \({SNR=0dB}\)

Full size image

In this part, we will demonstrate EE behavior of the proposed algorithm based on the definition of EE in 26 and the corresponding parameters: \(P_{maj}=10W, P_{RF}=100mW, P_s=10mW\) and \(P_{PA}=100mW\) [9]. The simulation result is displayed in Fig. 5, wherein EE is decaying with increasing the RF chains. This can be explained that phase shifters are linearly scaled with the number of used RF chains as shown by the second term of (25). Therefore, it has a significant impact at measuring power consumption.

Based on the previous results in Fig. 3 and Fig. 4b, we observe that the SE performance is fixed and the decaying rate of power consumption is faster than the increment of SE along \(N_{RF}\) range as depicted in second term of (25). This explains the dramatic decaying of EE. Further, increasing the number of data streams enhances the EE performance. For instance, the EE is boosted by about 3.6dB at \(N_s=8\) comparing with its counterpart at \(N_s=3\). Moreover, the two bits quantized EE performance is approximately equal the unquantized approach without significant loss for any scenario of stream number. Nevertheless, The EE of one bit quantized approach reveals quite performance loss at high number of data streams. This matches the divergence that has been explained for Fig. 4a.

5 Conclusions and Future Work

We have presented an effective hybrid precoding algorithm to approach the fully digital precoder which has high complex degree of implementation in mmWave massive MIMO systems. Mainly, our proposed algorithm has been built on the legacy of tight upper bound which approximates the analog precoder to an alternative one that have low processing cost. On the other hand, the digital precoder has been optimized considering data streams orthogonality which has been maintained through modified water filling solution. Furthermore, the proposed algorithm exhibits superior performance at any number of RF implementations where, the spectral efficiency displays a converged behavior along wide range of RF chains. Moreover, we have considered quantized analog beam-formers for practical issues wherein, the steering angles are quantized up to two bits of precision. In this case, quantized version of the proposed hybrid precoder reveals a remarkable performance without significant loss. Besides, tracing EE of our proposed approach returns a valuable insight for design criteria, where the hardware complexity may costs more power consumption than the expected/required growth of system capacity. As a result, network performance requires compromising between data rate demands and energy saving.

So far, it will be interesting to extend our proposal to the heterogeneous networks and further small dense cells to introduce a complete picture about the hybrid beamforming in the future networks. Also, more characterization for the hybrid precoding structure will be considered through integrating with one of new candidate modulation techniques which will be elected for future 5G networks.