Two-Way Secure Communication with Multiple Untrusted Half-Duplex AF Relays

Abstract

In this paper, we analyze the secrecy outage probability (SOP) of a cognitive cooperative radio network in a two-way communication in which two secondary source communicate with each other via multiple untrusted half-duplex amplify and forward relays in the absence of direct link. Due to the cognitive scenario, power is allocated to secondary nodes on the basis of outage constraint of the primary network. In the absence of direct link between two sources, communication completes in two time slots. In the first time slot, both of the sources broadcast the information signal and in the second time slot, a selected relay broadcasts the amplified information signals of both of the sources. Relays being untrusted, they can eavesdrop the message from the information signal. A particular relay, which maximizes the end-to-end secrecy capacity, is selected to broadcast the signal. The selected untrusted relay can only eavesdrop the message and other relays forcefully remain in idle condition. At the untrusted relay, information signals of both of the sources act as a jamming to each other. The selected untrusted relay harvests the energy using a power splitting ratio scheme. We observe the performance of the proposed model in terms of SOP. We find the optimal values of energy harvesting factor at which SOP becomes minimum. Several important parameters such as the impact of number of untrusted relays, primary transmit power, peak transmit power of secondary sources, threshold outage rate of primary receiver and threshold secrecy rate on SOP is indicated. An analytical expression for the SOP has been developed in a single integration form. Numerical results based on analytical expression are verified by MATLAB simulation.

1 Introduction

Physical layer security (PLS) [1] is an appealing approach to maintain secrecy of confidential message alternative to cryptography technique. In cryptographic approach, message becomes vulnerable if someone knows the private keys. At physical layer, message may not be secured always in the case, when an eavesdropper is very close to the source. In such case, cooperative jamming helps to improve security at physical layer [2].

1.1 Secrecy Capacity, Secrecy Outage Probability and Cooperative Jamming

The authors in [3] considered the Gaussian wire-tap channel and defined the secrecy capacity which is the difference between legitimate channel capacity and eavesdropper (EAV) channel capacity. For proper secrecy of the information signal, information channel capacity at destination should be greater than that at the EAV. The authors in [4] evaluated the ergodic secrecy capacity (ESC) via multiple untrusted amplify and forward (AF) relays. In the same, relays are assisted with directional antennas. They have found that the multiple untrusted relay does not improve the performance. The authors in [5] also proved that the ESC degrades with increase in number untrusted AF relays. Here relays are assisted with Omni-directional antennas. The authors in [2] have found the secrecy rate under the source and destination assisted jamming via multiple decode and forward (DF) relays.

The authors in [6] have evaluated the SOP in presence of an untrusted energy harvesting AF relay. In the same, to enhance the positive secrecy rate, cooperative destination assisted jamming has been used which is eliminated in the second time slot by the destination. The authors in [7] have evaluated the SOP under the scenario in which an EAV tries to eavesdrop the information signal from selected relay. An optimal relay selection is considered and the SOP is analyzed under such case. The authors in [8] evaluated the SOP in presence of multiple EAVs for a single hop communication. The authors in [9] evaluated the secrecy rate for multiple-input and multiple-output relay network. In the same, authors have used the cooperative jamming to improve positive secrecy rate. In [10], the authors considered a destination assisted jamming in the first time slot under the perfect knowledge of channel state information (CSI). The destination eliminates the known jamming on the basis of perfect knowledge of CSI.

1.2 Energy Harvesting

Intermediate helper nodes like relay or jammer, which are constrained by power, need to harvest energy. They can use this energy to forward the information signal or send the jamming signal. Popular schemes for harvesting energy from radio frequency (RF) signal exist such as power splitting ratio (PSR) based [6, 8, 11] and time switching relay (TSR) [12] or hybrid combination of these two. The authors in [6] power the relay with harvested energy based on power splitting scheme. In [8], all energy harvesters harvest the energy based on power splitting scheme. Power splitting based energy harvesting has been discussed in [11] which uses supplies the harvested power to both of the AF and DF relays. In [12], both of the relays and jammer are powered by harvested energy on the basis of time switching scheme.

1.3 Secrecy in Cognitive Radio Network

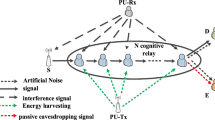
Due to multiple nodes in cognitive radio network (CRN), PLS is promising approach to secure the message of primary and secondary network. In [13], PLS has been estimated in terms of secrecy rate and SOP in a cognitive environment. In the same, there are multiple primary users (PUs) and multiple EAVs. Secrecy rate is maximized under the interference constraint of PU receiver (PU-RX). In [14], SOP has been evaluated in a cognitive environment which uses single hop communication. Power is allocated to cognitive nodes under the interference constraint of PU-RX. In the same, authors assume that the primary transmitter (PU-TX) is situated far away from the secondary receiving node. The signal received at destination is not interfered by the transmission of PU-TX. In [15], authors have evaluated the SOP in the CRN with coordinated and uncoordinated EAVs. Power allocation in the CRN is an important issue. Power can be allocated to cognitive nodes on the basis of outage constraint [16] and interference constraint [14].

1.4 Two-Way Communication

Two-way communication via half duplex AF relay increase the efficiency of utilization of bandwidth and also saves the time of communication. In two-way communication, two nodes share their information with the help of intermediate relay(s) which can work in half duplex mode or full duplex mode [12, 17]. In [17], the SOP is affected with number of relays, average signal to interference plus noise ratio (SINR) and average self-interference at full duplex relays. In [18], the SOP and the average secrecy rate have been analyzed for fifth generation network achieving two-way communication via multiple relays under attack of multiple EAVs. Relay has been selected following a low-complexity relay selection criterion. In [19], the secrecy performance has been analyzed using truth-telling mechanism via multiple AF relays under an EAV attack. Relays harvest the energy from RF sources. In [12], ergodic secrecy rate has been analyzed in a two-way communication with and without jammer. In the same, energy is harvested from RF source in the first time slot and in second time slot both the sources forward the information signal and jammer sends the jamming signal to confuse untrusted relay. In the third time slot, relay forwards the scaled version of the signal to both the sources.

1.5 Problem Addressed in the Paper

In the existing literature, as discussed above, secrecy performance of two-way communication via multiple energy harvesting untrusted relays in the cognitive scenario is not addressed to the best of our knowledge. In [6], only a single untrusted relay and only one-way communication is discussed where the relay also harvests energy. In [12], two-way communication is taking place between two sources via a single energy harvesting untrusted relay without considering any cognitive scenario. Thus, there is a need of analyzing the secrecy performance for the two-way communication with the help of multiple energy harvesting untrusted relays in a cognitive scenario which is the theme of this paper.

1.6 Contribution of the Present Paper

We have evaluated the SOP of CCRN in two-way communication via multiple energy harvesting half-duplex untrusted relays. The evaluation of SOP in such environment is our novel contribution. Major contribution of the present paper is outlined below as:

• We evaluate the SOP of the proposed model. Analytical expression of SOP involving a single integration is developed.

• In the considered model, the closed form expression of power allocation to cognitive nodes under the outage constraint of primary user in the first and second time slots have been evaluated.

• Optimal value of fraction of received energy has been evaluated at which SOP becomes minimum.

• Impact of several network parameters such as: outage constraints of primary user, fraction of received energy used for harvesting, primary transmit power, peak transmit power of secondary nodes, and threshold secrecy rate is shown on SOP.

• The diversity in number of relays is seen to improve the secrecy performance in terms of SOP significantly, even if relays are untrusted, in contrast to existing literature where multiple untrusted relay degrades SOP in one-way communication [4, 5].

1.7 Sections Organization

The Sect. 2 describes the system model. In Sect. 3, the performance analysis is presented. The numerical results have been presented and explained in Sect. 4. Finally Sect. 5 concludes the paper.

2 System Model

2.1 CCRN Model

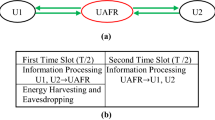
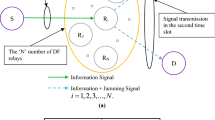
In this system model as shown in Fig. 1, secondary source one ($SS_1$) communicates with secondary source two ($SS_2$) via multiple half-duplex untrusted secondary amplify and forward relays (USAFRs) under a cognitive scenario. The relays being untrusted and can eavesdrop the message. But, the messages are eavesdropped by the selected relay only, which is selected to broadcast the information signal. The other non-selected relays forcefully remain in idle condition, i.e., they can not receive and transmit the signal. All secondary nodes (SNs) (i.e., $SS_1$, $SS_2$ and USAFRs) are assisted with omnidirectional antennas and thus there is a need of power allocation to SNs depending on outage constraint of primary network. Thus power is allocated to SNs on the basis of outage constraint of primary network. We assume that the SNs are far from the PU-TX, the interference from PU-TX to SNs is negligible [14]. There is no direct link between $SS_1$ and $SS_2$. Thus, communication is completed in two time slots as shown in Fig. 2. The relay is selected on the basis of maximizing secrecy rate. After relay selection, both the sources, i.e., $SS_1$ and $SS_2$, broadcast their confidential information signal via wireless channel to the selected USAFR in the first time slot. In the second time slot, selected relay broadcasts the amplified version of information signals of $SS_1$ and $SS_2$ which are received at $SS_2$ and $SS_1$. Meanwhile, the selected USAFR tries to eavesdrop the message of any one source at a particular time. The selected USAFR can not eavesdrop the messages of both the sources simultaneously at any particular time. Since, information signals of both the sources acts as a jamming to each other at the selected USAFR which degrades the signal strength at the USAFR. In the case of signal transmission with unequal power by both the sources, selected relay is able to eavesdrop the message of the information signal which is being transmitted with comparably higher power. Thus, we consider the signal transmission with equal power which provides signal to interference plus noise ratio (SINR) at the relay receiver almost same for both the senders. This assumption works if both the sources to relay links have independent identically distributed (i.i.d.) fading with same channel mean power.

We also assume that the perfect channel state information (CSI) are available at both the sources [10]. The $SS_1$ and $SS_2$ detect their own signal in second time slot on the basis of CSI and delete the same from the received signal as in [10]. The selected relay only tries to eavesdrop the message signal of either source while the message signal of other source acts as a jamming signal. In this way, both the sources decode the message successfully but, due to jamming nature of the signals to each other at the relay position, relay is unable to decode the message properly which leads to maintaining secrecy. However, the relay’s ability to decode the message leads to secrecy outage, the evaluation of probability of which is the main focus of the paper.

Fig. 1

System model of two-way communication via multiple half-duplex AF relays

Fig. 2

Time frame structure of complete communication

2.2 Channel Model

In this model as shown in Fig. 1, let ${h_{PP}}$, $h_{SS_1P}$, $h_{RP_i}$, $h_{SS_2P}$, $h_{SS_1R_i}$, $h_{R_iSS_1}$, $h_{R_iSS_2}$ and $h_{SS_2R_i}$ are the channel coefficients of links between PU-TX to PU-RX, $SS_1$ to PU-RX, $USAFR_i$ to PU-RX, $SS_2$ to PU-RX, $SS_1$ to $USAFR_i$, $USAFR_i$ to $SS_1$, $USAFR_i$ to $SS_2$ and $SS_2$ to $USAFR_i$, respectively. All channels are considered as flat Rayleigh fading.

These channel gains are independent identically distributed (i.i.d.) random variables. Square of the jth channel coefficient is the channel gain of that channel and it is expressed as:

$$\begin{aligned} {g_j} = {\left| {{h_j}} \right| ^2} \end{aligned}$$

(1)

The probability distribution function of channel gain is exponential and can be expressed as:

$$\begin{aligned} {f_{{g_j}}}\left( x \right) = \frac{1}{{{\varOmega _j}}}\exp \left( { - \frac{x}{{{\varOmega _j}}}} \right);\,\,\,\,\,\, x \ge 0 \end{aligned}$$

(2)

where the channel mean power of jth channel coefficient is $\varOmega _j$ .Additive white Gaussian noise (AWGN) of channel is circularly symmetry complex Gaussian noise with mean zero and two sided power spectral density of $N_0$ .Both the sources have the peak transmit power $\left( {{P_{PK}}} \right)$.

3 Performance Analysis

In this section, we are evaluating the power allocation to secondary nodes under primary constraint, signal to interference-plus-noise ratio (SINR) at different receiving nodes, global secrecy capacity of two-way communication, and finally SOP of the two-way communication network.

3.1 Power Allocation to Secondary Nodes

In the first time slot of the secondary network, both the sources broadcast the information signal which interfere with the information signal of primary network at the receiver of PU-RX. In this slot, we need to evaluate the maximum limit of the broadcasting power of both the sources. The ${g_{S{S_1}P}}$ and ${g_{S{S_2}P}}$ are the i.i.d. random variables indicating channel gains of two secondary sources to primary receiver respectively. The outage probability $P_{Out}^P$ of primary network in the duration of first time slot of secondary network is given as:

$$\begin{aligned} \begin{aligned} P_{Out}^P&= \left[ {P\left\{ {\left( {1 + \frac{{{P_P}{g_{PP}}}}{{{P_{{M_{SS}}}}\left( {{g_{S{S_1}P}} + {g_{S{S_2}P}}} \right) + {N_0}}}} \right) \le {R_P}} \right\} } \right] \le \varTheta \\&= 1 - \frac{{\exp \left( { - \frac{{\gamma _{TH}^P{N_0}}}{{{P_P}{\varOmega _{PP}}}}} \right) }}{{{{\left( {\frac{{\gamma _{TH}^P{P_{{M_{SS}}}}{\varOmega _{S{S_1}P}}}}{{{P_P}{\varOmega _{PP}}}} + 1} \right) }^2}}} \le \varTheta . \end{aligned} \end{aligned}$$

(3)

where $\gamma _{TH}^P = {2^{2{R_P}}}$ and $P_P$ is the primary user transmit power, $R_P$ is the threshold outage rate of PU-RX, $P_{M_{SS}}$ is the maximum allowable broadcasting power of $SS_1$ and $SS_2$, $N_0$ is the noise power of AWGN and $\varTheta$ is the constraint in outage probability of the primary network. On the basis of expression in Eq. (3), we can allocate the power to both of the sources which are in equal values as:

$$\begin{aligned} {P_{{M_{SS}}}} = \frac{{{P_P}{\varOmega _{PP}}}}{{\gamma _{TH}^P{\varOmega _{SP}}}}\left[ {{{\left\{ {\frac{{\exp \left( { - \frac{{\gamma _{TH}^P{N_O}}}{{{P_P}{\varOmega _{PP}}}}} \right) }}{{1 - \varTheta }}} \right\} }^{0.5}} - 1} \right] , \end{aligned}$$

(4)

Since both the sources have sufficient amount of available power, they can transmit the signal with assigned maximum allowable broadcasting power $\left( {{P_{{M_{SS}}}}} \right)$ maintaining constraint on primary outage. However, due to purpose of saving the power, they may not transmit the signal with this maximum allowable broadcasting power $\left( {{P_{{M_{SS}}}}} \right)$ estimated above under cognitive constraint. Considering the peak transmit power of secondary nodes (the limitation on peak transmit power arises due to device limitation), the actual assigned power to both the sources can be expressed as:

$$\begin{aligned} P_S = \min \left( {{P_{{M_{SS}}}},{P_{PK}}} \right) \end{aligned}$$

(5)

where $P_S$ is the assigned power to both the sources. In the second time slot of the secondary network, only the selected relay broadcasts the information signal using harvested energy which interfere with the information signal of primary network at PU-RX. In this time slot also, we can evaluate the maximum amount of broadcasting power with which relay can broadcast the information signal. The outage probability, $P_{Out}^P$ of primary network in this second duration is given as:

$$\begin{aligned} \begin{aligned} P_{Out}^P&= P\left\{ {lo{g_2}\left( {1 + \frac{{{P_P}{g_{PP}}}}{{{P_{{M_{SR}}}}{g_{RP}} + {N_O}}}} \right) \le {R_P}} \right\} \\&= 1 - \frac{{\exp \left( { - \frac{{\gamma _{TH}^P{N_0}}}{{{P_P}{\varOmega _{PP}}}}} \right) }}{{\left( {\frac{{\gamma _{TH}^P{P_{{M_{SR}}}}{\varOmega _{RP}}}}{{{P_P}{\varOmega _{PP}}}} + 1} \right) }} \le \varTheta . \end{aligned} \end{aligned}$$

(6)

The maximum allowable power of the selected ith relay is ${P_{{M_{SR_i}}}}$. We leave the subscript i from ${P_{{M_{SR_i}}}}$ for ease of notation, i.e., ${P_{{M_{SR}}}}= {P_{{M_{SR_i}}}}$. The maximum allowable power $\left( {{P_{{M_{SR}}}}} \right)$ of the selected ith relay, to amplify and broadcast the information signal, can be expressed as:

$$\begin{aligned} {P_{{M_{SR}}}} = \frac{{{P_P}{\varOmega _{PP}}}}{{\gamma _{TH}^P{\varOmega _{RP}}}}\left[ {\left\{ {\frac{{\exp \left( { - \frac{{\gamma _{TH}^P{N_O}}}{{{P_P}{\varOmega _{PP}}}}} \right) }}{{1 - \varTheta }}} \right\} - 1} \right] . \end{aligned}$$

(7)

But, the relay can not always broadcast the information signal with maximum allowable power $\left( {{P_{{M_{SR}}}}} \right)$ under cognitive constraint due to lack of sufficient amount of available power. If ith relay harvests more power which is greater than ${P_{{M_{SR}}}}$ then it can broadcast the information signal with ${P_{{M_{SR}}}}$, as obtained in Eq. (7), otherwise it broadcasts with maximum available harvesting power. Mathematically, it can be expressed as:

$$\begin{aligned} {P_{S{R_i}}} = \min \left( {{P_{{H_i}}},{P_{{M_{SR}}}}} \right) \end{aligned}$$

(8)

where ${P_{{H_i}}}$ is the harvested power by the ith USAFR which is used by the same in the second time slot and ${P_{S{R_i}}}$ is the transmit power of the ith relay.

3.2 Harvesting Energy and SINR Evaluation at Different Receiving Nodes of Secondary Network

AT first, an optimal relay is selected on the basis of maximizing global secrecy capacity as following the approach of maximizing the system secrecy capacity in [7]. The selection scheme of relay has been described in Subsection C of this Section. The $S{S_1}$ and $S{S_2}$ broadcast their information signal which is received at the selected ith USAFR as:

$$\begin{aligned} y_R^{\prime}= \sqrt{P}_S {h_{S{S_1}{R_i}}}{x_{S{S_1}}} + \sqrt{P}_S {h_{S{S_2}{R_i}}}{x_{S{S_2}}} + {n_0} \end{aligned}$$

(9)

where ${x_{S{S_1}}}$ and ${x_{S{S_2}}}$ are the messages of the $SS_1$ and $SS_2$ with unit power, respectively and $n_0$ is the AWGN sample. The selected relay harvests the energy using a fraction $\left( \beta \right)$ of the received energy following a PSR scheme [6, 8]. The expression of energy is expressed as:

$$\begin{aligned} {E_{{H_i}}} = \eta \beta P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) {\textstyle {T \over 2}} \end{aligned}$$

(10)

where $E_{H_i}$ is the harvested energy, $\beta$ is the fraction of received energy at relay with range $0< \beta < 1$ and $\eta$ is the energy conversion efficiency with range $0 < \eta \le 1$. Harvested power $\left( {{P_{{H_i}}}} \right)$, which is used by the relay in the second time slot to broadcast the information signal, is given as:

$$\begin{aligned} {P_{{H_i}}} = \eta \beta P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) \end{aligned}$$

(11)

The remaining fraction of received power of the information signal is used by the relay for processing the information which is given as:

$$\begin{aligned} {y_R} = \sqrt{\left( {1 - \beta } \right) P_S} {h_{S{S_1}{R_i}}}{x_{S{S_1}}} + \sqrt{\left( {1 - \beta } \right) P_S} {h_{S{S_2}{R_i}}}{x_{S{S_2}}} + {n_0} \end{aligned}$$

(12)

The relay is being untrusted and tries to eavesdrop the message from the information signal of both the sources. If relay tries to eavesdrop the message from information signal of $SS_1$ then the information signal of $SS_2$ acts as a jamming to the ith USAFR and vice versa. The SINRs at the relay in order to eavesdrop the messages from the information signal of $SS_1$ and $SS_2$, respectively are expressed as:

$$\begin{aligned} \left. \begin{array}{l} {\gamma _{S{S_1}{R_i}}} = \frac{{\left( {1 - \beta } \right) P_S{g_{S{S_1}{R_i}}}}}{{\left( {1 - \beta } \right) P_S{g_{S{S_2}{R_i}}} + {N_0}}},\\ {\gamma _{S{S_2}{R_i}}} = \frac{{\left( {1 - \beta } \right) P_S{g_{S{S_2}{R_i}}}}}{{\left( {1 - \beta } \right) P_S{g_{S{S_1}{R_i}}} + {N_0}}} \end{array} \right\} \end{aligned}$$

(13)

where ${\gamma _{S{S_1}{R_i}}}$ and ${\gamma _{S{S_2}{R_i}}}$ are the SINR at ith USAFR in order to eavesdrop the message of information signal of $SS_1$ and $SS_2$, respectively.

The ith USAFR amplifies the signal with a amplification factor $\left( {{\mu _i}} \right)$ [10] and broadcasts the information signal via wireless channel. It is clear that the energy of the broadcasting information signal at the relay should not be greater than the energy used by the relay to amplify and broadcast the information signal [10]. Mathematically it can be expressed as:

$$\begin{aligned} \left. \begin{array}{c} {\left| {{\mu _i}{y_R}} \right| ^2}{\textstyle {T \over 2}} = {P_{S{R_i}}}{\textstyle {T \over 2}}\\ {\left| {{\mu _i}{y_R}} \right| ^2} = {P_{S{R_i}}} \end{array} \right\} \end{aligned}$$

(14)

where ${\left| {{\mu _i}{y_R}} \right| ^2}{\textstyle {T \over 2}}$ is energy of transmitted signal from relay considering an amplification factor ${\mu _i}$ and ${P_{S{R_i}}}{\textstyle {T \over 2}}$ is the energy of transmitted signal from relay considering a transmit power of the relay as ${P_{S{R_i}}}$. An amplification factor of ith USAFR is $\mu _i$ and $P_{SR_i}$ is the transmit power of ith relay as defined in Eq. (8), i.e., the selected relay uses the power $P_{SR_i}$ to amplify and broadcast the information signal.

There are two cases of estimating the power of relay to amplify and broadcast the signal as: in case (1), when harvested power $\left( {{P_{{H_i}}}} \right)$ is less than the maximum allowable power $\left( {{P_{{M_{SR}}}}} \right)$ under cognitive constraint to amplify and broadcast the information signal. In case (2), when harvested power is greater or equal to the maximum allowable power $\left( {{P_{{M_{SR}}}}} \right)$ under cognitive constraint to amplify and broadcast the information signal. Mathematically, it can be expressed as:

Case (1), when ${P_{{H_i}}} < {P_{{M_{SR}}}}$

$$\begin{aligned} {P_{S{R_i}}} = {P_{{H_i}}} \end{aligned}$$

(15)

Case (2), when ${P_{{H_i}}} \ge {P_{{M_{SR}}}}$

$$\begin{aligned} {P_{S{R_i}}} = {P_{{M_{SR}}}} \end{aligned}$$

(16)

From Eq. (14), amplification factor $\left( \mu \right)$ can be expressed as:

$$\begin{aligned} {\mu _i} = \sqrt{\frac{{{P_{S{R_i}}}}}{{\left( {1 - \beta } \right) P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) + {N_0}}}} \end{aligned}$$

(17)

In cases (1) and (2), $\mu _i$ can be expressed, respectively as:

$$\begin{aligned} {\mu _i} = \left\{ \begin{array}{l} \sqrt{\frac{{{P_{{H_i}}}}}{{\left( {1 - \beta } \right) P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) + {N_0}}}} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{P_{{H_i}}} < {P_{{M_{SR}}}}\\ \\ \sqrt{\frac{{{P_{{M_{SR}}}}}}{{\left( {1 - \beta } \right) P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) + {N_0}}}} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{P_{{H_i}}} \ge {P_{{M_{SR}}}} \end{array} \right. \end{aligned}$$

(18)

Amplified and broadcasted information signal of relay can be expressed as:

$$\begin{aligned} {x_{{R_i}}} = {\mu _i}{y_R} \end{aligned}$$

(19)

Now, the received signal at the receiver of the both the sources are respectively, given as:

$$\begin{aligned} \left. \begin{array}{l} {y_{S{S_1}}} = {\mu _i}{y_R}{h_{{R_i}S{S_1}}} + {n_0},\\ {y_{S{S_2}}} = {\mu _i}{y_R}{h_{{R_i}S{S_2}}} + {n_0} \end{array} \right\} \end{aligned}$$

(20)

At $SS_2$, to identify the signal and noise part, received information signal can be expressed as:

$$\begin{aligned} \begin{aligned} {y_{S{S_2}}}&= \underbrace{{\mu _i}\sqrt{\left( {1 - \beta } \right) P_S} {h_{S{S_1}{R_i}}}{h_{{R_i}S{S_2}}}{x_{S{S_1}}}}_{Information\,Signal} + \underbrace{{\mu _i}\sqrt{\left( {1 - \beta } \right) P_S} {h_{S{S_2}{R_i}}}{h_{{R_i}S{S_2}}}{x_{S{S_2}}}}_{Self\,interference\,Signal}\\&\quad + \underbrace{{\mu _i}{n_0}{h_{{R_i}S{S_2}}} + {n_0}}_{Noise\,signal} \end{aligned} \end{aligned}$$

(21)

Similarly at $SS_1$, to identify the signal and noise part, received information signal can be expressed as:

$$\begin{aligned} \begin{aligned} {y_{S{S_1}}}&= \underbrace{{\mu _i}\sqrt{\left( {1 - \beta } \right) P_S} {h_{S{S_1}{R_i}}}{h_{{R_i}S{S_1}}}{x_{S{S_1}}}}_{Self\,interference\,Signal} + \underbrace{{\mu _i}\sqrt{\left( {1 - \beta } \right) P_S} {h_{S{S_2}{R_i}}}{h_{{R_i}S{S_1}}}{x_{S{S_2}}}}_{Information\,Signal}\\&\quad + \underbrace{{\mu _i}{n_0}{h_{{R_i}S{S_1}}} + {n_0}}_{Noise\,signal} \end{aligned} \end{aligned}$$

(22)

Both the sources know the self-interference signal which is detected with the help of perfect knowledge of CSI and can be subtracted [10]. From Eqs. (21) and (22), we can express the SINR at $SS_1$ and $SS_2$, respectively as:

$$\begin{aligned} \left. \begin{array}{l} {\gamma _{{R_i}S{S_2}}} = \frac{{\mu _i^2\left( {1 - \beta } \right) P_S{g_{S{S_1}{R_i}}}{g_{{R_i}S{S_2}}}}}{{\mu _i^2{N_0}{g_{{R_i}S{S_2}}} + {N_0}}},\\ {\gamma _{{R_i}S{S_1}}} = \frac{{\mu _i^2\left( {1 - \beta } \right) P_S{g_{S{S_2}{R_i}}}{g_{{R_i}S{S_1}}}}}{{\mu _i^2{N_0}{g_{{R_i}S{S_1}}} + {N_0}}} \end{array} \right\} . \end{aligned}$$

(23)

Considering case (1) and putting amplification factor in Eq. (23), we re-express it as:

$$\begin{aligned} \left. \begin{array}{l} {\gamma _{{R_i}S{S_2}}} = \frac{{\eta \beta \left( {1 - \beta } \right) P_S{g_{S{S_1}{R_i}}}{g_{{R_i}S{S_2}}}}}{{\eta \beta {g_{{R_i}S{S_2}}}{N_0} + \left( {1 - \beta } \right) {N_0} + {\textstyle {{N_0^2} \over {P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) }}}}},\\ {\gamma _{{R_i}S{S_1}}} = \frac{{\eta \beta \left( {1 - \beta } \right) P_S{g_{S{S_2}{R_i}}}{g_{{R_i}S{S_1}}}}}{{\eta \beta {g_{{R_i}S{S_1}}}{N_0} + \left( {1 - \beta } \right) {N_0} + {\textstyle {{N_0^2} \over {P_S\left( {{g_{S{S_1}{R_i}}} + {g_{S{S_2}{R_i}}}} \right) }}}}} \end{array} \right\} . \end{aligned}$$

(24)

For low values of $N_0$, we can make approximation of expressions in Eq. (24) (i.e., SINR at both of the receiving stage of the sources) as:

$$\begin{aligned} \left. \begin{array}{l} {\gamma _{{R_i}S{S_2}}} \approx \frac{{\eta \beta \left( {1 - \beta } \right) P_S{g_{S{S_1}{R_i}}}{g_{{R_i}S{S_2}}}}}{{\eta \beta {g_{{R_i}S{S_2}}}{N_0} + \left( {1 - \beta } \right) {N_0}}},\\ {\gamma _{{R_i}S{S_1}}} \approx \frac{{\eta \beta \left( {1 - \beta } \right) P_S{g_{S{S_2}{R_i}}}{g_{{R_i}S{S_1}}}}}{{\eta \beta {g_{{R_i}S{S_1}}}{N_0} + \left( {1 - \beta } \right) {N_0}}} \end{array} \right\} . \end{aligned}$$

(25)

For evaluating the SOP analytical expression, we utilize the approximated expressions given in Eq. (25).

3.3 Secrecy Capacity, Relay Selection and Secrecy Outage Probability (SOP) of Two-Way Communication

Capacities of links from ith USAFR to $SS_2$ and $SS_1$ can be expressed as:

$$\begin{aligned} \left. {\begin{array}{l} {{C_{{R_i}S{S_2}}} = \frac{1}{2}\log \left( {1 + {\gamma _{{R_i}S{S_2}}}} \right) ,}\\ {{C_{{R_i}S{S_1}}} = \frac{1}{2}\log \left( {1 + {\gamma _{{R_i}S{S_1}}}} \right) } \end{array}} \right\} , \end{aligned}$$

(26)

where ${C_{{R_i}S{S_2}}}$ and ${C_{{R_i}S{S_1}}}$ are the capacities from ith USAFR to $SS_2$ and $SS_1$, respectively. Next, capacities of channel links from sources to ith USAFR in order to eavesdrop the message of $SS_1$ and $SS_2$, respectively, can be expressed as:

$$\begin{aligned} \left. {\begin{array}{l} {{C_{S{S_1}{R_i}}} = \frac{1}{2}\log \left( {1 + {\gamma _{S{S_1}{R_i}}}} \right) ,}\\ {{C_{S{S_2}{R_i}}} = \frac{1}{2}\log \left( {1 + {\gamma _{S{S_2}{R_i}}}} \right) } \end{array}} \right\} , \end{aligned}$$

(27)

where ${C_{S{S_1}{R_i}}}$ and ${C_{S{S_2}{R_i}}}$ are the capacities of channel links from both the sources to ith USAFR in order to eavesdrop the message of $SS_1$ and $SS_2$, respectively. Further, secrecy capacity can be defined as the positive difference of capacity of legitimate link and that of ith USAFR link [3]. Mathematically, secrecy capacities of two-way communication can be defined individually as:

$$\begin{aligned} \left. {\begin{array}{l} {C_{{R_i}S{S_2}}^{SEC} = \frac{1}{2}\log \left( {1 + {\gamma _{{R_i}S{S_2}}}} \right) - \frac{1}{2}\log \left( {1 + {\gamma _{S{S_1}{R_i}}}} \right) ,}\\ {C_{{R_i}S{S_1}}^{SEC} = \frac{1}{2}\log \left( {1 + {\gamma _{{R_i}S{S_1}}}} \right) - \frac{1}{2}\log \left( {1 + {\gamma _{S{S_2}{R_i}}}} \right) } \end{array}} \right\} , \end{aligned}$$

(28)

where $C_{{R_i}S{S_2}}^{SEC}$ and $C_{{R_i}S{S_1}}^{SEC}$ are the secrecy capacities of link from $SS_1$ to $SS_2$ and from $SS_2$ to $SS_1$, respectively. Further, the above Eq. (28) is re-written as:

$$\begin{aligned} \left. {\begin{array}{l} {C_{{R_i}S{S_2}}^{SEC} = {{\left[ {\frac{1}{2}\log \left( {\frac{{1 + {\gamma _{{R_i}S{S_2}}}}}{{1 + {\gamma _{S{S_1}{R_i}}}}}} \right) } \right] }^ + },}\\ {C_{{R_i}S{S_1}}^{SEC} = {{\left[ {\frac{1}{2}\log \left( {\frac{{1 + {\gamma _{{R_i}S{S_1}}}}}{{1 + {\gamma _{S{S_2}{R_i}}}}}} \right) } \right] }^ + }} \end{array}} \right\} , \end{aligned}$$

(29)

where ${\left[ x \right] ^ + } = \max \left( {x,0} \right)$. In Eq. (29), only individual secrecy capacities corresponding to information signal of $SS_1$ and $SS_2$ are defined, respectively. However, in this formulation, if one information is secure, it does not necessarily guarantee security of the other information. So, there is a need of global secrecy capacity which is defined as [18]:

$$\begin{aligned} C_{{G_i}}^{SEC} = \min \left( {C_{{R_i}S{S_2}}^{SEC},C_{{R_i}S{S_1}}^{SEC}} \right) , \end{aligned}$$

(30)

where $C_{{G_i}}^{SEC}$ represents the global secrecy capacity via ith USAFR. The Eq. (30) explains that if minimum secrecy capacity of one of the two links is secure then it ensures that the other link have the comparably maximum secrecy capacity, which is also secured.

Relay selection is based on maximization of global secrecy rate via ith USAFR.

$$\begin{aligned} {i^*} = \arg \mathop {\max }\limits _{1 \le i \le N} \left( {C_{{G_i}}^{SEC}} \right) , \end{aligned}$$

(31)

where ${i^*}$ is the optimal selected relay and N indicates the number of untrusted half-duplex AF relays present in the network. Now, secrecy outage probability (SOP) can be defined as:

$$\begin{aligned} P_{OUT}^{SEC} = P\left( {\mathop {\max }\limits _{1 \le i \le N} C_{{G_i}}^{SEC} < R_{TH}^{SEC}} \right) \end{aligned}$$

(32)

where $R_{TH}^{SEC}$ is the threshold secrecy rate of the secondary network. Each of the two-way communication links is i.i.d. Applying order statistics and re-organizing the Eq. (32) becomes:

$$\begin{aligned} \left. \begin{array}{l} P_{OUT}^{SEC} = P\left[ {\mathop {\max }\limits _{1 \le i \le N} \left\{ {\min \left( {C_{{R_i}S{S_2}}^{SEC},C_{{R_i}S{S_1}}^{SEC}} \right) } \right\}< R_{TH}^{SEC}} \right] \\ \qquad \quad \; = \mathop \varPi \limits _{i = 1}^N \left[ {P\left\{ {\min \left( {C_{{R_i}S{S_2}}^{SEC},C_{{R_i}S{S_1}}^{SEC}} \right)< R_{TH}^{SEC}} \right\} } \right] \\ \qquad \quad \; = {\left[ {1 - \left\{ {1 - \underbrace{P\left( {C_{{R_i}S{S_2}}^{SEC}< R_{TH}^{SEC}} \right) }_{{I_1}}} \right\} \times \left\{ {1 - \underbrace{P\left( {C_{{R_i}S{S_1}}^{SEC} < R_{TH}^{SEC}} \right) }_{{I_2}}} \right\} } \right] ^N}\\ \qquad \quad \; = {\left[ {1 - {{\left( {1 - I} \right) }^2}} \right] ^N} \end{array} \right\} , \end{aligned}$$

(33)

here $I = {I_1} = {I_2}$ due to independent and symmetry about relay. Considering the two cases of power allocation at the ith USAFR, we can estimate the I as:

$$\begin{aligned} \begin{array}{l} I = P\left( {C_{{R_i}S{S_2}}^{SEC}< R_{TH}^{SEC}} \right) \\ \quad = \underbrace{P\left\{ {\left( {C_{{R_i}S{S_2}}^{SEC}< R_{TH}^{SEC}} \right) |\left( {{P_{{H_i}}}< {P_{{M_{SR}}}}} \right) } \right\} }_{{I_3}}P\left( {{P_{{H_i}}}< {P_{{M_{SR}}}}} \right) \\ \qquad + \underbrace{P\left\{ {\left( {C_{{R_i}S{S_2}}^{SEC} < R_{TH}^{SEC}} \right) |\left( {{P_{{H_i}}} \ge {P_{{M_{SR}}}}} \right) } \right\} }_{{I_4}}P\left( {{P_{{H_i}}} \ge {P_{{M_{SR}}}}} \right) \end{array} \end{aligned}$$

(34)

In case (1), when ${P_{{H_i}}} < {P_{{M_{SR}}}}$ then ${P_{S{R_i}}} = {P_{{H_i}}}$. Probability of event ${P_{{H_i}}} < {P_{{M_{SR}}}}$ can be expressed as:

$$\begin{aligned} P\left( {{P_{{H_i}}} < {P_R}} \right) = 1 - \left( {1 + \frac{{{P_R}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) \exp \left( { - \frac{{{P_R}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) , \end{aligned}$$

(35)

In this case, we assume that the $x = {\left| {{h_{S{S_2}{R_i}}}} \right| ^2}\mathrm{{and}}\,y = {\left| {{h_{{R_i}S{S_2}}}} \right| ^2}$. The $I_3$ in single integration from can be expressed as [6]:

$$\begin{aligned} \begin{aligned} {I_3}&= P\left\{ {\left( {C_{{R_i}S{S_2}}^{SEC}< R_{TH}^{SEC}} \right) |\left( {{P_{{H_i}}}< {P_{{M_{SR}}}}} \right) } \right\} \\&= P\left\{ {\frac{1}{2}{{\log }_2}\left( {{{1 + \frac{{\eta \beta \left( {1 - \beta } \right) P_Sxy}}{{\eta \beta {N_0}y + {N_0}\left( {1 - \beta } \right) }}} \Bigg / {1 + \frac{{\left( {1 - \beta } \right) P_Sx}}{{\left( {1 - \beta } \right) P_Sy + {N_0}}}}}} \right) \le R_{TH}^S} \right\} \\&= P\left\{ {\nu \left( y \right) x < \left( {\varDelta - 1} \right) } \right\} = 1 - \frac{1}{{{\varOmega _{{R_i}S{S_2}}}}}\int \limits _{{\theta _1}}^\infty {\exp \left( { - \frac{{\left( {\varDelta - 1} \right) }}{{\nu \left( y \right) {\varOmega _{S{S_1}{R_i}}}}} - \frac{y}{{{\varOmega _{{R_i}S{S_2}}}}}} \right) dy}, \end{aligned} \end{aligned}$$

(36)

where $y = {\left| {{h_{{R_i}S{S_2}}}} \right| ^2},\,\varDelta = {2^{2R_{TH}^{SEC}}}$, $\nu \left( y \right) = \left( {1 - \beta } \right) \left\{ {\frac{{\eta \beta P_Sy}}{{\eta \beta \mathrm{{y}}{N_0} + {N_0}\left( {1 - \beta } \right) }} - \frac{{\varDelta P_S}}{{\left( {1 - \beta } \right) P_Sy + {N_0}}}} \right\}$, $\mathrm{{and}}\,{\theta _1} = \frac{{\left( {\frac{{\varDelta - 1}}{{1 - \beta }}} \right) + \sqrt{{{\left( {\frac{{\varDelta - 1}}{{1 - \beta }}} \right) }^2} + \frac{{4\varDelta P_S}}{{{N_0}\eta \beta }}} }}{{2\left( {\frac{P_S}{{{N_0}}}} \right) }}$ In case (2), when ${P_{{H_i}}} \ge {P_{{M_{SR}}}}$ then ${P_{S{R_i}}} = {P_{{M_{SR}}}}$. Probability of this event is expressed as:

$$\begin{aligned} \begin{aligned}&P\left( {{P_{{H_i}}} \ge {P_{{M_{SR}}}}} \right) = 1 - P\left( {{P_{{H_i}}} < {P_{{M_{SR}}}}} \right) \\&\quad = \left( {1 + \frac{{{P_{{M_{SR}}}}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) \exp \left( { - \frac{{{P_{{M_{SR}}}}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) . \end{aligned} \end{aligned}$$

(37)

In this case, lower bound of SINR at $S{S_2}$, from Eq. (23) and with the help of Eq. (18), can be expressed as [4]:

$$\begin{aligned} \begin{aligned}&{\gamma _{{R_i}S{S_2}}} = \frac{{{P_{{M_{SR}}}}}}{{\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}}}\left[ {\frac{{\left\{ {\frac{{\left( {1 - \beta } \right) P_S}}{{{N_0}}}x} \right\} \left\{ {\frac{{\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}}}{{{N_0}}}y} \right\} }}{{1 + \left\{ {\frac{{\left( {1 - \beta } \right) P_S}}{{{N_0}}}x} \right\} + \left\{ {\frac{{\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}}}{{{N_0}}}y} \right\} }}} \right] \\&{\gamma _{{R_i}S{S_2}}} < {A_1}\min \left( {Q,\,R} \right) ;\,{\gamma _{{R_i}S{S_2}}} \ge \frac{{{A_1}}}{2}\min \left( {Q,\,R} \right) \\&\mathrm{{where}}\,Q = \frac{{\left( {1 - \beta } \right) P_S}}{{{N_0}}}x;R = \frac{{\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}}}{{{N_0}}}y;\,{A_1} = \frac{{{P_{{M_{SR}}}}}}{{\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}}} \end{aligned} \end{aligned}$$

(38)

From Eq. (38), we can find the PDF of SINR at $SS_2$ as:

$$\begin{aligned} {f_{{\gamma _{{R_i}S{S_2}}}}}\left( \tau \right) \approx \frac{1}{{{\varOmega _D}}}\exp \left( { - \frac{\tau }{{{\varOmega _D}}}} \right) ;\tau \ge 0, \end{aligned}$$

(39)

where ${\varOmega _D} = \frac{{{A_1}}}{2}{T_{QR}}$; ${A_1} = \frac{{{P_{{M_{SR}}}}}}{{\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}}}$; ${T_{QR}} = \frac{{{T_Q}{T_R}}}{{{T_Q} + {T_R}}}$; ${T_Q} = \frac{{\left( {1 - \beta } \right) P_S{\varOmega _{S{S_1}{R_i}}}}}{{{N_o}}}$; and ${T_R} = \frac{{\left\{ {\left( {1 - \beta } \right) P_S + {P_{{M_{SR}}}}} \right\} {\varOmega _{{R_i}S{S_2}}}}}{{{N_o}}}$.

PDF of SINR at the selected ith USAFR from Eq. (13) can be expressed as:

$$\begin{aligned} \begin{aligned} {f_{{\gamma _{S{S_1}{R_i}}}}}\left( \upsilon \right)&= \frac{{{N_0}}}{{\left( {1 - \beta } \right) P_S{\varOmega _{{R_i}S{S_2}}}}} \times \frac{{\exp \left( { - \frac{{{N_0}\upsilon }}{{\left( {1 - \beta } \right) P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) }}{{\upsilon + 1}}\\&\quad + \frac{{\exp \left( { - \frac{{{N_0}\upsilon }}{{\left( {1 - \beta } \right) P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) }}{{{{\left( {\upsilon + 1} \right) }^2}}};\,\,\,\upsilon \ge 0 \end{aligned} \end{aligned}$$

(40)

The $I_4$ in single integration from can be expressed as:

$$\begin{aligned} \begin{aligned} {I_4}&= P\left\{ {\left( {C_{{R_i}S{S_2}}^{SEC}< R_{TH}^{SEC}} \right) |\left( {{P_{{H_i}}} \ge {P_{{M_{SR}}}}} \right) } \right\} = P\left\{ {\tau < \left( {\varDelta \left( {1 + \upsilon } \right) - 1} \right) } \right\} \\&= \int \limits _0^\infty {\int \limits _0^{\left( {\varDelta \left( {1 + \upsilon } \right) - 1} \right) } {{f_{{\gamma _{{D_i}}}{\gamma _{{R_i}}}}}\left( {\tau ,\upsilon } \right) d\tau } d\upsilon } = \int \limits _0^\infty {\left\{ {\int \limits _0^{\left( {\varDelta \left( {1 + \upsilon } \right) - 1} \right) } {{f_{{\gamma _{{R_i}S{S_2}}}}}\left( {\frac{\tau }{\upsilon }} \right) d\tau } } \right\} {f_{{\gamma _{S{S_1}{R_i}}}}}\left( \upsilon \right) d\upsilon }\\&= \int \limits _0^\infty {\left[ {\upsilon \left\{ {1 - \exp \left( { - \frac{{\left( {\varDelta \left( {1 + \upsilon } \right) - 1} \right) }}{{{\varOmega _D}\upsilon }}} \right) } \right\} \left\{ {{A_2}\frac{{\exp \left( { - {A_2}\upsilon } \right) }}{{\upsilon + 1}} + \frac{{\exp \left( { - {A_2}\upsilon } \right) }}{{{{\left( {\upsilon + 1} \right) }^2}}}} \right\} } \right] d\upsilon } \end{aligned}, \end{aligned}$$

(41)

where ${A_2} = \frac{{{N_O}}}{{\left( {1 - \beta } \right) P_S{\varOmega _{S{S_1}{R_i}}}}}$. We can evaluate the I from Eqs. (34) (35) and (37), and the expressions of $I_3$ and $I_4$ given in Eqs. (36) and (41), respectively. The I of Eq. (33) [this I is also expressed in Eq. (34)] can be expressed as:

$$\begin{aligned} \begin{aligned} I&= {I_3}\left\{ {1 - \left( {1 + \frac{{{P_R}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) \exp \left( { - \frac{{{P_R}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) } \right\} \\&\quad + {I_4}\left\{ {\left( {1 + \frac{{{P_R}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) \exp \left( { - \frac{{{P_R}}}{{\rho \beta P_S{\varOmega _{{R_i}S{S_2}}}}}} \right) } \right\} \end{aligned} \end{aligned}$$

(42)

where $I_3$ and $I_4$ are given in Eqs. (36) and (41), respectively. Next, we plug I in Eq. (33) to obtain final expression of SOP which is given as:

$$\begin{aligned} P_{out}^{{\mathop {\mathrm{S}}\nolimits } EC} = {\left[ {1 - {{\left( {1 - I} \right) }^2}} \right] ^N} \end{aligned}$$

(43)

The expression of SOP in Eq. (42) is in single integration form which can be solved by numerical method of integration.

4 Numerical Results

In this Section, MATLAB based simulation results has been shown for secured two-way communication via the multiple half-duplex untrusted AF relays. We also have shown the approximated numerical results which closely match with simulated results. Assigned numerical values are given in Table 1.

Table 1 Name of different network parameters with their symbols and numerical values

4.1 Impact of Fraction of Received Energy $\left( \beta \right)$ at Relay on SOP

Figure 3 shows the performance in terms of SOP with respect to $\beta$. As $\beta$ increases, harvested energy increases as per Eq. (10). Harvested power corresponding to harvested energy also increases as per Eq. (11). This increased harvested power increases the signal quality at respective source destination. On the other hand, the information signal available for eavesdropping the message at the untrusted relay becomes poor with increase in $\beta$. Thus information signal strength increases at both the source destinations and decreases at the selected untrusted relay with increase in $\beta$. This leads to reduction in SOP with increase in $\beta$. However, after an optimal value of $\beta$, untrusted relay harvests more energy. The high value of harvested power corresponding to harvested energy can not increase the signal quality at the respective source destinations as the received signal strength reduces at the relay due to allocation of higher fraction of signal power for harvesting at relay. Due to more fraction of the information signal used in the harvesting, signal becomes noisy, and after amplification signal becomes comparably noisier which degrades the channel capacity at both the source destinations. Thus, SOP decreases with increase in $\beta$ after optimal value of it. We obtain the two optimal values of $\beta$ corresponding to different values of the peak transmit power. It is for as peak transmit power $\left( {{P_{PK}}} \right)$ of $0\,\mathrm{{dBW}}$ and 0.7 for $P_{PK}$ of $5\,\mathrm{{dBW}}$.

Fig. 3

SOP versus $\beta$ for different values of $P_{PK}$. There are different optimal values of $\beta$ for different values of $P_{PK}$

4.2 Impact of Transmit Power of Primary Network and Peak Transmit Power of Both of the Secondary Sources on SOP

Figure 4 shows the SOP variation with $P_P$ and $P_{PK}$ . Increase in $P_P$, assigned power to secondary nodes increases for a given outage constraint of primary network. With increase in signal strength at the selected relay, harvested power also increases for a particular value of $\beta$. Combined effect of increase in harvested power and power under cognitive constraint increases the signal strength at the receiving source destination. Thus, SOP decreases with increase in $P_P$. However, there is no effect on SOP for large value of $P_P$ due to peak transmit power constraint and we obtain the floor. Increase in peak transmit power increases the transmit power of information signal. Thus, SOP also decreases with increase in peak transmit power. For evaluating analytical expression, the lower bound of SINR [as given in Eq. (38)] at the respective source destination is used. Therefore, SOP value in an analytical results for a particular value of $P_P$ is some greater than the SOP value in a simulated results for that particular value of $P_P$. But, the nature of curves in the graphs are same.

Fig. 4

SOP versus $P_P$ for different values of $P_{PK}$

4.3 Impact of Threshold Outage Rate of PU-RX on SOP

Figure 5 shows the SOP versus $R_P$ for different values of peak transmit power. Increase in $R_P$ decreases the assigned power to secondary nodes as per Eqs. (4) and (7). Signal with low transmit power is received by relay in poor strength. Corresponding harvested power decreases with increase in $R_P$. Further, power assigned to relay under cognitive constraint decreases with increase in $R_P$. Next, combined effect of low harvested power and low assigned power provides the poor channel capacity to respective source destination. Decreasing rate of channel capacities at respective source destination dominates over the decreasing rate of channel capacities at the selected relay. Thus secrecy rate decreases and performance in terms of SOP increases.

Fig. 5

SOP versus $R_P$ for different values of $P_{PK}$

4.4 Impact of Number of Relays on SOP

Figure 6 shows the SOP versus number of relays. If number of relay increases then secrecy performance increases even if the relays are untrusted. However it is found in [4] and [5], if number of untrusted relays increases, then performance reduces because all relays are in active stage in first time slot. They can receive the information signal and try to eavesdrop the message. But, in our case, only selected relay is in active stage and all other relays are in idle stage, i.e., non-selected relays do not participate in signal processing, in the first time slot and in the second time slot. In this case diversity in number of relays is preserved and always provide best strength of signal to respective source destination. Thus, secrecy rate increases with increase in number of relays and SOP decreases.

Fig. 6

SOP versus N for different values of $P_{PK}$

4.5 Imapct of Channel Mean Power of Links Between the Sources and the Selected Relay $\left( {{\varOmega _{S{S_1}{R_i}}},\,{\varOmega _{S{S_2}{R_i}}}} \right)$ on SOP

Figure 7 shows SOP versus channel mean power of links between the sources and the selected relay $\left( {{\varOmega _{S{S_1}{R_i}}},\,{\varOmega _{S{S_2}{R_i}}}} \right)$. As the channel mean power increases, strength of the information signals corresponding to both the sources also increases. But due to jamming nature of the information signals to each other at the selected untrusted relay, the selected untrusted relay receives the signal strength with no further improvement. Thus, the selected untrusted relay is unable to eavesdrop the message successfully. On the other hand, after amplification and broadcasting by the selected relay, respective destination sources receive the signal in better strength with increase in channel mean power. Both the sources detects and removes the own signal from the received signal on the basis of CSI. After removal of own signals from the received signal, both the sources are able to decode the information signal of each other.

Fig. 7

SOP versus channel mean power of links between the sources and the selected relay $\left( {{\varOmega _{S{S_1}{R_i}}},\,{\varOmega _{S{S_2}{R_i}}}} \right)$ for different values of $P_{PK}$

5 Conclusion

The SOP of CCRN has been evaluated for a two-way communication via multiple half-duplex energy harvesting untrusted AF relays. We obtain optimal values of fraction of received energy at which SOP becomes minimum under a given scenario of primary transmit power and peak transmit power of secondary nodes. For a particular values of outage probability of primary network, SOP decreases with increase in primary transmit power. But, SOP increases with increase in threshold outage rate of PU-RX. Diversity in number of relays provide the benefit in performance even if relays are untrusted. As the number of relays increases, SOP decreases. Next, increase in channel mean power of links between the sources and the selected relay provides better secrecy of the messages. Further, both the sources can share the confidential information via untrusted relays maintaining a desired level of SOP without affecting the quality of service of primary network in terms of outage.