1 Introduction

Wireless networks have experienced an explosive growth in the past few years. A large portion of the radio spectrum is not fully utilized most of the time [1]. To improve the spectrum usage a new communication paradigm, named as Cognitive Radio (CR) has been derived from Software Defined Radio (SDR) [2, 3]. CR allows Secondary Users (SUs) to access the idle frequency spectrum opportunistically when it is not occupied by Primary User (PU) while maintaining the interference to PU below a permissible limit [4, 5]. Spectrum sensing technique has been used to identify the available spectrum and also prevents the harmful interference with PU and for improving the spectrum’s utilization [6,7,8]. However, in wireless scenario, it is almost not possible to achieve perfect sensing. Sensing errors occur owing to feedback delays, quantization error, interference and uncertainty of wireless channel [9,10,11].

To improve the spectrum efficiency in heterogeneous networks, CR is largely implemented and thus CR exists as HCRN [12, 13]. In HCRN both Single-Network (SN) and Multi-Homing (MH) secondary users may coexist and resource allocation for SUs is based on OFDM technique. In [14] OFDM multicarrier modulation technique is used to overcome many problems that arise with high bit rate communications. OFDM based CR system maximizes the overall bit rate by efficiently utilizing spectrum holes and keeping the interference to PUs within tolerable limits is studied in [15]. Resource allocation (RA) schemes for HCRN are discussed in [16,17,18,19]. In [20] the RA problem in multiuser OFDM-based CR networks with heterogeneous services under imperfect sensing is studied.

EE power allocation is of crucial importance for CRN [21]. In [22] energy consumption is minimized in amplify and forward CR network satisfying the throughput requirement and the interference threshold. In [23,24,25] an energy efficient resource allocation problem for CRN is proposed. EE resource allocation problem for heterogeneous users in cognitive radio systems has been addressed in [26,27,28,29] without considering sensing errors. In our work the EEPA algorithm is anticipated in OFDM-based HCRN networks for both SN and MH users under imperfect sensing.

In this work EE maximization problem subject to transmit power, interference and QoS Constraint in the occurrence of sensing errors for HCRN is formulated. The outline of the work is:

  1. 1.

    A system framework to maximize the EE for HCRN with imperfect spectrum sensing is entrenched.

  2. 2.

    The problem is formulated as mixed integer non-linear programming; we propose to address this issue by subcarrier assignment and optimal power allocation.

  3. 3.

    In subcarrier assignment algorithm, the non-polynomial log term is relaxed to convert to low complexity problem. The subcarrier assignment and network selection is done based on optimal solution of problem.

  4. 4.

    After the subcarrier assignment the original problem is transformed into convex optimization problem using fractional programming

  5. 5.

    Power to the subcarriers is allocated by EEPA algorithm in which sub-gradient method is adopted.

  6. 6.

    Based on the transmit power, interference and QoS constraints the EE is maximized and the normal communication is protected in the presence of imperfect sensing for HCRN.

  7. 7.

    Finally Simulation results are provided to verify the performance improvement of the proposal.

The rest of the work is structured as follows: Sect. 2 starts with system framework and problem conceptualization. In Sect. 3, the subcarrier assignment and EEPA algorithm is proposed. Simulation results are given in Sect. 4 with discussions. The paper is finally concluded in Sect. 5.

2 System Framework and Problem Conceptualization

2.1 System Framework

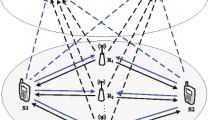
Consider a HCRN system as delineated in Fig. 1. M OFDM-based CRNs and N secondary users have been haphazardly distributed in the HCRN. Each CRN co-occurs with a PU and two types of secondary users such as SN and MH. The SN users access and transmit packets by selecting the best available wireless networks. The MH users can access multiple networks at the same time through Multiple Access Technologies. The Bandwidth of each CRN is divided into K subcarriers consequently the mth CRN has Km subcarriers and the bandwidth of each subcarrier is Bm Hz. The subcarriers in mth CRN are divided into available subcarriers \(\text{k}_{\text{m}}^{\text{a}}\) and unavailable subcarriers \(\text{k}_{\text{m}}^{\text{u}}\) for secondary users. In overlay mode subcarriers in SU is shared with primary user.

Fig. 1
figure 1

System framework for HCRN

Full size image

Sensing errors occurs in CRN are Miss Detection (MD) and False Alarm (FA). MD occurs when the subcarrier is occupied by PU but the sensing result states that as vacant. FA occurs when the subcarrier is available but the sensing result stated as busy. The Probabilities of MD and FA are denoted as \(\text{Q}_{{\text{m,k}}}^{{\text{msd}}}\) and \(\text{Q}_{{\text{m,k}}}^{{\text{fa}}}\). In mth CRN the event that the PU is available and unavailable in the kth subcarrier is denoted by \({\text{H}}_{{\text{m,k}}}^{1}\) and \({\text{H}}_{{\text{m,k}}}^{2}\). In mth CRN the event that the kth subcarrier is unavailable and available is denoted by \({\text{O}}_{{\text{m,k}}}^{1}\) and \({\text{O}}_{{\text{m,k}}}^{2}\).

The four possible spectrum sensing results are stated as

$$\begin{aligned} & \text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{1} |{\text{H}}_{{\text{m,k}}}^{1} } \right\} = 1 - \text{Q}_{{\text{m,k}}}^{{\text{msd}}} \\ & \text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{2} |{\text{H}}_{{\text{m,k}}}^{1} } \right\} = \text{Q}_{{\text{m,k}}}^{{\text{msd}}} \\ & \text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{2} |{\text{H}}_{{\text{m,k}}}^{2} } \right\} = 1 - \text{Q}_{{\text{m,k}}}^{{\text{fa}}} \\ & \text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{1} |{\text{H}}_{{\text{m,k}}}^{2} } \right\} = \text{Q}_{{\text{m,k}}}^{{\text{fa}}} \\ \end{aligned}$$
(1)

In mth CRN the probability that the kth subcarrier is really used by PUs and it is known to be not available can be written as

$$\begin{aligned} \uptheta_{{\text{m,k}}}^{1} & = \text{P}\left\{ {{\text{H}}_{{\text{m,k}}}^{1} |{\text{O}}_{{\text{m,k}}}^{1} } \right\} \\ & = \frac{{\text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{1} |{\text{H}}_{{\text{m,k}}}^{1} } \right\}\text{P}\left\{ {{\text{H}}_{{\text{m,k}}}^{1} } \right\}}}{{\text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{1} |{\text{H}}_{{\text{m,k}}}^{1} } \right\}\text{P}\left\{ {{\text{H}}_{{\text{m,k}}}^{1} } \right\} + \text{P}\left\{ {{\text{O}}_{{\text{m,k}}}^{1} |{\text{H}}_{{\text{m,k}}}^{2} } \right\}\text{P}\left\{ {{\text{H}}_{{\text{m,k}}}^{2} } \right\}}} \\ & = \frac{{\left( {1 - \text{Q}_{{\text{m,k}}}^{{\text{msd}}} } \right) \text{Q}_{{\text{m,k}}}^{\text{L}} }}{{\left( {1 - \text{Q}_{{\text{m,k}}}^{{\text{msd}}} } \right) \text{Q}_{{\text{m,k}}}^{\text{L}} + { \text{Q}_{{\text{m,k}}}^{{\text{fa}}} \left( {1 - \text{Q}_{{\text{m,k}}}^{\text{L}} } \right)}}} \\ \end{aligned}$$
(2)

where \(\text{Q}_{{\text{m,k}}}^{\text{L}}\) is the activity probability that the kth subcarrier in mth CRN is occupied by PU. The \(\uptheta_{{\text{m,k}}}^{2}\) is the probability that the kth subcarrier in mth CRN is not used by PUs and it is known to be available.

The total achievable rate Rn of nth SU in mth CRN can be expressed as

$$\text{R}_{\text{n}} = \text{B}_{\text{m}} \sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} {\mathrm{r}}_{{\text{n,m}}}^{\text{k}} } }$$
(3)
$$\uprho_{{\text{n,m}}}^{\text{k}} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{Kth}\,\text{subcarrier}\,\text{alloted}\,\text{to}\,\text{SU}\,\text{n}\,\text{in}\,\text{CRN}\,\text{m}} \hfill \\ {0,} \hfill & {\text{Others}} \hfill \\ \end{array} } \right.$$
(4)

where \(\uprho_{{\text{n,m}}}^{\text{k}}\) can be either 1 or 0 conveys if the subcarrier k in mth CRN is occupied by SU n or not. \({\text{r}}_{{\text{n,m}}}^{\text{k}}\) is the transmission rate of subcarrier k used by nth SU in mth CRN and it can be expressed as

$${\text{r}}_{{\text{n,m}}}^{\text{k}} = \log_{2} \left( {1 + \text{P}_{{\text{n,m}}}^{\text{k}} \upgamma_{{\text{n,m}}}^{\text{k}} } \right)$$
(5)

where \(\upgamma_{{\text{n,m}}}^{\text{k}}\) is the Signal-to-Noise Ratio (SNR) of subcarrier k used by nth SU in mth CRN with unit power can be denoted as

$$\upgamma_{{\text{n,m}}}^{\text{k}} = \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{{\sigma B}_{\text{m}} }}$$
(6)

where \(\text{P}_{{\text{n,m}}}^{\text{k}}\) the power allocated to the subcarrier k occupied by nth SU in mth CRN and \({\text{H}}_{{\text{n,m}}}^{\text{k}}\) is the channel gain from mth CRN Access Point (AP) to the nth SU over the kth subcarrier. \(\upsigma\) is the thermal noise power density.

The interference introduced by the secondary user n into the primary user of mth CRN on the kth subcarrier with unit transmission power can be written as

$${\text{i}}_{{\text{n,m}}}^{\text{k}} = \uptheta_{{\text{m,j}}}^{1} {\text{i}}_{{\text{n,m}}}^{{\text{j,k}}} + \uptheta_{{\text{m,j}}}^{2} {\text{i}}_{{\text{n,m}}}^{{\text{j,k}}}$$
(7)
$${\text{where}},\quad {\text{i}}_{{\text{n,m}}}^{{\text{j,k}}} = \int\limits_{{\text{(j} - \text{1)B}_{\text{m}} - \left( {\text{k} - \frac{1}{2}} \right)\text{B}_{\text{m}} }}^{{\text{jB}_{\text{m}} - \left( {\text{k} - \frac{1}{2}} \right)\text{B}_{\text{m}} }} {\mathrm{T}_{\text{s}} \left| {{\text{g}}_{{\text{n,m}}}^{\text{k}} } \right|^{2} \left( {\frac{{{\sin\Pi {\text{fT}}}_{\text{s}} }}{{{\Pi {\text{fT}}}}}} \right)^{2} \text{df}}$$
(8)

where \({\text{g}}_{{\text{n,m}}}^{\text{k}}\) is the channel gain between the nth SU and PU of mth CRN on the kth subcarrier. \({\text{i}}_{{\text{n,m}}}^{{\text{j,k}}}\) is the interference to PU of mth CRN on the jth subcarrier when nth SU transmits data on the kth subcarrier with unit transmission power. \({\varphi (f)} = \text{T}\left( {\frac{\sin\Pi{\text{fT}_{\text{s}} }}{\Pi {\text{fT}}}} \right)^{2}\) is the power spectral density (PSD) of the OFDM transmitted signal. \(\text{T}_{\text{s}}\) is the symbol duration.

The EE of OFDM based HCRN for imperfect sensing is given by

$$\upeta_{{\text{EE}}} = \frac{{\sum\nolimits_{{\text{m} = 1}}^{\text{M}} {\rm{R}_{\text{n}} } }}{{\sum\nolimits_{{\text{n} = 1}}^{\text{N}} {\sum\nolimits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\rm{m}}^{\text{a}} }} {\uprho_{{\rm{n,m}}}^{\text{k}} \text{P}_{{\rm{n,m}}}^{\text{k}} + \text{P}_{\rm{c}} } } } }}$$
(9)

The Capacity of HCRN is given by

$$\text{C} = \sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\mathrm{B}_{\text{m}} \log_{2} \left( {1 + \frac{{\text{P}_{{\text{n,m}}}^{\text{k}} {\mathrm{H}}_{{\text{n,m}}}^{\text{k}} }}{{{\sigma B}_{\text{m}} }}} \right)} } }$$
(10)

2.2 Network Selection

The subcarrier assignment is mentioned in Eq. (4). Each subcarrier can be allotted to one SU at a time, we have

$$\sum\limits_{{\text{m} = 1}}^{\text{M}} {\uprho_{{\text{n,m}}}^{\text{k}} } \le 1\quad \forall \text{m,k}$$
(11)

When a Single network user selects the network to access, the subcarriers over other networks can’t be used. For Multi Homing user, this condition is relaxed.

$$\uprho_{{\text{n,m}}}^{\text{k}} + \uprho_{{\text{n,m}^{\text{'}} }}^{{\text{k}^{{\prime }} }} \le \text{l}_{\text{n}} \quad\forall \text{n,}\,\text{m} \ne \text{m}^{{\prime }} \text{,k,k}^{{\prime }}$$
(12)

where \(\text{l}_{\text{n}}\) denotes the type of SU n and it is expressed as,

$$\text{l}_{\text{n}} = \left\{ {\begin{array}{*{20}l} {\text{1,}} \hfill & {\text{user}\,\text{n}\,\text{is}\,\text{single-network}\,\text{user}} \hfill \\ {{\text{M}},} \hfill & {\text{user}\,\text{n}\,\text{is}\,\text{multi-homing}\,\text{user}} \hfill \\ \end{array} } \right.$$
(13)

2.2.1 Constraint Selection

Total transmission power, interference and guaranteed QoS constraints are chosen in this paper to maximize the EE of HCRN.

To guarantee the QoS of each SU, it should satisfy

$$\text{R}_{\text{n}} \ge \text{R}_{{\text{min}}}$$
(14)

where \(\text{R}_{{\text{min}}}\) is the minimum capacity requirement of every SU. Guaranteeing the QoS is that the capacity of SU n must be higher than the \(\text{R}_{{\text{min}}}\). The subcarriers with good channel gain are allotted to the SU’s.

The total transmission power constraint and interference constraint are given by,

$$\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} \text{P}_{{\text{n,m}}}^{\text{k}} } } \le \text{P}_{\text{n}}\quad \forall \text{n}$$
(15)
$$\sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} \text{P}_{{\text{n,m}}}^{\text{k}} } } {\mathrm{i}}_{{\text{n,m}}}^{\text{k}} \le {\text{i}}_{\text{n}}^{{\text{th}}} \quad \forall \text{m}$$
(16)

where Pn is the total transmission power of SU n and Ithn is the interference limit of PU in every CRN. The transmission power assigned to the subcarrier k in mth CRN could not exceed the total transmission power of user n. If not assigned the transmission power is set to zero. Then we have,

$$\text{P}_{{\text{n,m}}}^{\text{k}} \le \text{P}_{\text{n}} \uprho_{{\text{n,m}}}^{\text{k}} \quad \forall \text{n,m,k}$$
(17)

2.3 Problem Conceptualization

The objective of this paper is to maximize the EE of HCRN by optimizing the subcarrier and power allocation. The constraints considered are total transmission power, interference and guaranteed QoS. The optimization problem can be formulated as follows:

$$\begin{aligned} & \quad {\text{OP1}}\,{\mathop {{\text{max}}}\limits_{{{\uprho_{{\text{n,m}}}}^{{\text{k}}} ,{\text{P}}_{{{\text{n,m}}}}^{{\text{k}}} }}}\upeta_{{\text{EE}}} \\ & {\text{s}}.{\text{t}}.\,{\text{C1}}.\sum\limits_{{\text{m} = 1}}^{\text{M}} {\uprho_{{\text{n,m}}}^{\text{k}} } \le 1\quad\forall \text{m,k} \\ & \quad {\text{C2}}.\,\uprho_{{\text{n,m}}}^{\text{k}} + \uprho_{{\text{n,m}^{\text{'}} }}^{{\text{k}^{{\prime }} }} \le \text{l}_{\text{n}}\quad \forall \text{n,}\,\,\text{m} \ne \text{m}^{{\prime }} ,\,\text{k,}\,\text{k}^{{\prime }} \\ & \quad {\text{C}}3.\,\text{P}_{{\text{n,m}}}^{\text{k}} - \text{P}_{\text{n}} \uprho_{{\text{n,m}}}^{\text{k}} \le 0\,\,\forall \text{n,m,k} \\ & \quad {\text{C}}4.\,\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} \text{P}_{{\text{n,m}}}^{\text{k}} } } \le \text{P}_{\text{n}} \quad\forall \text{n} \\ & \quad {\text{C}}5.\,\sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} \text{P}_{{\text{n,m}}}^{\text{k}} } } {\mathrm{i}}_{{\text{n,m}}}^{\text{k}} \le {\text{i}}_{\text{n}}^{{\text{th}}} \quad\forall \text{m} \\ & \quad {\text{C}}6.\,\text{R}_{\text{n}} \ge \text{R}_{{\text{min}}}\quad \forall \text{n} \\ & \quad {\text{C}}7.\,\sum\limits_{{\text{m} = 1}}^{\text{M}} {\mathrm{P}_{{\text{n,m}}}^{\text{k}} } \ge 0\quad\forall \text{n,m,k} \\ & \quad {\text{C}}8.\,\uprho_{{\text{n,m}}}^{\text{k}} \in \left\{ {\text{0,1}} \right\}\quad\forall \text{n,m,k} \\ \end{aligned}$$
(18)

3 Optimal Subcarrier and Power Allocation

Since the problem is a mixed integer non linear programming problem, it is relaxed first into a low complexity solution to find the optimal solutions for subcarrier assignment and next the problem is transformed into a convex problem for further simplification.

3.1 Relaxing the Problem

In relaxing the OP1, the integer variable \(\uprho_{{\text{n,m}}}^{\text{k}}\) is relaxed as a continuous variable over [0,1]. The non polynomial log term in (18) is relaxed into three linear constraints as in [30].

$${\text{r}}_{{\text{n,m}}}^{\text{k}} = \log_{2} \left( {1 + \text{P}_{{\text{n,m}}}^{\text{k}} \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{{\sigma B}_{\text{m}} }}} \right)$$

The linear constraints are

$$\begin{aligned} & {\text{r}}_{{\text{n,m}}}^{\text{k}} - \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{{ln2\sigma B}_{\text{m}} }}\,{\mathrm{P}}_{{\text{n,m}}}^{\text{k}} \le 0 \\ & {\text{r}}_{{\text{n,m}}}^{\text{k}} - \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{\mathrm{ln2}\left( {{\sigma B}_{\text{m}} + {\text{H}}_{{\text{n,m}}}^{\text{k}}\upbeta} \right)}}\,{\mathrm{P}}_{{\text{n,m}}}^{\text{k}} - \log_{2} \left( {1 + \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}}\upbeta}}{{{\sigma B}_{\text{m}} }}} \right) - \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}}\upbeta}}{{\mathrm{ln2}\left( {{\sigma B}_{\text{m}} + {\text{H}}_{{\text{n,m}}}^{\text{k}}\upbeta} \right)}} \le 0 \\ & {\text{r}}_{{\text{n,m}}}^{\text{k}} - \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{\mathrm{ln2}\left( {{\sigma B}_{\text{m}} + \text{P}_{\text{n}} } \right)}}\,{\mathrm{P}}_{{\text{n,m}}}^{\text{k}} - \log_{2} \left( {1 + \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{\text{n}} }}{{{\sigma B}_{\text{m}} }}} \right) - \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} \,{\mathrm{P}}_{\text{n}} }}{{\mathrm{ln2}\left( {{\sigma B}_{\text{m}} + {\text{H}}_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{\text{n}} } \right)}} \le 0 \\ \end{aligned}$$

where

$$\upbeta = \frac{{\log_{2} \left( {1 + \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{\text{n}} }}{{{\sigma B}_{\text{m}} }}} \right) - \frac{{{\mathrm{H}}_{{\text{n,m}}}^{\text{k}} \,{\mathrm{P}}_{\text{n}} }}{{\mathrm{ln2} \left( {{\sigma B}_{\text{m}} + {\text{H}}_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{\text{n}} } \right)}}}}{{\frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{\mathrm{ln2} {\sigma B}_{\text{m}} }} - \frac{{{\text{H}}_{{\text{n,m}}}^{\text{k}} }}{{\mathrm{ln2} \left( {{\sigma B}_{\text{m}} + {\text{H}}_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{\text{n}} } \right)}}}}$$
(19)

The optimal solution of \(({\text{P}}_{\text{n,m}}^{\text{k}})^{{*}}\),\((\uprho_{\text{n,m}}^{\text{k}})^{{*}}\), \(({\text{r}}_{\text{n,m}}^{\text{k}})^{{*}}\) can be achieved by interior point method in [31].

3.2 Subcarrier Assignment

It has been assumed that the kth subcarrier in mth CRN is used by the nth SU. For the heterogeneous network, Un,m has been denoted as the network selection parameter. For the SN user, only one network has been selected. The selection parameter for SN user is 1 when highest capacity is offered from mth CRN to nth SU and for MH user the Un,m is always 1.

The network selection is expressed as

$${\text{U}}_{{\text{n,m}}} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{m}} \ne {\text{m}}^{\prime } \,{\text{(or)}}\,\mathrm{l}_{\text{n}} = \, = {\text{M}} \hfill \\ 0, \hfill & {\text{Others}} \hfill \\ \end{array} } \right.$$
(20)

where

$$\text{m}^{{\prime }} = {\mathop {{\text{argmax}}}\limits_{{\rm{m}}}} \sum\limits_{{{k\varepsilon }{\text{k}}_{\rm{m}}^{\text{a}} }} {\left( {{\text{r}}_{{\rm{n,m}}}^{\text{k}} } \right)}^{{*}}$$
(21)

The set Um is indicated as network m is chosen by the users to access. Therefore we have,

$$\text{U}_{\text{m}} = \left\{ {\text{n|U}_{{\text{n,m}}} = \, = 1} \right\}$$
(22)

The subcarrier in CRN is pre-assigned as

$$\text{n}^{{\prime }} = {\mathop {{\text{argmax}}}\limits_{{\rm{m}} \in \text{U}_{\rm{m}} }} \left( {\uprho_{{\rm{n,m}}}^{\text{k}} } \right)^{{*}}$$
(23)
$$\uprho_{{\text{n,m}}}^{\text{k}} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\text{m}} = \, = {\text{m}}^{{\prime }} \hfill \\ 0, \hfill & {\text{Others}} \hfill \\ \end{array} } \right.$$
(24)

Assume each subcarrier in CRN \({k\varepsilon }\text{k}_{\text{m}}^{\text{a}}\) shares the equal responsibility to guarantee the normal communication of PU. The total power of SU is considered to be allotted equally to all subcarriers in CRN should not exceed Pn. The initial power can be written as

$${\tilde{\text{P}}}_{{\text{n,m}}}^{\text{k}} = \text{min}\left[ {\frac{{\text{P}_{\text{n}} }}{{\left| {\text{N}_{\text{n}} } \right|}},\frac{{{\text{i}}_{\text{n}}^{{\text{th}}} }}{{\left| {\text{K}_{\text{n}}^{\text{a}} } \right|{\text{i}}_{{\text{n,m}}}^{\text{k}} }}} \right]$$
(25)

where Nn is the set of subcarriers allotted to nth SU. The subcarrier k should be reassigned to the nth SU which maximizes the energy efficiency with the initial power allocation until each user’s QoS is guaranteed.

figure c

3.3 Power Allocation

The integer variables \(\uprho_{{\text{n,m}}}^{\text{k}}\) are fixed, meanwhile the integer constraints in OP1 are removed after the subcarrier assignment. Since OP1 is not convex, which is difficult to solve. To transform the problem into convex optimization problem, fractional programming is used [32].

To simplify the analysis, the maximization problem is rewritten into minimization form as

$${\mathop {{\text{min}}}\limits_{{\rm{P}}}}\,\upeta_{{\text{EE}}} \mathrm{(p)} = \frac{{\sum\nolimits_{{\text{n} = 1}}^{\text{N}} {\sum\nolimits_{{\text{m} = 1}}^{\text{M}} {\sum\nolimits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{{\text{n,m}}}^{\text{k}} + \text{P}_{\text{c}} } } } }}{{\sum\nolimits_{{\text{m} = 1}}^{\text{M}} {\mathrm{R}_{\text{n}} } }}$$
(26)

The new objective function is defined as

$$\text{h}\left( {{p,\alpha }} \right) = \left( {\sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}}\,{\mathrm{P}}_{{\text{n,m}}}^{\text{k}} + \text{P}_{\text{c}} } } } } \right) -\upalpha\sum\limits_{{\text{m} = 1}}^{\text{M}} {\left( {\text{B}_{\text{m}} \sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} {\log}_{2} \left( {1 + \text{P}_{{\text{n,m}}}^{\text{k}} \upgamma_{{\text{n,m}}}^{\text{k}} } \right)} } } \right)}$$
(27)

Where α is a positive parameter. The new problem is formulated as

$$\begin{aligned} & \text{OP2:}\, {\mathop {{\text{min}}}\limits_{{\rm{P}}}} {\rm{h}}\left( {{p,\alpha }} \right) \\ & {\text{s}}.{\mathrm{t}}\,\,{\text{C}}3{-}{\text{C}}7 \\ \end{aligned}$$
(28)

The optimal value of OP2 is defined as F(α) = minp\(\left\{ {\text{h}\left( {{p,\alpha }} \right)\text{|p} \in \text{S}} \right\}\), Where S is the feasible region of OP1 and OP2. The optimal solution of OP2 can be defined as

$${\text{f}\left( \alpha \right) = {\mathop {{\text{argmin}}}\limits_{{\rm{p}}} }} \left\{ {\text{h}\left( {{p,\alpha }} \right)\text{|p} \in \text{S}} \right\}$$
(29)

The following lemma introduced by Dinkelbach in [32] can relate OP1 and OP2. The detailed proof is given in [32].

Lemma 1

\(\upalpha^{{*}} = \text{min}_{\text{p}} \left\{ {\text{h}\left( {{p,\alpha }} \right)\text{|p} \in \text{S}} \right\} = {\eta (p}^{{*}} )\), if and only if

$${F(\alpha }^{{*}} ) = 0\,\,{\text{and}}\,\,{f(\alpha }^{{*}} ) = \text{(p}^{{*}} )$$
(30)

The lemma states that the optimal solution of OP1 is the optimal solution of OP1. For the given α the optimal power allocation of OP2 is obtained from this the solution of OP1 is realized. And then update α until (30) is fulfilled.

The Lagrangian function of OP2 with Lagrangian multipliers is \(\uplambda_{1} {,\lambda }_{2} {,\lambda }_{3}\) can be written as

$$\begin{aligned} \text{L} & = \left( {\sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }}\, {\mathrm{P}_{{\text{n,m}}}^{\text{k}} + \text{P}_{\text{c}} } } } } \right) -\upalpha\sum\limits_{{\text{m} = 1}}^{\text{M}} {\left( {\text{B}_{\text{m}} \sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {\uprho_{{\text{n,m}}}^{\text{k}} \log_{2} \left( {1 + \text{P}_{{\text{n,m}}}^{\text{k}} \upgamma_{{\text{n,m}}}^{\text{k}} } \right)} } } \right)} \\ & \quad + \sum\limits_{{\text{n} = 1}}^{\text{N}} {\uplambda_{1} \left( {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }}\, {\mathrm{P}_{{\text{n,m}}}^{\text{k}} } } - \text{P}_{\text{n}} } \right)} \\ & \quad + \sum\limits_{{\text{m} = 1}}^{\text{M}} {\uplambda_{2} \left( {\sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }}\, {\mathrm{P}_{{\text{n,m}}}^{\text{k}} } } {\mathrm{i}}_{{\text{n,m}}}^{\text{k}} - {\text{i}}_{\text{n}}^{{\text{th}}} } \right) - } \sum\limits_{{\text{n} = 1}}^{\text{N}} {\uplambda_{3} \left( {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {{\text{r}}_{{\text{n,m}}}^{\text{k}} - \text{R}_{{\text{min}}} } } } \right)} \\ \end{aligned}$$
(31)

The Lagrangian Multipliers \(\uplambda_{1} {,\lambda }_{2} {,\lambda }_{3}\) denotes the total transmission power limit of user n, total interference limit of mth CRN and guaranteed QoS constraint.

Using Karush–Kuhn–Tucker (KKT) conditions [31], the first derivative is

$$\frac{{\partial \text{L}}}{{\partial \text{P}_{{\text{n,m}}}^{\text{k}} }} = 1 - {\alpha B}_{\text{m}} \left( {\frac{{\upgamma_{{\text{n,m}}}^{\text{k}} }}{{\left( {1 + \text{P}_{{\text{n,m}}}^{\text{k}} \upgamma_{{\text{n,m}}}^{\text{k}} } \right)\text{ln2}}}} \right) +\uplambda_{1} +\uplambda_{2} {\text{i}}_{{\text{n,m}}}^{\text{k}} -\uplambda_{3} \left( {\frac{{\upgamma_{{\text{n,m}}}^{\text{k}} }}{{\left( {1 + \text{P}_{{\text{n,m}}}^{\text{k}} \upgamma_{{\text{n,m}}}^{\text{k}} } \right)\text{ln2}}}} \right) = 0$$
(32)

The optimal power allocation is obtained as,

$$\text{P}_{{\text{n,m}}}^{\text{k}} = \left( {\frac{{{(\alpha } +\uplambda_{3} \text{)B}_{\text{m}} }}{{\text{ln2(1} +\uplambda_{1} +\uplambda_{2} {\text{i}}_{{\text{n,m}}}^{\text{k}} }} - \frac{1}{{\upgamma_{{\text{n,m}}}^{\text{k}} }}} \right)^{ + }$$
(33)

where [x]+ = max(x,0). Sub-gradient method is introduced to update the lagrangian multipliers. To update \(\uplambda\) in sub-gradient method with a suitable step size \(\upxi\), the lagrangian multipliers \(\uplambda =\uplambda_{1} ,\lambda_{2} ,\lambda _{3}\) can be updated as:

$$\uplambda_{1} \text{(t} + \text{1)} = \left[ {\uplambda_{1} \text{(t)} +\upxi^{\text{t}} \left( {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }}\, {\mathrm{P}_{{\text{n,m}}}^{\text{k}} } } - \text{P}_{\text{n}} } \right)} \right]^{ + }$$
(34)
$$\uplambda_{2} \text{(t} + \text{1)} = \left[ {\uplambda_{2} \text{(t)} +\upxi^{\text{t}} \left( {\sum\limits_{{\text{n} = 1}}^{\text{N}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }}\,{\mathrm{P}_{{\text{n,m}}}^{\text{k}} } } {\mathrm{i}}_{{\text{n,m}}}^{\text{k}} - {\text{i}}_{\text{n}}^{{\text{th}}} } \right)} \right]^{ + }$$
(35)
$$\uplambda_{3} \text{(t} + \text{1)} = \left[ {\uplambda_{3} \text{(t)} +\upxi^{\text{t}} \left( {\sum\limits_{{\text{m} = 1}}^{\text{M}} {\sum\limits_{{{k\varepsilon }\text{k}_{\text{m}}^{\text{a}} }} {{\text{r}}_{{\text{n,m}}}^{\text{k}} - \text{R}_{{\text{min}}} } } } \right)} \right]^{ + }$$
(36)

where \(\upxi^{\text{t}} > 0\) a sequence of step size and t denotes the iteration time. The optimal values of Lagrangian multipliers can be obtained by sub-gradient method.

figure d

4 Simulation Results

The numerical results for the proposed algorithm have been validated in this section. The results have been simulated using MATLAB R2016a on a Laptop equipped with an Intel(R) Core(TM) i3 processor (2.3 GHz), Windows 10 pro 64 bit operating system (Table 1).

Table 1 Parameter settings
Full size table

The channel gain is modelled as path loss propagation model for CRN1 and CRN2

$$\text{P}_{{\text{loss}}}^{1} \text{(dB)} = \left\{ {\begin{array}{*{20}l} 122 + 38\log(0.05), \hfill & {\text{if}}\,{\text{d}} < 0.05 \hfill \\ 122 + 38\log(d), \hfill & {\text{if}}\,{\text{d}} \ge 0.05 \hfill \\ \end{array} } \right.$$
(37)
$$\text{P}_{{\text{loss}}}^{2} \text{(dB)} = \left\{ {\begin{array}{*{20}l} 128.1 + 37.6\log(0.05), \hfill & \text{if}\,{\text{d}} < 0.05 \hfill \\ 28.1 + 37.6\log(d), \hfill & {\text{if}}\,{\text{d}} \ge 0.05 \hfill \\ \end{array} } \right.$$
(38)

Figure 2 illustrates the Energy Efficiency versus total transmit power Pn performance curves for different interference thresholds under imperfect sensing respectively. The curves have been plotted for various interference threshold such as \({\text{i}}_{\text{n}}^{{\text{th}}}\) = 5 × 10−10 W and \({\text{i}}_{\text{n}}^{{\text{th}}}\) = 1 × 10−10 W. Initially EE increases as the total transmit power increases and then EE starts decreasing when the transmit power Pn becomes larger, which can be explained instinctively. The larger Pn can achieve more capacity when the transmission power limit is chosen to be small, at this time the Pc is the main part of total power consumption. When the circuit power gets ignored due to larger Pn, the EE will decrease as the total power budget is drained due to logarithmic growth of capacity. The curves of two interference threshold get to be horizontal at Pn = 0.8 × 10−3 W, as with the total transmit power getting larger the interference threshold turns to be the main constraint of the optimization problem.

Fig. 2
figure 2

Energy efficiency versus total transmit power with different interference thresholds

Full size image

In Fig. 3, it shows that the EE curves of the proposed EEPA algorithm under perfect and imperfect sensing. The curves have been plotted for various total transmit power such as Pn = 10−3 W and Pn = 10−4 W. It can be observed the EE increases as the \({\text{i}}_{\text{n}}^{{\text{th}}}\) increases for both perfect and imperfect sensing. EE is higher when the total transmit power is larger. When the transmit power is comparably high i.e. Pn is 10−3 W, the EE is mainly determined by the interference threshold. When the transit power is low enough i.e. Pn is 10−4 W, the EE is stifled by the total transmit power and will be constant as the \({\text{i}}_{\text{n}}^{{\text{th}}}\) increases.

Fig. 3
figure 3

Energy efficiency versus interference threshold under perfect and imperfect sensing

Full size image

Figure 4 shows the energy efficiency versus interference threshold curves of EEPA algorithm and EPA method with imperfect spectrum sensing where Pn is 10−3 W respectively. As the interference threshold increases, the EE of the proposed EEPA algorithm and EPA method increases respectively. It can be clearly seen that the proposed scheme offers approximately 30% greater performance than conventional EPA method. EPA distributes power reasonably to all the available subcarriers under imperfect sensing.

Fig. 4
figure 4

Energy efficiency versus interference threshold with Pn = 10−3 W for EEPA algorithm and EPA method

Full size image

Figure 5 exemplifies the capacity versus \({\text{i}}_{\text{n}}^{{\text{th}}}\) curves for both perfect and imperfect sensing of EEPA algorithm and EPA method. It is inferred that capacity increases as the interference threshold increases and it will reach a constant maximum when \({\text{i}}_{\text{n}}^{{\text{th}}}\) is 9 × 10−10 W. Perfect sensing performs better than the capacity of the system under imperfect sensing of the proposed EEPA algorithm and EPA method. The system capacity under imperfect sensing of the proposed EEPA algorithm is approximately 25% greater than EPA method.

Fig. 5
figure 5

Capacity versus interference threshold under different metrics

Full size image

In Fig. 6, the capacity of each user in HCRNS is graphically demonstrated for proposed algorithm and without guaranteeing QoS. From the figure it is inferred that our proposed algorithm guarantees each user’s QoS and when QoS is not guaranteed it leads to few users’ capacity below the minimum required capacity.

Fig. 6
figure 6

Capacity of each user in HCRN

Full size image

Figure 7 compares the interference introduced to each PU in CRN1 and CRN2 for both perfect and imperfect sensing. For imperfect sensing the interference introduced to PU is always below the interference threshold. When considering perfect sensing it violates the interference threshold, which is mainly caused by the SU’s access to the subcarriers used by the PU.

Fig. 7
figure 7

Interference introduced to PU with transmission power under perfect and imperfect sensing

Full size image

5 Conclusion

An optimal energy efficient power allocation scheme for OFDM based HCRN under imperfect sensing with guaranteed quality of service (QoS) has been presented in this work. Performance parameters such as energy efficiency and capacity under total transmission power, interference and QoS constraint have been analyzed. Simulation results show that the proposed EEPA algorithm can provide higher Energy Efficiency and data rate compared to the EPA method. The performance in system loss is unavoidable, while considering imperfect sensing scenario. However it can still achieve promising performance in energy efficiency of HCRN. In future the energy efficient power allocation problem can be extended for Femto cell network under cooperative spectrum sensing.