1 Introduction

In recent years, applications of global navigation satellite system (GNSS) are developing rapidly and new signals and new modulations are applied in different navigation systems. Binary offset carrier (BOC) [1, 2] and multiplexed binary offset carrier (MBOC) [3] modulations have been chosen as the chief candidate for several future navigation signals, for example, GPS L1C, GPS M-code, and Galileo open service (OS) signals. BOC signals have increased resilience against multipath and provide improved tracking performance. However, their autocorrelation functions (ACF) have multiple peaks, which may lead to false code lock on side peaks. Several solutions have been proposed in the literature. Several techniques that have been reported to avoid such ambiguity include BPSK-like technique [4, 5], Bump-Jumping (BJ) technique [6], Autocorrelation Side-peaks Cancellation (SC) Techniques [7], and double estimator (DE) [8, 9].

The BPSK-like technique described in [4] considers the sine-BOC signals as the sum of two BPSK signals. Thus each side band component leads to unambiguous correlation functions. However, it weakens the robustness of BOC signal against multipath needs an extra filter. Besides, signal to noise ratio (SNR) will be deteriorated. In BJ [6], the BOC autocorrelation function uses additional correlators includes very early (VE) and very late (VL) correlators to check whether the loop is locked on the main peak by comparing the output of VE, VL, and prompt (P) correlators. When locked on the main peak, it has high tracking accuracy. But when the SNR is low, the detection will have a high probability of false alarm. Side-peaks Cancellation Techniques remove the ambiguities of the correlation function by using other signals to correlate with BOC signal. An innovative unambiguous tracking method called ASPeCT is described in [7, 10]. In ASPeCT, BOC signal is correlated with its local replica and PRN code. It removes the side peaks from the correlation function and keeps the main peak, but it is only applicable to sine-BOC signals. It is important to design local signals for SC techniques.

In this paper a new unambiguous tracking method for BOC modulated GNSS signals is proposed. The properties of sine-BOC signals are given, at first. Then, analytical expression of linear fitting with multi-correlator function is presented. Its multipath mitigation and noise performance are investigated and finally conclusions are drawn in the end.

2 Backgrounds

A BOC signal is characterized by its spreading code frequency \(f_{c} = m \times 1.023\;{\text{MHz}}\), and its subcarrier frequency \(f_{s} = n \times 1.023\;{\text{MHz}}\) with m, n and the ratio \(k = 2n/m\) must be positive integers. Each family defined by these two parameters is referred to as a \(BOC\left( {n,m} \right)\) modulation and has its specific spectral characteristics. The sine sub-carrier can be modeled as:

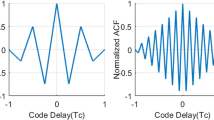
$$SC\left( t \right) = \text{sgn} \left( {\sin \left( {2\pi f_{s} t} \right)} \right)$$
(1)

The Auto-Correlation Function (ACF) of sine-BOC(n,n) and sine-BOC(2n,n) are shown in Fig. 1 along with BPSK (1) ACF.

Fig. 1
figure 1

Normalized ACF comparison with BOC and BPSK modulated signals

Full size image

From Fig. 1 we can see that the ACF of BPSK modulated signals is a triangle and have only one peak, but BOC signals have other side-peaks. The difference of spreading chip waveforms between BPSK signals and BOC signals leads their difference in ACF shapes, and makes the distinction of acquisition and tracking performance.

The output of traditional early-late discriminator in delay locked loop (DLL) can be expressed as [11]

$$E_{n} \left( \tau \right) = \left| {R\left( {\tau + D/2} \right)} \right|^{n} - \left| {R\left( {\tau - D/2} \right)} \right|^{n}$$
(2)

where \(n\) is usually either 1 or 2, \(D\) is the spacing between the early and late gates, and \(R\left( \tau \right)\) is the cross correlation function.

The normalized of Eq. (2) can be written as

$$S_{n} \left( \tau \right) = \frac{{\left| {R\left( {\tau + D/2} \right)} \right|^{n} - \left| {R\left( {\tau - D/2} \right)} \right|^{n} }}{{\left| {R\left( {\tau + D/2} \right)} \right|^{n} + \left| {R\left( {\tau - D/2} \right)} \right|^{n} }}$$
(3)

When we use traditional early-late correlator to track BOC modulated signals, it will lead to false lock on side-peaks, which is referred to as ambiguous tracking, as shown in Fig. 2.

Fig. 2
figure 2

Discriminator functions comparison with BOC and BPSK signals with early-late correlator

Full size image

As shown in Fig. 2, when using the traditional early-late correlator for BOC modulated signals, the output of discriminator function has some drawbacks as follows:

  1. (1)

    The linear region of discriminator output is narrow, which will deteriorate its performance in the absence of noise. From the Fig. 2, we can know the linear region of sine-BOC(n,n) is \(\left[ { - \;0.17,0.17} \right]\) and the sine-BOC(2n,n) is \(\left[ { - \;0.1,0.1} \right]\), however the linear region of BPSK is \(\left[ { - \;0.5,0.5} \right]\), which is wider than sine-BOC modulated signals.

  2. (2)

    The discriminator outputs have divergence zones, which will drive the code delay lock loop out of lock.

  3. (3)

    There is more than one zero-crossing point, which will result in false lock.

In order to solve those problems, this paper proposes a novel method to make the discriminator output of sine-BOC modulated signals similar to that of BPSK signals.

3 Proposed Method

We propose a multi-correlate approach for the design of the discriminator in code tracking loop. So the Eq. (2) can be replaced by:

$$E_{n} \left( \tau \right) = \sum\limits_{i = 1}^{N} {\alpha_{i} \left( {\left| {R\left( {\tau + D_{i} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{i} /2} \right)} \right|^{n} } \right)}$$
(4)

And Eq. (3) can be rewritten as:

$$S_{n} \left( \tau \right) = \frac{{\sum\nolimits_{i = 1}^{N} {\alpha_{i} \left( {\left| {R\left( {\tau + D_{i} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{i} /2} \right)} \right|^{n} } \right)} }}{{\sum\nolimits_{i = 1}^{N} {\alpha_{i} \left( {\left| {R\left( {\tau + D_{i} /2} \right)} \right|^{n} + \left| {R\left( {\tau - D_{i} /2} \right)} \right|^{n} } \right)} }}$$
(5)

Typically, the design requirements of the discriminator are follows:

  1. (1)

    The discriminator output \(E_{n} \left( \tau \right)\) is linear with \(\tau\) for \(\left| \tau \right| \le D_{\hbox{max} } /2\);

  2. (2)

    There is only one zero-crossing point in the convergence zone.

In the absence of noise and multipath, the requirement (1) can be expressed as:

$$E_{n} \left( \tau \right) = \beta \tau$$
(6)

where \(\beta\) is an arbitrary constant.The requirement (2) means:

$$E_{n} \left( \tau \right) \ne 0,\;\tau \ne 0,\;\left| \tau \right| \le D_{\hbox{max} } /2$$
(7)

We can’t get \(\alpha_{1} ,\alpha_{2} \ldots \alpha_{N}\) directly, but we can use the method of least function approximation as follows:

$$e = \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\left( {E_{n} \left( \tau \right) - \beta \tau } \right)^{2} d\tau }$$
(8)

And we minimize \(e\), which satisfies:

$$\frac{de}{{d\alpha_{i} }} = 0$$
(9)

For the sake of simplicity, we can concentrate on the situation of \(N = 2\), so we replace Eq. (8) by:

$$e = \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\left( \begin{aligned} & \alpha_{1} \left( {\left| {R\left( {\tau + D_{1} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{1} /2} \right)} \right|^{n} } \right) \hfill \\ &+ \alpha_{2} \left( {\left| {R\left( {\tau + D_{2} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{2} /2} \right)} \right|^{n} } \right) - \beta \tau \hfill \\ \end{aligned} \right)}^{2} d\tau$$
(10)

According to Eq. (9), we have

$$\begin{aligned} \frac{de}{{d\alpha_{1} }} & = 2\alpha_{1} \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\left( {\left| {R\left( {\tau + D_{1} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{1} /2} \right)} \right|^{n} } \right)^{2} d\tau } \\ & \quad + 2\alpha_{2} \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\left( {\left| {R\left( {\tau + D_{1} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{1} /2} \right)} \right|^{n} } \right)} \left( {\left| {R\left( {\tau + D_{2} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{2} /2} \right)} \right|^{n} } \right)d\tau \\ & \quad - 2\beta \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\tau \left( {\left| {R\left( {\tau + D_{1} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{1} /2} \right)} \right|^{n} } \right)} d\tau = 0 \\ \end{aligned}$$
(11)
$$\begin{aligned} \frac{de}{{d\alpha_{2} }} & = 2\alpha_{2} \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\left( {\left| {R\left( {\tau + D_{2} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{2} /2} \right)} \right|^{n} } \right)^{2} d\tau } \\ & \quad + 2\alpha_{1} \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\left( {\left| {R\left( {\tau + D_{1} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{1} /2} \right)} \right|^{n} } \right)} \left( {\left| {R\left( {\tau + D_{2} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{2} /2} \right)} \right|^{n} } \right)d\tau \\ & \quad - 2\beta \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\tau \left( {\left| {R\left( {\tau + D_{2} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{2} /2} \right)} \right|^{n} } \right)} d\tau = 0 \\ \end{aligned}$$
(12)

Equations (11) and (12) can be written as

$$\alpha_{1} \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\psi_{1}^{2} \left( \tau \right)d\tau + \alpha_{2} } \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\psi_{1} \left( \tau \right)} \psi_{2} \left( \tau \right)d\tau = \beta \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } }} {\tau \psi_{1} \left( \tau \right)} d\tau$$
(13)
$$\alpha_{2} \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\psi_{2}^{2} \left( \tau \right)d\tau + \alpha_{1} } \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\psi_{1} \left( \tau \right)} \psi_{2} \left( \tau \right)d\tau = \beta \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } }} {\tau \psi_{2} \left( \tau \right)} d\tau$$
(14)

where \(\psi_{i} \left( \tau \right) = \left| {R\left( {\tau + D_{i} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{i} /2} \right)} \right|^{n} ,\;i = 1,2\).

And they can be convert into:

$$\left[ {\begin{array}{*{20}c} {\theta_{11} } & {\theta_{12} } \\ {\theta_{12} } & {\theta_{22} } \\ \end{array} } \right]\left[ \begin{aligned} \alpha_{1} \hfill \\ \alpha_{2} \hfill \\ \end{aligned} \right] = \beta \left[ \begin{aligned} \lambda_{1} \hfill \\ \lambda_{2} \hfill \\ \end{aligned} \right]$$
(15)

where

$$\theta_{ij} = \theta_{ji} = \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\psi_{i} \left( \tau \right)\psi_{j} \left( \tau \right)} d\tau ,\;i,j = 1,2$$
(16)
$$\lambda_{i} = \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\tau \psi_{i} \left( \tau \right)} d\tau ,\;\;\;i = 1,2$$
(17)

When the number of correlator is \(N\), Eq. (15) can be replaced by:

$$\left[ {\begin{array}{*{20}c} {\theta_{11} } & {\theta_{12} } & \cdots & {\theta_{1N} } \\ {\theta_{21} } & {\theta_{22} } & \cdots & {\theta_{2N} } \\ \vdots & \vdots & \ddots & \vdots \\ {\theta_{N1} } & {\theta_{N1} } & \cdots & {\theta_{NN} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\alpha_{1} } \\ {\alpha_{2} } \\ \vdots \\ {\alpha_{N} } \\ \end{array} } \right] = \beta \left[ {\begin{array}{*{20}c} {\lambda_{1} } \\ {\lambda_{2} } \\ \vdots \\ {\lambda_{N} } \\ \end{array} } \right]$$
(18)

where

$$\theta_{ij} = \theta_{ji} = \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\psi_{i} \left( \tau \right)\psi_{j} \left( \tau \right)} d\tau ,\;i,j = 1,2, \ldots ,N$$
(19)
$$\lambda_{i} = \int\limits_{{ - D_{\hbox{max} } /2}}^{{D_{\hbox{max} } /2}} {\tau \psi_{i} \left( \tau \right)} d\tau ,\;i = 1,2, \ldots ,N$$
(20)
$$\psi_{i} \left( \tau \right) = \left| {R\left( {\tau + D_{i} /2} \right)} \right|^{n} - \left| {R\left( {\tau - D_{i} /2} \right)} \right|^{n} ,\;i = 1,2, \ldots ,N$$
(21)

It is shown that \(e\) is minimized if the coefficient \(\alpha\) satisfies:

$$\alpha = \beta \theta^{ - 1} \lambda$$
(22)

When \(\beta = 1\), we get the value of \(\alpha\) shown in the following Table 1.

Table 1 The value of \(\alpha\) for each correlator
Full size table

A novel architecture of the multi-correlator tracking loop based on linear fitting is depicted in Fig. 3. The received BOC modulated signal is down converted to baseband in-phase (I) and quadrature-phase (Q) signals and then the local generator generates early and late spreading sequence multiplying with the baseband I and Q signals. The discriminator output can be written as Eq. (4).

Fig. 3
figure 3

Novel DLL architecture based on linear fitting with multi-correlator

Full size image

4 Performance

4.1 Discriminator Output

According to Table 1, the discriminator output of each family of BOC modulated signals can be simulated. When N = 1, it is known as a traditional early-late correlator. From the Fig. 4, we can see that the discriminator output performs better with the increasing N and all of them has only one zero-crossing point, besides the linear zoon is better enough to accomplish unambiguous tracking for sine-BOC modulated signals, especially for sine-BOC(n,n) signals.

Fig. 4
figure 4

Discriminator functions with different N for some BOC modulated signals

Full size image

4.2 Impact of Multipath

The multipath error is generated because the line-of-sight signal is corrupted by the delayed reflected signal. Multipath error envelope (MEE) is a typical way to evaluate the multipath mitigation performance. The MEE commonly employs two paths, namely, in-phase and out-of phase [12]. The amplitude of the second-path is 6 dB lower than that of the line-of-sight path. The discriminator output with only one reflector path can be given by [13]

$$E_{s} \left( \tau \right) = \sum\limits_{i = 1}^{N} {\alpha_{i} \left\{ {\begin{array}{*{20}l} {\left( {\left| {R\left( {\tau + D_{i} /2} \right)} \right| + \beta_{1} \cos \theta_{m1} \left| {R\left( {\tau + D_{i} /2 + \delta_{1} } \right)} \right|} \right)^{2} } \hfill \\ { - \left( {\left| {R\left( {\tau - D_{i} /2} \right)} \right| + \beta_{1} \cos \theta_{m1} \left| {R\left( {\tau - D_{i} /2 + \delta_{1} } \right)} \right|} \right)^{2} } \hfill \\ \end{array} } \right\}}$$
(23)

where \(\beta_{1}\) and \(\delta_{1}\) denots the multipath to direct ratio (MDR) and multipath delay, respectively. Equation (23) can be replaced by its linear equivalent model

$$E_{s} \left( \tau \right) \approx E_{s} \left( 0 \right) + E_{s}^{{\prime }} \left( 0 \right)\tau_{e}$$
(24)

where \(\tau_{e}\) represents the multipath error. The delay lock loop (DLL) continuously solves the equation \(E_{s} = 0\) which is the balance condition of DLL. Thus we can get the multipath envelope error.

Figure 5 shows the MEE for sine-BOC(n,n) tracking, as well as for ASPeCT in [7] with \(\beta = 1\) for signal-to-multipath-amplitude ratio of 0.5 and an infinite front-end filter. The results show that the proposed method will be better when we increase the number of correlator. The main reason is that the proposed method has narrower correlate spacing with the increasing value of \(N\), which is discussed in [14]. And the difference between the proposed method and the ASPeCT is minimal.

Fig. 5
figure 5

Code tracking multipath envelope for \(BOC\left( {n,n} \right)\) with different value of \(N\) and ASPeCT with \(\beta = 1\) for early-late spacing of 0.5 chips and an infinite front-end filter

Full size image

4.3 Impact of Noise

The another tracking performance criteria is thermal noise range error which has the similar form as traditional early-minus-late discriminator for the proposed method. It can be given by [15]

$$\sigma^{2} = \frac{{4B_{L} \left( {1 - 0.5B_{L} T_{\text{int}} } \right)}}{{C/N_{0} }}\frac{1}{\chi }\left[ {\sigma_{1} + \frac{{\sigma_{2} }}{{T_{\text{int}} C/N_{0} }}} \right]$$
(25)

where \(T_{\text{int}}\), \(B_{L}\), \(C/N_{0}\) and \(\chi\) denotes integration time, noise bandwidth, carrier-to-noise ratio and the gain of the discriminator. \(\chi\), \(\sigma_{1}\) and \(\sigma_{2}\) can be expressed by

$$\chi = \frac{d}{d\tau }E_{n} \left( \tau \right)\left| {_{\tau = 0} } \right.$$
(25)

And

$$\sigma_{1} = R_{F} \left( 0 \right)\sum\limits_{i = 1}^{N} {\left\{ {R^{2} \left( {D_{i} /2} \right) + R^{2} \left( { - D_{i} /2} \right) - 2R_{F} \left( {D_{i} } \right)R\left( {D_{i} /2} \right)R\left( { - D_{i} /2} \right)} \right\}}$$
(26)
$$\sigma_{2} = \sum\limits_{i = 1}^{N} {R_{F}^{2} \left( 0 \right) - R_{F}^{2} } \left( {D_{i} } \right)$$
(27)

\(R_{F} \left( \tau \right)\) can be denoted by

$$R_{F} \left( \tau \right) = \int\limits_{{ - B_{r} }}^{{B_{r} }} {S\left( f \right)e^{ - j2\pi f\tau } df}$$
(28)

where \(B_{r}\) is the frontend bandwidth, and \(S\left( f \right)\) is the PSD of the baseband code.

Figure 6 shows the code tracking error standard deviation of the proposed method for sine-BOC(n,n) with integrate time of 1 ms. As we can see that the traditional BPSK method and the proposed method performs slight better than the ASPeCT (\(\beta = 1.4\)), while it is slightly more susceptible to noise than ASPeCT (\(\beta = 1\)).

Fig. 6
figure 6

Code tracking error standard deviation versus the C/N0 for the sine-BOC tracking with the proposed method and ASPeCT

Full size image

Figure 6 Code tracking error standard deviation versus the C/N0 for the sine-BOC tracking with the proposed method and ASPeCT (\(\beta = 1\) and \(\beta = 1.4\)) with correlate spacing of 0.2 chips and a coherent integration time of 1 ms.

5 Conclusion

This paper presents a novel tracking method based on multi-correlator, and the performance of this method is investigated. Applying linear fitting of multi-correlator to design an ideal discriminator, which has only one zero-crossing point and the linear region is wider. The proposed method can improve the performance of tracking BOC modulated signals. From the figure of discriminator output, we can know the proposed method performs best for sine-BOC(n,n). Besides, the correlators can be accomplished in a way of software. So this method will not need extra hardware resources.