1 Introduction

Increasing demand for high speed data has led to the popularity and adoption of multi-carrier modulation techniques such as orthogonal frequency division multiplexing (OFDM) in high speed wireless communication standards e.g. Digital Video Broadcast (DVB) and Long Term Evolution (LTE) for 4G mobile communication systems. OFDM is chosen because it provides immunity to multipath fading, offers high data transmission, and has high spectral efficiency [1]. However, it often produces signals with large peak-to-average power ratio (PAPR) levels, which may increase bit-error-rate (BER) [1–4]. A comprehensive review of common PAPR reduction techniques in OFDM can be found in [5–7]. Amongst these techniques, selected mapping (SLM) [8] is considered the most effective solution because it offers improved PAPR reduction performance compared to other methods such as partial transmit sequences (PTS) [9].

At the receiver of an SLM–OFDM system, some form of side information (SI) estimation is often required to enable the successful recovery of payload data [10–12]. This SI represents critical information, which must be accurately known or determined at the receiver to enable successful data recovery [13]. Through the use of some form of pilot-assisted SI estimation scheme, recent studies found in [13–15] have shown that it is possible to determine the SI without prior SI transmission and with no extra data overhead since the same pilots (training signals) are also used during channel estimation for coherent detection [16].

Amongst these pilot-assisted SI estimation schemes, the frequency-domain correlation (FDC) SI estimation scheme in [15] is chosen for comparisons in this paper because it uses similar conventional SLM method in [8] and not a modified SLM as used in the SI estimation method described in [14]. Aside from high computational complexity of SI estimation, another practical problem with SI estimation is that the receiver will only implement SI estimation when SLM is actually implemented. Hence, similar to the DVB standard specifications [17], an additional system flag or control signalling information is required to inform the receiver when the transmitter implements PAPR reduction. This is an extra system overhead that poses an additional implementation challenge, which will also be addressed in this paper.

This paper demonstrates the use of an alternative SLM–OFDM data decoding procedure known as Embedded Coded Modulation (ECM) that requires no SI estimation and as a consequence, requires no extra system overhead. Similar to the FDC method in [15], the ECM method is a pilot-assisted SLM–OFDM data decoding scheme and applies a similar SLM method described in [18] to reduce PAPR within a block-type frame structure. The performance of the ECM method is investigated through the evaluation of the BER performance and the computational complexity in comparison with a conventional SLM–OFDM receiver that performs SI estimation using, for example, the FDC method.

The paper is structured as follows. Section 2 describes an OFDM transmitted model and a form of block-type OFDM frame structure used for the investigations in this paper. Section  3 presents the FDC based SI estimation scheme and related data decoding procedures for a block-type OFDM frame. Section 4 describes the ECM method. Section 5 presents the simulation results and provides some discussion on these results. Finally, conclusions from the results are presented in Sect. 6.

2 System Model—Transmitter

This section briefly introduces an OFDM transmitter model and the considered block-type OFDM frame structure described in [19].

2.1 OFDM Signal Generation

Let \({\varvec{X}}\) be an OFDM sequence, which consists of \(N_{v}\) subcarriers, such that

$$\begin{aligned} {\varvec{X}}&= \left[ {\varvec{X}}(0)\,{\varvec{X}}(1)\,{\varvec{X}}(k)\,\dots\,{\varvec{X}}(N_v-1)\right] \end{aligned}$$
(1)

where k for \(0 \le k \le N_{v}-1\) represents the subcarrier index. Using an N-point inverse fast Fourier transform (IFFT), a time-domain signal \({\varvec{x}}\) of size N is obtained from \({\varvec{X}}\). For \(0 \le n \le N-1\), each discrete time-domain sample, \({\varvec{x}}(n)\) within \({\varvec{x}}\) is given by [20]

$$\begin{aligned} {\varvec{x}}(n)&= \frac{1}{N} \sum \limits _{k = 0}^{N_{\text {v}}-1} {\varvec{X}}(k)\exp (j2\pi nk/N) \nonumber \\&= \underset{N-\text {point}}{\text {IFFT}}\left\{ {\varvec{X}} \right\} , \end{aligned}$$
(2)

where \(\underset{N-\text {point}}{\text {IFFT}}\left\{ \cdot \right\}\) denotes an N-point IFFT function. Hence, \({\varvec{x}}\) can be written as

$$\begin{aligned} {\varvec{x}}&= \left[ {\varvec{x}}(0)\,{\varvec{x}}(1)\,{\varvec{x}}(n)\,\dots \,{\varvec{x}}(N-1)\right] . \end{aligned}$$
(3)

Finally, the length of OFDM signal \({\varvec{x}}\) is further extended by a cyclic prefix (CP) so as to mitigate channel fading and to facilitate the use of simpler frequency-domain equalization [21]. The PAPR of \({\varvec{x}}\) is calculated from [22]

$$\begin{aligned} PAPR\{{\varvec{x}}\}&= \frac{\text {max} \{ \vert {\varvec{x}}\vert ^{2} \}}{E\{ \vert {\varvec{x}}\vert ^{2}\}} \end{aligned}$$
(4)

where \(E\{ \cdot \}\) denotes the expectation function. Note that the use of CP has no significant influence on the PAPR evaluations [19].

Figure 1 shows a block diagram representation of a baseband OFDM transmitter structure for OFDM signal generation.

Fig. 1
figure 1

A block diagram representation of baseband OFDM signal generation (OFDM transmitter)

Full size image

2.2 Block-Type OFDM Frame Structure

In practical OFDM wireless systems, multiple OFDM symbol blocks in the form of a \(2-\hbox {D}\) pattern are usually transmitted in parallel [16]. This \(2-\hbox {D}\) pattern may be referred to as a frame. Several forms of OFDM frame structure exist in the literature and in various wireless communication systems. An example of a well-known OFDM frame structure, which is considered in this paper is the block-type OFDM frame, described in [19]. Figure  2 shows the considered data and pilot pattern within the considered block-type frame.

Fig. 2
figure 2

An example of a form of block-type OFDM frame structure [19]

Full size image

In the block-type frame, one of the OFDM symbol blocks contains only pilots or training sequence and is designated as the pilot block while other blocks, which consist of data subcarriers are regarded as data blocks. The block-type frame is considered to be most suitable in the case of a time-invariant channel condition such as indoor channels where there exists no or negligible variation in the channel gain between consecutive OFDM blocks in the frame [16].

Consider a block-type frame that comprises of G OFDM symbol blocks where each block has \(N_{v}\) subcarriers, then similar to \({\varvec{X}}(k)\) in (1) and for \(1 \le g \le G\) where g is the index of each block, a subcarrier index k in a given block g is denoted by \({\varvec{X}}(g, k)\). To indicate the data and the pilot block in the frame, let \(g_p\) and \(g_{d}\) be the g-index for the pilot and the data block respectively. Hence, each subcarrier in a pilot and a data block is respectively represented by \({\varvec{X}}(g_{p}, k)\) and \({\varvec{X}}(g_{d}, k)\).

2.3 OFDM Frame PAPR Reduction

To reduce PAPR in a block-type frame, the classical SLM method is considered [8]. However, since the frame consists of several OFDM symbol blocks, it is customary to reduce the PAPR of the whole frame rather than for each individual OFDM symbol [19].

For \(1 \le u \le U\) where U is the number of SLM sequence vectors, each SLM sequence is denoted by \({\varvec{P}}^{u}\) where

$$\begin{aligned} {\varvec{P}}^{u} = \left[ {\varvec{P}}^{u}(0)\,{\varvec{P}}^{u}(1)\,{\varvec{P}}^{u}(k)\,\dots\,{\varvec{P}}^{u}(N_v-1)\right] . \end{aligned}$$
(5)

With the application of \({\varvec{P}}^{u}\), U alternative frames are formed and the resulting time-domain signal (after IFFT) can be denoted by \({\varvec{x}}^u(g)\) where

$$\begin{aligned} {\varvec{x}}^u(g)&= \underset{N-\text {point}}{\text {IFFT}}\{ {\varvec{X}}(g, k) \cdot {\varvec{P}}^{u} \}. \end{aligned}$$
(6)

Then, each block, \({\varvec{x}}^{\bar{u}}(g)\) within the selected frame with the lowest PAPR is given by [19]

$$\begin{aligned} {\varvec{x}}^{\bar{u}}(g) = \underset{u}{\min } \left[ \underset{g=1,2~\dots ~G}{\max } PAPR\{ {\varvec{x}}^{u}(g)\} \right] \end{aligned}$$
(7)

where the variable \(\bar{u}\) in (7) is the SI and is given by [19]

$$\begin{aligned} \bar{u} = \underset{u=1,2~\dots ~U}{\arg \min } \left[ \underset{g=1,2~\dots ~G}{\max } PAPR\{ {\varvec{x}}^{u}(g)\} \right] . \end{aligned}$$
(8)

3 Conventional SLM–OFDM Frame Data Decoding

This section presents the FDC SI estimation method and conventional SLM–OFDM data decoding procedures for the considered block-type OFDM frame structure.

In the presence of complex-valued channel frequency response \({\varvec{H}}(g, k)\) and additive white Gaussian noise (AWGN) \(\varvec{V}(g, k)\), each received OFDM block \({\varvec{Y}}(g, k)\) (after FFT) is given by [19]

$$\begin{aligned} {\varvec{Y}}(g, k)&= {\varvec{H}}(g, k) {\varvec{X}}(g, k) {\varvec{P}}^{\bar{u}}(k) + \varvec{V}(g, k). \end{aligned}$$
(9)

From (9), it can be noted that before the transmitted data subcarrier \({\varvec{X}}(g_d, k)\) can be recovered at the receiver, the value \({\varvec{P}}^{\bar{u}}(k)\) must be known or determined through some form of SI estimation scheme. The purpose of SI estimation is to estimate the value of \(\bar{u}\), assuming all U SLM sequence vectors \({\varvec{P}}^{u}\) are deterministic and known at the receiver [13].

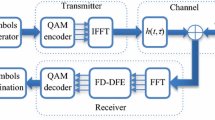
Figure 3 shows a block diagram representation of a baseband OFDM receiver. As previously mentioned, with SLM, the conventional data decoding procedure requires some of SI estimation [2].

Fig. 3
figure 3

A block diagram representation of baseband OFDM receiver

Full size image

3.1 FDC SI Estimation

A detailed description of the FDC SI estimation scheme is presented in [15]. From the received pilot block, an FDC function, \({\varvec{R}}^{u}\) is obtained from [15]

$$\begin{aligned} {\varvec{R}}^u = \frac{1}{N_v-1} \sum _{k=1}^{N_v-1} {{\bar{\varvec H}}}^{u}\left( g_p, k\right) \cdot {{\bar{\varvec H}}}^{u}\left( g_p, k-1\right) ^{*} \end{aligned}$$
(10)

where (\(^*\)) denotes complex conjugate and the term \({{\bar{\varvec H}}}^u(g_p, k)\) in (10) is obtained as

$$\begin{aligned} {{\bar{\varvec H}}}^u(g_p, k)&= \left( {\varvec{Y}}(g_p, k) {\varvec{P}}^{u}(k) \right) \Big / {\varvec{X}}(g_p, k)~. \end{aligned}$$
(11)

Note that for coherent detection, (11) assumes the transmitted pilot block \({\varvec{X}}(g_{p}, k)\) is known at the receiver.

Let \({\hat{u}}\) be the SI estimate. Then, using \({\varvec{R}}^u\), \({\hat{u}}\) is determined from [15]

$$\begin{aligned} {\hat{u}}& = \underset{u}{\hbox {arg}}\, {\hbox{max}} Re \{{\varvec{R}}^{u}\} \end{aligned}$$
(12)

where \(Re\{\cdot \}\) takes only the real component of a complex-valued number or variable.

The computational complexity of this FDC scheme is evaluated from (10) and (11). It can be noted that the FDC scheme requires \(2UN_{v}-U\) complex multiplications (CMs) and \(U(N_{v}-2)\) complex additions (CAs) [23]. Note that similar to [15], these evaluations ignore the division with the scaling parameter \(1/(N_{v}-1)\) in (10) and assumed \({\varvec{P}}^u(k) \in \pm 1\).

3.2 Channel Mitigation and QAM Demodulation

The required channel mitigation and QAM demodulation is now discussed.

3.2.1 Channel Mitigation

Using the SI estimate \({\hat{u}}\), the channel estimate, \({\hat{\varvec{H}}}(g_p, k)\) for the pilot block is obtained using, for example, a least squares (LS) method, where

$$\begin{aligned} {\hat{\varvec{H}}}(g_p, k)&= {\varvec{Y}}(g_p, k) \Big / \left( {\varvec{P}}^{{\hat{u}}}(k) {\varvec{X}}(g_p, k) \right) \nonumber \\&= \frac{{\varvec{H}}(g_p, k) {\varvec{X}}(g_p, k) {\varvec{P}}^{\bar{u}}(k) + \varvec{V}(g_p, k)}{\left( {\varvec{P}}^{{\hat{u}}}(k) {\varvec{X}}(g_p, k) \right) }. \end{aligned}$$
(13)

At high SNR, the additive terms in (13) are negligible. Thus, the expression for \({\hat{\varvec{H}}}(g_{p}, k)\) is reduced to

$$\begin{aligned} {\hat{\varvec{H}}}(g_p, k)&\approx \frac{{\varvec{H}}(g_p, k) {\varvec{X}}(g_p, k) {\varvec{P}}^{\bar{u}}(k)}{\left( {\varvec{P}}^{{\hat{u}}}(k) {\varvec{X}}(g_p, k) \right) } \nonumber \\&\approx {\varvec{H}}(g_p, k) {\varvec{P}}^{\bar{u}}(k) \Big / {\varvec{P}}^{{\hat{u}}}(k). \end{aligned}$$
(14)

From (14), it can be seen that when \({\hat{u}} = \bar{u}\) (i.e. the ideal case of perfect SI estimation), then

$$\begin{aligned} {\hat{\varvec{H}}}(g_p, k) \approx {\varvec{H}}(g_p, k). \end{aligned}$$
(15)

Since a time-invariant channel is assumed, then estimate of the channel gain on each data block, \({\hat{\varvec{H}}}(g_d, k)\) is approximately equivalent to \({\hat{\varvec{H}}}(g_p, k)\) i.e.,

$$\begin{aligned} {\hat{\varvec{H}}}(g_d, k) \approx {\hat{\varvec{H}}}(g_p, k). \end{aligned}$$
(16)

Now, using \({\hat{\varvec{H}}}(g_d, k)\) and the SI estimate \({\hat{u}}\), a channel equalized data term, \({\hat{{\varvec Y}}}(g_d, k)\) is computed from

$$\begin{aligned} {\hat{{\varvec Y}}}(g_d, k) = {\varvec{Y}}(g_d, k) \Big / \left( {\hat{\varvec{H}}}(g_d, k) {\varvec{P}}^{{\hat{u}}}(k) \right) . \end{aligned}$$
(17)

3.2.2 QAM Demodulation

Using a form of ML decision criterion, an estimate of the transmitted data, \({\hat{{\varvec X}}}(g_d, k)\) is obtained from \({\hat{{\varvec Y}}}(g_d, k)\) through [15]

$$\begin{aligned} {\hat{{\varvec X}}}(g_d, k)&= \underset{D[q] \in {\mathbb {Q}}}{\text {min}} \Big |{\hat{{\varvec Y}}}(g_d, k) - D[q]\Big |^2. \end{aligned}$$
(18)

By assuming a QAM modulation at the transmitter, \({\mathbb {Q}}\) is a set of Q QAM constellation points D[q] for \(1 \le q \le Q\) such that \({\hat{{\varvec X}}}(g_d, k) \in {\mathbb {Q}}\).

4 Embedded Coded Modulation

The ECM method is now described. ECM is an alternative pilot-assisted SLM–OFDM data decoding procedure that requires no SI estimation. Table 1 summarises the fundamental differences between conventional SLM–OFDM data decoding and the ECM decoding method.

In the ECM method, a term denoted by \(\tilde{{\varvec{H}}}(g_p, k)\) is obtained from the received pilot block, using

$$\begin{aligned} {\tilde{\varvec{H}}}(g_p, k)&= {\varvec{Y}}(g_p, k) \Big / {\varvec{X}}(g_p, k) \nonumber \\&= \frac{\left( {\varvec{H}}(g_p, k){\varvec{X}}(g_p, k){\varvec{P}}^{\bar{u}}(k) + \varvec{V}(g_p, k) \right) }{{\varvec{X}}(g_p, k)}. \end{aligned}$$
(19)

As before, at high SNR, the additive noise terms in (19) are negligible. Thus, an approximate expression for \({\tilde{\varvec{H}}}(g_p, k)\) becomes

$$\begin{aligned} {\tilde{\varvec{H}}}(g_p, k)&\approx {\varvec{H}}(g_p, k){\varvec{P}}^{\bar{u}}(k). \end{aligned}$$
(20)

Similarly, by applying \({\tilde{\varvec{H}}}(g_p, k)\) and by assuming a time-invariant channel, a simple channel mitigation procedure is implemented on each data block to produce

$$\begin{aligned} {\hat{{\varvec Y}}}(g_d, k)&= {\varvec{Y}}(g_d, k) \Big / {\tilde{\varvec{H}}}(g_p, k) \nonumber \\&= \frac{\left( {\varvec{H}}(g_d, k){\varvec{X}}(g_d, k){\varvec{P}}^{\bar{u}}(k) + \varvec{V}(g_d, k) \right) }{{\tilde{\varvec{H}}}(g_p, k)}. \end{aligned}$$
(21)
Table 1 Fundamental differences between conventional data decoding and ECM method
Full size table

As before, at high SNR, the additive noise terms in (21) are considered to be negligible. Hence, from the simplified expression in (20), the expression for \({\hat{{\varvec Y}}}(g_{d}, k)\) is reduced to

$$\begin{aligned} {\hat{{\varvec Y}}}(g_d, k)&\approx \frac{\left( {\varvec{H}}(g_d, k){\varvec{X}}(g_d, k){\varvec{P}}^{\bar{u}}(k)\right) }{{\varvec{H}}(g_p, k){\varvec{P}}^{\bar{u}}(k) }\nonumber \\&\approx \frac{\left( {\varvec{H}}(g_d, k){\varvec{X}}(g_d, k)\right) }{{\varvec{H}}(g_p, k)}. \end{aligned}$$
(22)

For time-invariant channel conditions where \({\varvec{H}}(g_{d}, k) \approx {\varvec{H}}(g_{p}, k)\), the expression for \({\hat{{\varvec Y}}}(g_{d}, k)\) is further reduced to

$$\begin{aligned} {\hat{{\varvec Y}}}(g_d, k)&\approx {\varvec{X}}(g_d, k). \end{aligned}$$
(23)

It can be seen from (22) that term SLM term \({\varvec{P}}^{\bar{u}}(k)\) is present on both numerator and denominator expressions, and is inherently cancelled with no SI estimation. Hence, the ECM method requires no SI estimation. The expression in (22) also implies that if \({\varvec{P}}^{\bar{u}}(k) =\) 1 (i.e. with no SLM), the ECM data decoding procedures remain the same. Therefore, the same ECM data decoding procedure is implemented regardless of whether SLM is used or not. The final stage of data decoding involves standard QAM demodulation on the channel equalized data term, \({\hat{{\varvec Y}}}(g_d, k)\) as previously described in (18).

5 Simulation Results and Computational Complexity

This section presents the comparison of the BER performance between the FDC SI estimation scheme and the ECM data decoding method, using a block-type frame structure. It also shows the PAPR reduction performance of the SLM method when applied to a block-type frame structure. The PAPR reduction performance is evaluated using the well-known complementary cumulative distribution function (CCDF) metric. The final aspect of this section compares the computational complexity of the ECM method against conventional SLM–OFDM receiver, which normally requires some form of SI estimation.

5.1 CCDF Results

The CCDF gives the probability of a PAPR value exceeding a certain threshold level \(\gamma\) and is computed from the original PAPR values (before SLM) and the resulting PAPR after SLM according to [19]. To evaluate the CCDF, 16—QAM data modulation is considered.

Fig. 4
figure 4

PAPR reduction of SLM in a block-type frame

Full size image

Using the OFDM architecture described in Fig. 1 and the block-type frame structure described in Figs. 2 and 4 shows CCDF comparisons with U set to 4 and 8 when \(N_{v} = 127\) and \(N = 1024\). As expected, results in Fig. 4 show that the PAPR reduction performance is improved as U is increased from 4 to 8. For instance, at a CCDF level of 0.01%, the PAPR reduction gain is estimated to be around 1.8and 2.5 dB when U is set to 4 and 8 respectively.

Table 2 Power-delay profiles of indoor JTC channels \({\varvec{A}}\) and \({\varvec{B}}\)
Full size table

5.2 BER Results

Simulations consider OFDM transmissions over two indoor residential channel (frequency selective) models, namely: \({\varvec{A}}\) and \({\varvec{B}}\) described by the joint technical committee (JTC) [24] with root mean square delay spread of 18 and 68 ns respectively. Table 2 shows the power-delay profiles of these two fading channels.

To evaluate the BER, simulations use parameter values outlined in Table 3.

Table 3 Simulation parameter values
Full size table
Fig. 5
figure 5

BER comparison with no HPA i.e. IBO = \(\infty\)

Full size image
Fig. 6
figure 6

BER comparison with IBO = 6 dB

Full size image

The BER is evaluated with and without the presence of non-linear amplifier distortion, characterised by the well-known input back off (IBO) parameter. The IBO is expressed as [23]

$$\begin{aligned} \text {IBO (dB)} = 10 \log _{10} \left( \frac{P_{sat}}{P_{avg}}\right) \end{aligned}$$
(24)

where \(P_{sat}\) and \(P_{avg}\) denote the input saturation power and mean power of the input signal respectively. In simulations, the non-linear high power amplifier (HPA) distortion is modelled using the well-known Rapp’s model described in [25]. The transfer function of the Rapp model is given by [25]

$$\begin{aligned} {\varvec{y}}(n) = \frac{{\varvec{x}}(n)}{\left[ 1 + \left( \frac{\left| {\varvec{x}}(n)\right| }{A_{sat}}\right) ^{2\rho }\right] ^{1/2\rho }} \end{aligned}$$
(25)

where \({\varvec{x}}(n)\) and \({\varvec{y}}(n)\) respectively represent the input/output signal of the amplifier, \(A_{sat}\) is the amplifier’s output saturation magnitude and \(\rho\) is the smoothing factor which controls the HPA’s transition from linear to saturation region i.e. the higher the value of \(\rho\), the sharper the transition from linear to non-linear operating region of the amplifier. Similar to [25], the smoothing parameter, \(\rho\) is set to 3.

With no HPA distortion, Fig. 5 shows the BER comparisons between the considered methods. Figure 6 shows similar results in the presence of amplifier distortion. Results in Figs. 5 and 6 show that the ECM method produces similar BER performance as the conventional method that performed SI estimation.

In both channel conditions and with a lower order data modulation i.e. 4—QAM, comparisons of results in Figs. 5 and 6 show that even in the presence of the considered level (IBO = 6 dB) of amplifier distortion, there is little or no change in the BER performance. However, with a higher order modulation such as 16—QAM, similar level of amplifier distortion causes small BER degradation (see Fig. 6) relative to the case when there is no HPA distortion (see Fig. 5). Results suggest the ECM method is therefore an attractive solution because it requires no SI estimation and it achieves identical data performance when compared to the conventional data decoding approach.

Though not presented, in the case of 64—QAM, the ECM technique produces identical BER performance as other methods.

5.3 Computational Complexity

This section describes the computational advantage of the ECM method over a conventional SLM–OFDM receiver that normally requires some form of SI estimation.

The computational complexity of the ECM approach is related to (19) and (21). The expressions in (19) and (21) respectively involves \(N_{v}\) and \(N_{v} \times (G-1)\) CMs. Hence, the ECM method requires a total \(G \times N_{v}\) CMs, which is identical to the sum of the computational complexity of (13) and (17). Therefore, the use of the ECM method completely eliminates the computational complexity of SI estimation. This is one of the significant advantages of the ECM data decoding procedure over conventional methods.

The percentage reduction in the computational complexity of the two methods is evaluated using the well-known computational complexity reduction ratio (CCRR) described in [15]. Given than \({C_{\text {conv}}}\) and \({C_{\text {ecm}}}\) respectively represent the computational complexity of conventional SLM–OFDM and an ECM based receiver, the CCRR is computed as [15]

$$\begin{aligned} \text {CCRR} = \left( 1 - \frac{{C_{\text {ecm}}}}{{C_{\text {conv}}}}\right) \times 100\%. \end{aligned}$$
(26)

The CCRR value represents the amount (expressed as a \(\%\)) of reduction in computational complexity offered by the ECM method relative to the conventional approach. With \(N_{v} = 127\), Table  4 shows the CCRR values as a function of U and G. Note that the CCRR values are computed based on number of CMs only since the ECM method requires no CA operation.

Results in Table 4 show that for a given value of G, the computational advantage of the ECM method increases as U increases. For instance, when \(G = 4\), the CCRR value is 50% when \(U = 2\) and 80% when U is 8. This is because unlike the conventional method, the computational complexity of the ECM approach is independent of the value of U. However, for a given of U, the computational advantage of the ECM method decreases as G increases because the computational complexity of both methods is dependent on the value of G. As an example, when \(U = 8\), the corresponding CCRR values when \(G = 2\) and 8 are 88 and 66% respectively. Therefore, the ECM method has a significant computational advantage over the conventional data decoding approach.

Table 4 Comparison of CCRR values as a function of U and G
Full size table

6 Conclusions

Using a block-type frame structure and conventional SLM PAPR reduction, this paper presented and investigated the data decoding performance of an alternative SLM–OFDM data decoding procedure called ECM. The ECM method required no SI estimation at the receiver. Hence, the use of ECM eliminated both the computational complexity and implementation issues associated with SI estimation. Under two indoor channel conditions, the ECM achieved similar data decoding performance to conventional SLM–OFDM receiver that uses FDC based SI estimation and when there is perfect SI estimation, even in the presence of non-linear amplifier distortions.

In future work, the implementation of the ECM method within a different frame structure used in, for example, LTE systems will be considered.