1 Introduction

By considering the properties of code division multiple access (CDMA) and orthogonal frequency-division multiplexing (OFDM), a hybrid multiple access technique is proposed in [1, 2]. This technique is called multicarrier-code division multiple access (MC-CDMA). MC-CDMA inherits the advantages of both CDMA and OFDM. Therefore, it has tolerance against frequency selective channels. Moreover, these systems have tolerance against ISI (intersymbol interference) and ICI (intercarrier interference) through the use of a cyclic prefix and equalization [3]. Also, MC-CDMA has an inherent frequency diversity because one symbol can be transmitted through different subcarriers. For these reasons, MC-CDMA is an interesting option for future broadband mobile communication systems [4,5,6,7].

Simulations and analysis of MC-CDMA systems were made [8,9,10,11,12], but only considering the own cell interference (or multiple access interference—\({\mathcal {MAI}}\)) and BPSK modulation. However, in practice, the performance of wireless cellular systems is not only limited by \({\mathcal {MAI}}\), but also by co-channel interference (\({\mathcal {CCI}}\)) due to the channels reuse. Therefore, the \({\mathcal {CCI}}\) is an important parameter to be considered in the performance evaluation of cellular systems. Also, wireless technologies aim is to increase the system throughput, thus, high order modulations (like M-QAM) should be used in the networks [13]. Moreover, it is important to accept that uplink interference is greater than downlink interference [14].

Although the bit error rate (BER) provides important information to guarantee the quality of a communications service, in practice, designers of cellular networks also deal with a trade-off between mitigating interference and increasing the spectral efficiency, focusing on the improvement of data rates and considering that the radio spectrum is a limited and expensive resource. Thus, the analysis of spectral efficiency of a cellular network is crucial to optimize the available bandwidth.

Therefore, the aim of this paper is to evaluate the mean spectral efficiency of cellular systems uplink employing the MC-CDMA technique, considering not only \({\mathcal {MAI}}\), but also \({\mathcal {CCI}}\). Also, the considered system employs a linear antenna array at the base stations, frequency domain interleaving, maximal ratio combining (MRC), adaptive modulation, perfect power control and a cyclic prefix large enough to eliminate the effects of ISI and ICI. The channel considers the presence of additive white Gaussian noise (AWGN), exponential path-loss and slow-frequency selective Rayleigh fading.

The paper is organized as follows. A description of the cellular system is discussed in Sect. 2. An analytical expression for the mean signal-to-interference ratio is obtained in Sect. 3. Section 4 describes the procedure to calculate the cell coverage radius in the system. An analytical expression to calculate the mean spectral efficiency is determined in Sect. 5. Section 6 shows the numerical results. Finally, the conclusions are made in Sect. 7.

2 System Description

2.1 Cellular System

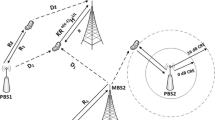
Consider the cellular system shown in Fig. 1, where each cell has a base station (BS) in its center. The distance (D) between two base stations located in the center of two co-cells is given by [15]:

$$\begin{aligned} D=R\sqrt{3{\mathcal {F}}} \end{aligned}$$
(1)

where R is the outer radius of the cell and \({\mathcal {F}}\) is the channel reuse factor, which establishes the number of cells in a cluster. A cluster is a group of contiguous cells which collectively use the complete set of available channels in the system. Also, almost all \({\mathcal {CCI}}\) is produced by the users in the first layer of co-cells [16], therefore, only this layer is considered in the analysis.

Fig. 1
figure 1

Cellular system with \({\mathcal {F}}=3\)

Full size image

2.2 Spatial Distribution of the Users

Suppose that \(N_{t}\) users are uniformly distributed in each cell, which has a circular shape, as shown in Fig. 2. The circular shape with an inner radius guarantee convergence in the average value of the received power. The distance between k-th user and the center of his cell is represented by \(r_{k}\), with \(R_{0} \le r_{k} \le R\), where \(R_{0}\) and R are the inner and outer radius of the cell, respectively. Also, \(\theta _{k}\) is the angle formed by the horizontal axis and the position of the k-th user. As the users are uniformly distributed in the cell area, it is easy to show that the probability density functions (PDF) of the independent random variables r and \(\theta\) are, respectively, given by:

$$\begin{aligned} f_{R}(r)=\frac{2r}{R^{2}-R_{0}^{2}}, \;\;\; R_{0}\le r \le R \end{aligned}$$
(2)

and

$$\begin{aligned} f_{\theta }(\theta )=\frac{1}{2\pi }, \;\;\; 0\le \theta \le 2\pi \end{aligned}$$
(3)

Employing geometry, it is possible to show that the distance between the k-th interferer user in a co-cell and the BS in the cell of interest can be written as:

$$\begin{aligned} d_{k}=\sqrt{\left[ D+r_{k}\cos {\theta _{k}}\right] ^{2}+\left[ r_{k} \sin {\theta _{k}}\right] ^{2}} \end{aligned}$$
(4)
Fig. 2
figure 2

Spatial distribution of the users in the cells

Full size image

2.3 Characteristics of Transmitters and Receivers

The MC-CDMA technique proposed in [1] is employed. A system with L data transmission subcarriers and \(L_{p}\) cyclic prefix subcarriers is considered. Therefore, the bandwidth and power increase factor (\(\rho\)) due to the cyclic prefix can be defined as:

$$\begin{aligned} \varrho =1+\frac{L_{p}}{L} \end{aligned}$$
(5)

All \(N_{t}\) users in the cell are distributed in b blocks. For each block are allocated G subcarriers. Thereby, the total number of subcarriers for data transmission can be written as \(L=bG\). For simplicity, we assume that the number of users in each block (\(N_{u}\)) is the same for all blocks, thus, \(N_{t}=bN_{u}\). Therefore, the \({\mathcal {MAI}}\) for each user is produced by the other \(N_{u}-1\) users in the same cell employing the same G subcarriers.

Figure 3 shows the transmitter of k-th user. In the transmitter of MC-CDMA, one data symbol is transcribed into G parallel copies. Then, each copy is multiplied by a chip from a spreading sequence of length G, where G is also the spreading factor. The chip duration is the same as the symbol duration (\(T_{s}\)). These outputs are modulated into G orthogonal subcarriers. Also, in order to obtain frequency diversity, the frequency separation between two adjacent subcarriers allocated to the same user, \(\Delta _{fe}\), should be greater than the channel coherence bandwidth, \((\Delta _{f})_{c}\), therefore experiencing independent fading in each subcarrier. For this purpose, a frequency domain interleaving is used in the transmitter. Its block diagram is shown in Fig. 4, where it is considered a single user in each block of G subcarriers for better understanding. Finally, an upconverter is employed in the transmitter in order to introduce the carrier. The parameters shown in Fig. 3 will be more detailed in Sect. 3.

Fig. 3
figure 3

Transmitter of the k-th user

Full size image
Fig. 4
figure 4

Frequency domain interleaving

Full size image

Figure 5 shows the k-th user receiver at the BS. It employs an uniform linear antenna array formed by \(\varUpsilon\) equally spaced antennas. Thus, the G signals from the different subcarriers and the \(\varUpsilon\) signals from the antennas are combined employing a Maximal Ratio Combining (MRC) stage. Therefore, it is assumed a perfect estimation of amplitudes and phases of the received signals. The specific parameters shown in Fig. 5 will be more detailed in Sect. 3.

Fig. 5
figure 5

Receiver of k-th user at BS

Full size image

Perfect power control is also considered. This control is performed by altering the output power of each user equipment (UE) in the cell in order to receive the same power for all users in the BS. With this strategy, the output power for each UE can be written as:

$$\begin{aligned} P_{t}=P_{r}r^{\beta } \end{aligned}$$
(6)

where \(P_{r}\) is the constant received power by BS and r is the distance between UE and BS in its cell. The factor \(r^{\beta }\) allows the transmitted signals by UEs reach the BS with the same power level, because, as is discussed in the following, the path-loss increases as a power of distance.

A slow and frequency selective Rayleigh fading channel with mean square value \(\overline{\alpha ^{2}}\) is supposed. Also, it is considered a channel with exponential path-loss. Thus, the received power (\(P_{r}\)) can be written as:

$$\begin{aligned} P_{r}=P_{t}d^{-\beta } \end{aligned}$$
(7)

where \(P_{t}\) is the output power of UE, d is the distance between transmitter and receiver and \(\beta\) is the propagation path-loss exponent, which depends on the characteristics of the propagation environment and it has values between 2 and 6. Typically, \(\beta = 4\) is employed for urban environments [15].

Finally, adaptive modulation is used. We consider that this technique employs 4-QAM, 16-QAM and 64-QAM.

3 Mean Signal-to-Interference Ratio

In this section, an expression for the mean Signal-to-Interference Ratio (SIR) is determined. Remember that an efficient implementation of OFDM-based systems is through the Fast Fourier Transform (FFT). However, for an easier analysis, an analog equivalent of this technique is employed.

The uplink of a cellular system has asynchronous nature because the signals of the users are asynchronous and because their distances to BS are different. Therefore, asynchronous random spreading sequences are considered in the analysis. For these sequences, the mean and the mean squared value of their cross-correlation have closed forms. Thus, it has zero mean and mean squared equals to \(\frac{2}{3G}\) [17]. Moreover, in [18], it was shown that random spreading sequences and Walsh spreading sequences have same performance when a frequency domain interleaving is employed.

The transmitted signal by k-th user during the i-th symbol time interval can be written as:

$$\begin{aligned} \begin{aligned} s_{k}(t)=&\frac{1}{\sqrt{G}}\sum _{m=1}^{G}c_{k,m} \left\{ {\mathcal {S}}_{P,k}\cos \left[ 2\pi (f_{c}+m\Delta _{f_{e}})t +\vartheta _{k}\right] \right. \\&\left. -{\mathcal {S}}_{Q,k}\sin \left[ 2\pi (f_{c} +m\Delta _{f_{e}})t+\vartheta _{k}\right] \right\} p(t-iT_{s}) \end{aligned} \end{aligned}$$
(8)

where \(c_{k,m}\) is the m-th chip of k-th user spreading sequence, whose amplitudes are \(c_{k,m}=\pm 1\), \(f_{c}\) is the carrier frequency, \(\Delta _{f_{e}}\) is the frequency separation between two adjacent subcarriers allocated to the same user when frequency interleaving is employed. Therefore, it is considered that \(\Delta _{f_{e}}>(\Delta _{f})_{c}\), where \((\Delta _{f})_{c}\) is the channel coherence bandwidth. Also, the subcarrier bandwidth is given by \(B_{sub}=\frac{1}{T_{s}}\), where \(T_{s}\) is the symbol duration. Furthermore, \(\vartheta _{k}\) is the random phase produced in the modulation stage of k-th user, p(t) is a baseband pulse of duration \(T_{s}\) and the factor \(\frac{1}{\sqrt{G}}\) normalizes the transmitted power per subcarrier. Finally, the transmitted symbol, \({\mathcal {S}}_{k}\), can be written as:

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_{k}&={\mathcal {S}}_{P,k}+\text {j}{\mathcal {S}}_{Q,k}\\&=\pm (2s-1)A_{k}\pm \text {j}(2s-1)A_{k}, \;\;\;\; s=\left\{ 1,2,\ldots ,\sqrt{M}/2\right\} \end{aligned} \end{aligned}$$
(9)

where \({\mathcal {S}}_{P,k}\) and \({\mathcal {S}}_{Q,k}\) are the in-phase and in-quadrature components of the transmitted symbol, respectively, \(\text {j}=\sqrt{-1}\), \(A_{k}\) is the signal amplitude and M is the modulation order.

In order to evaluate the interference effects, it is enough to consider only a block of G subcarriers, because interference occurs between users using the same radio resources. Therefore, the received signal at the a-th antenna in the BS during the i-th symbol time interval is given by:

$$\begin{aligned} \begin{aligned} r_{a}(t)=&\frac{1}{\sqrt{\varUpsilon G}}\sum _{m=1}^{G}\sum _{k=1}^{N_{u}} \alpha _{k,a,m}c_{k,m}p(t-iT_{s}-\tau _{k}) \\&\times \left\{ {\mathcal {S}}_{P,k}\cos [2\pi (f_{c}+m\Delta _{f_{e}})t +\phi _{k,a,m}]-{\mathcal {S}}_{Q,k}\sin [2\pi (f_{c}+m\Delta _{f_{e}})t +\phi _{k,a,m}] \right\} \\&+\frac{1}{\sqrt{\varUpsilon G}}\sum _{m=1}^{G}\sum _{\ell =1}^{N_{i}} \alpha _{\ell ,a,m}c_{\ell ,m}p(t-iT_{s}-\tau _{\ell })\\&\times \left\{ {\mathcal {S}}_{P,\ell }\cos [2\pi (f_{c}+m\Delta _{f_{e}})t +\phi _{\ell ,a,m}]-{\mathcal {S}}_{Q,\ell }\sin [2\pi (f_{c} +m\Delta _{f_{e}})t+\phi _{\ell ,a,m}] \right\} \\&+n(t) \end{aligned} \end{aligned}$$
(10)

where the factor \(\frac{1}{\sqrt{\varUpsilon }}\) normalizes the received power per antenna, \({N_{u}}\) is the number of users in the cell of interest employing a block of G subcarriers, \({N_{i}}\) is the number of co-cell interferers, \(\alpha _{k,a,m}\) and \(\alpha _{\ell ,a,m}\) are fading amplitudes experienced by the signals arriving at a-th antenna from the n-th subcarrier for users k and \(\ell\), respectively, \(\tau _{k}\) and \(\tau _{\ell }\) are the time delay of k-th and \(\ell\)-th users, respectively, which are uniformly distributed over \([0,T_{s})\), \(\phi _{k,a,m}\) is the received phase, which can be considered uniformly distributed over \([0,2\pi )\) due to the uniformly distribution of users in the cell area and the random phases introduced by the channel.

The first term of (10) is the signal arriving at BS from their own cell, the second term is the signal arriving at BS from the co-cells and the third term n(t) is the AWGN with zero mean and double-sided power spectral density \(N_{0}/2\). Also, it is considered that the separation between two adjacent antennas is \(d=\lambda /2\), where \(\lambda\) is the wavelength and c is light speed in vacuum. Thus, signals arriving at two different antennas of the array are affected by independent fadings [15]. Therefore, \(\alpha _{k,a,m}\) and \(\alpha _{\ell ,a,m}\) are considered to be independent and identically distributed (i.i.d) for different k, \(\ell\), a and m. Similarly, \(\phi _{k,a,m}\) and \(\phi _{\ell ,a,m}\) are i.i.d for different k, \(\ell\), a and m.

At k-th user receiver at BS, the decision variable at instant \(t_{i}+T_{s}\) is:

$$\begin{aligned} \begin{aligned} z_{k}=&\sum _{a=1}^{\varUpsilon }\sum _{n=1}^{G}\hat{\alpha }_{k,a,n} c_{k,n}\frac{1}{T_{s}}\int _{t_{i}}^{t_{i}+T_{s}}r_{a}(t)p(t-\hat{\tau }_{k})\\&\times \left\{ \cos \left[ 2\pi (f_{c}+n\Delta _{f_{e}})t +\hat{\phi }_{k,a,n}\right] -\sin \left[ 2\pi (f_{c}+n\Delta _{f_{e}})t +\hat{\phi }_{k,a,n}\right] \right\} dt \\ =&{\mathcal {D}}+{\mathcal {MAI}}+{\mathcal {CCI}}+\eta \end{aligned} \end{aligned}$$
(11)

where \(\hat{\alpha }_{k,a,n}\) is the estimated fading amplitude of n-th subcarrier at a-th antenna, \(c_{k,n}\) is the n-th chip from the spreading sequence of k-th user, \(\hat{\phi }_{k,a,n}\) is the estimated phase of n-th subcarrier at a-th antenna, \(\hat{\tau }_{k}\) represents the estimated delay of k-th user and \(\frac{1}{T_{s}}\) is a normalization factor. The received sample can be split into four terms: the first term, \({\mathcal {D}}\), is the desired signal from k-th user, the second term is the \({\mathcal {MAI}}\), the third term is the \({\mathcal {CCI}}\) and the fourth term, \(\eta\), is the noise sample.

In the following, we consider p(t) rectangular with duration \(T_{s}\) and perfect estimation of \(\alpha _{k,a,n}\), \(\phi _{k,a,n}\) and \(\tau _{k}\). Without loss of generality, user 1 is considered the target user. Substituting the first term of (10) in (11) and noting that the terms for \(m \ne n\) are zero due to the orthogonality between subcarriers, the in-phase (\({\mathcal {D}}_{P}\)) and in-quadrature (\({\mathcal {D}}_{Q}\)) components of the desired signal from target user are, respectively, given by:

$$\begin{aligned} {\mathcal {D}}_{P} =& \frac{{\mathcal {S}}_{P,1}}{2\sqrt{\varUpsilon G}} \sum _{a=1}^{\varUpsilon }\sum _{n=1}^{G}\alpha _{1,a,n}^{2} \end{aligned}$$
(12)
$$\begin{aligned} {\mathcal {D}}_{Q} =& \frac{{\mathcal {S}}_{Q,1}}{2\sqrt{\varUpsilon G}}\sum _{a=1}^{\varUpsilon } \sum _{n=1}^{G}\alpha _{1,a,n}^{2} \end{aligned}$$
(13)

Note that (12) and (13) are a sum of \(\varUpsilon G\) independent squared Rayleigh random variables, so they are a sum of \(2\varUpsilon G\) independent zero mean squared Gaussian random variables. Thus, they can be modeled by a Chi-squared distribution with \(2\varUpsilon G\) degrees of freedom. On this basis and considering the exponential path-loss channel, the mean squared of the desired signal can be written as:

$$\begin{aligned} \overline{{\mathcal {D}}^{2}}=\frac{1}{4}\; \overline{{\mathcal {S}}_{1}^{2}}(\varUpsilon G+1)\overline{{\alpha }^{2}}^{\;2}{r_{1}}^{-\beta } \end{aligned}$$
(14)

where \(r_{1}\) is the distance between the target user and the BS in its cell. Also, we have employed that \(\overline{{\mathcal {D}}^{2}}=\overline{{\mathcal {D}}^{2}_{P}}+\overline{{\mathcal {D}}^{2}_{Q}}\), that \(\overline{\alpha _{1,a,n}^{2}}=\overline{\alpha ^{2}}\) and the mean power of the constellation is given by \(\overline{{\mathcal {S}}_{1}^{2}}=\overline{{\mathcal {S}}_{P,1}^{2}}+\overline{{\mathcal {S}}_{Q,1}^{2}}\).

The \({\mathcal {CCI}}\) is produced by the \(N_{i}\) users in the co-cells employing the same subcarriers that the target user. Using the second term of (10) in (11), it is possible to show that in-phase and in-quadrature components of the \({\mathcal {CCI}}\) are equal and they are given by:

$$\begin{aligned} \begin{aligned} {\mathcal {CCI}}=&\frac{1}{2\sqrt{\varUpsilon G}}\sum _{\ell =1}^{N_{i}} \sum _{a=1}^{\varUpsilon }\sum _{n=1}^{G}\alpha _{1,a,n}\alpha _{\ell ,a,n}c_{1,n}c_{\ell ,n}\\&\times \left\{ {\mathcal {S}}_{P,\ell }\cos \left[ \phi _{\ell ,a,n}-\phi _{1,a,n}\right] -{\mathcal {S}}_{Q,\ell } \sin \left[ \phi _{\ell ,a,n}-\phi _{1,a,n}\right] \right\} \end{aligned} \end{aligned}$$
(15)

The \({\mathcal {CCI}}\) can be modeled by a Gaussian random variable conditioned to the fading amplitudes of the target user. Thus, the \({\mathcal {CCI}}\) components have zero mean because \(\overline{c_{1,n}c_{\ell ,n}}=0\), \(\overline{\cos (\phi _{\ell ,a,n}-\phi _{1,a,n})}=0\) and \(\overline{\sin (\phi _{\ell ,a,n}-\phi _{1,a,n})}=0\). Also, both \({\mathcal {CCI}}\) components have variance given by:

$$\begin{aligned} \text {Var}[{\mathcal {CCI}}|\alpha _{1,a,n}]=\frac{1}{12\varUpsilon G}\overline{{\mathcal {S}}_{\ell }^{2}}N_{i}\;\overline{\alpha _{\ell ,a,n}^{2}} \sum _{a=1}^{\varUpsilon }\sum _{n=1}^{G}\alpha _{1,a,n}^{2} \end{aligned}$$
(16)

where perfect power control is considered, i.e., \(A_{1}=A_{2}=\cdots =A_{N_{i}}\). Also, it was employed the mean squared value of the asynchronous random spreading sequences, also that \(\overline{\cos ^{2}(\phi _{\ell ,a,n}-\phi _{1,a,n})}=1/2\), that \(\overline{\sin ^{2}(\phi _{\ell ,a,n}-\phi _{1,a,n})}=1/2\) and that \(\overline{\cos [\phi _{\ell ,a,n}-\phi _{1,a,n}]\sin [\phi _{\ell ,a,n}-\phi _{1,a,n}]}=0\). The \(\overline{\alpha _{\ell ,a,n}^{2}}\) factor represents the mean squared of the fading amplitudes of the co-cell interferers.

Employing (16), the mean received power from the \({\mathcal {CCI}}\) can be written as:

$$\begin{aligned} \overline{\text {Var}[{\mathcal {CCI}}|\alpha ]} =\frac{1}{12}\;\overline{{\mathcal {S}}_{\ell }^{2}}N_{i} \overline{{\alpha }^{2}}^{\;2}\; \overline{{d}^{-\beta }} \end{aligned}$$
(17)

where we have employed that \(\overline{\alpha _{1,a,n}^{2}}=\overline{\alpha _{\ell ,a,n}^{2}}=\overline{\alpha ^{2}}\). Also, \(\overline{{d}^{-\beta }}\) represents the power decay average for the interferer users signals in the co-cells.

Considering perfect power control, the mean SIR can be written as:

$$\begin{aligned} \frac{S}{I}=\frac{\overline{{\mathcal {D}}^{2}} \;{r_{1}}^{\beta }}{\;\overline{ \text {Var}[{\mathcal {CCI}}|\alpha ]\;r^{\beta }}\;} =3\frac{(\varUpsilon G+1)}{6\overline{{d}^{-\beta }{r}^{\beta }}} \end{aligned}$$
(18)

where it is considered a predominant interferer in each co-cell of the first layer, i.e., \(N_{i}= 6\). Also, it is considered that the interferer users and the target user employ the same modulation, i.e., \(\overline{{\mathcal {S}}_{1}^{2}}=\overline{{\mathcal {S}}_{\ell }^{2}}\). Finally, the factor \(\overline{r^{\beta }}\) represents the power increase average for interferer users due to power control. From (1), (2), (3) and (4), the factor \(\overline{{d}^{-\beta }{r}^{\beta }}\) can be obtained by employing:

$$\begin{aligned} \overline{{d}^{-\beta }}\overline{{r}^{\beta }}=\int _{R_{0}}^{R}\int _{0}^{2\pi } \left[ \frac{1}{r}\sqrt{(R\sqrt{3{\mathcal {F}}}+r\cos {\theta })^{2}+(r\sin {\theta })^{2}}\right] ^{-\beta }f_{R}(r)f_{\theta }(\theta )drd\theta \end{aligned}$$
(19)

4 Cell Radius

In this section, our aim is to establish a procedure to calculate the coverage radius of the cell. This radius determines the cell region where the users have coverage to guarantee a maximum mean BER. Accordingly, the coverage radius depend of the modulation schemes and the interference levels. We can consider that \(R_{0}\;\le R_{c}^{(M)}\le R\), where \(R_{c}^{(M)}\) is the coverage radius as a function of the modulation order. The procedure to calculate the coverage radius is described below:

  1. 1.

    First, the maximum mean BER (\(\overline{P_{b}}\)) necessary to guarantee the quality of a communication service should be known. Also, the operating characteristics of the MC-CDMA cellular system as the number of antennas in the array (\(\varUpsilon\)), the channel reuse factor (\({\mathcal {L}}\)) and the maximum output power of the UE (\(P_{t,max}\)) must be established. The inner (\(R_{0}\)) and outer (R) cell radius must be known, which, typically depend of the antenna height, the downtilt angle and the vertical beamwidth. Regarding to the channel, it is necessary to know the propagation path-loss exponent (\(\beta\)).

  2. 2.

    A parameter related to the \({\mathcal {MAI}}\) is also necessary. This parameter is called load factor [18], which describes the ratio between the number of own cell interferer users and the spreading factor, i.e.:

    $$\begin{aligned} {\mathcal {L}}=\frac{N_{u}-1}{G} \end{aligned}$$
    (20)

    where \(0\le {\mathcal{L}} < 1\).

  3. 3.

    Next, the mean SIR must be calculated through (18) and (19).

  4. 4.

    Beginning with the highest order modulation, the mean normalized signal-to-noise ratio (\(E_{b}/N_{0}\)) necessary to guarantee the maximum mean BER established in step 1 is obtained recursively from [19]:

    $$\begin{aligned} \overline{P_{b}}=\frac{2}{\sqrt{M}\log _{2} \sqrt{M}}\sum _{\ell =1}^{\log _{2} \sqrt{M}}\;\sum _{\kappa =0}^{(1-2^{-\ell })\sqrt{M}-1}\left\{ (-1)^{\left\lfloor \frac{\kappa 2^{\ell -1}}{\sqrt{M}}\right\rfloor }\left( 2^{\ell -1} -\left\lfloor \frac{\kappa 2^{\ell -1}}{\sqrt{M}}+\frac{1}{2}\right\rfloor \right) I\right\} \end{aligned}$$
    (21)

    with

    $$\begin{aligned} I &= \left( \frac{1-\mu }{2}\right) ^{\varUpsilon G}\,\sum _{i=0}^{\varUpsilon G-1} \left( {\begin{array}{c}\varUpsilon G-1+i\\ i\end{array}}\right) \left( \frac{1+\mu }{2}\right) ^{i}\\ \mu &= \sqrt{\frac{\overline{\gamma _{b}}}{\varUpsilon Gw+\overline{\gamma _{b}}}}, \;\;\; w=\frac{2(M-1)}{3(\kappa +1)^{2}}\\ \overline{\gamma _{b}} &= \frac{1}{\frac{1}{\log _2 M}\varvec{\frac{N_{0}}{E_{b}}}\frac{1}{\;\overline{\alpha ^{2}}\;} +\frac{2}{3}\frac{{\mathcal {L}}}{\varUpsilon }+2\left( \frac{\varUpsilon G+1}{\varUpsilon G}\right) \frac{I}{S}} \end{aligned}$$

    where \(\lfloor x \rfloor\) represents floor operation and \(\overline{\gamma _{b}}\) is known as the mean signal-to-noise-plus-interference ratio.

  5. 5.

    Then, the received power by the BS \((P_{r})\) from the target user is obtained. The ratio between the received power and \(E_{b}/N_{0}\) ratio is given by:

    $$\begin{aligned} P_{r}=N_{0}R_{b}\frac{E_{b}}{N_{0}} \end{aligned}$$
    (22)

    where \(N_{0}\) is the noise power spectral density and \(R_{b}\) is the bit rate. According to the Nyquist criterion, \(R_{b}\) is directly related to the bandwidth. Because the bit rate is equal to the chip rate in a MC-CDMA system, the bit rate per user can be written as:

    $$\begin{aligned} R_{b}=B_{sub}\log _{2}M\left( r\right) \end{aligned}$$
    (23)

    where \(B_{sub}\) is the subcarrier bandwidth and \(M\left( r\right)\) is the modulation order as a function of the distance between the UE and the BS in its cell.

  6. 6.

    After, the maximum transmitted power allocated to the data subcarriers is obtained through:

    $$\begin{aligned} P_{t,d}=\frac{L_{p}}{L}P_{t,max}=\left( \lceil \varrho \rceil -\varrho \right) P_{t,max} \end{aligned}$$
    (24)

    where \(\lceil x \rceil\) is the ceiling operation and \(\varrho\) was given in (5).

  7. 7.

    Next, the coverage radius for the chosen modulation is determined. For this, we need to calculate the UE transmission power by considering perfect power control:

    $$\begin{aligned} P_{t}=P_{r}r^{\beta } \end{aligned}$$
    (25)

    In (25), vary r from \(R_{0}\) to R. If \(P_{t}\) outperforms \(P_{t,d}\) before r reaches the outer radius (R), then that value of r corresponds to the coverage radius for that modulation.

  8. 8.

    Finally, choose the immediately lower order modulation and repeat all the procedure from step 4. Repeat this until r reaches the value of R or until all modulations have been chosen. There may be scenarios in which no modulation achieves the maximum BER, and therefore the coverage of the cell is void. In other scenarios, even the lowest order modulation does not enable r to reach the value of R. Therefore, the largest coverage radius is smaller than the outer cell radius. In this case, we have a partial cell coverage. For a better understanding consider Fig. 6.

Fig. 6
figure 6

Coverage radius

Full size image

5 Mean Spectral Efficiency

In this section, an expression to evaluate the mean spectral efficiency of the cellular system is obtained. This mean spectral efficiency is given by the ratio between the cell bit rate and the total system bandwidth. Because all \(N_{t}\) simultaneous users in the cell employ subcarriers with the same bandwidth, the mean spectral efficiency of the system can be written as:

$$\begin{aligned} \xi =N_{t}\int _{R_{0}}^{R}\frac{B_{sub}\log _{2}M \left( r\right) }{B_{d}+B_{p}}f_{R}(r)dr \end{aligned}$$
(26)

where \(B_{sub}\) is the subcarrier bandwidth, M(r) is the modulation order as a function of the radius and the total system bandwidth is the data transmission bandwidth (\(B_{d}\)) plus the cyclic prefix bandwidth (\(B_{p}\)).

For a given channel reuse factor, the data transmission bandwidth in each cell is given by \(B_{d}/{\mathcal {F}}\). Now, refer to Fig. 7. Remember that in a MC-CDMA system, the available bandwidth per cell is divided in b blocks formed by G subcarriers. Each block is allocated for a group formed by \(N_{u}\) users. Therefore, it is possible to establish that the data bandwidth per cell is given by:

$$\begin{aligned} \frac{B_{d}}{{\mathcal {F}}}=B_{sub}Gb \end{aligned}$$
(27)
Fig. 7
figure 7

Allocation of the available bandwidth in each cell considering the channel reuse factor (\({\mathcal {F}}\))

Full size image

Employing (26), (27) and considering that the number of users per block (\(N_{u}\)) is the same for all blocks, i.e., \(N_{t}=b N_{u}\), the mean spectral efficiency for the MC-CDMA cellular system can be written as:

$$\begin{aligned} \xi =\frac{1}{{\mathcal {F}}\varrho }\left( {\mathcal {L}}+\frac{1}{G} \right) \int _{R_{0}}^{R}\log _{2}M\left( r\right) f_{R}(r)dr \end{aligned}$$
(28)

For a system employing m different modulations, (28) is obtained as a sum of m integrals, where their limits are given by the coverage radius of each modulation.

6 Numerical Results

In this section, the results shown employ the procedure and expressions established in the previous sections. Thus, the figures show the coverage radius and the mean spectral efficiency of the uplink of a MC-CDMA cellular system for different operating scenarios. The software MATLAB® was employed to do the simulations.

For the calculations, we have employed the parameters shown in Table 1. Some of these parameters were chosen from recommendations and technical specifications for UMTS and LTE standards.

Table 1 System parameters
Full size table

Figure 8 shows the coverage radius as a function of the load factor (\({\mathcal {L}}\)), the channel reuse factor (\({\mathcal {F}}\)), the modulation order and the number of antennas in the array at the BS (\(\varUpsilon\)) for a system employing \(G= 8\). Note that for high values of \({\mathcal {L}}\) and for \(\varUpsilon = 2\), the system does not operate, i.e., it can not achieve the maximum mean BER of \(10^{-4}\) due to the high levels of interference. However, using a large number of antennas (specifically \(\varUpsilon = 8\) in this scenario), the effects of \({\mathcal {MAI}}\) and \({\mathcal {CCI}}\) are diminished, and therefore, it is possible to use high values of \({\mathcal {L}}\). Also, increasing \({\mathcal {F}}\) and \(\varUpsilon\) not only improves the coverage radius, but also increases the cell throughput, because higher order modulations can be used mainly (for the scenario with \({\mathcal {L}}= 0\)). As a particular case, note that for \(\varUpsilon = 8\) and \({\mathcal {L}}= 0.75\) the system can not operate with \({\mathcal {F}}= 1\) and for other values of \({\mathcal {F}}\), there is a partial coverage of the cell because the coverage radius is smaller than the outer cell radius.

Figure 9 shows the mean spectral efficiency obtained for the coverage radius of Fig. 8. In this figure, it is observed that the system can employ 64-QAM modulation in some scenarios with no \({\mathcal {MAI}}\) (\({\mathcal {L}}= 0\)). However, allocating a group of \(G= 8\) subcarriers for one user decreases the mean spectral efficiency. Thus, it can be observed in Fig. 9 that the scenario with \({\mathcal {L}}= 0\) has the lowest spectral efficiency. Furthermore, for \(\varUpsilon = 8\), the mean spectral efficiency improves as \({\mathcal {L}}\) increases because the number of users per block in the cell is increased. Also, note that using \({\mathcal {F}}= 1\) if possible, the mean spectral efficiency is maximum for each load factor.

Fig. 8
figure 8

Coverage radius as a function of the load factor (\({\mathcal {L}}\)), the channel reuse factor (\({\mathcal {F}}\)), the modulation order, and the number of antennas in the array (\(\varUpsilon\)) for a system with \(G= 8\). a \(\varUpsilon = 2\), b \(\varUpsilon = 8\)

Full size image
Fig. 9
figure 9

Mean spectral efficiency as a function of the load factor (\({\mathcal {L}}\)), the channel reuse factor (\({\mathcal {F}}\)) and the number of antennas in the array (\(\varUpsilon\)) for a system with \(G= 8\). a \(\varUpsilon = 2\), b \(\varUpsilon = 8\)

Full size image

In the previous figures, it was verified that the antenna array is essential in a MC-CDMA system due to the interference. Also, another technique that allows to increase the system performance is frequency diversity. Therefore, the spreading factor plays an important role in spectral efficiency. It is observed that high load factors limit the MC-CDMA performance due to high levels of \({\mathcal {MAI}}\). Consequently, in practice \({\mathcal {L}}= 0.5\) is employed for cellular network dimensioning [14]. Given the above, Fig. 10 shows the coverage radius and the mean spectral efficiency of a MC-CDMA cellular system as a function of the spreading factor (G) considering a load factor of 0.5. Also, a scenario with 8 antennas in the array at BS is considered. It is important to mention that when \(G= 1\), the MC-CDMA system becomes an orthogonal frequency division multiple access (OFDMA) system, thus, there is no \({\mathcal {MAI}}\) (\({\mathcal {L}}= 0\)). Note in Fig. 10 that it is not possible to employ \({\mathcal {F}}= 1\) when \(G\le 2\), but when \(G\ge\) 2, it is possible to employ \({\mathcal {F}}= 1\) due to the frequency diversity gain. Also, observe that with \(G= 1\) it is possible to use higher order modulations (64-QAM and 16-QAM). Nevertheless, the mean spectral efficiency not only depends on the modulation schemes, but also on \({\mathcal {F}}\). Thus, observe that for \({\mathcal {F}}\ne 1\), the OFDMA system has better mean spectral efficiency. However, the maximum mean spectral efficiency obtained for the OFDMA system (\(G=\) 1, \({\mathcal {F}}= 3\)) is lower than the maximum mean spectral efficiency obtained for the MC-CDMA system (\(G= 8\), \({\mathcal {F}}=1\)).

Fig. 10
figure 10

Coverage radius and mean spectral efficiency of a MC-CDMA system employing \({\mathcal {L}}= 0.5\). a Coverage radius as a function of G, \({\mathcal {F}}\), M and \(\varUpsilon\). b Mean spectral efficiency as a function of G, \({\mathcal {F}}\) and \(\varUpsilon\)

Full size image

7 Conclusions

Analytic expressions to evaluate the mean spectral efficiency of the uplink of a cellular network employing MC-CDMA were obtained. These expressions depends on the channel reuse factor, the system load, the spreading factor and the cell radius. Also, parameters as modulation schemes order, bit error rate and length of the cyclic prefix are considered.

The existence of \({\mathcal {MAI}}\) and \({\mathcal {CCI}}\) in a channel characterized by the presence of AWGN, exponential path-loss and slow and frequency selective Rayleigh fading are considered. A linear antenna array at the base stations, a frequency domain interleaving, maximal ratio combining, adaptive modulation and perfect power control are also considered.

From the spectral efficiency viewpoint, it was determined that increasing the number of antennas in the array is more efficient than increasing the number of subcarriers for each block of users (i.e., increasing G) or increasing the channel reuse factor. In order to exploit frequency diversity gain, there should be few users allocated in each group of subcarriers. In other words, the load factor should be close to zero, but it should decrease the mean spectral efficiency. High levels of own cell interference appear due to the use of matched filters in the receivers. For this reason, multiuser detection techniques are a good alternative to use with MC-CDMA systems.

Furthermore, increasing the channel reuse factor decreases the number of channels per cell and consequently, the mean spectral efficiency decreases too. Also, the greater the bandwidth increase due to the cyclic prefix, the lower the mean spectral efficiency.

In the results, it is observed that unitary channel reuse factor presents the best mean spectral efficiency for almost all system load scenarios. However, this reuse factor is critical in relation to the bit rates, thus, in this scenario only the lowest modulation order can be employed.

Finally, when the spreading factor is equal to 1, OFDMA is a particular case of MC-CDMA. In this case, for a reuse factor different of 1, OFDMA has better mean spectral efficiency than MC-CDMA. However, in the studied scenario, the maximum mean spectral efficiency obtained with MC-CDMA is greater than the maximum mean spectral efficiency obtained with OFDMA.