1 Introduction

Recently, wireless sensor networks (WSNs) have become one of the most indispensable technologies in our modern life. WSNs typically consists of a large number of sensor nodes that are capable of not only sensing, but also interact with each other [1]. However, most of WSN applications suffer from limited energy resources issue when it come for large-scale deployment across a wide geographic area for collecting measurement data about environmental or physical condition, such as humidity, temperature, pressure, etc. Therefore, energy optimization became paramount in increasing the battery life and, consequently the network lifetime. There are several parameters govern the sensor node energy consumption, such as the transmitted power, modulation scheme, and packet structure. Some of these parameters directly affect the performance of probability of packet error which in turn affect the number of re-transmissions packets. For this reason, it will be more convenient to set up these parameters wisely to achieve efficient exploitation of available energy resources in WSN nodes.

The key success for optimized energy consumption comes from the knowledge of all sources that consume energy in WSNs. Tune with this idea and as it is known that most of the energy is consumed in physical (PHY) layer, an accurate energy consumption model is a must which considers parameters of PHY layer in addition to the type of channel models such as fading Rayleigh and Additive White Gaussian Noise (AWGN) channel models. In spite of the large number of energy consumption models, but most models have not been tested with real network and this raises suspicion in accuracy of these models. Previously, most of the research efforts in choosing of transmitted power, modulation size and other PHY layer parameters dedicated to consider AWGN channel model only with few works took the case of fading Rayleigh channel model. Moreover, most of the previous works use numerical evaluations to reach the solution and does not provide closed-form expressions for optimum value of these parameters. In spite of the great results obtained by [2,3,4,5,6,7,8,9] but it is only considered AWGN channel model. Unlike, in [10], the problem of energy-efficient is studied with consideration of fading Rayleigh channel. However, outage probability of fading channel is considered rather than the actual symbol error rate. In [11], the authors first review energy efficiency metrics pertinent to measuring network performance and designing its parameters. Then, relay network parameters are optimized to achieve better energy efficiency and full energy saving expectations. On the other hand, they assume that the bit error rate is constant, and determined by other layers.

In this paper, an energy consumption model is proposed considering PHY layer parameters which is used to optimize the transmitted power and modulation level for communication over fading Rayleigh and AWGN channels. The proposed energy consumption model is validated with real measurements. Results showed good agreement between proposed model and experimental measurements with mean absolute percentage error less than 6%. The validated model is used to optimize transmitted power and modulation level to achieve minimum energy consumption. As a final point, analytic expressions for the optimum transmitted power and modulation level at different modulation schemes are provided.

The rest of this paper is organized as follows. In Sect. 2, we present the energy consumption model while in Sect. 3, the energy consumption model will be tested with real data to measure the accuracy of the model. The model in Sect. 2 is used in Sects. 4 and 5 in order to optimize the transmitted power and modulation level to achieve minimum energy consumption. Finally, Sect. 6 summarizes our conclusions.

2 Energy Consumption Model

The importance of having model is coming from the necessity to lengthen the node lifetime operating as long as possible. As a consequence, our goal is to determine the energy consumption in transceiver by determining the total energy that is required for successfully received one bit, without error, between two sensor nodes. Two assumptions are made to achieve this goal. First, every packet transmitted in the forward direction is matched by an error-free feedback packet in the reverse direction, to acknowledge correct reception or requests a re-transmission as shown in Fig. 1. Second, the transceiver of transmitter node is by default in a low power mode (sleep state) and it must be brought online before it can make the transmission. In the sequel, firstly the packet structure and the components of energy consumption of a transceiver unit are analyzed. Then, the total energy required for successfully received one bit is determined.

Fig. 1
figure 1

Messaging mechanism

Full size image

2.1 Packet Structure

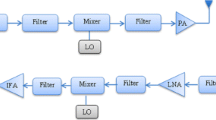
The general format of a packet structure in communications systems is shown in Fig. 2. Each packet consists of three main parts, a header with essential transmission parameters, a overhead for channel estimation, synchronization, etc., and a payload.

The data in a packet can be corrupted by bit or symbol errors due to channel noise. The probability of a symbol error at the PHY layer is primarily determined by the Signal to Noise Ratio (SNR), conditions of the radio channel and the modulation scheme employed. If the symbol errors are independent of each other and a packet gets corrupted when one or more bits are erroneous, then the packet error rate is given by

$$\begin{aligned} P_p=1-(1-P_{e,s})^{L_p/b} \end{aligned}$$
(1)

where \(P_{e,s}\), \(L_p\) and b are the probability of a symbol error, the packet size (in bits) and modulation level, respectively. Consequently, the expected amount of data received per packet correctly is obtained by multiplying the number of the payload bits per packet (N) by the probability of packet success (\(1-P_p\)) which can be expressed as

$$\begin{aligned} N_s=N (1-P_{e,s})^{L_p/b} \end{aligned}$$
(2)
Fig. 2
figure 2

The packet structure at physical layer

Full size image

2.2 Components of Transceiver Unit

In the transmitter node, there are three sources of energy consumption to transmit packet, and to receive a corresponding feedback packet, which are start-up energy consumption (\(E_{st}\)), energy consumption to forward payload packet, and energy consumption to receive the corresponding feedback packet. Therefore, the energy consumed by the transmitter to transmit one packet, and receives a corresponding feedback packet is given by:

$$\begin{aligned} E_{TX}=E_{st}+P_{tx} T_P+P_{rx} T_F \end{aligned}$$
(3)

where \(T_P\) is the duration time of the data packet and \(T_F\) is the duration time of the feedback packet, which is defined as \(T_F=L_F R_r\), where \(L_F\) is the number of bits that compose the feedback packet and \(R_r\) is the data rate. By analogy, the total energy used by the receiver node to receive one packet, and transmits a corresponding feedback packet is given by

$$\begin{aligned} E_{RX}=E_{st}+P_{tx} T_F+P_{rx} T_P \end{aligned}$$
(4)

From previous analysis, the total energy per successfully received bit (\(E_b\)) and the total energy per successfully received packet (\(E_p=NE_b\)) are given by:

$$\begin{aligned} E_b &= \frac{\text{Total amount of energy consumed per packet}}{\text{Total amount of data delivered per packet correctly}} \\&=\frac{E_{TX}+E_{RX}}{N_s} =\frac{E_{TX}+E_{RX}}{N (1-P_{e,s})^{L_p/b} } \end{aligned}$$
(5)
$$\begin{aligned} E_p &= \frac{E_{TX}+E_{RX}}{(1-P_{e,s})^{L_p/b} } \end{aligned}$$
(6)

3 Validation of the Energy Consumption Model

The energy consumption model stated in Sect. 2 will be tested with real system to measure the accuracy of the proposed model. In what follows, a solid background about energy consumption measuring methods is performed to override most of the drawbacks in the previous methods to come out with new methodology.

One of the main challenges associated with characterizing the energy consumption of radio transceivers is that their current draw varies greatly depending on the mode in which the transceivers is operating. Since radio transceivers usually operate at constant supply voltage, the measure of energy consumption can be carried out indirectly, by inserting a small resistance R (\(\le\) 10 \(\Omega\)) between the power supply and the radio transceiver and measuring the absorbed current. To this aim, various techniques are available to measure the energy consumption of radio transceivers, such as; Handheld Digital multi-meters (HDMs), DC power supplies (DCPS), Data Acquisition cards (DAQs) and Oscilloscopes (OSCs) [12,13,14,15]. In the following, the most significant features will be discussed for each method:

  • HDMs provide a simple method to measure the energy consumption with great measurement accuracy and low cost. On the other hand, HDMs are inadequate for measuring energy consumed during short active duty cycles of the radio transceiver.

  • DCPS are used to supply power to the radio transceivers with ability to communicate with a host PC to transfer measured data via a serial channel (e.g. USB) simultaneously. The major disadvantage of DCPS is its low sampling rate which is required to accurately capture RF activity on radio transceivers.

  • DAQs are a type of electronic test instrument which typically convert analog waveforms into digital values for processing. DAQ applications are controlled by software programs developed using various general purpose programming languages such as LabVIEW. DAQs have high sampling rates in comparison to DCPs which allowing to capture very short events such as RF activity. The main drawback of using a DAQ is its high price.

  • OSCs are general purpose instruments that provide a continuous plot of voltage signals as a function of time. OSCs have very high sampling rate and are easy to use when compared to a DAQs. On the other hand, OSCs have a limited ability to programming.

According to [12], comparison table between different methods of energy consumption measuring is provided and extended with our proposed method as illustrated in Table 1. Our proposed method is done by exploiting Digital Signal Processors DSPs. DSPs can be designed to measure voltage, current, and energy consumption of radio transceivers. DSPs, such as TI C2000 TMS320F2812, have high sampling rates, and low cost in comparison to DAQs.

Table 1 Comparison of energy consumption measurement methods
Full size table

The proposed method performed by using the Nordic Semiconductor nRF24L01+ 2.4 GHz wireless chips [16], a TI C2000 TMS320F28335 DSP microprocessor [17], the software Code Composer Studio (CCS), Arduino MCU (microcontroller), and 4.3 ohm shunt resistor. The Arduino MCU is used to design a radio system with the nRF24L01+ wireless chip. The shunt resistor is placed in series between the power supply and low power transceiver Nordic nRF24L01+ as shown in Fig. 3. The voltage drop across this shunt resistor is fed to TI C2000 TMS320F28335 DSP microprocessor which converts the analog signal to digital using one million samples per second data acquisition rate. Data exchange between computer and TMS320F28335 DSP board takes place thru USB JTAG emulator link. Figure 4 presents the hardware setup at work.

Fig. 3
figure 3

Experimental setup

Full size image
Fig. 4
figure 4

Experiment components

Full size image

For packet error probability (\(P_p\)) measurements, the transmitter node is programed to transmit a large number of packets (e.g. 3000 packets). Then, the correctly received packets are counted at the receiver node to determine the packet error probability.

Using the parameters in Table 2, the results acquired from the experiment are compared with the energy predicted by the proposed energy consumption model which are found to be in better agreement with mean absolute percentage error of 5.8% as shown in Fig. 5. Figure 6 shows the relative error between experiment and proposed energy consumption model as a function of the number of successfully received packets.

Table 2 Experiment parameters
Full size table
Fig. 5
figure 5

A comparison between the energy consumption predicted by the energy consumption model and energy consumption from real system

Full size image
Fig. 6
figure 6

Relative error over experiment

Full size image

4 Optimization of Transmitted Power

Considering (5), we note that a large transmitted power is preferred for lower symbol error rate, but it suffers from excessive transmitted power and energy per successfully received bit. On the other hand, using lower transmitted power increases the probability of symbol error and energy per successfully received bit. This trade-off is illustrated in the relation between the energy per successfully received bit and transmitted power as shown in Fig. 7. Moreover, Fig. 7 shows that the energy per successfully received bit has a unique minimum with respect to the transmitted power. This minimum can be found by minimizing (5) over \(P_t\). This can be done by taking derivative and equating the result to zero, which leads to the following implicit expression for the transmitted power \(P_t\) that minimizes energy per successfully received bit:

$$\begin{aligned} B(1-P_{e,s})+(L_p/b)(A+BP_t) \frac{\partial P_{e,s}}{\partial P_t }=0 \end{aligned}$$
(7)

where

$$\begin{aligned} A &= 2{E_{st}} + \left( {{T_F} + {T_P}} \right) {P_{rx}} + \left( {{T_F} + {T_P}} \right) {P_{t0}} \\ B &= \left( {\alpha + 1} \right) \left( {{T_F} + {T_P}} \right) \end{aligned}$$
Fig. 7
figure 7

The energy per successfully received bit as a function of the transmitted power using the parameters in Table 5

Full size image

The solution of Eq. (7) is depending on the type of radio channel which in our case is AWGN and fading Rayleigh channels that will be discussed profoundly in the following two subsections, to end up with closed-form expression derivation for optimum transmitted power in each case. Then, the accuracy of the results is tested by simulations in Sect. 4.3.

4.1 AWGN Channel

Under the condition of AWGN, the equations of symbol error rate as function of received SNR (\(\gamma\)) for different modulation schemes that stated in Table 3 [18] are approximated by fitting the curve \(b_0e^{-b_1\gamma }\), with \(b_0\) and \(b_1\) are constants that depend on the chosen modulation scheme (e.g. for BPSK \(b_0=0.2\) and \(b_1=1.1\) as illustrated in Table 3), and minimizing the mean square error. These approximations are valid for \(10^{-8} \le P_{e,s} \le 10^{-1}\). Figure 8 shows comparisons between the original expressions and the proposed simplified expressions of probability of symbol error of BPSK, MPSK and M-QAM modulating schemes. The proposed simplified expressions are closely matched to original expressions with relative error less than 1% of all cases.

Table 3 The original and approximate expressions of symbol error probabilities for AWGN channel
Full size table
Fig. 8
figure 8

A comparison between the original and approximate expressions of symbol error rate for different modulation schemes over AWGN channel. a BPSK, b M-PSK, c M-QAM

Full size image

The received SNR is defined as \(\gamma = {P_r}/2{B_0}{N_0}{N_f}{M_l}\), where \(P_r\) is the received power, \(B_0\) is the signal bandwidth, \(N_0\) is the spectral power density of AWGN, N(f) is the noise figure of the receivers front end, and \(M_l\) is a link margin term which represents any other additive noise or interference. Based on the signal propagation model, we have \({P_t} = \mathrm{{\;}}K{d^\mathrm{{\alpha }}}{P_r}\), where K is a parameter that depends on the transmission wavelength and transmitter and receiver antenna gains, d is the distance between transmitter and receiver and is the path loss exponent. Therefore, received SNR (\(\gamma\)) is related to \(P_t\) as

$$\begin{aligned} \gamma = \frac{{{P_t}}}{{2{B_0}{N_0}{N_f}{M_l}K{d^\mathrm{{\alpha }}}}} \end{aligned}$$
(8)

Consequently, the approximated symbol error rate for different modulation schemes over AWGN channel can be written as follows

$$\begin{aligned} {P_{e,s}} = {b_0}{e^{ - Y{P_t}}} \end{aligned}$$
(9)

where \(Y=b_1/2B_0 N_0 N_f M_l Kd^\alpha\). By replacing (9) in (7) we find

$$\begin{aligned} B\left( {1 - b_0{e^{ - Y{P_t}}}\mathrm{{\;\;}}} \right) - ({L_p}/b)\left( {A + B{P_t}} \right) \left( {b_0Y{e^{ - Y{P_t}}}} \right) = 0 \end{aligned}$$
(10)

By solving (10) for \(P_t>0\), the optimum transmitted power takes the following form

$$\begin{aligned} P_t^* = - \frac{{{W_{ - 1}}\left( Z \right) }}{Y} - \frac{{B + AY({L_p}/b)}}{{BY({L_p}/b)}} \end{aligned}$$
(11)

where \(W_{-1}(z)\) is a negative branch of Lambert function which defines by \(W(Z)e^{W(Z)}=Z\) [19], and Z is constant, which is given by

$$\begin{aligned} \mathrm{{Z}} = - \frac{1}{b_0 (L_p/b)} {e^{ - \frac{{B + AY({L_p}/b)}}{{B({L_p}/b)}}}} \end{aligned}$$
(12)

By using an approximation for negative branch of the Lambert function, which is found in [20], the optimum transmitted power can be eventually denoted as

$$\begin{aligned} P_t^* &= - \frac{{B + AY({L_p}/b)}}{{BY({L_p}/b)}}\\ &\quad + \frac{1}{Y}\left[ 1 + \sigma + \frac{2}{{{M_1}}} \left( {1 - \frac{1}{{1 + \left( {{M_1}\sqrt{\sigma /2} \;} \right) /\left( {1 + {M_2}\sigma {e^{{M_3}\sqrt{\sigma }}}} \right) }}}\right) \right] \end{aligned}$$
(13)

where \(\sigma =-1-ln(-Z), M_1=0.3361, M_2=-0.0042\) and \(M_3=-0.0201\).

4.2 Fast Fading Rayleigh Channel

Similarly as in AWGN condition, the equations of symbol error rate for different modulation schemes over Fast Fading Rayleigh channel, that stated in Table 4 [18, 21], are approximated by fitting the curve \(b_3/\gamma\), with \(b_3\) constant that depends on the modulation scheme (e.g. for BPSK \(b_3=0.25\)), and minimizing the mean square error. Also, the approximations are valid for \(10^{-8} \le P_{e,s} \le 10^{-1}\). In Fig. 9, the approximate symbol error rate is shown to be very close to the the original expressions for different modulation schemes over fading Rayleigh channel.

Table 4 The original and approximate expressions of symbol error probabilities for Rayleigh fading channel
Full size table
Fig. 9
figure 9

A comparison between the original and approximate expressions of symbol error rate for different modulation schemes over fading Rayleigh channel. a BPSK, b M-PSK, c M-QAM

Full size image

Thus, the symbol error rate for different modulation schemes over Rayleigh channel is related to \(P_t\) as

$$\begin{aligned} {P_{e,s}} = \frac{X}{{{P_t}}} \end{aligned}$$
(14)

where \(X=2B_0 N_0 N_f M_l Kd^\alpha b_3\). By replacing (14) in (7) we find:

$$\begin{aligned} B(1 - X/{P_t})P_t^2 - X({L_p}/b)(A + B{P_t}) = 0 \end{aligned}$$
(15)

By solving the previous equation, the optimum transmitted power over Rayleigh channel is determined as

$$\begin{aligned} P_t^* = \frac{{BX\left( {1 + {L_p}/b} \right) + \sqrt{{{\left( {BX\left( {1 + {L_p}/b} \right) } \right) }^2} + 4ABX{L_p}/b} }}{{2B}} \end{aligned}$$
(16)

4.3 Simulation Results

Using the parameters in Table 5, the energy per successfully received bit is calculated under the optimal transmitted power given by the various approximations developed in this section and compared with those obtained by finding the minimum of (5) numerically as shown in Fig. 10. The approximation results are closely matched to numerical results with relative error less than 2% in all cases.

Table 5 Simulation parameter settings
Full size table
Fig. 10
figure 10

The energy per successfully received bit at optimum transmitted power determined numerically form (12) and using the various approximations proposed in Sect. 4

Full size image

5 Optimization of Modulation Level for M-QAM

In the previous section, the energy saving gained from optimizing the transmitted power to minimize the energy per successfully received bit is investigated. In the following study, we assume a fixed bandwidth and target error rate, and choose the modulation level (b) that minimizes the energy per successfully received bit over AWGN. In this case, the transmitted power is computed under a target instantaneous error rate and the total time to transmit a packet of \(L_P\) bits (\(T_P\)) is given by [9]:

$$\begin{aligned} {T_P} = \frac{{{L_P}}}{{b{B_0}}} \end{aligned}$$
(17)

Thus, the energy per successfully received bit can be expressed as

$$\begin{aligned} {E_b}\left( b \right) = \mathrm{{\;}}\frac{{{U_0} + {U_2}\frac{{{U_1}}}{b} + \left( {{T_F} + \frac{{{U_1}}}{b}} \right) \left( {{\alpha _0} + 1} \right) {P_t}\left( b \right) }}{{N{{(1 - {P_{e,s}})}^{Lp/b}}}} \end{aligned}$$
(18)

where

$$\begin{aligned} {U_0} &= 2{E_{st}} + {T_F}{P_{r0}} + {T_F}{P_{ct}}\\ {U_1} &= \frac{{{L_P}}}{{{B_0}}}\\ {U_2} &= \left( {{P_{ct}} + {P_{rx}}} \right) \end{aligned}$$

Considering (18), a large constellation size is preferred for higher data rate, but it suffers from a high transmitted power for a given error probability. On the other hand, using small constellation size decreases the transmitted power, but also it suffers from a low data rate. This trade-off is illustrated in the relation between the energy per successfully received bit and constellation size as shown in Fig. 11. Also, Fig. 11 shows that the energy per successfully received bit has a unique minimum with respect to modulation level b. Moreover, we note that the optimal constellation size increases as the target symbol error probability increases. For example, the optimal modulation level is 3 bit/symbol at \(P_{e,s}=10^{-3}\), and as \(P_{e,s}\) increases to \(10^{-2}\) the optimal modulation level increases to 5 bit/symbol. To find this minimum, we set \(\partial E_b/\partial b =0\), which give us the following expression

Fig. 11
figure 11

The energy per successfully received bit as a function of the modulation level for M-QAM over AWGN channel using the parameters in Table 5

Full size image
$$\begin{aligned} &- {U_1}{U_2} + \left( {{T_F} + \frac{{{U_1}}}{b}} \right) \left( {{\alpha _0} + 1} \right) {b^2}\frac{{\partial {P_t}\left( b \right) }}{{\partial b}} - {U_1}\left( {{\alpha _0} + 1} \right) {P_t}\left( b \right) \\ &\quad +\left( {{U_0} + {U_2}\frac{{{U_1}}}{b} + \left( {{T_F} + \frac{{{U_1}}}{b}} \right) \left( {{\alpha _0} + 1} \right) {P_t}\left( b \right) } \right) \left( {{L_P}\ln \left( {1 - {P_{e,s}}} \right) } \right) = 0 \end{aligned}$$
(19)

From Table 3, the transmitted power \(P_t\) for M-QAM modulation can be expresses as:

$$\begin{aligned} \;{P_t} = \frac{{M - 1}}{{1.66{Y_0}}}\mathrm{{ln}}\left( {\frac{{0.78\left( {M - 1} \right) }}{{M{P_{e,s}}}}} \right) \end{aligned}$$
(20)

where \(Y_0=1/(2B_0 N_0 N_f M_l Kd^\alpha )\) and \(M=2^b\). By replacing (20) in (19) and ignore small terms, we get the optimum modulation level as:

$$\begin{aligned} {b^*} \approx \root 3 \of {{ - \frac{q}{2} + \sqrt{\frac{{{q^2}}}{4} + \frac{{{p^3}}}{{27}}} }} + \root 3 \of {{ - \frac{q}{2} - \sqrt{\frac{{{q^2}}}{4} + \frac{{{p^3}}}{{27}}} }} - \frac{{{a_1}}}{{3{a_0}}} \end{aligned}$$
(21)

where

$$\begin{aligned} q &= \left( {2{a_1}^3 - 9{a_0}{a_1}{a_2} + 27{a_0}^2{a_3}} \right) /27{a_0}^3\\ p &= \left( {3{a_0}{a_2} - {a_1}^2} \right) /3{a_0}^2\\ {a_0} &= \ln \left( 2 \right) \ln \left( {0.78/{P_{e,s}}} \right) \left( {{\alpha _0} + 1} \right) {\mathrm{{T}}_\mathrm{{f}}}\\ {a_1} &= \ln \left( 2 \right) \ln \left( {0.78/{P_{e,s}}} \right) \left( {{\alpha _0} + 1} \right) {U_1}\\ {a_2} &= \ln \left( {0.78/{P_{e,s}}} \right) \left( {{\alpha _0} + 1} \right) \left( {{\mathrm{{T}}_\mathrm{{f}}}\mathrm{{Lp}}\ln \left( {1 - {P_{e,s}}} \right) - {\mathrm{{U}}_1}} \right) \\ {a_3} &= {\mathrm{{U}}_1}{\mathrm{{L}}_\mathrm{{p}}}\ln \left( {1 - {P_{e,s}}} \right) \left( {{\alpha _0} + 1} \right) \mathrm{{ln}}\left( {0.78/{P_{e,s}}} \right) - \left( {1.66{\mathrm{{U}}_1}{\mathrm{{U}}_2}{\mathrm{{Y}}_0} + 1.66{\mathrm{{U}}_0}{\mathrm{{Y}}_0}} \right) /4\\ \end{aligned}$$

Using the parameters of Table 5, the energy per successfully received bit is calculated under the optimal modulation level given by the previous approximation developed in this section and compared with those obtained by finding the minimum of (5) numerically as shown in Fig. 12. The approximation results are closely matched to numerical results with relative error less than 3% of all cases.

Fig. 12
figure 12

The energy per successfully received bit using optimal modulation level for M-QAM modulation at target symbol error probability that determined numerically form minimizing (18) and using the approximation proposed in this section

Full size image

6 Conclusion

In this paper, the effect of transmitted power and modulation level selection on the energy consumption of WSNs is studied. In our study, an energy model for WSNs considering the physical layer parameters based on the energy per successfully received bit is derived. The model is validated with real data and the results found to be in good agreement with mean absolute percentage error is not exceeding 6%. It follows that the energy per successfully received bit as a function of transmitted power has a single minimum point for each type of wireless channels and depending on the packet size, modulation level and channel statistics. Furthermore, analytic expressions are derived for the optimal transmitted power under AWGN and Rayleigh channels using different modulation schemes. Also, the energy saving gained from optimizing the constellation size to minimize energy consumption with a target symbol error rate is investigated. The results show that the optimal modulation level increases as the target error probability increases. Finally, a closed-form expression for the optimal constellation size for M-QAM modulation at target symbol error probability is derived.