1 Introduction

Increasing demands on the frequency resources results in a shortage of spectrum. A survey of spectrum utilization indicates the licensed spectrum is rarely used in huge temporal and geographic dimensions [1]. Cognitive radio technology is viewed as an effective solution because the SU can share the frequency bands of PU while keeping the target outage probabilities of secondary system and primary system both maintained. However, there are different modes to choose when SU uses the spectrum of PU. In the underlay mode, it means SU is allowed to transmit when PU is active only if the inferences are under the required level. In the overlay mode, SU is allowed to transmit only when the spectrum of PU is detected as ‘idle’ (i.e. PU is inactive), otherwise, (i.e., PU is active), SU is not allowed to make transmission. The sensing problem was well investigated in the previous cognitive radio literatures. Distributed cooperative detection was put forward to conquer multi-path fading and hidden terminal problem [2,3,4,5]. [6,7,8] analyzed the influence of noise uncertainty to the sensing results. [9, 10] studied the system throughput while keeping the interferences of SU to PU limited below an “acceptable level”. [11, 12] investigated the sensing time optimization. Current trend is shifting from sensing to database management [13], however, the primary system needs to be involved and assist in the process. Besides, the networks model is considered to be static when system performance is discussed in those papers. Initiated by the seminal work of Gupta and Kumar [14], the studies for understanding the capacities of wireless ad hoc networks have made great progresses. Stochastic geometry theory is shown to be a very powerful mathematical tool for performance evaluation. Poisson point process (PPP) distribution was applied in [15,16,17,18] to analyze the performance of cognitive radio networks dynamically as used in the ad hoc networks.

As is known to all, a tradeoff is made between the user density of a system and the probability of successful transmission because larger interferences generate as more concurrent transmitting nodes exist (i.e., the user density is high) in ad hoc networks. Therefore, in cognitive radio networks, it is essential to verify the effect of SU on the networks.

In this paper, we employ stochastic geometry and define the TC as the user density of successful transmissions (user number per square meters multiply one minus outage probabilities, i.e., the overall spectrum efficiency per unit area) while satisfying the outage probability constraints of secondary system and primary systems as in [15, 16]. Jemin et al. [15] discussed the TC of secondary system in cognitive radio networks without analyzing that of primary system. On the contrary, Mohammad et al. [16] discussed the influence of secondary system parameters on the TC of primary system without considering the performance of SU. Changchuan et al. [17] studied the TC gain of spectrum sharing in the underlay mode over single primary mode without considering overlay mode. Jeemin et al. [18] did not compare the TC of spectrum sharing mode with single primary mode. In this paper, the TC in single primary system mode, overlay mode, and underlay mode are derived respectively. The ratios of transmission power and user density are obtained. Additionally, the constraint is found to make the TC of spectrum sharing mode exceed that of the single system mode. The upper bound of TC is derived and an accessing strategy to reach the maximum value is proposed, under which the TC of SU will be maximized when that of PU is fixed. The maximum TC is the larger value between overlay mode and underlay mode, which can approach the upper bound with high detection probabilities in short sensing time.

The rest of the paper is organized as follows. In Sect. 2, network model is introduced and outage probability of each system is derived. The TC in each mode, ratios, constraint, upper bound, and the accessing strategy to reach the maximum TC are derived in Sect. 3. In Sect. 4, the analyses are proved with numerical results. Finally, conclusions are drawn in Sect. 5.

2 Network Model and Outage Probability

2.1 A Model of Cognitive Radio Networks

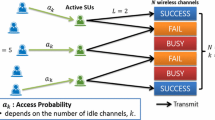
A model of cognitive radio networks is illustrated in Fig. 1. The networks consist of primary system and secondary system. The transmitting nodes and receiving nodes of two systems are uniformly distributed in the same area and share the spectrum. So, the interferences at a receiver are from the transmitting nodes of two systems.

Fig. 1
figure 1

A model of cognitive radio networks

Full size image

\(\upbeta = \{ {\text{p}},{\text{c}}\}\) is denoted as the set of spectrum sharing systems. The primary system is denoted as system p and the secondary system is denoted as system c. We assume that at a certain time instance the distribution of Primary TXs follows a homogeneous PPP \(\varPi_{\text{p}}\) with density λ p, and the distribution of Secondary TXs follows another independent homogeneous PPP \(\varPi_{\text{c}}\) with density λ c. In order to evaluate outage probability, a typical receiver of either primary system or secondary system is assumed to be located at the origin, and it does not give any effect on statistics by the Palm probabilities of a Poisson process [19]. Following the Slivnyak’s theory in stochastic geometry [20], these conditional distributions also follow homogeneous PPPs with the corresponding densities (i.e., λ p and λ c, respectively). The distance between the transmitter and a typical receiver of primary system is denoted by d p and the distance between the transmitter and a typical receiver of secondary system is denoted by d c. For simplicity, we limit our discussion to single-hop transmissions, and the common transmission data rate are the same for two systems. Besides, we assume that all Primary TXs use the same transmission power p p and all Secondary TXs use the same transmission power p c. For the wireless channel, we consider the large-scale path-loss with exponent \(\alpha\), and Rayleigh fading with the fading factor \(h_{ij}\) on the power transmitted from the jth node in system i to the typical receiver which has an exponential distribution with unit mean. \(d_{ij}\) is the location of the jth transmitting node in system i, and \(\left| {d_{ij} } \right|\) is the distance of \(d_{ij}\) from the origin. In the networks, the undesired transmitting nodes in each system generate interferences to a receiver, and the distribution of the interfering nodes in system i can be modeled by marked Poisson point process (MPPP), \(\varPi_{i} = \left\{ {\left( {d_{ij} ,h_{ij} } \right)} \right\},\forall i \in\upbeta\).

2.2 Outage Probability

The signal to interference-plus-noise ratio (SINR) at the receiver of primary system and secondary system are:

$$SINR_{\text{p}} = \frac{{p_{\text{p}} h_{{{\text{p}}0}} d_{\text{p}}^{ - \alpha } }}{{\sum_{{i \in\upbeta}} {\sum_{{d_{ij} \in \prod_{i} }} {p_{i} h_{ij} |d_{ij} |^{ - \alpha } + N_{0} } } }}$$
(1)
$$SINR_{\text{c}} = \frac{{p_{\text{c}} h_{{{\text{c}}0}} d_{\text{c}}^{ - \alpha } }}{{\sum\nolimits_{{i \in\upbeta}} {\sum\nolimits_{{d_{ij} \in \prod_{i} }} {p_{i} h_{ij} |d_{ij} |^{ - \alpha } + N_{0} } } }}$$
(2)

where \(h_{\text{p0}}\) is the fading factor on the power transmitted from the desired communication pairs in primary system, \(h_{\text{c0}}\) is the fading factor on the power transmitted from the desired communication pairs in secondary system, and N 0 is the thermal noise power.

Spectrum sharing systems are interference-limited systems, so the thermal noise is negligible in regimes of interest. The SIR can be used instead of SINR. Each system should satisfy the smallest allowable value of SIR at the receiver to guarantee its quality of service (QoS). Hence, the successful transmission of primary system can be possible only when SIRp ≥ \(\varepsilon_{\text{p}}\), where \(\varepsilon_{\text{p}}\) is the target SIR of primary system. The successful transmission of secondary system can be possible only when SIRc ≥ \(\varepsilon_{\text{c}}\), where \(\varepsilon_{\text{c}}\) is the target SIR of secondary system. The successful transmission probability of two systems can be respectively defined as

$$1 - P_{{{\text{out\_p}}}} = P\left( {SIR_{\text{p}} > \varepsilon_{\text{p}} } \right)$$
(3)
$$1 - P_{{{\text{out\_c}}}} = P\left( {SIR_{\text{c}} > \varepsilon_{\text{c}} } \right)$$
(4)

where \(P_{{{\text{out\_p}}}}\), \(P_{{{\text{out\_c}}}}\) represents the outage probability of primary system and secondary system respectively. Following the same procedure in [15], the outage probabilities can be denoted by:

$$P_{{{\text{out\_p}}}} = 1 - \exp \left( { - \lambda_{\text{c}} d_{\text{p}}^{2} \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right)^{{\frac{2}{\alpha }}} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} C_{\alpha } - \lambda_{\text{p}} d_{\text{p}}^{2} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} C_{\alpha } } \right)$$
(5)
$$P_{{{\text{out\_c}}}} = 1 - \exp \left( { - \lambda_{\text{p}} d_{\text{c}}^{2} \left( {\frac{{p_{\text{p}} }}{{p_{\text{c}} }}} \right)^{{\frac{2}{\alpha }}} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} C_{\alpha } - \lambda_{\text{c}} d_{\text{c}}^{2} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} C_{\alpha } } \right)$$
(6)

where \(C_{\alpha } = (2\pi /\alpha )\varGamma (2/\alpha )\varGamma (1 - 2/\alpha )\) with gamma function \(\varGamma (x) = \int_{0}^{\infty } {t^{x - 1} \text{e}^{ - t} } {\text{d}}t\). The random distance of interference transmission \(d_{ij}\) is no longer shown because of the integration of outage probability calculation procedure and the fixed \(d_{k}\) can be simply extended to the other (random) distance distribution by averaging the performance over the distance.

3 Tc, Ratios, Constraint, Upper Bound and Accessing Strategy

3.1 Tc

3.1.1 Instantaneous Tc

  1. 1.

    PU transmits alone with the maximum user density \(\lambda_{\text{p}}^{'}\) while satisfying the primary system outage probability. The instantaneous TC is \(e_{0}\):

    $$e_{0} = \lambda_{\text{p}}^{'} \left( {1 - P_{{{\text{out\_p}}}} } \right)$$
    (7)

    Substituting \(\lambda_{\text{c}} = 0\) into (5), we have

    $$\lambda_{\text{p}}^{'} = {{ - \ln \left( {1 - P_{{{\text{out\_p}}}} } \right)} \mathord{\left/ {\vphantom {{ - \ln \left( {1 - P_{{{\text{out\_p}}}} } \right)} {\left( {d_{\text{p}}^{2} \left( {\varepsilon_{\text{p}} } \right)^{2/\alpha } C_{\alpha } } \right)}}} \right. \kern-0pt} {\left( {d_{\text{p}}^{2} \left( {\varepsilon_{\text{p}} } \right)^{2/\alpha } C_{\alpha } } \right)}}$$
    (8)
  2. 2.

    PU is inactive, and SU transmits alone with the maximum user density \(\lambda_{\text{c}}^{'}\) while satisfying the secondary system outage probability. The instantaneous TC is \(a_{0}\):

    $$a_{0} = \lambda_{\text{c}}^{'} (1 - P_{{{\text{out\_c}}}} )$$
    (9)

    Substituting \(\lambda_{\text{p}} = 0\) into (6), we have

    $$\lambda_{\text{c}}^{'} = - \ln (1 - P_{{{\text{out\_c}}}} )/(d_{\text{c}}^{2} (\varepsilon_{\text{c}} )^{2/\alpha } C_{\alpha } )$$
    (10)
  3. 3.

    PU is inactive, and SU transmits with the user density to satisfy the outage probabilities of both secondary system and primary system because PU is considered to be active by mistake. The instantaneous TC is \(b_{0}\):

    $$b_{0} = \lambda_{\text{c}} (1 - P_{{{\text{out\_c}}}} )$$
    (11)

    where \(\lambda_{\text{c}}\) should satisfy (5) and (6).

  4. 4.

    PU and SU transmit at the same time when PU is undetected. SU will try to access the spectrum with its maximum user density, which leads the outage probabilities to change. The instantaneous TC is c:

    $$c = c_{1} + c_{0}$$
    (12)
    $$c_{1} = \lambda_{\text{p}} \left( {1 - P_{{{\text{out\_p}}}}^{'} } \right)$$
    (13)
    $$c_{0} = \lambda_{\text{c}}^{'} \left( {1 - P_{{{\text{out\_c}}}}^{'} } \right)$$
    (14)

    Following (5) and (6), we have

    $$P_{{{\text{out\_p}}}}^{'} = 1 - \exp \left( { - \lambda_{\text{c}}^{'} d_{\text{p}}^{2} \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right)^{{\frac{2}{\alpha }}} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} C_{\alpha } - \lambda_{\text{p}} d_{\text{p}}^{2} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} C_{\alpha } } \right)$$
    (15)
    $$P_{{{\text{out\_c}}}}^{'} = 1 - \exp \left( { - \lambda_{\text{p}} d_{\text{c}}^{2} \left( {\frac{{p_{\text{p}} }}{{p_{\text{c}} }}} \right)^{{\frac{2}{\alpha }}} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} C_{\alpha } - \lambda_{\text{c}}^{'} d_{\text{c}}^{2} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} C_{\alpha } } \right)$$
    (16)
  5. 5.

    PU and SU transmit at the same time with the user densities to satisfy the outage probabilities of both secondary system and primary system. The instantaneous TC is b:

    $$b = b_{1} + b_{0}$$
    (17)
    $$b_{1} = \lambda_{\text{p}} (1 - P_{{{\text{out\_p}}}} )$$
    (18)

    where \(\lambda_{\text{p} }\) should satisfy (5) and (6), and \(b_{0}\) is given in (11).

3.1.2 Tc in Different Mode

We assume each transmission frame time duration is T and the TC is the sum one of two systems TC in the cognitive radio networks after time normalization.

Proposition 1

The TC in overlay mode is \(C_{\text{ts}}\):

$$C_{\text{ts}} = (\frac{{T_{\text{s}} }}{T}e_{0} + \frac{{T - T_{\text{s}} }}{T}(bP_{\text{d}} + c(1 - P_{\text{d}} )))P_{\text{on}} + \frac{{T - T_{\text{s}} }}{T}(a_{0} (1 - P_{\text{f}} ) + b_{0} P_{\text{f}} )(1 - P_{\text{on}} )$$
(19)

where \(T_{\text{s}}\) is the sensing time, \(P_{\text{on}}\) is the PU activity probability, \(P_{\text{f}}\) is the false alarm probability and \(P_{\text{d}}\) is the detection probability.

Proof

In overlay mode, SU spends \(T_{\text{s}}\) to sense the spectrum and then decide to transmit or keep quiet in the left duration \(T - T_{\text{s}}\). During the sensing time \(T_{\text{s}}\), only PU transmits alone with \(e_{0}\) multiplied by activity probability \(P_{\text{on}}\), i.e., \(\frac{{T_{\text{s}} }}{T}P_{\text{on}} e_{0}\). If PU is actually inactive and spectrum is detected to be idle, SU transmits alone with \(a_{0}\) multiplied by inactivity probability \((1 - P_{\text{on}} )\) and probability \((1 - P_{\text{f}} )\) during the left duration \(T - T_{\text{s}}\), i.e., \(\frac{{T - T_{\text{s}} }}{T}\left( {a_{0} \left( {1 - P_{\text{f}} } \right)\left( {1 - P_{\text{on}} } \right)} \right)\), otherwise, if PU is actually inactive but spectrum is detected to be busy, SU transmits alone as if PU is active, and with \(b_{0}\) multiplied by inactivity probability \(\left( {1 - P_{\text{on}} } \right)\) as well as false alarm probability \(P_{\text{f}}\), i.e., \(\frac{{T - T_{\text{s}} }}{T}\left( {b_{0} P_{\text{f}} \left( {1 - P_{\text{on}} } \right)} \right)\). On the contrary, if PU is actually active but spectrum is detected to be idle, SU transmits as if PU is inactive, and with \(c\) multiplied by activity probability \(P_{\text{on}}\) and probability \(\left( {1 - P_{\text{d}} } \right)\) during the left duration \(T - T_{\text{s}}\), i.e., \(\frac{{T - T_{\text{s}} }}{T}\left( {c\left( {1 - P_{\text{d}} } \right)P_{\text{on}} } \right)\), otherwise, if PU is actually active and spectrum is detected to be busy, users of two systems transmit at the same time with \(b\) multiplied by activity probability \(P_{\text{on}}\) as well as detection probability \(P_{\text{d}}\), i.e., \(\frac{{T - T_{\text{s}} }}{T}\left( {bP_{\text{d}} P_{\text{on}} } \right)\). Those correspond to the instantaneous TC given in states 1–5, which is respectively multiplied by time proportional factor and relevant probability. Finally, five parts are summed to get (19).

This completes the proof of Proposition 1.

Proposition 2

The TC in underlay mode is \(C_{\text{pc}}\):

$$C_{\text{pc}} = P_{\text{on}} b_{1} + b_{0}$$
(20)

Proof

In underlay mode, in order to satisfy the outage probabilities of both primary system and secondary system, SU will keep transmitting with \(b_{0}\) during the whole frame and PU transmits with \(b_{1}\) multiplied by activity probability \(P_{\text{on}}\), i.e., \(P_{\text{on}} b_{1}\). Two parts are summed to get (20).

This completes the proof of Proposition 2.

Proposition 3

The TC in single primary system mode is \(C_{\text{p}}\):

$$C_{\text{p}} = P_{\text{on}} e_{0}$$
(21)

Proof

PU transmits alone in the whole frame with its maximum user density which satisfies the outage probability of its own system. Combining the activity probability and the instantaneous TC in situation 1, we get (21).

This completes the proof of Proposition 3.

3.2 Ratios and Constraint

3.2.1 Ratio of Transmission Power

Whether a certain system uses the spectrum alone or shares it with the other system, it should meet the identical outage probability of the corresponding systems.

Proposition 4

The transmission power ratio which satisfies the outage probabilities of both primary system and secondary system is:

$$\left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right) \, ^{{\frac{2}{\alpha }}} = \frac{{\ln \left( {1 - P_{{{\text{out\_p}}}} } \right)d_{\text{c}}^{2} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} }}{{\ln \left( {1 - P_{{{\text{out\_c}}}} } \right)d_{\text{p}}^{2} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} }}$$
(22)

Proof

According to (5), we can get expression of \(P_{{{\text{out\_p}}}}\) and substitute it into (8), having

$$\lambda_{\text{p}}^{'} = \lambda_{\text{p}} + \lambda_{\text{c}} \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right)^{{\frac{2}{\alpha }}}$$
(23)

Similarly, we can get the expression of \(P_{{{\text{out\_c}}}}\) from (6) and substitute it into (10), having

$$\lambda_{\text{c}}^{'} = \lambda_{\text{c}} + \lambda_{\text{p}} \left( {\frac{{p_{\text{p}} }}{{p_{\text{c}} }}} \right) \, ^{{\frac{2}{\alpha }}}$$
(24)

Multiplying \(\left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right) \, ^{{\frac{2}{\alpha }}}\) on each side of (24), its right side becomes the same as the right part of (23), so the left side of two equations should be equal. We have

$$\lambda_{\text{p}}^{'} = \lambda_{\text{c}}^{'} \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right)^{{\frac{2}{\alpha }}}$$
(25)

(8) is divide by (10), we have

$$\frac{{\lambda_{\text{p}}^{'} }}{{\lambda_{\text{c}}^{'} }} = \frac{{\ln \left( {1 - P_{{{\text{out\_p}}}} } \right)d_{\text{c}}^{2} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} }}{{\ln \left( {1 - P_{{{\text{out\_c}}}} } \right)d_{\text{p}}^{2} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} }}$$
(26)

Combining (25) and (26), (22) can be derived.

This completes the proof of Proposition 4.

3.2.2 Ratio of User Density

Proposition 5

The user density ratio is:

$$\frac{{\lambda_{\text{p}} }}{{\lambda_{\text{c}} }} = \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right) \, ^{{\frac{2}{\alpha }}} \left( {\frac{{k^{'} }}{k}} \right) = \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right) \, ^{{\frac{2}{\alpha }}} \left( {\frac{1 - k}{k}} \right),\quad \left( {0 < k^{'} ,k < 1} \right)$$
(27)

where \(k = \lambda_{\text{c}} /\lambda_{\text{c}}^{'}\) is the proportional factor of secondary system user density in spectrum sharing mode over single secondary system mode, and \(k^{'} = \lambda_{\text{p}} /\lambda_{\text{p}}^{'}\) is the proportional factor of primary system user density in spectrum sharing mode over single primary system mode.

Proof

In order to meet the identical outage probability, it is known from the common knowledge, (23), and (24), the user density \(\lambda_{\text{p}}\) and \(\lambda_{\text{c}}\) in spectrum sharing mode are respectively lower than \(\lambda_{\text{p}}^{'}\) and \(\lambda_{\text{c}}^{'}\) in single system mode. Under the same outage probability, the spectrum can be shared by other systems only when the user density of present system is lower than its maximum value. According to (23) and proportional factor, we have

$$\lambda_{\text{p}}^{'} = k^{'} \lambda_{\text{p}}^{'} + k\lambda_{\text{c}}^{'} \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right)^{{\frac{2}{\alpha }}}$$
(28)

Substituting (25) into (28), we have

$$k^{'} = 1 - k$$
(29)

According to (25) and (29), (27) can be derived.

This completes the proof of Proposition 5.

(22) and (27) can offer a criterion for parameters designing in practical networks.

3.2.3 Constraint to Make Tc Increase When Spectrum is Shared

In order to analyze the TC in three modes, the first differential of function \(C_{\text{ts}} - C_{\text{pc}}\) is derived according to (19) and (20):

$$\frac{{d(C_{\text{ts}} - C_{\text{pc}} )}}{{d(T_{\text{s}} )}} = \frac{T}{{(T - T_{\text{s}} )^{2} }}(P_{\text{on}} e_{0} - P_{\text{on}} b_{1} - b_{0} )$$
(30)

It is shown from (30) that \(C_{\text{ts}} - C_{\text{pc}}\) is monotonic increasing of \(T_{\text{s}}\) when \(P_{\text{on}} e_{0} - P_{\text{on}} b_{1} - b_{0} > 0\), the maximum TC should be achieved when \(T_{\text{s}} = T\). Substituting \(T_{\text{s}} = T\) into (19), the maximum value is equal to (21), i.e., \(P_{\text{on}} e_{0}\). It means the TC is maximized when PU transmits alone without spectrum sharing. Therefore, the TC will be increased by spectrum sharing only if the followed constraint is satisfied:

$$P_{\text{on}} e_{0} - P_{\text{on}} b_{1} - b_{0} < 0$$
(31)

In this case, \(P_{\text{on}} e_{0} < P_{\text{on}} b_{1} + b_{0}\). According to (20) and (21), \(C_{\text{p}} < C_{\text{pc}}\). Therefore, when PU transmits alone, \(C_{\text{p}}\) can never be the highest TC and the maximum value is between \(C_{\text{ts}}\) and \(C_{\text{pc}}\). We assume the constraint (31) is maintained and ignore \(C_{\text{p}}\) in the following discussion.

3.3 Upper Bound and Accessing Strategy

3.3.1 Upper Bound

\(C_{\text{ts}} - C_{\text{pc}}\) is monotonic decreasing of \(T_{\text{s}}\) when \(P_{\text{on}} e_{0} - P_{\text{on}} b_{1} - b_{0} < 0\), the maximum TC should be achieved when \(T_{\text{s}} = 0\). According to (19), the theoretic value is:

$$C_{{{\text{max\_sharing}}}} = (a_{0} (1 - P_{\text{f}} ) + b_{0} P_{\text{f}} )(1 - P_{\text{on}} ) + (bP_{\text{d}} + c(1 - P_{\text{d}} ))P_{\text{on}}$$
(32)

When spectrum sensing is perfect (\(P_{\text{f}} = 0\) and \(P_{\text{d}} = 1\)), following (32), the upper bound for TC is:

$$C_{{{\text{max\_bound}}}} = a_{0} (1 - P_{\text{on}} ) + bP_{\text{on}}$$
(33)

Because \(P_{\text{f}}\) always approaches 0 and \(P_{\text{d}}\) always approaches 1, this upper bound is very tight.

3.3.2 Accessing Strategy

\(C_{{{\text{max\_bound}}}}\) can be viewed as the limit value. The maximum TC is denoted as \(C_{{{\text{our\_strategy}}}}\).

$$C_{{{\text{our\_strategy}}}} = \hbox{max} \{ C_{\text{ts}} ,C_{\text{pc}} \}$$
(34)

In order to reach the maximum TC, the SU should access the spectrum according to sensing time \(T_{\text{s}}\).

Assuming normalized sensing time \(t_{\text{s}} = \frac{{T_{\text{s}} }}{T}\), according to the monotonic decreasing character of function \(C_{\text{ts}} - C_{\text{pc}}\), it is also monotonic decreasing of \(t_{\text{s}}\). If the normalized sensing time \(t_{\text{s}}^{*}\) satisfies \(C_{\text{ts}} (t_{\text{s}}^{*} ) = C_{\text{pc}}\), the accessing strategy to reach the maximum TC is listed as follows:

  1. (a)

    When the normalized sensing time \(t_{\text{s}} < t_{\text{s}}^{*}\)(\(C_{\text{ts}} > C_{\text{pc}}\)), the secondary user should first sense the activity of primary user and then access, i.e., taking the overlay mode;

  2. (b)

    When the normalized sensing time \(t_{\text{s}} > t_{\text{s}}^{*}\)(\(C_{\text{ts}} < C_{\text{pc}}\)), the secondary user should not sense the activity of primary user but directly access the spectrum with acceptable density while keeping both the outage probabilities constraints of two systems satisfied, i.e., taking the underlay mode.

Proposition 6

\(t_{\text{s}}^{*}\) which satisfy \(C_{\text{ts}} (t_{\text{s}}^{*} ) = C_{\text{pc}}\) is:

$$t_{\text{s}}^{*} = \frac{{(1 - P_{{{\text{out\_c}}}} )(1 - P_{\text{on}} )(1 - k)}}{{(1 - P_{{{\text{out\_c}}}} )(1 - P_{\text{on}} ) + k((1 - P_{{{\text{out\_c}}}} )P_{\text{on}} - \left( {\frac{{\ln (1 - P_{{{\text{out\_p}}}} )d_{\text{c}}^{2} \varepsilon_{\text{c}}^{{\frac{2}{\alpha }}} }}{{\ln (1 - P_{{{\text{out\_c}}}} )d_{\text{p}}^{2} \varepsilon_{\text{p}}^{{\frac{2}{\alpha }}} }}} \right)(1 - P_{{{\text{out\_p}}}} )P_{\text{on}} )}}$$
(35)

Proof

According to \(C_{\text{ts}} (t_{\text{s}}^{*} ) = C_{\text{pc}}\), (19), and (20), we have

$$t_{\text{s}}^{*} P_{\text{on}} e_{0} + C_{{{\text{max\_sharing}}}} = P_{\text{on}} b_{1} + b_{0}$$
(36)

For simplification, we use \(C_{{{\text{max\_bound}}}}\) instead of \(C_{{{\text{max\_sharing}}}}\) to manipulate and substitute (33) into (36), having

$$t_{\text{s}}^{*} P_{\text{on}} e_{0} + (1 - t_{\text{s}}^{*} )(a_{0} (1 - P_{\text{on}} ) + bP_{\text{on}} ) = P_{\text{on}} b_{1} + b_{0}$$
(37)

Combining (7), (9), (11), (17), and (18) in the process, we have

$$t_{\text{s}}^{*} = \frac{{T_{\text{s}}^{*} }}{T} = \frac{{(1 - P_{{{\text{out\_c}}}} )(1 - P_{\text{on}} )(1 - k)}}{{(1 - P_{{{\text{out\_c}}}} )(1 - P_{\text{on}} ) + k\left( {(1 - P_{{{\text{out\_c}}}} )P_{\text{on}} - \left( {\frac{{p_{\text{c}} }}{{p_{\text{p}} }}} \right)^{{\frac{2}{\alpha }}} (1 - P_{{{\text{out\_p}}}} )P_{\text{on}} } \right)}}$$
(38)

According to (22), \(t_{\text{s}}^{*}\) expressed in (38) can be rewritten by (35).

This completes the proof of Proposition 6.

It should be noticed that SU will access the spectrum with its maximum user density when PU is undetected, which the outage probabilities \(P_{{{\text{out\_p}}}}^{'}\) and \(P_{{{\text{out\_c}}}}^{'}\) of both systems will change according to (15) and (16). However, this is neglected because detection issue has been studied in many other literatures, in which the missed detection probability \(1 - P_{\text{d}}\) can approach 0. So, here we mainly focus on maximum TC. Specially, when \(t_{\text{s}} < t_{\text{s}}^{*}\) and sensing accuracy is guaranteed, the shorter sensing time \(t_{\text{s}}\) is, the larger TC will be. It approaches \(C_{{{\text{max\_bound}}}}\) when \(t_{\text{s}}\) approaches 0.

4 Numerical Results

For verification, the used parameters and part of their value in various numerical analysis contexts are listed in Table 1.

Table 1 Summary of parameters in numerical analysis
Full size table

User density against outage probability is shown in Fig. 2. The primary system outage probability and secondary outage probability are the same in the range as horizontal axis shows. According to (22), (27), and proportional factor k = 0.2, with the same outage probability, the user density of each system in single system mode is equal to the sum of two systems user density subjected to (23) and (24). The user density of each system in sharing mode is less than that in the single mode. When SU uses less transmission power (\(p_{\text{p}} > p_{\text{c}}\)), the spectrum can afford more transmitting nodes of secondary system than the primary one, and the total user density of sharing mode (\(\lambda_{\text{p}} + \lambda_{\text{c}}\)) is larger than the one (\(\lambda_{\text{p}}^{'}\)) in single primary system but less than the one (\(\lambda_{\text{c}}^{'}\)) in single secondary system. It indicates spectrum should be shared especially by a high-power system to a low-power system.

Fig. 2
figure 2

User densities against outage probability

Full size image

TC against proportional factor k is shown in Fig. 3. We can see the curve of \(C_{{{\text{max\_sharing}}}}\) approximates the curve of \(C_{{{\text{max\_bound}}}}\) very well, which proves the accuracy of our approximation used in the above derivation. The TC in the underlay mode and overlay mode are higher than that in the single primary system mode. The curves of two spectrum sharing modes cross as the proportional factor k changes but the TC of our accessing strategy \(C_{{{\text{our\_strategy}}}} \,\) is always the larger one of them.

Fig. 3
figure 3

The TC against proportional factor k (\(P_{{{\text{out\_p}}}}\) = 0.08,\(P_{{{\text{out\_c}}}}\) = 0.1, \(t_{\text{s}}\) = 0.4)

Full size image

In Fig. 4, the TC in different spectrum sharing modes against outage probability is shown. First, the network \(C_{\text{p}}\) is the minimum one. Second, according to (35), parameters in Table 1, and k = 0.2, \(t_{\text{s}}^{*}\) is derived to be 0.56. When the normalized sensing time is 0.8, following our accessing strategy, the spectrum should be accessed by SU without sensing at all. \(C_{{{\text{our\_strategy}}}} \,\) is equal to the one in underlay mode, which is higher than the one in overlay mode. However, the situation will be different when sensing time changes.

Fig. 4
figure 4

The TC against outage probability with long sensing time

Full size image

As shown in Fig. 5, other parameters are the same as Fig. 4, only the normalized sensing time are changed into 0.2 and 0.4 respectively. According to our accessing strategy, overlay spectrum sharing mode should be taken when the sensing time is shorter than the \(t_{\text{s}}^{*}\) (i.e., 0.56 as above-mentioned) and \(C_{{{\text{our\_strategy}}}} \,\) is higher than that in single system mode and underlay mode. It also can be seen from Fig. 5, with the same false alarm probability and detection probability, \(C_{{{\text{our\_strategy}}}} \,\) will be further improved and even approach the upper bound when the sensing time decreases and approaches zero.

Fig. 5
figure 5

The TC against outage probability with short sensing time

Full size image

5 Conclusion

In this paper, the TC of cognitive radio networks in different spectrum sharing modes is obtained based on stochastic geometry theory. The ratios of transmission power and user density are found. The constraint is derived to make the TC increase when spectrum is shared. The upper bound of TC is obtained and an accessing strategy to reach the maximum value is proposed. In the spectrum sharing mode, the way SU access the spectrum is dependant on the sensing time. The TC derived by our accessing strategy is always larger than the one in single system mode or fixed spectrum sharing mode and it can approach the upper bound with high sensing performance. In the future, the sensing accuracy could be considered in overlay mode and the arbitrary user density with outage constraints could be discussed. Besides, the concrete and feasible control strategy to coordinate two user systems for sharing the spectrum with designated transmission power and user density will be further studied.