Probability-Based Multi-hop Diffusion Method for Influence Maximization in Social Networks

Abstract

Influence maximization is the problem of finding a subset of nodes that maximizes the spread of information in a social network. Many solutions have been developed, including greedy and heuristics based algorithms. While the former is very time consuming that might be impractical in many cases, the later is feasible in terms of computational time, but its influence spread is not guaranteed because of limitations in the algorithm. In this study, we propose a new heuristic algorithm which considers the propagation probabilities of nodes in the network individually and takes into account the effect of multi-hop neighbors, thus, it can achieve higher influence spread. A realistic network model with non-uniform propagation probabilities between nodes is assumed in our algorithm. We also examine the optimal number of hops of neighbors to be considered in the algorithm. Experiments using real-world social networks showed that our proposed method outperformed the previous heuristic-based approaches.

1 Introduction

Nowadays, social networks (SNs) play important roles as powerful media for broadcasting and collecting information. SN services allow users to share their activities and interesting news from other websites with the friends, as well as communicate directly to discuss issues such as sports, politics, etc. With the SNs emerging and quickly developing in the past few years, information diffusion has attracted considerable attention by researchers in different kinds of areas such as social advertising, viral marketing, etc. In the studies of information diffusion, a central problem that received much attention is the influence maximization problem, which specifies a small subset of individuals in a social network as seeds that produce a large word-of-mouth effect in the network.

Influence maximization problem was the first studied by Domingos and Richardson from algorithmic perspective [1, 2]. Kempe et al. [3] considered the problem as a discrete optimization problem and proved that the optimization problem is NP-hard. They proposed a greedy algorithm to approximate the optimal solution within a factor of $(1-1/e-\varepsilon )$, where $\varepsilon$ depends on the accuracy of influence spread estimation. In order to obtain an accurate estimate of influence spread, Kempe’s greedy algorithm run Monte-Carlo simulations of the influence cascade model for sufficiently many times, making it very slow and not scalable. Therefore, several studies were developed to optimize Kempe’s greedy algorithm in term of running time without affecting its guaranteed accuracy. The “cost-effective lazy forward” (CELF) optimization strategy [4] and CELF++ strategy [5] were proposed to reduce the complexity of Kempe’s greedy algorithm by exploiting the submodularity property of influence maximization. Chen et al. [6] proposed the NewGreedy algorithm and MixedGreedy algorithm. NewGreedy algorithm reuses the results of Monte Carlo simulations to estimate the influence spread for all candidate nodes in the same iteration. MixedGreedy algorithm integrated the advantages of both the CELF strategy and the NewGreedy algorithm. Unfortunately, even though those improved greedy algorithms can speed up the original greedy algorithm in several orders of magnitude, they are still impractical in real-life social networks.

A number of follow-up works tackle the problem by designing more efficient heuristics. Kimura and Saito [7] suggested the shortest-path based influence cascade models and proposed efficient algorithms to compute the influence spread under these models. Because these models are special models, this algorithm cannot be applied in general cases. Kim and Yoneki [8] proposed a new concept of k-neighbors selection for the diffusion process. In their diffusion model, every edge has the same propagation probability, which is too simple to correctly reflect the characteristics of the information diffusion process in real-world situations. Chen et al. [6] proposed the DegreeDiscount heuristic to find the effective seed nodes in feasible time. DegreeDiscount simply assumes that the nodes having more neighbors tends to have higher influence and consequently will be selected as seed nodes. This way of choosing seed nodes has two drawbacks. Firstly, the effects of two, three, or more hop neighbor nodes in the information diffusion process are ignored. Secondly, by assuming the node with high degree having higher influence, the current heuristic algorithms simply ignore the diversity of the propagation probabilities in the network. Two nodes having a tight relationship are likely to influence each other, which means the propagation probability between them would be high. The influence of a node depends on not only the number of neighbors but also the propagation probabilities between this node and its neighbors.

Recently, the research on using genetic algorithms (GA) for influence maximization is just starting and as preliminary works suggest, it can have a great potential in tackling the influence maximization problem. In Weskida et al. [9] used the genetic algorithm, which uses simple genetic operators typically used in discrete optimization, to tackle the influence maximization. The results show that the GA is at least as good as some of the known heuristics and outdoes the greedy algorithm for some data points. However, the running time is also the disadvantage of GA. Although the running time of GA is approximately half as big as the running time if the greedy algorithm, it is still significantly bigger than existing heuristic method.

In this study, we propose a new heuristic algorithm that addresses the limitations mentioned above. While the proposed algorithm still has a rapid calculation rate as other heuristic approaches, it can achieve higher influence spread by two major changes. Firstly, the effects of both direct and multi-hop neighbors are considered. Secondly, the diversity of the propagation probability between different pair of nodes are taken into account. We also examine the optimal number of hops of neighbor to be considered in the algorithm. To verify our analysis and to show the effectiveness of our influence maximization algorithm when applied in reality, we use the real-world data sets and conduct extensive simulations on realistic network model in which the propagation probabilities between users are non-uniform.

The remainder of this paper is organized as follows. Section 2 provides the background to our study and introduces our new heuristic algorithm. Section 3 presents our experimental setups and results. Finally, Sect. 4 offers the concluding remarks.

2 Probability-Based Multi-hop Diffusion Method

In this section, we present the problem statement and information diffusion model in Sect. 2.1. The proposed algorithm is introduced in Sect. 2.2. We consider the impact of three and more-hop neighbor in Sect. 2.3.

2.1 Problem Statement and Information Diffusion Model

A social network is modeled as an undirected graph $G = (V,E,P)$, where the set of nodes V represents all users in the network, the set of edges E represents the relationships between users, and P denotes the set of diffusion probabilities, which is the probability that the information spreads from one user to another user. In general, two users who have close relationship would have high diffusion probability since the information shared by one user is likely to be received by the other. Each edge (v, w) in the set E is mapped to a probability $p_{v,w}$ in the set P. This mapping is formalized as $p:E \rightarrow [0,1]$. The set of neighbor nodes of v is denoted as N(v). The degree of node v is denoted as $d_{v} = \left| {N(v)} \right|$. Express influence maximization as a discrete optimization problem, it can be described as below:

Given a social network $G = (V,E,P)$ and a parameter k, information spread in G by a specific diffusion model, the goal is to find a set S with k active nodes, which can result in the largest number of active nodes.

In this paper, we adopt the most standard information diffusion model, called the independent cascade (IC) model [10, 11]. The diffusion process starts with the initial set of active nodes S. Each active node v in S has only one chance to activate each of its inactive neighbors w. The probability that v successfully actives w is $p_{v,w}$. Note that the probability $p_{v,w}$ depends only on the characteristics of the connection between nodes. All newly activated nodes will be inserted to S. Then a new iteration of this process will run with these newly activated nodes. The diffusion process stops when there is no more node being activated.

2.2 Proposed Approach

The degree (i.e. number of neighbors) is a common parameter used to select the initial active nodes during information diffusion. The simplest method to use this parameter is selecting nodes with highest degree as the initial seed nodes. The DegreeDiscount [6] method used in IC model applies the same approach with the contributions of the already active neighbors being discounted and thus achieving higher accuracy.

However, both the Degree and DegreeDiscount method have the same drawback. Let us consider the following example. Assume that node v has |N(v)| neighbors, where the diffusion probability to each neighbor is $P_v = \{ {p_{v},w_{1}},{p_{v},w_{2}},\ldots ,{p_{v},w_{|N(v)|}}\} ,w_i \in N(v)$. Node u has |N(u)| neighbors, and $P_u = \{{p_{u},t_{1}},{p_{u},t_{2}},\ldots ,{p_{u},t_{|N(u)|}}\} , t \in N(u)$. Given the condition $|N\left( v \right) | > |N(u)|$ and $\sum \nolimits _{{\text{w}} \in N(v)} {{p_{v,{\text{w}}}} < \sum \nolimits _{t \in N(u)} {{p_{u,t}}} }$. In other words, node v has more neighbors, but the total probability that information from v spreads to its neighbors is lower than that of w. The question is which node u or v has greater influence. In this situation, the classic degree method and the DegreeDiscount heuristic approach will definitely choose node v as the seed node because it has the greatest number of neighbors. However, the size of the influenced area also depends on the diffusion probability. In some specific cases, where the difference in this probability is sufficiently large, the node with a smaller number of neighbors, but with high diffusion probability, may have a greater influence.

Our proposed approach takes the advantages of both the Degree and the DegreeDiscount method, and offers a better solution to the influence maximization problem. In our method, a seed node is chosen based on not only the number of neighbors but also its diffusion probability. In addition, the effect of two-hop away neighbors, which might have the strong impact on the information diffusion is also taken into account.

Fig. 1

Model used for information diffusion

Figure 1 illustrates our model. Node v is the seed node. Nodes $w_1$, $w_2$, $w_3$ are the neighbor nodes of v, which are connected to v with diffusion probabilities ${p_{v},w_{1}},{p_{v},w_{2}},{p_{v},w_{3}}$. The two-hops away neighbors of v are the neighbors of $w_1,w_2,w_3$. The diffusion path from a seed node to other nodes will create a tree without loops, where the seed node is the root.

In this paper, we propose a new measurement for evaluating the influence which takes into account the diffusion probability and the effect of two-hop neighbors:

$$\begin{aligned} dp_v = d_v + \sum \limits _{w \in N(v)}^{} {{p_{v,w}}} .{d_\text{{w}}}, \end{aligned}$$

(1)

where $dp_v$ is the diffusion score of node v, $d_v$ represents the degree of node v, and $d_w$ represents the degree of each two-hop neighbor w. The node with higher score of $dp_v$ will have higher chance to be selected as a seed node.

As in DegreeDiscount method, when calculating the degree of a node, the impact of the active neighbors will be subtracted from the final degree value of that node. In our method, the seed nodes must not be adjacent nodes.

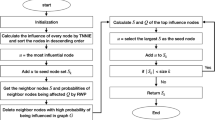
The pseudo-code of probability-based multi-hop diffusion algorithm is described in Algorithm 1. The subset of nodes selected to initiate the influence of diffusion (or the seed set) is S and n is the number of nodes in the networks. This algorithm uses the graph G and the parameter k as the input, and computes a seed set of candidates, where the goal is to maximize the ultimate number of nodes that accept information from the seed set. Our algorithm consists of two parts. Firstly, in Lines 2–5, the algorithm calculates the value of candidates by combine the degree and the diffusion probability according to Eq. 1. In this step, because the graph G is stored by adjacency list, the running time for evaluating the degree and value of candidates is total O(2m). Then in Lines 6–11, the algorithm selects the nodes with the highest values as seeding nodes, provided that the node selected is not a neighbor of the previous nodes. By using heap structure for storing dp[], the running time of this step is $O(k\log n)$. When k nodes are selected, the algorithm stop this process and return the seed set at Line 12. The total running time of Algorithm 1 is $O(k\log n + m)$, which is much faster than the original greedy algorithm with O(knNm) running time [3] and fast as well as DegreeDiscount algorithm with the same running time [6] in theory.

2.3 Impact of Three and More-Hop Neighbor

Figure 2 illustrates a graph with a seed node v, set of direct neighbors $H(1)=\{w_i\}$, set of two-hop neighbors $H(2)=\{u_i\}$, and set of three-hop neighbors $H(3)=\{t_i\}$. In Eq. 1, the effect of two-hop neighbors is taken into account by adding the term $\sum \nolimits _{w \in N(v)}^{} {{p_{v,w}}} .{d_w}$ to the diffusion score. Similarly, the impact of three-hop neighbors is counted by adding the term $\sum \nolimits _{u \in N(w)}^{} {{p_{v,u}}} .{d_u}$ into Eq. 1 as follow:

$$\begin{aligned} d{p_v} = {d_v} + \sum \limits _{w \in N(v)}^{} {{p_{v,w}}} .{d_\text{{w}}} + \sum \limits _{u \in N(\text{{w}})}^{} {{p_{v,u}}} .{d_u}, \end{aligned}$$

(2)

where $d_u$ is the degree of u and $p_{v,u}$ is the diffusion probability from v to u defined as:

$$\begin{aligned} p_{v,u}=p_{v,w}.p_{w,u}, \end{aligned}$$

(3)

where w is the bridge node between v and u.

Fig. 2

Model used for three-hop diffusion case

Through Fig. 2, it can be seen that the average number of activated nodes at first hop is given by:

$$\begin{aligned} {a_0} = \sum \limits _{{\text{{w}}_i} \in H(1)} {{p_{\text{{v,}}{\text{{w}}_i}}}} . \end{aligned}$$

(4)

The average number of activated nodes at two-hop away is given as:

$$\begin{aligned} {a_1} = \sum \limits _{{\text{{w}}_i} \in H(1)} {\sum \limits _{{\text{{u}}_j} \in H(2)} {{p_{v,{w_i}}}} {p_{{w_i},{u_j}}}} . \end{aligned}$$

(5)

And the average number of activated three-hop nodes is given as:

$$\begin{aligned} {a_2} = \sum \limits _{{\text{{w}}_i} \in H(1)} {\sum \limits _{{\text{{u}}_j} \in H(2)} {\sum \limits _{{t_k} \in H(3)} {{p_{v,{w_i}}}} } {p_{{w_i},{u_j}}}} {p_{{u_j},{t_k}}}. \end{aligned}$$

(6)

Because the diffusion probability of the nodes is small (<0.1), and the SNs are normally sparse as well, the value $a_2$ is very small, in comparison with $a_0$ and $a_1$. For that reason, the contribution of three and more hop neighbors can be ignored in the selection process. In the next section, we will demonstrate with experimental results that the three-hop neighbors have little impact on information diffusion.

3 Experiments

In this section, we conduct experiments on real data sets to show the performance of the proposed scheme compared to two existing algorithms: Degree and DegreeDiscount. Section 3.1 describes the experimental setups and Sect. 3.2 describes our experimental results.

3.1 Experimental Setups

In the comparison process, two real life data sets were used. Details of these data sets are given in Table 1.

Table 1 Data sets description

The first, which is called Netscience, contains a co-authorship network of scientists working on network theory and experiment, as compiled by Newman [12]. Each node in the network represents an author, and the number of edges between a pair of nodes is equal to the authors collaborated. The version used in the present study contains all of the network components, i.e., a total of 1589 scientists; with 2743 connections among them. The second data set, which is referred HEP-TH, contains the collaboration network of scientists posting preprints on the high-energy theory archive at www.arxiv.org, 1995–1999, as compiled by Newman [13]. Each node represents an author and an edge is added between two authors whenever they jointly wrote a paper. The numbers of nodes and edges are 8361 and 15,751, respectively. The two data sets are available at Mark Newman’s data sets website.¹

The experiment is implemented with the basic influence cascade model of the IC model. We compare the following algorithms:

• Greedy: The original greedy algorithm on the IC model [3].

• ProbDegree: Our new heuristic approach based on the degree, diffusion probability, and the effect of two-hops neighbors. (Algorithm 1).

• DegreeDiscount: The degree discount heuristic developed for the uniform IC model, which is also evaluated in [6].

• Degree: A basic heuristic that selects the candidate with the largest degree, which is also evaluated in [3].

All algorithms are written by C++ programming language. The running environment is a PC with Intel Core i3 3.33 GHz CPU, 4.00 GB main memory.

To get a detailed comparison of these algorithms’ performances, we calculate the information diffusion capacity with different numbers of initial active nodes (seed set size) for each algorithm, which ranged from 5 to 30. We run 20,000 iterated simulations with each five-node incremental step, and take the average value, to accurately estimate the influence size for every seed set selected by these algorithms.

Fig. 3

Diffusion probability of nodes in the Netscience data set

The diffusion probabilities between nodes are generated in two way: uniform distribution, and an exponential distribution. With uniform distribution, all probabilities have the same value of 0.1. With exponential distribution, the probabilities are generated randomly with exponential distribution and the mean of 0.1. Note that the exponential distribution is closer to the network in real life since relationship and interaction between different nodes are different and thus the diffusion probabilities between nodes would be different. Figure 3 shows the different diffusion probabilities of nodes in the Netscience data set.

3.2 Experimental Results

Figures 4 and 5 show the performance of four algorithms on two data sets with the diffusion probability following the uniform distribution $p = 0.1$. The x-axis indicates the number of seeds and y-axis indicates the number of influenced nodes. From the figures, we see that with all algorithms, the number of influenced nodes increases as the number of seed nodes increases. In addition, with all data sets, the Degree algorithm has the the worst while our proposed algorithm—ProDegree 2-hop has the best performance among three heuristic-based algorithms. More specifically, as can be seen in Fig. 4, our proposed algorithm outperforms the DegreeDiscount by 6 to 8% with the Netscience data set. With the HEP-TH data set, the performance of our proposed algorithm is higher than that of DegreeDiscount by 8 to 10% as can be seen in Fig. 5.

Fig. 4

Influence spread in Netscience with uniform distribution of diffusion probability

Fig. 5

Influence spread in HEP-TH with uniform distribution of diffusion probability

Fig. 6

Influence spread in Netscience with exponential distribution of diffusion probability

Fig. 7

Influence spread in HEP-TH with exponential distribution of diffusion probability

Figures 6 and 7 show the performance of various algorithms on two data sets with the diffusion probability following the exponential distribution with mean of 0.1. Similar to the previous case, with all algorithm, the number of influenced nodes increases when the size of seed set increases. In two data sets, the performance of Degree algorithm is still the worst, and that of the proposed algorithm is still the best among the three heuristic-based algorithms. As shown in Fig. 6, with Netscience data set, the proposed algorithm outperforms the DegreeDiscount by 8 to 11%. With the HEP-TH data set, the gap between the proposed algorithm and the DegreeDiscount is even larger: up to 16%. Since the diffusion probability between nodes in reality usually follows the exponential distribution, this result means that the proposed algorithm works even better in real-life applications.

Figures 1, 2, 3, and 4 also show the results on influence spreads of the traditional greedy algorithm. In general, in both two datasets, the Greedy produces the best influence spread, but our method—ProbDegree is very close to Greedy.

Fig. 8

Effects of multi-hop neighbors in the Netscience data set

Fig. 9

Effects of multi-hop neighbors in the HEP-TH data set

Figures 8 and 9 show the effect of three-hop neighbors on the proposed algorithm on two data sets Netscience and HEP-TH. The diffusion probabilities are generated following the exponential distribution. Note that the effect of three-hop neighbor is taken into account by using Eq. 2 for calculating the diffusion score. As mentioned earlier, the three-hop neighbors have small effect on the seed node selection since the probability for the information spread through three-hops is small. Figures 8 and 9 show that in both data sets, the proposed algorithm with considering the three-hop neighbor is almost identical with that of the proposed algorithm considering only two-hop neighbor. In other words, considering the effect of three-hop neighbor does not help much for choosing seed nodes. The same goes for the effect of four, five, or higher hop neighbors.

In term of running time, all of the heuristic-based algorithms find the seed set within an acceptable time. On the other hand, the greedy algorithm, which relies on a huge number of Monte Carlo simulations to achieve a fair solution, requires much longer time to find the seed set. More specifically, with the Netscience and HEP-TH datasets used in this paper, the greedy method takes several hours to finish the task while the heuristic-based methods, which use the simple operations to calculate the value and select the suitable nodes, only take a second. In large-scale social network, the running time of the greedy algorithm would be unacceptable.

From the conducted experiments, simulation results on real-world graphs show that the effects of multi-hop neighbors on the spread of information, and also demonstrate that our algorithm is more effective than previous heuristic-based algorithms for influence maximization problem in social networks.

4 Conclusion

In this study, we propose a probability-based multi-hop diffusion algorithm to solve the diffusion maximization problem in social network. Compared to existing algorithms, the proposed one takes into account the diversity of diffusion probabilities between nodes in the network and the effect of two-hop neighbors, thus achieving higher performance. Experiments are conducted using two real data sets to examine and compare the performance of the proposed algorithm and its counterparts. The results show that the proposed algorithm always outperforms its counterpart by 6–16%.