1 Introduction

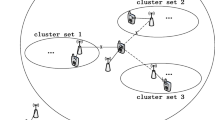
Nowadays, ultra-dense networks (UDNs) are deemed as a promising solution to fulfill the ever-increasing demands of wireless network capacity through the densification of access points (APs) far beyond today’s network [1]. Due to the ubiquitous APs in UDN, the distances between users and APs are statistically shortened. Thus, users are liable to access to closer APs, which is helpful to improve the network performance. However, the inter-cell interference (ICI) brought by the denser and closer interfering APs becomes even more severe, which is considered to be a main obstacle in UDNs. As a key technology for future dense networks, coordinated multi-point (CoMP) transmission is capable of mitigating the ICI efficiently as well as increasing the sum rate and cell-edge performance by grouping APs into different clusters to jointly serve the users within the cluster [2–5]. Generally, CoMP is mainly categorized into joint transmission (JT) and coordinated scheduling/beamforming (CS/CB, simplified as CSB for convenience). In JT (a.k.a. full coordination), a pool of APs are involved to jointly transmit useful signals to the users in the cluster. In this transmission mode, ICI can be effectively reduced by changing strongest interference into useful signals. In CSB (a.k.a. limited coordination), each user only receives the signal from its home AP and ICI is mitigated by efficient scheduling and beamforming. To illustrate specifically, these two CoMP schemes are shown in Fig. 1.

Fig. 1
figure 1

Illustration of two different CoMP schemes including JT and CSB

Full size image

While the network benefits greatly from CoMP transmission, applying coordination among APs also requires high capacity of backhaul links, which is one of the major setbacks of CoMP [6]. However, in practice, the capacity of backhaul links is restricted by the deployment costs of backhaul links [7]. And due to the growing demand for data devices and multimedia services, backhaul problem becomes even more serious, especially in CoMP systems where higher backhaul capacity (BC, also refers to backhaul consumption for simplicity) is required. Recently, the effect of BC constraint on CoMP transmission has attracted much attention, which can be recognized in two ways. The first one is that BC is implicitly reflected, for example, by cluster size or traffic load. The authors in [3] employ an efficiency metric called “per station goodput” taking multiple resources consumption into account, which limits network performance by cluster size. Meanwhile, a maximum loading based clustering and a biased signal strength based clustering algorithms are proposed, both of which put a constraint on BC by the load of each base station. The second one is a widely accepted indicator of BC quantified by the accumulated data rates of users associated with the AP, which is reasonable because data sharing is considered to be the dominant part of BC [8]. But most of the previous works only model it as a constraint to optimize network performance [9–15] and few works give the closed-form expressions of BC due to its complexity and intractability. In conclusion, there is one thing in common that limited BC poses a great threat to the network performance and deserves more attention.

Regardless of BC, JT is considered to be superior to CSB in achieving higher performance gains by changing strongest interference into desired signals while CSB aims at avoiding it. However, taking BC constraint into consideration, the aforementioned conclusion doesn’t necessarily hold and these two CoMP schemes become comparable to some degree. Compared with CSB, JT exhibits better performance at the expense of high BC for sharing CSI, users’ data and baseband received signals within the cluster [16]. But for CSB scheme, less BC is needed because only the CSI and other side information are required to be exchanged within the cooperative cluster [17]. In this light, it’s difficult to determine which scheme is preferable. Accordingly, there is a large body of literature focusing on performance comparison between JT and CSB transmission with limited BC. In [18], CSB mode shows better performance exhibiting by higher mean sum rate than JT with low BC constraint or high transmit power, which is illustrated by simulations but related theoretical analysis is absent. Similarly, the authors in [9] compare the average sum rates of these two schemes specifically and conclude that the performance of JT outperforms CSB with low edge SNR, at high BC constraint region, or in the case of more antennas at each AP. And in [19], spectrum efficiency (SE) comparison of multi-user multiple input multiple output (MU-MIMO) and different CoMP schemes including coordinated scheduling (CS), CSB and JT are conducted. Numerical results show that JT achieves highest SE in both cell center and cell edge for intra- and inter- site CoMP transmissions, then followed CS and CSB, and the worst is MU-MIMO. Meanwhile, energy efficiency (EE) comparison of JT and CSB is carried out in [16] and conclusions reveal that JT provides more EE while CSB requires lower BC. In conclusion, the prior works imply that either of these two schemes shows its advantages respectively in different cases. Additionally, there is a tradeoff between performance gain (mean sum rate, SE and EE) and operational expense (BC), which is also pointed out in [6] and [20].

To the best of our knowledge, there are a few defects in these precious works and some open questions still exist:

  1. (1)

    Although BC is crucial to evaluate the network operational expense, it’s always regarded as a constraint to optimize network performance in [9–15] and related theoretical analysis is rarely mentioned due to its complexity and intractability, let alone the explicit quantification of BC.

  2. (2)

    Previous literature [9, 16, 18, 19] mainly focus on the performance comparison of the two CoMP schemes from the user’s view concerning mean sum rate, SE as well as EE. Whereas, few works involves the comparison from a network perspective taking both of users’ performance and APs’ BC into account, which also reveals the lack of relevant network performance metrics.

  3. (3)

    Cluster size issue especially the optimal cluster size for various types of CoMP schemes has been recognized as a critical and urgent problem [21]. However, few works study the impact of cluster size on the network performance theoretically and give out the optimal cluster size but only show its influence by simulations.

Focusing on the above issues, this paper carries out the performance analysis of both JT and CSB in downlink UDN with limited BC. More specifically, the performance comparison of these two schemes is conducted from three aspects: a typical user’s perspective, a typical AP’s perspective and a network perspective. And the main contributions are summarized as follows:

  • Explicit qualification of BC For the two CoMP schemes, per-AP BC is explicitly quantified and given by close-forms expressed as the function of cluster size and AP density. As far as we know, we are the first to give the closed-form of BC to measure the backhaul cost for data sharing.

  • New performance metrics For a typical AP, successful serving probability (SSP) is propounded to capture its robustness to limited BC. Meanwhile, we also propose a network performance metric called effective ergodic capacity (EEC) considering performance gain (EC) and backhaul cost (SSP) simultaneously, which aims at evaluating JT and CSB from a network perspective.

  • Comprehensive comparison Unlike unilateral comparison between JT and CSB in [9, 16, 18, 19], our paper evaluate these two schemes roundly from a typical user’s perspective, a typical AP’s perspective as well as a network perspective.

  • Optimal cluster size With the help of the proposed performance metrics (SSP and EEC) and mean approximation method, the optimal cluster size problem is investigated theoretically and also verified by simulation, which provides useful insight for the set of cluster size in practical.

The rest of the paper is organized as follows. Section 2 introduces the system model. Section 3 conducts performance comparison between JT and CSB in theoretical from the aspects of a typical user and a typical AP as well as from a network perspective. Meanwhile, related performance metrics including CP, EC, BC, SSP and EEC as well as their approximations are derived. Then numerical and simulation results are shown to compare the performance of these two schemes in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 System Model

Consider a single-tier downlink UDN with single-antenna APs and single-antenna users, where APs and users are distributed according to two independent homogeneous Poisson point processes (HPPPs) \(\Phi_{a}\) and \(\Phi_{u}\) with density \(\lambda_{a}\) and \(\lambda_{u}\) respectively.Footnote 1 Specially, \(\lambda_{a}\) may be close to or even larger than \(\lambda_{u}\) due to the characteristic of UDNs. Without loss of generality, we focus the analysis on a typical user (denoted by \(U_{0}\)) and a typical AP (denoted by \(AP_{0}\)) located at the origin.

In this paper, user-centric clustering method is adopted because its advantages in allowing each user to select most beneficial serving APs in the whole network coverage and removing the traditional cell edges when compared with disjoint clustering method [3, 22, 23]. Specifically, each user can select a set of beneficial APs from \(\Phi_{a}\) as a cluster \(\Phi_{c}\) based on the average reference signal received power (RSRP) maximization strategy, which is similar to [24], i.e., n closest APs are assigned to each user. For CS, each user is only served by one AP which can provide the maximum RSRP, i.e., the closest AP while other APs within the cluster aim at avoiding ICI. For JT, each user can receive a sum of multipath useful signals from all the APs within the cluster, i.e., n closest APs. The intra-cluster interference is mitigated by utilizing orthogonal resources in the overlapped parts of different clusters while the APs outside the cluster act as interfering APs.

In this paper, the large-scale fading is expressed by \(r_{i}^{ - \alpha }\), where \(r_{i}\) denotes the distance between the \(ith\) closest AP (denoted by \(AP_{i}\)) and \(U_{0}\), and \(\alpha\) is the path loss exponent. For the small-scale fading, we assume that \(U_{0}\) experiences Rayleigh fading from its serving APs, which is denoted by \(h_{i}\) and follows an exponential distribution with unit mean, i.e. \(h_{i} \sim \exp (1)\). Correspondingly, the distance between the \(ith\) closest user (denoted by \(U_{i}\)) and \(AP_{0}\) is represented by \(l_{i}\), and \(g_{i}\) denotes the small-scale fading from \(AP_{0}\) to \(U_{i}\), which also follows \(\exp (1)\). Therefore, the power received by \(U_{0}\) from \(AP_{i}\) (\(U_{i}\) from \(AP_{0}\)) can be given by \(P_{t} h_{i} r_{i}^{ - \alpha }\) (\(P_{t} g_{i} l_{i}^{ - \alpha }\)), where \(P_{t}\) is the transmit power and assumed to be identical for all the APs. In addition, the noise is assumed additive with power \(\sigma^{2}\). Then the received signal to interference and noise ratio (SINR) of \(U_{0}\) concerning JT and CSB can be given by

$$SINR_{n}^{JT} = \frac{{\sum\nolimits_{{k \in \Phi_{c} }} {P_{t} h_{k} r_{k}^{ - \alpha } } }}{{\sum\nolimits_{{m \in \Phi_{a} \backslash \Phi_{c} }} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }} = \frac{{\sum\nolimits_{k = 1}^{n} {P_{t} h_{k} r_{k}^{ - \alpha } } }}{{\sum\nolimits_{m > n} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }}$$
(1)

and

$$SINR_{n}^{CSB} = \frac{{P_{t} h_{1} r_{1}^{ - \alpha } }}{{\sum\nolimits_{{m \in \Phi_{a} \backslash \Phi_{c} }} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }} = \frac{{P_{t} h_{1} r_{1}^{ - \alpha } }}{{\sum\nolimits_{m > n} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }}$$
(2)

We suppose that each AP is connected with the central unit (CU) through a limited-capacity backhaul link as is depicted in Fig. 1. Some necessary information including the downlink data, CSI, and baseband received signals is conveyed via the backhaul links whose capacities are all assumed to be \(\gamma^{BC}\). Note that we only consider BC as the users’ data sharing budget which is the dominant part of BC [8].

3 Performance Analysis

In this section, performance analysis of JT and CSB is conducted from the perspectives of a typical user and a typical AP as well as from a network perspective. By modeling the APs and the users into two independent HPPPs like [2, 24–26], we can use the theoretical results of stochastic geometry in [27–29] and derive closed-forms of related performance metrics for efficient theoretical comparison and numerical computation of different CoMP schemes.

3.1 Joint Transmission (JT)

JT with user-centric clustering refers to the case in which all the coordinated APs form a network MIMO by transmitting signals to the centric user of the cluster. Focusing on a typical user located at the origin, we have the following theorems.

3.1.1 Performance Analysis of a Typical User

3.1.1.1 Coverage Probability (CP)

CP specifies the probability that a user is able to access to the network under a target SINR threshold, which can also be viewed as the fraction of users in the network coverage.

Theorem 1

The CP with threshold \(\theta\) for a typical user in UDN downlink systems with JT can be expressed by

$$\begin{aligned} CP_{n}^{JT} \left( {\theta ,\lambda_{a} ,\alpha } \right) & = \int\limits_{{0 < r_{1} < \cdots < r_{n} < \infty }} {\exp \left( { - \frac{{\pi \lambda_{a} \theta^{{\frac{2}{\alpha }}} \int_{{\zeta_{cp}^{JT} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left( {\sum\nolimits_{k = 1}^{n} {r_{k}^{ - \alpha } } } \right)^{{\frac{2}{\alpha }}} }}} \right)} \\ & \quad \times \exp \left( { - \frac{{\theta \sigma^{2} }}{{P_{t} \sum\nolimits_{k = 1}^{n} {r_{k}^{ - \alpha } } }}} \right)f_{R} \left( {r_{1} , \ldots ,r_{n} } \right)dr_{1} \ldots dr_{n} \\ \end{aligned}$$
(3)

where \(\zeta_{cp}^{JT} = \theta^{{ - \frac{2}{\alpha }}} \left( {\sum\nolimits_{k = 1}^{n} {r_{k}^{ - \alpha } } } \right)^{{\frac{2}{\alpha }}} r_{n}^{2}\) and the joint distance distribution of \(\left\{ {r_{1} ,r_{2} , \ldots ,r_{n} } \right\}\) is \(f_{R} \left( {r_{1} ,r_{2} , \ldots ,r_{n} } \right) = e^{{ - \pi \lambda_{a} r_{n}^{2} }} \left( {2\pi \lambda_{a} } \right)^{n} r_{1} r_{2} \cdots r_{n} dr_{1} dr_{2} \cdots dr_{n}\) [30].

Proof

See Appendix 1.

Note that the above expression is still too complicated due to the n-fold integrals and the inaccessible probability distribution function (PDF) of \(\sum\nolimits_{k = 1}^{n} {r_{k}^{ - \alpha } }\). For better analysis of the impact of cluster size theoretically, the approximation form expressed by \(n\) is highly expected, which is specified as follows.

Lemma 1

Considering the property of HPPP that the accumulated area \(\pi r_{n}^{2}\) follows gamma distribution, i.e., \(\pi r_{n}^{2} \sim \Gamma (n,\frac{1}{{\lambda_{a} }})\) , the expectation of \(r_{n}^{2}\) and \(r_{n}^{ - \alpha }\) can be derived as

$$E\left( {r_{n}^{2} } \right) = \frac{n}{{\pi \lambda_{a} }}$$
(4)

and

$$E\left( {r_{n}^{ - \alpha } } \right) = \left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} \Gamma \left( {n - \frac{\alpha }{2}} \right)/\Gamma \left( n \right);\left( {n \ge \alpha /2} \right) .$$
(5)

Corollary 1

Utilizing the expectation to perform approximation proves to be feasible and accurate [20]. Hence, the CP can be approximated as

$$\begin{aligned} CP_{n}^{JT} \left( {\theta ,\lambda_{a} ,\alpha } \right) & \approx \int\limits_{{0 < r_{1} < \cdots < r_{\beta } < \infty }} {\exp \left\{ { - \frac{{\theta^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{cp}^{{^{JT} }} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left[ {\sum\nolimits_{i = 1}^{\beta } {\frac{{r_{i}^{ - \alpha } }}{{\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} }} + } \sum\nolimits_{k = \beta + 1}^{n} {\frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} }}} \right.} \\ & \quad \left. { - \frac{{\theta \sigma^{2} }}{{P_{t} \left[ {\sum\nolimits_{i = 1}^{\beta } {r_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{n} {\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]}}} \right\}f_{R} \left( {r_{1} , \ldots ,r_{\beta } } \right)dr_{1} \cdots dr_{\beta } \\ \end{aligned}$$
(6)

where \(\beta = \left\lfloor {\alpha /2} \right\rfloor\), (\(ith\) is the floor function) and

$$\tilde{\zeta }_{cp}^{JT} = n\theta^{{ - \frac{2}{\alpha }}} \left[ {\sum\nolimits_{i = 1}^{\beta } {\frac{{r_{i}^{ - \alpha } }}{{\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} }} + } \sum\nolimits_{k = \beta + 1}^{n} {\frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} .$$

By approximation, the computational complexity of CP is largely reduced and becomes much easier to compute because the number of integrations of (6) decreases from \(n\) to \(\beta\) (1–2). For the ease of evaluations, a special case with \(\alpha = 4\) and \(\sigma^{2} = 0\) (no noise) is considered, where (6) can be simplified to

$$\begin{aligned} CP_{n}^{JT} \left( {\theta ,\lambda_{a} ,4} \right) &\approx \int\limits_{{0 < r_{1} < r_{2} < \infty }} {\exp \left( { - \frac{{\theta^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \left( {\tilde{\zeta }_{cp}^{JT} \left| {_{\alpha = 4} } \right.} \right)} \right)}}{{\left[ {\left( {r_{1}^{ - 4} + r_{2}^{ - 4} } \right)/\left( {\pi \lambda_{a} } \right)^{2} + g\left( n \right)} \right]^{{\frac{1}{2}}} }}} \right)} \hfill \\ & \quad\times f_{R} \left( {r_{1} ,r_{2} } \right)dr_{1} dr_{2} ;(n \ge 2) \hfill \\ \end{aligned}$$
(7)

where \(\tilde{\zeta }_{cp}^{JT} \left| {_{\alpha = 4} } \right. = n\theta^{{ - \frac{1}{2}}} \left( {\left( {r_{1}^{ - 4} + r_{2}^{ - 4} } \right)/\left( {\pi \lambda_{a} } \right)^{2} + g\left( n \right)} \right)^{{\frac{1}{2}}}\) and \(g(n) = \frac{n - 2}{n - 1}\).

3.1.1.2 Ergodic Capacity (EC)

The discussion related to the EC of a typical user is conducted following similar steps to CP in this part and the detailed proof lines are omitted to avoid unnecessary repetition.

Theorem 2

The EC (bit/s/Hz) of a typical user in UDN downlink systems with JT can be given by

$$\begin{aligned} EC_{n}^{JT} \left( {\lambda_{a} ,\alpha } \right) & = {\mathbb{E}}\left[ {\ln \left( {1 + SINR_{n}^{JT} } \right)} \right] \\ & \approx \int\limits_{{0 < r_{1} < \cdots < r_{\beta } < \infty }} {\int\limits_{t > 0} {\exp \left\{ - \frac{{\left( {e^{t} - 1} \right)^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{ec}^{JT} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left[ {\sum\nolimits_{i = 1}^{\beta } {\frac{{r_{i}^{ - \alpha } }}{{\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} }} + } \sum\nolimits_{k = \beta + 1}^{n} {\frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} }} \right.}}\\ & \quad \left. - \frac{{\left( {e^{t} - 1} \right)\sigma^{2} }}{{P_{t} \left[ {\sum\nolimits_{i = 1}^{\beta } {r_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{n} {\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]}}\right\} dt \times f_{R} \left( {r_{1} , \cdots ,r_{\beta } } \right)dr_{1} \cdots dr_{\beta } \\ \end{aligned}$$
(8)

where \(\tilde{\zeta }_{ec}^{JT} = n\left( {e^{t} - 1} \right)^{{ - \frac{2}{\alpha }}} \left[ {\sum\nolimits_{i = 1}^{\beta } {\frac{{r_{i}^{ - \alpha } }}{{\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} }} + } \sum\nolimits_{k = \beta + 1}^{n} {\frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}}\).

Similarly, it allows simplification of (8)–(9) in the case of \(\alpha = 4\) and \(\sigma^{2} = 0\), which is shown as

$$\begin{aligned} EC_{n}^{JT} \left( {\lambda_{a} ,4} \right) & \approx \int\limits_{{0 < r_{1} < r_{2} < \infty }} {\int\limits_{t > 0} {\exp \left( { - \frac{{\left( {e^{t} - 1} \right)^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \left( {\tilde{\zeta }_{ec}^{JT} \left| {_{\alpha = 4} } \right.} \right)} \right)}}{{\left[ {\frac{{\left( {r_{1}^{ - 4} + r_{2}^{ - 4} } \right)}}{{\left( {\pi \lambda_{a} } \right)^{2} }} + g\left( n \right)} \right]^{{\frac{1}{2}}} }}} \right)} } dt \\ & \quad \times f_{R} \left( {r_{1} ,r_{2} } \right)dr_{1} dr_{2} ;(n \ge 2) \\ \end{aligned}$$
(9)

where \(\tilde{\zeta }_{ec}^{JT} \left| {_{\alpha = 4} } \right. = n\left( {e^{t} - 1} \right)^{{ - \frac{1}{2}}} \left[ {\frac{{\left( {r_{1}^{ - 4} + r_{2}^{ - 4} } \right)}}{{\left( {\pi \lambda_{a} } \right)^{2} }} + g\left( n \right)} \right]^{{\frac{1}{2}}}\).

According to (6)–(9), it can be clearly seen that both CP and EC are an increasing function of cluster size. Meanwhile, we can infer that CP and EC also increase with AP density, which can be explained as: Take the CP in (6) for example. There are two parts in the exponent of integration variable. The first part is hardly affected by \(\lambda_{a}\) since \({\mathbb{E}}\left[ {\frac{{r_{i}^{ - \alpha } }}{{\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}} }}} \right] = {\mathbb{E}}\left[ {\frac{1}{{\left( {\lambda_{a} \pi r_{i}^{2} } \right)^{{\frac{\alpha }{2}}} }}} \right] = i^{{ - \frac{\alpha }{2}}}\) while the second part grows with \(\lambda_{a}\) because the corresponding increase of both \(\sum\nolimits_{i = 1}^{\beta } {r_{i}^{ - \alpha } }\) and \(\left( {\pi \lambda_{a} } \right)^{{\frac{\alpha }{2}}}\). It follows that either of a large cluster size and a denser network is beneficial to improve the network performance in UDN.

Note that the aforementioned performance gains are derived from the view of a typical user. Meanwhile, the variation of cluster size and AP density would also influence the performance of APs. In this light, the performance analysis from the aspect of AP is shown in the following part to provide a measurement reference for BC.

3.1.2 Performance Analysis of a Typical AP

Concerning user-centric clustering method in UDN, each user is able to choose n closest serving APs to form a “virtual cell” (the left shaded area in Fig. 2) [31]. And in terms of a typical AP, it can be considered that there are \(k_{JT}\) users in its coverage (the right shaded area in Fig. 2) and the typical AP need to exchange all these users’ data information with its coordinated APs. Likewise, the related theorems focus on a typical AP located at the origin can be given.

Fig. 2
figure 2

Illustration of an AP cluster from the view of a typical user (left) and AP coverage from the view of a typical AP (right) with JT

Full size image
3.1.2.1 Backhaul Consumption (BC)

As assumed before, we only consider the backhaul required for sharing the users’ data which is equal to the accumulated rates of users associated with the typical AP.

Theorem 3

The BC (bit/s/Hz) of a typical AP in UDN downlink systems with JT is

$$\begin{aligned} BC_{n}^{JT} \left( {\lambda_{a} ,\alpha } \right) & \approx \int\limits_{{0 < l_{1} < \cdots < l_{\beta } < \infty }} {\int\limits_{t > 0} {\exp \left\{ { - \frac{{\pi \lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{bc}^{JT} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{JT} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} }}} \right.} } \\ & \quad \left. { - \frac{{\left( {e^{t} - 1} \right)\sigma^{2} }}{{P_{t} \left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{JT} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]}}} \right\}dt \times f_{L} \left( {l_{1} , \cdots ,l_{\beta } } \right)dl_{1} \cdots dl_{\beta } \\ \end{aligned}$$
(10)

where \(k_{JT} = \left\lceil {n\lambda_{u} /\lambda_{a} } \right\rceil\), \(\tilde{\zeta }_{bc}^{JT} = \frac{{n\left( {e^{t} - 1} \right)^{{ - \frac{2}{\alpha }}} }}{{\pi \lambda_{a} }}\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{JT} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}}\) , the joint distance distribution of \(\left\{ {l_{1} ,l_{2} , \ldots ,l_{n} } \right\}\) is \(f_{L} \left( {l_{1} , \ldots ,l_{{k_{JT} }} } \right) = e^{{ - \pi \lambda_{u} l_{{k_{JT} }}^{2} }} \left( {2\pi \lambda_{u} } \right)^{{k_{JT} }} l_{1} \ldots l_{{k_{JT} }}\) and the distance distribution of \(r_{n}\) is \(f_{R} \left( {r_{n} } \right) = \frac{{2\left( {\pi \lambda_{a} } \right)^{n} }}{{\left( {n - 1} \right)!}}r_{n}^{2n - 1} e^{{ - \pi \lambda_{a} r_{n}^{2} }}\).

Proof

See Appendix 2.

In the special case with \(\alpha = 4\) and \(\sigma^{2} = 0\), (10) can be simplified to

$$\begin{aligned} BC_{n}^{JT} \left( {\lambda_{a} ,4} \right) & \approx \int\limits_{{0 < l_{1} < l_{2} < \infty }} {\int\limits_{t > 0} {\exp \left( { - \frac{{\pi \lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \tilde{\zeta }_{bc}^{JT} \left| {_{\alpha = 4} } \right.} \right)}}{{\left[ {l_{1}^{ - 4} + l_{2}^{ - 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{JT} } \right)} \right]^{{\frac{1}{2}}} }}} \right)} } dt \\ & \quad \times \,f_{L} \left( {l_{1} ,l_{2} } \right)dl_{1} dl_{2} \\ \end{aligned}$$
(11)

where \(\tilde{\zeta }_{bc}^{JT} \left| {_{\alpha = 4} } \right. = \frac{{n\left( {e^{t} - 1} \right)^{{ - \frac{1}{2}}} }}{{\pi \lambda_{a} }}\left[ {l_{1}^{ - 4} + l_{2}^{ - 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{JT} } \right)} \right]^{{\frac{1}{2}}}\).

Comparison between (8) and (10) reveals that EC and BC share the similar form with a slight difference in the denominator of the exponent part. This is because these two metrics aim at evaluating the network from different views. And interestingly, we find that (11) is also an increasing function of cluster size (BC increases with \(k_{JT} = \left\lceil {n\lambda_{u} /\lambda_{a} } \right\rceil\)) but decline with AP density. It follows that network benefits from a larger cluster size at the expense of higher BC while a denser deployment of network can help to release each AP’s burden.

3.1.2.2 Successful Serving Probability (SSP)

To offer a measurement of the robustness to limited BC for the AP, we define SSP as the probability that per-AP BC is subject to a constraint \(\gamma^{BC}\). In other words, for the user, there’s no point in achieving higher performance gain if the BC of its serving APs exceeds the capacity of backhaul links.

Theorem 4

Given the BC constraint \(\gamma^{BC}\)(bit/s/Hz), the SSP \(p_{s}^{JT}\) in UDN downlink systems with JT can be given by

$$\begin{aligned} p_{s}^{JT} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right) & \approx 1 - \int\limits_{{0 < l_{1} < \cdots < l_{\beta } < \infty }} {\exp \left\{ { - \frac{{\pi \lambda_{a} \left( {e^{{\gamma^{BC} }} - 1} \right)^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{ssp}^{JT} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{JT} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} }}} \right.} \\ & \quad \left. { - \frac{{\left( {e^{{\gamma^{BC} }} - 1} \right)\sigma^{2} }}{{P_{t} \left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{JT} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]}}} \right\}f_{L} \left( {l_{1} , \ldots ,l_{\beta } } \right)dl_{1} \cdots dl_{\beta } \\ \end{aligned}$$
(12)

where \(\tilde{\zeta }_{ssp}^{JT} = \frac{{n\left( {e^{{\gamma^{BC} }} - 1} \right)^{{ - \frac{2}{\alpha }}} }}{{\pi \lambda_{a} }}\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{JT} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}}\).

Proof

See Appendix 3.

Similarly, in the case of \(\alpha = 4,\sigma^{2} = 0\), (12) can also be simplified by

$$\begin{aligned} \tilde{p}_{s}^{JT} \left( {\gamma^{BC} ,\lambda_{a} ,4} \right) & = 1 - \int\limits_{{0 < l_{1} < l_{2} < \infty }} {\exp \left( { - \frac{{\pi \lambda_{a} \left( {e^{{\gamma^{BC} }} - 1} \right)^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \tilde{\zeta }_{ssp}^{JT} \left| {_{\alpha = 4} } \right.} \right)}}{{\left[ {l_{1}^{ - 4} + l_{2}^{ - 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{JT} } \right)} \right]^{{\frac{1}{2}}} }}} \right)} \\ & \quad \times f_{L} \left( {l_{1} ,l_{2} } \right)dl_{1} dl_{2} \\ \end{aligned}$$
(13)

where \(\tilde{\zeta }_{ssp}^{JT} \left| {_{\alpha = 4} } \right. = \frac{{n\left( {e^{{\gamma^{BC} }} - 1} \right)^{{ - \frac{1}{2}}} }}{{\pi \lambda_{a} }}\left[ {l_{1}^{ - 4} + l_{2}^{ - 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{JT} } \right)} \right]^{{\frac{1}{2}}}\).

The above analysis demonstrates that: although JT is expected to have a higher SSP with the increase of cluster size (SSP increases with \(k_{JT} = \left\lceil {n\lambda_{u} /\lambda_{a} } \right\rceil\)) and AP density, the SSP is restricted by BC constraint.

3.1.3 Performance Analysis from a Network Perspective

In this part, EEC is proposed to provide a comprehensive and quantitative picture of the performance of CoMP schemes with limited BC. EEC is defined as the available effective EC for users under a given BC constraint \(\gamma^{BC}\) and it can also be interpreted as the part of EC successfully provided by serving APs. In this light, EEC introduces a balance between the user’s performance gain and the AP’s BC. More elaborately, the EEC (bit/s/Hz) of a typical user in UDN downlink systems with JT can be expressed by

$$C_{eff}^{JT} \left( {n,\lambda_{a} ,\alpha ,\gamma^{BC} } \right) = p_{s}^{JT} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right) \times EC_{n}^{JT} \left( {\lambda_{a} ,\alpha } \right)$$
(14)

where \(EC_{n}^{JT} \left( {\lambda_{a} ,\alpha } \right)\) and \(p_{s}^{JT} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right)\) are given by (8) and (12).

Considering a special case of \(\alpha = 4\) and \(\sigma^{2} = 0\), the approximation of (14) can be simplified as

$$\begin{aligned} \tilde{C}_{eff}^{JT} \left( {n,\lambda_{a},4,\gamma^{BC} } \right) & \approx p_{s}^{JT} \left({\gamma^{BC} ,\lambda_{a} ,4} \right) \times EC_{n}^{JT} \left({\lambda_{a} ,4} \right) \\ & = \left\{ {1 - \int\limits_{{0 < l_{1} < l_{2} < \infty }} {\exp \left( { - \frac{{\pi \lambda_{a} \left( {e^{{\gamma^{BC} }} - 1} \right)^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \tilde{\zeta }_{bc}^{JT} \left| {_{\alpha = 4} } \right.} \right)}}{{\left[ {l_{1}^{ - 4} + l_{2}^{- 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{JT} } \right)} \right]^{{\frac{1}{2}}} }}} \right)} } \right. \\ & \quad \left. \times\, f_{L} \left( {l_{1} ,l_{2} } \right)dl_{1} dl_{2} \right\} \\&\quad \times \left\{ {\int\limits_{{0 < r_{1} < r_{2} < \infty }} {\int\limits_{t > 0} {\exp \left( { - \frac{{\pi \lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \tilde{\zeta }_{ec}^{JT} \left| {_{\alpha = 4} } \right.} \right)}}{{\left[ {r_{1}^{ - 4} + r_{2}^{ - 4} + \left( {\pi \lambda_{a} } \right)^{2} g\left( n \right)} \right]^{{\frac{1}{2}}} }}} \right)} } dt} \right. \\ & \quad \left. \times\, f_{R} \left( {r_{1} ,r_{2} } \right)dr_{1} dr_{2} \right\} \\ \end{aligned}$$
(15)

According to (15), we notice that there are three main influence factors: AP density, cluster size and BC threshold. With respect to AP density, a denser network (increasing AP density) is beneficial to both of improving EC and releasing AP’s burden, which brings high EEC gain. For BC threshold, EEC grows with the increase of BC threshold due to more relaxed constraint. And for the cluster size, although JT is expected to have a higher EC with the increase of cluster size, the EEC is restricted by BC constraint reflected by a lower SSP. However, it’s not easy to tell which one is dominant. In the following, two cases are thereby considered, i.e., low BC constraint case and high BC constraint case.

In the case of low BC constraint, as cluster size increases, it’s the improvement of EC gain that matters at first but the decline of SSP becomes dominant gradually. In this context, an optimal size is expected to be found to achieve a tradeoff between the performance gain of the user and the BC of the AP, which can be obtained by

$$N_{opt}^{JT} = \arg \mathop {\hbox{max} }\nolimits_{n} C_{eff}^{JT} \left( {n,\lambda_{a} ,\alpha ,\gamma^{BC} } \right)$$
(16)

In the case of high BC constraint, EEC would keep increasing with cluster size, which can be explained by the predominant growing EC under relaxed BC constraint. In this case, the optimal cluster size may not be got in theoretical. Hence, we can conclude that the existence of optimal cluster size remains agnostic and depends on the related factors including BC threshold and AP density.

3.2 Coordinated Scheduling/Beamforming (CSB)

In this section, we turn our attention to the performance analysis of CSB transmission. CSB with user-centric clustering refers to the CoMP strategy in which only the nearest AP is selected to transmit useful signals within the cluster while the other APs aim at interference cancellation. Since the analysis of CSB is easier to handle than JT, similar steps are followed and related derivations are simplified.

3.2.1 Performance Analysis of A Typical User

3.2.1.1 Coverage Probability (CP)

Theorem 5

The CP with threshold \(\theta\) for a typical user in UDN downlink systems with CSB can be expressed by

$$CP_{n}^{CSB} \left( {\theta ,\lambda_{a} ,\alpha } \right) \approx \int_{0}^{\infty } {\exp \left( { - \frac{{\pi \lambda_{a} \theta^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{cp}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{r_{1}^{ - 2} }} - \frac{{\theta \sigma^{2} }}{{P_{t} r_{1}^{ - \alpha } }}} \right)f_{R} \left( {r_{1} } \right)dr_{1} }$$
(17)

where \(\tilde{\zeta }_{cp}^{CSB} = n\theta^{{ - \frac{2}{\alpha }}} r_{1}^{ - 2} /\left( {\pi \lambda_{a} } \right)\).

Proof

Considering CSB in downlink UDN and following the similar steps of JT, the CP of a typical user is

$$\begin{aligned} CP_{n}^{CSB} \left( {\theta ,\lambda_{a} ,\alpha } \right) & = {\mathbb{P}}\left( {SINR_{n}^{CSB} > \theta } \right) = {\mathbb{P}}\left( {\frac{{P_{t} h_{1} r_{1}^{ - \alpha } }}{{\sum\nolimits_{m > n} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }} > \theta } \right) \\ & = {\mathbb{E}}_{r,I} \left[ {\exp \left( { - \frac{{\theta \left( {I + \frac{{\sigma^{2} }}{{P_{t} }}} \right)}}{{r_{1}^{ - \alpha } }}} \right)} \right] \\ & = {\mathbb{E}}_{r} \left[ {{\mathcal{L}}_{I} \left( {\frac{\theta }{{r_{1}^{ - \alpha } }}} \right)\exp \left( { - \frac{{\theta \sigma^{2} }}{{P_{t} r_{1}^{ - \alpha } }}} \right)} \right] \\ & = \int\limits_{{0 < r_{1} < r_{n} < \infty }} {\exp \left( { - \frac{{\pi \lambda_{a} \theta^{{\frac{2}{\alpha }}} \int_{{\zeta_{cp}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{r_{1}^{ - 2} }} - \frac{{\theta \sigma^{2} }}{{P_{t} r_{1}^{ - \alpha } }}} \right)} f_{R} \left( {r_{1} } \right)f_{R} \left( {r_{n} } \right)dr_{1} dr_{n} \\ & \approx \int_{0}^{\infty } {\exp \left( { - \frac{{\pi \lambda_{a} \theta^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{cp}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{r_{1}^{ - 2} }} - \frac{{\theta \sigma^{2} }}{{P_{t} r_{1}^{ - \alpha } }}} \right)f_{R} \left( {r_{1} } \right)dr_{1} } \\ \end{aligned}$$
(18)

where \(\zeta_{cp}^{CSB} = \theta^{{ - \frac{2}{\alpha }}} r_{1}^{ - 2} r_{n}^{2}\).

In the special case of \(\alpha = 4\) and \(\sigma^{2} = 0\), the CP of CSB can be further simplified by

$$CP_{n}^{CSB} \left( {\theta ,\lambda_{a} ,4} \right) \approx \int_{0}^{\infty } {\exp \left( { - \pi \lambda_{a} \theta^{{\frac{1}{2}}} r_{1}^{2} \left[ {\frac{\pi }{2} - \arctan \left( {\frac{{n\theta^{{ - \frac{1}{2}}} r_{1}^{ - 2} }}{{\pi \lambda_{a} }}} \right)} \right]} \right)} f_{R} \left( {r_{1} } \right)dr_{1}$$
(19)
3.2.1.2 Ergodic Capacity (EC)

Theorem 6

The EC (bit/s/Hz) of a typical user in UDN downlink systems with CSB can be given by

$$\begin{aligned} EC_{n}^{CSB} \left( {\lambda_{a} ,\alpha }\right) & = \int\limits_{{0 < r_{1} < r_{n} < \infty }}{\int\limits_{t > 0} {\exp \left[ { - \pi \lambda_{a} \left({e^{t} - 1} \right)^{{\frac{2}{\alpha }}} r_{1}^{2} \int_{{\zeta_{ec}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha}{2}}} }}d\mu } } \right.} } \\ &\left. \quad - \frac{{\left({e^{t} - 1} \right)\sigma^{2} }}{{P_{t} r_{1}^{ - \alpha } }}\right]f_{R} \left( {r_{1} } \right)f_{R} \left( {r_{n} }\right)dr_{1} dr_{n} dt \\ \end{aligned}$$
(20)

where \(\zeta_{ec}^{CSB} = \left( {e^{t} - 1} \right)^{{ - \frac{2}{\alpha }}} r_{1}^{ - 2} r_{n}^{2}\).

Further, it can be approximated by

$$EC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right) \approx \int_{0}^{\infty } {\int_{0}^{\infty } {\exp \left[ - \pi\lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{2}{\alpha }}}r_{1}^{2} \int_{{\tilde{\zeta }_{ec}^{CSB} }}^{\infty } {\frac{1}{{1+ \mu^{{\frac{\alpha }{2}}} }}d\mu } - \frac{{\left( {e^{t} - 1}\right)\sigma^{2} }}{{P_{t} r_{1}^{ - \alpha } }} \right]}} f_{R}\left( {r_{1} } \right)dr_{1} dt$$
(21)

where \(\tilde{\zeta }_{ec}^{CSB} = n\left( {e^{t} - 1} \right)^{{ - \frac{2}{\alpha }}} r_{1}^{ - 2} /\left( {\pi \lambda_{a} } \right)\).

Observe (3) and (17) as well as (8) and (20), we can find the differences between JT and CSB with respect to CP and EC lie in the part of useful signals (expressed by \(\varphi = \sum\nolimits_{k = 1}^{n} {r_{k}^{ - \alpha } } or \, r_{1}^{ - \alpha }\) in the denominator) and the lower limit of the integral \(\int_{\zeta }^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu }\) (\(\zeta = \zeta_{cp}^{JT} , \, \zeta_{cp}^{CSB} , \, \zeta_{ec}^{JT} or \, \zeta_{ec}^{CSB}\)). Since both CP and EC increase with \(\varphi\) and \(\zeta\), we can conclude that JT achieves better performance than CSB under the same conditions (same cluster size, AP density, user density, etc.).

3.2.2 Performance Analysis of A Typical AP

Likewise, there is also a “virtual cell” (the left shaded area in Fig. 3) in the case of CSB but only the closest AP transmits. And from the perspective of a typical AP, \(k_{CSB}\) users are in its coverage (the right shaded area in Fig. 3). Although no data sharing is needed in CSB scheme, a typical AP is required to access the data information of its served users in the circular coverage with radius of \(r_{1}\) (the circle area with red solid borders in the right of Fig. 3). In CSB scheme, we refer to BC as the accumulated data rates of the served users to make these two schemes comparable.

Fig. 3
figure 3

Illustration of an AP cluster from the view of a typical user (left) and AP coverage from the view of a typical AP (right) with CSB

Full size image
3.2.2.1 Backhaul Consumption (BC)

Theorem 7

The BC (bit/s/Hz) of a typical AP in UDN downlink systems with CSB can be expressed by

$$\begin{aligned} BC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right) & \approx \int\limits_{{0 < l_{1} < \cdots < l_{\beta } < \infty }} {\int\limits_{t > 0} {\exp \left\{ { - \frac{{\pi \lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{bc}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{CSB} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} }}} \right.} } \\ & \quad \left. { - \frac{{\left( {e^{t} - 1} \right)\sigma^{2} }}{{P_{t} \left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{CSB} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]}}} \right\}dt \times f_{L} \left( {l_{1} , \ldots ,l_{\beta } } \right)dl_{1} \cdots dl_{\beta } \\ \end{aligned}$$
(22)

where \(k_{CSB} = round\left( {\frac{{\lambda_{u} }}{{\lambda_{a} }}} \right)\) and \(\tilde{\zeta }_{bc}^{CSB} = \frac{{n\left( {e^{t} - 1} \right)^{{ - \frac{2}{\alpha }}} }}{{\pi \lambda_{a} }}\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{CSB} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}}\).

Proof

Considering CSB in downlink UDN and following the similar steps of JT, the BC of a typical AP is

$$\begin{aligned} BC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right) & = {\mathbb{E}}_{l,I} \left[ {\ln \left( {1 + \frac{{\sum\nolimits_{i = 1}^{{k_{CSB} }} {P_{t} g_{i} l_{i}^{ - \alpha } } }}{{\sum\nolimits_{m > n} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }}} \right)} \right] \\ & = \int\limits_{{0 < l_{1} < \cdots < l_{{k_{CSB} }} < \infty }} {\int\limits_{{r_{n} > 0}} {\int\limits_{t > 0} {\exp \left[ { - \frac{{\left( {e^{t} - 1} \right)\sigma^{2} }}{{P_{t} \sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } }}} \right]{\mathcal{L}}_{I} \left[ {\frac{{e^{t} - 1}}{{\sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } }}} \right]dt} } } \\ & \quad \times f_{R} \left( {r_{n} } \right)f_{L} \left( {l_{1} , \ldots ,l_{{k_{CSB} }} } \right)dr_{n} dl_{1} \ldots dl_{{k_{CSB} }} \\ & = \int\limits_{{0 < l_{1} < \cdots < l_{{k_{CSB} }} < \infty }} {\int\limits_{{r_{n} > 0}} {\int\limits_{t > 0} {\exp \left[ { - \frac{{\pi \lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{2}{\alpha }}} }}{{\left( {\sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } } \right)^{{\frac{2}{\alpha }}} }}\int_{{\zeta_{bc}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } - \frac{{\left( {e^{t} - 1} \right)\sigma^{2} }}{{P_{t} \sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } }}} \right]} } } \\ & \quad \times f_{R} \left( {r_{n} } \right)f_{L} \left( {l_{1} , \ldots ,l_{{k_{CSB} }} } \right)dr_{n} dl_{1} \ldots dl_{{k_{CSB} }} \\ \end{aligned}$$
(23)

where \(\zeta_{bc}^{CSB} = \left( {e^{t} - 1} \right)^{{ - \frac{2}{\alpha }}} \left( {\sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } } \right)^{{\frac{2}{\alpha }}} r_{n}^{2}\).

Using the expectation (5) to perform approximation, the result in Theorem 7 can be got.

3.2.2.2 Successful Serving Probability (SSP)

Theorem 8

Given the BC threshold \(\gamma^{BC}\) , the SSP \(p_{s}^{CSB}\) in UDN downlink systems with CSB can be expressed by

$$\begin{aligned} p_{s}^{CSB} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right) & \approx 1 - \int\limits_{{0 < l_{1} < \cdots < l_{\beta } < \infty }} {\exp \left\{ { - \frac{{\pi \lambda_{a} \left( {e^{{\gamma^{BC} }} - 1} \right)^{{\frac{2}{\alpha }}} \int_{{\tilde{\zeta }_{bc}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } }}{{\left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{CSB} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]^{{\frac{2}{\alpha }}} }}} \right.} \\ & \quad \left. { - \frac{{\left( {e^{{\gamma^{BC} }} - 1} \right)\sigma^{2} }}{{P_{t} \left[ {\sum\nolimits_{i = 1}^{\beta } {l_{i}^{ - \alpha } + } \sum\nolimits_{k = \beta + 1}^{{k_{CSB} }} {\left( {\pi \lambda_{u} } \right)^{{\frac{\alpha }{2}}} \frac{{\Gamma \left( {k - \frac{\alpha }{2}} \right)}}{\Gamma \left( k \right)}} } \right]}}} \right\}f_{L} \left( {l_{1} , \ldots ,l_{\beta } } \right)dl_{1} \cdots dl_{\beta } \\ \end{aligned}$$
(24)

Proof

Considering CSB in downlink UDN and following the similar steps of JT, the SSP of a typical AP is

$$\begin{aligned} p_{s}^{CSB} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right) & = {\mathbb{P}}\left[ {BC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right) \le \gamma^{BC} } \right] \\ & = 1 - {\mathbb{P}}\left[ {BC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right) > \gamma^{BC} } \right] \\ & = 1 - {\mathbb{P}}\left[ {\ln \left( {1 + \frac{{\sum\nolimits_{i = 1}^{{k_{CSB} }} {P_{t} g_{i} l_{i}^{ - \alpha } } }}{{\sum\nolimits_{m > n} {P_{t} h_{m} r_{m}^{ - \alpha } } + \sigma^{2} }} > \gamma^{BC} } \right)} \right] \\ & = 1 - {\mathbb{P}}\left[ {\sum\limits_{i = 1}^{{k_{CSB} }} {g_{i} l_{i}^{ - \alpha } } > \left( {e^{{\gamma^{BC} }} - 1} \right)\left( {I + \frac{{\sigma^{2} }}{{P_{t} }}} \right)} \right] \\ & = 1 - \int\limits_{{0 < l_{1} < \cdots < l_{{k_{CSB} }} < \infty }} {\int\limits_{{r_{n} > 0}} {\exp \left[ { - \frac{{\pi \lambda_{a} \left( {e^{{\gamma^{BC} }} - 1} \right)^{{\frac{2}{\alpha }}} }}{{\left( {\sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } } \right)^{{\frac{2}{\alpha }}} }}\int_{{\zeta_{bc}^{CSB} }}^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu } - \frac{{\left( {e^{{\gamma^{BC} }} - 1} \right)\sigma^{2} }}{{P_{t} \sum\nolimits_{i = 1}^{{k_{CSB} }} {l_{i}^{ - \alpha } } }}} \right]} } \\ & \quad \times f_{R} \left( {r_{n} } \right)f_{L} \left( {l_{1} , \ldots ,l_{{k_{CSB} }} } \right)dr_{n} dl_{1} \ldots dl_{{k_{CSB} }} \\ \end{aligned}$$
(25)

Likewise, the result in Theorem 8 can be derived by expectation approximating.

Comparing (10) and (12) with (22) and (24), we find that the most important differences between JT and CSB concerning BC and SSP are \(K = k_{JT} \, or \, k_{CSB}\) and the lower limit of the integral \(\int_{\zeta }^{\infty } {\frac{1}{{1 + \mu^{{\frac{\alpha }{2}}} }}d\mu }\). With respect to BC, higher BC is required for JT because of larger \(K\) and \(\zeta\) under the same condition. But for SSP, CSB would achieve a higher SSP in the same case since SSP decreases with \(K\) and \(\zeta\).

3.2.3 Performance Analysis from a Network Perspective

The EEC of a typical user in UDN downlink systems with CSB can be expressed by

$$C_{eff}^{CSB} \left( {n,\lambda_{a} ,\alpha ,\gamma^{BC} } \right) = p_{s}^{CSB} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right) \times EC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right)$$
(26)

where \(EC_{n}^{CSB} \left( {\lambda_{a} ,\alpha } \right)\) and \(p_{s}^{CSB} \left( {\gamma^{BC} ,\lambda_{a} ,\alpha } \right)\) are given by (20) and (24).

In the special case of \(\alpha = 4,\sigma^{2} = 0\), (26) can be simplified by expectation approximating as

$$\begin{aligned} C_{eff}^{CSB} \left( {n,\lambda_{a} ,4,\gamma^{BC} } \right) & = p_{s}^{CSB} \left( {\gamma^{BC} ,\lambda_{a} ,4} \right) \times EC_{n}^{CSB} \left( {\lambda_{a} ,4} \right) \\ & \approx \left\{ {1 - \int\limits_{{0 < l_{1} < l_{2} < \infty }} {\exp \left( { - \frac{{\pi \lambda_{a} \left( {e^{{\gamma^{BC} }} - 1} \right)^{{\frac{1}{2}}} \left( {\frac{\pi }{2} - \arctan \tilde{\zeta }_{bc}^{CSB} \left| {_{\alpha = 4} } \right.} \right)}}{{\left[ {l_{1}^{ - 4} + l_{2}^{ - 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{CSB} } \right)} \right]^{{\frac{1}{2}}} }}} \right)} } \right. \\ &\quad \left. { \times f_{L} \left( {l_{1} ,l_{2} } \right)dl_{1} dl_{2} } \right\} \\ &\quad \times \left\{ {\int_{0}^{\infty } {\int_{0}^{\infty } {\left( {\exp - \pi \lambda_{a} \left( {e^{t} - 1} \right)^{{\frac{1}{2}}} r_{1}^{2} \left( {\frac{\pi }{2} - \arctan \tilde{\zeta }_{ec}^{CSB} \left| {_{\alpha = 4} } \right.} \right)} \right)} } } \right. \\ &\quad \left. { \times f_{R} \left( {r_{1} } \right)dr_{1} dt} \right\} \\ \end{aligned}$$
(27)

where \(\tilde{\zeta }_{bc}^{CSB} \left| {_{\alpha = 4} } \right. = \frac{{n\left( {e^{t} - 1} \right)^{{ - \frac{1}{2}}} }}{{\pi \lambda_{a} }}\left[ {l_{1}^{ - 4} + l_{2}^{ - 4} + \left( {\pi \lambda_{u} } \right)^{2} g\left( {k_{CSB} } \right)} \right]^{{\frac{1}{2}}}\) and

$$\tilde{\zeta }_{ec}^{CSB} \left| {_{\alpha = 4} } \right. = n\left( {e^{t} - 1} \right)^{{ - \frac{1}{2}}} r_{1}^{ - 2} /\left( {\pi \lambda_{a} } \right).$$

As is expressed in (27), we also pay attention to the three factors, i.e., AP density, cluster size and BC threshold. Similarly conclusion can be drawn in CSB scheme. Optimal cluster size still remains unknown and if there is one, it can be got by

$$N_{opt}^{CSB} = \arg \mathop {\hbox{max} }\nolimits_{n} C_{eff}^{CSB} \left( {n,\lambda_{a} ,\alpha ,\gamma^{BC} } \right)$$
(28)

Interestingly, we can infer that \(N_{opt}^{CSB} \ge N_{opt}^{JT}\) if the optimal cluster sizes of both schemes exist. This is because JT is more sensitive to BC threshold and more liable to exceed BC constraint than CSB under the same condition.

4 Numerical Results

In this section, we firstly evaluate the accuracy of the above closed-form expressions derived in Section 3. Then we focus on the performance comparison between JT and CS. In the simulation part, the network coverage radius is set at 500 m, where the AP density and user density are assumed to be 0.004 and 0.005/m2 respectively. The transmit power is 20 mW and pathloss exponent \(\alpha\) is set at 4. Meanwhile, we assume that the BC threshold \(\gamma^{BC} = 2.28\) bit/s/Hz, and the power of additive noise is set at −174 dBm/Hz.

4.1 Validation of Expectation Approximation Method

Compared with the Monte Carlo experiments, the analytical integrations outperform by computing more efficiently, which is verified with simulations as in Figs. 4 and 5.

Fig. 4
figure 4

Comparison between the CP evaluated using Theorem 1, Theorem 1 approximation and simulation results for JT

Full size image
Fig. 5
figure 5

Comparison between the CP evaluated using Theorem 5, Theorem 5 approximation and simulation results for CSB

Full size image

In Fig. 4, we compare the CP of a typical user with JT scheme evaluated by analytical (Theorem1 as well as its approximation) and simulation results for different cluster sizes. The curves all exhibit the same shape and the gaps between two analytical curves and the simulation one become very small (\(< 1\,{\text{dB}}\)) when \(\theta > 5\,{\text{dB}}\). Additionally, the CP curves keep rising with \(n\) since JT improves the system performance by transforming strongest interfering signals into useful signals, which is also can be inferred from (3) to (6).

Likewise, Fig. 5 depicts the CP of a typical user with CSB scheme captured by analytical (Theorem 5 and its approximation) and simulation results. We observe that the proposed approximated expression is also tight in the case of CSB. Similarly, the CP is also improved by increasing cluster size due to the effective mitigation of the dominant interfering signals. Both of Figs. 4 and 5 illustrates that our proposed approximated expressions are proved to be feasible and effective to evaluate the user’s performance.

4.2 Performance Comparison Between JT and CSB

In this section, we compare JT and CSB from the aspects of a typical user, a typical AP and a comprehensive perspective. Specifically, the performance metrics of these two schemes including CP, EC, BC, SSP as well as EEC are presented in Figs. 6, 7, 8, 9, 10, 11 and 12.

Fig. 6
figure 6

CP Comparison between JT and CSB with different cluster sizes

Full size image
Fig. 7
figure 7

EC Comparison between JT and CSB as a function of cluster size under different AP densities

Full size image
Fig. 8
figure 8

BC Comparison between JT and CSB as a function of cluster size under different AP densities

Full size image
Fig. 9
figure 9

SSP Comparison between JT and CSB as a function of BC threshold under different AP densities

Full size image
Fig. 10
figure 10

SSP Comparison between JT and CSB as a function of cluster size under different AP densities

Full size image
Fig. 11
figure 11

EEC Comparison between JT and CSB as a function of BC threshold under different AP densities (n = 4)

Full size image
Fig. 12
figure 12

a EEC Comparison between JT and CSB with low BC threshold (\(\gamma^{BC} = 1.5\) bit/s/Hz, a, b denotes the optimal cluster size and its corresponding EEC). b EEC Comparison between JT and CSB with high BC threshold (\(\gamma^{BC} = 3\) bit/s/Hz)

Full size image

4.2.1 From the Perspective of a Typical User

4.2.1.1 CP Comparison

Figure 6 compares the CP of JT and CSB with varying SINR thresholds. It can be observed that the CP for both schemes benefits most when \(n\) increases from 1 (no cooperation) to 2 (with cooperation) and the CP gain gets smaller with increasing \(n\). Take JT for example, the CP improves 17 and 4 % respectively when \(n\) increases from 1 to 2 and from 5 to 6 in the case of \(\theta = 10\,{\text{dB}}\). In comparison with CSB scheme, JT scheme can achieve better coverage performance at both low SINR thresholds and high SINR thresholds.

4.2.1.2 EC Comparison

The impact of cluster size and AP density on per-user EC are illustrated in Fig. 7. Firstly, we can see that the EC of both JT and CSB grows monotonically as n increases. However, the two groups of curves exhibit a slight increase at large cluster sizes because the effect of distant APs is negligible. Take the case of \(\lambda_{a} = 0.005/m^{2}\) for example, the EC of JT raises 78.2 and 2.5 % respectively when \(n\) increases from 1 to 5 and from 5 to 10. Secondly, per-user EC increases substantially with the AP density due to more APs selected in each cooperative cluster, which implies that dense network is a promising way to improve network capacity. Last but not least, it can be observed that JT is preferable to CSB in EC with varying cluster sizes or AP densities.

From Figs. 6 and 7, it can be concluded that JT scheme outperforms CSB scheme in the typical user’s performance concerning CP and EC, which is in accordance with the conclusions in [9, 16, 19]. This is because JT reduces ICI through changing dominant interference into useful signals while CSB tries to avoid it, which implies that JT scheme can provide better coverage and higher capacity for the network system. Whereas, the superior performance gained by JT also costs larger BC for the APs. To evaluate the schemes objectively, performance comparison from the perspective of a typical AP is highly required, which is depicted as follows.

4.2.2 From the Perspective of a Typical AP

4.2.2.1 BC Comparison

Figure 8 shows the evolution of per-AP BC of JT and CSB as a function of cluster size with different AP densities. It’s shown that the two groups of curves both increase with cluster size and the curves of JT exhibit higher and steeper. This happens because: for JT, all the APs within the cluster need to share the centric user’s data information while considering CS, only the single serving AP is required to access the useful signal. So for JT, more BC is needed and BC is more sensible to the increase of cluster size. Besides, we obeserve that per-AP BC of both JT and CSB decreases with AP density, which proves that UDN helps to release the burden of each AP effectively.

4.2.2.2 SSP Comparison

The SSP versus different BC thresholds and cluster sizes is investigated in Figs. 9 and 10 separately. First, as shown in Fig. 9, larger BC threshold results in higher SSP for both schemes due to more relaxed BC constraint. Meanwhile, Fig. 10 reveals that the SSP for both schemes decreases with cluster size. The reason lies in that larger cluster size means more data information is required to be shared, which shall cost more BC and further leads to lower SSP. Second, it’s worth noting that the SSP of JT is always lower than that of CSB in the same condition (same BC threshold, cluster size and AP density), which illustrates that BC imposes more rigid constraint on JT than CS. Last but not least, as is depicted in Figs. 9 and 10, the SSP of both schemes increases with AP density because denser deployment of APs can effectively reduce each AP’s burden.

4.2.3 From a Network Perspective

Our performance comparison between JT and CSB in terms of the proposed EEC versus BC threshold and cluster size under different AP densities are illustrated in Fig. 11 and 12. Specifically, two cases with different BC thresholds are considered in Fig. 12: (a) is for low BC threshold case, (b) is for high BC threshold case.

4.2.3.1 Impact of BC Threshold

As is described in Fig. 11, the EEC of the two schemes increase with BC threshold and JT outperforms CSB in high BC threshold regime. Besides, the EEC of the two schemes also increases with AP density due to the benefit of UDN in releasing each AP’s BC burden. Last but not least, the corresponding values of BC threshold at the intersection points of the two group curves decrease with AP density, which implies that the advantage of JT is highlighted in UDN.

4.2.3.2 Impact of Cluter Size

From Fig. 12a, i.e., low BC threshold case, we can observe that there exists an optimal cluster size for both schemes and \(N_{opt}^{CB}\) is no less than \(N_{opt}^{JT}\). The reasons are as follows: (1) In the condition of small cluster size, EC increases quickly with cluster size while SSP decreases slightly due to low backhaul cost in this condition. So it’s the increase of EC that matters. And in the condition of high cluster size, the decrease of SSP becomes dominant with the increase of cluster size due to the low BC constraint. Note that EEC is derived by the product of SSP and EC, so the EEC curves of both JT and CSB grow at first and then show a decline. (2) JT is more sensitive to the increase of cluster size (high BC), as is shown in Figs. 8 and 10. Therefore, JT is more liable to reach the optimal EEC, that is to say, a smaller optimal cluster size. Meanwhile, as depicted in Fig. 12b, i.e., high BC threshold case, both two group curves keep growing but the growth rate gets less distinct after \(n > 8\) and there is no local optimal cluster size. This happens because EEC is mainly determined by EC with relaxed BC constraint. Another observation from Fig. 12a, b is that a comparative small cluster size is advisable whether there exists an optimal cluster size or not. More specifically, the cluster size should be set at 2 or 3 with low BC constraint while 4 or 5 is preferable in high BC threshold case because it has already obtained rather good network performance (more than 90 % of the EEC in the case of \(n = 8\)).

4.2.3.3 Impact of AP Density

From Figs. 11 and 12a, b, EEC is observed to increase substantially with AP density. This can be explained by two aspects: On one hand, denser network allows users to select more beneficial cooperative APs which are closer in distance. On the other hand, there’s no doubt that the backhaul burden is effectively released by more APs with denser deployment. Hence, UDN is proved to be a potential technology in future network.

5 Conclusions

This paper has investigated the performance of JT and CSB in downlink UDN from a typical user’s perspective, a typical AP’s perspective as well as a network perspective. The explicit qualification of BC and the proposed performance metrics (SSP and EEC) effectively facilitate the comparison of these two schemes. Simulation results show that our proposed closed-form expressions perform well in capturing the network performance. Based on theoretical analysis and simulation verification, we are able to conclude that JT outperforms CSB in high BC threshold, small cluster size or high AP density regime. Additionally, numerical results also demonstrate that the existence of optimal cluster size remains unknown depending on the value of related factors including BC threshold and AP density. However, one thing is sure for both schemes: a comparative small cluster size is preferable in practice. Finally, this work still has many extensions: Firstly, note that the performance comparison is carried out in single-tier UDN in this paper, similar works can be extended to multi-tier networks. Secondly, the conclusion that both of two CoMP schemes have their merits in different cases can provide new insights into the design of hybrid transmission mode in CoMP system.