Performance Analysis of Multiantenna MC DS CDMA System Over Correlated η–µ Multipath Fading Channels

Abstract

In wireless communication channels, the performance of the wireless communication systems deteriorate due to the severe influence of interference, multipath fading, path loss, shadowing, and noise, respectively. In this paper, we investigate the performance of the system transmitting over correlated η–µ frequency selective fading channels in terms of average error rates. Based on moment generating function approach, closed form expressions for average error probabilities for the system are derived and represented in terms of Appell’s hypergeometric functions and Lauricella’s multivariate hypergeometric functions. In addition, probability density function based approach is employed to determine the formulae for average error probabilities of the system operating over correlated η–µ multipath fading channels. The numerical results reveal that, the effects of correlation, decaying power factor and signal constellation size can be reduced using frequency, spatial antennas and path diversities, respectively. Furthermore, we confirm the correctness of the analytical approaches through Monte Carlo simulation technique.

1 Introduction

The influence of multipath fading, intentional and unintentional interference, noise and other destructive obstacles on wireless communication systems performance operating in hostile environment results in system performance degradation. Then, the use of multiantenna systems in conjunction with wireless communication systems can increase spatial diversity, improves channel capacity and reduces the detrimental effects of multipath fading and other obstructions as well. Therefore, multicarrier direct sequence code division multiple access (MC DS-CDMA) system coupled with MIMO systems has the potential to mitigate the deleterious impact of multipath fading, interference and noise respectively. In this case, MC DS-CDMA is a digital modulation and multicarrier technique formed by combining orthogonal frequency division multiplexing (OFDM) with direct sequence code division multiple access (DS-CDMA) [1]. The operation of this system is based on time domain spreading code or combination of time domain and frequency domain spreading codes respectively. Hence, the input data stream is serial to parallel converted and spread using spreading code in time domain and then each subcarrier is modulated differently with each of the data stream [2]. In addition, the application of multiple input multiple output systems to multicarrier wireless communication systems can significantly increase the channel capacity and lower the error probability without any increase in the transmission power or expansion of the required bandwidth. In this case, wireless communication systems will be highly complex in structure and costly because of the involvement of multiple radio frequency (RF) devices. Thus, the portable mobile terminals may accommodate a small number of antennas due to the size and power limitation [3]. The antennas are connected to both ends of the system forming multiple input multiple output MC DS-CDMA (MIMO MC DS-CDMA) system. Based on space time coding technique, information is spread across the transmit antennas and allows the receiver to achieve transmit diversity. This, on the other hand, maximizes the diversity gain of the wireless communication system over fading channels. Furthermore, space time block codes (STBC) are utilised to orthogonalise the MIMO wireless channels, i.e., STBC simplify maximum-likelihood decoding by decoupling the vector detection problem into a simpler scalar detection problem [4]. Therefore, the operation of the system is based on channel state information available at the receiver side and exploits space time block code at the transmitter side. In addition, we incorporate a RAKE receiver into the system receiver side to reduce the impact of multipath fading.

The performance of broadband multicarrier DS CDMA system operating over Rayleigh frequency selective fading channels using space time spreading assisted transmit diversity is explored [5]. The authors considered both the conventional MC DS CDMA system using only time domain spreading code and broadband multicarrier DS CDMA system employing time and frequency domain spreading codes respectively. They analysed the systems in terms of average bit error probability of binary phase shift keying. In [6], the authors explored the performance of space time block code multicarrier direct sequence code division multiple access functioning over Rayleigh multipath fading channels in terms of average bit error probability of BPSK modulation technique. They analysed multiuser interference using standard Gaussian approximation method to derive instantaneous signal to interference noise ratio (SINR) at the output of the RAKE receiver. Hence, based on probability density function (PDF) of instantaneous SINR, the expression for average bit error probability was derived. The authors in [7] proposed a wireless communication system (multicarrier) that reduces the effect of correlation among the subcarriers, suppresses partial band interference and operates over frequency selective Rayleigh fading channels. They employed average bit error probability as a metric to evaluate system’s performance. Elnoubi and Hashem [8] studied the bit error rate performance of MIMO MC DS CDMA system operating over Nakagami-m multipath fading channels. The impact of RAKE receiver in conjunction with maximal ratio combining diversity on the system performance was also taken into account. Yang [9] studied the bit error rate performance of multiantenna MC DS CDMA system operating over correlated time selective Rayleigh fading channels. The space time spreading technique based on the family of orthogonal variable spreading factor (OVSF) code was proposed in order to attain time diversity. He investigated the performance of the multiantenna MC DS CDMA system over correlated time selective Rayleigh fading channels in terms of average bit error probability. Peppas et al. [10] studied the performance of a wireless communication system operating over η–µ frequency selective, slowly fading channels with arbitrary fading parameters in terms of average channel capacity, average error probability and outage probability respectively. Furthermore, they also evaluated the performance of DS CDMA system.

In this paper, we include the RAKE receiver at the receiver side of the multiantenna MC DS CDMA system and evaluate its performance over correlated η–µ frequency selective fading channels in terms of average error probability. We derive instantaneous signal to interference noise ratio (SINR) at the output of the RAKE receiver. Furthermore, we develop moment generating function (MGF) and PDF of the instantaneous SINR of the system. In this case, we exploit both MGF and PDF based approaches to derive average error probabilities of binary phase shift keying (BPSK), multilevel phase shift keying (MPSK) and square M-ary quadrature amplitude modulation (MQAM) modulation format of the system communicating over correlated η–µ frequency selective fading channels and express them in terms of Gauss hypergeometric functions, Appell’s hypergeometric functions and Laurricella’s multivariate hypergeometric functions, respectively. The closed form expressions for average error probabilities obtained are novel contributions of the authors.

The next section describes system model which includes transmitted signal, channel model and received signal, respectively. In Sect. 3, we analyse the system and derive instantaneous SINR at the RAKE receiver output. In addition, we obtain MGF and PDF of the instantaneous SINR of the system transmitting over correlated η–µ frequency selective fading channels. The average error probabilities of BPSK, MPSK and square MQAM modulation schemes for MIMO MC DS CDMA system operating over η–µ frequency selective fading channels are developed in Sect. 4. Whilst in Sect. 5, the numerical results and discussions that illustrates the performance of the system are presented. Finally, Sect. 6 outlines the conclusion of the paper.

2 System Model Description

In this section, we describe multiantenna MC DS CDMA system within the framework of the transmitted signal, channel model and receiver model, respectively. In addition, brief explanation about η–µ fading distribution is considered.

2.1 Transmitted Signal

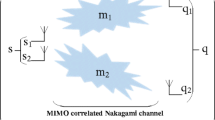
In this subsection, it is assumed that the system has M _t transmit antennas and N _r receive antennas respectively. Thus, the configuration of the system is called multiple input multiple output MC DS-CDMA (MIMO MC DS-CDMA) system. Basically, the system operation assumption depends on channel state information known at the receiver side while the transmitter utilises space time block codes (STBC) for the receiver to achieve transmit diversity. The input datastream is first serial to parallel converted to U substreams. In this way, the symbols in each substream are spread in time domain and mapped to M _t transmit antennas. So each subcarrier signal is multicarrier modulated by invoking inverse fast Fourier transform (IFFT) and then summation of the modulated signals is carried out and transmitted [2]. On the other hand, it is assumed that each subcarrier signal experiences flat η–µ fading. In this case, let us suppose that the system MIMO MC DS-CDMA uses two transmit antennas and two receive antennas respectively. Hence, we also assume two symbols say $x_{k}^{1} (t)$ and $x_{k}^{2} (t)$ to be transmitted simultaneously based on Alamouti technique [4] from transmit antenna 1 and transmit antennas 2 at the same first time slot. At the second time slot, the complex conjugate of symbol $- x_{k}^{2} (t)$ is transmitted from antenna 1 and complex conjugate of symbol $x_{k}^{1} (t)$ is transmitted from antenna 2 simultaneously. In addition, we presume that the channel from either of the transmitters to any of the receivers experience frequency selective η–µ fading. The two transmitted symbols of user k are given by

$$\begin{aligned} x_{k}^{1} (t) & = \sum\limits_{i = 1}^{q} {\sum\limits_{j = 1}^{U} {\sqrt {\frac{2P}{{M_{t} U}}} } } \, c_{k}^{1} (t) \, b_{k,i,j}^{1} (t)\cos \left( {2\pi f_{ij} t + \phi_{ij}^{1} } \right) \\ x_{k}^{2} (t) & = \sum\limits_{i = 1}^{q} {\sum\limits_{j = 1}^{U} {\sqrt {\frac{2P}{{M_{t} U}}} } } \, c_{k}^{2} (t) \, b_{k,i,j}^{2} (t)\cos \left( {2\pi f_{ij} + \phi_{ij}^{2} } \right), \\ \end{aligned}$$

(1)

where $b_{k}^{1} (t)$ and $b_{k}^{2} (t)$ are odd and even data stream transmitted by the kth user, where $b_{u}^{k} (t) = \sum\nolimits_{n = - \infty }^{\infty } {b_{u}^{k} } [n ] { }P_{{T_{s} }} (t - nT_{s} )$, $b_{u}^{k} [n] \in \{ + 1, - 1\}$ represent binary data sequence with equal probability, modulating the uth subcarriers, P _Ts (t) is a rectangular pulse uniformly distributed in [0, T_s) interval, $c_{k}^{1} (t)$ and $c_{k}^{2} (t)$ represent spreading codes in time domain in transmitters 1 and 2, respectively, where $c_{k} (t) = \sum\nolimits_{n = - \infty }^{\infty } {c_{k} } [n ] { }\psi (t - nT_{c} )$ is the spreading code waveform of user k and T _c is the chip duration, where $c_{n}^{k} \in \{ + 1, - 1\}$, with equal probability, while ψ(t) is a rectangular chip waveform of T-domain spreading sequence which is defined over the interval [0, T_c), U is the number of subcarriers, q is the number of bits in the data stream, P is the transmitted power, f _ij is the subcarrier frequency of the ith bit at jth subcarrier, and ϕ _ij is the phase due to the multicarrier modulations. The channel between the transmitter and the receiver during one time slot is assumed to be invariant, i.e., the conditions of the two symbols during this interval of time slot remain unchanged. But the characteristics of the channel vary after another interval of the time slot or another symbol frame.

2.2 Channel Model

The link between M _t transmit antennas and N _r receive antennas is assumed to be frequency flat fading channels for each subcarrier. The fading envelope of the received signal is modelled as η–µ fading distribution [11]. Hence, the impulse response for the kth transmitted data over the jth subcarrier is given by

$$h_{k} (t) = \sum\limits_{l = 1}^{L} {\alpha_{l}^{k} \delta (t - \tau_{kl} ) \, e^{{ - j\psi_{l}^{k} }} } ,$$

(2)

where α, τ, δ(.) and ψ denotes attenuation factor, time delay, Kronecker delta function and phase shift respectively. The time delay (τ_k) for the kth data is assumed to be uniformly distributed over [0, T_s). Thus, the attenuation factor, time delay and phase shift are presumed to be constant over two symbol intervals.

The η–µ fading distribution is a generalized distribution that includes one-sided Gaussian, Rayleigh, Hoyt (Nakagami-q) and Nakagami-m distribution as special cases, respectively. Therefore, this distribution characterized a small scale variation of the fading signal in a non-line of sight circumstance. Then, the power PDF of the instantaneous signal to noise ratio in both formats is given by [11]

$$f(\gamma ) = \frac{{2\sqrt \pi \mu^{\mu + 0.5} h^{\mu } \gamma^{\mu - 0.5} }}{{\Gamma \left( \mu \right)H^{\mu - 0.5} \overline{\gamma }^{\mu + 0.5} }}\exp \left( { - \frac{2\mu h\gamma }{{\overline{\gamma } }}} \right)I_{\mu - 0.5} \left( {\frac{2\mu H\gamma }{{\overline{\gamma } }}} \right)$$

(3)

where Γ(.) is the gamma function, I _x (.) is the modified Bessel function of the first kind and order x, $\mu = \frac{{E^{2} \left( \gamma \right)}}{2Var\left( \gamma \right)}\left( {1 + \left( {\frac{H}{h}} \right)^{2} } \right)$ is the number of multipath cluster, H and h are functions of η in both formats differently, $\overline{\gamma } = E[\gamma ]$ is the average signal to noise ratio, E[.] and Var[.] represent expectation and variance operators, respectively. In case of format 1, h = (2 + η ⁻¹ + η)/4, and H = (η ⁻¹ − η)/4, where η > 0 is the ratio between the powers of the in-phase and quadrature scattered waves in each multipath cluster. In addition, for the case of format 2, h = 1/(1 − η ²), and H = η/(1 − η ²), where η is the correlation coefficient between the power of the in-phase and quadrature scattered waves in each multipath cluster. I.e., −1 < η < 1. Therefore, the two formats are related mathematically as in [11].

2.3 Received Signal

It is assumed that multiantenna orthogonal MC DS-CDMA system supports K asynchronous CDMA active users communicating with the base station in a single cell. They use the same number of subcarriers and spreading factor as well. It is also presumed that the average power received from each user at the base station is the same, i.e., perfect power control condition. In this case, the operation of the receiver is in a reverse form to that of the transmitter. Thus, the received signal is demodulated by employing fast Fourier transform (FFT) based multicarrier demodulation in order to obtain U number of parallel streams that corresponds to that transmitted on U subcarriers [5]. Therefore, each stream is space time despread to form a decision variable for each of the transmitted data bits. Consequently, combining and detection of the received signals is carried out. Finally, parallel to serial conversion is performed to yield output data. The received signals during the first time slot interval is [12]

$$\begin{aligned} r_{1}^{1} (t) & = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {\left( {h_{1,1}^{l} x_{1,k}^{l} \left( {t - \tau_{k,l} } \right) + h_{1,2}^{l} x_{2,k}^{l} \left( {t - \tau_{k,l} } \right)} \right)} } + n_{1}^{1} , \\ r_{2}^{1} (t) & = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {\left( {h_{2,1}^{l} x_{1,k}^{l} \left( {t - \tau_{k,l} } \right) + h_{2,2}^{l} x_{2,k}^{l} \left( {t - \tau_{k,l} } \right)} \right)} } + n_{2}^{1} \\ \end{aligned}$$

(4)

Similarly, the received signals during the second time slot is

$$\begin{aligned} r_{1}^{2} (t) & = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {\left( { - h_{1,1}^{l} x_{2,k}^{*l} \left( {t - \tau_{k,l} } \right) + h_{1,2}^{l} x_{1,k}^{*l} \left( {t - \tau_{k,l} } \right)} \right)} } + n_{1}^{2} \\ r_{2}^{2} (t) & = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {\left( { - h_{2,1}^{l} x_{2,k}^{*l} \left( {t - \tau_{k,l} } \right) + h_{2,2}^{l} x_{1,k}^{*l} \left( {t - \tau_{k,l} } \right)} \right)} } + n_{2}^{2} \\ \end{aligned}$$

(5)

where K is the number of active users of the system, L is the number of resolvable path, τ_k,l is the time delay, h_n,m is the channel impulse response or fading coefficients from nth receive antenna and mth transmit antenna respectively, n ¹₁ and n ¹₂ , n ²₁ and n ²₂ denote an additive white Gaussian noise (AWGN) at the first and second time slot on receiver antenna 1 and antenna 2 and modelled as independent identically distributed (i.i.d) complex Gaussian random variables with zero mean and double sided power spectral density (psd) of N ₀/2.

3 System Analysis

The system is analysed by employing Gaussian approximation method for modelling multiple access interference in order to derive the PDF of the instantaneous signal to interference noise ratio (SINR) by employing MGF based method. But, first we have to take the complex conjugate of (5) and express the results with (4) in matrix form as

$$r(t) = \sum\limits_{k = 1}^{K} {\sum\limits_{l = 1}^{L} {HX_{k} \left( {t - \tau_{k,l} } \right)} } + n$$

(6)

where $r(t) = \left[ {r_{1}^{1} (t), r_{2}^{1} (t), r_{1}^{2*} (t), r_{2}^{2*} (t)} \right]^{T} ,H = \left[ \begin{array}{cccc} h_{1,1}^{l} & h_{2,1}^{l} & h_{1,2 }^{l*} & h_{2,2}^{l*} \hfill \\ h_{1,2}^{l} &h_{2,2}^{l} & - h_{1,1}^{l*} & - h_{2,1}^{l*} \hfill \\ \end{array} \right]^{T}$, $X_{k} ( {t - \tau_{k,l} }) = [ {x_{1,k}^{l} ( {t - \tau_{k,l} }) \, x_{2,k}^{l} ({t - \tau_{k,l} })}]^{T}$ $n = [ {n_{1}^{1} \, n_{2}^{1} \, n_{1}^{2*} \, n_{2}^{2*} } ]^{T}$ and T is transpose.

Therefore, (6) is decoded as in [4] and expressed in terms of desired user, interference due to other users with the same subcarriers frequency, interference due to other users with different subcarrier frequencies, and noise caused by AWGN. The detail analysis of the system is similar to that carried out in [13]. The instantaneous SINR of the system with two transmit antennas and two receive antennas is given as

$$\gamma = \frac{{\gamma_{c}^{\prime } }}{R}\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{2} {\sum\limits_{n = 1}^{2} {\sum\limits_{l = 1}^{{L_{r} }} {\left| {h_{vmnl} } \right|^{2} } } } }$$

(7)

Hence, it is simple to generalise that the instantaneous SINR of the system with M_t transmit antennas and N _r receive antennas is

$$\gamma = \frac{{\gamma_{c} }}{R}\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} { \, \sum\limits_{l = 1}^{Lr} {\left| {{\text{h}}_{\text{vmnl}} } \right|^{2} } } } } ,$$

(8a)

where

$$\begin{aligned} \gamma_{c}^{ - 1} & = \frac{{M_{t} }}{{2\Omega _{0} SNR}} + \frac{{\left( {K - 1} \right)X\left( {L,\delta } \right)}}{{3N_{e} }} + \frac{{N_{e} \left( {K - 1} \right)X\left( {L,\delta } \right)}}{{2\pi^{2} \lambda^{2} q}} \\ & \quad \times \sum\limits_{u = 1}^{q} {\sum\limits_{v = 0}^{U - 1} {\sum\limits_{i = 1}^{q} {\sum\limits_{j = 1 + v}^{U} {\left( {\frac{{1 - {\text{sinc}}\left( {\frac{{2\pi \lambda \left( {\left( {{\text{i}} - {\text{u}}} \right) + q\left( {j - v} \right)} \right)}}{{N_{e} }}} \right)}}{{\left( {\left( {i - u} \right) + q\left( {j - v} \right)} \right)^{2} }}} \right)} } } } , \\ \end{aligned}$$

(8b)

$X\left( {L, \delta } \right) = \sum _{l = 0}^{L} e^{ - l\delta }$ and R is the code rate of the orthogonal space time block code. If U = 1, the system reduces to a single carrier MIMO system and its instantaneous SINR (8a) diminishes to that in [14, Eq. (4)]. In this case, it is assumed that the diversity branches (antennas) of the wireless communication system are correlated at the receiver end. The analysis of the correlated diversity branches is similar to that of the independent fading scenario, i.e., if the system operation is in conjunction with maximal ratio combining diversity, the MRC needs the knowledge of MGF of the combiner output SINR in order to determine the average error probability [15]. Hence, we can find the MGF of the instantaneous signal to interference noise ratio at the RAKE receiver output. Since the envelope of the fading signal is modelled by η–µ fading distribution, then, for arbitrary correlated η–µ fading channels, we obtain the MGF as Eq. (55) in “Appendix 1”

$$\Phi (s) = \prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{\partial } }} {\left( {\det \left( {I + 2sC_{xx}^{{\prime }} } \right)\det \left( {I + 2sD_{yy}^{{\prime }} } \right)} \right)^{{ - \mu_{vmnl} }} } } } }$$

(9)

where I is the identity matrix, det represent determinant, $C_{xx}^{\prime } = B_{vmnl} C_{xx}^{vmnl}$ is the covariance matrix of the inphase component and $D_{yy}^{{\prime }} = B_{vmnl} D_{yy}^{vmnl}$ is the covariance matrix of the quadrature component of signal fading envelope. Furthermore, we can represent (9) in terms of eigenvalues of the covariance matrices ${\mathbf{C}}_{{{\mathbf{xx}}}}^{{\prime }}$ and ${\mathbf{D}}_{{{\mathbf{yy}}}}^{\prime }$, respectively [16, 17].

$$\Phi (s) = \prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + 2s\lambda_{vmnl \le }^{x} } \right)^{{ - \mu_{vmnl} }} \left( {1 + 2s\lambda_{vmnl}^{y} } \right)^{{ - \mu_{vmnl} }} } } } }$$

(10)

Hence, Eq. (10) represent an MGF of arbitrary correlation. For confirmation, putting U = 1, M _t = 1, N _r = 1, and K (user) = 1 into (10), it reduces to [18, Eq. (12)]. I.e., the system drops to a single carrier and single user system. Similarly, we can obtain PDF of (10) by first expressing it in partial fraction form and taking inverse Laplace transform [19, 20]

$$\Phi \left( \gamma \right) = \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\alpha_{i}^{vmnl} \gamma^{i - 1} e^{{ - \frac{1}{{2\lambda_{vmnl}^{x} }}\gamma }} }}{{\left( {2\lambda_{vmnl}^{x} } \right)^{i} \left( {i - 1} \right)!}}} } } } } + \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\beta_{i}^{vmnl} \gamma^{i - 1} e^{{ - \frac{1}{{2\lambda_{vmnl}^{y} }}\gamma }} }}{{\left( {2\lambda_{vmnl}^{y} } \right)^{i} \left( {i - 1} \right)!}}} } } } }$$

(11)

where α_i and β_i are residues to be determined, i.e.,

$$\alpha_{i}^{vmnl} = \frac{1}{{\left( {\mu_{vmnl} - i} \right)!}}\frac{{d^{{\mu_{vmnl} - i}} }}{{ds^{{\mu_{vmnl} - i}} }}\left( {\left( {1 + 2s\lambda_{vmnl}^{x} } \right)^{{\mu_{vmnl} }}\Phi (s)} \right)_{{s = - 1/2\lambda_{vmnl}^{x} }}$$

and

$$\beta_{i}^{vmnl} = \frac{1}{{\left( {\mu_{vmnl} - i} \right)!}}\frac{{d^{{\mu_{vmnl} - i}} }}{{ds^{{\mu_{vmnl} - i}} }}\left( {\left( {1 + 2s\lambda_{vmnl}^{y} } \right)^{\mu vmnl}\Phi (s)} \right)_{{s = - 1/2\lambda_{vmnl}^{y} }}$$

In case of validation, substitute U = 1, M _t  = 1 into (11), it lessens to [20, Eq. (44)], since Nakagami-m is a particular case of η–µ fading distribution. On the other hand, we can consider constant correlation as a particular case in this system analysis. That is to say, all channels are assumed to have the same average SINR and the same fading parameters η and µ with constant correlation across all channels. In this case, we assume that the power correlation coefficient ρ is the same between all the channel pairs, hence

$$\rho = \rho_{{ss^{{\prime }} }} = \frac{{Cov\left( {\gamma_{s} ,\gamma_{{s^{{\prime }} }} } \right)}}{{\sqrt {Var\left( {\gamma_{s} } \right)Var\left( {\gamma_{{s^{{\prime }} }} } \right)} }},\quad s \ne s^{{\prime }} ,\quad 0 \le \rho \le 1$$

(12)

Therefore, the eigenvalues of the covariance matrices $C_{xx}^{{\prime }}$ and $D_{yy}^{\prime }$ are given by [21–23]

$$\lambda_{1}^{x} = \sigma_{x}^{2} \left( {1 - \rho } \right)\,{\text{for}}\,{\text{k}} - 1\,{\text{fold}}\,{\text{zeros}},\quad \lambda_{2}^{x} = \sigma_{x}^{2} \left( {1 + \rho \left( {k - 1} \right)} \right)\,{\text{for}}\,{\text{single}}\,{\text{zero}}$$

and

$$\lambda_{1}^{y} = \sigma_{y}^{2} \left( {1 - \rho } \right)\,{\text{for}}\,{\text{k}} - 1\,{\text{fold}}\,{\text{zeros}},\quad \lambda_{2}^{y} = \sigma_{y}^{2} \left( {1 + \rho \left( {k - 1} \right)} \right)\,{\text{for}}\,{\text{single}}\,{\text{zero}}$$

where k = UM _t N _r L _r . Therefore, the MGF becomes [24, 25]

$$\Phi (s) = \left(1+2s\lambda_{1}^{x} \right)^{{ - \mu \left( {k - 1} \right)}} \left( 1+2s\lambda_{1}^{y} \right)^{{ - \mu \left( {k - 1} \right)}} \left(1+2s\lambda_{2}^{x} \right)^{ - \mu } \left(1+2s\lambda_{2}^{y} \right)^{ - \mu }$$

(13)

where ρ is the correlation coefficient between two adjacent antennas, σ ² _x and σ ² _y are the variances of the inphase component and quadrature component of the signal envelope. Alternatively, we can express (13) in partial fraction form and obtain its inverse Laplace transform [19, 20]

$$\Phi \left( \gamma \right) = \sum\limits_{i = 1}^{D} {\frac{{\alpha_{i} \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{x} }}}} }}{{\left( {2\lambda_{1}^{x} } \right)^{i} \left( {i - 1} \right)!}}} + \sum\limits_{i = 1}^{D} {\frac{{\beta_{i} \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{y} }}}} }}{{\left( {2\lambda_{1}^{y} } \right)^{i} \left( {i - 1} \right)!}}} + \sum\limits_{j = 1}^{\mu } {\frac{{c_{j} \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{x} }}}} }}{{\left( {2\lambda_{2}^{x} } \right)^{j} \left( {j - 1} \right)!}}} +\sum\limits_{j = 1}^{\mu } {\frac{{E_{j} \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{y} }}}} }}{{\left( {2\lambda_{2}^{y} } \right)^{j} \left( {j - 1} \right)!}}}$$

(14)

where D = µ(k − 1), α _i , β _i , C _j and E _j are residues to be obtained from the following differential expressions

$$\begin{aligned} \alpha_{i} & = \frac{1}{{\left( {D - i} \right)!}}\frac{{d^{D - i} }}{{ds^{D - i} }}\left( {\left( {1 + 2s\lambda_{1}^{x} } \right)^{D}\Phi (s)} \right)_{{s = - 1/2\lambda_{1}^{x} }} , \\ \beta_{i} & = \frac{1}{{\left( {D - i} \right)!}}\frac{{d^{D - i} }}{{ds^{D - i} }}\left( {\left( {1 + 2s\lambda_{1}^{y} } \right)^{D}\Phi (s)} \right)_{{s = - 1/2\lambda_{1}^{y} }} , \\ \end{aligned}$$

$$\begin{aligned} C_{j} & = \frac{1}{{\left( {\mu - j} \right)!}}\frac{{d^{\mu - j} }}{{ds^{\mu - j} }}\left( {\left( {1 + 2s\lambda_{2}^{x} } \right)^{\mu }\Phi (s)} \right)_{{s = - 1/2\lambda_{2}^{x} }} , \\ E_{j} & = \frac{1}{{\left( {\mu - j} \right)!}}\frac{{d^{\mu - j} }}{{ds^{\mu - j} }}\left( {\left( {1 + 2s\lambda_{2}^{y} } \right)^{\mu }\Phi (s)} \right)_{{s = - 1/2\lambda_{2}^{y} }} \\ \end{aligned}$$

4 Average Error Probability Performance Analysis

In this section, the average error probabilities of binary phase shift keying (BPSK), M-ary phase shift keying (MPSK) and square multilevel quadrature amplitude modulation (MQAM) modulation techniques for MIMO MC DS CDMA system operating over correlated η–µ frequency selective, slowly fading channels are determined. First, the conditional error probabilities of BPSK, MPSK and MQAM modulation schemes under the influence of additive white Gaussian noise (AWGN) is provided and then averaged over the PDF of the instantaneous SINR at the RAKE receiver output to yield average error probability of each modulation scheme for the system. In this case, both MGF and PDF of the instantaneous SINR is employed for determining the average error probability of the system.

4.1 Average Bit Error Probability of BPSK Modulation Technique

The average bit error probability of BPSK modulation scheme for MIMO MC DS CDMA system working over arbitrarily correlated η–µ frequency selective fading channels is obtained using (10) and (16). The conditional error probability of BPSK modulation scheme is given as in [24]

$$P_{b} \left( {E\left| \gamma \right.} \right) = Q\left( {\sqrt {2\gamma } } \right)$$

(15)

Then, the average error probability using MGF is as given in [24]

$$P_{b} \left( E \right) = \frac{1}{\pi }\int\limits_{0}^{0.5\pi } {M_{\gamma } } \left( {\frac{1}{{\sin^{2} \theta }}} \right)d\theta$$

(16)

So putting (10) into (16), the average bit error probability of BPSK modulation scheme using MGF is

$$P_{b} \left( E \right) = \frac{1}{\pi }\int\limits_{0}^{\infty } {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + \frac{{2\lambda_{vmnl}^{x} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} \left( {1 + \frac{{2\lambda_{vmnl}^{y} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} d\theta } } } } }$$

(17)

Then, carrying out substitution t = cos²θ and using further mathematical manipulations, the average bit error probability becomes

$$\begin{aligned} P_{b} \left( E \right) & = \frac{1}{2\sqrt \pi }\frac{{\Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 0.5} } } } } \right)}}{{\Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 1} } } } } \right)}} \\ & \quad \times \left( {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + 2\lambda_{vmnl}^{x} } \right)^{{ - \mu_{vmnl} }} \left( {1 + 2\lambda_{vmnl}^{y} } \right)^{{ - \mu_{vmnl} }} } } } } } \right) \\ & \quad \times F_{D}^{{\left( {2UM_{t} N_{r} L_{r} } \right)}} \left( {0.5,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ;} \right. \\ & \quad \quad 2\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 1} } } ;\frac{1}{{1 + 2\lambda_{1111}^{x} }},\frac{1}{{1 + 2\lambda_{1112}^{x} }}} , \ldots ,\frac{1}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{x} }}, \\ & \quad \quad \left. {\frac{1}{{1 + 2\lambda_{1111}^{y} }},\frac{1}{{1 + 2\lambda_{1112}^{y} }}, \ldots ,\frac{1}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{y} }}} \right), \\ \end{aligned}$$

(18)

For verification, suppose U = 1, K = 1, M_t = 1 and N_r = 1, then (18) diminishes to [18, Eq. (19)]. Alternatively, we determine the average bit error probability of BPSK modulation technique for the system communicating over arbitrary correlated η–µ frequency selective fading channels by averaging the conditional error probability (15) over the PDF (11) of the instantaneous SINR at the RAKE receiver output. i.e.,

$$\begin{aligned} P_{b} \left( E \right) & = \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\alpha_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{x} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma } } \right)} \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{x} }}}} d\gamma \\ & \quad + \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\beta_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{y} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma } } \right)\gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{y} }}}} d\gamma } \\ \end{aligned}$$

(19)

Therefore, carrying out integration as in [26], we have

$$\begin{aligned} P_{b} \left( E \right) & = \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\alpha_{i}^{vmnl} \left( {\frac{{1 - w_{1} }}{2}} \right)} } } } }^{i - 1} \sum\limits_{k = 0}^{i - 1} {\left( \begin{array}{c} i - 1 + k \hfill \\ k \\ \end{array} \right)} \left( {\frac{{1 + w_{1} }}{2}} \right)^{k} \\ & \quad + \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\beta_{i}^{vmnl} } \left( {\frac{{1 - w_{2} }}{2}} \right)} } } }^{i - 1} \sum\limits_{k1 = 0}^{i - 1} {\left( \begin{array}{c} i - 1 + k1 \hfill \\ {k1} \\ \end{array} \right)} \left( {\frac{{1 + w_{2} }}{2}} \right)^{k1} \\ \end{aligned}$$

(20)

where $w_{1} = \sqrt {\frac{{2\lambda_{vmnl}^{x} }}{{1 + 2\lambda_{vmnl}^{x} }}}$ and $w_{2} = \sqrt {\frac{{2\lambda_{vmnl}^{y} }}{{1 + 2\lambda_{vmnl}^{y} }}}$.

On the other hand, we reduce arbitrary correlation to its particular case constant correlation and obtain the average bit error probability of BPSK modulation scheme using MGF based approach. Upon substituting (13) into (16), yields

$$\begin{aligned} P_{b} \left( E \right) & = \frac{1}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {\left( {1 + \frac{{2\lambda_{1}^{x} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} } \left( {1 + \frac{{2\lambda_{1}^{y} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + \frac{{2\lambda_{2}^{x} }}{{\sin^{2} \theta }}} \right)^{ - \mu } \left( {1 + \frac{{2\lambda_{2}^{y} }}{{\sin^{2} \theta }}} \right)^{ - \mu } d\gamma , \\ \end{aligned}$$

(21)

Hence, let t = cos²θ be put in (21), simplifying further, then, we have

$$\begin{aligned} P_{b} \left( E \right) & = \frac{{\Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 0.5} \right)}}{{2\sqrt \pi \Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 1} \right)}}\left( {1 + 2\lambda_{1}^{x} } \right)^{{ - \left( {UM_{t} N_{r} L_{r} - 1} \right)\mu }} \left( {1 + 2\lambda_{1}^{y} } \right)^{{ - \left( {UM_{t} N_{r} L_{r} - 1} \right)\mu }} \\ & \quad \times \left( {1 + 2\lambda_{2}^{x} } \right)^{ - \mu } \left( {1 + 2\lambda_{2}^{y} } \right)^{ - \mu } \times F_{D}^{4} \left( {0.5,\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu ,\mu ;} \right. \\ & \quad \quad \left. {2UM_{t} N_{r} L_{r} \mu + 1;\frac{1}{{1 + 2\lambda_{1}^{x} }},\frac{1}{{1 + 2\lambda_{1}^{y} }},\frac{1}{{1 + 2\lambda_{2}^{x} }},\frac{1}{{1 + 2\lambda_{2}^{y} }}} \right), \\ \end{aligned}$$

(22)

Similarly, we use PDF based approach to find the average bit error probability of BPSK modulation format by averaging the conditional error probability over the PDF in (14), i.e.,

$$\begin{aligned} P_{b} \left( E \right) & = \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\alpha_{i} }}{{\left( {2\lambda_{1}^{x} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{x} }}}} d\gamma \\ & \quad + \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\beta_{i} }}{{\left( {2\lambda_{1}^{y} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{y} }}}} d\gamma \\ & \quad + \sum\limits_{j = 1}^{\mu } {\frac{{c_{j} }}{{\left( {2\lambda_{2}^{x} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt \gamma } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{x} }}}} d\gamma \\ & \quad + \sum\limits_{j = 1}^{\mu } {\frac{{E_{j} }}{{\left( {2\lambda_{2}^{y} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{y} }}}} d\gamma \\ \end{aligned}$$

(23)

Hence, carrying out integration by parts [26, 27], gives

$$\begin{aligned} P_{b} \left( E \right) & = \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\alpha_{i} } \left( {\frac{{1 - d_{1} }}{2}} \right)^{i - 1} \sum\limits_{k = 0}^{i - 1} {\left( \begin{array}{c} i - 1 + k \hfill \\ \begin{array}{*{20}c} {} & k \\ \end{array} \hfill \\ \end{array} \right)} \left( {\frac{{1 + d_{1} }}{2}} \right)^{k} \\ & \quad + \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\beta_{i} } \left( {\frac{{1 - d_{2} }}{2}} \right)^{i - 1} \sum\limits_{k = 0}^{i - 1} {\left( \begin{array}{c} i - 1 + k \hfill \\ \begin{array}{*{20}c} {} & k \\ \end{array} \hfill \\ \end{array} \right)\left( {\frac{{1 + d_{2} }}{2}} \right)^{k} } \\ & \quad + \sum\limits_{j = 1}^{\mu } {C_{j} } \left( {\frac{{1 - Z_{1} }}{2}} \right)^{j - 1} \sum\limits_{l = 1}^{j - 1} {\left( \begin{array}{c} j - 1 + l \hfill \\ \begin{array}{*{20}c} {} & l \\ \end{array} \hfill \\ \end{array} \right)\left( {\frac{{1 + Z_{1} }}{2}} \right)^{l} } \\ & \quad + \sum\limits_{j = 1}^{\mu } {E_{j} } \left( {\frac{{1 - Z_{2} }}{2}} \right)^{j - 1} \sum\limits_{l = 0}^{j - 1} {\left( \begin{array}{c} j - 1 + l \hfill \\ \begin{array}{*{20}c} {} & l \\ \end{array} \hfill \\ \end{array} \right)} \left( {\frac{{1 + Z_{2} }}{2}} \right)^{l} \\ \end{aligned}$$

(24)

where $d_{1} = \sqrt {\frac{{2\lambda_{1}^{x} }}{{1 + 2\lambda_{1}^{x} }}} ,d_{2} = \sqrt {\frac{{2\lambda_{1}^{y} }}{{1 + 2\lambda_{1}^{y} }}} ,Z_{1} = \sqrt {\frac{{2\lambda_{2}^{x} }}{{1 + 2\lambda_{2}^{x} }}} \quad {\text{and}}\quad Z_{2} = \sqrt {\frac{{2\lambda_{2}^{y} }}{{1 + 2\lambda_{2}^{y} }}} .$

4.2 Average Symbol Error Probability of MPSK Modulation Scheme

In this subsection, the average symbol error probability of MPSK modulation format for MIMO MC DS CDMA system transmitting over arbitrarily correlated η–µ frequency selective fading channels is first obtained using MGF based approach. The conditional error probability of MPSK modulation scheme is given as

$$P_{mpsk} \left( {E\left| \gamma \right.} \right) = 2Q\left( {\sqrt {2g_{mpsk} \gamma } } \right)$$

(25)

Hence, the average error probability of MPSK based on MGF approach is given by

$$P_{mpsk} \left( E \right) = \frac{1}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {M_{\gamma } } \left( {\frac{{g_{mpsk} }}{{\sin^{2} \theta }}} \right)d\theta + \frac{1}{\pi }\int\limits_{{\frac{\pi }{2}}}^{{\frac{\pi }{M}\left( {M - 1} \right)}} {M_{\gamma } \left( {\frac{{g_{mpsk} }}{{\sin^{2} \theta }}} \right)} \, d\theta$$

(26)

where g_mpsk = sin²(π/M) and M = 2ⁱ, I is a positive integer (i = 1, 2, 3,…).

From (10) and (26), we have

$$\begin{aligned} P_{mpsk} \left( E \right) & = \frac{1}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + \frac{{2\lambda_{vmnl}^{x} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} } } } } } \left( {1 + \frac{{2\lambda_{vmnl}^{y} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} d\theta \\ & \quad + \frac{1}{\pi }\int\limits_{{\frac{\pi }{2}}}^{{\pi - \frac{\pi }{M}}} {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + \frac{{2\lambda_{vmnl}^{x} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} \left( {1 + \frac{{2\lambda_{vmnl}^{y} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} d\theta } } } } } \\ \end{aligned}$$

(27)

So in integrating the first integral, we set t = cos²θ and making necessary mathematical manipulation, we arrived at

$$\begin{aligned} I_{1} & = \frac{{\Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 0.5} } } } } \right)}}{{2\sqrt \pi \Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} } + 0.5} } } } \right)}} \\ & \quad \times \left( {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + 2\lambda_{vmnl}^{x} g_{mpsk} } \right)^{{ - \mu_{vmnl} }} \left( {1 + 2\lambda_{vmnl}^{y} g_{mpsk} } \right)^{{ - \mu_{vmnl} }} } } } } } \right) \\ & \quad \times F_{D}^{{\left( {2UM_{t} N_{r} L_{r} } \right)}} \left( {0.5,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ,\mu_{1111} } \right.,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ; \\ & \quad \times2\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\mu_{vmnl} } + 1} } } ;\frac{1}{{1 + 2\lambda_{1111}^{x} g_{mpsk} }},\frac{1}{{1 + 2\lambda_{1112}^{x} g_{mpsk} }}, \ldots , \\ & \quad\quad \left. {\frac{1}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{x} g_{mpsk} }},\frac{1}{{1 + 2\lambda_{1111}^{y} g_{mpsk} }},\frac{1}{{1 + 2\lambda_{1112}^{y} g_{mpsk} }}, \ldots ,\frac{1}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{y} g_{mpsk} }}} \right), \\ \end{aligned}$$

(28)

Hence, Eq. (28) reduces to (18) if g_mpsk = 1. Similarly, we put t = cos²θ/cos²(π/M) in the second integral of (27) and manipulate, we have

$$\begin{aligned} I_{2} & = \frac{\cos (\pi /M)}{\pi }\left( {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + 2\lambda_{vmnl}^{x} g_{vmnl} } \right)^{{ - \mu_{vmnl} }} \left( {1 + 2\lambda_{vmnl}^{y} g_{mpsk} } \right)^{{ - \mu_{vmnl} }} } } } } } \right) \\ & \quad \times F_{D}^{{\left( {2UM_{t} N_{r} L_{r} + 1} \right)}} \left( {0.5,0.5 - 2\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{r} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\mu_{vmnl} } } } } } \right.,\mu_{1111} ,\mu_{1112} ,..,\mu_{{UM_{t} N_{r} L_{r} }} , \\ & \quad \quad \mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ;1.5;\cos^{2} (\pi /M),\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{1111}^{x} g_{mpsk} }},\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{1112}^{x} g_{mpsk} }}, \ldots , \\ & \quad \quad \frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{x} g_{mpsk} }},\left. {\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{1111}^{y} g_{mpsk} }},\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{1112}^{y} g_{mpsk} }}, \ldots ,\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{y} g_{mpsk} }}} \right) \\ \end{aligned}$$

(29)

Therefore, the average symbol error probability of MPSK modulation technique for the system operating over arbitrarily correlated η–µ frequency selective fading channels is the summation of I₁ and I₂.

Alternatively, we employ PDF based approach to determine the average symbol error probability of MPSK modulation technique for MIMO MC DS CDMA system working over arbitrarily correlated η–µ frequency selective fading channels. We average (25) over (11), hence, ASEP becomes

$$\begin{aligned} P_{mpsk} \left( E \right) & = \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\alpha_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{x} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g_{mpsk} } } \right)} \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{x} }}}} d\gamma \\ & \quad + \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\beta_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{y} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g_{mpsk} } } \right)\gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{y} }}}} d\gamma } \\ \end{aligned}$$

(30)

Using integration by parts, we have as Eq. (58) in “Appendix 2”

$$\begin{aligned} P_{mpsk} \left( E \right) & = \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\alpha_{i}^{vmnl} } } } } } \left( {1 - \sqrt {\frac{{2\lambda_{vmnl}^{x} g_{mpsk} }}{{\pi \left( {1 + 2\lambda_{vmnl}^{x} g_{mpsk} } \right)}}} \, \sum\limits_{j = 0}^{i - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {1 + 2\lambda_{vmnl}^{x} g_{mpsk} } \right)^{j} }}} } \right) \\ & \quad + \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\beta_{i}^{vmnl} } } } } } \left( {1 - \sqrt {\frac{{2\lambda_{vmnl}^{y} g_{mpsk} }}{{\pi \left( {1 + 2\lambda_{vmnl}^{y} g_{mpsk} } \right)}}} \, \sum\limits_{j = 0}^{i - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {1 + 2\lambda_{vmnl}^{y} g_{mpsk} } \right)^{j} }}} } \right) \\ \end{aligned}$$

(31)

For the case of special cases, we employ (13) to obtain the average symbol error probability of MPSK for MIMO MC DS CDMA system operating over constant correlation η–µ frequency selective fading channels. Then, putting (13) into (26), ASEP becomes

$$\begin{aligned} P_{mpsk} \left( E \right) & = \frac{1}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {\left( {1 + \frac{{2\lambda_{1}^{x} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} } \left( {1 + \frac{{2\lambda_{1}^{y} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + \frac{{2\lambda_{2}^{x} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{ - \mu } \left( {1 + \frac{{2\lambda_{2}^{y} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{ - \mu } d\theta \\ & \quad + \frac{1}{\pi }\int\limits_{{\frac{\pi }{2}}}^{{\pi - \frac{\pi }{M}}} {\left( {1 + \frac{{2\lambda_{1}^{x} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} } \left( {1 + \frac{{2\lambda_{1}^{y} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + \frac{{2\lambda_{2}^{x} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{ - \mu } \left( {1 + \frac{{2\lambda_{2}^{y} g_{mpsk} }}{{\sin^{2} \theta }}} \right)^{ - \mu } d\theta \\ \end{aligned}$$

(32)

Substituting t = cos²θ to the first integral and manipulate mathematically, we have

$$\begin{aligned} I_{1} & = \frac{{\Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 0.5} \right)}}{{2\sqrt \pi \Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 1} \right)}}\left( {1 + 2\lambda_{1}^{x} g_{mpsk} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \left( {1 + 2\lambda_{1}^{y} g_{mpsk} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + 2\lambda_{2}^{x} g_{mpsk} } \right)^{ - \mu } \left( {1 + 2\lambda_{2}^{y} g_{mpsk} } \right)^{ - \mu } F_{D}^{4} \left( {0.5,} \right.\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu ,\mu ; \\ & \quad \quad 2\mu \left( {UM_{t} N_{r} L_{r} - 1} \right) + 1;\left. {\frac{1}{{1 + 2\lambda_{1}^{x} g_{mpsk} }},\frac{1}{{1 + 2\lambda_{1}^{y} g_{mpsk} }},\frac{1}{{1 + 2\lambda_{2}^{x} g_{mpsk} }},\frac{1}{{1 + 2\lambda_{2}^{y} g_{mpsk} }}} \right) \\ \end{aligned}$$

(33)

Analogously, putting t = cos²θ/cos²(π/M) to the second integral and manipulate using algebra and calculus, we have

$$\begin{aligned} I_{2} & = \frac{\cos (\pi /M)}{\pi }\left( {1 + 2\lambda_{1}^{x} g_{mpsk} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \left( {1 + 2\lambda_{1}^{y} g_{mpsk} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + 2\lambda_{2}^{x} g_{mpsk} } \right)^{ - \mu } \left( {1 + 2\lambda_{2}^{y} g_{mpsk} } \right)^{ - \mu } F_{D}^{5} \left( {0.5,0.5 - 2\mu \left( {UM_{t} N_{r} L_{r} - 1} \right)} \right., \\ & \quad \quad \mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu ,\mu ;1.5;\cos^{2} (\pi /M), \\ & \quad \quad \left. {\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{1}^{x} g_{mpsk} }},\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{1}^{y} g_{mpsk} }},\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{2}^{x} g_{mpsk} }},\frac{{\cos^{2} (\pi /M)}}{{1 + 2\lambda_{2}^{y} g_{mpsk} }}} \right) \\ \end{aligned}$$

(34)

Hence, the summation of I₁ and I₂ yields the required average symbol error probability of MPSK modulation scheme for the system working over constant correlated η–µ frequency selective fading channels.

On the other hand, we utilise PDF based approach to calculate the average symbol error probability of MPSK modulation format for MIMO MC DS CDMA system operating over constant correlated η–µ frequency selective fading channels. Using (14) and (25), we have

$$\begin{aligned} P_{mpsk} \left( E \right) & = \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\alpha_{i} }}{{\left( {2\lambda_{1}^{x} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g_{mpsk} } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{x} }}}} d \\ & \quad + \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\beta_{i} }}{{\left( {2\lambda_{1}^{y} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g_{mpsk} } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{y} }}}} d\gamma \\ & \quad + \sum\limits_{j = 1}^{\mu } {\frac{{c_{j} }}{{\left( {2\lambda_{2}^{x} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g_{mpsk} } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{x} }}}} d\gamma \\ & \quad +\sum\limits_{j = 1}^{\mu } {\frac{{E_{j} }}{{\left( {2\lambda_{2}^{y} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g_{mpsk} } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{y} }}}} d\gamma \\ \end{aligned}$$

(35)

Hence, solving using integration by parts as Eq. (58) in “Appendix 2”, we have

$$\begin{aligned} P_{mpsk} \left( E \right) & = \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\alpha_{i} } \left( {1 - \sqrt {\frac{{2\lambda_{1}^{x} g_{mpsk} }}{{\pi \left( {1 + 2\lambda_{1}^{x} g_{mpsk} } \right)}}} \, \sum\limits_{l = 0}^{i - 1} {\frac{{\Gamma \left( {l + 0.5} \right)}}{{l!\left( {1 + 2\lambda_{1}^{x} g_{mpsk} } \right)^{l} }}} } \right) \\ & \quad + \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\beta_{i} } \left( {1 - \sqrt {\frac{{2\lambda_{1}^{y} g_{mpsk} }}{{\pi \left( {1 + 2\lambda_{1}^{y} g_{mpsk} } \right)}}} \, \sum\limits_{l = 0}^{i - 1} {\frac{{\Gamma \left( {l + 0.5} \right)}}{{l!\left( {1 + 2\lambda_{1}^{y} g_{mpsk} } \right)}}} } \right) \\ & \quad + \sum\limits_{j = 1}^{\mu } {C_{j} } \left( {1 - \sqrt {\frac{{2\lambda_{2}^{x} g_{mpsk} }}{{\pi \left( {1 + 2\lambda_{2}^{x} g_{mpsk} } \right)}}} \, \sum\limits_{l = 0}^{j - 1} {\frac{{\Gamma \left( {l + 0.5} \right)}}{{l!\left( {1 + 2\lambda_{2}^{x} g_{mpsk} } \right)^{l} }}} } \right) \\ & \quad + \sum\limits_{j = 1}^{\mu } {E_{j} } \left( {1 - \sqrt {\frac{{2\lambda_{2}^{y} g_{mpsk} }}{{\pi \left( {1 + 2\lambda_{2}^{y} g_{mpsk} } \right)}}} \, \sum\limits_{l = 0}^{j - 1} {\frac{{\Gamma \left( {l + 0.5} \right)}}{{l!\left( {1 + 2\lambda_{2}^{y} g_{mpsk} } \right)^{l} }}} } \right) \\ \end{aligned}$$

(36)

4.3 Average Symbol Error Probability of Square MQAM Modulation Technique

In case of arbitrary correlation, the average symbol error probability of MQAM modulation scheme for MIMO MC DS CDMA system is first obtained using MGF based approach. The conditional error probability of square MQAM modulation technique is given by [26]

$$P_{mqam} \left( {E\left| \gamma \right.} \right) = 4qQ\left( {\sqrt {2g_{mqam} \gamma } } \right) - 4q^{2} Q^{2} \left( {\sqrt {2g_{mqam} \gamma } } \right)$$

(37)

Then, the average symbol error probability of square MQAM modulation scheme based on MGF approach is given by

$$P_{mqam} \left( E \right) = \frac{4q}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {M_{\gamma } } \left( {\frac{{g_{mqam} }}{{\sin^{2} \theta }}} \right)d\theta - \frac{{4q^{2} }}{\pi }\int\limits_{0}^{{\frac{\pi }{4}}} {M_{\gamma } } \left( {\frac{{g_{mqam} }}{{\sin^{2} \theta }}} \right)d\theta$$

(38)

where $q = 1 - \sqrt {M^{ - 1} }$ and g _mqam  = 1.5(M − 1)⁻¹, M = 2ⁱ is the constellation size, i is an even positive integer (i = 2, 4, 6, …). Therefore, putting (10) into (38), we have

$$\begin{aligned} P_{mqam} \left( E \right) & = \frac{4q}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + \frac{{2\lambda_{vmnl}^{x} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} } } } } } \left( {1 + \frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} d\theta \\ & \quad -\frac{{4q^{2} }}{\pi }\int\limits_{0}^{{\frac{\pi }{4}}} {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + \frac{{2\lambda_{vmnl}^{x} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} } } } } } \left( {1 + \frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu_{vmnl} }} d\theta \\ \end{aligned}$$

(39)

Let t = cos²θ be put in the first integral and carry out further mathematical approaches, we have

$$\begin{aligned} I_{1} & = \frac{{2q\Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 0.5} } } } } \right)}}{{\sqrt \pi \Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 1} } } } } \right)}} \\ & \quad \times \left( {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + 2\lambda_{vmnl}^{x} g_{mqam} } \right)^{{ - \mu_{vmnl} }} \left( {1 + 2\lambda_{vmnl}^{y} g_{mqam} } \right)^{{ - \mu_{vmnl} }} } } } } } \right) \\ & \quad \times F_{D}^{{\left( {2UM_{t} N_{r} L_{r} } \right)}} \left( {0.5,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ;} \right. \\ & \quad \quad 2\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 1} } } } ;\frac{1}{{1 + 2\lambda_{1111}^{x} g_{mqam} }},\frac{1}{{1 + 2\lambda_{1112}^{x} g_{mqam} }}, \ldots , \\ &\quad \quad \frac{1}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{x} g_{mqam} }}\left. {,\frac{1}{{1 + 2\lambda_{1111}^{y} g_{mqam} }},\frac{1}{{1 + 2\lambda_{1112}^{y} g_{mqam} }}, \ldots ,\frac{1}{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{y} g_{mqam} }}} \right) \\ \end{aligned}$$

(40)

Similarly, putting t = 1 − tan²θ in the second integral of (39) and applying essential mathematical manipulations, we have

$$\begin{aligned} I_{2} & = \frac{{q^{2} \Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 0.5} } } } } \right)}}{{\pi \Gamma \left( {2\sum\nolimits_{v = 1}^{U} {\sum\nolimits_{m = 1}^{{M_{t} }} {\sum\nolimits_{n = 1}^{{N_{r} }} {\sum\nolimits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 1.5} } } } } \right)}} \\ & \quad \times \left( {\prod\limits_{v = 1}^{U} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {1 + 4\lambda_{vmnl}^{x} g_{mqam} } \right)^{{ - \mu_{vmnl} }} \left( {1 + 4\lambda_{vmnl}^{y} g_{mqam} } \right)^{{ - \mu_{vmnl} }} } } } } } \right) \\ & \quad \times F_{D}^{{\left( {2UM_{t} N_{r} L_{r} + 1} \right)}} \left( {1,1,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ,\mu_{1111} ,\mu_{1112} , \ldots ,\mu_{{UM_{t} N_{r} L_{r} }} ;} \right. \\ &\quad \quad 2\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\mu_{vmnl} + 1} } } } .5;0.5,\frac{{1 + 2\lambda_{1111}^{x} g_{mqam} }}{{1 + 4\lambda_{1111}^{x} g_{mqam} }},\frac{{1 + 2\lambda_{1112}^{x} g_{mqam} }}{{1 + 4\lambda_{1112}^{x} g_{mqam} }}, \ldots , \\ &\quad \quad \left. {\frac{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{x} g_{mqam} }}{{1 + 4\lambda_{{UM_{t} N_{r} L_{r} }}^{x} g_{mqam} }},\frac{{1 + 2\lambda_{1111}^{y} g_{mqam} }}{{1 + 4\lambda_{1111}^{y} g_{mqam} }},\frac{{1 + 2\lambda_{1112}^{y} g_{mqam} }}{{1 + 4\lambda_{1112}^{y} g_{mqam} }}, \ldots ,\frac{{1 + 2\lambda_{{UM_{t} N_{r} L_{r} }}^{y} g_{mqam} }}{{1 + 4\lambda_{{UM_{t} N_{r} L_{r} }}^{y} g_{mqam} }}} \right) \\ \end{aligned}$$

(41)

Therefore, the difference between I₁ and I₂ yields the required average symbol error probability.

On the other hand, we can determine the average symbol error probability of MQAM modulation scheme for MIMO MC DS CDMA system operating over arbitrarily correlated η–µ multipath fading channels using PDF based approach. That is to say, averaging (37) over (11), we have

$$\begin{aligned} P_{mqam} \left( E \right) & = 4q\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\alpha_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{x} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma g_{mqam} } } \right)} \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{x} }}}} d\gamma \\ & \quad + 4q\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\beta_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{y} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma g_{mqam} } } \right)\gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{y} }}}} d\gamma } \\ & \quad -4q^{2} \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\alpha_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{x} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {Q^{2} \left( {\sqrt {2\gamma g_{mqam} } } \right)} \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{x} }}}} d\gamma \\ & \quad -4q^{2} \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\frac{{\beta_{i}^{vmnl} }}{{\left( {2\lambda_{vmnl}^{y} } \right)^{i} \left( {i - 1} \right)!}}} } } } } \int\limits_{0}^{\infty } {Q^{2} \left( {\sqrt {2\gamma g_{mqam} } } \right)\gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{vmnl}^{y} }}}} d\gamma } \\ \end{aligned}$$

(42)

Therefore, carrying out integration by parts as Eqs. (58) and (60) in “Appendix 2”, we have

$$\begin{aligned} & P_{mqam} \left( E \right) = 2q\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\alpha_{i}^{vmnl} } } } } } \left( {1 - \sqrt {\frac{{2\lambda_{vmnl}^{x} g_{mqam} }}{{\pi \left( {2\lambda_{vmnl}^{x} g_{mqam} + 1} \right)}}} \, \sum\limits_{j = 0}^{i - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {2\lambda_{vmnl}^{x} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad + 2q\sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\beta_{i}^{vmnl} } } } } } \left( {1 - \sqrt {\frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{\pi \left( {2\lambda_{vmnl}^{y} g_{mqam} + 1} \right)}}} \, \sum\limits_{j = 0}^{i - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {2\lambda_{vmnl}^{y} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad -q^{2} \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\alpha_{i}^{vmnl} } } } } } \left( {1 - \frac{4}{\pi }\left( {\frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{4\lambda_{vmnl}^{y} g_{mqam} + 1}}} \right)\sum\limits_{j = 0}^{i - 1} {\frac{{_{2} F_{1} \left( {1,j + 1;j + 1.5;\frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{4\lambda_{vmnl}^{y} g_{mqam} + 1}}} \right)}}{{\left( {2j + 1} \right)\left( {4\lambda_{vmnl}^{y} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad -q^{2} \sum\limits_{v = 1}^{U} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{{\mu_{vmnl} }} {\beta_{i}^{vmnl} } } } } } \left( {1 - \frac{4}{\pi }\left( {\frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{4\lambda_{vmnl}^{y} g_{mqam} + 1}}} \right)\sum\limits_{j = 0}^{i - 1} {\frac{{_{2} F_{1} \left( {1,j + 1;j + 1.5;\frac{{2\lambda_{vmnl}^{y} g_{mqam} }}{{4\lambda_{vmnl}^{y} g_{mqam} + 1}}} \right)}}{{\left( {2j + 1} \right)\left( {4\lambda_{vmnl}^{y} g_{mqam} + 1} \right)^{j} }}} } \right), \\ \end{aligned}$$

(43)

For the case of special cases, we consider constant correlation as a particular case of arbitrary correlation, then based on MGF approach, the average symbol error probability of MQAM modulation technique is obtained by putting (13) into (38), we have

$$\begin{aligned} P_{mqam} \left( E \right) & = \frac{4q}{\pi }\int\limits_{0}^{{\frac{\pi }{2}}} {\left( {1 + \frac{{2\lambda_{1}^{x} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} } \left( {1 + \frac{{2\lambda_{1}^{y} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + \frac{{2\lambda_{2}^{x} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{ - \mu } \left( {1 + \frac{{2\lambda_{2}^{y} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{ - \mu } d\theta \\ & \quad -\frac{{4q^{2} }}{\pi }\int\limits_{0}^{{\frac{\pi }{4}}} {\left( {1 + \frac{{2\lambda_{1}^{x} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} } \left( {1 + \frac{{2\lambda_{1}^{y} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + \frac{{2\lambda_{2}^{x} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{ - \mu } \left( {1 + \frac{{2\lambda_{2}^{y} g_{mqam} }}{{\sin^{2} \theta }}} \right)^{ - \mu } d\theta \\ \end{aligned}$$

(44)

Putting t = cos²θ in the first integral and apply algebraic and calculus manipulation, we have

$$\begin{aligned} I_{1} & = \frac{{2q\Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 0.5} \right)}}{{\sqrt \pi \Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 1} \right)}}\left( {1 + 2\lambda_{1}^{x} g_{mqam} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \left( {1 + 2\lambda_{1}^{y} g_{mqam} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + 2\lambda_{2}^{x} g_{mqam} } \right)^{ - \mu } \left( {1 + 2\lambda_{2}^{y} g_{mqam} } \right)^{ - \mu } F_{D}^{4} \left( {0.5,\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu ,\mu ;} \right. \\ & \quad \quad 2UM_{t} N_{r} L_{r} \mu + 1;\left. {\frac{1}{{1 + 2\lambda_{1}^{x} g_{mqam} }},\frac{1}{{1 + 2\lambda_{1}^{y} g_{mqam} }},\frac{1}{{1 + 2\lambda_{2}^{x} g_{mqam} }},\frac{1}{{1 + 2\lambda_{2}^{y} g_{mqam} }}} \right) \\ \end{aligned}$$

(45)

In the same way, substituting t = 1 − tan²θ in the second integral of (44), and manipulating further, we have

$$\begin{aligned} I_{2} & = \frac{{q^{2} \Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 0.5} \right)}}{{\pi \Gamma \left( {2UM_{t} N_{r} L_{r} \mu + 1.5} \right)}}\left( {1 + 2\lambda_{1}^{x} g_{mqam} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \left( {1 + 2\lambda_{1}^{y} g_{mqam} } \right)^{{ - \mu \left( {UM_{t} N_{r} L_{r} - 1} \right)}} \\ & \quad \times \left( {1 + 2\lambda_{2}^{x} g_{mqam} } \right)^{ - \mu } \left( {1 + 2\lambda_{2}^{y} g_{mqam} } \right)^{ - \mu } F_{D}^{4 + 1} \left( {1,1,\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu \left( {UM_{t} N_{r} L_{r} - 1} \right),\mu ,\mu ;} \right. \\ & \quad \quad 2UM_{t} N_{r} L_{r} \mu + 1.5;0.5,\left. {\frac{{1 + 2\lambda_{1}^{x} g_{mqam} }}{{1 + 4\lambda_{1}^{x} g_{mqam} }},\frac{{1 + 2\lambda_{1}^{y} g_{mqam} }}{{1 + 4\lambda_{1}^{y} g_{mqam} }},\frac{{1 + 2\lambda_{2}^{x} g_{mqam} }}{{1 + 4\lambda_{2}^{x} g_{mqam} }},\frac{{1 + 2\lambda_{2}^{y} g_{mqam} }}{{1 + 4\lambda_{2}^{y} g_{mqam} }}} \right) \\ \end{aligned}$$

(46)

Hence, the difference between I₁ and I₂ yields the average symbol error probability of MQAM modulation format for MIMO MC DS CDMA system operating over constant correlation η–µ frequency selective fading channels.

On the other hand, we employ PDF based approach to calculate the average symbol error probability of MQAM modulation format for MIMO MC DS CDMA system operating over constant correlated η–µ frequency selective fading channels. Using (14) and (37), we have

$$\begin{aligned} P_{mqam} \left( E \right) & = 4q\sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\alpha_{i} }}{{\left( {2\lambda_{1}^{x} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{x} }}}} d\gamma \\ & \quad + 4q\sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\beta_{i} }}{{\left( {2\lambda_{1}^{y} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{y} }}}} d\gamma \\ & \quad + 4q\sum\limits_{j = 1}^{\mu } {\frac{{c_{j} }}{{\left( {2\lambda_{2}^{x} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{x} }}}} d\gamma \\ & \quad + 4q\sum\limits_{j = 1}^{\mu } {\frac{{E_{j} }}{{\left( {2\lambda_{2}^{y} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {Q\left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{y} }}}} d\gamma \\ & \quad -4q^{2} \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\alpha_{i} }}{{\left( {2\lambda_{1}^{x} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {Q^{2} \left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{x} }}}} d\gamma \\ & \quad -4q^{2} \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\frac{{\beta_{i} }}{{\left( {2\lambda_{1}^{y} } \right)^{i} \left( {i - 1} \right)!}}} \int\limits_{0}^{\infty } {Q^{2} \left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{i - 1} e^{{ - \frac{\gamma }{{2\lambda_{1}^{y} }}}} d\gamma \\ & \quad -4q^{2} \sum\limits_{j = 1}^{\mu } {\frac{{c_{j} }}{{\left( {2\lambda_{2}^{x} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {Q^{2} \left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{x} }}}} d\gamma \\ & \quad -4q^{2} \sum\limits_{j = 1}^{\mu } {\frac{{E_{j} }}{{\left( {2\lambda_{2}^{y} } \right)^{j} \left( {j - 1} \right)!}}} \int\limits_{0}^{\infty } {Q^{2} \left( {\sqrt {2\gamma g_{mqam} } } \right)} \, \gamma^{j - 1} e^{{ - \frac{\gamma }{{2\lambda_{2}^{y} }}}} d\gamma \\ \end{aligned}$$

(47)

Hence, integrating by parts as Eqs. (58) and (60) in “Appendix 2”, we have

$$\begin{aligned} P_{mqam} \left( E \right) & = 2q\sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\alpha_{i} } \left( {1 - \sqrt {\frac{{2\lambda_{1}^{x} g_{mqam} }}{{\pi \left( {2\lambda_{1}^{x} g_{mqam} + 1} \right)}}} \, \sum\limits_{j = 0}^{i - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {2\lambda_{1}^{x} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad + 2q\sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\beta_{i} } \left( {1 - \sqrt {\frac{{2\lambda_{1}^{y} g_{mqam} }}{{\pi \left( {2\lambda_{1}^{y} g_{mqam} + 1} \right)}}} \, \sum\limits_{j = 0}^{i - 1} {\frac{{\Gamma \left( {i + 0.5} \right)}}{{j!\left( {2\lambda_{1}^{y} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad + 2q\sum\limits_{l = 1}^{\mu } {c_{l} } \left( {1 - \sqrt {\frac{{2\lambda_{2}^{x} g_{mqam} }}{{\pi \left( {2\lambda_{2}^{x} g_{mqam} + 1} \right)}}} \, \sum\limits_{j = 0}^{l - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {2\lambda_{2}^{x} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad + 2q\sum\limits_{l = 1}^{\mu } {E_{l} } \left( {1 - \sqrt {\frac{{2\lambda_{2}^{y} g_{mqam} }}{{\pi \left( {2\lambda_{2}^{y} g_{mqam} + 1} \right)}}} \, \sum\limits_{j = 0}^{l - 1} {\frac{{\Gamma \left( {j + 0.5} \right)}}{{j!\left( {2\lambda_{2}^{y} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad -q^{2} \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\alpha_{i} } \left( {1 - \frac{4}{\pi }\left( {\frac{{2\lambda_{1}^{x} g_{mqam} }}{{4\lambda_{1}^{x} g_{mqam} + 1}}} \right)\sum\limits_{j = 0}^{i - 1} {\frac{{_{2} F_{1} \left( {1,j + 1;j + 1.5;\frac{{2\lambda_{1}^{x} g_{mqam} }}{{4\lambda_{1}^{x} g_{mqam} + 1}}} \right)}}{{\left( {2j + 1} \right)\left( {4\lambda_{1}^{x} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad -q^{2} \sum\limits_{i = 1}^{{UM_{t} N_{r} L_{r} \mu - \mu }} {\beta_{i} } \left( {1 - \frac{4}{\pi }\left( {\frac{{2\lambda_{1}^{y} g_{mqam} }}{{4\lambda_{1}^{y} g_{mqam} + 1}}} \right)\sum\limits_{j = 0}^{i - 1} {\frac{{_{2} F_{1} \left( {1,j + 1;j + 1.5;\frac{{2\lambda_{1}^{y} g_{mqam} }}{{4\lambda_{1}^{y} g_{mqam} + 1}}} \right)}}{{\left( {2j + 1} \right)\left( {4\lambda_{1}^{y} g_{mqam} + 1} \right)^{j} }}} } \right) \\ & \quad -q^{2} \sum\limits_{l = 1}^{\mu } {c_{l} \left( {1 - \frac{4}{\pi }\left( {\frac{{2\lambda_{2}^{x} g_{mqam} }}{{4\lambda_{2}^{x} g_{mqam} + 1}}} \right)\sum\limits_{j = 0}^{l - 1} {\frac{{_{2} F_{1} \left( {1,j + 1;j + 1.5;\frac{{2\lambda_{2}^{x} g_{mqam} }}{{4\lambda_{2}^{x} g_{mqam} + 1}}} \right)}}{{\left( {2j + 1} \right)\left( {4\lambda_{2}^{x} g_{mqam} + 1} \right)^{j} }}} } \right)} \\ & \quad -q^{2} \sum\limits_{l = 1}^{\mu } {E_{l} } \left( {1 - \frac{4}{\pi }\left( {\frac{{2\lambda_{2}^{y} g_{mqam} }}{{4\lambda_{2}^{y} g_{mqam} + 1}}} \right)\sum\limits_{j = 0}^{i - 1} {\frac{{_{2} F_{1} \left( {1,j + 1;j + 1.5;\frac{{2\lambda_{2}^{y} g_{mqam} }}{{4\lambda_{2}^{y} g_{mqam} + 1}}} \right)}}{{\left( {2j + 1} \right)\left( {4\lambda_{2}^{y} g_{mqam} + 1} \right)^{j} }}} } \right) \\ \end{aligned}$$

(48)

Generally, Eqs. (18), (20), (22), (24), (28) + (29), (31), (33) + (34), (36), (40)–(41), (43), (45)–(46) and (48) are the novel contributions of the authors.

5 Numerical Examples and Discussions

In this section, the derived closed form expressions for average error probabilities of BPSK, MPSK, and square MQAM modulation techniques for multiantenna MC DS CDMA system communicating over correlated η–µ frequency selective fading channels are analysed and represented graphically. Invariable parameters are indicated at the top of each figure and changeable ones are placed within the graphs respectively. Throughout the system analysis, it is assumed that lambda (λ), that is the space between two adjacent subcarriers, and spreading gain are fixed and equal because the system represent orthogonal MC DS CDMA multicarrier communication system.

Figure 1 exemplifies the effect of correlation coefficient on the system’s performance over η–µ multipath fading channels in terms of average bit error probability. It is noted that increasing the correlation coefficient increases the average bit error probability of the system. Hence, the performance of the system degrades. But as shown, increasing the number of RAKE branches reduces the effect of correlation coefficient on the system’s performance. In Fig. 2, we demonstrate the performance of the system over correlated η–µ multipath fading channels under the influence of multipath intensity profile. In this case, increasing the multipath intensity profile increases the average bit error probability of the system and diminishes the system’s performance. It is seen that the effect of decaying power factor on the system’s performance is more diminishing if the correlation coefficient is small otherwise it is less destructive. In Fig. 3, the influence of η fading parameter on the system’s performance is considered in format 1 scenario. As shown in the figure, it is observed that the performance of the system improves if η fading parameter increases. This is due to the increase in in-phase and quadrature components power ratio of the received signal within a cluster. Figure 4 shows average bit error probability of BPSK modulation scheme versus average SNR of the system operating over correlated η–µ frequency selective fading channels in format 2 scenario. In this figure, it is noted that as η fading parameter increases the performance of the system deteriorates. This is because the in-phase and quadrature components of the received signal in one cluster are correlated. Hence, Figs. 1, 2, 3 and 4 are derived from (22).

Fig. 1

Average bit error probability of BPSK digital modulation scheme versus average SNR for multiantenna MC DS CDMA system transmitting over correlated η–µ multipath fading channels (µ = 1, η = 0.5: format 1 scenario)

Fig. 2

Effect of multipath intensity profile on average bit error probability of the system communicating over correlated η–µ multipath fading channels (η = 0.5, µ = 1: format 1 scenario)

Fig. 3

Average bit error probability of BPSK modulation technique against average SNR for multiantenna MC DS CDMA system operating over correlated η–µ frequency selective fading channels with varying η parameter in format 1 scenario (µ = 1)

Fig. 4

Average bit error probability of BPSK modulation technique versus average SNR for MIMO MC DS CDMA system transmitting over correlated η–µ multipath fading channels with variable η parameter in format 2 scenario (µ = 1)

On the other hand, Figs. 5, 6 and 7 are obtained from (33) + (34). Figure 5 illustrates average symbol error probability of MPSK modulation scheme against average SNR for SIMO MC DS CDMA system operating over correlated η–µ multipath fading channels in format 1 scenario. It exemplifies the effects of correlation coefficient and signal constellations on the performance of the system functioning over correlated η–µ multipath fading channels with two users. It is shown that the system performance degrades as the correlation coefficient increases and also when the signal constellation size increases as well. Similarly, Fig. 6 shows the effects of correlation coefficient and signal constellation size. It is noticed that the effect of correlation on the performance of the system is more severe than that of the signal constellation size. Figure 7 demonstrates the average symbol error probability of MPSK modulation technique versus average SNR. In this figure, the effects of multipath power profile and signal constellation size are considered. We observe that the average symbol error probability increases if either the constellation size or decaying power profile increases. Therefore, the performance of the system degrades. It is also noticed that the effects of signal constellation size and correlation coefficient on the system’s performance can be reduced by increasing the number of RAKE branches, i.e., multipath diversity.

Fig. 5

Average symbol error probability versus average SNR of MPSK modulation technique against average SNR for SIMO MC DS CDMA system working over correlated η–µ multipath fading channels (η = 0.5, µ = 0.5: format 1 scenario)

Fig. 6

Average symbol error probability of MPSK modulation scheme versus average SNR for SIMO MC DS CDMA system operating over correlated η–µ multipath fading channels with two active users (η = 0.5, µ = 0.5: format 1 scenario)

Fig. 7

Average error probability of MPSK modulation technique as a function of average SNR for SIMO MC DS CDMA system communicating over correlated η–µ multipath fading channels (η = 0.5, µ = 0.5: format 1 scenario)

Based on (45) − (46), Figs. 8, 9 and 10 are plotted to illustrate the influence of correlation on the system’s performance. Figure 8 represents the effect of correlation coefficient on the system’s performance in terms of average symbol error probability. We note that when the correlation coefficient increases, the symbol error probability increases as well which leads to the deterioration in system’s performance over η–µ fading channels. In this case, we cannot also ignore the influence of the signal constellation size on the system operation. Furthermore, Fig. 9 demonstrates the impact of fading parameter µ on the system operation over correlated η–µ multipath fading channels in terms of average symbol error probability. It is seen from the figure that increasing the fading parameter µ decreases the average symbol error probability and enhances the system’s performance. Figure 10 depicts average symbol error probability of square MQAM modulation scheme versus average SNR. It demonstrates the impact of decaying power factor and signal constellation size. We observe that both decaying power factor and constellation size affect the system’s performance.

Fig. 8

Average symbol error probability of MQAM modulation scheme against average SNR for multiantenna MC DS CDMA system transmitting over correlated η–µ multipath fading channels with varying correlation coefficients (η = 1.5, µ = 1, δ = 0.2: format 1 scenario)

Fig. 9

Average symbol error probability of 4.16 QAM modulation technique against average SNR for multiantenna MC CDMA system functioning over correlated η–µ multipath fading channels with varying fading parameter µ (η = 1.5, δ = 0.2, ρ = 0.2: format 1 scenario)

Fig. 10

Average symbol error probability of square MQAM modulation scheme versus average SNR for multiantenna MC DS CDMA system transmitting over correlated η–µ frequency selective fading channels in format 1 scenario (η = 1.5, µ = 1.5)

Generally, providing sufficient space between two adjacent antennas can alleviate the destructive effect of correlation and enhances the system’s performance. In addition, increasing spatial diversity as well as path diversity can further improves the performance of the system operating over fading channels. We confirm the correctness of the analytical approaches via Monte Carlo simulation technique.

6 Conclusion

In this paper, we have incorporated a RAKE receiver into the system (MIMO MC DS CDMA) receiver side and investigated its communication over correlated η–µ frequency selective fading channels. The performance of the multiantenna MC DS CDMA system over correlated η–µ frequency selective fading channels in terms of average error probability have been explored. Based on MGF, closed form expressions for average probability of error for the system have been derived and expressed in terms of Appell’s hypergeometric functions and Lauricella’s multivariate hypergeometric functions, respectively. Similarly, PDF have been employed to determine closed form formulae for average error probability of the system operating over correlated η–µ multipath fading channels.

Based on average error probabilities of BPSK, MPSK, and square MQAM digital modulation technique for the system operating over correlated η–µ frequency selective fading channels, we obtained the numerical results. From these results, we deduced that the effects of correlation, decaying power factor, and signal constellation size on the system’s performance increases the average error probability. Consequently, the performance of the system over correlated η–µ frequency selective fading channels is reduced. On the other hand, we employed spatial and path diversity to enhance the system performance. Finally, we validated our results by reducing the expressions for average error probabilities to those already available in the literature and the exactness of the analytical methods through Monte Carlo simulation approach.

Appendices

Appendix 1

The MGF of the instantaneous SINR at the output of the RAKE receiver is derived in this appendix. The envelope (R) of the fading signal is modelled by η–µ fading distribution. Then, the random variable γ = ‖R ²‖ has the PDF of η–µ distribution. Hence, a set of N_rM_tUL_r variates of η–µ random variables is equivalent to a set of 2µ independent Gaussian random variable vectors with N_rM_tUL_r dimensions. Since the instantaneous signal to interference noise ratio is given as in (8a)

$$\gamma_{s} = \gamma_{c} \sum\limits_{n = 1}^{{N_{t} }} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{j = 1}^{U} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{2\mu } {R_{nmjli}^{2} } } } } }$$

(49)

where $R_{nmjli}^{2} = R_{nmjli}^{T} R_{nmjli} = X_{nmjli}^{T} X_{nmjli} + Y_{nmjli}^{T} Y_{nmjli}$, X_i1=nmjl = [X_i11, X_i12, …, X_i2µ]^T where i ₁  = nmjl = 1, 2, …, N_rM_tUL_r represent dependent inphase random variables. Hence, X_i1k are independent and identically distributed Gaussian random variables with zero mean and variance $E[X_{i1k}^{2} ]$, k = 1, 2, …, 2µ. Similarly, Y_i1=nmjl = [Y_i11, Y_i12, …, Y_i12µ]^T denote dependent quadrature random variables. Therefore, Y_i1k are independent identically distributed Gaussian random variables with zero mean and variance $E[Y_{i1k}^{2} ]$ [27]. Both are mutually independent Gaussian variables with $E[X_{nmjli} ] = E[Y_{nmjli} ] = 0, E[X_{nmjli}^{2} ] = \rho_{x}^{2} , E[Y_{nmjli}^{2} ] = \rho_{y}^{2}$, µ is the number of clusters of multipath. Therefore, the instantaneous SINR can be rewritten as

$$\gamma_{s} = \gamma_{c} \sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{j = 1}^{U} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{2\mu } {X_{nmjli}^{2} } } } } } + \gamma_{c} \sum\limits_{n = 1}^{{N_{r} }} {\sum\limits_{m = 1}^{{M_{t} }} {\sum\limits_{j = 1}^{U} {\sum\limits_{l = 1}^{{L_{r} }} {\sum\limits_{i = 1}^{2\mu } {Y_{nmjli}^{2} } } } } }$$

(50)

Considering the inphase random variates $X_{i1k}^{T} X_{i1k}$, similarly for quadrature random $Y_{i1k}^{T} Y_{i1k}$. For the case of inphase random variates, we assume the arbitrary covariance matrix as C_xx, then we can form a scalar quadratic function of vector X, i.e., suppose ${\text{Z}} = {\mathbf{X}}_{nmli}^{T} B_{nmli} {\mathbf{X}}_{nmli}$, where B_nmli is a 2µ by 2µ matrix. Hence, the joint PDF of $[{\text{X}}_{\text{nmlil}}^{2} + {\text{X}}_{{{\text{nmli}}2}}^{2} + \cdots + X_{{{\text{nmli}}2\upmu}}^{2} ]$ is [16, 28]

$$f\left( {X_{nmli} } \right) = \frac{1}{{\sqrt {\left( {2\pi } \right)^{2\mu } \det \left( {C_{xx} } \right)} }} \, \exp \left( { - \frac{1}{2}X_{nmli}^{T} C_{nmli}^{ - 1} X_{nmli} } \right)$$

(51)

Then, the MGF of Z is

$$\begin{aligned} \Phi_{x} (s) & = E\left[ {e^{{ - sX_{nmli}^{T} B_{nmli} X_{nmli} }} } \right] = \int\limits_{0}^{\infty } {\frac{1}{{\sqrt {\left( {2\pi } \right)^{2\mu } \det \left( {C_{xx} } \right)} }}} {\text{ e}}^{{ - \frac{ 1}{ 2}\left( {X_{nmli}^{T} C_{xx}^{ - 1} X_{nmli} } \right)}} {\text{ e}}^{{ - sX_{nmli}^{T} B_{nmli} X_{nmli} }} {\text{dX}}_{\text{nmli}} \\ & = \int\limits_{0}^{\infty } {\frac{1}{{\sqrt {\left( {2\pi } \right)^{2\mu } \det \left( {C_{xx} } \right)} }}} {\text{ e}}^{{ - \frac{ 1}{ 2}\left( {X_{nmli}^{T} \left( {C_{xx}^{ - 1} + 2sB_{nmli} } \right)X_{nmli} } \right)}} {\text{ dX}}_{\text{nmli}} \\ & = \frac{{\sqrt {\left( {\det \left( {F^{ - 1} } \right)} \right)} }}{{\sqrt {\left( {\det \left( {C_{xx} } \right)} \right)} }} \, \int\limits_{ 0}^{\infty } {\frac{ 1}{{\sqrt {\left( { 2\pi } \right)^{2\mu } \left( {\det \left( F \right)} \right)} }}} {\text{ e}}^{{ - \frac{ 1}{ 2}X^{T} F^{ - 1} X}} {\text{ dX}} \\ & = \frac{1}{{\det \left( {I_{nmli} + 2sB_{nmli} Cxx} \right)^{\mu } }} \\ \end{aligned}$$

(52)

where det denotes determinant. Therefore, for N_rM_tUL_r diversity branches, we have

$$\Phi_{x} (s) = \prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{i = 1}^{U} {\prod\limits_{l = 1}^{{L_{r} }} {\frac{1}{{\det \left( {I_{nmil} + 2sB_{nmil} C_{xx}^{nmil} } \right)^{{\mu_{nmil} }} }}} } } }$$

(53)

Similarly, for Y_nmil (quadrature Gaussian variates), we have

$$\Phi_{y} (s) = \prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{i = 1}^{U} {\prod\limits_{l = 1}^{{L_{r} }} {\frac{1}{{\det \left( {I_{nmil} + s2B_{nmil} D_{yy}^{nmil} } \right)^{{\mu_{nmil} }} }}} } } } ,$$

(54)

where D is the matrix. Therefore, overall MGF of instantaneous SINR at the RAKE receiver output is

$$\Phi_{x + y} (s) = \prod\limits_{n = 1}^{{N_{r} }} {\prod\limits_{m = 1}^{{M_{t} }} {\prod\limits_{i = 1}^{U} {\prod\limits_{l = 1}^{{L_{r} }} {\left( {\frac{1}{{\det \left( {I_{nmil} + 2sB_{nmil} C_{xx}^{nmil} } \right)^{{\mu_{nmil} }} \det \left( {I_{nmil} + 2sB_{nmil} D_{yy}^{nmil} } \right)^{{\mu_{nmil} }} }}} \right)} } } }$$

(55)

Appendix 2

In this appendix, we provide some hints for the solutions of (31), (36), (43), and (48), respectively. We consider

$$G_{1} = \int\limits_{0}^{\infty } {2Q\left( {\sqrt {2\gamma g} } \right)} \gamma^{i - 1} e^{ - \alpha \gamma } d\gamma = \int\limits_{0}^{\infty } {erfc\left( {\sqrt {g\gamma } } \right)} \gamma^{i - 1} e^{ - \alpha \gamma } d\gamma$$

(56)

Hence, we integrate using by parts

$$U = erfc\left( {\sqrt {g\gamma } } \right)\gamma^{i - 1} = \left( {\frac{2}{\sqrt \pi }\int\limits_{{\sqrt {g\gamma } }}^{\infty } {e^{{ - t^{2} }} } dt} \right)\gamma^{i - 1}$$

and dV = e ^−αγ dγ, then

$$dU = \left( { - \sqrt {\frac{g}{\pi }} \gamma^{i - 1.5} e^{ - g\gamma } + \left( {i - 1} \right)\gamma^{i - 2} erfc\left( {\sqrt {g\gamma } } \right)} \right)d\gamma$$

and $V = - \frac{1}{\alpha }e^{ - \alpha \gamma }$, then

$$\frac{{\left( {i - 1} \right)}}{\alpha }\int\limits_{0}^{\infty } {\gamma^{i - 2} } erfc\left( {\sqrt {g\gamma } } \right)e^{ - \alpha \gamma } d\gamma - \sqrt {\frac{g}{{\pi \alpha^{2} }}} \int\limits_{0}^{\infty } {\gamma^{i - 1.5} } e^{{ - \left( {\alpha + g} \right)\gamma }} d\gamma .$$

We have to integrate the first integral by parts, yields

$$\begin{aligned} & \frac{{\left( {i - 1} \right)\left( {i - 2} \right)}}{{\alpha^{2} }}\int\limits_{0}^{\infty } {\gamma^{i - 3} } erfc\left( {\sqrt {g\gamma } } \right)e^{ - \alpha \gamma } d\gamma - \frac{{\left( {i - 1} \right)}}{{\alpha^{2} }}\sqrt {\frac{g}{\pi }} \int\limits_{0}^{\infty } {\gamma^{i - 2.5} } e^{{ - \left( {\alpha + g} \right)\gamma }} d\gamma \\ & \quad - \sqrt {\frac{g}{{\pi \alpha^{2} }}} \int\limits_{0}^{\infty } {\gamma^{i - 1.5} } e^{{ - \left( {\alpha + g} \right)\gamma }} d\gamma \\ \end{aligned}$$

(57)

Therefore, the last two integrals are obtained from [29, 30, 31, Eq. (3.371)], again applying successive integration by parts to first integral, the general solution is given as

$$G_{1} = \frac{{\left( {i - 1} \right)!}}{{\alpha^{i} }}\left[ {1 - \sqrt {\frac{g}{{\pi \left( {g + \alpha } \right)}}} \sum\limits_{l = 0}^{i - 1} {\frac{{\alpha^{l} \Gamma \left( {l + 0.5} \right)}}{{l!\left( {g + \alpha } \right)^{l} }}} } \right]$$

(58)

Next, we consider the integral given below

$$G_{2} = \int\limits_{0}^{\infty } {2Q^{2} } \left( {\sqrt {2g\gamma } } \right)\gamma^{i - 1} e^{ - \alpha \gamma } d\gamma = \int\limits_{0}^{\infty } {erfc^{2} } \left( {\sqrt {g\gamma } } \right)\gamma^{i - 1} e^{ - \alpha \gamma } d\gamma$$

(59)

Then, let $z = \sqrt {g\gamma }$ and $\gamma = z^{2} /g,{\text{ d}}\gamma {\text{ = 2zdz/g}}$, we have

$$G_{2} = \frac{2}{{g^{i} }}\int\limits_{0}^{\infty } {z^{2i - 1} } erfc^{2} \left( z \right)e^{{ - kz^{2} }} dz$$

where k = α/g, then integrating by parts

$$U = erfc^{2} \left( z \right), \quad dU = - \frac{4}{\sqrt \pi }erfc\left( z \right)e^{{ - z^{2} }} dz$$

and

$$dV = z^{2i - 1} e^{{ - kz^{2} }} dz, \quad V = \int {z^{2i - 1} } e^{{ - kz^{2} }} dz$$

Hence, from [31, Eq. (2.326.11)]

$$V = - \frac{{\left( {i - 1} \right)!}}{{k^{i} }}e^{{ - kz^{2} }} \sum\limits_{l = 0}^{i - 1} {\frac{{\left( {kz^{2} } \right)^{l} }}{l!}} ,$$

then the integral becomes

$$\frac{{\left( {i - 1} \right)!}}{{k^{i} }} - \frac{{4\left( {i - 1} \right)!}}{{\sqrt \pi k^{i} }}\sum\limits_{l = 0}^{i - 1} {\frac{{k^{l} }}{l!}} \int\limits_{0}^{\infty } {erfc\left( z \right)} e^{{ - \left( {1 + k} \right)z^{2} }} dz,$$

then considering the integral part

$$y = \left( {1 + k} \right)z^{2} ,\quad z = \sqrt {\frac{1}{1 + k}} y^{0.5} ,\quad dz = 0.5\sqrt {\frac{1}{k + 1}} y^{ - 0.5} dy$$

and putting

$$erfc\left( {\sqrt {A\gamma } } \right) = \frac{{\Gamma \left( {0.5,A\gamma } \right)}}{\sqrt \pi }$$

Then from [27, 32, 31, Eq. (6.455.1)], the solution is

$$G_{2} = \left( {\frac{g}{\alpha }} \right)^{i} \left( {i - 1} \right)!\left[ {1 - \frac{4}{\pi }\left( {\frac{g}{2g + \alpha }} \right)\sum\limits_{l = 0}^{i - 1} {\frac{{\alpha^{l} }}{{\left( {2l + 1} \right)\left( {2g + \alpha } \right)^{l} }} \, {}_{2}F_{1} \left( {1,l + 1;l + 1.5;\frac{g + \alpha }{2g + \alpha }} \right)} } \right]$$

(60)

Therefore, the expressions for G₁ can be employed in (30), (35), while for both G₁ and G₂ in (42), and (47), respectively.