1 Introduction

IoT [1] refers to the network formed by objects with the identification, perception and intelligent processing ability based on the communication technology, and these objects can realize collaboration and interaction without manual intervention so as to provide an intelligent network information system that covers all people and objects in the world. With the development of IoT, especially the wireless sensor network (WSN) technology, the WSN consisting of it can connect the physical world and the digital world, so WSN is the basis of IoT. WSN has been extensively applied to the various fields, such as natural disaster monitoring, medical and health, intelligent traffic, aviation and aerospace and so on [2]. During its applications in multiple fields, the location information of nodes is usually the precondition of their applications, which plays a critical role, and the related literature [3] shows that about 80 % contextual information is related to the location. Through the GPS carried by the nodes or the manually set method, the location information of event occurrence can be obtained, however, in many applications, hundreds or thousands of sensor nodes might be involved and it is not practical to use GPS for all the sensor nodes because of cost concerns and some technical problems related to line-of-sight (LOS). Therefore, under the scenario that that it is not accessible by the personnel or the application of GPS is restricted, other approaches are required to determine the location information of event occurrence within the monitoring area.

Through many years’ development, researchers have proposed many localization strategies and methods. According to whether distance information in the localization is required, the localization techniques of IoT can be roughly divided into the range-based and the range-free [4, 5]. The former usually implements their localization requires to obtain the distance or angle information between two neighboring nodes. The range-based localization has a relatively higher localization accuracy, but it also has a strict requirement of hardware and it costs more, so it is generally not suitable for large-scale deployment. In order to reduce various expenditures such as energy and hardware, range-free technology is generally adopted in large-scale IoT localization. Most of the range-free methods obtain the inter-node hop-counts through the connection information between nodes, and then estimate the locations of unknown nodes. However, similar to many key technologies, during the practical application, the multihop range-free technology is still affected by many technical problems, among which, the most critical one is that the range-free localization method can only obtain ideal localization result in the isotropic network with high nodes density and uniform distribution, but its localization result is poor in the complicated environment (anisotropic network environment) when the node distributions are not uniform and sparse.

The issue that causes the low performance of multihop range-free method mainly consists of three aspects [6–8], i.e.,:

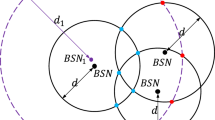
  • The ambiguity problem of hop-counts and physical distances: when there is the same hop-counts between nodes, it does not necessarily mean they also have the same physical distances; similarly, when they have the same physical distances, it does not necessarily mean they also have the same hop-counts, as shown in Fig. 1a. In Fig. 1a, we can see that the distances between nodes A, B, C and node D are the same, but their corresponding hop-counts are different, and at this moment, if hop-distance (average physical distance of one hop multiplies hop-count) is used to replace the physical distance, it will definitely cause the decrease in the localization performance.

    Fig. 1
    figure 1

    WSN topologies with different shapes. a Hop-distance ambiguity network. b Isotropic topology network. c Anisotropic topology network due to bigger barrier. d Anisotropic topology network due to difference radio ranges

    Full size image

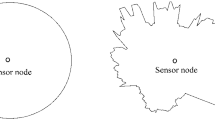
  • The anisotropy problem of network topology: it is caused by various reasons such as lack of coverage, bigger barrier and that certain nodes cannot work, as showed in Fig. 1c. In Fig. 1b, when each direction of the node presents the same property, this kind of network is called the isotropic network; otherwise, it will be called the anisotropic network, and C-shape network (Fig. 1c) is a classic network with anisotropic network topology. The causes in the anisotropy of C-shape network include various reasons, such as lack of coverage and bigger barrier etc. The hop-counts of previous nodes with close distances have increased, which has increased the measurement errors between the nodes.

  • The anisotropy problem of radio ranges: it is caused by various reasons such as the environmental disturbance and node quality, as showed in Fig. 1d (its node distribution is the same as in Fig. 1a). Due to the anisotropy of radio ranges, the nodes that could be connected previously become unable to be connected, while nodes that could not be connected previously become able to be connected, which has caused errors in the hop-count estimation, and it has further reduced the localization performance.

In view of the above questions, this paper proposes a localization approach with lower computational complexity, higher localization precision and stronger adaptability, which more suits the application under complicated environments, called LE-KPLS. The KPLS-based localization method tries to use the network topological structure of IoT and its peculiar properties to further improve the performance of localization algorithm to make it adapt to different complex environments. First of all, the LE-KPLS uses kernel trick to map the data from the previous low-dimensional space to the high-dimensional feature space, which transfers the ambiguous relation between hop-counts and physical distances in the original input space to linear problem in the feature space; then, in the feature space, partial least squares (PLS) is used to guide and build the mapping function from hop-counts to physical distances; finally, the collected hop-count information is used to predict the inter-node physical distances for some pairs of nodes through the mapping function, in this way to obtain the locations of unknown nodes.

The remainder of the paper is structured as follows. Section 2 describes the related work and Sect. 3 presents our localization method. Section 4 shows simulated results, and Sect. 5 gives the conclusions.

2 Related Works

In recent years, in accordance with different monitoring environments some researchers have proposed different multihop range-free localization strategies, which can, to a certain extent, obtain higher localization precision under certain application scenarios. For example, Niculescu et al. [9] proposed a classic multihop range-free localization method—DV-Hop. It is assumed that the hop-counts between nodes have a mapping function with the physical distances, and then hop-distances are used to replace the physical distances to estimate the locations of unknown nodes. However, this mapping function does not exist under complicated environments, and it will cause huge estimation error by using the DV-Hop method directly and simply. Zhong et al. [10] used the RSSI signal carried by the inter-node communication to sense the neighborhood relative distances, and further obtained relatively accurate relation between hop-counts and physical distances through recombination. However, this method has assumed that the radio range is regular (isotropic) and the deployments of nodes are uniform. In accordance with the topology anisotropy problem caused by lack of coverage, Li et al. [11] proposed REndered Path (REP) Protocol. REP assumes that all lacked boundary nodes have been identified, and the included angle between various sub-segments are calculated by generating unit circles at the endpoints of various sub-segments, and then, the law of cosines and the measured lengths of various sub-segments are used to determine the physical distances between various sub-segments. The REP method has noticed the impact on the measurement of inter-node distance caused by deployment problem and was trying to solve it. However, in this method, both the generation of unit circles at the endpoints of sub-segments and application of the law of cosines highly depend on the high deployment density of nodes. In addition, boundary identification for the lacked part in deployment which this method is based on is very difficult to achieve the actual application environment. Recently, Tan et al. [12] have proposed a novel localization algorithm, called CATL, and this algorithm realizes the improvement of the localization performance by finding the incision node where the hop-count of the shortest path between nodes deviates from the physical distance. However, to a great extent, the performance of CATL method depends on the accurate deployment of beacons. In addition, the CATL method is an iterative algorithm. The nodes located during each round of iteration will be used as the new beacons to participate into the next round of localization process, and the localization error of each round of iteration will also be accumulated into the next round of location estimation.

In recent years, it has been one of the research hotspots to make use of machine learning to conduct modeling and algorithm design of the localization mechanism [13]. This method finds the location dependence relation between nodes in accordance with the similarity or dissimilarity between nodes, and uses these dependence relations to make as accurate estimation of the locations of unknown nodes as possible. Compared to the previous methods, machine learning tolerates certain measurement noise, and certain algorithms are even insensitive to the measurement noise, so it does not have a very high requirement for using what measurement technology to measure the distance between nodes. Shang et al. [14] proposed the MDS-MAP localization algorithm based on the machine learning in accordance with the connectivity between nodes, and this method assumes there are no isolated nodes in the network and uses the minimum hop-counts between any random nodes as their distance, which transfers the localization problem into the dimension reduction problem. This method has a high requirement for the connectivity of nodes, which also require the global connectivity of the network, but under the anisotropic network, the hop-distance is significantly different from the physical distances between nodes, so the localization performance is significantly reduced. Therefore, Shang made improvement of the MDS-MAP method and proposed MDS-MAP(P) method [15]. First of all, this method uses the MDS method to build a local relative coordinate system for each node and its adjacent nodes, and then, various local relative coordinate systems are combined to build the global coordinate system. Because MDS is not directly applied in the whole network, the localization performance of MDS-MAP(P) has great improvement under anisotropic network. This method to address the problem separately can improve the localization precision in a certain degree, but the MDS-MAP(P) method has a high computational complexity and big communication traffic, and it’s affected by the selection of local area sizes. In order to avoid the size selection problem of local area, Lim et al. [8] proposed a PDM algorithm based on the overall information. First of all, the PDM method uses matrices to express the collected physical distances and the hop-counts between known nodes; then, TSVD [16] is used to conduct linear transformation of two matrices to obtain an optimum linear transformation model; next, the hop-counts from the unknown nodes to the known nodes will be applied to this model to estimate the physical distances between unknown nodes and beacons. In essence, TSVD is a multivariable linear regularization learning method; the estimated physical distance obtained through method is actually the weighted sum of the estimated values of other known nodes in the monitoring area, and therefore, the obtained estimated value is close to the actual value. In addition, the TSVD method has abandoned the small singular values, which can reduce the impact of noise during the transformation process to a certain extent, so the ill-posed problem during the localization process can be avoided, and the stability of algorithm can be increased. All these have caused the algorithm to have a low requirement for the deployment of sensor nodes, connection and signal attenuation method, which more benefits its use in complex application environments. In a certain degree, TSVD can solve the problem of range-free method on three aspects, but the literature and experiment [17, 18] show that the PDM method only works under certain conditions, and when the beacons are sparse or various radio ranges have serious anisotropy, the performance of TSVD method will sharply decrease. Firstly, it is because by setting a threshold parameter k, TSVD directly sets the singular values smaller than the threshold parameter k as zero, and if k is properly chosen, the solution of TSVD is stable, otherwise, it will reduce the algorithms performance; secondly, the PDM method has not conducted standard processing to the hop-counts and physical distances, and different dimensions have caused a certain degree of data submergence; lastly, the most fatal problem of PDM method is: the TSVD method is a linear method, while the ambiguous relation between the inter-node hop-counts and physical distances are essentially a nonlinear relation. It’s more difficult to use the linear TSVD method to obtain the optimal solution if the nonlinear degree is higher.

The researchers found that the kernel trick is a great solution for the nonlinear problem [19]. The kernel trick can map the original data into the proper feature space, in this way to transform the nonlinear problem difficult to solve in the original space to the linear problem in the feature space, and compared to the traditional methods used to solve the nonlinear problem, the kernel method can not only increase the computational speed, but also make the computation more flexible. Inspired by the PDM method, Lee et al. [17, 18] proposed two kernel regression methods based on the traditional SVR to solve the hop-distance ambiguity problem, i.e., LSVR and LMSVR. The LSVR and LMSVR methods can well solve the problem that affects the localization performance of the range-free method on three aspects, which can still obtain excellent localization accuracy with a small sample. SVR is the most important and common application of the kernel regression, and the structure which it is based on has the smallest risk, and it can well solve various problems such as small sample, nonlinearity, over-fitting and local minimum, which has great generalization and promotion ability. However, the traditional SVM regression method has to solve the convex quadratic programming problem with constraint conditions, which has a slow convergence rate and a low computational efficiency, and it also has to conduct optimization selection of penalty coefficient and nuclear parameter in advance. In addition, in order to avoid the ill-posed problem during the training process, the LSVR/LMSVR method also needs to manually set the regularization parameter, so the model built with this method cannot adapt to the continuously changing localization scale. In the meantime, we can also see that the SVR [20] method is a single-output method. For the multi-input and multi-output model, this method has to repeatedly build the model in accordance with each beacon node, which will not only significantly increase the computational complexity, but with the growth of beacon number. The time and space required for the localization computation will also have geometric growth, and when there are correlation problems between the training samples, the estimation precision will be poor. In addition, for regression forecasting, what’s important is not to obtain a hyper-plane with the smallest structural risk, but to use regression estimation to estimate the accuracy that the output can reach. The hyper-plane with the smallest distance obtained only through the SVM might not be related to the forecasting goal, but it could have a strong forecasting in a direction not with the smallest distances from all sample points.

Rosipal et al. [21] made further promotion based on the linear PLS and proposed kernel-based PLS (KPLS), in order to solve the regression problem between nonlinear data. KPLS has strong predictability, which can be used to solve various problems such as small sample and the multicollinearity between independent variables; it also has strong anti-noise property and great generalization ability; it does not require obtaining the distribution model of the sample in advance, and it also has various characteristics such as a high predication precision. KPLS has equal performance with SVR on single prediction precision and training time, but when the input variables are correlated, its performance is significantly superior to the SVR method.

Inspired by the PDM and SVR-based localization methods, this paper has designed a novel localization method with relatively lower computational complexity and higher localization precision, which is more suitable to be used under the complicated environments, that is LE-KPLS. The LE-KPLS method can be used to construct modelling of the hop-counts and physical distances of known nodes, in this way to obtain the accurate mapping relation between the hop-counts and distances, so that this localization method could have a high localization precision, and it can adapt to different complicated environment.

3 Localization by Kernel Partial Least Squares

KPLS is a kernel version of the partial least squares, which performs as well as or better than traditional SVR for moderately sized problems with the advantages of simple implementation, less training cost, and easier setting of parameters. Its commonly used in machine learning tasks, e.g., face detection, character recognition. In this paper, we employ KPLS to solve the location estimation problem.

3.1 Problem Statement

Consider a WSN which is comprised of n sensor nodes deployed in \( \left\{ S \right\}_{i = 1}^{n} \) deployed in a 2D geographic area. Without loss of generality, let the first m (m ≪ n) sensor nodes be beacons, whose locations are known. We assume that beacon S i (i ∊ m) is capable of transmitting localization to each of its neighbor beacons and there are two kinds of location data, i.e., smallest hop-count vector h i and corresponding pair-wise physical distances d i .

Smallest hop-count vector h i . We use h ij to denote the smallest hop-count beacon S i from beacon S j . We set h ii  = 1 and \( {\mathbf{h}}_{i} = \left[ {h_{i1} ,h_{i2} , \ldots ,h_{im} } \right]^{T} \) for all i = 1, …, m.

Physical distances \( {\mathbf{d}}_{i} \). For every pair of beacons S i and S j . d ij denotes their measured physical distance. We set \( {\mathbf{d}}_{i} = \left[ {d_{i1} ,d_{i2} , \ldots ,d_{im} } \right]^{T} \) for all i = 1, …, m.

After communication for a while, two data matrices can be obtained between the beacons, i.e., the smallest hop-count matrix \( {\mathbf{H}}_{i} = \left[ {{\mathbf{h}}_{1} ,{\mathbf{h}}_{2} , \ldots ,{\mathbf{h}}_{m} } \right] \) and the distance matrix \( {\mathbf{D}}_{i} = \left[ {{\mathbf{d}}_{1} ,{\mathbf{d}}_{2} , \ldots ,{\mathbf{d}}_{m} } \right] \). There is an ambiguous relation between the hop-counts and physical distances between the beacons, and this ambiguous relation is a nonlinear relation. In accordance with the kernel theory, the data can be mapped into the feature space H through “dimensionality increase”, i.e., \( \varPhi\,{:}\,{\mathbf{H}} \subseteq {\mathbb{R}}^{m}\,\mapsto\,\varPhi \left( {\mathbf{H}} \right) \subseteq \varvec{H} \). Therefore, the relation between the hop-counts and physical distances can be expressed as:

$$ {\tilde{\mathbf{D}}} = \tilde{\varPhi }\left( {\mathbf{H}} \right){\varvec{\upeta}} + {\varvec{\upvarepsilon}} $$
(1)

where, \( {\tilde{\mathbf{D}}} \) and \( \tilde{\varPhi }\left( {\mathbf{H}} \right) \) are the matrices D and Φ(H) after centralization respectively, \( {\tilde{\mathbf{D}}}=\left( {{\mathbf{I}}_{m} - \frac{1}{m}{\mathbf{1}}_{m} {\mathbf{1}}_{m}^{T} } \right){\mathbf{D}} \), \( \tilde{\varPhi }\left( {\mathbf{H}} \right) = \left( {\tilde{\phi }\left( {{\mathbf{h}}_{1} } \right), \ldots ,\tilde{\phi }\left( {{\mathbf{h}}_{m} } \right)} \right)^{T} \) and \( \sum\nolimits_{i = 1}^{m} ={ \tilde{\phi }\left( {{\mathbf{h}}_{i} } \right) = 0} \); \( {\boldsymbol{\upeta}}=\left( {\eta_{1} ,\eta_{2} , \ldots ,\eta_{m} } \right)^{T} \) is the regression coefficient vector; \( {\varvec{\upvarepsilon}} \) is the random error vector of feature space.

In order to obtain the optimal relation between the hop-counts and physical distances, the equation needs to obtain the optimal estimate \( {\hat{\boldsymbol{\upeta }}} \) of \( {\varvec{\upeta}} \). To this end, \( \left\| {\varvec{\upvarepsilon}} \right\|^{2} \) should be the smallest, and when \( \left\| {\varvec{\upvarepsilon}} \right\|^{2} \) is the smallest, we can obtain:

$$ \tilde{\varPhi }^{\rm T} \tilde{\varPhi }{\hat{\boldsymbol{\upeta }}} = \tilde{\varPhi }^{\rm T} {\tilde{\mathbf{D}}} $$
(2)

In the feature space, there are also severe multiple correlations among the variables of \( \tilde{\varPhi }\left( {\mathbf{H}} \right) \), or the number of sample points in \( \tilde{\varPhi }\left( {\mathbf{H}} \right) \) is smaller than that of variables. In addition, the precision of the estimate \( {\hat{\upeta }} \) is not only related to the input variable, but also related to the output variable, and the input and output co-decide the prediction direction of \( {\hat{\boldsymbol{\upeta}}} \). KPLS uses the covariance of input and output variables to guide the selection of features, which can be used in the multihop range-free application, and it can adapt to different complex scenarios and obtain great localization precision.

3.2 Localization Model Building

In the multihop range-free localization approach based on KPLS, the localization process can be divided into two phases: offline training phase and online localization phase. In the offline phase, through the learning training of the hop-counts and physical distances between the known nodes, the mapping model from the hop-counts to physical distances is obtained; in the online phase, through the hop-counts from the unknown nodes to the beacons, the unknown nodes uses the mapping model obtained through the training to conduct location estimation.

In this section, we mainly consider how to use the KPLS method to build the model after obtaining the hop-count matrix H and corresponding physical distance matrix D of the know nodes. Solution of KPLS should satisfy: and (t refers to the linear combination of independent variables; u refers to the linear combination of dependent variables); they should carry the variation information in their respective data tables; the correlation between t and u can reach the maximum, i.e., the covariance to solve t and u reaches the maximum.

$$ {max} \left\| {{cov} \left( {t,u} \right)} \right\|^{2} = {max} \left[ {{cov} \left( {\tilde{\varPhi }\left( {\mathbf{H}} \right)w,\tilde{\varPhi }\left( {\mathbf{H}} \right)c} \right)} \right]^{2} $$
(3)

in which, w and c refer to the weight vectors.

After the data is mapped into the feature space H, the feature space has both enriched the function expression ability and increased the computation quantity, which will reduce the generalization ability of related learning algorithm. Therefore, an implicit approach can be adopted in order to complete the transformation process of data, i.e., through the method of kernel function. The kernel function can transfer the inner product operation in the feature space after nonlinear transformation into the kernel function computation in the original space, which has significantly simplified the computation quantity. Kernel function is defined as the inner product in the feature space H, i.e.,:

$$ {\mathbf{K}} =\varPhi \varPhi^{T} $$
(4)

During the actual application, there are three common kernel functions [19]: Gaussian kernel function, polynomial kernel function and sigmoid kernel function. Literature [22] points it out by selecting different kernel functions or setting different kernel parameters. It will in a certain degree affect the distribution of the sample mapped into the feature space. The Gaussian kernel function has the characteristics of maintaining the distance similarity of the input space, therefore, this paper has chosen Gaussian kernel function to calculate the similarity between nodes, and its definition is as the following:

$$ \kappa \left( {{\mathbf{h}}_{i} ,{\mathbf{h}}_{j} } \right) = exp \left( {{{ - \left\| {{\mathbf{h}}_{i} - {\mathbf{h}}_{j} } \right\|^{2} } \mathord{\left/ {\vphantom {{ - \left\| {{\mathbf{h}}_{i} - {\mathbf{h}}_{j} } \right\|^{2} } {2\sigma^{2} }}} \right. \kern-0pt} {2\sigma^{2} }}} \right) $$
(5)

For the multihop range-free method, assume the mapping of the hop-count matrix H of the known node in the feature space is \( \varPhi \left( {\mathbf{H}} \right) \), and make \( {\mathbf{K}} = \varPhi \left( {\mathbf{H}} \right)\varPhi \left( {\mathbf{H}} \right)^{T} \), in the meantime, assume l is the number of principal elements set by the prediction, before modelling, conduct centralization to K, and obtain \( \tilde{\mathbf{K}} = {{\bf K}} - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}}{\mathbf{1}}_{m} {\mathbf{1}}_{m}^{T} {\mathbf{K}} - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}}{\mathbf{K1}}_{m} {\mathbf{1}}_{m}^{T} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {m^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${m^{2} }$}}\left( {{\mathbf{1}}_{m}^{T} {\mathbf{K1}}_{m} } \right){\mathbf{1}}_{m} {\mathbf{1}}_{m}^{T} \). At this moment, the process of using KPLS to build a model for the hop-counts—physical distances between the beacons can be concluded as Algorithm 1:

Algorithm 1 Localization model building by KPLS

Input: The smallest hop-count matrix \( {\mathbf{H}} = \left[ {{\mathbf{h}}_{1} , \ldots ,{\mathbf{h}}_{m} } \right] \); The physical distance matrix \( {\mathbf{D}} = \left[ {{\mathbf{d}}_{1} , \ldots ,{\mathbf{d}}_{m} } \right] \); the number l of principal elements

1:

Calculate the kernel matrix in terms of the smallest hop-count, where \( {\mathbf{K}}_{ij} = \varPhi \left( {\mathbf{H}} \right)\varPhi \left( {\mathbf{H}} \right)^{T} = \kappa \left( {{\mathbf{h}}_{i} ,{\mathbf{h}}_{j} } \right),{\kern 1pt} {\kern 1pt} i,j = 1, \ldots ,m \), and then center matrix D and matrix K obtain matrix \( {\tilde{\mathbf{D}}} \) and matrix \( {\tilde{\mathbf{K}}} \);

2:

Set \( {\mathbf{K}}_{1} = {\tilde{\mathbf{K}}} \), \( {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }} = {\tilde{\mathbf{D}}} \);

3:

for k = 1 to l do

4:

        δ k  = first column of \( {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }} \)

5:

        normalization δ k , δ k  = δ k /‖δ k ‖

6:

         repeat

7:

                \( \delta_{k} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{T} {\mathbf{K}}_{k} \)

8:

                δ k  = δ k /‖δ k ‖

9:

        until convergence

10:

        \( t_{k} = {\tilde{\mathbf{K}}}_{k} \delta_{k} \)

11:

        \( c_{k} = {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{T} t_{k} } \mathord{\left/ {\vphantom {{{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }}^{T} t_{k} } {\left\| {t_{k} } \right\|}}} \right. \kern-0pt} {\left\| {t_{k} } \right\|}}^{2} \)

12:

        \( {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D} }} - t_{k} c_{k}^{T} \)

13:

        \( {\mathbf{K}}_{k + 1} = \left( {{{{\mathbf{I}}_{m} - t_{k} t_{k}^{T} } \mathord{\left/ {\vphantom {{{\mathbf{I}}_{m} - t_{k} t_{k}^{T} } {\left\| {t_{k} } \right\|^{2} }}} \right. \kern-0pt} {\left\| {t_{k} } \right\|^{2} }}} \right){\mathbf{K}}_{k} \left( {{{{\mathbf{I}}_{m} - t_{k} t_{k}^{T} } \mathord{\left/ {\vphantom {{{\mathbf{I}}_{m} - t_{k} t_{k}^{T} } {\left\| {t_{k} } \right\|^{2} }}} \right. \kern-0pt} {\left\| {t_{k} } \right\|^{2} }}} \right) \)

14:

end for

15:

\( \Delta = \left[ {\delta_{1} , \ldots ,\delta_{k} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{T}} = \left[ {{\mathbf{t}}_{1} , \ldots ,{\mathbf{t}}_{2} } \right] \)

16:

\( {\hat{\boldsymbol{\upeta }}}={ \Delta }\left( {{\mathbf{T}}^{T} {\mathbf{K}}\Delta } \right)^{ - 1} {\mathbf{T}}^{T} {\mathbf{D}} \)

17:

return \( {\hat{\boldsymbol{\upeta }}} \)

Therefore, the prediction model can also be expressed as:

$$ f\left( \text{h} \right) = {\tilde{\mathbf{d}}} + \sum\limits_{i = 1}^{m} {\eta_{i} {\mathbf{K}}\left( {{\mathbf{h}},{\mathbf{h}}_{i} } \right)} $$
(6)

in which, \( {\varvec{\upeta}}={\Delta }\left( {{\mathbf{T}}^{T} {\mathbf{K}}\Delta } \right)^{ - 1} {\mathbf{T}}^{T} {\mathbf{D}} \), the kernel function is \( {\mathbf{K}}\left( {{\mathbf{h}},{\mathbf{h}}_{i} } \right) \), and \( {\tilde{d}}= {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}}{\mathbf{1}}_{m}^{T} {\mathbf{D}} \) is the average value of each sample.

3.3 Location Estimation

After obtaining the hop-counts of various connected beacons, the unknown node \( \left\{ S \right\}_{i = m + 1}^{n} \) uses the prediction mode to estimate its distance from the corresponding known node. Before the estimation, conduct centralization to the kernel function \( {\mathbf{K}}\left( {\text{h},\text{h}_{i} } \right) \), and its centralization method is:

$$ {\tilde{\mathbf{K}}}_{t} = \left( {{\tilde{\mathbf{K}}}_{t} - \left( {{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}} \right){\mathbf{1}}_{n - m} {\mathbf{1}}_{m}^{T} {\tilde{\mathbf{K}}}} \right)\left( {{\mathbf{I}}_{m} - \left( {{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}} \right){\mathbf{1}}_{m} {\mathbf{1}}_{m}^{T} } \right) $$

where, \( {\tilde{\mathbf{K}}} \) refers to the kernel matrix during offline training phase; \( {\tilde{\mathbf{K}}}_{t} \) refers to the kernel matrix obtained by using the smallest hop-counts from the unknown nodes to the known nodes during the online phase, and \( {\mathbf{1}}_{n - m} \) represent the vectors whose elements are ones, with length n − m.

After the hop-counts from the unknown node to the known node is substituted in accordance with formula 6, estimate corresponding physical distance, finally, use the trilateration or multilateration method to estimate the coordinate location of unknown node, and see the algorithm for the specific Algorithm 2:

Algorithm 2 Estimation location

Input: The smallest hop-count matrix between unknown nodes and beacons \( {\mathbf{H}}_{t} = \left[ {{\mathbf{h}}_{m + 1} , \ldots ,{\mathbf{h}}_{n} } \right]_{{m \times \left( {n - m} \right)}} \). The location of beacons \( \left\{ {{\mathbf{c}}_{i} = \left( {x_{i} ,y_{i} } \right)} \right\}_{i = 1}^{m} \)

Output: The estimated location of the non-beacons: \( \left\{ {{\hat{\mathbf{c}}}_{i} = \left( {\hat{x}_{i} ,\hat{y}_{i} } \right)} \right\}_{i = m + 1}^{n} \)

1:          for k = m + 1 to n do

2:                    Set \( {\mathbf{A}} = 2 \times \left[ {\begin{array}{*{20}c} {\left( {x_{1} - x_{m} } \right)} \\ \vdots \\ {\left( {x_{m - 1} - x_{m} } \right)} \\ \end{array} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}c} {\left( {y_{1} - y_{m} } \right)} \\ \vdots \\ {\left( {y_{m - 1} - y_{m} } \right)} \\ \end{array} } \right] \)

3:                    \( {\mathbf{b}} = 2 \times \left[ {\begin{array}{*{20}c} {x_{1}^{2} - x_{m}^{2} + y_{1}^{2} - y_{m}^{2} + d_{km}^{2} - d_{k1}^{2} } \\ \vdots \\ {x_{m - 1}^{2} - x_{m}^{2} + y_{m - 1}^{2} - y_{m}^{2} + d_{km}^{2} - d_{km - 1}^{2} } \\ \end{array} } \right] \)

4:                    Obtain estimated location of node \( S_{k} \text{:}{\hat{\mathbf{c}}}_{k} = \left[ {\begin{array}{*{20}c} {\hat{x}_{k} } \\ {\hat{y}_{k} } \\ \end{array} } \right] = \left( {{\mathbf{A}}^{T} {\mathbf{A}}} \right)^{ - 1} {\mathbf{A}}^{T} {\mathbf{b}} \)

5:          end for

6:          Obtain estimated location matrix of unknown nodes: \( {\hat{\mathbf{C}}}= \left[ {\hat{c}_{m + 1} , \ldots ,\hat{c}_{n} } \right] \)

3.4 Complexity Analysis of Localization Algorithm

The LE-KPLS localization method proposed in this paper and its performance are related to its communication and computation, so the complexity of algorithm mainly consists of the communication complexity and the computational complexity of localization estimation. The LE-KPLS method has similar communication process with various methods such as PDM, LSVR and DV-Hop, and each node requires calculating the hop-count between nodes through the flood method, so they have the same communication complexity. The communication overhead of four methods is all around O(m 2 n), in which, n refers to number of nodes, and m refers to number of beacons. The communication process consists of two parts: first of all, through m times of broadcasting, the beacon node notices the residual nodes of their shortest hops from the beacon node, and this overhead is around O(mn); however, it requires collecting all information from the beacon node pair to the base station, after the hop-count and actual relation are calculated at the base station, it will be distributed to the whole network, so the communication overhead is all around O(m 2 n). The MDS-MAP(P) localization algorithm is improved based on MDS. It is calculated through local MDS, then various parts are integrated, and the algorithm uses the binary aggregation tree to conduct communication, therefore, the overall communication complexity is around O(n log n).

For the computational complexity: in DV-Hop, each known node needs to receive and send the feedback information, so the computational complexity is approximately O(n); while in the MDS-MAP(P) algorithm, due to adoption of the SVD method, for each part, its computation complexity is around O(k 3), in which, k refers to the average number of its neighbor nodes. When various parts are integrated into a whole, the computational complexity is approximately O(nk 3), in which n refers to the number of network nodes, and in the meantime, during the phase of building global coordinate and transforming the relative coordinate into absolute coordinate, it will require O(n 3) and O(m 3 + n), respectively; the TSVD method adopted by PDM conducts modelling to m known nodes, so it will require a computation quantity of O(m 3); during calculation of SVM in SVR, it requires solving a quadratic programming problem. In accordance with different optimization methods, its computational complexity is generally between O(m 2) to O(m 3). However, because the traditional SVR is multi-input and single-output, for m training samples, the computational complexity of its modelling is between O(m 3) ∼ O(m 4); the computational complexity of LE-KPLS is mainly decided by the KPLS method, so its computational complexity is around O(km 2), in which, k refers to the number of potential vectors. In Table 1, the communication and computational complexities of DV-Hop, PDM, LSVR and the LE-KPLS method proposed in this paper are specifically compared.

Table 1 Complexity comparison
Full size table

4 Performance Evaluation

The important characteristic of the multihop range-free method is the application to large-scale deployment, which requires deploying hundreds and even thousands of sensor nodes, but under current experiment conditions, it is very difficult to realize a real network of such scale. Therefore, during the research of large-scale application of the multihop range-free method, the method of software simulation is generally adopted to evaluate the advantages and disadvantages of the localization algorithm. We analyze the localization methods with Matlab 2013b. To evaluate the performance of the proposed algorithm LE-KPLS, we suppose the sensor nodes are randomly placed in 2D region and run the localization method on various topologies.

The localization precision, the power consumption, the applicable environment and scale, the proportion of beacons, the adaptability of network topologic structure, the self-adaption and the fault tolerance are the common technical standards used to evaluate the localization method. The improved method proposed in this paper mainly aims at the three aspects problems that affect the precision of the multihop range-free method, so during the experiment, two groups of experiment proposals have been designed to analyze and evaluate the algorithm performance:

  1. 1.

    The inter-node communication adopts the logarithmic attenuation model (LAM). By changing the node distribution and the number of beacons, the experiment tested the relationship ambiguity between hop-counts and physical distances and the anisotropy of network topology on the algorithm performance. The network topologies set by the experiment are respectively: (1) random deployment in a square region; (2) regular deployment in a square region; (3) randomly deploying nodes in a C-shape region; (4) and regularly deploying nodes in a C-shape region.

  2. 2.

    An irregular radio range is used for the communication between nodes. The experiment simulated the anisotropy of transmission radius by parameter degree of irregular (DOI) [25], and in the meantime, by combining different node distribution in the experiment of Group A, the algorithm performance was tested under different beacons.

To avoid the one-sidedness of single one result, all of the reported results are the average over 50 trials’ root mean square error (RMS) [23] and all nodes are to be randomly re-deployed in each region. This experiment also compare our method with three previous methods: (1) the classic DV-Hop method proposed in [9]; (2) PDM proposed in [8]; and (3) LSVR proposed in [17] in two group experiments. In addition, considering that the TSVD method needs to set the rejection eigenvalue threshold, and the SVR method needs to set the kernel parameter, the penalty coefficient C and the width of insensitive loss function parameter ε, for fairness, during the experiment, the TSVD method sets the rejection eigenvalue no bigger than the corresponding eigenvalue of 2; about the setting of C and ε in the SVR method, please refer to the literature [24]; on the aspect of kernel function, this paper has chosen the Gaussian kernel function, and its kernel function is related to the distance of the training sample, so the kernel parameter is set as the 40 times of the average distance of the training sample.

4.1 Simulation Experiments Based on Logarithmic Attenuation Model

In this set of experiments, the nodes were placed in a 300 × 300 area; the number of beacons was gradually increased from 20 to 40, with a step size of 2, and the node’s communication radius was 40. The experiments were divided into the two types of random deployment and regular deployment, of which, the random deployment was: 300 nodes were randomly and uniformly distributed in the deployment area; the regular deployment was: the distance between nodes was 20; for the C-shape network topology, a 100 × 200 rectangular obstruction was put at the centre of the monitoring area. Figure 2a–d is the final localization result of nodes of certain deployment in square area under the circumstance that there are 28 beacons, in which circle denotes unknown node. Box denotes beacon node, and the straight line connects the actual coordinates of the unknown node with its estimated coordinates.

Fig. 2
figure 2

Localization results based on LE-KPLS under different topologies. a RMS error is 3.651. b RMS error is 3.9131. c RMS error is 3.751. d RMS error is 3.952

Full size image

Figure 3a–d describes the impact of the number of beacons on the localization precision under different node distributions. Beacons are the priori conditions to estimate the location of unknown node, and it is generally believed that with the increase of beacons, the localization precision will increase. We can find that, for the DV-Hop method, this is not the case: under the C-shape topology, the RMS error is bigger than that under the corresponding square deployment; the regular deployment has significantly more fluctuations than the random deployment; in addition, the curve presents up and down fluctuation with the increase of beacons, which is very unstable. Furthermore, under four kinds network topologies, the RMS error of DV-Hop is greater than the other three methods. We can see that the biggest RMS error of DV-Hop occurs under the C-shape random distribution, at this moment, the number of beacons are 32, and the RMS is 9.131. There are two reasons that could cause the poor localization performance of DV-Hop and its failure to adapt to the anisotropy of network topology: first of all, it only uses the hop-distance to replace the inter-node physical distance; when there is change to the topology, the relation between the hop-distances and physical distances cannot adapt to this change, especially the C-shape network topology, and due to the lack of network topology, the coverage area of nodes presents irregularity, which will further increase the distance error between some of the adjacent nodes; secondly, due to the random deployment of nodes, it is inevitable that some beacons are in the same straight lines, so during the regular deployment, the probability of collineation between the beacons are even higher, which has caused the collineation between beacons, while DV-Hop has adopted the least squares to conduct estimation of the unknown node, and least squares are very sensitive to colinearity, so if DV-Hop has not taken corresponding measures, it will definitely aggravate the fluctuation of RMS error.

Fig. 3
figure 3

RMS error of different methods under different deployment with different number of beacons. a RMS error of random deployment in square area. b RMS error of random deployment in C-shape area. c RMS error of regular deployment in square area. d RMS error of regular deployment in C-shape area

Full size image

The estimation model obtained by the PDM method by adopting TSVD can in a certain degree reflect the relation between the hop-distance and distance, especially in the C-shape area, which has realized compensation of distance evaluation in area with uneven node distribution. Therefore, in Fig. 3b, d, we can see that its localization precision is significantly better than that of the DV-Hop method; in addition, through the method of TSVD rejection, it can reduce the impact of noise, avoiding the impact of colinearity and increasing the precision and stability, that all these make the PDM method has superior localization performance than the DV-Hop method under different deployment conditions, and the average localization precision has increased by about 25.6 %. However, the relation between the hop-counts and physical distances built by the PDM method by using TSVD is a linear optimal relation, while in the actual environment, they have a nonlinear relation, and it will not necessarily obtain the optimal solution by using the linear method to solve the nonlinear problem. Both LSVR and LE-KPLS method proposed by this paper are kernel-based algorithms. By mapping the data into high-dimensional feature space, they make the nonlinear data become linearly separable, so that they can capture the actual relation between the hop-counts and physical distances and obtain high localization precision, and compared to the DV-Hop method, the average localization precision of LSVR has increased by 38.8 %. However, LSVR has adopted a multi-input and single-output model, which has not considered the correlation between samples or the impact of the output variable on the predictive variable, which has caused SVR has a lower prediction precision than LE-KPLS, and the average localization precision of KPLS is approximately 41.2 % higher than that of DV-Hop.

The above experiments have adopted multiple deployments, and the average value of RMS has been used to estimate the performances of various localization methods. The average value reflects the degree of data aggregation, and for the actual application, the stability of the method should also be considered. This section has used the box diagram to investigate the estimation error ranges of different methods under different conditions. The box diagram can be used to present the coverage scale of a group of data, so it can be used to investigate the localization error range in order to determine the stability of the experiment. Figure 4a–d shows the localization error ranges of various algorithms with the change of the beacon node number under different distributions. We can see that the DV-Hop method does not only have a low localization precision, but also a big error range. No matter whether the number of beacons is high or low, its error range has no rule whatsoever; its biggest RMS error can reach 5.01 (in Fig. 4b, the number of beacons is 40), and its smallest RMS error is 0.073 (in Fig. 4a, the number of beacons is 38); the other three methods have optimized the localization data, and the corresponding error ranges present certain rules with the change of the beacon node number: the biggest RMS error of the PDM method is 0.82 (in Fig. 4d, the number of beacons is 20), while its smallest RMS error is 0.075 (in Fig. 4a, the number of beacons is 32); the kernel-based localization method is superior to the linear method; the biggest RMS error of the LSVR method is 0.34 (in Fig. 4b, the number of beacons is 20), and its smallest RMS error is 0.069 (in Fig. 4d, the number of beacons is 40); compared to the other three methods, the KPLS-based method proposed by this paper has the smallest error range; its biggest RMS error is 0.246 (in Fig. 4b, the number of beacons is 20), and its smallest RMS error is 0.041 (in Fig. 4b, the number of beacons is 38).

Fig. 4
figure 4

Performance of different algorithms in different network topologies. a Error range of random deployment in square area. b Error range of random deployment in C-shape area. c Error range of regular deployment in square area. d Error range of regular deployment in C-shape area

Full size image

Therefore, on the other hand, we can see that the method based on machine learning can in a certain degree accurately build the relation between the hop-counts and distances, in particular, compared to the existing methods, the LE-KPLS can better adapt to complicated environment, and the algorithm does not only have a high precision, but also it also has a high stability.

4.2 Simulation Experiments Based on Radio Irregularity model

In the experiment in Sect. 4.1, it is assumed that the communication between nodes adopts the LAM, which is a transmission mode with isotropic communication radius, i.e., the signal won’t change with the change of direction, and however, under the actual environment, the signal presents anisotropy under the impact of its physical property and the external disturbance. In order to prove the adaptability and stability of the algorithm proposed in this paper toward the anisotropy of communication radius, the experiment introduced the parameter of DOI, and the algorithm’s adaptability toward the anisotropy of communication radius was evaluated by setting different DOI values. DOI [25] is defined as the percentage change of maximum path loss on the unit direction during the wireless communication.

Fig. 5
figure 5

Degree of irregular

Full size image

As shown in Fig. 5, When DOI = 0, the communication radius did not change, and the communication radius was circular, which equalled to the isotropic communication model. With the increase of DOI value, the communication radius started to become irregular, so an irregular transmission model is a wireless communication model close to the real situation. During this set of experiments, it was assumed that in a certain deployment area and under certain number of beacons, the DOI value was increased, which was increased from 0.005 (see Fig. 5) to 0.019 (see Fig. 5) with a step of 0.002. In the experiment in this section, it was also assumed the nodes were randomly or regularly distributed in a 300 × 300 area: under the scenario of random deployment, it was assumed 300 nodes were deployed in this experiment, and the number of beacons was increased from 30 to 57 with a step of 3; under the scenario of regular deployment, it was assumed that the interval between nodes was 20 units, and the number of beacons was increased from 25 to 49 with a step of 3; for the C-shape area, a 100 × 200 obstacle was also set.

4.2.1 Square Area

In this set of experiments, it was assumed the nodes were deployed in a square area, and in the experiment, 3D surface charts were used to investigate the change of RMS error in accordance with the changes of beacon number and DOI value. Figure 6a–d shows the RMS error surface charts of four methods to change in accordance with the changes of beacon number and DOI value when 300 nodes were randomly distributed in the monitoring area; Fig. 7a–d shows the RMS surface charts of four methods to change in accordance with the changes of beacon number and DOI value when the nodes were regularly distributed in the monitoring area.

Fig. 6
figure 6

Comparison of the RMS error for random deployment under square area. a RMS error of DV-Hop with different DOI and number of beacons. b RMS error of PDM with different DOI and number of beacons. c RMS error of LSVR with different DOI and number of beacons. d RMS error of LE-KPLS with different DOI and number of beacons

Full size image
Fig. 7
figure 7

Comparison of the RMS error for regular deployment under square area. a RMS error of DV-Hop with different DOI and number of beacons. b RMS error of PDM with different DOI and number of beacons. c RMS error of LSVR with different DOI and number of beacons. d RMS error of LE-KPLS with different DOI and number of beacons

Full size image

Figures 6a and 7a show the surface charts of the change of RMS error in the random and regular deployments of the DV-Hop method, respectively. Thereinto, Fig. 6a shows that the RMS error is between 7.498 and 4.121; Fig. 7a shows that the RMS error is between 7.78 and 4.14. In both charts, the change of RMS error presents irregular up and down fluctuation, which means DV-Hop is very sensitive to irregular transmission.

Figure 6b shows the surface chart of the change of RMS error in the random and regular deployments of the PDM method in the square area, and the surface shown in Fig. 6b is smoother compared to that in the DV-Hop method. In it, RMS error shown in Fig. 6b is between 6.572 and 3.791, and shown in Fig. 7b is between 6.572 and 3.791. That’s because the PDM method has used TSVD to modify the measured distance between nodes, and certain data with low signal to noise ratios are rejected through certain threshold, so that the estimation feature from the node to beacon node is maintained in a certain degree, which has increased the localization precision. However, because TSVD is a linear method, its applicable scenarios are limited, and when the number of beacons is low and the DOI value is high, the corresponding RMS error will be high.

Figures 6c, d and 7c, d show the surface charts of the change of RMS error in the random and regular deployments of the LSVR and LE-KPLS, respectively. In Figs. 6c, d and 7c, d, we can see that both the LSVR method and the LE-KPLS method proposed in this paper are significantly superior to the PDM and DV-Hop methods, and this is because the kernel method calculates the similarity function in the original feature space, which can help addressing the nonlinear problem. From the corresponding chart, we can also find that the KPLS-based localization has superior performance to LSVR which adopts the kernel method, and this is because LE-KPLS can combine the input and output data and also eliminate the correlation between data, so it can obtain great prediction precision after using the known data to build model. Among them, in Fig. 6c, the scale of RMS error is between 5.601 and 3.197; in Fig. 7c, the scale of RMS error is between 5.282 and 3.267; in Fig. 6d, the scale of RMS error is between 5.613 and 3.269; in Fig. 7d, the scale of RMS error is between 5.657 and 3.301.

4.2.2 C-Shape Area

In this set of experiments, it was assumed that nodes were deployed in a C-shape area, and the algorithm’s performance is simultaneously investigated through the anisotropy of network topology and the irregular of radio ranges.

Figures 8a–d and 9a–d show the surface charts of the change of RMS error in accordance with the change of beacon number and DOI value in the random and regular deployments in the C-shape area, respectively. Figures 8a and 9a show the changing RMS surface chart in the DV-Hop method, in which, we can see that in this set of experiments, the surface fluctuation for the DV-Hop method is fiercer than the last set of experiments. No matter whether the beacon number is high and the DOI value is small or the beacon number is low and the DOI value is big, the corresponding RMS values are both high. In Fig. 8a, the RMS error is between 7.31 and 9.1976; in Fig. 9a, the scale of RMS error is between 7.49 and 9.12.

Fig. 8
figure 8

Comparison of the RMS error for random deployment under C-shape area. a RMS error of DV-Hop with different DOI and number of beacons. b RMS error of PDM with different DOI and number of beacons. c RMS error of LSVR with different DOI and number of beacons. d RMS error of LE-KPLS with different DOI and number of beacons

Full size image
Fig. 9
figure 9

Comparison of the RMS error for regular deployment under C-shape area. a RMS error of DV-Hop with different DOI and number of beacons. b RMS error of PDM with different DOI and number of beacons. c RMS error of LSVR with different DOI and number of beacons. d RMS error of LE-KPLS with different DOI and number of beacons

Full size image

Figures 8a and 9d show the surface chart of the change of RMS error under two deployments in the C-shape area in the PDM method. Its surface chart has slower change than the DV-Hop method, but in accordance with Fig. 8b, we can also see the sharp increase of RMS error when DOI ≥ 0.011 and number of beacons ≤48 or DOI ≤ 0.013 and number of beacon ≥48; in Fig. 9b, when DOI ≥ 0.015 and number of beacons ≤34 or DOI ≥ 0.017 and number of beacons ≤34, the RMS error increases sharply, which proves PDM’s adaptation to the severe environment is under limited condition: under the regular of radio ranges, PDM can well adapt to the anisotropy of network topology; however, when the radio ranges have high irregular and there is anisotropy of network topology, there will be a big error.

Figures 8c, d and 9c–d show the distributions of the SVR method and KPLS-based method in the C-shape area, especially under the two types of random and regular deployments, respectively. The change of their RMS errors presents certain regularity, and especially during the process, the RMS errors are between 3.444–5.406 and 3.656–5.581, respectively. Under corresponding DOI value and beacon number, the RMS error of KPLS is smaller than that of the SVR method, and the change of KPLS surface is smoother.

In accordance with the above two sets of experiments under the scenarios of the anisotropy of network topology and the anisotropy of communication radius respectively, we can see that the KPLS method proposed in this paper can obtain high localization precision and stability in both the scenarios of the anisotropy of network topology and the anisotropy of node communication radius.

5 Conclusion

IoT has the characteristics of heterogeneous network and volatile environment, and it is difficult for current range-free localization methods to adapt to it. By using KPLS to build the mapping relation between the hop-counts and distances, the KPLS-based localization algorithm proposed in this paper makes the new range-free method be able to adapt to various problems, such as the complicated topology and irregular communication radius in the environment of internet of things. Compared to algorithms of the same kind, the LE-KPLS algorithm has not only maintained the original characteristics of the range-free method, but also improved the localization precision based on that, which has increased its adaptability under different environments, and this algorithm is stable. Considering that compared to the linear learning method, it will take a longer time by using the kernel learning method. The next step of work is to make improvement based on that, in this way to increase the localization efficiency.